Abstract
The origin of anomalous Hall effect (AHE) in magnetic materials is one of the most intriguing aspects in condensed matter physics and has been a controversial topic for a long time. Recent studies indicate that the intrinsic AHE is closely related to the Berry curvature of occupied electronic states. In a magnetic Weyl semimetal with broken time-reversal symmetry, there are significant contributions to Berry curvature around Weyl nodes, possibly leading to a large intrinsic AHE. Here, we report the quite large AHE in the half-metallic ferromagnet Co3Sn2S2 single crystal. By systematically mapping out the electronic structure of Co3Sn2S2 both theoretically and experimentally, we demonstrate that the intrinsic AHE from the Weyl fermions near the Fermi energy is dominating. The intrinsic anomalous Hall conductivity depends linearly on the magnetization and can be reproduced by theoretical simulation, in which the Weyl nodes monotonically move with the constrained magnetic moment on Co atom.
The large intrinsic anomalous Hall effect (AHE) in magnetic Weyl semimetals is expected but rarely verified experimentally. Here, Wang et al. report large intrinsic AHE with linear dependence on magnetization in a half-metallic ferromagnet Co3Sn2S2 single crystal with Kagome lattice of Co atoms, arising dominantly from the Weyl fermions.
Introduction
The ordinary Hall effect that arises from the Lorentz force deflecting the moving charge carriers has been well understood1. In contrast, the anomalous Hall effect (AHE)2,3 has attracted tremendous interests because of the fundamental physics and great potential in technical application4,5, but the microscopic origin of AHE is still not fully solved. The key issue is whether the effect is intrinsic or extrinsic. It is now recognized that there are three mechanisms to account for the AHE6. One is the extrinsic mechanism related to the scattering affected by the spin–orbit interaction, i.e., the skew scattering and side jump mechanisms7–9. The skew scattering model predicts that the is linearly proportional to ρxx, whereas, the side jump models give . The other is intrinsic Kaplus–Luttinger (KL) mechanism related to spin–orbit interaction of Bloch electronic bands, originally proposed by Karplus and Luttinger, which also gives 10. Importantly, recent studies indicate that there is an intimate relation between the AHE and the Berry curvature of occupied electronic Bloch states11–14.
Recently-discovered topological semimetals (TSMs) are characterized by the topologically robust or symmetry-protected bulk band crossings near the Fermi energy (EF)15–18. Classified by the degeneracy of nodes, Dirac and Weyl semimetals (WSMs) with the 4- and 2-fold degenerate Dirac or Weyl points, respectively, have been theoretically predicted and experimentally confirmed18–22. Especially, in a magnetic WSM with broken time-reversal symmetry (TRS), Weyl node can be seen as a magnetic monopole in momentum space23, around which there are significant contributions to Berry curvature24. Thus, if the position of Weyl nodes are proper, especially close to EF, and the individual Fermi surface (FS) sheets have nonzero Chern numbers, there should be large intrinsic AHE in magnetic WSMs nearly proportional to the distance between a pair of Weyl nodes with opposite chirality24. On the other hand, the half-metallic ferromagnets (HMFMs) can also exhibit AHE, such as ferromagnetic (FM) Heusler alloy Co2MnGa, NiMnSb and related intermetallic compounds25,26. Different from traditional ferromagnets, the HMFMs have attracted extensive interests because of the (nearly) 100% spin polarization of conduction electrons at EF27. They can be perfectly applied to spintronic devices.
In this work, we study the AHE and electronic structure of HMFM Co3Sn2S2 with kagome layers of Co. As previous experimental results reported on polycrystalline samples, the compound orders ferromagnetically at TC = 177 K and the spontaneous magnetic moment is about 0.3 μB/Co28–30. By employing systematic first-principles calculations, transport, and angle-resolved photoemission spectroscopy (ARPES) measurements on Co3Sn2S2 single crystals, we reveal the quadratically scaling relationship between anomalous Hall resistivity and ρxx, and the linear behavior between intrinsic anomalous Hall conductivity (AHC) and the magnetization. Furthermore, the agreement between the experimental band structures and theoretical calculations support the existence of magnetic Weyl fermions in Co3Sn2S2. Our findings suggest the main contribution of observed large AHE originates from the intrinsic mechanism, which is intimately related to the Weyl nodes near EF.
Results
Structure and Ferromagnetic state in Co3Sn2S2
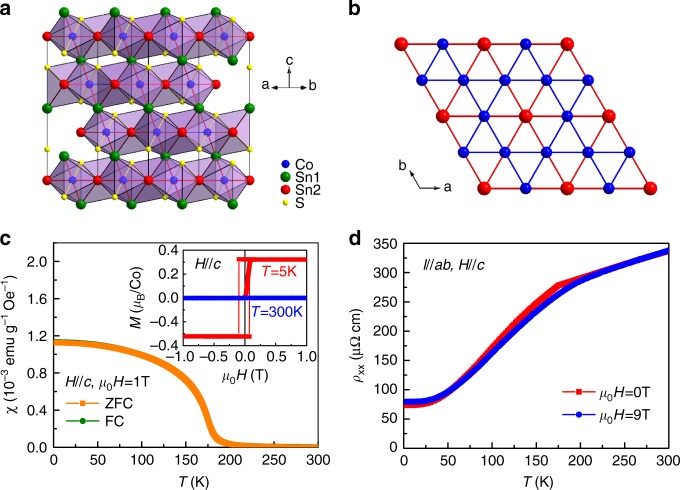
Co3Sn2S2 is crystalized in a hexagonal lattice with space group of (No. 166). As shown in Fig. 1a, the crystal structure of Co3Sn2S2 is composed of the slabs of CoSn4S2 octahedra stacking in a hexagonal packing (A-B-C fashion) along the c axis. Each Co atom is surrounded by four Sn and two S atoms, forming a distorted octahedron. The Co and S atoms are located at Wyckoff position 9e (1/2, 0, 0) and 6c (0, 0, 0.219), respectively. The CoSn4S2 octahedra connect each other along ab plane by face-sharing and along c axis by corner-sharing. On the other hand, the Co atoms form perfect kagome layer with corner-sharing triangles of Co atoms in Co–Sn layer. There are two kinds of Sn sites. A half of Sn atoms lie in the centers of the kagome hexagons (Sn2 sites, Wyckoff position 3a (0, 0, 0)) (Fig. 1b) and another half of Sn atoms located between the Co–Sn bilayers (Sn1 sites, Wyckoff position 3b (0, 0, 1/2)), connecting adjacent Co–Sn2 layers. S atoms are located below and above the Co–Sn2 layers. For the plate-like Co3Sn2S2 single crystal, the c axis is perpendicular to the crystal surface (Supplementary Fig. 1).
Fig. 1.
Structure, magnetization and longitudinal resistivity of Co3Sn2S2. a, b Crystal structure of Co3Sn2S2 and kagome layer made of Co atoms. The small blue and yellow balls represent Co and S atoms, respectively, and the big green and red balls represent Sn atoms at Sn1 and Sn2 sites, respectively. c Temperature dependence of magnetic susceptibility χ(T) with ZFC and FC modes at μ0H = 1 T for H||c. Inset: field dependence of magnetization M(μ0H) at 5 and 300 K for H||c. d Longitudinal resistivity ρxx(T, μ0H) as a function of temperature T at μ0H = 0 and 9 T along the c axis
The χ(T) curves with zero-field-cooling (ZFC) and field-cooling (FC) modes at μ0H = 1 T for H||c increase rapidly when T is below the Curie temperature TC (~174 K) (Fig. 1c), well agree with previous results in the literatures28–30. Moreover, the ZFC and FC χ(T) curves overlap each other very well, suggesting that magnetic domains have aligned with the direction of external field when μ0H = 1 T. The field dependence of magnetization M(μ0H) at T = 5 K for H||c further confirms the ferromagnetism at low temperature (inset of Fig. 1c). The M(μ0H) curve shows a pronounced hysteresis. The hysteresis loop is square and changes its direction at very little coercive field μ0Hc close to 0.08–0.1 T. The saturated magnetization Ms is about 0.3 μB/Co, consistent with previous results28,30. In contrast, when , the hysteresis behavior vanishes and the M(μ0H) curve only shows a paramagnetic behavior (inset of Fig. 1c).
As shown in Fig. 1d, the zero-field longitudinal resistivity ρxx(T, 0) of Co3Sn2S2 shows a metallic behavior in the whole measuring temperature range. A kink can be clearly observed in the ρxx(T, 0) curve around TC. The resistivity decreases rapidly with decreasing temperature below TC due to the decrease of spin disorder scattering. When the external magnetic field is applied (μ0H = 9 T), the metallic behavior of ρxx(T) has almost no change, but the kink of ρxx(T) near TC becomes smooth and the staring temperature where the ρxx(T) curve changes the slope shifts to higher temperature.
Calculated electronic structure, Weyl nodes and AHC
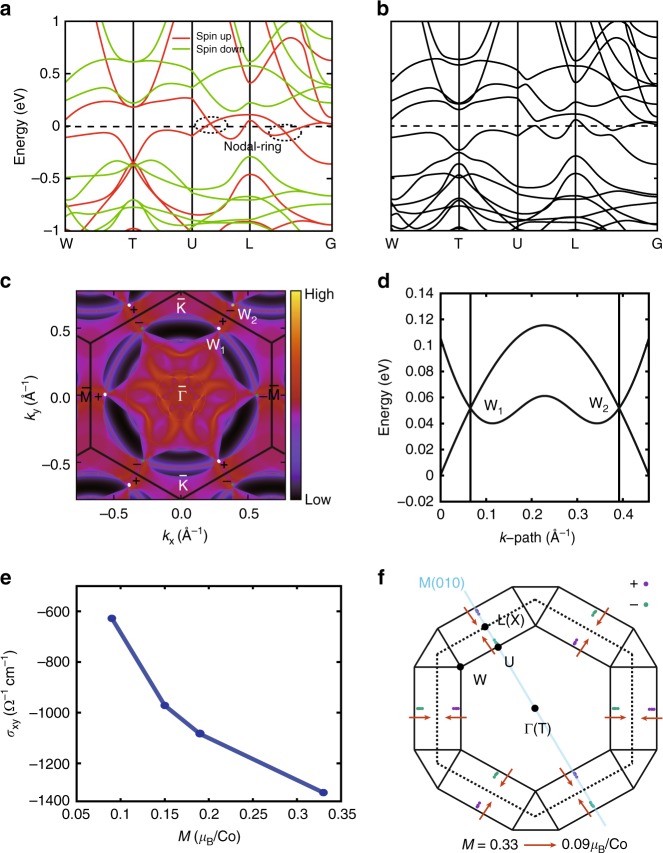
The results of the first principle calculation indicate the half-metallic feature of Co3Sn2S2 at FM state (Fig. 2a) and reveal that the bands dispersion near the EF are contributed mainly by the 3d orbitals of Co with the polarized magnetic momentum about 0.33 μB/Co irrespective of the presence of spin–orbit coupling (SOC). Co3Sn2S2 belongs to the type IA half metallic ferromagnets and the spins of all electrons are fully polarized along the up direction (defined in c axis)31. When the SOC is absent, the valence and conductance bands inverse near the L point and form a nodal ring (signed by the dashed circles in Fig. 2a), which is protected by the mirror symmetry of the plane M(010) shown in Fig. 2f. When the SOC is further included, it will decay into a pair of Weyl points (WPs) with opposite chirality off the high-symmetry lines (Fig. 2b). The precise positions of the WPs have been obtained by calculating the Wilson-loop evolution32 on a much denser k-grid in the Brillouin zone (BZ). The evolution of the Wannier charge center (WCC) on a sphere that enclosing a WP in Brillion Zone is demonstrated in Supplementary Fig. 2. There are three pairs of WPs in the BZ in total related by C3 rotation symmetry and inversion symmetry, as illustrated in Fig. 2c and Supplementary Table 1. From the energy dispersion along the direction connecting the WPs of W1 and W2, the splitting distance of them is about 0.3 Å−1 (Fig. 2d), which is far enough to guarantee the robustness of the WPs. We have also calculated the Fermi surface (FS) of (001) surface at the energy of WPs with Green function method33,34. As shown in Fig. 2c, the pairs of the WPs with opposite chirality projected on (001) surface are indicated by green and white dots, respectively. Since all of the WPs are mixed with bulk states, it is not easy to clarify the details of how the Fermi arcs connecting the WPs although there are arc-like FSs with large weight of local density of states on surface and preserving C3 rotation symmetry. In order to distinguish the topological surface states in Fig. 2c, we have redefined a k-dependent Fermi energy EF(k) = α[EN(k) + EN + 1(k)]/2, where 0 ≤ α ≤ 1. EN(k) is the low branch of the two bands crossing at the Weyl nodes and EN + 1(k) is the up branch. Thus, if α = 1, the k-dependent EF(k) will lead to an ideal Weyl semimetal state with and only with Weyl nodes appearing at the Fermi level. When α ranges from 0.1 to 0.9 (as shown in Supplementary Fig. 3), we can gradually remove the projected bulk state and identify the Fermi-arc patterns from the other topologically trivial surface states. In Supplementary Fig. 4, the calculations using unrelaxed experimental crystal structure are also shown. The Weyl nodes and magnetic properties are the same as those calculated from relaxed structure. But the WPs and Fermi arcs altered slightly and separated from the projected bulk states. Both the Fermi arcs and the corresponding topological surface states can be identified.
Fig. 2.
Band structure obtained from first-principle calculations. a The spin-resolved band structure without SOC. b The band structure with SOC included. The definition of high-symmetry points are shown in Fig. 3a. c Fermi surface on the (001) surface cutting on the energy of WPs. The white and green dots represent the projected WPs with positive and negative chirality respectively. d The energy dispersion along the direction connecting the WPs W1 and W2 in c. e The intrinsic anomalous Hall conductivity with the magnetic momentum of 0.09, 0.15, 0.19, and 0.33 μB/Co at 0 K. f The evolution of WPs in the BZ with the magnetic momentum decreased from 0.33 to 0.09 μB/Co. The directions of the evolution are indicated by the red arrows. The EF is set to 0
The existence of WPs implies that there would be a large intrinsic AHE in Co3Sn2S2. The AHC σxy obtained from the integral of Berry curvature along kz in the BZ has a very large value of about −1310 Ω cm−1 at 0 K (Fig. 2e). Moreover, because the time-reversal symmetry is broken in the FM state, the AHE has a direct relation with the intrinsic magnetic momentum. We constrained the local magnetic momentum as 0.09, 0.15, 0.19, and 0.33 μB/Co and as illustrated in Fig. 2e, the AHC decreases almost linearly with the decreasing of magnetic momentum. Meanwhile, the WPs evolve monotonically with the magnetic momentum decreasing from 0.33 to 0.09 μB/Co as indicated by the red arrows in Fig. 2f. The WPs with opposite chirality approach each other along kz direction when the spin polarization is reduced. In addition, the AHC of magnetic Weyl semimetals can also be related to the distance of WPs. We can estimate the intrinsic AHC by the formula of σxy = Ke2/4π224, where K is the distance of WPs with opposite chirality along the direction of magnetization. The result also confirms the decrease of intrinsic AHC with decreasing magnetization strength (Supplementary Fig. 6). However, before the pair of Weyl nodes meet each other to annihilate, the two bands composing them become spin degenerate with their time-reversal symmetric partners due to Kramer degeneracy in paramagnetic state.
Experimental electronic structure observed by ARPES measurements
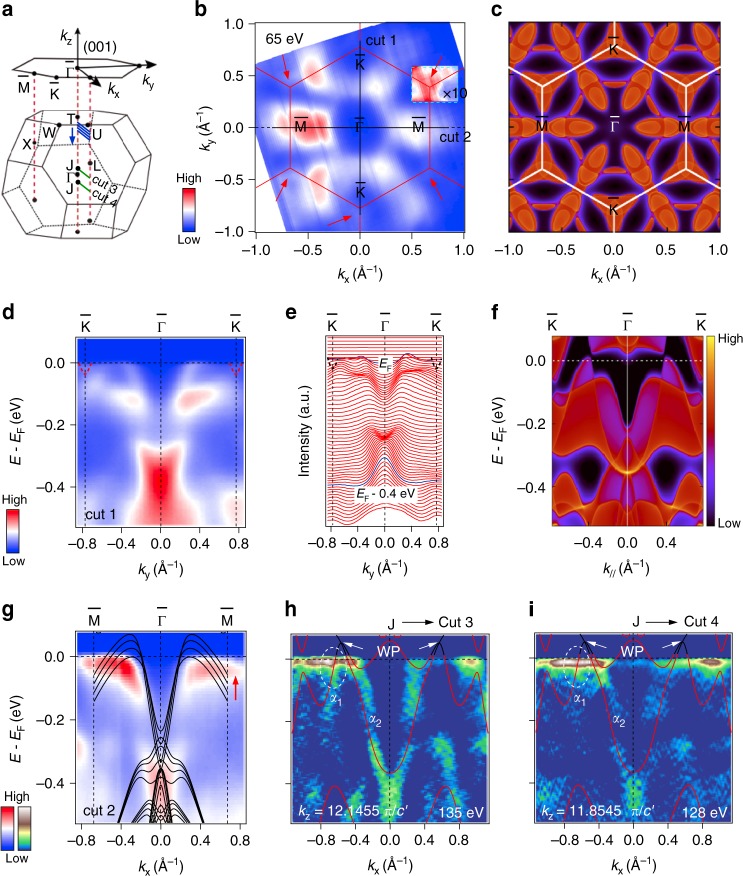
In order to further uncover the electronic origin of AHE in Co3Sn2S2, we performed ARPES experiments on the (001) surface of the samples. The overall band structures are summarized in Fig. 3. The experimental FSs in Fig. 3b are in good agreement with the projections of calculated bulk FSs on the (001) surface in Fig. 3c. The spindle-shaped FSs centered at points, the triangle-shaped FSs centered at point, and the ring-like ones connecting the spindle-shaped FSs are all captured by ARPES. Specifically, the agreement of the spindle-shaped FSs is significant since the projection of bands on the (001) surface that creates the WPs are located along the direction, i.e., the (001)-surface projections of WPs W1 and W2 are located along this direction as illustrated in Fig. 2c, although the WPs are buried into bulk continuum states at the chemical potential.
Fig. 3.
Near-EF ARPES spectra compared with first-principle calculations of Co3Sn2S2. a Schematic primitive BZ and 2D projected BZ of the (001) surface. Blue lines parallel to the direction indicate the momentum locations of calculated band structures in g, with the kz momenta of 0.96, 0.92, 0.88, and 0.84 π from top to bottom, respectively. Cuts 3 and 4 illustrate the momentum locations of the predicted WPs, which are parallel to the direction in the kz = ± 0.1455 π planes. b Constant energy ARPES image obtained by integrating the spectral weight within EF ± 10 meV recorded with 65 eV photons. Cuts 1 and 2 indicate the momentum locations of the experimental band structures in d–i. Red lines represent the (001) surface BZs. Red arrows indicate the triangle-shaped FSs centered at points in c. The intensity within the cyan dashed rectangle has been multiplied by 10. c Projections of calculated bulk FSs on the (001) surface. White lines represent the (001) surface BZs. d, e ARPES intensity plot and corresponding momentum distribution curves along the direction [cut 1 in b], respectively. Red and black dashed curves illuminate the electron bands forming the triangle-shaped FSs centered at points. f Projections of calculated bulk bands along the direction. g ARPES intensity plot along the direction [cut 2 in b]. Black curves represent the calculated bulk bands along the four directions indicated by blue lines in a, where the bands from bottom to top correspond to the cuts from top to bottom, respectively. h, i Second derivative intensity plots along cuts 3 and 4 recorded at hν = 135 and 128 eV (kz = ± 0.1455 π), respectively, with corresponding bulk calculations (superimposed red curves). The band crossings for WPs are highlighted by black curves. The crossing-EF features of the α1 bands are marked out by white dashed ellipses
The detailed near-EF band structures along the and directions are presented in Fig. 3d–g. We first focus on the results along the direction (Fig. 3d–f), the projections of calculated bulk bands along this direction in Fig. 3f well reproduce the experimental band features in Fig. 3d, e, i.e., the hole bands at near half of corresponding to the ring-like FSs and the electron bands (dashed curves in Fig. 3d, e) at points for the triangle-like FSs, whose intensities are relatively weak due to the matrix element effect. The band structures along the direction are displayed in Fig. 3g. One can obtain that the observed band dispersions are consistent with calculated bulk bands close to the kz ~ π plane, as illustrated by black curves in Fig. 3g. Indicated by the four blue cuts in Fig. 3a, these bulk bands are located in the kx−kz plane with ky = 0 and kz = 0.96, 0.92, 0.88, and 0.84 π from bottom to top, respectively, which are parallel to the direction. This consistency demonstrates the electronic states at high-symmetry kz planes (kz = π here) have main contributions to the ARPES spectra in the frame of kz broadening effect35–37.
Based on the first-principles calculations, the WPs are not located on the high-symmetry kz planes, they are embedded in the kz = ±0.1455 π planes instead. By performing detailed photon-energy-dependent measurements in Supplementary Fig. 7, we can determine the specific kz positions of predicted WPs. As shown in Supplementary Fig. 7a, the band dispersions along the direction show periodic modulation when varying the photon energy. The inner potential (V0) is thus estimated to be 10 eV. We illustrate the kz = ±0.1455 π planes, where the Weyl fermions with opposite chirality are located, respectively, as blue curves in Supplementary Fig. 7b. To demonstrate the existence of WPs without any interference from possible trivial surface states, we utilize the photons with higher energies to record the band structure. The energies of 138 and 125 eV correspond to the kz = ±0.1455 π planes in the neighbor BZ to that in Supplementary Fig. 7b, respectively. The measured second derivative intensity plots along cuts 3 and 4 (Fig. 3a), which are parallel to the direction in the kz = ±0.1455 π planes, are displayed in Fig. 3h, i, respectively. The overlaid bulk band calculations well reproduce the experimental results, especially the α1 and α2 bands forming the WPs. The intensity asymmetry of the α1 band in opposite kx regions derives from the matrix element effect. Since the cone nature of the Weyl dispersion is an important character proving the realization of massless Weyl fermions, we perform a FS mapping with the photon energy of 135 eV, and study the evolution of band structures gradually off the direction. As shown in Supplementary Fig. 8b, c, when measuring off the ky = 0 line, the slopes of the near-EF band dispersions (α1 and α2) forming the Weyl nodes decrease monotonically. This evolution is in accord with a cone nature within energy–momentum space. We would like to stress that, although the predicted WPs are located at ~50 meV above EF, the good agreement between theory and experiment, including the two specific kz positions of WPs and the band structures forming the WPs below EF, combined with the valid Weyl–cone structure in experiment, could plausibly demonstrate the existence of Weyl fermions in Co3Sn2S2.
AHE of Co3Sn2S2
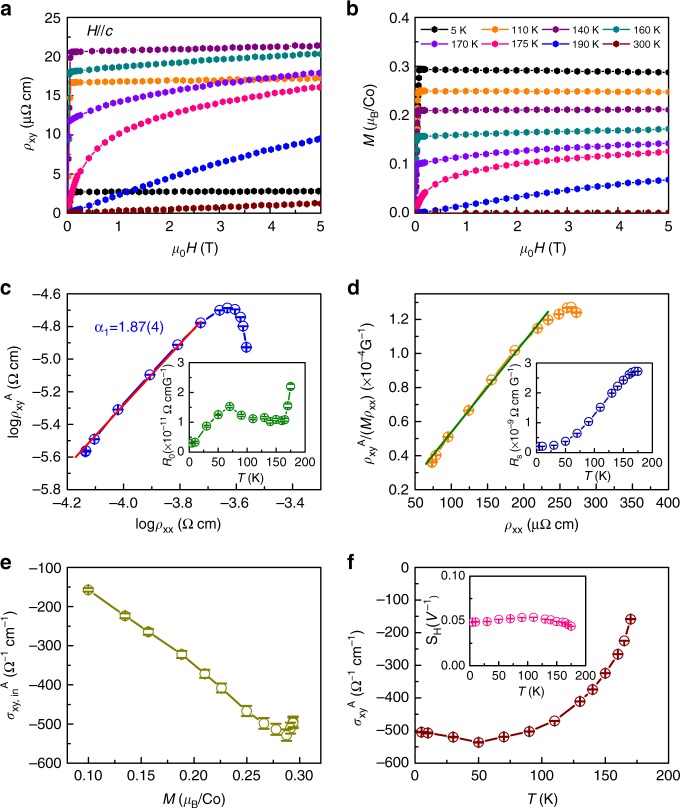
Next, we move to the AHE of Co3Sn2S2. As shown in Fig. 4a, the Hall resistivity ρxy of Co3Sn2S2 at high temperature shows the linear field dependence. When T is close to TC, the ρxy(μ0H) curve starts to bend significantly at low field region. For , the ρxy(μ0H) curve increases steeply at low field and then becomes weakly field-dependent at high field (above ~0.1 T). The field dependence of ρxy(μ0H) resembles those of M(μ0H) (Fig. 4b), typical ones for ferromagnets. But the saturation values follow opposed temperature dependencies at . When the saturation magnetization increases with decreasing temperature, the saturation value of the ρxy(μ0H) decreases below TC. The maximum saturated value of ρxy(μ0H) is ~21 μΩ cm at T = 140 K. We also measured the ρxy(μ0H) of several crystals at the same temperature. They exhibit similar values, spanning between 19.59 and 24.22 μΩ cm at μ0H = 5 T (Supplementary Fig. 9). The standard deviation of determined sample thickness is also below 5% (Supplementary Fig. 10). Moreover, the ρxy(μ0H) at various field directions are also measured. When the magnetic field is titled away from the c axis of Co3Sn2S2 crystal up to ±30°, the change of ρxy(μ0H) is small and the [ρxy(μ0H)(30°) − ρxy(0°)]/ρxy(0°) at 5 T is only about 1% (Supplementary Fig. 11). All of these results clearly indicate that the experimental ρxy(μ0H) is reproducible and reliable.
Fig. 4.
AHE of Co3Sn2S2. a, b Hall resistivity ρxy(μ0H) and M(μ0H) as a function of magnetic field at various temperatures for H||c, respectively. c Plot of log vs. log ρxx(T). The red solid line is the fit using the relation . d Plot of vs. ρxx. The green solid line is the linear fit when ρxx ≤ 250 μΩ cm. Insets of c and d show the temperature dependence of R0(T) and Rs(T) at T ≤ TC, respectively. e Intrinsic AHC as a function of M. f AHC as a function of temperature. Inset: temperature dependence of scale factor SH(T). Error bars in c–f are the standard deviations of the fits when determining the (Supplementary Note 1)
It is known that the Hall resistivity ρxy in ferromagnets arises from two parts4, ρxy = = R0B + 4πRsM, where is the normal Hall resistivity due to the Lorentz force, is the anomalous Hall resistivity, R0 is the ordinary Hall coefficient, and Rs is the anomalous Hall coefficient. From the ρxy(μ0H) and M(μ0H) curves (Supplementary Fig. 12 and Supplementary Note 1), the R0 and Rs can be determined. The R0 is positive at entire temperature region (inset of Fig. 4c), indicating that the dominant carrier is hole-type. The apparent charge carrier density na can be deduced using the relation of na ~ −1/|e|R0 (Supplementary Fig. 13), and it reaches 2.1 × 1022 cm−3 at 5 K, corresponding to about 0.7 carriers per formula unit of Co3Sn2S2. The Rs(T) is also positive but the absolute value is much larger than R0 (inset of Fig. 4d). It increases monotonically with increasing temperature. The obtained Rs value is 2.7 × 10−9 Ω cm G−1 at 170 K, which exhibits an enhancement of two orders of magnitude when compared with the conventional itinerant ferromagnets, such as pure Fe and Ni38,39.
Discussion
The relation between log and log ρxx at low temperature region (Fig. 4c) can be fitted using the formula , which gives the scaling exponent α = 1.87(4). It suggests that the intrinsic KL or extrinsic side-jump mechanism are mainly responsible for the AHE in Co3Sn2S2. On the other hand, the dominant mechanism of AHE can also be decided by fitting the relationship between and ρxx using the formula = . The first term corresponds to the skew scattering contribution, while the second term represents the intrinsic or side-jump contribution40. For the skew scattering contribution, the a(M) is usually proportional to M linearly41, and for the intrinsic contribution, the b(M) = is directly related to the intrinsic AHC . Previous study suggests that the is also proportional to M linearly40, thus the linear fit of vs. ρxx can separate the intrinsic and extrinsic contributions. The relation between and ρxx (Fig. 4d) shows the linear dependence when ρxx ≤ 250 μΩ cm. After subtracting the skew-scattering contribution, the obtained value of at 5 K is about 505 Ω−1 cm−1, which is comparable with the predicted value by using the formula of σxy = Ke2/4π2 (~525 Ω−1 cm−1) (Supplementary Fig. 6) but smaller than that calculated from the integral of Berry curvature along kz in the BZ (~1310 Ω−1 cm−1) when setting the moment of Co as 0.33 μB (Fig. 2e). The discrepancy between experimental results and the theoretical results from the latter method is still not clear. But such kind of difference has also been observed in other systems, such as Fe [751 Ω−1 cm−1 (experiment) vs. 1032 Ω−1 cm−1 (theory)], and Ni [−2073 Ω−1 cm−1 (experiment) vs. −646 Ω−1 cm−1 (theory)]14,42. On the other hand, the exhibits the linear dependence of M when T < TC (Fig. 4e), well consistent with the KL theory10. Importantly, this result is also well in agreement with the theoretical predictions that the smaller moment of Co leads to the nearly linear decrease of (Fig. 2e and Supplementary Fig. 6). In contrast to the , the for the side-jump contribution can be estimated using an expression (e2/(ha)(εSO/EF), where εSO is the spin–orbit interaction energy41,43. Using the lattice constant a ~ V1/3 = 9.96 Å and εSO/EF ~ 0.01 for the metallic ferromagnets, the derived is only about 3.9 Ω−1 cm−1, thus the extrinsic side-jump contribution to could be very small when compared to . To further investigate the mechanism of AHE in Co3Sn2S2, the temperature dependence of is shown in Fig. 4f. The shows fairly large values at low temperature region and it is insensitive to the change of temperatures. Above 140 K, however, it decreases quickly with increasing temperature and reaches to about 150 Ω−1 cm−1 at 175 K. In contrast, the scale factor SH () is almost constant when T < TC (inset of Fig. 4f). Therefore it further confirms that the temperature dependence of originates from the temperature dependence of M, i.e., the dramatic decrease of above 140 K is mainly due to the sharp decrease of M(T) as the temperature approaches TC. Above results clearly indicate that the large intrinsic AHC is dominant in HMFM Co3Sn2S2, and it is closely related to the nontrivial topology of band structure with Weyl nodes near EF.
In summary, we have investigated the AHE and electronic structure of HMFM Co3Sn2S2 single crystal. The nearly quadratic relationship between and ρxx indicates that the mechanism of AHE in Co3Sn2S2 is dominated by the intrinsic contribution. The consistency between the experimental band structures and first-principles calculations, especially the spindle-shaped FSs along the direction and the band dispersions forming the WPs, combined with the Weyl-cone structure presented in ARPES, indicate that the intrinsic AHE in Co3Sn2S2 originates from the existence of magnetic Weyl fermions near EF. Moreover, the steep decrease of at high temperature can be mainly ascribed to the sharp decrease of magnetic moment, causing the change of topological properties in band structure. Current work will not only deepen our understanding on the exotic physical phenomena associated with nontrivial band topology, but also shed light on exploring novel electronic/spintronic devices based on AHE and/or half metallicity.
Methods
Single crystal growth and structural characterization
Co3Sn2S2 single crystals were grown by the Sn flux44. The starting materials Co lumps (purity 99.99%), Sn grains (purity 99.99%) and S flakes (purity 99.999%) were mixed together in a molar ratio of Co:Sn:S = 8:86:6 and placed in an alumina crucible. Then, the crucible was sealed in the quartz ampoule under partial argon atmosphere. The sealed quartz ampoule was initially heated at 673 K for 2 h in order to avoid bursting of ampoule due to the high vapor pressure of S. And then it was heated up to 1323 K and kept there for 6 h to ensure the homogeneity of melt. Finally the ampoule was cooled down slowly to 973 K with 5 K/h. At this temperature, the ampoule was taken out from the furnace rapidly and decanted with a centrifuge to extract Co3Sn2S2 single crystals from the Sn flux. X-ray diffraction (XRD) patterns were measured using a Bruker D8 X-ray machine with CuKα radiation (λ = 0.15418 nm) at room temperature.
Magnetization and transport measurements
Magnetization and electrical transport measurements were performed in a Quantum design MPMS3 and PPMS, respectively. Both longitudinal and Hall electrical resistivity were measured using a standard four-probe method on rectangular shape single crystals with current flowing in the ab plane. In order to effectively avoid the longitudinal resistivity contribution due to voltage probe misalignment, the Hall resistivity was measured by sweeping the field from −5 T to 5 T at various temperatures, and the total Hall resistivity was determined by ρxy(μ0H) = [ρ(+μ0H) − ρ(−μ0H)]/2, where ρxy(±μ0H) is the transverse resistivity under a positive or negative magnetic field.
ARPES measurements
ARPES measurements were performed at the Dreamline beamline of the Shanghai Synchrotron Radiation Facility (SSRF) with a Scienta D80 analyzer and at the 1-cubed ARPES end-station of BESSY using a Scienta R4000 analyzer. The energy and angular resolutions were set to 15 meV and 0.2°, respectively. All samples were cleaved in situ along the (001) plane and measured at T = 20 K in a working vacuum better than 5 × 10−11 Torr.
Theoretical calculation
We have simulated the electronic structure of Co3Sn2S2 with first-principle calculations using Vienna ab initio Simulation Package (VASP)45, and the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) type exchange correlation potential46 was employed. The spin–orbit coupling was taken into account in all of the calculations. We have relaxed the crystal structure and the lattice constants a = b = 5.3892 Å, and c = 13.1519 Å are adopted in our calculation. The surface states and anomalous Hall conductivity were calculated based on the tight binding Hamiltonian constructed by using Wannier90 package47. The maximally localized Wannier functions for 3d orbitals on Co, 5p orbitals on Sn, and 3p orbitals on S have been used as the basis of the tight-binding Hamiltonian. We calculate the anomalous Hall conductivity (AHC) as the sum of Berry curvatures over all of the occupied bands48,
| 1 |
where fn(k) is the Fermi–Dirac distribution function, and n is the index of the occupied bands. The Berry curvature can be arisen from the Kubo-formula derivation,
| 2 |
where vx(y) is the velocity operator. The intrinsic AHC is calculated with 200 × 200 × 200 k-point grid based on the tight binding Hamiltonian.
Electronic supplementary material
Acknowledgements
This work was supported by the National Key R&D Program of China (Grant nos. 2016YFA0300504, 2016YFA0300600), the National Natural Science Foundation of China (Nos. 11574394, 11774423, 11774421, and 11674369), the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (RUC) (15XNLF06, 15XNLQ07, 17XNH055, 18XNLG14, 18XNH057). Z.L. acknowledges Shanghai Sailing Program (17YF1422900). Y.X and H.W are also supported by the “Strategic Priority Research Program (B)” of the Chinese Academy of Sciences (Grant no. XDB07020100).
Author contributions
H.L., H.W., and S.W. provided strategy and advice for the research; Q.W. performed the crystal growth, magnetization and transport measurements and fundamental data analysis; R.L., Z.L., M.L., Y.H. and D.S. performed the ARPES measurements and analyzed the data; Y.X. and H.W. carried out the theoretical calculation; H.L. wrote the manuscript based on discussion with all the authors.
Data availability
Data measured or analyzed during this study are available from the corresponding authors on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Qi Wang, Yuanfeng Xu, Rui Lou.
Change history
10/8/2018
The original version of this Article incorrectly omitted an affiliation of Hongming Weng: “Beijing National Laboratory for Condensed Matter Physics and Institute of Physics, Chinese Academy of Sciences, 100190, Beijing, China”
This has been corrected in both the PDF and HTML versions of the Article.
Contributor Information
Hongming Weng, Email: hmweng@iphy.ac.cn.
Shancai Wang, Email: scw@ruc.edu.cn.
Hechang Lei, Email: hlei@ruc.edu.cn.
Electronic supplementary material
Supplementary Information accompanies this paper at 10.1038/s41467-018-06088-2.
References
- 1.Hall EH. On a new action of the magnet on electric currents. Am. J. Math. 1879;2:287–292. doi: 10.2307/2369245. [DOI] [Google Scholar]
- 2.Hall EH. On the new action of magnetism on a permanent electric current. Philos. Mag. 1880;10:301–328. doi: 10.1080/14786448008626936. [DOI] [Google Scholar]
- 3.Hall EH. On the “Rotational coefficient” in nickel and cobalt. Philos. Mag. 1881;12:157–172. doi: 10.1080/14786448108627086. [DOI] [Google Scholar]
- 4.Hurd CM. The Hall Effect in Metals and Alloys. New York: Plenum Press; 1972. [Google Scholar]
- 5.Chien CL, Westgate CR. The Hall Effect and Its Applications. New York: Plenum Press; 1980. [Google Scholar]
- 6.Nagaosa N, Sinova J, Onoda S, MacDonald AH, Ong NP. Anomalous Hall effect. Rev. Mod. Phys. 2010;82:1539–1592. doi: 10.1103/RevModPhys.82.1539. [DOI] [Google Scholar]
- 7.Smit J. The spontaneous Hall effect in ferromagnetics I. Physica. 1955;21:877–887. doi: 10.1016/S0031-8914(55)92596-9. [DOI] [Google Scholar]
- 8.Smit J. The spontaneous Hall effect in ferromagnetics II. Physica. 1958;24:39–51. doi: 10.1016/S0031-8914(58)93541-9. [DOI] [Google Scholar]
- 9.Berger L. Side-jump mechanism for the Hall effect of ferromagnets. Phys. Rev. B. 1970;2:4559–4566. doi: 10.1103/PhysRevB.2.4559. [DOI] [Google Scholar]
- 10.Karplus R, Luttinger JM. Hall effect in ferromagnetics. Phys. Rev. 1954;95:1154–1160. doi: 10.1103/PhysRev.95.1154. [DOI] [Google Scholar]
- 11.Jungwirth T, Niu Q, MacDonald AH. Anomalous Hall effect in ferromagnetic semiconductors. Phys. Rev. Lett. 2002;88:207208. doi: 10.1103/PhysRevLett.88.207208. [DOI] [PubMed] [Google Scholar]
- 12.Onoda M, Nagaosa N. Quantized anomalous Hall effect in two-dimensional ferromagnets: quantum Hall effect in metals. Phys. Rev. Lett. 2003;90:206601. doi: 10.1103/PhysRevLett.90.206601. [DOI] [PubMed] [Google Scholar]
- 13.Haldane FDM. Berry curvature on the fermi surface: anomalous Hall effect as a topological fermi-liquid property. Phys. Rev. Lett. 2004;93:206602. doi: 10.1103/PhysRevLett.93.206602. [DOI] [PubMed] [Google Scholar]
- 14.Yao YG, et al. First principles calculation of anomalous Hall conductivity in ferromagnetic bcc Fe. Phys. Rev. Lett. 2004;92:037204. doi: 10.1103/PhysRevLett.92.037204. [DOI] [PubMed] [Google Scholar]
- 15.Burkov AA, Hook MD, Balents L. Topological nodal semimetals. Phys. Rev. B. 2011;84:235126. doi: 10.1103/PhysRevB.84.235126. [DOI] [Google Scholar]
- 16.Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B. 2011;83:205101. doi: 10.1103/PhysRevB.83.205101. [DOI] [Google Scholar]
- 17.Xu G, Weng H, Wang Z, Dai X, Fang Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4. Phys. Rev. Lett. 2011;107:186806. doi: 10.1103/PhysRevLett.107.186806. [DOI] [PubMed] [Google Scholar]
- 18.Wang Z, et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb) Phys. Rev. B. 2012;85:195320. doi: 10.1103/PhysRevB.85.195320. [DOI] [Google Scholar]
- 19.Liu ZK, et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science. 2014;343:864–867. doi: 10.1126/science.1245085. [DOI] [PubMed] [Google Scholar]
- 20.Weng H, Fang C, Fang Z, Bernevig BA, Dai X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X. 2015;5:011029. [Google Scholar]
- 21.Xu SY, et al. Discovery of a Weyl Fermion semimetal and topological Fermi arcs. Science. 2015;349:613–618. doi: 10.1126/science.aaa9297. [DOI] [PubMed] [Google Scholar]
- 22.Lv BQ, et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X. 2015;5:031013. [Google Scholar]
- 23.Fang Z, et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science. 2003;302:93–95. doi: 10.1126/science.1089408. [DOI] [PubMed] [Google Scholar]
- 24.Burkov AA. Anomalous Hall effect in Weyl metals. Phys. Rev. Lett. 2014;113:187202. doi: 10.1103/PhysRevLett.113.187202. [DOI] [PubMed] [Google Scholar]
- 25.Ludbrook BM, Ruck BJ, Granville S. Perpendicular magnetic anisotropy in Co3MnGa and its anomalous Hall effect. Appl. Phys. Lett. 2017;110:062408. doi: 10.1063/1.4976078. [DOI] [Google Scholar]
- 26.Otto MJ, et al. Half-metallic ferromagnets II. Transport properties of NiMnSb and related inter-metallic compounds. J. Phys. Condens. Matter. 1989;1:2351–2360. doi: 10.1088/0953-8984/1/13/008. [DOI] [Google Scholar]
- 27.de Groot RA, Mueller FM, Engen PGv, Buschow KHJ. New class of materials: half-metallic ferromagnets. Phys. Rev. Lett. 1983;50:2024–2027. doi: 10.1103/PhysRevLett.50.2024. [DOI] [Google Scholar]
- 28.Vaqueiro P, Sobany GG. A powder neutron diffraction study of the metallic ferromagnet Co3Sn2S2. Solid State Sci. 2009;11:513–518. doi: 10.1016/j.solidstatesciences.2008.06.017. [DOI] [Google Scholar]
- 29.Kubodera T, Okabe H, Kamihara Y, Matoba M. Ni substitution effect on magnetic and transport properties in metallic ferromagnet Co3Sn2S2. Phys. B. 2006;378–380:1142–1143. doi: 10.1016/j.physb.2006.01.458. [DOI] [Google Scholar]
- 30.Schnelle W, et al. Ferromagnetic ordering and half-metallic state of Sn2Co3S2 with the shandite-type structure. Phys. Rev. B. 2013;88:144404. doi: 10.1103/PhysRevB.88.144404. [DOI] [Google Scholar]
- 31.Coey JMD, Sanvito S. Magnetic semiconductors and half-metals. J. Phys. D. Appl. Phys. 2004;37:988–993. doi: 10.1088/0022-3727/37/7/005. [DOI] [Google Scholar]
- 32.Yu R, Qi XL, Bernevig A, Fang Z, Dai X. Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection. Phys. Rev. B. 2011;84:075119. doi: 10.1103/PhysRevB.84.075119. [DOI] [Google Scholar]
- 33.Sancho MPL, Sancho JML, Sancho JML, Rubio J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F Met. Phys. 1985;15:851–858. doi: 10.1088/0305-4608/15/4/009. [DOI] [Google Scholar]
- 34.Wu Q, Zhang S, Song HF, Troyer M, Soluyanov AA. WannierTools: an open-source software package for novel topological materials. Comp. Phys. Commun. 2018;224:405–416. doi: 10.1016/j.cpc.2017.09.033. [DOI] [Google Scholar]
- 35.Strocov VN. Intrinsic accuracy in 3-dimensional photoemission band mapping. J. Electron Spectrosc. Relat. Phenom. 2003;130:65–78. doi: 10.1016/S0368-2048(03)00054-9. [DOI] [Google Scholar]
- 36.Kumigashira H, et al. High-resolution angle-resolved photoemission study of LaSb. Phys. Rev. B. 1998;58:7675–7680. doi: 10.1103/PhysRevB.58.7675. [DOI] [Google Scholar]
- 37.Takane D, et al. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B. 2016;94:121108(R). doi: 10.1103/PhysRevB.94.121108. [DOI] [Google Scholar]
- 38.Volkenshtein NV, Fedorov GV. Temperature dependence of the Hall effect of pure ferromagnets. Sov. Phys. JETP. 1960;11:48–50. [Google Scholar]
- 39.Kaul SN. Anomalous Hall effect in nickel and nickel-rich nickel–copper alloys. Phys. Rev. B. 1979;20:5122–5130. doi: 10.1103/PhysRevB.20.5122. [DOI] [Google Scholar]
- 40.Zeng C, Yao Y, Niu Q, Weitering HH. Linear magnetization dependence of the intrinsic anomalous Hall effect. Phys. Rev. Lett. 2006;96:037204. doi: 10.1103/PhysRevLett.96.037204. [DOI] [PubMed] [Google Scholar]
- 41.Nozières P, Lewiner C. A simple theory of the anomalous Hall effect in semiconductors. J. Phys. 1973;34:901–915. doi: 10.1051/jphys:019730034010090100. [DOI] [Google Scholar]
- 42.Wang X, Vanderbilt D, Yates JR, Souza I. Fermi-surface calculation of the anomalous Hall conductivity. Phys. Rev. B. 2007;76:195109. doi: 10.1103/PhysRevB.76.195109. [DOI] [Google Scholar]
- 43.Onoda S, Sugimoto N, Nagaosa N. Intrinsic versus extrinsic anomalous hall effect in ferromagnets. Phys. Rev. Lett. 2006;97:126602. doi: 10.1103/PhysRevLett.97.126602. [DOI] [PubMed] [Google Scholar]
- 44.Kassem MA, Tabata Y, Waki T, Nakamura H. Single crystal growth and characterization of kagomé-lattice shandites Co3Sn2−xInxS2. J. Cryst. Growth. 2015;426:208–213. doi: 10.1016/j.jcrysgro.2015.06.017. [DOI] [Google Scholar]
- 45.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- 46.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 47.Mostofi AA, et al. Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2008;178:685–699. doi: 10.1016/j.cpc.2007.11.016. [DOI] [Google Scholar]
- 48.Weng HM, Yu R, Hu X, Dai X, Fang Z. Quantum anomalous Hall effect and related topological electronic states. Adv. Phys. 2015;64:227–282. doi: 10.1080/00018732.2015.1068524. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data measured or analyzed during this study are available from the corresponding authors on reasonable request.