Towards patient-specific modeling of brain tumor growth and formation of secondary nodes guided by DTI-MRI

Abstract

Previous studies to simulate brain tumor progression, often investigate either temporal changes in cancer cell density or the overall tissue-level growth of the tumor mass. Here, we developed a computational model to bridge these two approaches. The model incorporates the tumor biomechanical response at the tissue level and accounts for cellular events by modeling cancer cell proliferation, infiltration to surrounding tissues, and invasion to distant locations. Moreover, acquisition of high resolution human data from anatomical magnetic resonance imaging, diffusion tensor imaging and perfusion imaging was employed within the simulations towards a realistic and patient specific model. The model predicted the intratumoral mechanical stresses to range from 20 to 34 kPa, which caused an up to 4.5 mm displacement to the adjacent healthy tissue. Furthermore, the model predicted plausible cancer cell invasion patterns within the brain along the white matter fiber tracts. Finally, by varying the tumor vascular density and its invasive outer ring thickness, our model showed the potential of these parameters for guiding the timing (83–90 days) of cancer cell distant invasion as well as the number (0–2 sites) and location (temportal and/or parietal lobe) of the invasion sites.

1. Introduction

Dysfunctional cells exhibiting uncontrolled proliferation give rise to malignant growths (tumors) that are able to invade and ultimately destruct vital organs. In recent years, as mathematical and computational models evolve, their application to neuro-oncology enables the formation of predictive systems that can model and simulate malignancies in the brain. Such systems can improve our understanding of growth and invasive patterns, and potentially lead to useful clinical tools (Martirosyan et al., 2015; Engwer et al., 2016). In regards to brain tumor modeling this can be viewed from two perspectives: i) the microscopic approach that accounts for cellular processes within the tumor and in the surrounding tissue, and ii) the macroscopic approach that investigates the tissue-level growth of the tumor (Konukoglu et al., 2010; Martirosyan et al., 2015).

The microscopic models account for the discrete nature of cells either by single cell approaches or by approaches modeling the tumor as a collection of interacting self-organizing cells (Juffer et al., 2008). In cellular automation studies, the cells are considered as discrete entities, in a particular state (dead, alive, vacant, etc.) within a large lattice, which proliferate, with the daughter cell occupying a neighboring vacant lattice site (Juffer et al., 2008). Such lattice-based models with discrete cellular components have managed to address the tumor cell heterogeneity, growth pattern, invasiveness (Rubenstein and Kaufman, 2008; Zhang et al., 2009; Baker et al., 2014) and response to treatment (Alfonso et al., 2014). The migration-proliferation dichotomy of the cells has also been investigated by phenomenological models (Alfonso et al., 2017) applying continuous time random walks (Iomin, 2015), “go or grow” mechanisms (Hatzikirou et al., 2012), as well as phenotypic switching (Tektonidis et al., 2011; Alfonso et al., 2016). Finally, evolutionary game theory has been used to study the interplay between different cell phenotypes and how these affect tumor progression (Basanta et al., 2008).

Continuum-based models focus on the evolution of cancer cell density over time, using the diffusion-reaction equation to describe tumor growth and infiltration. These models initially assumed a homogeneous and isotropic diffusion/invasion of cancer cells in the entire brain (Tracqui et al., 1995; Swanson et al., 2000). Later efforts increased the level of sophistication by accounting for different diffusion coefficients for each of the brain's substances (Swanson et al., 2003; Szeto et al., 2009; Unkelbach et al., 2014). More recently, models for brain tumor growth recognize the importance of incorporating the inhomogeneous and anisotropic diffusion of cancer cells in the brain and are most often driven by data acquired from magnetic resonance diffusion tensor imaging (DTI-MRI) (Konukoglu et al., 2010; Roniotis et al., 2012; Colombo et al., 2015; Engwer et al., 2016).

The realization that not only biological factors but also biomechanical forces affect tumor dynamics (Jain et al., 2014) drove mathematical models of brain tumors to investigate the macroscopic, tissue-level behavior of the tumor and its mechanical interaction with the surrounding structures (Konukoglu et al., 2010). Earlier models of this type, assumed the brain to consist of a single solid phase and modeled its mechanical response using an external force proportional to the concentration gradient of cancer cells (Wasserman et al., 1996; Clatz et al., 2005; Hogea et al., 2008; Zacharaki et al., 2008). More comprehensive biomechanical models have also been developed that address the biphasic (i.e., fluid and solid phase) nature of the brain and simulate brain tumor growth by accounting for the varying mechanical properties of the brain's grey and white matter and cerebrospinal fluid using a realistic geometry extracted from MRI data (Angeli and Stylianopoulos, 2016).

The need of an approach to couple cellular and tissue-level events, becomes imperative in the case of brain tumors. The infiltration and invasion of glioma cells frequently causes relapse after treatment (Yangjin and Soyeon, 2013; Hunt and Surulescu, 2017), whereas the inhomogeneous and irregular growth patterns of brain tumors are affected by the physical anatomical structures of the surrounding tissue (Tysnes and Mahesparan, 2001; Esmaeili et al., 2018). Furthermore, as population-level data are shown to be poor predictors of patients' response to treatment due to an increased inter-individual variability (Johnson and O'Neill, 2012), the necessity of patient specific models becomes more essential (Jackson et al., 2015).

To address these limitations, we build on previous work (Mpekris et al., 2015; Angeli and Stylianopoulos, 2016; Mpekris et al., 2017) and developed a biomechanical finite elements model of brain tumor growth accounting for the entire human brain as well as for the infiltration of cancer cells in the surrounding normal tissue and their invasion to distant areas within the brain. Cancer cell infiltration and distant invasion were described by the diffusion-reaction equation using an anisotropic and inhomogeneous diffusion tensor acquired from DTI-MRI (Tuch et al., 2003; Zhang et al., 2009), in accordance with previous studies reporting that the preferred dispersion routes of tumor cells is along white matter fiber tracts (Vertosick Jr and Selker, 1990; Yangjin and Soyeon, 2013; Alfonso et al., 2017). The vascular density of the tumor was derived from human data of perfusion MRI, while the biphasic and continuum mechanics basis of the formulation enabled the calculation of solid stresses, tissue displacements and interstitial fluid pressure (IFP).

Our mathematical formulation is therefor able to, i) couple the diffusion-reaction models with the tissue level tumor behavior, ii) account for the effects of mechanical forces and perfusion on tumor growth and distant invasion and iii) predict satellite/secondary growths in distant sites within the brain. Additionally, we employed the model's predictions to investigate the effect of the tumoral vascular density (i.e., perfusion) and the invasive potential of cancer cells on the number, location and time of appearance of the secondary growths. The proposed mathematical framework along with the utilization of information acquired from various imaging protocols, produces a patient tailored “personalized” outcome, which can ultimately have considerable clinical impact and utility.

2. Methods

2.1. MR imaging and 3D geometry extraction

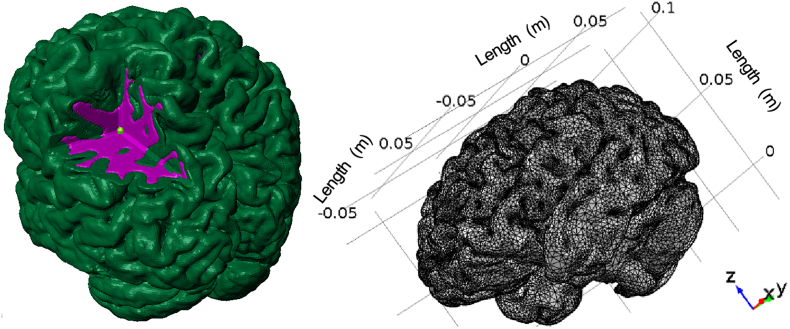
Brain morphological imaging followed by geometrical model extraction was performed according to our previously described methodology (Angeli and Stylianopoulos, 2016). The model, included the full brain and consisted of two different computational domains, corresponding to the grey and white matter. Additionally, a third domain was manually positioned at the left parietal lobe to act as the initial tumor seed. The final model is presented in Fig. 1 along with its size in meters. It consisted of 777,397 tetrahedral and 202,349 triangular elements resulting in 2,335,057 degrees of freedom.

Fig. 1.

(Left) Three-dimensional representation of the computational mesh showing the individual domains for the grey (green), white (purple) matter and tumor seed (light green). (Right) Computational finite element mesh employed in the present study consisting of 777,397 tetrahedral and 202,349 triangular elements. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In the same session as the morphological brain imaging, using the same slice stack positioning and orientation, DTI-MRI was performed for the same healthy volunteer employing an 1.5 Philips Achieva Magnetic Resonance Imaging Scanner (Philips Healthcare, Netherlands) and a SENSE 16-channel head coil. The spatial resolution of the scan was 1.75 × 1.75 × 2 mm with a repetition time of 4907 ms an echo time of 80 ms, 15 gradient directions and b-values of 0 and 800 s/mm². The acquired magnetic resonance (MR) images were exported as standard DICOM format and imported into the Diffusion Toolkit (Massachusetts General Hospital, Boston, MA) along with the corresponding gradient table and b-values to enable the calculation of the diffusion tensors for every imaged voxel (Angeli et al., 2014). The calculated diffusion tensors were then imported in Matlab (Mathworks, MA) and were used to direct tumor cells invasion within the healthy tissue domains as described in the Section 2.3.

2.2. Biomechanical model of brain tumor growth

The model accounted for both the solid and fluid phase of the tumor and normal brain tissue (white and grey matter) as well as for tumor growth and oxygen transport. To model tumor growth, the decomposition of the total deformation gradient tensor F was employed according to the expression (Skalak et al., 1996; Ambrosi and Mollica, 2002):

$$\mathrm{F}={\mathrm{F}}_e{\mathrm{F}}_g$$ (1)

where F_e is the elastic component of F used to account for interactions with the normal brain and F_g was assumed to be an isotropic tensor that describes tumor growth due to cancer cell proliferation and it was associated with the growth stretch ratio λ_g as follows (Roose et al., 2003; Kim et al., 2011; Stylianopoulos et al., 2013; Mpekris et al., 2015):

$${\mathrm{F}}_g={\lambda }_g\mathrm{{\rm I}}$$ (2)

where Ι is the identity tensor. The elastic component F_e was determined by rearranging Eq. (1).

The growth stretch ratio was formulated by considering a growth rate which accounts for the effects of Cauchy solid stress (σ^s) and oxygen on tumor growth, the volume fraction of the solid (Φ^s) and fluid phase (1 − Φ^s), along with the normalized cancer cell density (T_cell), according to the following expression (Roose et al., 2003; Kim et al., 2011; MacLaurin et al., 2012; Voutouri and Stylianopoulos, 2014; Mpekris et al., 2015):

$$\frac{d{\lambda }_g}{\mathit{dt}}=\frac{1}{3}{R}_{\mathit{tumor}}{\lambda }_g$$ (3)

with

$$R_{\mathit{tumor}}=G(1+\beta \overline{\sigma }){\mathrm{\Phi }}^S\left(1-{\mathrm{\Phi }}^S\right)T{}_{\mathit{cell}}$$ (4)

where R_tumor describes the proliferation rate of cancer cells, $\overline{\sigma }=\left({\sigma }_{\mathit{rr}}^s+{\sigma }_{\mathit{\theta \theta }}^s+{\sigma }_{\mathit{\phi \phi }}^s\right)/3$ is the average (bulk) of the solid phase Cauchy stress and β is a constant to describe the dependence of growth on solid stress. The term $\left(1+\beta \overline{\sigma }\right)$ is taken to be positive but less than unity when the bulk stress was compressive, and set equal to unity when the bulk stress was tensile (Helmlinger et al., 1997; Cheng et al., 2009). The ⅓ multiplier in the right-hand side of the equation appears owing to the assumption of isotropic tumor growth. The growth stretch ratio, λ_g, describes tumor growth in each of the three coordinate directions. For isotropic growth λ_g becomes the same in all three directions and thus, the ⅓ denotes that the cancer cell proliferation term, R_tumor is equally divided among the three coordinates. Finally, the term G describes the effect of oxygen on tumor growth. A Michaelis-Menten expression is used for G, reflecting the fact that an increase in oxygen concentration will increase cancer cell proliferation rate, until a plateau is reached corresponding to the state that oxygen supply is higher than the maximum consumption capacity of cancer cells (Casciari et al., 1992):

$$\begin{array}{l}G=\frac{k_1{c}_{\mathit{ox}}}{k_2+c_{\mathit{ox}}}\end{array}$$ (5)

where c_ox is the oxygen concentration and k₁, k₂ are growth rate constants, the values of which are listed in Table 1, along with all other parameter values used in this study.

Table 1.

Values of model's parameters employed in the simulation.

Parameter	Description	Domain	Value	Reference
β	Growth stress dependence	Tumor	0.000025 Pa−1	(Voutouri et al., 2014)
Ciox	Initial oxygen concentration	All	0.2 mol·m−3	(Casciari et al., 1992)
Dox	Oxygen diffusion coefficient	All	1.55 × 10−4 m2·day−1	(Kim et al., 2011)
Aox	Oxygen consumption rate	All	2200 mol·m−3·day−1	(Casciari et al., 1992; Kim et al., 2011)
kox	Oxygen concentration at which the reaction rate is half	All	0.00464 mol·m−3	(Casciari et al., 1992; Kim et al., 2011)
k1	Growth rate parameter	Tumor	0.16 day−1	This Study
k2	Growth rate parameter	Tumor	0,0083 mol m−3	(Casciari et al., 1992)
ρTcell	Tumor cell proliferation rate	Brain	0.012 day−1	(Swanson et al., 2008)
To	Reference cancer cell density	Tumor	107 cells/cm3	(Stein et al., 2007)
Tcell,i	Normalized initial cancer cell density	Brain	0	–
		Tumor	1

The equations for the mass balance of the fluid and solid phase, for the interstitial fluid transport as well as the constitute equation for the mechanical behavior of the tumor and normal tissues are presented in the Appendix A - Supplementary Material.

2.3. Cancer cell proliferation and diffusion

The normalized/dimensionless density of cancer cells, T_cell was derived by division of the cancer cell density to a reference cancer cell density (T_o = 10⁷ cells/cm³) (Stein et al., 2007). Such a normalization does not affect model predictions and acts towards eliminating their quantitative reliance from the dimensional cancer cell density. T_cell in the tumor and normal brain was given by a diffusion-reaction type equation that accounted for the proliferation of cancer cells and their invasion to the adjacent healthy tissues (Mpekris et al., 2017):

$$\frac{\partial T_{\mathit{cel}}}{\partial t}+\nabla \cdot \left(-D_T\left(x\right)\nabla T_{\mathit{cells}}\right)=R$$ (6)

where D_T(x) is the inhomogeneous and anisotropic diffusion tensor acquired from the DTI-MRI in accordance with previous studies (Roniotis et al., 2012; Engwer et al., 2016) and R is a reaction term used to describe cancer cell proliferation. Within the tumor domain, R is given by Eq. (4), while for the cells that invade into the normal brain is given by:

$$R_{\mathit{tissue}}={\rho }_{\mathit{cell}}{T}_{\mathit{cell}}$$ (7)

where ρ_cell is the proliferation rate of cancer cells diffusing away from the tumor found from the literature (Table 1).

2.4. Oxygen transport

Transport of oxygen is modeled taking into account: the oxygen entering the brain from the blood vessels, the convective and diffusive oxygen transport within the brain, and the amount of oxygen consumed by cancer cells (Roose et al., 2003; Kim et al., 2011; Mpekris et al., 2015), that is,

$$\frac{\partial c_{\mathit{ox}}}{\partial t}+\nabla \cdot \left(c_{\mathit{ox}}{\mathrm{v}}^f\right)=D_{\mathit{ox}}{\nabla }^2{c}_{\mathit{ox}}-\frac{A_{\mathit{ox}}{c}_{\mathit{ox}}}{c_{\mathit{ox}}+k_{\mathit{ox}}}{T}_{\mathit{cell}}+P_{\mathit{er}}{S}_V\left(c_{\mathit{iox}}-c_{\mathit{ox}}\right),$$ (8)

where D_ox is the diffusion coefficient of oxygen in the tumor interstitial space, A_ox is the oxygen consumption rate and k_ox is the oxygen concentration at which the reaction rate is half, P_er is the vascular permeability of oxygen that describes diffusion across the tumor vessel wall, and C_iox is the oxygen concentration in the vessels.

The values of the model's parameters were taken from the literature and are summarized in Table 1. The vascular density of the tumor, S_v, was calculated from human perfusion data derived from MR imaging (Section 2.5).

2.5. Perfusion data from human brain tumors

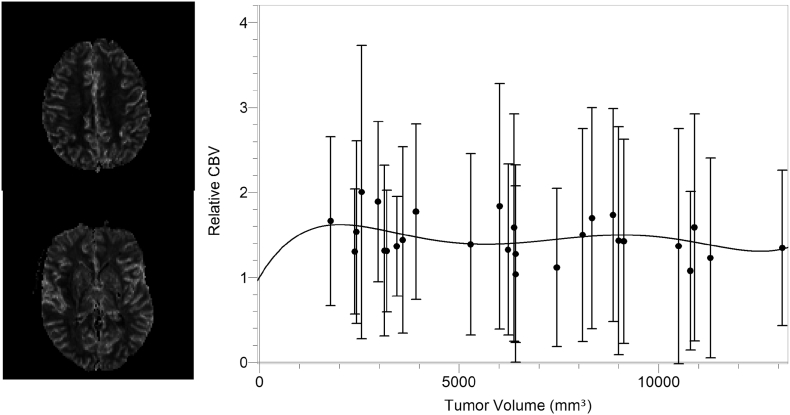
The perfusion MRI data of 12 adult patients with an intra-cranial brain lesion (age: 44 ± 16 y) were acquired at Oslo University Hospital and allowed for the calculation of normalized cerebral blood volume (CBV), i.e. the fraction of blood-to-tissue in a given voxel, for 69 aggregated tumor volumes as follows; Dynamic susceptibility contrast MRI was performed by gradient-echo echo-planar imaging during contrast agent administration (0.2 mmol/kg of gadobutrol) with repetition time 1430 ms, echo time 46 ms, 1.8 × 1.8 mm in-plane resolution and 5 mm slice thickness. Normalized CBV maps were created using nordicICE (NordicNeuroLab, Oslo, Norway) as previous described (Emblem et al., 2015). This included a fully automatic estimation of the area under the contrast-enhanced first-pass curve, voxel-wise normalization to a combined grey- and white-matter reference tissue value and correction for contrast agent extravasation. The resulting CBV values were then fitted with a 5th order polynomial function and the obtained fit, presented in Fig. 2, was used to relate the functional vascular density (Lin et al., 2002) of the tumor with the tumor size. Such a fit was chosen since it was the lowest degree polynomial that was able to cross the vertical axis at the point y 1 (i.e., in the absence of the tumor, vascular density becomes equal to the vascular density of the normal tissue), and provided a proper qualitative response throughout the data range.

Fig. 2.

(Left) Typical relative Cerebral Blood Volume (rCBV) maps extracted from perfusion MRI. (Right) rCBV as a function of tumor volume along with the performed 5^th order fit used to correlate the vascular density and the tumor size within the simulation setup according to the equation rCBV = 1.0 + (7.8 × 10⁻⁴)V_t − (3.4 × 10⁻⁷)V_t² + (5.8 × 10⁻¹¹)V_t³ − (4.4 × 10⁻¹⁵)V_t⁴ + (1.2 × 10⁻¹⁹)Vt⁵.

2.6. Implementation of computational model and boundary conditions

The model equations were solved in COMSOL Multiphysics 5.2 (COMSOL, Inc., Burlington, USA). During the preparation phases of the simulation, a COMSOL – Matlab integration was employed to read the anisotropic and inhomogeneous diffusion tensors for all the nodes of the computational mesh. Such diffusion tensors were subsequently used throughout the time evolution of the tumor growth model to drive tumor cell diffusion within the grey and white matter as described in Section 2.3.

At all internal boundaries (i.e., internal interfaces of the computational domains namely between the grey matter, the white matter and the tumor), COMSOL automatically assigned continuity of the stress and displacement fields, i.e., n · σ^s|₊ = n · σ^s|₋ and n · u|₊ = n · u|₋ where n is the unit normal to the surface vector, u the displacement field and the plus(+) and minus(−) signs denote the two sides of the interface. Furthermore, the interstitial fluid flux exiting from one domain was set equal to the fluid flux entering the other domain of the interface, i.e., n · k_th∇p|₊ = n · k_th∇p|₋, where k_th is the hydraulic conductivity of the tissue and ∇p is the IFP gradient at both sides of the interface.

At the external boundaries, a no-flux condition was employed for the fluid phase (i.e., ∇p = 0) to avoid fluid leakage from the boundaries of the brain while the solid phase was set fixed, to allow deformation only within the brain and not at the periphery, which is in contact with the fixed skull.

A thin layer around the tumor was defined to limit the cells evading the tumor domain and act as its invasive front. While being a computational barrier to the diffusion of cancer cells, this layer allows only a portion of cancer cells to evade the tumor in inverse proportion to its thickness i.e., the thicker the layer the less cells evade the tumor. Such a layer is employed in an effort to approximate previous reports of cells' dichotomy, stating that only a portion of intratumoral cancer cells, with migratory phenotype, have the tendency to escape the tumor through a tumoral outer ring (Tektonidis et al., 2011; Hatzikirou et al., 2012; Alfonso et al., 2016). Additionally, a parametric study was performed to investigate the effect of the thickness of this layer on the model predictions by varying its thickness from 1.0–2.5 mm, considering as baseline the 2 mm thickness. Moreover, the effect of the vascular density on the model predictions was also studied by changing its value by 50% and 150%.

3. Results

3.1. Baseline simulations for tumor growth and cancer cell infiltration

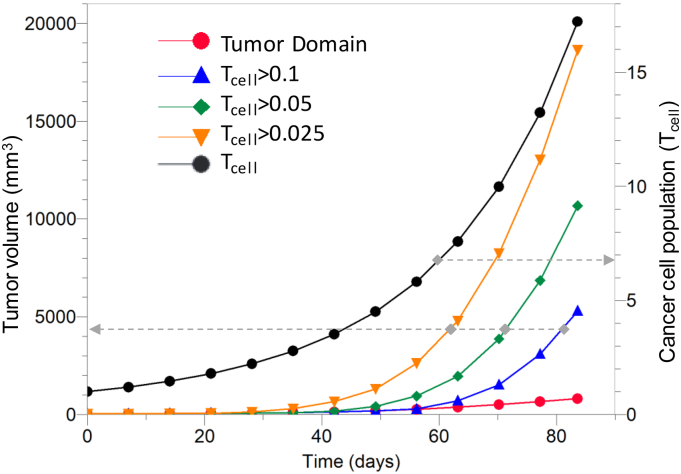
Fig. 3 (left y-axis) presents the growth curve of the initial tumor seed (tumor domain) appearing to increase in size from 32 to 660 mm³. The growth rate of the simulated tumor, defined by the Volume Doubling Time (VDT) (Yamashita and Kuwabara, 1983), was found to be 18.0 days, which is in agreement with the human data of 16.7 and 14.9 days reported in previous studies (Huang et al., 1995; Stensjoen et al., 2015).

Fig. 3.

(Left y-axis) Tumor volume as a function of time for the tumor domain and the three isosurfaces corresponding to different cell densities infiltrating the proximal tissues. (Right y-axis) Cell density as a function of time for the tumor domain showing the proliferation of cancer cells as the tumor grows. The dashed grey arrows connect each curve with its corresponding vertical axis.

Volume estimation was also performed to account for the tumor cells escaping the tumor domain and infiltrating the surrounding tissue. Such volume estimations were performed for isosurfaces with cell population, T_cell, of 0.1, 0.05 and 0.025 and resulted in final tumor volumes of 5296, 10,680 and 18,639 mm³, respectively. The average cell population within the tumor domain increased from the normalized initial unitary value to 17.2, corresponding to a 17-fold increase, (Fig. 3, right y-axis).

3.2. Tissue deformation and stress accumulation in normal and tumor tissue

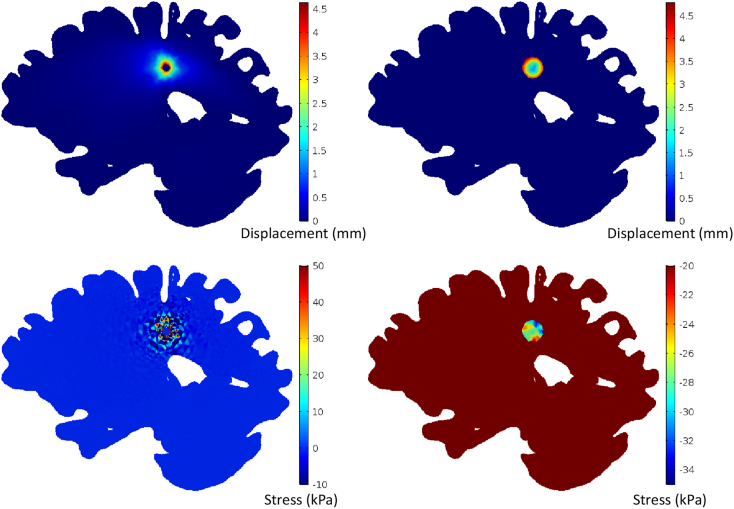
A direct consequence of tumor growth is the displacement and compression of the tumor and the surrounding structures. Such displacements increased from 0.2 mm within the tumor center to 4.5 mm at the tumor periphery. Similarly, in the surrounding tissue the deformations also peaked at 4.5 mm. Contour plots of the displacement distribution are presented in Fig. 4 for both the tumor and the surrounding tissue domains.

Fig. 4.

(Top) Displacement maps and (bottom) stress $\overline{\sigma }=\left({\sigma }_{\mathit{rr}}^s+{\sigma }_{\mathit{\theta \theta }}^s+{\sigma }_{\mathit{\phi \phi }}^s\right)/3$ for the host tissue presented over the reference configuration (right), and for the tumor presented over the final/deformed mesh configuration (left).

The continuum mechanics basis of the model allows for the calculation of the mechanical stresses exhibited during tumor growth. These stresses were found to be heterogeneously distributed and to range from −20 to −34 kPa (−150 to −255 mmHg) within the tumor domain and from −35 to +49 kPa (−262.5 to 367.5 mmHg) in the surrounding tissues (Fig. 4), with negative values to denote compressive stress.

3.3. Tumor cells infiltrate and invade within the brain to form satellite nodes

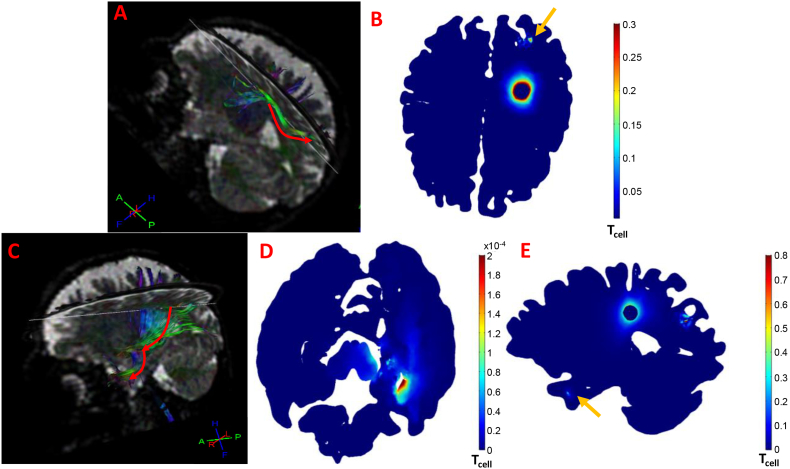
The inhomogeneous and anisotropic diffusion coefficients acquired from DTI-MRI and incorporated into the model, resulted in anisotropic diffusion of cancer cells from the tumor to the normal brain. Fig. 5 presents two slice plots of the population of the cancer cells within the tumor and the normal tissue for two different orientations (transversal and sagittal).

Fig. 5.

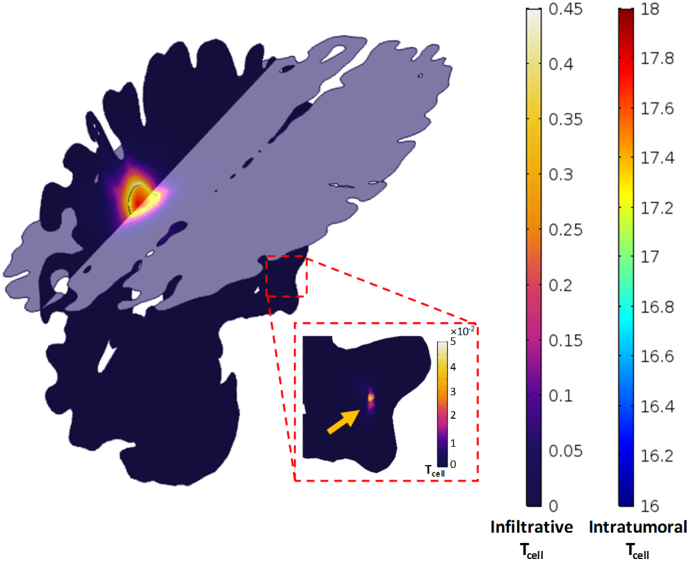
Sagittal and axial surface plots of cancer cell density showing inhomogeneous distribution within the tumor and anisotropic infiltration at the proximal tissue, owing to the inhomogeneous and anisotropic geometry and diffusion tensors. Distant invasion of cancer cells to the right temporal node formed satellite lesion indicated by the yellow arrow in the zoomed region. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Interestingly, the simulation showed cell invasion from the tumor and its proximal areas, to distant locations in the brain. Within the computational domains, we consider a satellite node to be defined as any cell density with no apparent connection to the primary tumor domain and exceeds 1% of the initial cancer cell density. Such cell density was formed in the right temporal lobe at day 83 and is marked by the yellow arrow in Fig. 5 (see also Fig. 6B).

Fig. 6.

(Α) Tumor volume as a function of time (Left y-axis) for the tumor domain and the 2.5% isosurface of cancer cell density, along with the tumor domain's cell density as a function of time (right y-axis) for the additional runs of the parametric study. The dashed grey arrows connect each curve with its corresponding vertical axis. (Β) Sagittal view of T_cell outside the tumor domain showing secondary nodes (yellow arrows) only in the right temporal lobe for the 1.5, 2.5 mm thickness tumor outer rings. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.4. Tumoral outer ring size is crucial for the number of distant satellite nodes

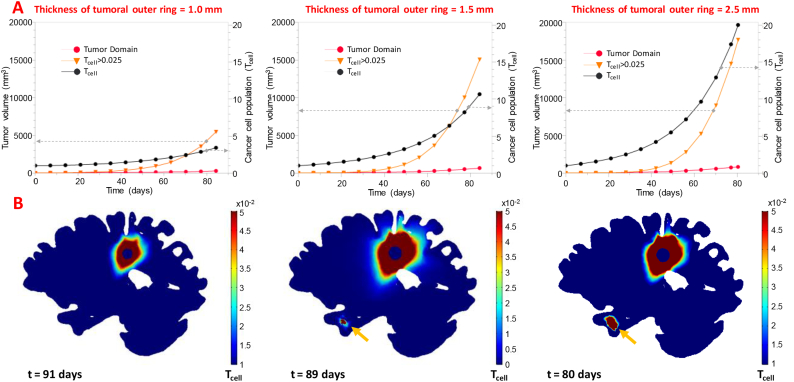
In an effort to investigate the effect of the tumoral outer ring on the simulation results, its thickness was varied from 1.0–2.5 mm. Fig. 6A presents the tumor growth curves (left y-axis) of the parametric analysis. The curves show the tumor domain to reach at day 83 a volume of 284, 658 and 814 mm³ for the 1.0, 1.5 and 2.5 mm of tumoral outer ring thickness, respectively. Additionally, the volume estimation for the 0.05 isosurface resulted in tumor volumes of 1826, 7947 and 10,024 mm³ (5481, 15,086 and 17,691 mm³ for the 0.025 isosurface) at the same day. Fig. 6A depicts the cancer cell proliferation curves (right y-axis), showing the tumor cells to increase from 3.4, to 19.9 at day 83 following the increase in the tumoral outer ring thickness. Also, presented in Supplementary Fig. 1 (A-C) are two slice plots of the population of the cancer cells within the tumor and the surrounding tissue for two different orientations (transversal and sagittal) of the parametric study.

Fig. 6B presents a sagittal view of the brain, depicting the cell density outside the original tumor domain. The formation of satellite nodes was observed only for the 1.5 and 2.5 mm thickness of tumoral outer rings to the right temporal lobe and first appeared at day 77 and 70, respectively. For outer ring thickness of 1 mm, cancer cells did not form any secondary growths.

3.5. Vascular density significantly affects tumor growth rate, cancer cell infiltration and number of satellite nodes

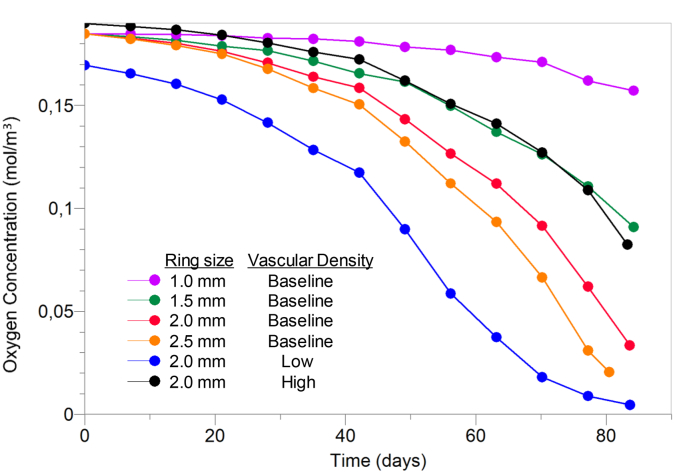
To simulate and investigate the effect of functional vascular density on the model's predictions, its value was decreased by 50% (low vascular density) and increased by 150% (high vascular density) compared to that of the baseline. Fig. 7 shows the oxygen concentration calculated within the tumor during the time evolution of its growth. A marked variability is observed among the different conditions showing that at day 83 the oxygen concentration ranged from 0.004 to 0.16 mol/m³.

Fig. 7.

Intratumoral oxygen concentration as a function of time for varying tumoral outer ring and vascular density conditions. Low and high vascular density corresponds to values 50% and 150% of that of the baseline, respectively.

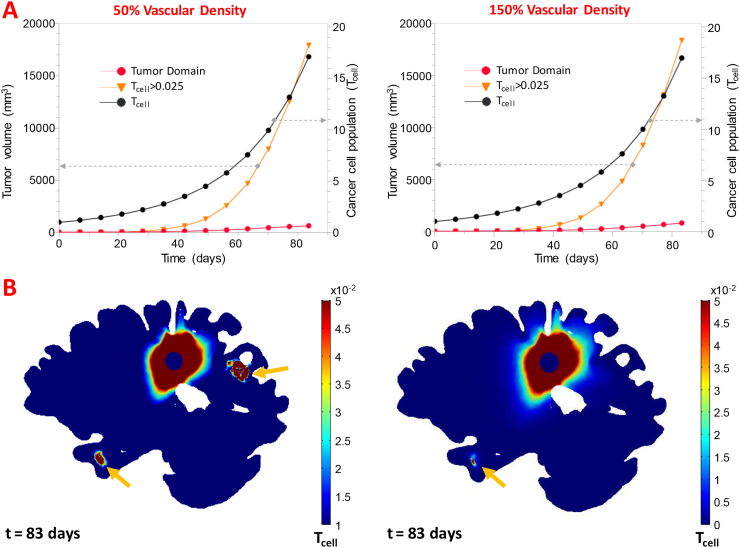
Fig. 8A shows the tumor growth curves (left y-axis) for low and high vascular density, which is related to the number of functional tumor vessels. The curves show the tumor domain to reach a volume of 647 and 824 mm³ at day 83 for low and high vascular densities, respectively. Additionally, the volume estimation for the 0.05 isosurface resulted in tumor volumes of 9945 and 10,511 mm³ (17,908 and 18,365 mm³ for the 0.025 isosurface) at the same day and for low and high vascular densities, respectively. The cancer cell proliferation curves (right y-axis) show the tumor cell density to increase to 17, at day 83. In Supplementary Fig. 1 (D,E) the slice plots of the population of the cancer cells within the tumor and the surrounding tissue for two different orientations (transversal and sagittal) are presented while in the brain sagittal views shown in Fig. 8B, the cell density outside the original tumor domain is plotted. The formation of a satellite node in the right temporal node is first observed in both runs at day 77, interestingly however, for low vascular density a second satellite region was formed in the right posterior parietal lobe at day 83.

Fig. 8.

(Α) Tumor volume as a function of time (Left y-axis) for the tumor domain and the 2.5% isosurface of cancer cell density, along with the tumor domain's cell density as a function of time (right y-axis) for the additional runs of the parametric study. (Β) Sagittal view of T_cell outside the tumor domain showing secondary nodes (yellow arrows) the right temporal posterior parietal lobe for the 50% vascular density run and the only the right temporal lobe for the 150% vascular density run. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.6. Connectivity of satellite regions to the initial tumor location using fiber tractography

In order to visualize the fiber tracts connecting the initial tumor location to the secondary locations, tractography was performed at the Philips MR Console and results are presented in Fig. 9A and C showing numerous fiber bundles connecting the initial to the satellite locations.

Fig. 9.

(A, C) Tractography depicting numerous fiber tracts connecting the initial tumor location with the secondary nodes. (B, E) Distant invasion of cancer cells at distant locations within the brain, forming secondary nodes at the right posterior parietal lobe (B) and the right temporal lobe (E) (yellow arrows) along with the intermediate “cell pool” (D). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Interestingly, while for the case of the right posterior parietal lobe, in which the DTI-based fiber bundles connect the primary tumor to the secondary site directly (Fig. 9A), this is not the case with the temporal lobe where no apparent DTI-based fiber bundles connect the primary lesion to the secondary node. Instead, fibers passing through the tumor encounter the fibers passing through the temporal lobe near the brainstem (Fig. 9C). At this specific location, a “cell pool” is observed (Fig. 9D), indicating that the cells move from the primary tumor to this region, and then relocate to the temporal lobe to form the satellite node (Fig. 9E).

4. Discussion

In this study, a mathematical framework was proposed to investigate brain tumor progression in a patient specific model using data acquired from MRI. The model was based on principles from continuum mechanics (Mpekris et al., 2015; Angeli and Stylianopoulos, 2016) and accounted for the infiltration and distant invasion of cancer cells to the surrounding tissues. Our approach attempts to bridge the gap of existing models, which either model the temporal evolution of cancer cell density (Wang et al., 2009; Chen et al., 2011; Mi et al., 2014) or the macroscopic/tissue-level response of tumor growth (Kyriacou et al., 1999; Hogea et al., 2007; Zacharaki et al., 2008). Even though coupling of cancer cell invasion with the generation of intratumoral mechanical stresses has recently been investigated (Hormuth 2nd et al., 2017; Weis et al., 2017), our model accounts additionally for the interstitial fluid pressure, the oxygen concentration and the anisotropic nature of the diffusion tensors within the brain; in a patient specific three-dimensional, whole brain geometry, employing distinct computational domains for the tumor, the white and the grey matter. Furthermore, while in previous studies, mechanical stress was indirectly accounting for, as a function of cancer cell concentration gradient (Chen et al., 2013; Liu et al., 2014), here we directly model the effects of mechanical stress with the explicit solution of the biomechanical formalism presented. In spite of the strenuous computational demands of our approach, its application is justified by its ability to provide information not only about the heterogeneous tumor growth, the exhibited stresses, and the surrounding tissue displacements, but also about the cancer cell infiltration to the vicinity of the tumor and the invasion to distal locations within the brain.

To our knowledge, this is the first model to predict non-random cancer cell distant invasion, to secondary foci within the brain. Unlike a less sophisticated, directionless and uniform growth, these secondary growths are connected to the primary tumor domain through numerous fiber bundles, as shown in Fig. 9 and are presumed to guide cells distant invasion. The above mechanisms support the validity of the model and show that the cellular formations away from the initial tumor domain are not due to errors of the computational solution.

The parametric study performed herein, highlights the importance of the tumoral outer ring and the vascular density for tumor cell infiltration and distant invasion. We observed that in all simulations, the tumor formed satellite nodes away from its initial location except for the case of the 1 mm outer ring thickness. In this case, even though the distant invasion potential of the cells increases, the population of cancer cells drops significantly, the tumor does not grow big enough to reach a fiber bundle suitable to guide cell distant invasion and/or the cancer cell density is not high enough to establish a diffusion gradient sufficient to drive invasion to distant sites. Therefore, while the percentage of cells evading the tumor is greater than in the other scenarios due to the presence of a thinner outer ring, cancer cells are not able to migrate away from the tumor owing to insufficient density. Additionally, our conclusion is further supported by the fact that for the 2.5 mm outer ring thickness, the formation of the satellite node occurs 7 days earlier than in the other cases. The thickest outer ring accounts for more proliferative cells by reducing the percentage of cells evading the tumor. Therefore, the cells reach a sufficient density for distant invasion earlier, they do invade and form the temporal lobe node, one week earlier than in the other simulations. An additional observation is that the 2 mm ring thickness and 50% vascular density favors the formation of multiple satellite nodes, not observed for the other values tested. This fact, points towards the conclusion that apart from the outer ring size, the change in perfusion, affected tumor growth rate and cancer cell population, enabling distant invasion to the posterior parietal lobe. There appears to be a balance between cancer cell density, tumor growth rate and tumoral outer ring thickness that benefits cancer cell distant invasion and allows formation of multiple secondary nodes.

The two parameters (tumor growth rate/cell density and fiber bundles) shown to affect the formation of satellite nodes are directly affected by the mechanical forces. Therefore, mechanical forces are related to cancer cell invasion to distant sites. Firstly, mechanical forces (in terms of solid stress) determine in the model both the growth of the tumor and the density of cancer cells (Eqs. (3), (4)), and thus they should affect the formation of secondary nodes. Secondly, mechanical forces deform the healthy tissue, which affects the fiber bundles configuration. Fiber bundles, in turn, guide cancer cells to distant regions (Fig. 9).

The model has several limitations. A first limitation is that even though the simulated geometry and the diffusion tensors corresponded to the same healthy volunteer and during the same imaging session, the perfusion data were acquired independently from other imaging studies, at a different institution, for patients with brain tumors who received treatment after scanning. This restrains the comparison of the model results with actual medical data, limiting its clinical validation. However, the accuracy of the model is supported by the physiologically meaningful results of stress, displacement and VDT, which compare well with previous studies (Huang et al., 1995; Stensjoen et al., 2015; Angeli and Stylianopoulos, 2016), and by the identification of a mechanism to support the formation of secondary nodes in all simulations (Fig. 9).

Another limitation of our study is the fact that the values of several model's parameters, listed in Table 1 and in the Supplementary Material, were not derived from patient data but instead they were found in the literature. Incorporation in the model of patient-specific data, could further improve the model's accuracy and specificity. A more detailed specification of the model would require other relevant imaging techniques such as MR elastography (Johnson et al., 2013) to accurately characterize the mechanical properties of the brain tissue and the tumor in individual patients, while arterial spin labeling could be used to acquire perfusion data without the need of a contrast agent (Noguchi et al., 2008).

An additional limitation of the model is the approximation of the cells' dichotomy using the tumoral outer ring. The model's precision could benefit from the explicit description of the migratory phenotype of cells and their behavior (Tektonidis et al., 2011; Hatzikirou et al., 2012). In the model, however, the effect of the invasive potential of cancer cells was indirectly accounted for by varying the thickness of the tumoral outer ring. A direct description of the population of such cells, and employing equations from related studies (Altrock et al., 2015), could improve the accuracy and the specificity of the model.

Collectively, in this study we attempted to unite the bulk mechanical response of a tumor with the tumor's cellular environment in a realistic geometry. The formalism of the model is general and can account for additional cell types shown to affect tumor growth and therapy, such as different phenotypes of cancer cells, immune cells and macrophages (Mpekris et al., 2017). Ultimately, this study could prove to be a valuable tool, capable of describing realistically tumor growth and cell kinetics, with the ability to eventually assist towards a personalized treatment planning.

Appendix A. Supplementary data

Supplementary material