Abstract
Background:
Despite the recent advancements in the modeling of glycemic dynamics for type 1 diabetes mellitus, automatically considering unannounced meals and exercise without manual user inputs remains challenging.
Method:
An adaptive model identification technique that incorporates exercise information and estimates of the effects of unannounced meals obtained automatically without user input is proposed in this work. The effects of the unknown consumed carbohydrates are estimated using an individualized unscented Kalman filtering algorithm employing an augmented glucose-insulin dynamic model, and exercise information is acquired from noninvasive physiological measurements. The additional information on meals and exercise is incorporated with personalized estimates of plasma insulin concentration and glucose measurement data in an adaptive model identification algorithm.
Results:
The efficacy of the proposed personalized and adaptive modeling algorithm is demonstrated using clinical data involving closed-loop experiments of the artificial pancreas system, and the results demonstrate accurate glycemic modeling with the average root-mean-square error (mean absolute error) of 25.50 mg/dL (18.18 mg/dL) for six-step (30 minutes ahead) predictions.
Conclusions:
The approach presented is able to identify reliable time-varying individualized glucose-insulin models.
Keywords: modeling and identification, artificial pancreas, biomedical system, subspace methods, recursive identification, linear systems
Improved glycemic control in individuals with type 1 diabetes mellitus (T1DM) via the use of artificial pancreas (AP) systems, which integrate a continuous glucose monitoring (CGM) sensor, continuous subcutaneous insulin infusion (CSII) pump, and insulin dosing control algorithm, reduces the risks of immediate life-threatening conditions, such as severe hypoglycemia and ketoacidosis, and long-term health complications, such as cardiovascular disease, nephropathy, neuropathy, and retinopathy.1-13 A fully automated AP system eliminating the need for patients with T1DM to enter user inputs for meal and exercise announcements represents a substantial step toward achieving better insulin delivery systems. Although AP systems are shown to be effective compared to conventional multiple daily insulin injections or sensor augmented pump therapy, improvements in the insulin dosing algorithms are needed if the AP systems are to compensate for meals and exercise without requiring patients to manually interact with the systems. Model-based predictive control has emerged as an effective insulin dosing algorithm for AP systems as it inherently considers future projections of the glycemic dynamics for predictive hypo- and hyperglycemia alarms and manipulating insulin delivery when glucose concentrations are forecast to deviate from the desired outcomes. The ability of the predictive controllers is dependent on accurate models of the metabolic system that can effectively encode a comprehensive understanding of the physiology of T1DM, handle the long dynamical effects of the insulin action, and characterize the effects of various diurnal disturbances on glycemic dynamics. Furthermore, many mathematical models of the glucose and insulin dynamics employ real-time feedback solely from the CGM signal, which limits their ability to automatically accommodate meals and exercise without manual interventions by people with T1DM.
One of the challenges to achieve a fully automated and reliable AP is the lack of an accurate model to represent the dynamic changes in physiology under various conditions. The future glucose measurements are difficult to predict accurately as glycemic dynamics vary substantially due to the effects of numerous factors such as current and historical glucose trends, carbohydrate consumption, previously administered insulin, exercise or physical activity levels, and concentrations of certain hormones. Moreover, metabolic processes vary substantially among subjects and temporally within people due to the diversified lifestyles and erratic routines of individuals. The diversity of physiology and behaviors in people causes the glucose-insulin dynamics and insulin sensitivities of individuals to vary over time, while large perturbations such as meals and physical activity cause significant excursions in glucose concentrations that may not be described accurately by generalized models. Hence, the necessity in AP systems of personalized glucose-insulin models rather than models with generalized parameters that do not reflect the dynamic characteristics of subjects in different situations.14-19
The glycemic models proposed in literature can be categorized as either physiological or data-driven models, often with carbohydrate intake and infused insulin as inputs. Physiological models, usually based on compartmental models, consist of simultaneous differential equations describing the insulin and glucose metabolism with a number of physiological parameters to be identified. Detailed physiological models are very useful in simulations, though model complexity and computational load impede their real-time implementation in AP systems. In contrast to physiological models, data-driven models with relatively simpler structures that effectively characterize the intricate relationships among the measured variables generally require less computational effort.15 Among the various empirical modeling approaches proposed to predict future glycemic measurements, subspace-based system identification methods are capable of efficiently identifying linear state-space models from multi-input, multi-output sampled data of a dynamic system. Nevertheless, a fixed empirical model may not predict glycemic measurements well in all scenarios and across all subjects due to the significant variability in glycemic dynamics. Therefore, the empirical models need to be appropriately adapted on-line to characterize the current dynamics of the individuals and make accurate short-term predictions of glucose concentration measurements. For this purpose, adaptive system identification approaches are proposed to determine linear, time-varying models and effectively characterize the evolving glycemic dynamics, thus allowing the adaptive models to be valid over a diverse range of daily conditions.
Despite the predictive ability of the adaptive system identification approach, the discrete basal changes and acute bolus impulses present a challenging configuration for empirical modeling techniques. Further complicating the model identification procedure is the fact that administered insulin (basal or bolus) gradually accumulates in the bloodstream and is eventually utilized by the body. One of the factors that prolongs the utilization of administered insulin is the significant time delays involved in the diffusion and absorption of the subcutaneously injected insulin analogues. For instance, the plasma insulin response to subcutaneously infused fast-acting insulin has a time lag of approximately 15 minutes, peak effect at about 45-90 minutes, and an overall effective duration of 4-6 hours. The protracted effects of the administered insulin may cause glucose concentration measurements to continue rising in response to carbohydrate consumption even though sufficient insulin is already administered. Under such postprandial circumstances where insulin effects are not observed in CGM measurements for lengthy periods of time after insulin infusion, methods relying entirely on data-driven models may lead to inappropriate generalizations with regards to the effects of insulin. This well-recognized artifact of modeling glycemic measurements can be addressed by filtering the administered insulin dose into a newly constructed variable that readily accommodates the effects of previously administered insulin. It is well recognized that filtering the input variables has a significant effect on the predictive performance of the identified model. Although such schemes are shown to improve glycemic prediction accuracy, the filtering algorithms utilized, whether based on numerical signal processing techniques or derived from compartment models describing the underlying physiological phenomena, are often time-invariant. The application of fixed time-invariant filters thus may be suboptimal and may diminish the potential for improvement, especially when employed simultaneously with adaptive system identification techniques. Utilizing PIC estimates from an adaptive and personalized PIC estimator as the newly established input for the identification algorithm provides a filtered variable that improves prediction ability. In contrast to the conventional insulin on board approach that estimates the amount of active insulin in the body through static appropriations of action profiles and decay curves, the estimated PIC is a physically meaningful and quantifiable measure of insulin the bloodstream that may benefit control design as well. The estimated plasma insulin concentration (PIC) can be considered as a more appropriate input variable in the identification of a dynamic model for predicting future glucose concentrations because it directly quantifies the insulin in the bloodstream that affects the glycemic evolution.20-24
Besides the effects of administered insulin, another limitation of current AP systems is the requirement of manual meal and exercise announcements. Several studies have incorporated unannounced meals through the estimation of time-varying parameters or analysis of glucose trends.25-30 Concerning the automation of AP systems, additional physiological variables related to physical activity are also considered to automatically accommodate exercise.31-34 Despite this progress, automatically handling of unannounced meals and exercise in adaptive and personalized glycemic models for AP systems is not sufficiently studied.
Motivated by the above considerations, in this work, an adaptive and personalized compartment model that translates the abrupt bolus and discrete basal changes into estimates of PIC is integrated with an adaptive system identification approach to characterize the transient dynamics of glycemic measurements. The adaptations by the recursive system identification assist in handling stochastic disturbances like the effects of meal consumption and physical activities. Furthermore, the system identification algorithm is extended to improve reliability for use in fully automated artificial pancreas systems. The proposed approach involves the modification of the recursive predictor-based subspace identification (PBSID) algorithm to incorporate constraints on the fidelity and accuracy of the identified models, correctness of the sign of the input-to-output gains, and the integration of heuristics to ensure the stability of the recursively identified models. To achieve this, the proposed adaptive models also include estimated meal effects and the reported exercise related biometric variables by BodyMedia SenseWear armband as additional inputs to automatically accommodate unannounced meals and exercise. The proposed adaptive and personalized modeling approach considering the effects of unannounced meals and exercise on the transient glycemic dynamics is applied to 15 clinical data sets involving closed-loop experiments of the AP systems.
Methods
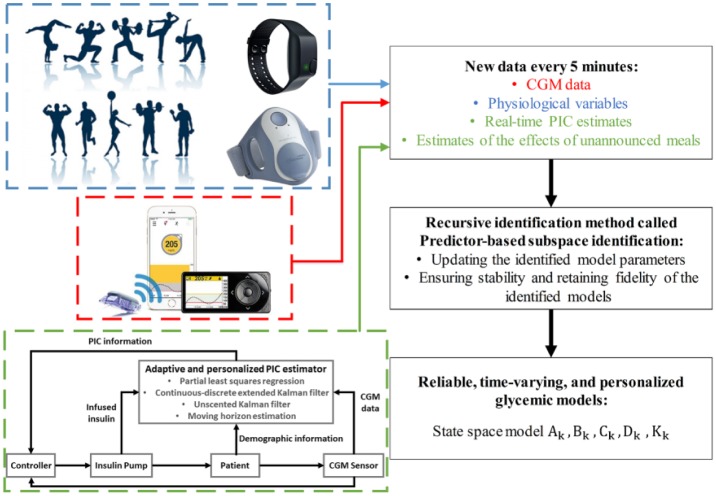
The predictor-based subspace identification (PBSID) approach is used to identify a recursively updated state-space model characterizing the glucose-insulin dynamics. The PBSID algorithm estimates a vector autoregressive with exogenous inputs model and uses it to construct matrices related to the state-space model parameters. A low-rank approximation then identifies a state sequence, and the state-space model parameters are recursively updated. The PBSID technique is further extended to provide stable, time-varying, and individualized models for glycemic predictions by using estimates of PIC and meal effects, and measured physiological signals. The estimates of PIC and meal effects are obtained by-using an adaptive and personalized PIC estimator designed based on the Hovorka’s glucose-insulin dynamic model. In this section, a review of the PBSID algorithm for the identification of linear, time-varying state-space models is provided, followed by a brief overview of the adaptive and personalized PIC estimator. Figure 1 shows a flowchart of the proposed personalized and adaptive modeling algorithm.
Figure 1.
Flowchart of the proposed personalized and adaptive modeling algorithm.
Adaptive Modeling Approach
In this work, a recursive subspace-based system identification approach is used to build linear, time-varying state-space models of the form:
| (1) |
where , and denote vectors of the state, input, and output variables, respectively, with and denoting the vectors of process disturbance and measurement noise (respectively) that are assumed to be zero-mean white Gaussian sequences. The input variables considered are the insulin concentration in the bloodstream, energy expenditure, and the estimated meal effects, and the output variable is the CGM measurement. The system matrices and are the state transition, input, output, and direct feedthrough matrices of appropriate dimensions (respectively) that are adaptively estimated at each sampling instance using subspace identification techniques. A detailed description of the proposed technique is provided in Appendix A, as well as in Hajizadeh et al14 and Houtzager et al.35 The identification procedure employs constraints on the estimated model coefficient matrices to ensure that the appropriate gains are determined relating the insulin to the glucose outputs. In another consideration of the fidelity of the identified models, constraints are also imposed to restrict the identified model to be stable. Consider the system matrices to constrain for fidelity and stability of the identification. Then the constrained optimization problem becomes
| (2) |
where a weighted quadratic norm of the deviation of the predicted CGM outputs is penalized from the actual CGM measurements while ensuring that the estimated model coefficients satisfy the imposed constraints for model fidelity and stability purposes. The constrained optimization problems are solved using the computationally efficient quadratic programming solver, which seeks to minimize a scalar function in multiple variables within a region specified by constraints and bounds. A detailed description of the proposed technique is provided in Appendices B and C.
One modification compared to traditional glycemic models is the use of PIC as an input to the system identification procedure. The insulin present in the bloodstream is derived from the insulin subsystem of Hovorka’s model, which translates the abrupt basal and discrete bolus inputs into PIC estimates with time-varying model parameters simultaneously estimated using a nonlinear observer.36,37 The observer is of the form
where denotes the estimated state vector, with PIC an estimated state variable, is the infused (basal and bolus) insulin, is the CGM measurements providing feedback correction for the estimation of states and parameters, and are the model parameters that are estimated simultaneously with the state variables to characterize the time-varying physiological processes of people. The estimated parameters of Hovorka’s model include the time to maximum insulin absorption (), the fractional elimination rate of insulin from the bloodstream (), and the gut absorption rate () representing the rate of appearance of glucose in the blood from consumed meals. The on-line estimation of the insulin compartment parameters characterizes the transient pharmacodynamics of subcutaneously administered insulin. The estimation of the glucose appearance rate allows for quantification of the effects of unannounced meals on the glycemic dynamics without requiring user specified information on the amounts of carbohydrates consumed. The easily attainable demographic information of subjects, such as weight, height, BMI, age, total daily insulin and duration with T1DM, is exploited to personalize the initialization of the PIC estimator. To this end, the readily available demographic information is used to identify a relationship between the demographic variables and the model parameters to be individually initialized to each patient. Data-driven approaches, such as partial least squares (PLS) regression models, are widely used when the exact underlying mathematical relationship between two sets of data, demographic inputs and the output parameters, is not explicitly and mathematically formalized through fundamental physiological models. PLS is a multivariate regression method for modeling the relationship between two groups of data consisting of numerous noisy and correlated variables while appropriately handling potentially incomplete measurements with missing data. The PLS based regression relationship is derived from data collected from several experiments. The latent variables of the PLS model are identified to maximize the prediction performance of the model. This is achieved by finding components that maximize the covariance between the independent and the dependent variables. The independent variables matrix consists of the demographic information of the patients, such as bodyweight, height, BMI, total daily insulin dose, and the dependent variables matrix is defined to be the parameters of the PIC estimator that were determined for each patient using actual clinical experimental PIC measurements. Following the initialization of the parameter values using the PLS regression models, the proposed estimation technique can rapidly converge to provide good estimates of the PIC in a timely manner by using only the CGM measurements and infused insulin data. A detailed description of the proposed technique is provided in Appendix D, as well as in Hajizadeh et al.22-24
| (3) |
Subjects and Clinical Study Experiments
The subjects involved in this study were recruited by the Kovler Diabetes Center, University of Chicago Medical Center, Chicago, Illinois, and were scheduled for a visit at the University of Chicago General Clinical Research Center. The subjects included adults 19-39 years with T1DM. All subjects used CSII pump therapy by adjusting the insulin infusion flow rate based on suggestions from a generalized predictive controller.6,30,31,38 Subjects wore their personal insulin pump, a continuous glucose monitor (CGM; Medtronic Guardian-Real Time Continuous Glucose Monitors [Medtronic, Northridge, CA] or Dexcom G4 Platinum [Dexcom, San Diego, CA]) and a BodyMedia SenseWear Pro3 (BodyMedia, Pittsburgh, PA) armband reporting physiological signals. Each patient’s visit was approximately 60 hours long during the closed-loop experiment using a multimodule multivariable adaptive artificial pancreas system.24,29,39-42 The subjects’ own insulin type and pumps were used during the experiments. Subjects participated in two exercise bouts of 20- to 30-minute sessions before and after lunch. Overall 10 subjects participated in the 15 clinical closed-loop experiments. Table 1 shows the characteristics of the participants of the closed-loop studies.
Table 1.
Demographic Information of the Clinical Subjects.
| Demographic criteria | Mean ± standard deviation |
|---|---|
| Age (years) | 26.13 ± 5.76 |
| Body weight (kg) | 79.29 ± 15.40 |
| Height (m) | 1.73 ± 0.08 |
| Body mass index (kg/m2) | 26.33 ± 4.18 |
| Total daily insulin dose [basal] (U) | 45.75 [26.79] ± 12.73 [11.66] |
| Duration of time with diabetes (years) | 18.30 ± 8.10 |
| Waist (cm) | 90.72 ± 13.57 |
Results
The efficacy of the proposed adaptive system identification algorithm for identifying high fidelity glycemic models is demonstrated using 15 clinical datasets. The output of the model is the predicted CGM measurements and the inputs are the estimates of the PIC, meal effect (), and energy expenditure values in units of metabolic equivalents (MET). The two performance indices used to evaluate the performance of the proposed method are the mean absolute error (MAE) and root mean square error (RMSE).
The MAE and RMSE are calculated based on the following equations:
| (4) |
| (5) |
The MAE and RMSE are two of the most common metrics used to measure the prediction accuracy. MAE measures the average magnitude of the errors in a set of predictions, without considering their direction. It’s the average over all samples of the absolute differences between prediction and actual observation where all individual differences have equal weight. RMSE is a quadratic scoring rule that also measures the average magnitude of the error. It is the square root of the average of squared differences between prediction and actual observation. Both the MAE and RMSE express average model prediction error in units of the variable of interest. Both metrics can range from 0 to ∞ and are indifferent to the direction of errors. They are negatively oriented scores, which means lower values are better. Taking the square root of the average squared errors has some interesting implications for the RMSE. Since the errors are squared before they are averaged, the RMSE gives a relatively high weight to large errors. This means the RMSE should be more useful when large errors are particularly undesirable.
The quantitative results for all 15 clinical experiments are presented in Tables 2 and 3. These performance indices are computed based on one- and six-step-ahead predictions. The one- and six-step-ahead prediction are used to show the performance of the proposed technique in predicting the future outputs. The average RMSE (MAE) for one- and six-step-ahead CGM prediction are 4.93 (3.17) and 25.50 mg/dL (18.18 mg/dL), respectively. The RMSE (MAE) values for the one-step-ahead predicted CGM are less than 8.44 mg/dL (4.25 mg/dl), and for the six-step-ahead predicted CGM is less than 32.96 mg/dL (22.02 mg/dL), which demonstrates the effective performance of the adaptive system identification technique to model the glycemic dynamics.
Table 2.
Performance Indices Values for the Modeling Results Using the Proposed Personalized and Adaptive Modeling Algorithm for All Clinical Experiments Based on the One-Step-Ahead Prediction.
| No. | MAE (mg/dL) | RMSE (mg/dL) | Median (mg/dL) | First quartile (mg/dL) | Third quartile (mg/dL) |
|---|---|---|---|---|---|
| 1 | 3.16 | 4.50 | 1.96 | 0.83 | 3.80 |
| 2 | 2.86 | 3.80 | 2.66 | 1.28 | 4.24 |
| 3 | 3.22 | 5.78 | 1.66 | 0.62 | 3.67 |
| 4 | 3.91 | 5.22 | 3.03 | 1.48 | 5.65 |
| 5 | 2.97 | 4.15 | 2.02 | 0.93 | 3.65 |
| 6 | 2.56 | 4.10 | 1.86 | 0.78 | 3.49 |
| 7 | 2.90 | 4.50 | 2.03 | 0.89 | 3.45 |
| 8 | 3.16 | 4.27 | 2.58 | 1.15 | 4.67 |
| 9 | 2.71 | 4.29 | 1.72 | 0.80 | 3.50 |
| 10 | 3.79 | 6.58 | 2.37 | 1.05 | 4.37 |
| 11 | 3.89 | 5.79 | 2.61 | 1.19 | 5.02 |
| 12 | 2.88 | 4.84 | 1.85 | 0.72 | 3.57 |
| 13 | 2.29 | 3.30 | 1.61 | 0.67 | 3.15 |
| 14 | 4.25 | 8.44 | 2.50 | 1.21 | 4.48 |
| 15 | 3.06 | 4.45 | 2.13 | 0.97 | 4.25 |
| Avg | 3.17 | 4.93 | 2.17 | 0.97 | 4.07 |
Table 3.
Performance Indices Values for the Modeling Results Using the Proposed Personalized and Adaptive Modeling Algorithm for all Clinical Experiments Based on the Six-Step-Ahead Prediction.
| No. | MAE (mg/dL) | RMSE (mg/dL) | Median (mg/dL) | First quartile (mg/dL) | Third quartile (mg/dL) |
|---|---|---|---|---|---|
| 1 | 18.28 | 26.01 | 10.47 | 4.80 | 24.86 |
| 2 | 16.45 | 20.45 | 14.23 | 8.44 | 22.47 |
| 3 | 17.31 | 25.94 | 10.58 | 4.13 | 21.85 |
| 4 | 21.45 | 27.29 | 16.28 | 7.30 | 30.03 |
| 5 | 21.66 | 30.26 | 13.90 | 5.76 | 27.60 |
| 6 | 16.12 | 21.91 | 11.70 | 5.80 | 22.53 |
| 7 | 17.71 | 25.22 | 11.56 | 5.21 | 24.62 |
| 8 | 18.36 | 24.80 | 13.54 | 6.59 | 24.77 |
| 9 | 17.51 | 26.92 | 10.65 | 4.45 | 22.27 |
| 10 | 19.35 | 27.09 | 13.95 | 7.18 | 24.56 |
| 11 | 19.08 | 25.11 | 14.08 | 6.84 | 26.71 |
| 12 | 16.82 | 25.43 | 9.89 | 4.77 | 18.93 |
| 13 | 14.71 | 20.96 | 10.00 | 4.65 | 19.32 |
| 14 | 22.02 | 32.96 | 14.87 | 6.69 | 27.15 |
| 15 | 15.89 | 22.13 | 9.95 | 4.73 | 19.74 |
| Avg | 18.18 | 25.50 | 12.38 | 5.82 | 23.83 |
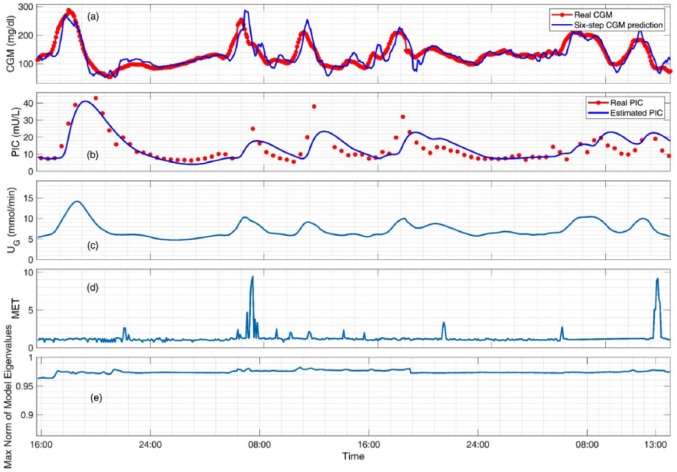
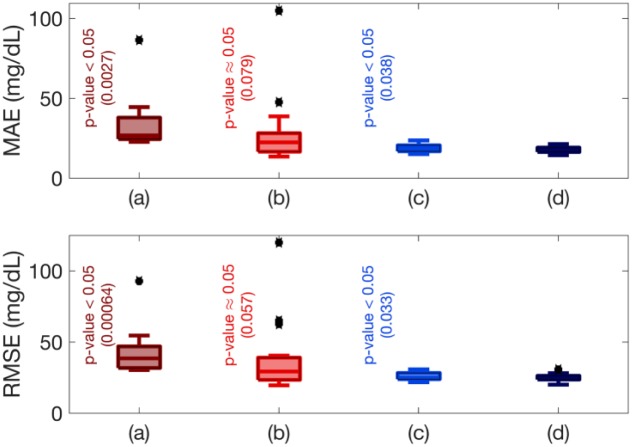
The proposed adaptive system identification method is able to provide stable and adaptive state-space models at each sampling time. Figure 2 shows the predicted and actual CGM values along with the inputs of the model (the estimates of the PIC and meal effect parameter, and the energy expenditure values) and maximum norm of model eigenvalues for a selected experiment. The results for the clinical experiments (Figure 2) show that the maximum norm of eigenvalues of the models is maintained within the unit circle and evolve over time to best describe the available input and output data, thus ensuring stability of the identified models. Furthermore, the estimated and predicted CGM values closely track the actual CGM measurements. The state-space model is identified such that the available input-output data is well characterized by the system realization while the stability and fidelity of the identified models is guaranteed. Compared to only using the PIC as a model input, additional inputs capturing the effects of meals and physical activity, such as the estimated meal effect parameter and energy expenditure, significantly improve the prediction ability of the modeling approach (Figure 3). Although the model using PIC and meal effect as inputs does not show statistical significance compared to the proposed model using PIC, meal effect and energy expenditures as input variables, the standard deviation is biased by the outliers, which influences the statistical hypothesis test. To elucidate this bias caused by the outliers, a one-sided test for statistical significance is used to compare the model (b) with the proposed model (d), which shows statistical significance (P value = 0.04 for MAE and 0.029 for RMSE). The results demonstrate that the use of the PIC as a filtered insulin input, the incorporation of estimates of the meal effect obtained through the nonlinear observer algorithm, and the inclusion of energy expenditure as an auxiliary input from the BodyMedia SenseWear armband improve the identified glucose-insulin dynamic models.
Figure 2.
Modeling results for a select experiment (subject 7) showing (a) the six-step (30 minutes ahead) predicted and actual CGM values, (b) the estimated plasma insulin concentration and actual PIC values (not used in model development), (c) the estimated meal effect parameter for capturing unannounced meals, (d) the energy expenditure in units of metabolic equivalent (MET) for incorporating unannounced exercise, and (e) the maximum norm of eigenvalues of the stable time-varying identified models.
Figure 3.
Comparison of six-step (30 minutes ahead) prediction accuracies across all experiments using the mean absolute error (MAE) and root mean square error (RMSE) for prediction with different model inputs: (a) PIC; (b) PIC and energy expenditure; (c) PIC and meal effect; and (d) PIC, energy expenditure, and meal effect. All hypothesis tests computed using two-sided paired t-tests at 5% significance level and are relative to the proposed model (d), which considers PIC, energy expenditure, and meal effect as input variables.
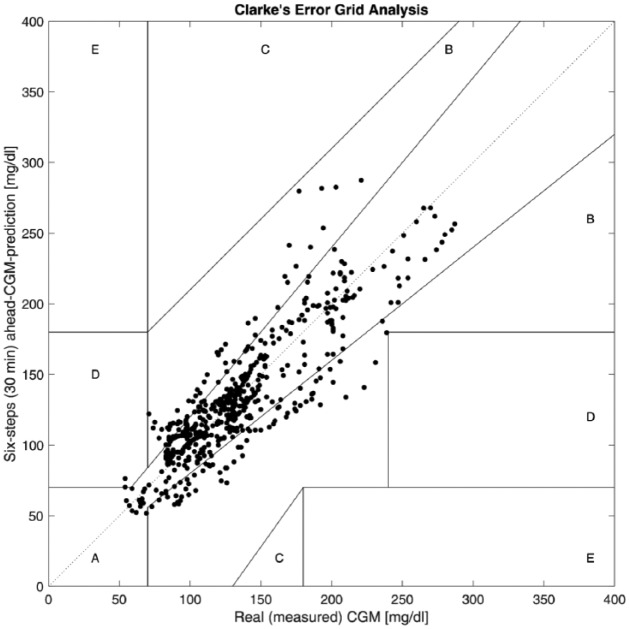
The Clarke error grid approach is used to assess the clinical significance of differences between glucose predictions generated by the proposed technique and measured values.43-46 The method uses a Cartesian diagram, in which the six-step-ahead CGM predictions obtained by the presented technique are displayed on the y-axis, whereas the real (measured) CGM values are displayed on the x-axis. The diagonal represents the perfect agreement between the two, whereas the points below and above the line indicate, respectively, overestimation and underestimation of the actual values. Zone A (acceptable) represents the glucose values that deviate from the real values by ±20% or are in the hypoglycemic range (<70 mg/dl), when the reference is also within the hypoglycemic range. The values within this range are clinically exact and are thus characterized by correct clinical treatment. Zone B (benign errors) is located above and below zone A; this zone represents those values that deviate from the reference values, which are incremented by 20%. The values that fall within zones A and B are clinically acceptable, whereas the values included in areas C-E are potentially dangerous, and there is a possibility of making clinically significant mistakes. Based on the results presented in the Table 4, we can see that 98.87% of values fall within zones A and B. There is no cases fall within zone E that is the most dangerous case and just 1.13% of values fall within zones C and D. Figure 4 shows of the Clarke error grid analysis for a select experiment (subject 7).
Table 4.
Percentages in Each Zone Based on Clarke Error Grid Analysis for the Modeling Results Using the Proposed Personalized and Adaptive Modeling Algorithm for All Clinical Experiments Based on the Six-Step-Ahead Prediction.
| No. | A | B | C | D | E |
|---|---|---|---|---|---|
| 1 | 77.30 | 21.44 | 0.00 | 1.26 | 0.00 |
| 2 | 79.67 | 19.42 | 0.91 | 0.00 | 0.00 |
| 3 | 85.43 | 14.37 | 0.20 | 0.00 | 0.00 |
| 4 | 66.48 | 31.25 | 0.00 | 2.27 | 0.00 |
| 5 | 77.08 | 21.48 | 0.18 | 1.26 | 0.00 |
| 6 | 78.46 | 21.18 | 0.00 | 0.36 | 0.00 |
| 7 | 82.64 | 17.15 | 0.00 | 0.21 | 0.00 |
| 8 | 77.84 | 21.26 | 0.00 | 0.90 | 0.00 |
| 9 | 88.60 | 10.40 | 0.00 | 1.00 | 0.00 |
| 10 | 76.65 | 22.37 | 0.19 | 0.78 | 0.00 |
| 11 | 70.48 | 27.24 | 0.19 | 2.10 | 0.00 |
| 12 | 83.62 | 16.19 | 0.00 | 0.19 | 0.00 |
| 13 | 81.95 | 17.13 | 0.00 | 0.92 | 0.00 |
| 14 | 76.04 | 21.80 | 0.90 | 1.26 | 0.00 |
| 15 | 78.87 | 19.25 | 0.00 | 1.89 | 0.00 |
| Avg | 78.74 | 20.13 | 0.17 | 0.96 | 0.00 |
Figure 4.
Figure of the Clarke error grid analysis for a select experiment.
In addition to the MAE and RMSE performance indices and Clarke error grid analysis, the low risk of missing hypoglycemia (below 70 mg/dL) or hyperglycemia (above 200 mg/dL) is a key feature of an efficient and reliable identified glucose-insulin dynamic model. We have also calculated the results for the percentage of the cases which the hypoglycemia or hyperglycemia are missed. Nine out of 15 experiments have CGM values below 70 mg/dl, and the average and standard deviation of missed hypoglycemia for these 9 experiments are 24.09% ± 16.50%. Thirteen out of 15 experiments have CGM values above 200 mg/dl, and the average and standard deviation of missed hyperglycemia for these 13 experiments are 07.83% ± 05.29%.
Discussion
A physiological model derived from the insulin compartment subsystem of Hovorka’s model is incorporated in this work with adaptive data-driven models developed using a recursive subspace identification technique. A computationally efficient nonlinear observer is used to estimate the time-varying parameters and the meal effect, thus facilitating the explicit incorporation of unannounced meals. The results for the proposed integrated compartment model with adaptive subspace identification techniques are promising. The proposed adaptive models may be used in the design of a model-based predictive control algorithm.
There are several benefits to the integration of compartment models with adaptive models. First, the PIC estimates are adaptive and individualized to particular patients, thus providing accurate real-time estimates of the amount of active insulin present in the bloodstream. The plasma insulin information can be readily used to impose constraints on the insulin dosing computation algorithm. Second, in contrast to the discrete basal and acute bolus insulin variations, the estimated PIC from the compartment model readily provides a more appropriate and filtered input variable for model identification. Third, the adaptive subspace identification technique renders the recursively identified glycemic models valid over a diverse range of daily activities without requiring onerous and obscure information such as the amount of carbohydrate consumption or quantification of physical activity levels.
Although meal and exercise announcements may improve the prediction ability of the proposed approach, unannounced meals and exercise are considered in this work to refrain from the inconvenience of user inputs and avoid the potential hazards of erroneous entries. The proposed adaptive modeling approach with an integrated compartment model utilizes additional auxiliary input variables such as the energy expenditure bio-signals to consider the effects of physical activity on glycemic dynamics.
Any insulin model capable to translate the abrupt bolus and discrete basal changes into estimates of PIC can be used. In this work, insulin subsystem of Hovorka’s model has been used since the PIC estimator is designed based on the Hovorka’s glucose-insulin dynamic model and we have developed personalization techniques based on the PLS models to individualize the parameters of this insulin subsystem for each specific patient.
PIC measurements are available from the clinical experiments, however, this information is not used in the development of the PIC estimation model and the on-line and real-time prediction of future CGM values. We use the clinical measurements of PIC to validate the estimates of the PIC obtained through the nonlinear simultaneous state and parameter estimation technique. As the PIC estimates are accurate, we employ the PIC estimates in the identification of adaptive state-space models. This ensures that only CGM measurements, infused insulin information, and physiological measurements from an nonintrusive wearable activity tracker are used in the on-line modeling and predictions of future glucose values.
For any data-driven modeling approaches where the model is obtained based only on input and output data measured form the underlying system, the quality and accuracy of the data play an important role on the performance of identified model. The time and frequency of calibrations have a significant effect on accuracy of the CGM measurements and consequently on the predictions accuracy. Subjects calibrated the CGM at least twice each day according to manufacturer instructions. The participants used their personal glucometers, and the CGM calibration may have occurred in nonideal glucose trends. CGM accuracy is greatest when the CGM is calibrated during a stable glucose period (flat arrows on CGM), but this was not always the case when the subjects chose to calibrate.
The steady-state value of the gut appearance rate (UG) parameter should be zero during fasting time, provided all model parameters are personalized for each subject and the basal insulin rate stabilizes the BGC around a steady-state value. The purpose of considering the UG in the PIC estimator is to handle any unknown disturbances present in the system, including the effects of unannounced meals (such as main meals or fast-acting carbohydrates for treatment of hypoglycemia) or any other uncertainties in the model parameters (such as EGP0, and FR parameters). To design the PIC estimator, other than the two model parameters ( and ) that are individualized using the PLS models, the other parameters of Hovorka’s model are not personalized because personalization of all parameters requires sufficient data (more detailed information) on the subject’s glucose-insulin dynamics. Since the steady-state value of UG is a function of several factors including the parameters of Hovorka’s model, the steady state value of the UG can be a nonzero value even during fasting period.
The most challenging periods for the CGM predictions are the times that exercise and meal affect the glucose-insulin dynamics. Since, any information about these unknown disturbances such as their time, intensity, amount and duration are not known in advance, the accuracy of multistep-ahead predictions that is just based on current and past data decreases during these periods until the model parameters are updated based on measurements in those specific periods. One of the reasons that a recursively updated model is necessary for a fully automated artificial pancreas system (unannounced meal and exercise) is to update the model parameters at each sampling time using new measurements to adapt the model for that specific period. As shown in Figure 3, including the MET values and meal effects estimates improves the performance of the identified model for predicting the CGM values. In addition to analyzing the global error metrics, investigating the local error variabilities around the unannounced meals and exercises can be useful.
To design a fully automated artificial pancreas system that can operate without any user input, in addition to CGM data, information that could help the artificial pancreas control system to detect exercise and act properly for that period is needed. This information can be physical activity signals measured by wearable devices. To achieve this, different bio-signals have been used in artificial pancreas systems. The metabolic equivalent task (MET), or simply metabolic equivalent, is a physiological measure expressing the energy cost of physical activity (PA) and is defined as the ratio of metabolic rate (and therefore the rate of energy consumption) during a specific PA to a reference metabolic rate. MET is used as a means of expressing the intensity and energy expenditure of activities in a way that is comparable among people. We have developed a real-time MET estimation algorithm by using noninvasive measurements of physiological variables by our research group at Illinois Institute of Technology. In this approach, these MET values are derived using heart rate, galvanic skin response, skin temperature, blood volume pulse, and accelerometer.
The performance of proposed technique has been verified using different indices based on one-step-ahead predictions and six-step-ahead predictions. Different indices are considered to show the ability of the identified model in tracking the real measurements as well as predicting the future trend in CGM measurements. As we extend the prediction horizon, the accuracy of the predicted values decreases (as it can be seen from 1 step to 6 steps ahead of prediction) due to several reasons including unknown phenomena like exercise, stress or meal that may take place. So choosing the prediction horizon is a trade-off between knowing long-term information about the future measurements and their accuracy.
For few clinical experiments (e.g. No. 14 in Table 3) the relative high value of performance indices (MAE and RMSE values) is observed in comparison to the average values. The proposed technique is a data-driven technique and the quality of the measured data (eg, CGM and physiological variables that may be corrupted with noise and outliers) have a significant effect of the performance, as well as the fact that any information about the meal and exercises are not used. Predicting such abnormal measurements is very challenging and updating the glucose-insulin dynamic models using poor quality of data may result in bad performance in predicting the future trend of measurements.
One of the limitations of our clinical experiments is the exercise times are close to the meal times. Although people with type 1 diabetes usually consume carbohydrates before, during, and after exercise to avoid hypoglycemia and the proposed approach demonstrates that the effects of meals and exercise have well been captured by the modeling technique, in our future clinical work, the clinical experiments will be conducted to test the algorithm under different conditions such as. no meals very close to the exercise time.
Conclusion
An adaptive system identification algorithm is proposed to determine reliable dynamic glycemic models for use in AP systems. The proposed modifications to the recursive system identification algorithm assist in handling uncertain disturbances such as unannounced meals and exercise, stochastic measurement noise, and other adverse phenomena. The efficacy of the proposed approach is demonstrated using case studies involving the modeling of time-varying glucose-insulin dynamics in clinical experiments, and the results demonstrate the approach is able to identify reliable, time-varying, and personalized glycemic models.
Appendix A
Recursive System Identification Algorithm
The dynamics of the system can be described using a linear, time-varying state-space model of the form:
| (A1) |
where , and denote vectors of the state, input, and output variables, respectively, with and denoting the vectors of process disturbance and measurement noise (respectively) that are assumed to be zero-mean white Gaussian sequences. The system matrices and are the state transition, input, output, and direct feedthrough matrices of appropriate dimensions, respectively. Using Kalman filter theory, equation A1 can be reformulated to the innovation form:
| (A2) |
where denotes the predicted state vector, , and denotes the Kalman gain matrix. The feedback through the Kalman gain is capable of mitigating the effects of some disturbances and smoothing out the measurement noise.
The foundation of the recursive PBSID approach is the one-step-ahead vector autoregressive with exogenous inputs (VARX) model given by:
| (A3) |
where is the predicted output for sampling instance given the prior inputs and outputs for some horizon into the past.35 The VARX model parameters to be estimated are:
| (A4) |
The conventional approach for recursive implementation of the PBSID algorithm involves the use of adaptive filters, such as recursive least squares (RLS), that can efficiently estimate the VARX model parameters by tracking the dynamic changes in the data. Such an approach is effective as it assigns less weight to the older measurements that may no longer be representative of the current state of the system than the newer measurements.
The following briefly describes the PBSID algorithm for completeness. To obtain the state estimates, and hence a realization of the system matrices, the stacked vector of output measurement variables is defined with respect to the past window of length as , and the stacked vector of input variables is defined similarly. Recognizing that the predicted state is given by:
| (A5) |
where and denote the extended controllability matrices and , and assuming that the state transition matrix is nilpotent with degree , meaning that the contribution of the initial state is negligible for sufficiently large (that is, Ap≈ 0 for some sufficiently large ), the predicted state can be expressed as:
| (A6) |
Premultiplying the predicted state in equation A6 by the extended observability matrix gives:
| (A7) |
where the extended observability matrix is
| (A8) |
It is readily observed that the product of the matrices and can be constructed from the estimated VARX model coefficient matrices as:
| (A9) |
and
| (A10) |
where is the future window length. Therefore, after estimating the VARX coefficient matrices, the estimated coefficient matrices and can be used to determine all quantities on the right-hand side of equation A7, and a singular value decomposition (SVD) can be carried out to readily obtain a low-rank approximation of the state sequence. Nevertheless, updating the SVD factorization while maintaining a consistent basis is not straightforward.
To avoid the complications of repeatedly updating an SVD factorization in recursive identification, a selection matrix of appropriate dimensions can be determined at each sampling time such that the basis of the state estimation is consistent. Using the selection matrix, equation A7 can be reformulated as:
| (A11) |
where is a predefined weight matrix. The selection matrix can be recursively updated through the projection approximation subspace tracking (PAST) method.47 The estimated state sequence is then employed along with the inputs and measured outputs to estimate the system matrices and by solution of recursive least squares problems.
Appendix B
Ensuring Stability of Identified Models
A concern regarding the typical recursive identification algorithm is that stochastic disturbances and measurement noise may render the identified models unstable even though the underlying system in inherently stable. Although an optimization problem may find the most appropriate and stable system realization, the solution time may be prohibitive. In this work, the optimization problem is substituted with a simple algorithm that incorporates line search mechanism to reduce the innovation term in the RLS filter. The optimization problems to be solved at each sampling instance for determining the system matrices are:
| (B1) |
where and as well as
| (B2) |
where and The solutions to these optimization problems can be updated at each sampling time through recursive least squares filters. If the identified system becomes unstable, the innovation term is reduced by multiplication with a scalar as:
| (B3) |
where is successively reduced in a line search approach until is stable and is the error covariance matrix. Reducing the innovation term translates to discarding the new information, perhaps including disturbance or noise effects, that caused the identified system to become unstable. Note that without knowing the stochastic noise and disturbance characteristics, it is difficult to remove all the effects from the state transition matrix that cause the instability. Therefore, reducing the innovation term in the RLS algorithm until the identified system is stable provides a verifiable stable system realization for implementation.
Appendix C
Retaining Fidelity of Identified Models
The RLS filters can efficiently estimate the VARX model parameters employed in the PBSID algorithm by tracking the dynamic changes in the data. Nevertheless, measurement noise and unknown disturbances can cause inopportune overfitting and may lead to incorrect signs for the input-output gain terms, which is problematic as the controller designed using the inaccurate model may suggest wrong input actions. Although this undesired adverse effect can be reduced through larger forgetting factors that reduce sensitivity to noise and disturbances, the drawbacks of a sluggish response may be too onerous for certain applications. To overcome the adverse effects of the adaptive filters, the filtering approach is replaced with a constrained convex linear least squares optimization problem in this work. The problem of updating the VARX model parameters is then recast as finding the optimal parameters for the most recently available historical data over a past window as follows
| (C1) |
with the objective function
| (C2) |
where denotes the region of admissible VARX model parameter and is the array of (constrained) VARX model parameters, taking values in a nonempty convex set , and and denote the lower and upper bounds on the VARX model parameters. Incorporating constraints on the VARX model parameters ensures the sign of the gain relating the inputs to the outputs is correct in the identified state-space model, which improves the prediction ability. Note that the computational load of the optimization problem can be minimized through appropriate initialization by using the solution from the previous sampling time as an initial guess of the optimum solution.
Appendix D
Estimating and Incorporating Disturbance Variables
To estimate the unmeasured disturbances and incorporate the disturbance estimates in the system identification algorithm, the unscented Kalman filter (UKF) is used with a fundamental first-principles model. Hovorka’s model, a widely utilized physiological model for describing the insulin action and the glucose kinetics system, is used in this study for designing the UKF estimator.36,37 A brief description of Hovorka’s model is provided for completeness. The model consists of nine state variables and various differential equations that describe the glucose-insulin dynamics, the subsystem pertaining to the BGC dynamics, the subsystem concerning the subcutaneous insulin infusion, and the subsystem for the glucose transport from plasma to interstitial tissues. The BGC dynamics are described using a two-compartment model. The two state variables and denote the mass of glucose in the accessible and nonaccessible compartments, respectively. As precise information about the time and quantity of meals is difficult to ascertain, meal information is considered as an unknown disturbance characterized by the gut absorption rate, . To capture the meal intake, the time-varying gut absorption rate parameter in the dynamics of the state variable is determined by the PIC estimator to automatically quantify the effects of the consumed carbohydrates. Another two-compartment model, with state variables and , defines the absorption rate of subcutaneously administered insulin. The PIC, denoted , is represented by a first-order differential equation. The measure of insulin action on glucose kinetics is calculated through three variables: the influence on glucose transport and distribution ; the utilization and phosphorylation of glucose in adipose tissue ; and the endogenous glucose production in the liver . The relationship between BGC and subcutaneous glucose reported by CGM measurements is considered a first-order dynamic equation.
The glucose-insulin dynamic model can be written in the form
| (D1) |
where
denotes the vector of state variables, denotes the measurement function and as the subcutaneous glucose output measurement given by . As precise information about the time and quantity of meals is difficult to ascertain, meal information is considered as an unknown disturbance to be characterized by the gut absorption rate , which is included as an extended state in the model to capture the effect of meal intake.
The dynamics of the augmented system, after incorporating uncertainty in the dynamics of the system (referred to as process noise) and measurement noise in the discrete-time sampled outputs, can be expressed as
| (D2) |
where and represent the process and observation noise vectors, respectively, and denote the covariance and variance of the process and measurement noise, respectively, and denotes the augmented state vector including the uncertain model parameters to be simultaneously estimated.
In the UKF algorithm, the unscented transformation (UT) method is employed for calculating the statistics of a random variable that undergoes a nonlinear transformation such as the augmented Hovorka’s glucose-insulin dynamic model.
The UKF algorithm can handle the nonlinear dynamics of the glucose-insulin model, is robust to noise, and has the ability to compensate for deviations and converge to the true value of the augmented states through the Kalman-gain-based correction term added to the estimation. The UKF captures the statistical distribution characteristics of a nonlinear system through a series of sigma points and each point is associated with a corresponding weight The sigma points are propagated through the nonlinear system dynamics to yield the propagated states and the corresponding weighted average of the transformed points and the weighted covariance of the prior state estimates . Similarly propagating the sigma points through the measurement function yields the outputs and the associated weighted average . Furthermore, the covariance matrices and are obtained through the sigma points. The Kalman gain and posterior updates for the state estimate as well as the posterior error covariance matrix of the augmented state estimate are given by the standard Kalman update equations:
| (D3) |
| (D4) |
| (D5) |
Furthermore, the estimated vector of state variables can be augmented with disturbance variables or time-varying model parameters for simultaneous state and parameter estimation, provided that the augmented system is also observable. The estimated values are then considered as additional input variables in the recursive system identification approach to improve the prediction ability.
Footnotes
Abbreviations: AP, artificial pancreas; CGM, continuous glucose monitoring; CSII, continuous subcutaneous insulin infusion; MAE, mean absolute error; MET, metabolic equivalent task; PA, physical activity; PAST, projection approximation subspace tracking; PBSID, predictor-based subspace identification; PIC, plasma insulin concentration; PLS, partial least squares; RLS, recursive least squares; RMSE, root mean square error; SVD, singular value decomposition; T1DM, type 1 diabetes mellitus; UKF, unscented Kalman filter; UT, unscented transformation; VARX, vector autoregressive with exogenous inputs.
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Financial support by NIH with grants NIDDK DP3 DK101075-01 and DP3 DK101077-01 is gratefully acknowledged.
References
- 1. Thabit H, Tauschmann M, Allen JM, et al. Home use of an artificial beta cell in type 1 diabetes. N Engl J Med. 2015;373:2129-2140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Russell SJ, El-Khatib FH, Sinha M, et al. Outpatient glycemic control with a bionic pancreas in type 1 diabetes. N Engl J Med. 2014;371:313-325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Ly TT, Weinzimer SA, Maahs DM, et al. Automated hybrid closed-loop control with a proportional-integral-derivative based system in adolescents and adults with type 1 diabetes: individualizing settings for optimal performance. Pediatr Diabetes. 2017;18:348-355. [DOI] [PubMed] [Google Scholar]
- 4. Breton M, Farret A, Bruttomesso D, et al. Fully integrated artificial pancreas in type 1 diabetes. Diabetes. 2012;61:2230-2237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Sánchez-Peña R, Colmegna P, Grosembacher L, et al. Artificial pancreas: first clinical trials in Argentina. IFAC-PapersOnLine. 2017;50:7731-7736. [Google Scholar]
- 6. Turksoy K, Bayrak ES, Quinn L, Littlejohn E, Cinar A. Multivariable adaptive closed-loop control of an artificial pancreas without meal and activity announcement. Diabetes Technol Ther. 2013;15:386-400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Cameron FM, Ly TT, Buckingham BA, et al. Closed-loop control without meal announcement in type 1 diabetes. Diabetes Technol Ther. 2017;19:527-532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Pinsker JE, Lee JB, Dassau E, et al. Randomized crossover comparison of personalized MPC and PID control algorithms for the artificial pancreas. Diabetes Care. 2016;39:1135-1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Forlenza GP, Deshpande S, Ly TT, et al. Application of zone model predictive control artificial pancreas during extended use of infusion set and sensor: a randomized crossover-controlled home-use trial. Diabetes Care. 2017;40:1096-1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Garg SK, Weinzimer SA, Tamborlane WV, et al. Glucose outcomes with the in-home use of a hybrid closed-loop insulin delivery system in adolescents and adults with type 1 diabetes. Diabetes Technol Ther. 2017;19:155-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Haidar A, Legault L, Messier V, Mitre TM, Leroux C, Rabasa-Lhoret R. Comparison of dual-hormone artificial pancreas, single-hormone artificial pancreas, and conventional insulin pump therapy for glycaemic control in patients with type 1 diabetes: an open-label randomised controlled crossover trial. Lancet Diabetes Endocrinol. 2015;3:17-26. [DOI] [PubMed] [Google Scholar]
- 12. Messori M, Kropff J, Del Favero S, et al. Individually adaptive artificial pancreas in subjects with type 1 diabetes: a one-month proof-of-concept trial in free-living conditions. Diabetes Technol Ther. 2017;19:560-571. [Google Scholar]
- 13. Rossetti P, Quiros C, Moscardo V, et al. Closed-loop control of postprandial glycemia using an insulin-on-board limitation through continuous action on glucose target. Diabetes Technol Ther. 2017;19:355-362. [DOI] [PubMed] [Google Scholar]
- 14. Hajizadeh I, Rashid M, Turksoy K, et al. Multivariable recursive subspace identification with application to artificial pancreas systems. IFAC-PapersOnLine. 2017;50:886-891. [Google Scholar]
- 15. Oviedo S, Vehí J, Calm R, Armengol J. A review of personalized blood glucose prediction strategies for T1DM patients. Int J Numer Methods Biomed Eng. 2017;33. doi: 10.1002/cnm.2833. [DOI] [PubMed] [Google Scholar]
- 16. Xie J, Wang Q. A nonlinear data-driven model of glucose dynamics accounting for physical activity for type 1 diabetes: an in silico study. ASME 2016 Dyn Syst Control Conf 2016;V001T09A002-V001T09A002. [Google Scholar]
- 17. Boiroux D, Hagdrup M, Mahmoudi Z, Poulsen NK, Madsen H, Jørgensen JB. Model identification using continuous glucose monitoring data for type 1 diabetes. IFAC-PapersOnLine. 2016;49:759-764. [Google Scholar]
- 18. Messori M, Toffanin C, Del Favero S, De Nicolao G, Cobelli C, Magni L. Model individualization for artificial pancreas [published online ahead of print July 5, 2016]. Comput Methods Programs Biomed. doi: 10.1016/j.cmpb.2016.06.006. [DOI] [PubMed] [Google Scholar]
- 19. Toffanin C, Favero S, Del, Aiello EM, Messori M, Cobelli C, Magni L. Glucose-insulin model identified in free-living conditions for hypoglycaemia prevention. J Process Control. 2018;64:27-36. [Google Scholar]
- 20. Hajizadeh I, Rashid M, Cinar A. Ensuring stability and fidelity of recursively identified control-relevant models. Paper presented at: 18th IFAC Symposium on System Identification; 2018; Stockholm, Sweden. [Google Scholar]
- 21. Hajizadeh I, Rashid M, Cinar A. Integrating compartment models with recursive system identification. Paper presented at: American Control Conference; 2018; Milwaukee, WI. [Google Scholar]
- 22. Hajizadeh I, Rashid M, Turksoy K, et al. Plasma insulin estimation in people with type 1 diabetes mellitus. Ind Eng Chem Res. 2017;56:9846-9857. [Google Scholar]
- 23. Hajizadeh I, Turksoy K, Cengiz E, Cinar A. Real-time estimation of plasma insulin concentration using continuous subcutaneous glucose measurements in people with type 1 diabetes. Paper presented at: American Control Conference; 2017; Seattle, WA. [Google Scholar]
- 24. Hajizadeh I, Rashid M, Samadi S, et al. Adaptive and personalized plasma insulin concentration estimation for artificial pancreas systems. J Diabetes Sci Technol. 2018;12:639-649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Colmegna P, Garelli F, De Battista H, Sánchez-Peña R. Automatic regulatory control in type 1 diabetes without carbohydrate counting. Control Eng Pr. 2018;74. [Google Scholar]
- 26. Ramkissoon C, Herrero P, Bondia J, Vehi J. Unannounced meals in the artificial pancreas: detection using continuous glucose monitoring. Sensors. 2018;18:884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Turksoy K, Samadi S, Feng J, Littlejohn E, Quinn L, Cinar A. Meal detection in patients with type 1 diabetes: a new module for the multivariable adaptive artificial pancreas control system. IEEE J Biomed Heal Inform. 2016;20:47-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Samadi S, Rashid M, Turksoy K, et al. Automatic detection and estimation of unannounced meals for multivariable artificial pancreas system. Diabetes Technol Ther. 2018;20:dia.2017.0364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Samadi S, Turksoy K, Hajizadeh I, Feng J, Sevil M, Cinar A. Meal detection and carbohydrate estimation using continuous glucose sensor data. IEEE J Biomed Heal Inform. 2017;21:619-627. [DOI] [PubMed] [Google Scholar]
- 30. Turksoy K, Hajizadeh I, Samadi S, et al. Real-time insulin bolusing for unannounced meals with artificial pancreas. Control Eng Pr. 2017;59:159-164. [Google Scholar]
- 31. Turksoy K, Quinn LT, Littlejohn E, Cinar A. An integrated multivariable artificial pancreas control system. J Diabetes Sci Technol. 2014;8:498-507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Jacobs PG, El Youssef J, Reddy R, et al. Randomized trial of a dual-hormone artificial pancreas with dosing adjustment during exercise compared with no adjustment and sensor-augmented pump therapy. Diabetes Obes Metab. 2016;18:1110-1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Beneyto A, Vehi J. Closed-loop blood glucose control using insulin and carbohydrates in front meals and exercise. IFAC-PapersOnLine. 2017;50:2058-2063. [Google Scholar]
- 34. DeBoer MD, Cherñavvsky DR, Topchyan K, Kovatchev BP, Francis GL, Breton MD. Heart rate informed artificial pancreas system enhances glycemic control during exercise in adolescents with T1D. Pediatr Diabetes. 2017;18:540-546. [DOI] [PubMed] [Google Scholar]
- 35. Houtzager I, van Wingerden J-W, Verhaegen M. Recursive predictor-based subspace identification with application to the real-time closed-loop tracking of flutter. IEEE Trans Control Syst Technol. 2012;20:934-949. [Google Scholar]
- 36. Kolås S, Foss BA, Schei TS. Constrained nonlinear state estimation based on the UKF approach. Comput Chem Eng. 2009;33:1386-1401. [Google Scholar]
- 37. Hovorka R, Canonico V, Chassin LJ, et al. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol Meas. 2004;25:905-920. [DOI] [PubMed] [Google Scholar]
- 38. Turksoy K, Quinn L, Littlejohn E, Cinar A. Multivariable adaptive identification and control for artificial pancreas systems. IEEE Trans Biomed Eng. 2014;61:883-891. [DOI] [PubMed] [Google Scholar]
- 39. Feng J, Turksoy K, Samadi S, Hajizadeh I, Littlejohn E, Cinar A. Hybrid online sensor error detection and functional redundancy for systems with time-varying parameters. J Process Control. 2017;60:115-127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Cinar A, Turksoy K, Hajizadeh I. Multivariable artificial pancreas method and system. US Patent App. 15/171,355, 2016. [Google Scholar]
- 41. Feng J, Hajizadeh I, Yu X, et al. Multi-level supervision and modification of artificial pancreas control system. Comput Chem Eng. 2018;112:57-69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Turksoy K, Kilkus J, Hajizadeh I, et al. Hypoglycemia detection and carbohydrate suggestion in an artificial pancreas. J Diabetes Sci Technol. 2016;10:1236-1244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Guevara E, González FJ. Joint optical-electrical technique for noninvasive glucose monitoring. Rev Mex Fis. 2010;56:430-434. [Google Scholar]
- 44. Kovatchev BP, Gonder-Frederick LA, Cox DJ, Clarke WL. Evaluating the accuracy of continuous glucose-monitoring sensors: continuous glucose-error grid analysis illustrated by TheraSense Freestyle Navigator data. Diabetes Care. 2004;27:1922-1928. [DOI] [PubMed] [Google Scholar]
- 45. Maran A, Crepaldi C, Tiengo A, et al. Continuous subcutaneous glucose monitoring in diabetic patients: a multicenter analysis. Diabetes Care. 2002;25:347-352. [DOI] [PubMed] [Google Scholar]
- 46. Guevara E, González FJ. Prediction of glucose concentration by impedance phase measurements. AIP Conf Proc. 2008;1032:259-261. [Google Scholar]
- 47. Chiuso A. The role of vector autoregressive modeling in predictor-based subspace identification. Automatica. 2007;43:1034-1048. [Google Scholar]