Identifiability Analysis of Three Control-Oriented Models for Use in Artificial Pancreas Systems

Abstract

Objective:

Our aim is to analyze the identifiability of three commonly used control-oriented models for glucose control in patients with type 1 diabetes (T1D).

Methods:

Structural and practical identifiability analysis were performed on three published control-oriented models for glucose control in patients with type 1 diabetes (T1D): the subcutaneous oral glucose minimal model (SOGMM), the intensive control insulin-nutrition-glucose (ICING) model, and the minimal model control-oriented (MMC). Structural identifiability was addressed with a combination of the generating series (GS) approach and identifiability tableaus whereas practical identifiability was studied by means of (1) global ranking of parameters via sensitivity analysis together with the Latin hypercube sampling method (LHS) and (2) collinearity analysis among parameters. For practical identifiability and model identification, continuous glucose monitor (CGM), insulin pump, and meal records were selected from a set of patients (n = 5) on continuous subcutaneous insulin infusion (CSII) that underwent a clinical trial in an outpatient setting. The performance of the identified models was analyzed by means of the root mean square (RMS) criterion.

Results:

A reliable set of identifiable parameters was found for every studied model after analyzing the possible identifiability issues of the original parameter sets. According to an importance factor (${\mathrm{\delta }}^{msqr}$), it was shown that insulin sensitivity is not the most influential parameter from the dynamical point of view, that is, is not the parameter impacting the outputs the most of the three models, contrary to what is assumed in the literature. For the test data, the models demonstrated similar performance with most RMS values around 20 mg/dl (min: 15.64 mg/dl, max: 51.32 mg/dl). However, MMC failed to identify the model for patient 4. Also, considering the three models, the MMC model showed the higher parameter variability when reidentified every 6 hours.

Conclusion:

This study shows that both structural and practical identifiability analysis need to be considered prior to the model identification/individualization in patients with T1D. It was shown that all the studied models are able to represent the CGM data, yet their usefulness in a hypothetical artificial pancreas could be a matter of debate. In spite that the three models do not capture all the dynamics and metabolic effects as a maximal model (ie, our FDA-accepted UVa/Padova simulator), SOGMM and ICING appear to be more appealing than MMC regarding both the performance and parameter variability after reidentification. Although the model predictions of ICING are comparable to the ones of the SOGMM model, the large parameter set makes the model prone to overfitting if all parameters are identified. Moreover, the existence of a high nonlinear function like $\max (\cdot ,\cdot )$ prevents the use of tools from the linear systems theory.

Type 1 diabetes mellitus (T1DM) is an autoimmune condition resulting in absolute insulin deficiency and a life-long need for insulin replacement.¹ Glycemic control in T1D remains a challenge, despite the availability of modern insulin analogs,² and the improvement in insulin therapy by means of either multiple daily injections (MDI), the combined use of CGM³ and continuous subcutaneous insulin infusion (CSII), and lately the use of automated insulin delivery systems, that is, the artificial pancreas (AP).⁴

Regarding the design of control structures for AP, a large volume of available literature is specifically devoted to the design of model predictive control (MPC)-based schemes.^5-13 However, in spite of the well-known advantages of this strategy, the lack of reliable control-oriented models of the glucose-insulin system limits the success of such approaches, for both physiology inspired models^14-16 or black-box models.^9,17,18 As stated in the literature, model individualization with “manageable” models (ie, minimal models) remains a challenge for two main reasons: (1) errors in CGM devices and (2) the complex and variable dynamics of the glucose homeostasis which is largely dependent on many uncontrolled factors like patient behavior, circadian rhythm, and other metabolic disturbances.^14,17,19 Therefore, in spite of the large structural uncertainty, in order to obtain the best out of the available models for AP design, appropriate model identification (individualization) should be performed to minimize the overall model uncertainty.

Model identification consists in finding the model parameters’ numerical values such that the model describes the available data in predefined optimal way (e.g., deviation/cost minimization). However, nonlinear model identification is in general a very challenging task due to the lack of either practical or structural identifiability.²⁰

Model identification of control-oriented models in diabetes technology has been typically carried out in an informal way, giving most priority to insulin sensitivity (the gain of insulin action onto glucose uptake) for model individualization without assessing the role and impact of this and other parameters on the system output (measurements).^14-17,^21-31 For example, in Patek et al¹⁴ the insulin sensitivity is the only parameter used for model individualization of SOGMM with the remaining parameters fixed at population values. In Lin et al,¹⁵ the authors used an alternative representation of the minimal model for glucose control in patients at the intensive care unit (ICU). In this contribution, the authors identified the model in two steps: first on the glucose compartment and then on the insulin pharmacodynamics. The insulin sensitivity is considered as a critical parameter to be fitted every hour. The authors used parameter sensitivity analysis to assess the goodness of fit of the identified model. In Magdelaine et al,¹⁶ a linear model of the glucose-insulin system is proposed. This model exhibits beneficial stability properties to correct non desired steady-state behaviors if compared with existing minimal models. After stating the structural identifiability property of the model, the model is directly identified using a least-square cost function. In this contribution, the authors claim that their model fits over two days of clinical data for a given patient with T1D. In Hann et al,²¹ the minimal model is rewritten in integro-differential form. In a first attempt, almost all parameters were fixed with population values and only the insulin sensitivity $S_I$ and the time-varying fractional clearance of plasma glucose at basal insulin $p_G$ are identified. After a sensitivity analysis is performed on the model parameters, the authors realized about the little influence of $p_G$ on the model output and the importance of including ${\mathrm{\alpha }}_G,$ a parameter for the glucose clearance saturation, into the identification process. In Cobelli et al,²² Caumo et al,²³ Pillonetto et al,²⁴ and Dalla Man et al,²⁵ the structural identifiability of the minimal model is studied using different scenarios. In the latter publication, the model is analyzed with three different representations of the rate of glucose appearance. In this analysis, the volume of distribution of glucose $V$ is found nonidentifiable and the rate parameter $p_1$ is found to be nonuniquely identifiable (ie, locally structurally identifiable). After fixing $V$and $p_1$, the remaining identifiable parameters are identified using data from 22 normal subjects after a meal glucose tolerance test (MGTT). In Chin and Chappell,²⁶ the authors addressed the structural identifiability analysis of the minimal model by assuming different setups. First, the identifiability of the two-equation minimal model is studied by assuming only the measurement of plasma glucose. According to their findings, $p_2,$ the insulin action time constant, is not identifiable. When expanded to a three-equation minimal model with switching state ($G\left(t\right)<p_5$ and $G\left(t\right)>p_5$), the authors showed that the model remains structurally globally identifiable, under the assumption of measured plasma insulin and glucose. In Kanderian et al,^27,28 the Medtronic Virtual Patient (MVP) model, which is based on Bergman’s minimal model, is identified with closed loop data (insulin and glucose). The identification was performed in three steps: (1) known insulin delivery rates were used to estimate parameters of the insulin PK model, (2) measured insulin profile and known meal CHO content is used to identify six additional parameters, (3) inclusion of intraday variation for insulin sensitivity $S_I$, endogenous glucose production $EGP$, glucose effectiveness at zero insulin $GEZI$ whether results are not satisfactory. In Messori et al,¹⁷ the authors individualized the linearized UVa/Padova model around a basal working point. Identification is performed using closed-loop in silico data from the simulator (100 virtual subjects) and a cost function minimizing the square deviation of the model with respect to the entire dataset with two additional terms acting as soft constraints over low and high glycemic values. The solution of the proposed optimization problem was found by means of simulated annealing (SA) heuristic.

Alternative methods have also been presented.^29,30 In Herrero et al,²⁹ the minimal model is reparametrized to render globally structural identifiable. The parameter identification is performed through the set inversion via interval analysis (SIVIA) assuming a set of acceptable errors (intervals) from standard intravenous glucose tolerance test (IVGTT) data. The authors claimed the use of a computationally efficient implementation to overcome the extensive computational complexity derived from the method. In Laguna et al,³⁰ the authors used the Cambridge model¹² (Hovorka’s model) together with interval analysis, tackling the model uncertainties with interval models. Unlike the above methods, interval analysis provides an envelope of glucose covering all the possible glucose trajectories given an allowed parameter variability.

As it was evidenced, model individualization in diabetes technology has been typically addressed without a formal procedure or method, that is, direct identification is made without exploring possible problems in the model structure or in the amount and quality of the available data. A possible hypothesis explaining why identifiability analysis is usually overlooked by some researchers is perhaps due to the availability of powerful software suits able to solve complex numerical optimization problems.²⁶ However, disregarding possible identifiability issues will probably produce ill-posed problems, and with this, multiple solutions for a given parameter set. In some cases, structural identifiability is studied under different conditions and using different model structures; only few contributions addresses possible practical identifiability issues.

Analyzing both structural and practical identifiability give a clear path to obtain unique representations for a given experimental dataset. In this regard, this manuscript presents a complete identifiability analysis of three commonly used models for AP design. The models are selected according to (1) the number of equations and (2) different model structures, that is, models are control-oriented models with similar number of equations but with alternative descriptions of the main variables in the glucose metabolism. Our study differs from the existing ones as possible structural and practical (related to the amount and quality of data) limitations of the analyzed models are carefully addressed to guarantee a reliable model identification/individualization.

Methods

Participants and Data Selection

CGM (Dexcom G5, San Diego, CA) and insulin pump data (Tandem Diabetes Care, Inc, San Diego, CA) together with meal information (timing and carbohydrate counting) and physical activity data (fitbit, San Francisco, CA) were collected during an IRB-approved clinical trial (clinicaltrials.org NCT02558491) at the University of Virginia (Charlottesville, VA, USA) for 15 study subjects on continuous subcutaneous insulin infusion (CSII) and 10 study subjects on multiple daily injections (MDI), all having been diagnosed with type 1 diabetes for at least six months. Each patient experienced two identical outpatient admissions of 48 hours (separated by four weeks or more), experiencing both meal and exercise challenges designed to induce glucose variability. In the time in between the admissions, the patients were asked to perform at least three exercise bouts every week. In order to go through the details of the role of identifiability on model individualization, 7-day data in between the admission periods was selected from five subjects (group CSII) in rest periods, that is, data from 1h before to 3h after exercise periods were excluded. For analysis purposes, the data is divided into 6h intervals, every 6h interval corresponding to an experiment.

Models Under Study

In all the models, it is assumed that the only measurement comes from the CGM. Therefore, $\mathrm{y}$ will correspond to the plasma glucose concentration in every model.

The Subcutaneous Oral Glucose Minimal Model—SOGMM

Consider an extended version of the minimal model, known as the subcutaneous oral glucose minimal model (SOGMM)¹⁴

$${\stackrel{.}{x}}_1\left(t\right)=-\left(S_g+x_2\left(t\right)\right)\cdot x_1\left(t\right)+S_g\cdot G_b+\frac{k_{abs}\cdot f}{BW\cdot V_g}\cdot x_4\left(t\right)$$ (1a)

$${\stackrel{.}{x}}_2\left(t\right)=-p_2\cdot x_2\left(t\right)+p_2\cdot S_I\left(I\left(t\right)-I_b\right)$$ (1b)

$${\stackrel{.}{x}}_3\left(t\right)=-k_{\tau }{x}_3\left(t\right)+\mathrm{\omega }\left(t\right)$$ (1c)

$${\stackrel{.}{x}}_4\left(t\right)=-k_{abs}{x}_4\left(t\right)+k_{\tau }{x}_3\left(t\right)$$ (1d)

$${\stackrel{.}{x}}_5\left(t\right)=-k_d{x}_5\left(t\right)+J_{ctrl}\left(t\right)$$ (1e)

$${\stackrel{.}{x}}_6\left(t\right)=-k_d{x}_6\left(t\right)+k_d{x}_5\left(t\right)$$ (1f)

$${\stackrel{.}{x}}_7\left(t\right)=-k_{cl}{x}_7\left(t\right)+k_d{x}_6\left(t\right)$$ (1g)

with $I(t)=x_7/\left(V_I\cdot BW\right)$ the insulin concentration (mU/l), $x_1(t),\cdots ,x_7(t)$ the state variables of the system, namely, plasma glucose concentration (mg/dl), proportion of insulin in the remote compartment (1/min), glucose mass in the stomach (mg), glucose mass in the gut (mg), insulin amount in the first compartment (mU), insulin amount in the second compartment (mU), and plasma insulin (mU), respectively, $\mathrm{\omega }(t)$ the rate of mixed-meal carbohydrate absorption (mg/min), and $J_{ctrl}$ the insulin input signal (mU/min). The parameters of (1) are presented in Table 1. Basal glucose is computed as indicated in Patek et al:¹⁴

Table 1.

Model Parameters With Population Values for SOGMM.

Symbol	Meaning	Value	Range	Units
$S_g$	Fractional glucose effectiveness	0.01	$\left[0,0.1\right]$	1/min
$V_g$	Distribution volume of glucose	1.6	Fixed	dl/kg
$k_{abs}$	Rate constant—oral glucose consumption	0.01193	Fixed	1/min
$k_{\tau }$	Time constant related with oral glucose absorption	0.08930	Fixed	1/min
$p_2$	Rate constant of the remote insulin compartment	0.02	Fixed	1/min
$f$	Fraction of intestinal absorption	0.9	Fixed	—
$V_I$	Distribution volume of insulin	0.06005	$\left[0,5\right]$	1/kg
$k_{cl}$	Rate constant of subcutaneous insulin transport	0.16	$\left[0,0.1\right]$	1/min
$k_d$	Rate constant of subcutaneous insulin transport	0.02	$\left[0,0.1\right]$	1/min
$S_I$	Insulin sensitivity	0.0006	$[0.5\times {10}^{-4},12\times {10}^{-4}]$	1/min/mU/l
$BW$	Body weight	Known	Fixed	kg
$G_b$	Basal glucose concentration	Eq. (2)	Fixed	mg/dl
$I_b$	Reference value for $I(t)$, associated with the fasting plasma glucose concentration.	Steady-state	Fixed	mU/l

$$G_b=HbA1c\cdot 28.7-46.7$$ (2)

where HbA1c is the patient’s most recent glycated hemoglobin.

The Intensive Control Insulin-Nutrition-Glucose (ICING) Model

Consider an extended version of the Bergman’s minimal model, known as the intensive control insulin-nutrition-glucose model (ICING) presented elsewhere.¹⁵ Although this model is originally used for tight glycemic control at the intensive care unit (ICU), it was found to be suited for patients with T1D after some modifications: the terms for parenteral feeding and endogenous insulin production are neglected to represent the glucose-insulin dynamics for a patient with T1D in an outpatient setting.

$${\stackrel{.}{x}}_1\left(t\right)=-P_G{x}_1\left(t\right)-S_I\frac{x_1\left(t\right)x_2\left(t\right)}{1+{\mathrm{\alpha }}_G{x}_2\left(t\right)}+\frac{P+EG{P}_b-CNS}{V_G}$$ (3a)

$${\stackrel{.}{x}}_2\left(t\right)=n_I\left(x_3\left(t\right)-x_2\left(t\right)\right)-n_C\frac{x_{2\left(t\right)}}{1+{\mathrm{\alpha }}_{G}x{\left(t\right)}_2}$$ (3b)

$$\begin{array}{l}{\stackrel{.}{x}}_3\left(t\right)=-n_K{x}_3\left(t\right)-n_L\frac{x_3\left(t\right)}{1+{\mathrm{\alpha }}_I{x}_3\left(t\right)}-n_I\left(x_3\left(t\right)-x_2\left(t\right)\right)\\ +\frac{u_{ex}}{V_I}\end{array}$$ (3c)

$${\stackrel{.}{x}}_4\left(t\right)=-d_1{x}_4\left(t\right)+D$$ (3d)

$${\stackrel{.}{x}}_5\left(t\right)=-\min \left(d_2{x}_5\left(t\right),P_{max}\right)+d_1{x}_4\left(t\right)$$ (3e)

where $x_1$(mmol/l) is the blood glucose or plasma glucose, $x_2$(mU/l) the insulin concentration in the interstice, $x_3$(mU/l) the insulin concentration in plasma, $x_4$(mmol) the amount of glucose in the stomach, $x_5$(mmol) the amount of glucose in the gut, $u_{ex}$(mU/min) the exogenous insulin, and $D$(mmol/min) the amount of ingested carbohydrates. $P$(mmol/min), as defined below, corresponds to the glucose appearance into the blood stream from the enteral nutrition

$$P=min\left(d_2{x}_5\left(t\right),P_{max}\right)$$ (4)

The description of the model parameters together with its units and numerical values (seed or population values) are presented in Table 2.

Table 2.

Model Parameters With Population Values for ICING Model.

Symbol	Meaning	Value	Range	Units
$P_G$	Patient endogenous glucose removal	0.006	$\left[0,1\right]$	1/min
$S_I$	Insulin sensitivity	0.002	$[0.5\times {10}^{-4},12\times {10}^{-4}]$	l/mU/min
${\mathrm{\alpha }}_G$	Saturation of insulin-stimulated glucose	0.0154	Fixed	l/mU
$EG{P}_b$	Basal endogenous glucose production	1.16	$\left[0,5\right]$	mmol/l
$CNS$	Insulin independent central nervous system glucose uptake	0.3	Fixed	mmol/min
$V_G$	Glucose distribution volume	13.3	$\left[0,50\right]$	l
$V_I$	Insulin distribution volume	3.15	Fixed	l
${\alpha }_I$	Saturation of plasma insulin disappearance	0.0017	Fixed	l/mU
$n_C$	Rate parameter	0.003	Fixed	1/min
$n_I$	Transcapillary diffusion rate	0.003	Fixed	l/min
$n_K$	kidney clearance rate of insulin from plasma	0.0542	Fixed	1/min
$n_L$	Patient specific liver clearance	0.1578	Fixed	l/mU
$d_1$	Transport rate	0.0347	Fixed	1/min
$d_2$	Transport rate	0.0069	Fixed	1/min
$P_{max}$	Saturation value of $x_5$	6.11	Fixed	1/min

The Minimal Model Control-Oriented

Consider a control-oriented model of the glucose-insulin system, presented elsewhere in Magdelaine et al.¹⁶

$$\stackrel{.}{x}(t)=Ax(t)+\left[\begin{array}{cc}{B}_u& B_r\end{array}\right]\cdot \left[\begin{array}{c}u(t)\\ r(t)\end{array}\right]+E$$ (5)

with

$$\begin{array}{l}A=\left[\begin{array}{lllll}0\hfill & -k_{si}\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & -\frac{1}{T_u^2}\hfill & -\frac{2}{T_u}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill \\ 0\hfill & 0\hfill & 0\hfill & -\frac{1}{T_r^2}\hfill & -\frac{2}{T_r}\hfill \end{array}\right],\\ \left[\begin{array}{cc}{B}_u& B_r\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& 0\\ \frac{k_u}{V_i\cdot T_u^2}& 0\\ 0& 0\\ 0& \frac{k_r}{V_B\cdot T_r^2}\end{array}\right]\\ E=\left[\begin{array}{c}{k}_l-k_b\\ 0\\ 0\\ 0\\ 0\end{array}\right],C=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\end{array}\right]\end{array}$$

where $x_1(t),\cdots ,x_5(t)$denotes the plasma glucose concentration in (mg/dl), the plasma insulin concentration in (U/l) and its derivative in (U/l/min), and the carbohydrate digestion in (g/min) and its derivative in (g/min/min). The description of the model parameters together with its units and numerical values (seed or population values) are presented in Table 3.

Table 3.

Model Parameters With Population Values for MMC Model.

Symbol	Meaning	Value	Range	Units
$V_i$	Insulin distribution volume	2.5 BW	—	dl
$V_B$	Glucose distribution volume	0.65 BW	—	dl
$k_b$	Insulin independent glucose utilization	128/BW	—	mg/dl/min
$BW$	Body weight	known	—	kg
$k_{si}$	Insulin dependent glucose utilization	300	$\left[0,500\right]$	mg/U/min
$T_u$	Time constant	82.6	$\left[0,500\right]$	min
$k_u$	Static gain	16.45	$\left[0,100\right]$	min
$T_r$	Time constant	75.4	Fixed	min
$k_r$	Static gain	18.28	Fixed	min
$k_l$	Endogenous glucose production	2.24	Fixed	mg/dl/min

Identification Methodology

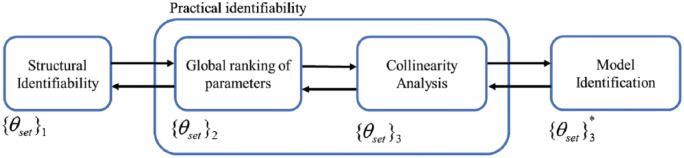
In the present study, it is considered that the only available source of information (measurement) comes from the plasma glucose concentration (CGM). We follow the procedure in Figure 1. The arrows indicate the (possible) existence of an iterative process where a subprocedure can be revisited once preliminary results from the following/preceding subprocedure is obtained. At the end, model identification is performed by the minimization of the mean square error (MSE) through the defined dataset.

Figure 1.

Identification procedure. ${\left\{{\mathrm{\theta }}_{set}\right\}}_j$ indicates the evolution of the identification parameter set according to the identifiability analysis. The star indicates the final set for identification.

The performance of the models after identification will be assessed by means of the root mean square (RMS) criterion

$$RMS=\frac{1}{N}{\sum }_{i=1}^N\sqrt{{\left(y_i-{\widehat{y}}_i\right)}^2}$$ (6)

where $N$, $y$, and $\widehat{y}$ stand for the number of data points, the CGM measurements, and model output, respectively.

Identifiability Analysis

Let’s consider the following nonlinear ODE model representing the system dynamics of the phenomena of interest

$$\mathrm{\Sigma }(\mathrm{\theta }):\{\begin{array}{l}\stackrel{.}{x}\left(t\right)=f_0(x\left(t\right),\mathrm{\theta },t)+{\displaystyle {\sum }_{j=1}^m{f}_i}(x\left(t\right),\mathrm{\theta },t)\cdot u_i\left(t\right)\\ y=g(x\left(t\right),\mathrm{\theta },t)\end{array}$$ (7)

where $x\in {ℝ}^n$ is the system state, $u\in {ℝ}^m$is the input (external excitations), $y\in {ℝ}^{n_0}$ the system output (measurements), $f_0$ and $f_i$ with $i=1,\dots ,m$ are a vector fields whose entries are analytic functions of their arguments, and $\mathrm{\theta }\in \mathrm{\Theta }\subset x\in {ℝ}^{n_p}$ is the vector of parameters within a feasible space $\mathrm{\Theta }$. In this regard, we define an experiment setup with $n_e$ different experiments and $n_s$ different sampling times.

Structural Identifiability

Structural identifiability is a theoretical property of the model structure depending only on the system dynamics, the observation and the stimuli functions.³² Formally, this property is defined as the possibility of assigning unique values to model parameters from the observables (system outputs) but assuming noise-free and continuous-time data.³² In this regard, a parameter ${\mathrm{\theta }}_i,i=1,\dots ,n_p$ is said structurally globally identifiable if for almost any ${\mathbf{\theta }}^{*}=\left({\mathrm{\theta }}_1^{*},{\mathrm{\theta }}_2^{*},\dots ,{\mathrm{\theta }}_{n_p}^{*}\right)\in {ℝ}^{n_p}$

$$\mathrm{\Sigma }(\mathbf{\theta })=\mathrm{\Sigma }({\mathbf{\theta }}^{*})\Rightarrow {\mathrm{\theta }}_i={\mathrm{\theta }}_i^{*}$$ (8)

This property means that if a parameter or set of parameters under study are found to be structurally globally identifiable, it is possible to obtain a unique numerical value for every parameter under the stated conditions (noise-free and continuous-time data). Global structural identifiability can be hard to characterize, therefore, as an alternative, a parameter ${\mathrm{\theta }}_i,i=1,\dots ,n_p$ is said structurally locally identifiable if for almost any ${\mathbf{\theta }}^{*}=({\mathrm{\theta }}_1^{*},{\mathrm{\theta }}_2^{*},\dots ,{\mathrm{\theta }}_{n_p}^{*})\in \mathbf{\Theta }$, there exists a neighborhood $V({\mathrm{\theta }}^{*})$ such that

$$\mathbf{\theta }\in V({\mathrm{\theta }}^{*})\mathrm{and}\mathrm{\Sigma }(\mathbf{\theta })=\mathrm{\Sigma }({\mathbf{\theta }}^{*})\Rightarrow {\mathrm{\theta }}_i={\mathrm{\theta }}_i^{*}$$ (9)

Methods assessing structural identifiability can be found in the literature, and the reader is directed to the review from Chis et al.³³ Here, we chose the method of the generating series approach (GS).³⁴ The method relies on the fact that the system outputs can be expanded in series with respect to time and inputs, using as coefficients the function $g(x,\mathrm{\theta },0)$ and all the successive Lie derivatives along the vector fields $f_0\mathrm{and}{f}_i,$ that is, ${\mathcal{L}}_{f_0}g,{\mathcal{L}}_{f_i}g,$ ${\mathcal{L}}_{f_0}{\mathcal{L}}_{f_0}g,$ ${\mathcal{L}}_{f_0}{\mathcal{L}}_{f_i}g,$ and so on. As a matter of illustration, the Lie derivative of $g$ along $f_0$ can be written as

$${\mathcal{L}}_{f_0}g=〈\frac{\partial g}{\partial x},f_0〉$$

where 〈⋅,⋅〉 denotes the scalar product between two vectors. It is important to emphasize that the GS approach does not specify an upper bound for the order of the derivatives to be taken to prove/disprove the property. Therefore, either the Lie derivatives are taken until a solvable set of algebraic equations in the parameters is found or until, after some coefficient, all subsequent coefficients become zero. The advantage of this method over the Taylor series approach is that the obtained mathematical expressions are easier to handle.³³ Since the amount of Lie derivatives can be overwhelming, Balsa-Canto et al introduced the concept of the identifiability tableaus³³ to (1) organize the Lie derivatives, (2) systematize the resulting algebraic equations, and (3) handle possible structural identification issues. The tableau depicts the nonzero elements of the Jacobian of the series coefficients with respect to the parameters. In this sense, the tableau is an array with as many columns as parameters and as many rows as nonzero computed coefficients. Once enough nonzero coefficients guarantee the full-rank condition of this array, at least the local identifiability of the parameters can be stated. Structural identifiability of the models is studied by a combination of the GS approach³⁴ and identifiability tableaus³⁵ by means of the GenSSI tool.³⁶

Practical Identifiability

Structurally identifiable parameters may not though be identifiable in practice. Practical identifiability deals with whether the parameters can be estimated with sufficient precision using experimental data.³⁷ Lack of practical identifiability can result from (i) parameters without influence on the system outputs and (ii) correlated parameters, that is, the effect of some parameter is affected or overshadowed by the effect of some other parameter or parameters.

Global Parameter Ranking

Global parameter ranking proposes to sort the model parameters with respect to their impact on the system outputs. In this sense, the parameters impacting the outputs the most can be either selected for a further structural identifiability analysis or for model identification. The most common approach for parameter ranking involves the use of parametric sensitivities³⁸ like

$$S_{i,j}(\mathrm{\theta })={\left(\frac{\partial y_j}{\partial {\mathrm{\theta }}_i}\right)}_{y=y(t,\widehat{\mathrm{\theta }}),\mathrm{\theta }=\widehat{\mathrm{\theta }}}$$ (10)

where $\mathrm{\theta }$ is evaluated at some nominal value $\widehat{\mathrm{\theta }}$. A relative parametric sensitivity is easily found by normalizing both outputs and parameters. However, in order to make the analysis valid to the entire parameter space, a global approach needs to be used.^35,39 Although Monte Carlo approaches stand out as the most common approaches, these techniques require considerable computational effort and a large number of samples.⁴⁰ Balsa-Canto et al showed a global parameter ranking strategy based on the Latin hypercube sampling (LHS) method and the use of five importance factors which give more precise estimates with lower computational effort compared to Monte Carlo approaches.³⁵

Once the sensitivities are computed for every sample, the importance factor for parameter ${\mathrm{\theta }}_i$is defined as

$${\mathrm{\delta }}_{{\mathrm{\theta }}_i}^{msqr}=\frac{1}{n_D}\sqrt{{\displaystyle \sum _{l=1}^{n_{lhs}}{\displaystyle \sum _{e=1}^{n_e}{\displaystyle \sum _{j=1}^{n_o}{\displaystyle \sum _{t_{s_i}=1}^{n_s}{\left(s_{{\mathrm{\theta }}_i,j}^{l,e}\left(t_{s_i}\right)\right)}^2}}}}}$$ (11)

where $n_e$ refers to the number of experiments, $n_o$ the number of observables, $n_{lhs}$the number of samples in the LHS algorithm, $n_s$to the specific sampling times used in a given experiment with a given observable, $n_D=n_{lhs}\cdot n_e\cdot n_o\cdot n_s,$ and $s_{{\mathrm{\theta }}_i,j}^{l,e}\left(t_{s_i}\right)$the sensitivity of parameter ${\mathrm{\theta }}_i$ with the observable $j$,in experiment $e$ (using $t_{s_i}$sampling time), and sample $l$ in the LHS method. Then, parameters can be ordered according with their ${\mathrm{\delta }}_{{\mathrm{\theta }}_i}^{msqr}$values. In the specific case of the glucose-insulin system (1.6) can be simplified as

$${\mathrm{\delta }}_{{\mathrm{\theta }}_i}^{msqr}=\frac{1}{n_D}\sqrt{{\displaystyle \sum _{l=1}^{n_{lhs}}{\displaystyle \sum _{e=1}^{n_e}{\left(s_{{\mathrm{\theta }}_i}^{l,e}\right)}^2}}}$$ (12)

since there is only one observable (CGM trace) and in every experiment the same sampling time is used. Note that (12) depends on the number of samples in the LHS method as well as the number of experiments. Our findings show similar results using $n_{lhs}=1000$and either $n_e=7$ (1-day data for every experiment) or $n_e=28$ (6h data for every experiment). Ranking of parameters is performed using the following parameter clusters: (1) Sensitive parameters are in order of importance and sum more than the 80% of the total ${\mathrm{\delta }}^{msqr},$ (2) almost insensitive parameters are parameter subsets gathering less than the 1% of their respective total ${\mathrm{\delta }}^{msqr},$ and (3) mildly sensitive parameters are in between. The latter parameters can be used to refine the identification procedure when allowed, that is, whether identifiability is not compromised. Sensitive parameters are then selected to continue with the identification analysis.

Correlation Among Parameters

As stated before, even the effect of most significant parameter(s) might be overshadowed by the effect of others.^35,41 Analysis of the correlation between parameters can indicate such deficiency.^35,37 To avoid a pair-by-pair analysis of parameters, a collinearity analysis of the entire subgroup can be performed instead.^41,42 The collinearity analysis is based on the linear dependence definition: the parameters are linearly dependent (collinear) if there exist $k$ scalars ${\alpha }_i\ne 0$ with $i=1,\dots ,k$ such that

$${\mathrm{\alpha }}_1{\widehat{s}}_{1,:}+{\mathrm{\alpha }}_2{\widehat{s}}_{2,:}+\cdots +{\mathrm{\alpha }}_k{\widehat{s}}_{k,:}=0$$

where ${\widehat{s}}_{i,:}$is a vector of the sensitivity matrix related to parameter ${\mathrm{\theta }}_i$. A way to approximate this result is by means of the degree of collinearity among a group of parameters which is defined as^41,42

$$C_D({\mathrm{\theta }}_{set})=\frac{1}{{\min }_{\Vert \mathrm{\alpha }\Vert =1}\Vert {\widehat{S}}_{{\mathrm{\theta }}_{set}}\Vert }=\frac{1}{\sqrt{{\underset{\_}{\lambda }}_{{\mathrm{\theta }}_{set}}}}$$ (13)

where ${\mathrm{\theta }}_{set}$is the set of considered parameters for the collinearity analysis, ${\widehat{S}}_{{\mathrm{\theta }}_{set}}$is the submatrix of the sensitivity matrix with the vectors related to the set ${\mathrm{\theta }}_{set}$, and ${\underset{\_}{\lambda }}_{{\mathrm{\theta }}_{set}}$ is the smallest eigenvalue of the matrix ${{\widehat{S}}_{{\mathrm{\theta }}_{set}}}^T{\widehat{S}}_{{\mathrm{\theta }}_{set}}.$ The larger the collinearity index the more dependent the set of parameters are. According to Brun et al,⁴² a threshold of $C_D({\mathrm{\theta }}_{set})<20$is highly desired. Due to the complexity and high variability of the glucose dynamics, the collinearity analyses were performed in 6h datasets instead of 1-day datasets.

Results

Structural Identifiability Analysis

It is important to note that none of the three models considered in this analysis is either locally or globally structurally identifiable considering the original parameter set, that is,

$$\begin{array}{l}{\theta }_{0,SOGMM}=\left[BWf{S}_g{V}_g{k}_{abs}{k}_{\tau }{p}_2{V}_I{k}_{cl}{k}_d{S}_I{G}_b{I}_b\right]\\ {\theta }_{0,ICING}=\left[\begin{array}{l}{P}_G{S}_I{\alpha }_{G}EG{P}_{b}CNS{V}_G{V}_I{\alpha }_I{n}_C{n}_I{n}_L{d}_1\\ d_2{P}_{max}\end{array}\right]\\ {\theta }_{0,MMC}=\left[V_i{V}_B{k}_b{k}_{si}{T}_u{k}_u{T}_r{k}_r{k}_l\right]\end{array}$$

In the case of SOGMM and MMC models, the authors indicated a reduction of the parameter sets to

$$\begin{array}{c}{\mathrm{\theta }}_{1,SOGMM}=\left[\begin{array}{lllllllllll}{S}_g\hfill & V_g\hfill & k_{abs}\hfill & k_{\tau }\hfill & p_2\hfill & V_I\hfill & k_{cl}\hfill & k_d\hfill & S_I\hfill & G_b\hfill & I_b\hfill \end{array}\right]\\ {\mathrm{\theta }}_{1,MMC}=\left[\begin{array}{llllll}{k}_{si}\hfill & T_u\hfill & k_u\hfill & T_r\hfill & k_r\hfill & k_l\hfill \end{array}\right]\end{array}$$

since both $BW$ and $f$are a priori known (and then fixed) in SOGMM and because constitutive equations are provided for $V_B,V_I,\mathrm{and}{k}_b$ in the MMC in terms of the body weight (BW)

$$\begin{array}{c}{V}_i[dl]=2.5BW\\ V_B=0.65BW\\ k_b[mg/dl/\min ]=128/BW\end{array}$$

which lead again to nonidentifiable models (from the structure). With the above scenario, there exist many combinations of parameters to be analyzed from every model in order to obtain a subset of structurally identifiable parameters, making the procedure cumbersome. Therefore, a method helping in that selection is of paramount importance. In this case, we circumvented the above issue by means of the global ranking of the parameters in terms of the parameter sensitivity, that is, what are the parameters impacting the output the most.

SOGMM

Consider the parameter set ${\mathrm{\theta }}_{1,SOGMM}.$ Using the global ranking of parameters, we found the six most impacting parameters in this model, that is,

$${\mathrm{\theta }}_{2,SOGMM}=\left[\begin{array}{llllll}{I}_b\hfill & V_i\hfill & S_i\hfill & k_{cl}\hfill & S_g\hfill & k_d\hfill \end{array}\right]$$

However, as it will be confirmed later, $I_b$ is found to be highly correlated to other parameters (from the given experimental data). After dropping $I_b$, the new set becomes

$${\mathrm{\theta }}_{3,SOGMM}=\left[\begin{array}{lllll}{V}_I\hfill & S_i\hfill & k_{cl}\hfill & S_g\hfill & k_d\hfill \end{array}\right]$$

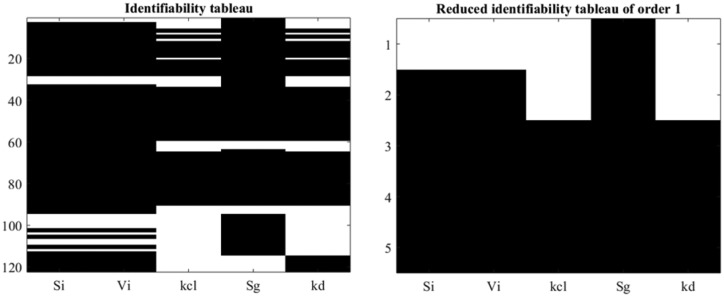
where is found, by means of GS method and the identifiability tableaus, that all the parameters are locally structurally identifiable as shown in Figure 2. Note that 120 coefficients are generated by means of the Lie derivatives (left) from which 5 coefficients are found to fulfill the rank condition (right).

Figure 2.

Identifiability tableaus for SOGMM.

ICING Model

Using the global ranking of parameters and a similar analysis as before we found that the set

$${\mathrm{\theta }}_{1,ICING}=\left[\begin{array}{lllllllllll}{V}_G\hfill & P_G\hfill & EG{P}_b\hfill & d_2\hfill & S_I\hfill & {\alpha }_G\hfill & V_I\hfill & n_K\hfill & n_L\hfill & n_I\hfill & n_C\hfill \end{array}\right]$$

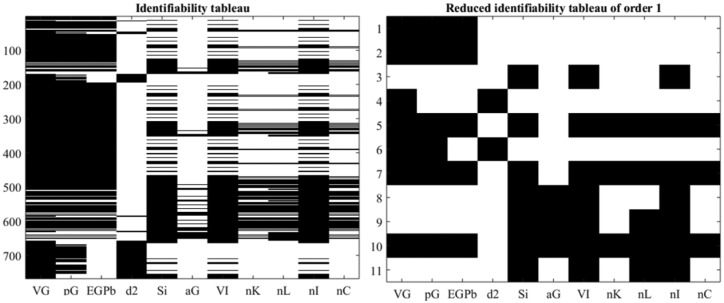
is globally structurally identifiable. Figure 3 show the identifiability tableaus with more than 700 coefficients of the series (left) and 11 relations fulfilling the rank condition. Moreover, $P_{max}$ was determined to be nonidentifiable which is explainable by the use of the “min” function in (3) and (4).

Figure 3.

Identifiability tableaus for ICING model.

MMC

Using the global ranking of parameters and a similar analysis as before we found that

$${\mathrm{\theta }}_{2,MMC}=\left[\begin{array}{lllll}{k}_{si}\hfill & T_u\hfill & T_r\hfill & k_r\hfill & k_l\hfill \end{array}\right]$$

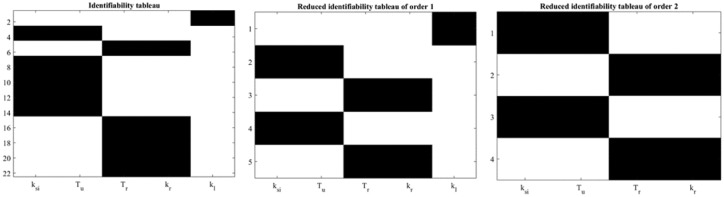
is globally structurally identifiable. Figure 4 show the identifiability tableaus with around 22 coefficients of the series (left) and reduced tableaus indicating the fulfillment of the rank condition (and the uniqueness in the solution).

Figure 4.

Identifiability tableaus for MMC.

Practical Identifiability Analysis

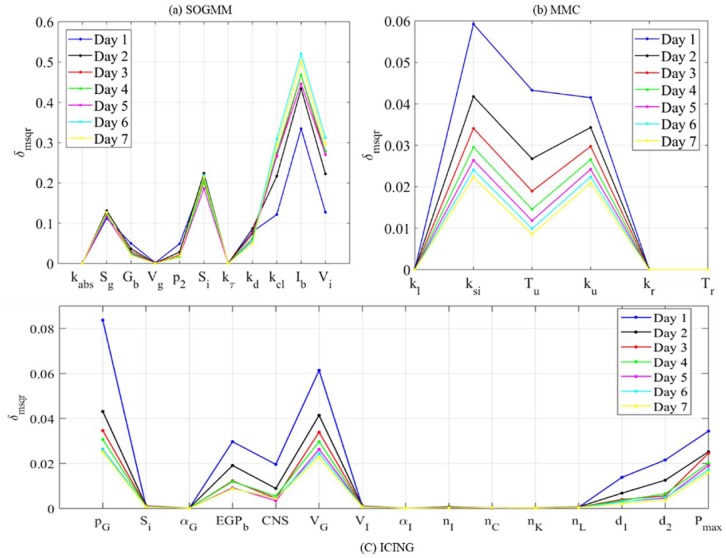
The parameters of every model are ranked with respect to ${\mathrm{\delta }}^{msqr}$ in (1.6) as importance factor using AMIGO2 toolbox.⁴³ As stated before, similar results were found by using $n_{lhs}=1000$ and either $n_e=7$ (1-day datasets) or $n_e=28$ (6h datasets). Figure 5 shows the importance factor ${\mathrm{\delta }}^{msqr}$for all the parameters in the three studied models considering every experiment as 1-day of data in patient 1. Although ${\mathrm{\delta }}^{msqr}$ does vary from one experiment to the next, the variation pattern (ranking) is almost homogeneous, leading to robust ordering of the parameters.

Figure 5.

Global ranking of parameters for patient 1 in seven days using the three models.

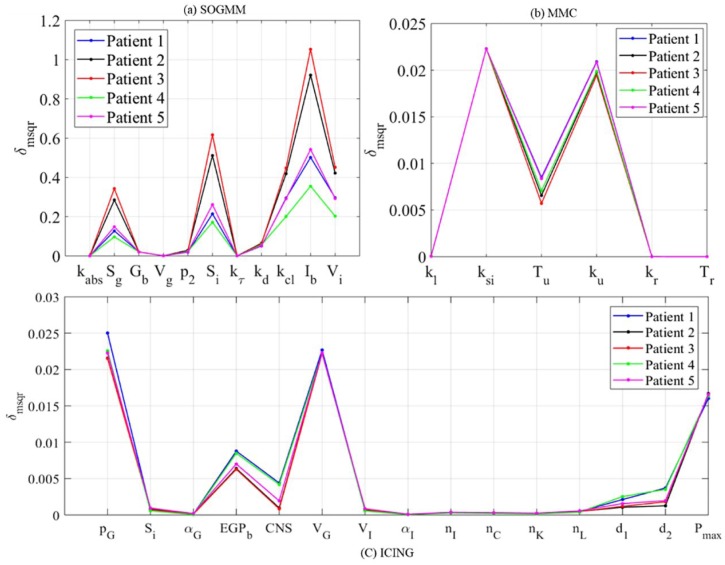
Figure 6 shows the global ranking of the parameters for all the selected patients during the last dataset. In spite of the numerical differences, the relations among parameters within a subject are maintained, therefore the rank remains with no change. Table 4 summarizes the different effects of the parameters on the system output (plasma glucose concentration). Sensitive parameters sum the 97%, 99%, and 85% of total ${\mathrm{\delta }}^{msqr}$ for SOGMM, MMC, and ICING, respectively.

Figure 6.

Global ranking of parameters for patients 1-5 during day seven using the three models.

Table 4.

Parameter Clustering in the Studied Models.

Model	Sensitive	Mildly sensitive	Almost insensitive
SOGMM	$I_b,V_I,k_{cl},S_I,S_g,k_d$	$G_b$,$p_2$	$V_g,k_{abs},k_{\tau }$
ICING	$P_G,V_G,EG{P}_b,P_{max},CNS$	$S_I,{\mathrm{\alpha }}_G,V_I,d_1,d_2$	${\mathrm{\alpha }}_I,n_I,n_C,n_K,n_L$
MMC	$k_{si},T_u,k_u$	−	$k_l,k_r,T_r$

Using the above results, the parameters labeled as “almost insensitive” are fixed with population values. Then, considering the results from the structural identifiability analysis, we update the sets of parameters to be identified as

$$\begin{array}{c}{\mathrm{\theta }}_{3,SOGMM}=\left[\begin{array}{lllll}{V}_I\hfill & S_I\hfill & k_{cl}\hfill & S_g\hfill & k_d\hfill \end{array}\right]\\ {\mathrm{\theta }}_{2,ICING}=\left[\begin{array}{lllllll}{V}_G\hfill & P_G\hfill & EG{P}_b\hfill & d_2\hfill & S_I\hfill & {\alpha }_G\hfill & V_I\hfill \end{array}\right]\\ {\mathrm{\theta }}_{3,MMC}=\left[\begin{array}{ccc}{k}_{si}& T_u& k_u\end{array}\right]\end{array}$$

From the above parameter sets, the collinearity of the parametric sensitivities is investigated for every patient in different time windows. As stated before, datasets with 6h data each are used in this analysis to account for the intrapatient variability and dynamic changes contained in the CGM traces. Moreover, this short-term analysis will also allow further investigation of the data reliability for model identification at different times of the day. After evaluating the collinearity of the parametric sensitivities for the different combinations of parameters, the following sets were found to be the best conditioned in most of the evaluated time windows

$$\begin{array}{c}{\mathrm{\theta }}_{4,SOGMM}=\left[\begin{array}{lllll}{V}_I\hfill & S_I\hfill & k_{cl}\hfill & S_g\hfill & k_d\hfill \end{array}\right]\\ {\mathrm{\theta }}_{3,ICING}=\left[\begin{array}{ccc}{V}_G& P_G& EG{P}_b\end{array}\right]\\ {\mathrm{\theta }}_{3,MMC}=\left[\begin{array}{ccc}{k}_{si}& T_u& k_u\end{array}\right]\end{array}$$

Tables 5-7 show the evaluation of the condition $C_D({\mathrm{\theta }}_{set})<20$for the five evaluated patients (#P) in all the defined time windows (1-28) for the three models. “x” marks show datasets where the parameters are possibly correlated and hence are not suitable for identification. From the visual inspection of these tables, we found that the above parameters sets have correlation issues in 41, 35, and 71 out of the 140 datasets for SOGMM, ICING, and MMC, respectively.

Table 5.

Collinearity Test for ${\mathrm{\theta }}_{4,SOGMM}$ in the Defined 6h Datasets.

	Day 1				Day 2				Day 3				Day 4				Day 5				Day 6				Day 7
#P	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
1	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔	✔	✘	✘	✘	✔	✔	✘	✘	✘	✔	✘	✔	✔	✘	✔	✔	✘	✘
2	✔	✔	✔	✔	✔	✔	✔	✘	✘	✔	✔	✔	✔	✔	✔	✔	✘	✔	✔	✔	✘	✔	✔	✔	✘	✘	✔	✘
3	✘	✔	✔	✔	✔	✔	✘	✔	✘	✔	✔	✔	✘	✔	✔	✔	✘	✔	✔	✘	✘	✔	✔	✔	✘	✔	✘	✔
4	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔	✘	✘	✔	✔	✔	✔	✔	✔	✘	✔	✔	✘	✘	✘	✔	✔
5	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔	✔	✘	✔	✔	✘	✔	✘	✔	✔	✔	✘	✘	✔	✔	✔	✔	✔	✘

Check marks indicate that the condition $C_D({\mathrm{\theta }}_{set})<20$ is met in the corresponding dataset. Otherwise, an “x” mark is used.

Table 6.

Collinearity Test for ${\mathrm{\theta }}_{3,ICING}$ in the Defined 6h Datasets.

	Day 1				Day 2				Day 3				Day 4				Day 5				Day 6				Day 7
#P	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
1	✘	✔	✔	✘	✘	✘	✘	✔	✘	✔	✔	✔	✘	✔	✘	✘	✘	✔	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔
2	✘	✔	✔	✔	✔	✔	✔	✘	✔	✔	✘	✔	✘	✔	✘	✘	✔	✔	✘	✔	✔	✔	✘	✔	✘	✔	✔	✔
3	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔	✔	✔
4	✔	✔	✔	✘	✔	✔	✘	✘	✘	✔	✔	✔	✔	✔	✔	✘	✔	✔	✘	✔	✔	✘	✔	✔	✔	✔	✔	✔
5	✔	✔	✘	✘	✔	✔	✘	✔	✔	✔	✔	✘	✘	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✘	✔	✔

Check marks indicate that the condition $C_D({\mathrm{\theta }}_{set})<20$ is met in the corresponding dataset. Otherwise, an “x” mark is used.

Table 7.

Collinearity Test for ${\mathrm{\theta }}_{3,MMC}$ in the Defined 6h Datasets.

	Day 1				Day 2				Day 3				Day 4				Day 5				Day 6				Day 7
#P	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
1	✔	✔	✘	✘	✘	✔	✔	✔	✘	✘	✔	✘	✘	✘	✘	✔	✘	✘	✘	✔	✘	✔	✔	✔	✘	✘	✘	✔
2	✔	✔	✘	✔	✔	✔	✘	✘	✘	✔	✔	✘	✘	✔	✔	✔	✘	✔	✔	✔	✘	✔	✔	✔	✔	✔	✘	✘
3	✘	✔	✔	✘	✘	✔	✘	✘	✘	✔	✔	✘	✘	✘	✔	✘	✘	✔	✔	✘	✘	✘	✘	✘	✘	✘	✔	✘
4	✔	✘	✘	✘	✘	✔	✔	✔	✘	✘	✔	✔	✘	✘	✔	✔	✘	✔	✔	✔	✘	✔	✔	✘	✘	✔	✘	✔
5	✘	✔	✔	✔	✘	✔	✔	✔	✘	✘	✘	✘	✘	✔	✔	✔	✘	✔	✘	✔	✘	✘	✘	✔	✔	✔	✔	✘

Check marks indicate that the condition $C_D({\mathrm{\theta }}_{set})<20$ is met in the corresponding dataset. Otherwise, an “x” mark is used.

Model Identification

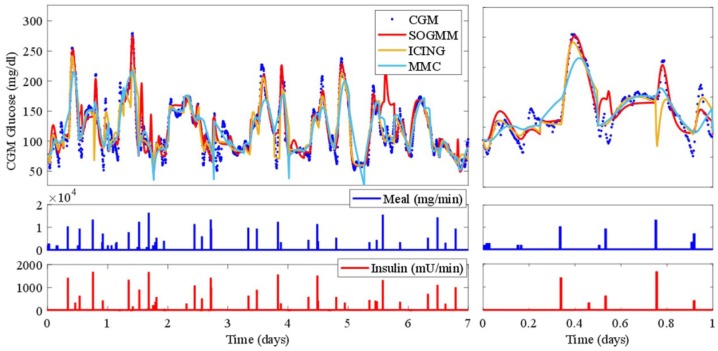
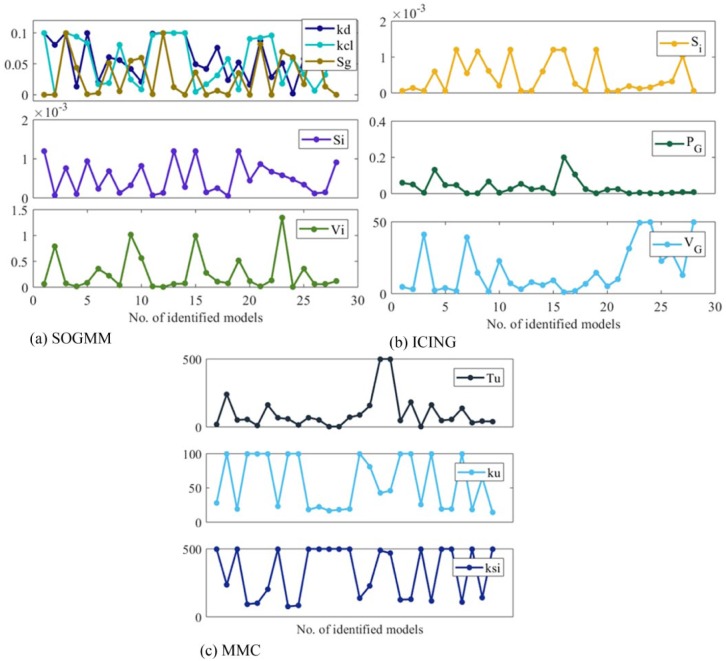
The three models are identified with the parameter sets defined above and with the suitable datasets for identification as presented in Tables 5-7. The variation intervals of the parameters to be identified are presented in Tables 1-3. Figure 7 shows the model identification for patient 1 using the three models. The parameter variability of the models after every 6h identification is presented in Figure 8. The RMS index is presented in Table 8 for all patients. Note that MMC model was not able to provide results for patient 4, possibly for limitations in the model structure.

Figure 7.

Model calibration of the three analyzed models for patient 1. The rightmost figure shows a zoom of the first day.

Figure 8.

Parameter variation (after identification) in all the used data batches.

Table 8.

Model Performance Using the RMS (mg/dl) in All Patients (#).

Model	RMS (#P1)	RMS (#P2)	RMS (#P3)	RMS (#P4)	RMS (#P5)
SOGMM	15.64	18.46	51.32	22.16	18.15
ICING	15.80	20.75	17.61	21.81	26.61
MMC	18.62	18.85	30.35	−	29.51

Several runs were performed by comparing ${\mathrm{\theta }}_{4,SOGMM}$ vs ${\mathrm{\theta }}_{all,SOGMM}$, ${\mathrm{\theta }}_{3,ICING}$ vs ${\mathrm{\theta }}_{all,ICING}$, and ${\mathrm{\theta }}_{3,MMC}$ vs ${\mathrm{\theta }}_{all,MMC}$ (where ${\mathrm{\theta }}_{all,model}$ refers to all parameters of the corresponding model) after modifying either the initial guess on the parameters and the state’s initial condition. Although some times the models fit the data very well (according to the RMS criterion), the identified parameters ${\mathrm{\theta }}_{all,model}$ did not converge to any specific value which show the nonuniqueness of the solutions.

Discussion

In this study, three commonly used control-oriented models for artificial pancreas systems are investigated in terms of their properties to be individualized (identified) to field collected data. While previous contributions gave a big role to the insulin sensitivity, likely due to its role in the evolution of mathematical models of glucose metabolism,^44,45 the presented results indicate that insulin sensitivity is not the parameter impacting the model output the most in the three studied models.

While structural identifiability^16,22-26 has been significantly more studied than practical identifiability^24,31 in control-oriented models for artificial pancreas design, it appears that direct identification is typically performed disregarding the potential pitfalls from the misestimation of model parameters. However, as it has been widely shown in diverse contributions,^20,35,41 both properties are necessary to guarantee the uniqueness of the identified parameters and hence the model usefulness.

In this contribution, we showed a straightforward identification/individualization methodology for control-oriented models in diabetes technology capable of reproducing outpatient data from patients with T1D. Our methodology uses existing procedures and tools such as the generating series approach, identifiability tableaus, global parameter ranking, and collinearity analysis to investigate possible structural or practical issues before performing parameter identification. When compared to direct identification of the whole parameter set, our approach gives a subset of identifiable parameters which in turn reduces the computational load from the solution of the identification problem while guaranteeing the uniqueness of the solution.

Results from the present study showed that the studied models are able to reproduce the experimental data in 6h intervals or less in spite of their different model structure. This may be explained by the structural uncertainty of minimal models when compared to maximal models which are able to reproduce experimental data for longer periods of time.⁴⁶ This fact and high intrapatient and interpatient variability makes online identification a desired feature for use of these models in dosing strategies.

As it was evidenced, structural identifiability analysis needs to be revisited once the global ranking of parameters is performed. Therefore, a good idea is to start with the global parameter ranking and propose a candidate parameter set for structural identifiability. If the structural identifiability test rejects a sensitive parameter then this parameter should be dropped (as with $P_{max}$ in ICING model).

Global parameter ranking reveals possible insensitivity of the observables to some parameters. Moreover, using the global ranking, we may define the parameter set with most influence on the system output. In our case, we obtained parameter sets summing the 97%, 99%, and 85% of total ${\mathrm{\delta }}^{msqr}$ for SOGMM, MMC, and ICING, respectively, although more than 80% would give a yield tradeoff. It is important to point out that alternative importance factors may give different rankings and therefore this fact needs to be further studied.

The collinearity test shows possible linear dependence among candidate parameters as a whole for a given dataset instead of examining the correlation for every pair of parameters. In this way, ill-conditioned data (sometimes referred as weak data) need to be avoided or replaced if possible. As shown in Tables 5-7, not every dataset was conditioned for identification for the given sets of parameter candidates ${\mathrm{\theta }}_{4,SOGMM},{\mathrm{\theta }}_{3,ICING},$ and ${\mathrm{\theta }}_{2,MMC}.$ A possible explanation for this is perhaps the inputs were applied in such a way that provided indistinguishable input-output relationships from the available information. In this regard, design of experiments may play an important role for model individualization.^47,48

While a good model fitting is shown in Figure 7 for the three models in almost all the scenarios, what is important to highlight is the uniqueness of the identified parameters (since similar performances may be obtained with the full parameter sets). However, we found that the optimization did not converge for MMC (patient 4) as the linear model might be found limited to represent such complex data.

From the three studied models, ICING is perhaps more prone to overfitting if all parameters are used for identification since it has more parameters (degrees of freedom) and almost the same number of equations if compared with SOGMM and MMC. Although MMC is found to be the simplest model, the lack of parameter interpretability hampers the definition of practical parameter ranges. Moreover, our analysis indicates larger variability over the parameters of this model, inferior accuracy, and high correlation.

Conclusion

Model individualization in diabetes technology has typically been carried directly, that is, given a parameter set determined in an arbitrary way, the parameters are identified from the optimization of a certain cost function. In this contribution, we presented a thorough and easy-to-follow identification procedure based on the structural and practical identifiability properties. In this sense, it was found that structural identifiability, global parameter rank, and correlation analysis of the parameters give a complete picture for parameter selection in terms of model individualization (patient-adjusted models). Identification results show acceptable fitting with the studied models with respect to real CGM and insulin pump data from patients with T1D in an outpatient setting while guaranteeing the uniqueness of the parameter selection. As far as we are aware, this is the first time that a thorough identifiability analysis is performed on control-oriented models for artificial pancreas systems.