Abstract
Understanding how proteins fold has remained a problem of great interest in biophysical research. Atomistic computer simulations using physics-based force fields can provide important insights on the interplay of different interactions and energetics and their roles in governing the folding thermodynamics and mechanism. In particular, generalized Born (GB)-based implicit solvent force fields can be optimized to provide an appropriate balance between solvation and intramolecular interactions and successfully recapitulate experimental conformational equilibria for a set of helical and β-hairpin peptides. Here, we further demonstrate that key thermodynamic properties and their temperature dependence obtained from replica exchange molecular dynamics simulations of these peptides are in quantitative agreement with experimental results. Useful lessons can be learned on how the interplay of entropy and sequentially long-range interactions governs the mechanism and cooperativity of folding. These results highlight the great potential of high-quality implicit solvent force fields for studying protein folding and large-scale conformational transitions.
Introduction
The protein folding problem, i.e., understanding how natural proteins fold reliably into unique three-dimensional structures, remains one of the major tasks in molecular biology1. Significant advances in both theoretical and experimental aspects have been made in the last few decades and the general mechanism of protein folding is now considered to be known2–5. In particular, the statistical mechanics view, i.e., the energy landscape theory, has become a central framework for understanding protein folding, structure prediction and protein design6–8. The key ideas are that the global energy landscape of a naturally evolved protein resembles a partially rugged funnel and that the protein folds through multiple routes to the basin of global free energy minimum. The state-of-the-art explicit solvent protein force fields have also steadily improved over the years9–13, and achieved remarkable successes in recent atomistic protein folding simulations5,14. Nevertheless, a complete and unambiguous picture of protein folding at the atomic level has yet to emerge. For example, there are still controversies even on how a 16-residue β-hairpin from the C-terminus of the protein G B1 domain (GB1p) folds in isolation15–25. This reflects some of the limitations in current computational and experimental methodologies. Direct all-atom molecular dynamics (MD) or Monte Carlo (MC) simulations can provide insight at levels of detail and fast timescales that cannot be currently reached by experiments, but remain limited by accessible simulation timescales and force field accuracy. The speed limit of the fastest folding proteins ranges from a few microsecond (μs) to tens of μs26, mostly out of direct reach of statistically meaningful atomistic simulations when solvent is treated explicitly. As such, efficient implicit solvent models, where average properties of water are described macroscopically, can be particularly useful in reducing the timescale gap27–32.
An important advance in the experimental frontier of protein folding studies is the discovery and design of ultrafast folding peptides and proteins33. These systems are more amenable to detailed simulations and provide a unique opportunity to bridge the gap between theoretical and experimental investigations. In particular, empirical protein force fields, originally calibrated to characterize conformations near the native basin, have important limitations for protein folding studies34,35; virtually all of them tend to generate overly compact ensembles for unfolded protein states36–38. Availability of fast folding peptides makes it more feasible to recalibrate these force fields to include the non-native/unfolded conformational space39. Such optimization requires extensive conformational sampling and can substantially benefit from enhanced sampling methods, particularly the replica exchange (REX) class of sampling techniques40–42. For example, we have previous parameterized a generalized Born with smooth switching (GBSW)43 implicit solvent force field, by rebalancing solvation and intramolecular interactions to reproduce the experimental conformational equilibria of two helical peptides and a range of β-hairpins derived from GB1p44,45. These hairpins are sequentially homologous but display either reduced or enhanced stability compared to the native sequence46, offering excellent controls for optimization of various implicit and explicit solvent force fields9,13,47,48. The optimized GBSW force field demonstrates a good level of transferability, successfully folding both trpzip249, a designed β-hairpin, and Trp-cage50, a designed mini-protein, to ~1.0 Å accuracy. It has also been successfully applied to calculate the conformational equilibria of small proteins51–53 and to describe non-trivial structural features of several IDPs54–57.
In the present study, we apply the optimized GBSW protein force field to examine the detailed thermodynamics and mechanisms of β-hairpin formation using the set of GB1p-derived peptides. Despite their small size, these hairpins are good model systems for understanding the folding of larger proteins, with cooperative folding transitions at multi-μs timescales and involvement of sequentially long-range hydrophobic and backbone hydrogen-bonding (H-bond) interactions15. The findings here are also made more relevant with the use of a single physics-based force field tuned to preserve the delicate balance of competing interactions. Coupling implicit solvent and REX enhanced sampling allows derivation of key thermodynamic properties with good statistical convergence for direct comparison with available experimental data on these peptides. Together, the results reveal an interesting interplay between chain entropy and long-range interactions in determining the cooperativity and mechanism of peptide folding.
Results
Structure and energetics of GB1p series β-hairpin folding
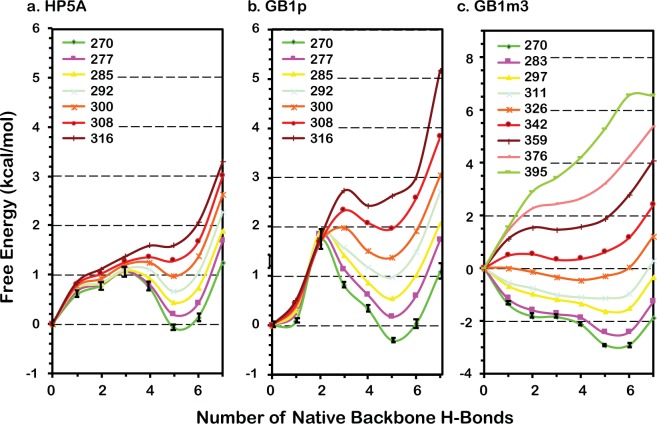
All three GB1p-series peptides can fold into β-hairpin structures in the GBSW implicit solvent (see Fig. 1), with the same backbone H-bond registry as observed in the intact protein G B1 domain. Key hydrophobic sidechains also form cross-strand contacts as expected. Interestingly, the hairpin structures formed by these peptides display significant differences in the level of curving, with HP5A showing the least bending. As it will be discussed later, this is likely due to different relative importance of hydrophobic side chain interactions and backbone H-bonds. The force field also correctly recapitulates the experimental observation that the folded hairpin state is the most stable for GB1m3 and least stable for HP5A49. Examination of the free energy profiles as a function of the number of native backbone H-bonds formed (NHB), shown in Fig. 2, suggests that all three hairpins fold cooperatively. It has been demonstrated that the number (or fraction) of native contacts formed provides an excellent reaction coordinate for describing protein folding using both coarse-grained58 and atomistic26 simulations. For both GB1p and HP5A, there are two well-defined folded and unfolded free energy minima, separated by a single major barrier. That is, both peptides display strong cooperative folding, with most native structural features formed together. This is highly consistent with previous experimental studies demonstrating that the isolated GB1p hairpin retains the folding cooperativity15,18. For GB1m3, there is a single free energy minimum that corresponds to the folded state at low temperatures, suggesting that it may follow ‘downhill folding’59. However, a mild free energy barrier is present near the melting temperature (Tm), around 330 K (e.g., see the T = 342 K trace in Fig. 2c).
Figure 1.
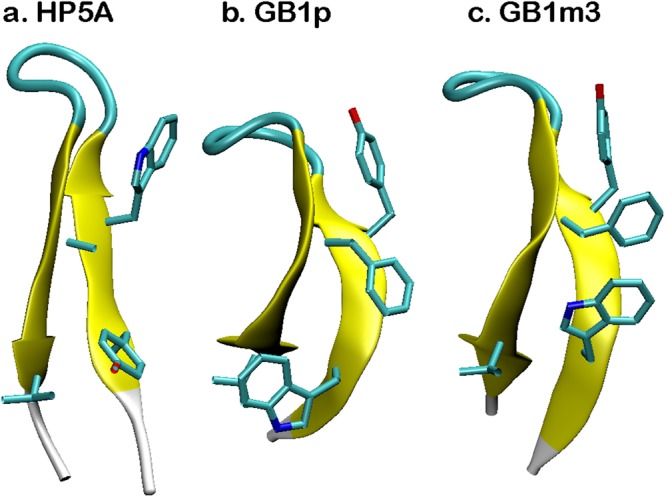
Representative folded structures of GB1p β-hairpins at 270 K. Key hydrophobic sidechains are shown in bonds. Peptide sequences and native contacts are given under Methods.
Figure 2.
Free energy profiles of GB1p β-hairpins at different temperatures. All profiles were calculated directly from distributions sampled at various temperatures during the last 60 ns of REX-MD. Error bars are shown only for results at 270 K for clarity, which are standard errors estimated based on the differences calculated using first and second half of the production ensembles.
The cooperative folding behavior allows one to derive folding thermodynamics directly from the simulated ensembles sampled during REX-MD simulations (see Methods for details). The results for 270 K are summarized in Table 1 and compared with existing experimental data. Implicit solvent simulations were able to reproduce the order of stabilities of these hairpins, which is expected as they have been used in GBSW force field optimization45. Importantly, both folding enthalpy and folding entropy of GB1p derived from simulations are in quantitative agreement with values derived from NMR and T-jump tryptophan fluorescence experiments15,18,46. We note that implicit-solvent derived folding entropies do not include contributions from solvent. Nonetheless, the agreement re-affirms that the optimized GBSW force field offers a realistic balance between solvent-mediated protein-protein interactions vs. conformational flexibility, which may be directly attributed to the optimization strategy that involves both calibration of pair-wise interactions of backbone and side chain moieties and calculation of conformational equilibria of carefully selected model peptides45. Consistent with realistic estimation of folding entropy, the melting temperatures derived from REX-MD are also highly consistent with experimental results for all three hairpins46.
Table 1.
Key folding thermodynamic parameters of β-hairpins at 270 K.
| ΔG (kcal/mol) | ΔU (kcal/mol) | ΔS (cal/mol/K) | Tm (K) | |||||
|---|---|---|---|---|---|---|---|---|
| MD | Expra | MD | Expr | MD | Expr | MD | Expr | |
| HP5A | 0.35 ± 0.1 | 0.82 ± 0.4 | −2.4 ± 0.4 | −7.6 ± 4 | — | <270 | <27346 | |
| GB1p | −0.44 ± 0.3 | −0.8 ± 0.6 | −9.9 ± 0.8 | −11.615 | −38 ± 4 | −3915 | ~273 | <27846 |
| −12.6 ± 1.218 | −43 ± 418 | 293 ± 4.318 | ||||||
| GB1m3 | −1.3 ± 0.2 | −1.1 ± 0.2 | — | — | ~−7.6 | — | ~330 | 333 ± 246 |
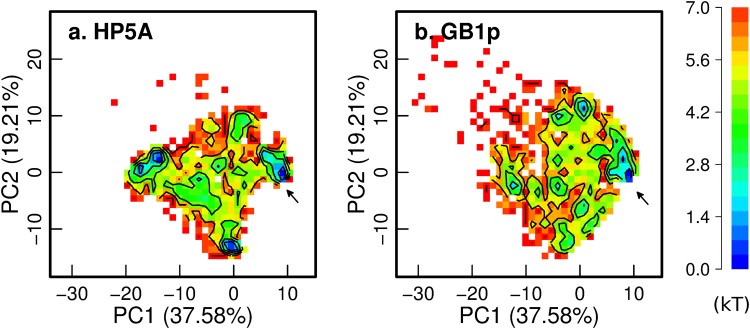
Even though both HP5A and GB1p hairpins are marginally stable (~35% vs ~65% folded), the underlying entropic and enthalpic contributions differ dramatically. The conformational entropic cost of folding for GB1p, ~38 cal/mol/K, is about 5-fold greater than for HP5A, which is only 7.6 cal/mol/K. This is mainly due to the proline-rigidified loop (-PATG-) in HP5A (and GB1m3), which was designed to replace the highly flexible -DATK- loop in the original GB1p sequence46. Analysis of the equilibrium conformational distributions, shown in Fig. 3, clearly shows that GB1p samples a wider conformational space compared to HP5A. In particular, HP5A samples two major nonnative basins beside the native state. Representative snapshots of these conformations are shown in Fig. S1, which suggests that the reduced conformational space sampled by HP5A can be primarily attributed to the loop. The loop forms a native-like turn in one of the nonnative states while adopting extended conformations in the other. This is also reflected in the loop distance distributions, where the -PATG- loop in HP5A occupied two major sub-states (dashed red line in Fig. 4) and has substantial probability of sampling folded like conformations (black traces in Fig. 4). In comparison, the -DATK- loop in GB1p rarely adopts folded-like configurations and can sample a broad and largely continuous range of disordered states (solid red trace in Fig. 4).
Figure 3.
Free energy surfaces projected along the first two principal components. (a) HP5A and (b) GB1p. Only conformations sampled at 270 K during the last 60 ns of REX-MD were included and the principal components were derived by including backbone structures of both HP5A and GB1p. The arrows mark the location of folded basins. Contours are drawn at every kT.
Figure 4.
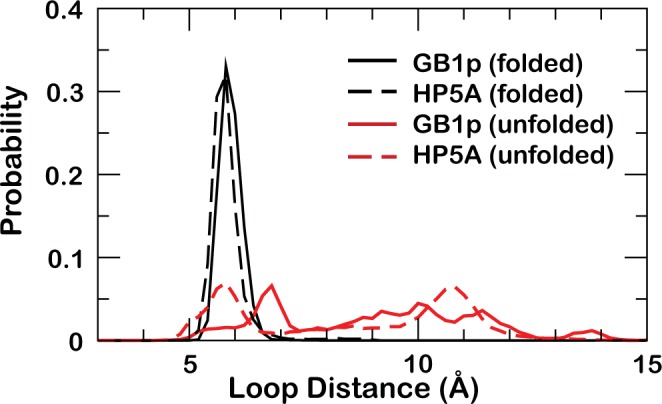
Distributions of loop distances in folded and unfolded GB1p and HP5A. The loop distance was calculated as the distance between Cα atoms of residues 6 and 11.
Intriguingly, the enthalpic stabilization of folding, −2.4 ± 0.4 kcal/mol, is also much smaller for HP5A, which is only about one fourth of that of GB1p (−9.9 ± 0.8 kcal/mol). The design of HP5A sequence involves replacement of larger hydrophobic contacts (Trp-Val and Tyr-Phe in GB1p and GB1m3) with the smaller ones (Trp-Ala and Tyr-Val), and at the same time introduces two Lys residues in the N-terminus to potentially stabilize the folded state via salt-bridge interactions with negatively charged C-terminus46. Yet, analysis of the contributions of various interactions, summarized in Table 2, revealed that the largest contribution to larger folding enthalpy of GB1p came from solvent-screened electrostatic contributions, which is ~7.0 kcal/mol stabilizing vs ~2.5 kcal/mol de-stabilizing for HP5A. Contributions of salt-bridge interactions to protein stabilities are highly context dependent, and it has been shown that exposed ones (such as those could potentially form between N-terminal Lys residues and C-terminal Glu and the carboxyl group) are often destabilizing or contribute only slightly to protein stability55,60,61. This seems to be true for HP5A as well. Instead, presence of larger sidechains in GB1p (and GB1m3) reduces the solvent exposure of backbone H-bonds and enhances their stabilities, leading to a much larger total electrostatic contribution to the folding enthalpy of GB1p. These energetic effects also likely explain higher bending of the folded hairpin structures observed for GB1p and GB1m3 (Fig. 1), which apparently increase the level of side chain-backbone contacts. We note that significant bending of GB1p hairpin structure was also observed in explicit solvent simulations23.
Table 2.
Detailed folding energetics of HP5A and GB1p β-hairpins (all in kcal/mol).
| vdW | ASP | Elec | GB Ener | Elec + GB | Total | |
|---|---|---|---|---|---|---|
| HP5A | −3.5 ± 0.1 | −0.10 ± 0.1 | 12.2 ± 1.6 | −9.7 ± 2.1 | 2.5 ± 0.4 | −2.4 ± 0.4 |
| GB1p | −0.50 ± 0.06 | −0.40 ± 0.1 | −14.9 ± 1.7 | 7.9 ± 2.1 | −7.0 ± 0.4 | −9.9 ± 0.8 |
Standard errors were estimated based on the differences calculated using first and second half of the production ensembles (last 60 ns of REX-MD).
Cooperative folding of GB1p: hydrophobic interactions vs backbone H-bonds
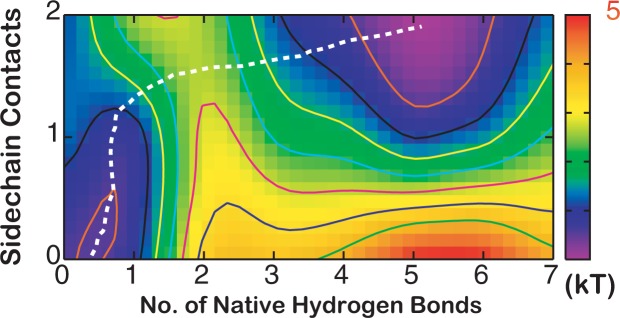
The ability of REX-MD simulations in GBSW implicit solvent to quantitatively recapitulate the stabilities and folding energetics of GB1p-series hairpins provides a unique opportunity to revisit several key questions regarding GB1p folding mechanism, particularly the roles of loop dynamics, hydrophobic side chain interactions and backbone H-bond formation. Folding of GB1p is clearly highly cooperative with a single major barrier separating the folded and unfolded states (Fig. 2), which is in agreement with existing experimental and computational studies16,18,62,63. Further examination of the 2D free energy surface demonstrates that the collapse of the peptide and formation of hydrophobic side chain contacts precede the backbone H-bond formation (e.g., see dashed line in Fig. 5). Such a sidechain driven cooperative folding mechanism is highly consistent previous NMR analyses18,64. A representative folding event sampled during REX-MD is shown in Fig. S2. Formation of native backbone H-bonds requires the loop making the correct turn and hydrophobic side chains making native-like contacts, which represent the rate limiting steps. Complete folding is almost always initiated by H-bonds near the turn, which leads to very fast zipping up of the rest of native backbone contacts (e.g., see Fig. S2). Consistent with simulations using latest optimized explicit solvent force fields23, there are no partially helical intermediate state not well populated at equilibrium (Fig. S3). Previous observation of such states was likely a consequence of inherent biases in early force fields, which have now been shown to yield over-stabilized helical and nonspecific compact states9–13. We also note that, despite the appearance of a single dominant folding pathway in Fig. 5, specific native side chain and backbone contacts can form in different orders, giving rise to relatively diverse microscopic folding pathways even for these small hairpins.
Figure 5.
2D Free energy profiles of GB1p as a function of the numbers of native side chain contacts formed and backbone H-bond formed. The dashed line illustrates the minimal energy path connecting unfolded and folded states. Contours are drawn at every kT.
Entropy, long-range interactions and folding cooperativity
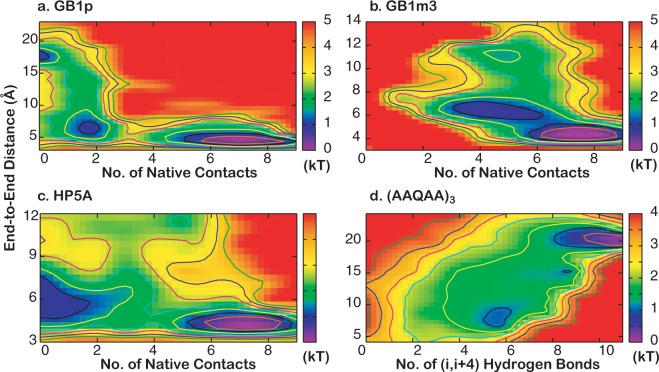
The funneled energy landscape theory predicts that cooperativity of folding arises naturally as a consequence of imperfect cancellation of (conformational) entropy and enthalpy6–8. The three GB1b-series hairpins simulated here provide a nice case study that illustrates how the magnitude of conformational entropy and strengths and (topological) distribution of native (sequentially) long-range interactions together determines the level of folding cooperativity. Folding of GB1p is the most cooperative among the three hairpins. Formation of multiple energetically favorable contacts is required in order to overcome the large conformational entropy of folding due to the flexible loop, which enforces cooperative folding. As shown in Fig. 6a, the peptide can readily sample collapsed conformations in the unfolded state where both sidechain hydrophobic contacts are frequently formed. However, it requires formation of about two additional backbone H-bonds to fully overcome the entropic cost and precede to the fully folded state sharply downhill in free energy (Fig. 2b). For HP5A, the entropic cost of folding is much smaller (Table 1), but the net energetic stabilization effects of side chain and backbone native contacts are also much smaller (Table 2). This leads a more gradual compensation of the entropic cost through formation of native contacts and folding does not turn downhill until over three backbone H-bonds are formed together with both side chain contacts (Figs 2a and 6c). In contrast, GB1m3 contains the same rigidified loop of HP5A but retains large hydrophobic side chains of GB1p. As a result, the modest entropic cost of folding can be readily compensated by formation of side chain hydrophobic interactions alone and the folding is virtually downhill as a function of the number of backbone H-bonds (Fig. 2c). Examination of the 2D free energy surface as a function of the end-to-end distance and number of native contacts also reveal minimal barriers (Fig. 6b). It resembles the surface for folding of helical peptide (AAQAA)3, where the entropic cost of helix-coil transitions is continuously compensated by formation of additional backbone H-bonds in a largely downhill fashion towards the folded state (Fig. 6d). However, there remains an important difference between folding of (AAQAA)3 helix and GB1m3 β-hairpin. While helix formation may be initiated virtually anywhere along the sequence of (AAQAA)3, the rigid loop of GB1m3 strongly restricts the accessible conformation space in the unfold state. Folding of the GB1m3 hairpin appears to largely follow similar folding pathways as observed in GB1p and HP5A, which is initiated near the turn and involve formation of hydrophobic side chain contacts followed by rapid zipping up of backbone H-bonds (e.g., see Fig. S2). Note that the coil state of (AAQAA)3 appears overly compact in GBSW compared to previous explicit solvent simulations65, and the actual folding landscape of (AAQAA)3 folding is thus likely more downhill than what is shown in Fig. 6d.
Figure 6.
2D Free energy profiles as a function of the end-to-end distance and number of native side chain and backbone H-bond contacts formed. (a) GB1p, (b) GB1m3, (c) HP5A and (d) (AAQAA)3. Contours are drawn at every kT.
Discussion
While the energy landscape theory has provided a general statistical mechanics framework for understanding the thermodynamics and kinetics of protein folding, atomistic simulations using physics-based empirical energy functions are usually required to provide quantitative description of the detailed folding mechanism and energetics for a specific protein or peptide. This has increasingly become a reality with recent development of carefully optimized implicit and explicit solvent force fields9,10,13,47,48 as well as development of advanced sampling methods and powerful hardware4,66. In this work, we combine an optimized implicit solvent force field and REX-MD enhanced sampling to analyze the folding of three related GB1p-series β-hairpins. The calculation was able to quantitatively recapitulate known mechanistic features as well as folding thermodynamics of these model systems. The results nicely illustrate how conformational entropy and long-range interactions together dictate various cooperative and downhill-like folding behaviors. This case study highlights the great potential of combining atomistic force fields and enhanced sampling for predictive studies of protein folding and large conformational transitions associated with various biological processes.
Methods
Model Peptides
Four peptides are used in this study, including helical (AAQAA)3 and three GB1p-series β-hairpins. Consistent with the experimental conditions18,46,67, termini of (AAQAA)3 peptide were blocked with Ace and NH2 respectively, and all hairpins with unblocked termini. The β-hairpin sequences are: G41EWTY DDATK TFTVT E56 (GB1p), KKYTW NPATG KATVQ E (HP5A), and KKWTY NPATG KFTVQ E (GB1m3) (the loop segments are underlined). Note that HP5A and GB1m3 are derived from the native sequence of the C-terminal hairpin (residues 41–56) of the B1 domain of protein G (GB1p) with modified stabilities (folded populations at 298 K estimated from NMR chemical shirts46 shown in parenthesis): HP5A (21 ± 10%) < GB1p (ca. 30%) < GB1m3 (86 ± 3%). Note that the folded population of GB1p has also been estimated to be ~42% at 278 K based on NMR68 and ~80% at 273 K based on tryptophan fluorescence experiment15. Native side chain contacts (for Gb1p) include: Trp43-Val54 and Tyr45-Phe52; a total of 7 native backbone contacts for these hairpins include: Glu42 NH-Thr55 CO, Glu42 CO-Thr55 NH, Thr44 NH-Thr53 CO, Thr44 CO-Thr53 NH, Asp46 NH-Thr51 CO, Asp46 CO-Thr51 NH, and Asp47 CO-Lys50 NH. (AAQAA)3 was estimated to be about 50% helical at 270 K based on NMR chemical shifts67.
REX simulations in GBSW implicit solvent
As previously described45, all peptides were simulated using the previously optimized GBSW protein implicit solvent force field45, which was built on the CHARMM22/CMAP all-atom force field69–71. GBSW is generalized Born (GB)-class of implicit solvent that describes the solvent as a high dielectric continuum. GB offers a pair-wise, analytical approximation for calculating the electrostatic solvation free energy and is particularly suitable for molecular dynamics (MD) simulations72. GBSW in particular employs a van der Waals (vdW)-based surface with a smooth dielectric boundary, and the effective Born radii (the key quantities in the GB approximation) are calculated by a rapid volume integration scheme that includes a higher-order correction term to the Coulomb field approximation73. Default GBSW parameters were used along with 50 Lebedev angular integration points and 24 radial integration points up to 20 Å for each atom45. The nonpolar solvation energy was estimated from the solvent-exposed surface area with a phenomenological surface tension coefficient of 0.005 kcal/mol/Å2.
REX-MD simulations in GBSW were performed using the MMTSB Tool Set74 together with the CHARMM program75,76. REX involves multiple copies (replicas) of the peptide simulated at different temperatures independently and replicas attempt to exchange simulation temperatures periodically using Metropolis criteria that preserve the detailed balance. Replicas can travel up and down the temperature space during REX, which facilitates barrier crossing and reduces the probability of being trapped in states of local energy minima. 16 replicas were used in all simulations. The temperatures were distributed exponentially between 270 to 400 K for HP5A and GB1p and 270 to 550 K for (AAQAA)3 and GB1m345. SHAKE was applied to fix the lengths of all bonds with hydrogen atoms and a time-step of 2 femtoseconds (fs) was used. Temperature exchanges were attempted every 2.0 picoseconds (ps) of MD between neighboring replicas. The total simulation lengths were 20 nanoseconds (ns) for (AAQAA)3 and 100 ns for the β-hairpins. In this work we only analyze ensembles derived from folding simulations that were initiated from fully extended structures. Previous comparison with results from control simulations initiated from folded structures suggested that the simulated ensembles were well converged within 100 ns77.
Structural and energetic analysis
The post-analysis was done largely with CHARMM and the MMTSB Tool Set. The helicity was computed from the average 1–4 H-bond frequency, identified when the distance between the carbonyl oxygen of residue i, Oi, and the amide hydrogen of residue i + 4, HNi+4, d(Oi···HNi+4) ≤ 2.6 Å. Similar distance criteria were used to count the number of native backbone H-bonds in the β-hairpins. Sidechains are considered to be in contact if the shortest distance among heavy atoms is no greater than 4.2 Å. All distributions (or equivalently free energy profiles) were derived from conformations sampled during the last 60 ns of REX simulations. For principal component analysis (PCA), backbone structures of both GB1p and HP5A were first aligned using Cα atoms and then projected onto the first two principal components (PCs) to generate the 2D distributions/free energy profiles.
For folding energetic analysis, all conformations sampled during the last 60 ns of REX at 270 K were assigned to the folded state if NHB ≥ 4 and unfolded states if NHB ≤ 1. The free energy of folding was then calculated as ΔG = −RT ln (Pf/Pu). The folding energy, ΔU, was calculated as the difference between average potential energies of the folded and unfolded sub-ensembles. Given ΔG and ΔU, the folding entropy was estimated as ΔS = (ΔU − ΔG)/T. For GB1m3, the free energy profile (and equivalently the ensemble distribution) is dominated by the folded state (Fig. 2c) and the unfolded minimum is absent. ΔG was thus estimated by setting Pu = 1 − Pf. The low occupancy of the unfolded state at 270 K also prevents reliable estimation of ΔU directly from average potential energies. GB1m3 and HP5A contains the same rigidified loop and ΔS for GB1m3 was thus estimated to be similar to that of HP5A in Table 1. The folding transition temperature (Tm) was estimated as the temperature where Pf = Pu.
Electronic supplementary material
Acknowledgements
All simulations were performed on the Pikes GPU cluster housed in the Massachusetts Green High-Performance Computing Center (MGHPCC). This work was supported by National Institutes of Health (R01 GM114300) and National Science Foundation (MCB 1817332).
Author Contributions
J.L. Chen and J.H. Chen, conception and design of the study; J.H. Chen, performing the simulation and analysis; J.L. Chen, X.L. and J.H. Chen, analysis and interpretation of data, drafting and revising the manuscript.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-018-32028-7.
References
- 1.Anfinsen CB. Principles That Govern Folding of Protein Chains. Science. 1973;181(4096):223. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 2.Onuchic JN, LutheySchulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu. Rev. Phys. Chem. 1997;48:545. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 3.Shea JE, Brooks CL. From folding theories to folding proteins: A review and assessment of simulation studies of protein folding and unfolding. Annu. Rev. Phys. Chem. 2001;52:499. doi: 10.1146/annurev.physchem.52.1.499. [DOI] [PubMed] [Google Scholar]
- 4.Best RB. Atomistic molecular simulations of protein folding. Curr. Opin. Struct. Biol. 2012;22(1):52. doi: 10.1016/j.sbi.2011.12.001. [DOI] [PubMed] [Google Scholar]
- 5.Lane TJ, Shukla D, Beauchamp KA, Pande VS. To milliseconds and beyond: challenges in the simulation of protein folding. Curr. Opin. Struct. Biol. 2013;23(1):58. doi: 10.1016/j.sbi.2012.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wolynes PG, Onuchic JN, Thirumalai D. Navigating the Folding Routes. Science. 1995;267(5204):1619. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
- 7.Dill KA, Chan HS. From Levinthal to pathways to funnels. Nat. Struct. Biol. 1997;4(1):10. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 8.Schueler-Furman O, Wang C, Bradley P, Misura K, Baker D. Progress in modeling of protein structures and interactions. Science. 2005;310(5748):638. doi: 10.1126/science.1112160. [DOI] [PubMed] [Google Scholar]
- 9.Best RB, et al. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone φ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012;8(9):3257. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lindorff-Larsen K, et al. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78(8):1950. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Piana S, Lindorff-Larsen K, Shaw DE. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011;100(9):L47. doi: 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Maier JA, et al. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015;11(8):3696. doi: 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang J, et al. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods. 2017;14(1):71. doi: 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334(6055):517. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 15.Munoz V, Thompson PA, Hofrichter J, Eaton WA. Folding dynamics and mechanism of beta-hairpin formation. Nature. 1997;390(6656):196. doi: 10.1038/36626. [DOI] [PubMed] [Google Scholar]
- 16.Dinner AR, Lazaridis T, Karplus M. Understanding beta-hairpin formation. Proc. Natl. Acad. Sci. USA. 1999;96(16):9068. doi: 10.1073/pnas.96.16.9068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Klimov DK, Thirumalai D. Mechanisms and kinetics of beta-hairpin formation. Proc. Natl. Acad. Sci. USA. 2000;97(6):2544. doi: 10.1073/pnas.97.6.2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Honda S, Kobayashi N, Munekata E. Thermodynamics of a beta-hairpin structure: evidence for cooperative formation of folding nucleus. J. Mol. Biol. 2000;295(2):269. doi: 10.1006/jmbi.1999.3346. [DOI] [PubMed] [Google Scholar]
- 19.Gnanakaran S, Nymeyer H, Portman J, Sanbonmatsu KY, Garcia AE. Peptide folding simulations. Curr. Opin. Struct. Biol. 2003;13(2):168. doi: 10.1016/s0959-440x(03)00040-x. [DOI] [PubMed] [Google Scholar]
- 20.Zhang J, Qin M, Wang W. Folding mechanism of beta-hairpins studied by replica exchange molecular simulations. Proteins-Structure Function and Bioinformatics. 2006;62(3):672. doi: 10.1002/prot.20813. [DOI] [PubMed] [Google Scholar]
- 21.Jas GS, Hegefeld WA, Middaugh CR, Johnson CK, Kuczera K. Detailed Microscopic Unfolding Pathways of an alpha-Helix and a beta-Hairpin: Direct Observation and Molecular Dynamics. J. Phys. Chem. B. 2014;118(26):7233. doi: 10.1021/jp500955z. [DOI] [PubMed] [Google Scholar]
- 22.Markiewicz BN, Yang LJ, Culik RM, Gao YQ, Gai F. How Quickly Can a beta-Hairpin Fold from Its Transition State? J. Phys. Chem. B. 2014;118(12):3317. doi: 10.1021/jp500774q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zerze GH, Uz B, Mittal J. Folding thermodynamics of beta-hairpins studied by replica-exchange molecular dynamics simulations. Proteins-Structure Function and Bioinformatics. 2015;83(7):1307. doi: 10.1002/prot.24827. [DOI] [PubMed] [Google Scholar]
- 24.Bille, A., Mohanty, S. & Irback, A. Peptide folding in the presence of interacting protein crowders. J. Chem. Phys. 144 (17) (2016). [DOI] [PubMed]
- 25.Best RB, Mittal J. Microscopic events in beta-hairpin folding from alternative unfolded ensembles. Proc. Natl. Acad. Sci. USA. 2011;108(27):11087. doi: 10.1073/pnas.1016685108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Best, R. B., Hummer, G. & Eaton, W. A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA (2013). [DOI] [PMC free article] [PubMed]
- 27.Roux B, Simonson T. Implicit solvent models. Biophys. Chem. 1999;78(1–2):1. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 28.Bashford D, Case DA. Generalized Born Models of Macromolecular Solvation Effects. Annu. Rev. Phys. Chem. 2000;51:129. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 29.Chen J, Brooks CL. Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Phys. Chem. Chem. Phys. 2008;10:471. doi: 10.1039/b714141f. [DOI] [PubMed] [Google Scholar]
- 30.Chen J, Brooks CL, Khandogin J. Recent advances in implicit solvent based methods for biomolecular simulations. Curr. Opin. Struct. Biol. 2008;18:140. doi: 10.1016/j.sbi.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zheng W, Andrec M, Gallicchio E, Levy RM. Simulating replica exchange simulations of protein folding with a kinetic network model. Proc. Natl. Acad. Sci. USA. 2007;104(39):15340. doi: 10.1073/pnas.0704418104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nguyen H, Maier J, Huang H, Perrone V, Simmerling C. Folding simulations for proteins with diverse topologies are accessible in days with a physics-based force field and implicit solvent. J. Am. Chem. Soc. 2014;136(40):13959. doi: 10.1021/ja5032776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kubelka J, Hofrichter J, Eaton WA. The protein folding ‘speed limit’. Curr. Opin. Struct. Biol. 2004;14(1):76. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 34.Mackerell AD. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem. 2004;25(13):1584. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 35.Snow CD, Sorin EJ, Rhee YM, Pande VS. How well can simulation predict protein folding kinetics and thermodynamics? Annu. Rev. Biophys. Biomol. Struct. 2005;34:43. doi: 10.1146/annurev.biophys.34.040204.144447. [DOI] [PubMed] [Google Scholar]
- 36.Best RB, Zheng W, Mittal J. Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014;10(11):5113. doi: 10.1021/ct500569b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nerenberg PS, Head-Gordon T. Optimizing Protein−Solvent Force Fields to Reproduce Intrinsic Conformational Preferences of Model Peptides. Journal of Chemical Theory and Computation. 2011;7(4):1220. doi: 10.1021/ct2000183. [DOI] [PubMed] [Google Scholar]
- 38.Palazzesi F, Prakash MK, Bonomi M, Barducci A. Accuracy of Current All-Atom Force-Fields in Modeling Protein Disordered States. J. Chem. Theory Comput. 2015;11(1):2. doi: 10.1021/ct500718s. [DOI] [PubMed] [Google Scholar]
- 39.Huang J, MacKerell AD., Jr. Force field development and simulations of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2018;48:40. doi: 10.1016/j.sbi.2017.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314(1–2):141. [Google Scholar]
- 41.Hansmann UHE, Okamoto Y. Numerical comparisons of three recently proposed algorithms in the protein folding problem. J. Comput. Chem. 1997;18(7):920. [Google Scholar]
- 42.Liwo A, Czaplewski C, Oldziej S, Scheraga HA. Computational techniques for efficient conformational sampling of proteins. Curr. Opin. Struct. Biol. 2008;18(2):134. doi: 10.1016/j.sbi.2007.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Im WP, Lee MS, Brooks CL. Generalized born model with a simple smoothing function. J. Comput. Chem. 2003;24(14):1691. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
- 44.Im W, Chen J, Brooks CL., III. Peptide and protein folding and conformational equilibria: theoretical treatment of electrostatics and hydrogen bonding with implicit solvent models. Adv. Protein Chem. 2005;72:173. doi: 10.1016/S0065-3233(05)72007-6. [DOI] [PubMed] [Google Scholar]
- 45.Chen J, Im W, Brooks CL. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. J. Am. Chem. Soc. 2006;128(11):3728. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fesinmeyer RM, Hudson FM, Andersen NH. Enhanced hairpin stability through loop design: the case of the protein G B1 domain hairpin. J. Am. Chem. Soc. 2004;126(23):7238. doi: 10.1021/ja0379520. [DOI] [PubMed] [Google Scholar]
- 47.Lee KH, Chen JH. Optimization of the GBMV2 implicit solvent force field for accurate simulation of protein conformational equilibria. J. Comput. Chem. 2017;38(16):1332. doi: 10.1002/jcc.24734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nguyen H, Roe DR, Simmerling C. Improved Generalized Born Solvent Model Parameters for Protein Simulations. J. Chem. Theory Comput. 2013;9(4):2020. doi: 10.1021/ct3010485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cochran AG, Skelton NJ, Starovasnik MA. Tryptophan zippers: Stable, monomeric beta-hairpins. Proc. Natl. Acad. Sci. USA. 2001;98(10):5578. doi: 10.1073/pnas.091100898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Neidigh JW, Fesinmeyer RM, Andersen NH. Designing a 20-residue protein. Nat. Struct. Biol. 2002;9(6):425. doi: 10.1038/nsb798. [DOI] [PubMed] [Google Scholar]
- 51.Khandogin J, Chen JH, Brooks CL. Exploring atomistic details of pH-dependent peptide folding. Proc. Natl. Acad. Sci. USA. 2006;103(49):18546. doi: 10.1073/pnas.0605216103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Khandogin J, Brooks CL. Linking folding with aggregation in Alzheimer’s beta-amyloid peptides. Proc. Natl. Acad. Sci. USA. 2007;104(43):16880. doi: 10.1073/pnas.0703832104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Khandogin J, Raleigh DP, Brooks CL. Folding intermediate in the villin headpiece domain arises from disruption of a N-terminal hydrogen-bonded network. J. Am. Chem. Soc. 2007;129(11):3056. doi: 10.1021/ja0688880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen J. Intrinsically disordered p53 extreme C-terminus binds to S100B(betabeta) through “fly-casting”. J. Am. Chem. Soc. 2009;131(6):2088. doi: 10.1021/ja809547p. [DOI] [PubMed] [Google Scholar]
- 55.Ganguly D, Chen J. Atomistic details of the disordered states of KID and pKID. implications in coupled binding and folding. J. Am. Chem. Soc. 2009;131(14):5214. doi: 10.1021/ja808999m. [DOI] [PubMed] [Google Scholar]
- 56.Zhang W, Ganguly D, Chen J. Residual structures, conformational fluctuations, and electrostatic interactions in the synergistic folding of two intrinsically disordered proteins. Plos Comput. Biol. 2012;8(1):e1002353. doi: 10.1371/journal.pcbi.1002353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ganguly D, Chen J. Modulation of the disordered conformational ensembles of the p53 transactivation domain by cancer-associated mutations. PLoS Comput. Biol. 2015;11(4):e1004247. doi: 10.1371/journal.pcbi.1004247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cho SS, Levy Y, Wolynes PG. P versus Q: structural reaction coordinates capture protein folding on smooth landscapes. Proc. Natl. Acad. Sci. USA. 2006;103(3):586. doi: 10.1073/pnas.0509768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Dyer RB. Ultrafast and downhill protein folding. Curr. Opin. Struct. Biol. 2007;17(1):38. doi: 10.1016/j.sbi.2007.01.001. [DOI] [PubMed] [Google Scholar]
- 60.Luo R, David L, Hung H, Devaney J, Gilson MK. Strength of solvent-exposed salt-bridges. J. Phys. Chem. B. 1999;103(4):727. [Google Scholar]
- 61.Yang A-S, Honig B. Electrostatic effects on protein stability. Curr. Opin. Struct. Biol. 1992;2(1):40. [Google Scholar]
- 62.Zhou R, Berne BJ, Germain R. The free energy landscape for beta hairpin folding in explicit water. Proc. Natl. Acad. Sci. USA. 2001;98(26):14931. doi: 10.1073/pnas.201543998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Felts AK, Harano Y, Gallicchio E, Levy RM. Free energy surfaces of beta-hairpin and alpha-helical peptides generated by replica exchange molecular dynamics with the AGBNP implicit solvent model. Proteins. 2004;56(2):310. doi: 10.1002/prot.20104. [DOI] [PubMed] [Google Scholar]
- 64.Kobayashi N, Honda S, Yoshii H, Munekata E. Role of side-chains in the cooperative beta-hairpin folding of the short C-terminal fragment derived from streptococcal protein G. Biochemistry (Mosc.) 2000;39(21):6564. doi: 10.1021/bi000013p. [DOI] [PubMed] [Google Scholar]
- 65.Huang J, MacKerell AD., Jr. Induction of peptide bond dipoles drives cooperative helix formation in the (AAQAA)3 peptide. Biophys. J. 2014;107(4):991. doi: 10.1016/j.bpj.2014.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dror RO, Dirks RM, Grossman JP, Xu H, Shaw DE. Biomolecular simulation: a computational microscope for molecular biology. Annu Rev Biophys. 2012;41:429. doi: 10.1146/annurev-biophys-042910-155245. [DOI] [PubMed] [Google Scholar]
- 67.Shalongo W, Dugad L, Stellwagen E. Distribution of Helicity within the Model Peptide Acetyl (Aaqaa) (3) Amide. J. Am. Chem. Soc. 1994;116(18):8288. [Google Scholar]
- 68.Blanco FJ, Rivas G, Serrano L. A short linear peptide that folds into a native stable beta-hairpin in aqueous solution. Nat. Struct. Biol. 1994;1(9):584. doi: 10.1038/nsb0994-584. [DOI] [PubMed] [Google Scholar]
- 69.MacKerell AD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102(18):3586. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 70.Feig M, MacKerell AD, Brooks CL. Force field influence on the observation of pi-helical protein structures in molecular dynamics simulations. J. Phys. Chem. B. 2003;107(12):2831. [Google Scholar]
- 71.Mackerell AD, Feig M, Brooks CL. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25(11):1400. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 72.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. J. Am. Chem. Soc. 1990;112(16):6127. [Google Scholar]
- 73.Lee MS, Salsbury FR, Brooks CL. Novel generalized Born methods. J. Chem. Phys. 2002;116(24):10606. [Google Scholar]
- 74.Feig M, Karanicolas J, Brooks CL. MMTSB Tool Set: enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graphics Modell. 2004;22(5):377. doi: 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 75.Brooks BR, et al. Charmm - a Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem. 1983;4(2):187. [Google Scholar]
- 76.Brooks BR, et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009;30(10):1545. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Zhang W, Chen J. Accelerate Sampling in Atomistic Energy Landscapes Using Topology-Based Coarse-Grained Models. J. Chem. Theory Comput. 2014;10(3):918. doi: 10.1021/ct500031v. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.