Differential analysis of disease risk assessment using binary logistic regression with different analysis strategies

Short abstract

Objective

To investigate the importance of controlling confounding factors during binary logistic regression analysis.

Methods

Male coronary heart disease (CHD) patients (n = 664) and healthy control subjects (n = 400) were enrolled. Fourteen indexes were collected: age, uric acid, cholesterol, triglyceride, high density lipoprotein cholesterol, low density lipoprotein cholesterol, apolipoprotein A1, apolipoprotein B100, lipoprotein a, homocysteine, total bilirubin, direct bilirubin, indirect bilirubin, and γ-glutamyl transferase. Associations between these indexes and CHD were assessed by logistic regression, and results were compared by using different analysis strategies.

Results

1) Without controlling for confounding factors, 14 indexes were directly inputted in the analysis process, and 11 indexes were finally retained. A model was obtained with conflicting results. 2) According to the application conditions for logistic regression analysis, all 14 indexes were weighed according to their variances and the results of correlation analysis. Seven indexes were finally included in the model. The model was verified by receiver operating characteristic curve, with an area under the curve of 0.927.

Conclusions

When binary logistic regression analysis is used to evaluate the complex relationships between risk factors and CHD, strict control of confounding factors can improve the reliability and validity of the analysis.

Introduction

Logistic regression has become a relatively commonly used statistical method for studies involving risk assessment of complex diseases. The most common and mature method is binary logistic regression analysis.¹ A large number of studies and applications have shown that the logistic regression model can meet the requirements of classification data modeling, and it has become the standard method for modeling categorical dependent variables.² However, the application of the binary logistic regression model has strict requirements. If the conditions in which the model is used are inappropriate or inappropriately controlled, this may lead to unexplained results and erroneous conclusions.³ In this study, we compare two logistic regression results obtained by different analysis strategies through the use of a practical case, and then discuss the necessity and importance of confounding factor control in binary logistic regression analysis. In this case, we studied the correlations between 14 physiological and biochemical indexes and the risk of coronary heart disease (CHD); we attempted to establish a CHD risk assessment model through binary logistic regression analysis. Although there were gender differences in CHD risk factors, the results were similar between genders. For brevity, we have limited this report to the results from analyses involving male patients.

Materials and methods

Participants

This study was approved by the ethics review committee of Yuxi People’s Hospital of Yunnan Province. All subjects in this study were recruited from People’s Hospital of Yuxi City, and provided written informed consent to participate. Inclusion criteria for CHD patients were: 1. Coronary angiography clearly showed at least one instance of vascular stenosis >50%. 2. A history of coronary stent implantation. Inclusion criteria for the control group were: 1. Coronary angiography results were normal; 2. There were no symptoms of clinical ischemic chest pain (i.e., myocardial markers were normal and exercise electrocardiogram was flat). Exclusion criteria for CHD patients were any one of the following: 1. Coronary angiography showed stenosis of <50%. 2. Serious systemic disease (e.g., cancer, respiratory failure, liver or kidney dysfunction). 3. A history of immunosuppressive therapy, trauma, cancer chemotherapy, infection, radiotherapy, or a recent operation (within 2 months). 4. Incomplete medical record or partial data collection.

Biochemical analysis

The following serum biochemical indicators were examined in the laboratory: uric acid (UA), cholesterol (TC), triglyceride (TG), high density lipoprotein cholesterol (HDL-C), low density lipoprotein cholesterol (LDL-C), apolipoprotein A1 (ApoA1), apolipoprotein B100 (ApoB100), lipoprotein a (Lp(a)), homocysteine (HCY), total bilirubin (TBIL), direct bilirubin (DBIL), indirect bilirubin (IBIL), and γ-glutamyl transferase (γ-GT). All testing was performed by using Switzerland-imported Roche Cobas C 701 automatic biochemical analyzer (Roche Diagnostics Co., Ltd., Shanghai, China) and supporting reagents.

Statistical analysis

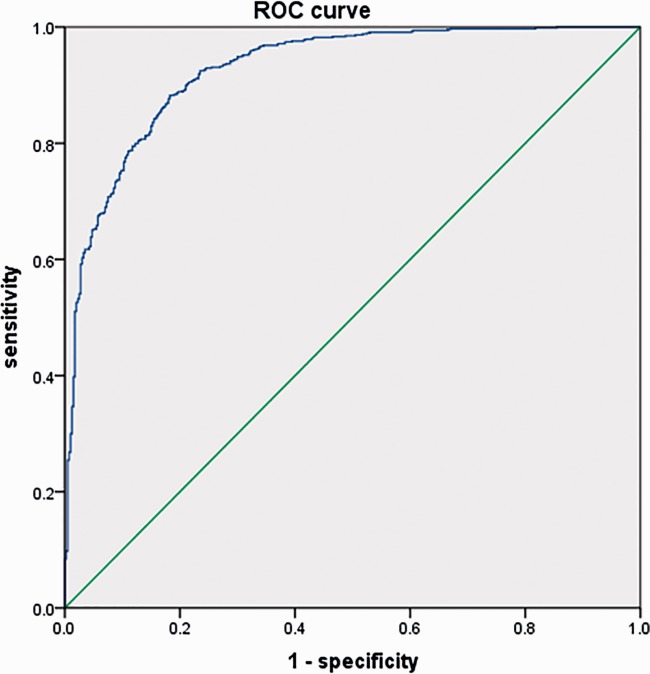
IBM SPSS Statistics, version 20.0 (IBM Corp., Armonk, NY, USA) was used for statistical analysis. All variables were first evaluated for conformance to a normal distribution, to check for uniformity in concentration and dispersion. Logarithmic transformation of variables with skewed distributions ensured consistency in subsequent analyses. Mean and standard deviation were used to describe each variable; independent samples t-tests were used to compare means between case and control groups. The Pearson Correlation coefficient matrix was used to assess correlations between variables. Conditional forward method binary logistic regression analysis was used to establish a mathematical model of the relationship between the variables and CHD. The validity of the mathematical model was evaluated through receiver operating characteristic curve (ROC curve) analysis and the area under the ROC curve (AUC) was measured. The significance level was set at α = 0.05 (Figure 1).

Figure 1.

Receiver operating characteristic curve of the evaluation model.

Results

Patients

We analyzed a total of 664 male patients with CHD, who were initially diagnosed at the Internal Medicine-Cardiovascular Department of our hospital between October 2010 and March 2013. Patient ages were 27-87 years old, mean age 62.2 years. Additionally, we analyzed a total of 400 healthy males, ages 24-84 years old, mean age 45.5 years, during the same period (control group).

Logistic regression without controls for confounding factors

Without correcting for the distribution characteristics and internal correlation of the 14 independent variables, the conditional forward method of binary logistic regression of independent and dependent variables was performed directly; the results are shown in Table 1. After 11 step regressions, of all 14 variables, only TC, TBIL, and IBIL were excluded. Age, APOB100, Lp(a), and HCY were positively correlated with CHD, the OR value of APOB100 [Odds ratio equation for Exp (B)] was 35.959, and LDL-C showed a negative correlation with CHD (Exp(B) value is 0.396). These are all incomprehensible results. If the application conditions for binary logistic regression are adequately controlled, such a result will not appear, as shown in the follow-up analysis. UA, TG, HDL-C, LDL-C, APOA1, and DBIL were negatively correlated with CHD.

Table 1.

Binary logistic regression results without confounding factor correction

		B	SE	Wald	df	P	Exp(B)	95% CI of Exp(B)
Step 11	Age	0.106	0.010	112.713	1	<0.001	1.112	1.090–1.134
	UA	−0.004	0.001	12.842	1	<0.001	0.996	0.993–0.998
	TG	−0.538	0.081	43.631	1	<0.001	0.584	0.498–0.685
	HDL-C	−2.846	0.511	31.006	1	<0.001	0.058	0.021–0.158
	LDL-C	−0.925	0.152	37.011	1	<0.001	0.396	0.294–0.534
	APOA1	−2.503	0.571	19.195	1	<0.001	0.082	0.027–0.251
	APOB100	3.582	0.690	26.924	1	<0.001	35.959	9.293–139.149
	Lp(a)	0.001	0.001	5.726	1	0.017	1.001	1.000–1.002
	HCY	0.198	0.024	69.720	1	<0.001	1.219	1.164–1.277
	DBIL	−0.197	0.065	9.339	1	0.002	0.821	0.723–0.932
	γ-GT	0.010	0.002	16.406	1	<0.001	1.010	1.005–1.014
	Constant	1.053	1.226	0.738	1	0.390	2.866

B, coefficient value; SE, standard error; df, degrees of freedom; 95% CI, 95% confidence interval; UA, uric acid; TG, triglycerides; HDL-C, high density lipoprotein cholesterol; LDL-C, low density lipoprotein cholesterol; APOA1, apolipoprotein A1; APOB100, apolipoprotein B100; Lp(a), lipoprotein a; HCY, homocysteine; DBIL, direct bilirubin; γ-GT, γ-glutamyl transferase.

Logistic regression with controls for confounding factors

After normality testing (K-S test) for the 14 indexes, we found that UA, TC, HDL-C, LDL-C, and APOA1 conform to the normal distribution, so the actual values were used in subsequent analyses. In contrast, APOB100, TG, Lp (a), HCY, TBIL, DBIL, IBIL, and γ-GT exhibited non-normal distributions, so these indexes were converted by logarithm transformation. Notably, age does not conform to the normal distribution; however, to understand the relationship between age and CHD, the actual value of age was used in this analysis. Difference analysis of the 14 indexes showed no significant differences between the case group and the control group in terms of lnγ-GT; for all other variables, the differences were significant. Detailed data are shown in Table 2.

Table 2.

Data summary and t-test results

	Controls (n=400)	CHD (n=664)	t	P
Age (years)	45.46 ± 12.13	62.16 ± 11.04	−23.016	<0.001
UA (μmol/L)	404.92 ± 86.14	376.08 ± 95.79	5.069	<0.001
TC (mmol/L)	4.92 ± 0.88	4.57 ± 1.08	5.821	<0.001
ln TG (mmol/L)	0.69 ± 0.63	0.53 ± 0.56	4.385	<0.001
HDL-C (mmol/L)	1.34 ± 0.33	1.13 ± 0.26	10.979	<0.001
LDL-C (mmol/L)	3.00 ± 0.76	2.83 ± 0.96	3.216	0.001
APOA1 (g/L)	1.42 ± 0.27	1.20 ± 0.23	13.518	<0.001
ln APOB100 (g/L)	−0.23 ± 0.20	−0.15 ± 0.23	−5.862	<0.001
ln Lp(a) (mg/L)	4.74 ± 0.88	4.99 ± 1.01	−4.241	<0.001
ln HCY (μmol/L)	2.39 ± 0.45	2.90 ± 0.36	−19.373	<0.001
ln TBIL (μmol/L)	2.61 ± 0.35	2.47 ± 0.41	5.958	<0.001
ln DBIL (μmol/L)	1.26 ± 0.39	1.11 ± 0.54	4.909	<0.001
ln IBIL (μmol/L)	2.31 ± 0.37	2.12 ± 0.52	7.066	<0.001
ln γ-GT (IU/L)	3.65 ± 0.77	3.69 ± 0.69	−0.859	0.391

Data are presented as mean± standard deviation. UA, uric acid; TC, total cholesterol; TG, triglycerides; HDL-C, high density lipoprotein cholesterol; LDL-C, low density lipoprotein cholesterol; APOA1, apolipoprotein A1; APOB100, apolipoprotein B100; Lp(a), lipoprotein a; HCY, homocysteine; TBIL, total bilirubin; DBIL, direct bilirubin; IBIL, indirect bilirubin; γ-GT, γ-glutamyl transferase.

Correlation analysis

To clearly assess the internal correlation of each variable, and to analyze the influences of confounding factors, Pearson correlation analysis was used to quantify correlations among variables; these results are shown in Table 3. There was a strong correlation between age and lnHCY (0.413); UA showed a relatively strong independence; TC exhibited strong correlations with LDL-C (0.748) and lnAPOB100 (0.645); a strong correlation was observed between HDL-C and APOA1 (0.651); there was a strong correlation between LDL-C and lnAPOB100 (0.569); there is a strong correlation between lnTG and lnγ-GT (0.351); lnLp (a) is relatively independent, and the correlation coefficient with respect to every other variable is lower; lnTBIL and lnDBIL (0.633) exhibit a strong correlation and especially with lnIBIL (0.930); lnγ-GT has strong independence.

Table 3.

Pearson correlation analysis results

		Age	UA	TC	HDL-C	LDL-C	APOA1	ln TG	ln APOB100	ln Lp(a)	ln HCY	ln TBIL	ln DBIL	ln IBIL	ln γ-GT
Age	PCC	1.000	−0.164**	−0.153**	−0.097**	−0.071*	−0.170**	−0.266**	0.040	0.144**	0.413**	−0.117**	−0.022	−0.158**	−0.155**
UA	PCC	−0.164**	1.000	0.092**	−0.023	0.010	0.010	0.251**	0.053	−0.075*	0.050	−0.051	−0.077*	−0.033	0.141**
TC	PCC	−0.153**	0.092**	1.000	0.282**	0.748**	0.020	0.324**	0.645**	0.084**	−0.082**	0.002	−0.163**	0.067*	0.177**
HDL-C	PCC	−0.097**	−0.023	0.282**	1.000	0.131**	0.651**	−0.322**	−0.069*	0.107**	−0.196**	0.198**	0.145**	0.191**	−0.025
LDL-C	PCC	−0.071*	0.010	0.748**	0.131**	1.000	−0.129**	0.042	0.569**	0.098**	−0.021	0.038	−0.114**	0.105**	0.028
APOA1	PCC	−0.170**	0.010	0.020	0.651**	−0.129**	1.000	−0.135**	−0.288**	0.027	−0.246**	0.173**	0.123**	0.176**	−0.036
ln TG	PCC	−0.266**	0.251**	0.324**	−0.322**	0.042	−0.135**	1.000	0.269**	−0.172**	−0.109**	−0.122**	−0.294**	−0.028	0.351**
ln APOB100	PCC	0.040	0.053	0.645**	−0.069*	0.569**	−0.288**	0.269**	1.000	0.129**	0.112**	−0.061*	−0.230**	0.008	0.165**
ln Lp(a)	PCC	0.144**	−0.075*	0.084**	0.107**	0.098**	0.027	−0.172**	0.129**	1.000	0.055	0.013	−0.009	0.001	−0.079*
ln HCY	PCC	0.413**	0.050	−0.082**	−0.196**	−0.021	−0.246**	−0.109**	0.112**	0.055	1.000	−0.112**	−0.073*	−0.129**	−0.003
ln TBIL	PCC	−0.117**	−0.051	0.002	0.198**	0.038	0.173**	−0.122**	−0.061*	0.013	−0.112**	1.000	0.633**	0.930**	−0.010
ln DBIL	PCC	−0.022	−0.077*	−0.163**	0.145**	−0.114**	0.123**	−0.294**	−0.230**	−0.009	−0.073*	0.633**	1.000	0.342**	−0.003
ln IBIL	PCC	−0.158**	−0.033	0.067*	0.191**	0.105**	0.176**	−0.028	0.008	0.001	−0.129**	0.930**	0.342**	1.000	−0.015
ln γ-GT	PCC	−0.155**	0.141**	0.177**	−0.025	0.028	−0.036	0.351**	0.165**	−0.079*	−0.003	−0.010	−0.003	−0.015	1.000

Note: **Correlation is significant at the 0.01 level, *Correlation is significant at the 0.05 level. PCC: Pearson Correlation coefficient, PCC > 0.5 are marked in bold. UA, uric acid; TC, total cholesterol; TG, triglycerides; HDL-C, high density lipoprotein cholesterol; LDL-C, low density lipoprotein cholesterol; APOA1, apolipoprotein A1; APOB100, apolipoprotein B100; Lp(a), lipoprotein a; HCY, homocysteine; TBIL, total bilirubin; DBIL, direct bilirubin; IBIL, indirect bilirubin; γ-GT, γ-glutamyl transferase.

Characterization of the final model

According to the difference and correlation analysis results, and combined with the appropriate application conditions for binary logistic regression, age, UA, TC, lnTG, lnLp (a), lnHCY, HDL-C, LDL-C and lnTBIL (nine indicators) were finally added to the binary logistic regression analysis. After seven step regressions, age, UA, HDL-C, the lnTG, lnLp (a), lnHCY, and lnTBIL were fitted into the regression model; detailed results are shown in Table 4. The model fitting effect was tested by ROC and the result is shown in Figure 1. Age, UA, HDL, lnTG, lnLp (a), lnHCY, and lnTBIL jointly predicted the risk of CHD with an AUC of 0.927 (95% confidence interval: 0.911–0.942); thus, this evaluation model has relatively better sensitivity and specificity.

Table 4.

Binary logistic regression results with confounding factor correction

		B	SE	Wald	df	P	Exp(B)	95% CI of Exp(B)
Step 7	Age	0.098	0.009	120.44	1	<0.001	1.103	1.084–1.122
	UA	−0.004	0.001	10.459	1	0.001	0.997	0.994–0.999
	HDL-C	−3.515	0.397	78.562	1	<0.001	0.030	0.014–0.065
	ln TG	−0.534	0.188	8.112	1	0.004	0.586	0.406–0.847
	ln Lp(a)	0.252	0.101	6.261	1	0.012	1.286	1.056–1.567
	ln HCY	2.821	0.291	94.217	1	<0.001	16.789	9.499–26.675
	ln TBIL	−0.619	0.258	5.77	1	0.016	0.538	0.325–0.892
	Constant	−5.907	1.314	20.201	1	<0.001	0.003

B, coefficient value; SE, standard error; df, degrees of freedom; 95% CI, 95% confidence interval; UA, uric acid; TG, triglycerides; HDL-C, high density lipoprotein cholesterol; Lp(a), lipoprotein a; HCY, homocysteine; TBIL, total bilirubin.

Discussion

The aim of this study was to explore the correlations among 14 physiological and biochemical indexes and CHD, in order to establish a disease risk assessment model, as this is a commonly used method for the study of risk factors of complex diseases. For methodology selection, “whether suffering from CHD” constitutes the typical binary classification variable, whereas the 14 indicators are all continuous variables. The most common and mature analysis strategy is binary logistic regression when studying the direction of weak intensity correlation between continuous variables and two classification variables. Each medical statistical method has its scope of application and its confounding factor control strategy; if these are ignored during the scope of its application, erroneous results may be obtained, such that the effectiveness of the research will be questioned.^4–12

In this study, the initial binary logistic regression was performed without any confounding factor control, and the results seemed to be satisfactory, but there were some results that were questionable. For instance, (1) “recognized” cardiovascular risk factor LDL-C is displayed as a protective factor; (2) γ-GT showed no significant difference between CHD group and control group in difference analysis, while γ-GT has been proven as an independent risk factor of CHD in the logistic regression modeling, and the level of γ-GT shows a positive correlation with CHD; (3) the Exp(B) value of APOB100 is 35.959, which is abnormally high in context of the modeling. According to the statistical guidelines, the application of binary logistic regression should meet with the following conditions: a, the dependent variable should be a binary variable; b, the correlation of dependent variables and logit (P) is a linear relationship; c, residual approaches 0 and is subject to binomial distribution; d, the source of binary logistic regression cannot complete multicollinearity diagnosis, so that the requirements of the observation values should be mutually independent.¹ In this study, “whether suffering from CHD” is the typical binary classification variable, meeting the requirement a; maximum likelihood method can examine coincidence, meeting the requirements for b and c; regarding the independence mentioned in requirement d, there are no repeat individuals or at least no genetically repeat individuals in the research population in this study. The confounding factors that were generated from the independent variables impact the results to a great extent, such that we have to rely on the relevant statistical analysis and biochemical knowledge to judge and screening.

In this study, the scope of the application and the confounding factor control were given full consideration when using the binary logistic regression, specifically regarding performance in: first, strict evaluation was implemented regarding the data distribution characteristics, and we conducted normality tests: Kolmogorov-Smirnov test and trend analysis of P-P (the results were not shown for brevity), and part of the data was transformed. For APOB100, TG, Lp (a), HCY, TBIL, DBIL, IBIL, and γ-GT, a natural log transformation was used to ensure that these variables could be incorporated into subsequent linear analysis. Second, the internal correlation of all variables was analyzed by Pearson correlation matrix analysis, and the regression index was screened according to the correlation or independence of the variables. The results showed that UA, lnTG, lnLp (a), and lnHCY were relatively independent and were used in subsequent logistic analysis; in the blood lipid spectrum, although lnTG has a wide correlation with other indicators, the correlation coefficient is < 0.5, so it was also included in the subsequent logistic analysis. HDL-C and LDL-C are common clinical indexes that serve as common risk factors for CHD, but their role in the prediction of CHD is still in dispute,^13,14 and needs to be confirmed by research analyses, so they were also included in the subsequent logistic analysis. Pearson correlation matrix analysis showed that LDL-C and lnAPOB100 have a strong correlation, and that HDL-C and APOA1 have a strong correlation; in order to ensure the reliability of the results analysis regarding HDL-C and LDL-C, APOA1 and lnAPOB100 were not included in the regression indexes. As a risk factor of CHD, TC was analyzed in the subsequent logistic analysis. The traditional four liver function indexes, lnTBIL, lnDBIL, lnIBIL, and lnγ-GT were analyzed: although lnγ-GT has strong independence, difference analysis showed that there was no significant difference between the case and control groups; therefore, it was not included in the subsequent analysis. Thus, only lnTBIL was selected as the representative index of the three bilirubin indicators in the following analyses. Third, through the series of statistical processing steps, the final modeling variables were confirmed; these variables respectively represent individual blood lipid level and metabolic characteristics. Fourth, in the processing of the binary logistic regression, through the score test, −2 log like-lihood value, model prediction accuracy based on two classification logistic regression analysis process, ROC curves and a series of statistical confounding factor control methods, we evaluated the reliability, likelihood, and effectiveness of the binary logistic regression analysis. Through all these means of effective control, a CHD risk assessment model with higher diagnostic efficiency was finally obtained.

The study of correlation factors is the premise of prevention and control of complex diseases, such as CHD. However, the use of related factors in CHD prevention and control is not simple. Although the various risk factors have been studied over decades, there are few risk factors can be directly applied in the prediction of CHD. Age, smoking, hypertension, gender, and other factors have been widely used in prior prediction models for CHD (e.g., Framingham, FHS 1991, FHS 2008, ASSIGN, QRISK2, SCORE, Reynolds, and PROCAM). Other risk factors, such as blood lipids, have generally not been included in the above prediction models. In addition to the blood lipid detection methods and indicators of representative underlying characteristics, the lack of rigorous statistical analysis is one of the reasons leading to instability.¹⁵ Therefore, in the study of complex disease risk factors, it is particularly important to grasp the statistical methods. This study, which includes confounding factor control of the binary logistic regression analysis as the breakthrough point and compares regression results under different analysis strategies, preliminarily confirms the importance of confounding factor control for the reliability of logistic regression results. However, due to the limitations of our non-professionals statistical backgrounds, there are many shortcomings in the application and presentation of these statistical methods, which will be strengthened and improved in the future studies.

Declaration of conflicting interest

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was supported by the Regional Fund Project [grant number: 81460326] of the National Natural Science Foundation of China; Yunnan Provincial Science and Technology Department of Basic Research on the Application of Self-Financing Projects [2013FZ257]; Joint Special Funds [2013FZ283] from the Yunnan Province Science and Technology Department and Department of Applied Basic Research of Kunming Medical University; the Scientific Research Fund of Yunnan Provincial Education Department [2011C083]; and the Training Special Funds of High Level Health and Family Planning Technical Personnel in Yunnan Province [D-201644]. The funders had no role in study design; in the collection, analysis, and interpretation of data; in writing the report; or in the decision to submit the article for publication.