Association Between 24-Hour Intraocular Pressure Monitored With Contact Lens Sensor and Visual Field Progression in Older Adults With Glaucoma

Carlos Gustavo De Moraes; Kaweh Mansouri; Jeffrey M Liebmann; Robert Ritch

doi:10.1001/jamaophthalmol.2018.1746

. 2018 May 24;136(7):779–785. doi: 10.1001/jamaophthalmol.2018.1746

Association Between 24-Hour Intraocular Pressure Monitored With Contact Lens Sensor and Visual Field Progression in Older Adults With Glaucoma

Carlos Gustavo De Moraes ^1,^✉, Kaweh Mansouri ^2,³, Jeffrey M Liebmann ¹, Robert Ritch ⁴, for the Triggerfish Consortium

¹Bernard and Shirlee Brown Glaucoma Research Laboratory, Edward S. Harkness Eye Institute, Columbia University Medical Center, New York, New York

²Glaucoma Research Center, Montchoisi Clinic, Swiss Vision Network, Lausanne, Switzerland

³Department of Ophthalmology, University of Colorado, Denver, Colorado

⁴Einhorn Clinical Research Center, New York Eye and Ear Infirmary of Mount Sinai, New York, New York

Group Information: The Triggerfish Consortium group members are listed at the end of this article.

Accepted for Publication: March 29, 2018.

^✉

Corresponding Author: Carlos Gustavo De Moraes, MD, MPH, Bernard and Shirlee Brown Glaucoma Research Laboratory, Edward S. Harkness Eye Institute, Columbia University Medical Center, 635 W 165th St, PO Box 69, New York, NY 10022 (cvd2109@cumc.columbia.edu).

Published Online: May 24, 2018. doi:10.1001/jamaophthalmol.2018.1746

Author Contributions: Dr De Moraes had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis

Study concept and design: All authors.

Acquisition, analysis, or interpretation of data: De Moraes, Liebmann, Mansouri.

Drafting of the manuscript: De Moraes.

Critical revision of the manuscript for important intellectual content: All authors.

Statistical analysis: De Moraes.

Administrative, technical, or material support: Liebmann.

Study supervision: All authors.

Conflict of Interest Disclosures: All authors have completed and submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Dr De Moraes has received research support from Heidelberg Engineering GmbH, Carl Zeiss Meditec Inc, and Topcon Inc. Dr Mansouri has served as a consultant for Sensimed AG. Dr Liebmann has served as a consultant for Sensimed AG, Arie Pharmaceuticals Inc, Alcon Laboratories Inc, Allergan Inc, Bausch & Lomb Inc, Carl Zeiss Meditec Inc, Forsight Visio5, Heidelberg Engineering GmbH, Inotek Pharmaceuticals Inc, Quark Pharmaceuticals Inc, Reichert Inc, and Sustained Nanosystems; has received research support from Heidelberg Engineering GmbH; and is equity owner of Forsight Visio5 and Sustained Nanosystems. Dr Ritch has served as a consultant for Sensimed AG, Aeon Astron Europe, Gerson Lehrman Group, Diopsys Inc, GLIA, and Guardion Health Sciences; is a member of the advisory board for Intelon Optics and iSonic Medical; has received speaker fees from Santen Pharmaceutical; and has received royalties from Ocular Instruments. No other disclosures were reported.

Funding/Support: The study was supported by an unrestricted departmental grant from Research to Prevent Blindness (Department of Ophthalmology, Columbia University Medical Center).

Role of the Funder/Sponsor: The funding organization had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication.

The Triggerfish Consortium: Tomas Grippo, MD (Argentina); Katrin Lorentz, MD (Germany); Antonio Duch, MD, Maria Jesus Muniesa Royo, MD, Nicola Alejandre, MD, Aitor Lanzagorta, MD, and Fernando Hussa Herrera, MD (Spain); Jean-Philippe Nordmann, MD, Denis Gruber, MD, Philippe Buffière, MD, Muriel Poli, MD, Isabelle Riss, MD, Corinne Dot, MD, and Yves Lachkar, MD (France); Suneeta Dubey, MD, and Shilpa N. Patil, MD (India); Luca Agnifili, MD, Daniela Paoli, MD, Marco Nardi, MD, Francesco Nasini, MD, Stefano Gandolfi, MD, Enzo D’Ambrozio, MD, and Luca Rossetti, MD (Italy); Jemaima Che Hamzah, MD, Geetha Ramakrishnan, MD, Fang Seng Kheong, MD, and Wei Loon, MD (Malaysia); Felix Gil Carasco, MD (Mexico); Jan Askvik, MD, and Albrecht Gerstenberger, MD (Norway); Dorin Chiselita, MD, and Horia Stanca, MD (Romania); and Rohit Sharma, MD, Andrew J Tatham, MD, and Fernando Hussa Herrera, MD (United Kingdom).

Meeting Presentation: This study was presented at the Annual Meeting of the American Glaucoma Society; March 4, 2017; Coronado, California.

^✉

Corresponding author.

PMCID: PMC6136041 PMID: 29800011

Key Points

Question

Does a single 24-hour curve with a contact lens sensor that measures intraocular pressure–related patterns correlate with the rates of visual field progression in patients with treated glaucoma?

Findings

In a cohort study including 445 patients (445 eyes) with glaucoma, a combination of contact lens sensor–derived variables was associated with prior rates of visual field progression of glaucoma. These variables performed better than Goldmann intraocular pressure measurements taken over follow-up.

Meaning

These findings suggest that a single 24-hour contact lens sensor session can help in risk stratification of patients with treated glaucoma.

Abstract

Importance

Twenty-four–hour intraocular pressure (IOP) patterns may provide more information regarding rates of visual field progression than office-hour measurements. However, little is known about the added value of 24-hour monitoring when stratifying glaucoma risk based on rates of progression.

Objective

To test the hypothesis that 24-hour IOP-related patterns recorded with a contact lens sensor (CLS) correlate with prior rates of visual field progression.

Design, Setting, and Participants

A multicenter, retrospective cohort study was conducted at 50 ophthalmology care centers in 13 countries. Participants included 445 patients (445 eyes) with treated, manifest open-angle glaucoma. The study was conducted from November 8, 1999, to September 17, 2016.

Interventions

Twenty-four–hour recordings of IOP-related patterns were prospectively collected with a CLS system. Retrospective visual field data of patients who underwent at least 3 prior reliable visual field tests were examined.

Main Outcomes and Measures

Association between CLS variables and rates of visual field mean deviation (MD) change.

Results

Of the 445 patients included, 238 (53.5%) were women and 394 (88.5%) were white. The mean (SD) age and MD values at the time of CLS recording were 68.9 (11.2) years and −9.0 (7.0) dB. The mean rate of MD change was −0.46 (0.5) dB/y in 5.2 (3) years of follow-up. After adjusting for baseline MD severity, age, and treatment, the following CLS variables were associated with fast visual field progression: mean peak ratio while awake (β = −0.021; 95% CI, −0.04 to −0.003), number of long peaks during sleep (β = 0.036; 95% CI, 0.005 to 0.067), night bursts ocular pulse frequency SD (β = 0.027; 95% CI, 0.004 to 0.051), and night bursts ocular pulse amplitude SD (β = 19.739; 95% CI, 1.333 to 38.145). Regression models including CLS variables had better fit than Goldmann IOP when testing the association with rates of progression.

Conclusions and Relevance

Results of this study indicate that 24-hour CLS recordings may be associated with prior rates of visual field progression of glaucoma. This association appears to be better than Goldmann mean IOP measured multiple times during office hours. Therefore, the CLS may be useful to assess the risk of future functional loss, even in situations when insufficient historical visual field information is available.

This cohort study examines the use of 24-hour monitoring of intraocular pressure with a contact lens sensor in assessing risk for change in the visual field of older adult patients with glaucoma.

Introduction

Intraocular pressure (IOP) is a risk factor for glaucoma onset¹ and progression^2,3,4,5 and is characterized by both short- and long-term fluctuations, either physiologic or related to efficacy and duration of antiglaucoma medications.⁶ Nonetheless, glaucoma management is often based on single IOP measurements determined during office hours that can miss peaks in over 60% of patients.^7,8

Different methods have been proposed to provide a more comprehensive assessment of IOP patterns, including office-hour diurnal curve testing, self-tonometry,^9,10 and 24-hour monitoring in sleep laboratories.⁸ More recently, 24-hour IOP estimation has been possible using a contact lens sensor (CLS) system (Triggerfish; Sensimed AG) that records patterns of changes of ocular dimensions related to IOP.¹¹ The inbuilt sensor captures spontaneous circumferential changes at the corneoscleral limbus that occur owing to IOP and volume changes. Output signals from the CLS are in electronic units of millivolt equivalents whose mean 24-hour patterns have been correlated with the mean 24-hour tonometric curve.¹²

A recent study demonstrated that certain variables derived from CLS signals provide a signature that can differentiate patients experiencing fast vs slow visual field progression of glaucoma.¹³ In addition, this signature obtained during a 1-day session had a better association with rates of visual field progression than Goldmann applanation tonometry (GAT) measurements taken multiple times over years. However, that study had limitations that prevented the generalizability of the results, such as a relatively small sample size, stringent inclusion and exclusion criteria, and patients coming from a single referral glaucoma practice.

To overcome these limitations and test the generalizability of the previous findings, we analyzed the data of a large, multicenter consortium of patients with treated open-angle glaucoma who underwent 24-hour CLS recordings and had a series of previously measured visual field test results available to evaluate the association between CLS variables and rates of glaucoma progression.

Methods

The Triggerfish Consortium compiled data from 50 centers in 13 countries in which CLS recording was performed in a total of 1355 eyes; 445 eyes of 445 patients were evaluated in the present study. The CLS data were obtained as part of different prospective studies or registries approved by a qualified body or institutional review board in each center (eAppendix 1 in the Supplement), whereas visual field data were collected retrospectively. The study was conducted from November 8, 1999, to September 17, 2016. The study followed the tenets of the Declaration of Helsinki¹⁴ and written informed consent was obtained from all participants. No financial compensation was provided.

eFigure 1 in the Supplement summarizes the exclusion and inclusion criteria for this study. We included patients with open-angle glaucoma defined as follows: open angles on gonioscopic examination, glaucomatous optic neuropathy defined based on evaluation of optic disc photographs by glaucoma specialists, visual field abnormalities consistent with the findings on optic disc photographs and repeatable on at least 2 consecutive tests, and at least 3 reliable visual field tests performed before the date of recording with the CLS.

All visual fields were performed using the Humphrey perimeter (Humphrey Field Analyzer, Carl Zeiss Meditec Inc) with 24-2 or 30-2 tests and required reliability indices with false-positive responses of less than 15%. We did not use cutoff values for fixation losses and false-negative responses.¹⁵ Both Swedish Interactive Testing Algorithm (SITA)-Standard and SITA-Fast tests were included; both the tests (24-2 or 30-2) and algorithms (SITA-Standard or SITA-Fast) had to be consistent within each patient during the follow-up period.

The CLS System

All patients underwent a 24-hour recording session with a wireless CLS.¹⁶ The device can record IOP-related fluctuations for up to 24 hours and remains active during undisturbed sleep. Three hundred data points are acquired during a 30-second measurement period, which is repeated every 5 minutes. The technology is described in more detail elsewhere.¹¹ eFigure 2 in the Supplement depicts the output of a 24-hour CLS recording.

Statistical Analysis

Mean deviation (MD) slopes (in decibels per year) were calculated with best linear unbiased prediction following mixed-effects linear models testing the association between MD (in decibels as dependent variable) and time (in years as independent variable). We used an unstructured variance-covariance matrix to model the random effects. To test the association between CLS variables and prior visual field progression, we used 2 types of regression models. First, we created linear regression models with the MD slopes as a continuous outcome. Second, we used binary logistic regression models with a dichotomous classification of MD slopes (fast vs slow), with cutoff at MD slopes less than −1.0 dB/y.¹⁷

A large number of variables (n = 55) can be derived from the CLS output (eFigure 2 and eAppendix 2 in the Supplement). For each of the models described above (linear and logistic), we tested the association between the dependent variables and CLS variables with 2 different approaches, using (1) each variable (n = 55) in univariable and multivariable models and (2) principal component (PC) analysis to reduce the number of the above-mentioned factors. The details of the PC analysis method have been described elsewhere.¹⁸ A brief description of how we derived the 14 PCs is reported in eAppendix 3, eFigure 3, and eTable 1 in the Supplement.

The following covariates were also tested in each model: age, visual field MD value closest to the date of CLS recording (henceforth called baseline MD), number of medical IOP-lowering interventions, number of laser trabeculoplasty procedures, and number of incisional glaucoma surgeries during the visual field testing period. After the CLS variables were tested in univariable models, those with P values <.20 were evaluated in multivariable models with the covariates, using backward stepwise selection to eliminate those with P values >.05, although the covariates were kept as locked terms (regardless of their P values).

Finally, to determine whether regression models including CLS variables had better fit than when using mean IOP (ie, the mean of all GAT IOP measurements during the sequence of visual fields used to calculate the MD slopes), we compared Akaike information criteria (AIC) between the models. In brief, this statistic enables the comparison of the goodness-of-fit between models while taking into account their complexity, which can be influenced by the number of variables. The model with a smaller AIC value suggests better fit. We also reported the adjusted R² values for each model to measure the proportion of the total variance of the outcome that is explained by the set of variables.

We used the Benjamini-Hochberg procedure to account for family-wise error rates. False discovery rates were set at 10%. All tests were 2-tailed. Statistical analyses were performed using commercially available software (Stata, version 14; StataCorp LP).

Results

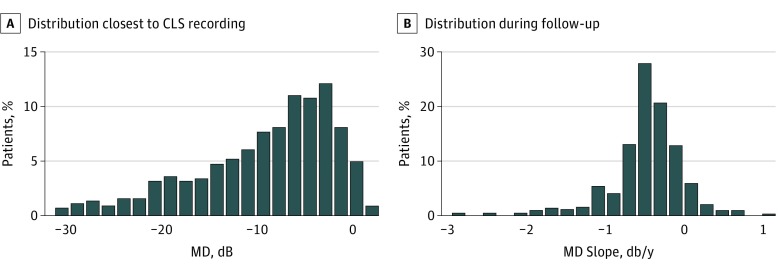
We analyzed the data of 445 eyes of 445 patients (238 [53.5%] women]; 394 [88.5%] white). The mean (SD) age at the time of CLS testing was 68.9 (11.2) years, and patients were examined with a mean of 7.5 (5.4) visual field tests spanning 4.7 (5.4) years. The mean time between the first and last visual field test and the CLS recording was −1975 (range, −5923 to −220) and −39 (range, −1015 to +397) days, respectively (“−” indicates before the CLS recording, and “+” is after the recording). The Figure shows the distribution of MD values (closest to the date of CLS recording) and MD slopes. The mean baseline MD was −9 (7) dB and mean MD slope was −0.46 (0.5) dB/y.

Figure. — A, Histogram showing the distribution of mean (SD) of the mean deviation (MD) values (dB) closest to the date of contact lens sensor recording (mean, −9.0 [7.0] dB). B, Histogram showing the distribution of MD slopes (dB) during the 5.2 (3.0) years of follow-up (mean, −0.46 [0.5] dB/y).

eTable 2 in the Supplement provides the correlation table testing of the association among CLS PCs, age, MD severity, MD slopes, and GAT IOP. Eyes with lower GAT IOP experienced faster rates of MD change prior to CLS testing, suggesting escalation of therapy as progression was detected or suspected. Also, eyes with a lower IOP had worse baseline MD. The PC3, PC8, and PC10 findings were associated with GAT IOP. In addition, many PCs were associated with age (PC1, PC3, PC4, PC5, PC7, PC11, and PC12).

Linear Regression Models

CLS Variables as Independent Variables

Table 1 reports the multivariable model including the set of confounders. The model had an AIC value of 515.7 and an adjusted R² value of 27.9%. Table 2 reports the results of the univariable analysis of each CLS variable. Those with a significance level of P < .20 were entered in the multivariable model with the covariates discussed above (Table 3). The significant CLS variable after the Benjamini-Hochberg procedure was the mean peak ratio while awake. The model had an AIC value of 506.5 and an adjusted R² value of 30.1%. The model including mean GAT IOP instead of CLS variables had an AIC value of 517.3 and an adjusted R² value of 27.8% (eTable 3 in the Supplement).

Table 1. Multivariable Linear Regression Analysis With Covariates Included as Confounders^a.

Covariate	β (95% CI)	P Value
Laser	−0.050 (−0.143 to 0.042)	.28
Medications	−0.032 (−0.053 to −0.011)	.003
Surgery	0.027 (−0.056 to 0.111)	.52
Baseline MD (per dB)	0.035 (0.029 to 0.041)	<.001
Age (per decade)	−0.018 (−0.054 to 0.017)	.30

Open in a new tab

Abbreviation: MD, mean deviation.

^{^a}

The dependent variable is the MD slope in decibels per year. Akaike information criterion, 515.7; adjusted R² = 27.9%.

Table 2. Univariable Linear Regression Analysis of 55 Individual Contact Lens Sensor Variables^a .

Variable	β (95% CI)	P Value
All bursts amplitude mean (per unit)	0.008 (−0.095 to 0.111)	.88
All bursts amplitude SD (per 0.1 U)	−0.003 (−0.017 to 0.010)	.60
All bursts OPA mean (per 0.01 U)	0.004 (−0.010 to 0.019)	.53
All bursts OPA SD (per 0.01 U)	0.030 (−0.006 to 0.067)	.11
All bursts OPF mean (per 10 U)	−0.006 (−0.062 to 0.048)	.81
All bursts OPF SD (per unit)	0.020 (−0.003 to 0.043)	.09
All bursts peak count mean (per unit)	0.002 (−0.010 to 0.015)	.69
All bursts peak count SD (per unit)	0.001 (−0.015 to 0.016)	.94
All bursts SD mean (per 0.1 U)	0.016 (−0.051 to 0.085)	.63
Amplitude (per 100 U)	−0.005 (−0.043 to 0.031)	.76
Amplitude of the cosine curve (per 100 U)	0.022 (−0.057 to 0.103)	.58
Auc sleep (per 10 U)	−0.000 (−0.015 to 0.013)	.92
Cosinor OPA acrophase (per 0.1 U)	0.004 (−0.012 to 0.022)	.59
Cosinor OPA amplitude (per 0.01 U)	0.010 (−0.013 to 0.033)	.39
Cosinor OPA mesor (per 0.01 U)	0.007 (−0.006 to 0.021)	.29
Day1 bursts amplitude mean (per unit)	−0.008 (−0.074 to 0.057)	.80
Day1 bursts amplitude SD (per unit)	0.027 (−0.108 to 0.161)	.70
Day1 bursts peak count mean (per unit)	−0.002 (−0.010 to 0.006)	.57
Day1 bursts peak count SD (per unit)	0.002 (−0.017 to 0.021)	.85
Day1 bursts SD mean (per 0.1 U)	−0.007 (−0.050 to 0.036)	.75
Level sleep start (per 100 U)	−0.090 (−0.182 to 0.001)	.05
Mean peak ratio 24 h (per 10 U)	−0.014 (−0.038 to 0.009)	.23
Mean peak ratio sleep (per 10 U)	0.000 (−0.020 to 0.021)	.97
Mean peak ratio wake (per 10 U)	−0.018 (−0.038 to 0.001)	.07
No. of brief peaks 24 h (per unit)	−0.016 (−0.049 to 0.017)	.34
No. of brief peaks sleep (per unit)	−0.029 (−0.087 to 0.030)	.34
No. of brief peaks wake (per unit)	−0.026 (−0.065 to 0.012)	.18
Night bursts amplitude mean (per 0.1 U)	0.017 (−0.003 to 0.038)	.11
Night bursts amplitude SD (per unit)	0.020 (−0.113 to 0.153)	.77
Night bursts OPA mean (per 0.01 U)	0.003 (−0.010 to 0.017)	.66
Night bursts OPA SD (per 0.1 U)	0.383 (−0.148 to 0.915)	.16
Night bursts OPF mean (per 10 U)	−0.014 (−0.068 to 0.040)	.62
Night bursts OPF SD (per unit)	0.020 (−0.007 to 0.047)	.15
Night bursts peak count mean (per unit)	0.024 (−0.033 to 0.082)	.40
Night bursts peak count SD (per unit)	−0.001 (−0.031 to 0.029)	.96
Night bursts SD mean (per 0.01 U)	0.014 (0.001 to 0.027)	.04
No. of long peaks 24 h (per unit)	0.008 (−0.005 to 0.021)	.24
No. of long peaks sleep (per unit)	0.023 (−0.011 to 0.057)	.18
No. of brief peaks wake (per unit)	0.007 (−0.010 to 0.024)	.43
OPA maximum (per 0.01 U)	0.003 (−0.005 to 0.012)	.42
OPA minimum (per 0.01 U)	−0.003 (−0.002 to 0.001)	.75
OPA night amplitude smoothed (per 0.1 U)	0.054 (−0.134 to 0.243)	.57
OPA night delta (per 0.1 U)	−0.042 (−0.139 to 0.055)	.39
OPA night delta smoothed (per 0.1 U)	−0.045 (−0.187 to 0.096)	.53
OPA night noise (per 0.01 U)	0.055 (−0.012 to 0.012)	.11
OPA SD (per 0.01 U)	0.037 (−0.016 to 0.090)	.17
SD (per 100 U)	0.023 (−0.094 to 0.140)	.70
Tojo (per 100 U)^b	0.019 (−0.027 to 0.066)	.42
Variability from mean 24 h (per 100 U)	0.064 (−0.062 to 0.191)	.32
Variability from mean sleep (per 100 U)	0.016 (−0.180 to 0.214)	.87
Variability from mean wake (per 100 U)	−0.015 (−0.136 to 0.105)	.80
Variability from smooth 24 h (per 10 U)	−0.076 (−0.202 to 0.049)	.23
Variability from smooth sleep (per 10 U)	0.139 (0.007 to 0.271)	.04
Variability from smooth wake (per 10 U)	−0.113 (−0.210 to −0.015)	.02
Wake-to-sleep slope (per 100 U)	0.141 (0.041 to 0.240)	.005

Open in a new tab

Abbreviations: AUC, area under the curve; OPA, ocular pulse amplitude; OPF, ocular pulse frequency.

^{^a}

The dependent variable is the mean deviation slope in decibels per year.

^{^b}

This feature is defined as maximum (Triggerfish burst curve during sleep) − minimum (Triggerfish burst curve during sleep). By Triggerfish burst curve we mean the curve composed of the 288 medians from the actual curve.¹⁹

Table 3. Multivariable Linear Regression Analysis With Stepwise Backward Selection of Contact Lens Variables and the Set of Covariates^a.

Covariates	β (95% CI)	P Value
Night bursts OPF SD (per unit)	0.027 (0.004 to 0.051)	.02^b
Night bursts OPA SD (per 0.1 U)	19.739 (1.333 to 38.145)	.04^b
No. of long peaks sleep (per unit)	0.036 (0.005 to 0.067)	.02^b
Mean peak ratio wake (per 10 U)	−0.021 (−0.04 to −0.003)	.02^b
OPA SD (per 0.01 U)	−1.928 (−3.771 to −0.084)	.04
Age (per decade)	−0.028 (−0.064 to 0.008)	.13
Baseline MD (per dB)	0.034 (0.028 to 0.040)	<.001^b
Laser	−0.042 (−0.133 to 0.050)	.37
Medications	−0.032 (−0.053 to −0.011)	.003^b
Surgery	0.006 (−0.078 to 0.090)	.90

Open in a new tab

Abbreviations: MD, mean deviation; OPA, ocular pulse amplitude; OPF, ocular pulse frequency.

^{^a}

Akaike information criterion, 506.5; adjusted R² = 30.1%. The covariates laser, surgery, medications, age, and baseline MD are set as locked terms. The dependent variable is the MD slope in decibels per year.

^{^b}

Significant after Benjamini-Hochberg procedure.

PCs as Independent Variables

eTable 4 in the Supplement provides the results of the univariable analysis of each PC. Those with a significance level of P < .20 were entered into the multivariable model (eTable 5 in the Supplement). The model had an AIC value of 513.5 and an adjusted R² value of 28.4%.

Binary Logistic Regression Models

CLS Variables as Independent Variables

eTable 6 in the Supplement reports the multivariable model including the set of confounders. The model had an AIC value of 263.8 and a pseudo R² value of 21.5%. eTable 7 in the Supplement provides the results of the univariable analysis of each CLS variable. Those with P < .20 were entered in the multivariable model with the covariates described above (eTable 8 in the Supplement). Significant CLS variables after the Benjamini-Hochberg procedure were the variability from smooth while awake. The model had an AIC value of 256.5 and a pseudo R² value of 25.0%. The model including mean GAT IOP instead of CLS variables had an AIC value of 265.6 and a pseudo R² value of 21.5% (eTable 9 in the Supplement).

PCs as Independent Variables

eTable 10 in the Supplement provides the results of the univariable analysis of each PC. Those with significance of P < .20 were entered in the multivariable model presented in eTable 11 in the Supplement. Significant CLS PCs after the Benjamini-Hochberg procedure were PC6 and PC10. The model had an AIC value of 254.6 and a pseudo R² value of 25.6%.

Discussion

We tested the hypothesis that a combination of features derived from a CLS output was associated with rates of visual field progression of patients with treated glaucoma. We found that a combination of CLS variables obtained during a single 24-hour recording session was associated with prior global rates of progression. Moreover, the models including CLS variables had better fit compared with measurements taken with the current standard, that is, the mean IOP measured with GAT over the entire follow-up period.

Among the tested CLS variables, the mean peak ratio while the patient was awake was the best variable associated with faster visual field progression of glaucoma. As described in eAppendix 2 in the Supplement, a CLS output peak will have a high peak ratio if the height is greater, the time to peak is shorter, or both. This ratio describes peaks that are more likely to be clinically significant. Our results show that, for every 10-U increase in this ratio, the mean rate of MD change was 0.02 dB/y faster on average. To put this finding in perspective, when analyzing data from the Ocular Hypertension Treatment Study, De Moraes et al²⁰ showed that a 1–mm Hg IOP reduction led to a mean MD rate of change improvement of 0.03 dB/y on average. Among the tested CLS PCs, PC6 was associated with faster progression. The variables with strongest loading to this component were the night bursts amplitude mean and night bursts peak count mean. However, the direction of the association is opposite from what one would expect: the higher PC6 score, the slowest the rate of MD change (mean, 0.02 dB/y slower on average for each unit increase). There are at least 3 potential explanations for this finding. First, eyes with faster progression may have been treated more aggressively, which probably dampened the nocturnal bursts by the time of CLS testing. This finding can be implied based on the effect of medications and baseline MD severity in the multivariable model (Table 1). In addition, the mean GAT IOP was lower in eyes with faster MD slopes, which also had worse baseline MD (eAppendix 4 in the Supplement). Another possibility is related to the definition of these nocturnal bursts, which are small signals measured within 30 seconds and may not have the same clinical implications as the larger, longer peaks depicted with the mean peak ratio. These short signals may be physiologic phenomena that reflect the plasticity of the globe. For instance, in eyes with stiffer sclera, changes in IOP may lead to greater deformation of the corneoscleral junction that translate into large, long CLS signals; in more plastic eyes, the energy from the same amount of IOP change may be absorbed and result in these short signals. A greater number of these bursts would then suggest more plasticity and more protective biomechanical properties of the eye. Finally, a third possibility is that this is a spurious result given the multiple comparisons performed in this study and thus the increased false-discovery rates.

The MD slope findings were mean, −0.46; median, −0.38; and 95% CI, −0.51 to −0.41 dB/y. Given the progressive and irreversible nature of glaucomatous damage, risk assessment plays an important role in clinical decision making. Glaucoma in patients experiencing faster visual field progression is more likely to continue advancing at faster rates if no changes in treatment are made. Bengtsson et al²¹ investigated how well prior visual field progression rates can estimate future visual field outcomes in patients with glaucoma followed up for a mean of 8 years. By using the rates of change of the first half of follow-up to estimate the entire sequence of 10 or more visual field tests, the investigators were able to estimate the final global indices within ±10% of the estimated final visual field index in 70% of the patients. Applying these findings to ours, patients deemed to have fast-progressing glaucoma prior to CLS recordings are more likely to sustain faster progression in the future. Nonetheless, in clinical practice, preexisting rates of visual field change are not always available to estimate future outcomes. Therefore, our findings suggest that 24-hour CLS recordings are significantly correlated with prior rates of progression and thus may be useful to assess the risk of future functional loss, even in situations when insufficient historical visual field information is available.

One characteristic of CLS recording is that, although the patterns are correlated with IOP, it does not measure pressure, but rather electric signals owing to volumetric changes in the eye.¹¹ Nonetheless, the fact that the CLS system measures how the ocular structures respond to pressure may provide additional information to IOP alone. It is therefore possible that IOP findings alone may not fully explain mechanical damage that occurs in glaucoma, but may rather be a function of how tissues respond to a mechanical stimulus based on their biomechanical properties. It is thus possible that CLS-derived signals reflect not only the pressure-related component of glaucomatous damage, but also the susceptibility of ocular tissues to pressure.²²

In particular, studies in human posterior ocular tissues have shown that the biomechanical properties of the peripapillary sclera and lamina cribrosa can help to explain how the optic nerve neural tissue may respond to pressure mechanical insult.^21,23,24,25 In eyes with stiffer sclera, for instance, pressure may be transmitted to the lamina cribrosa, causing greater back-bowing compared with eyes with more elastic sclera. The sclera becomes stiffer with aging,^26,27 and this may help to explain why age increases susceptibility to glaucomatous damage and progression. Although age was not associated with progression in our sample, we found a significant association between age and a number of PCs (eAppendix 4 in the Supplement). It is therefore possible that aging and its effect on scleral stiffness may help to explain CLS signals and how they relate to glaucoma progression. Given that CLS signals are the result of changes in the curvature of the corneoscleral junction, it is plausible that the effects of IOP on the anterior and posterior portions of the scleral canal are correlated. Future studies investigating the association between aging, biomechanical properties of the sclera (or corneascleral junction), and CLS signals are warranted to test the afore-described hypothesis.

Limitations and Strengths

Although we included data from studies that prospectively collected 24-hour IOP-related profiles with the CLS, the present study is a secondary data analysis based on retrospective visual field data collection, thus being subject to the inherent limitations of retrospective study designs. For instance, patients experiencing fast progression during follow-up may have received more aggressive treatment, which in turn could have altered the CLS signals by the time of recording. It is possible, therefore, that stronger effects might have been detected had glaucoma remained untreated—or treatment had not been escalated—during follow-up. This is an issue that future prospective studies should take into account, as not treating or not advancing therapy in the face of progression would be ethically challenging. Given the mainly retrospective study design, it is therefore difficult to determine whether the underlying nature of the association between CLS variables and rates of visual field progression, that is, whether CLS variables are indeed able to estimate faster progression or they reflect changes to treatment as the result of detected or suspected progression prior to CLS testing.

In addition, we were able to test the association, but not the predictive ability, between the 24-hour CLS signals and rates of visual field progression. Future studies with prospective collection of visual field tests after CLS recording ought to be performed to evaluate its performance to possibly recognize the patients at highest risk of visual field progression. If confirmed, these findings could have clinical application on risk stratification in glaucoma. For now, it is relevant that a single 24-hour recording with a device that measures volumetric changes related to IOP is associated with prior rates of visual field progression. The findings show that this association was better than that seen when using the present standard for IOP monitoring (ie, the mean follow-up IOP with GAT). Finally, the present study provides support for previous work by including a larger sample size and evaluating more features of the CLS output, including PCs that summarize most of the variance of its 24-hour signals.

Conclusions

In a large multicentric cohort of patients with treated glaucoma, a single 24-hour monitoring of IOP-related patterns provided a signature that was associated with prior rates of visual field progression. Moreover, this signature performed better than the mean GAT IOP during follow-up. Future studies addressing the present limitations and testing the predictive ability of this device are warranted.

Supplement.

eAppendix 1. Institutional Review Boards

eAppendix 2. Triggerfish Parameters Tested in the Present Study

eAppendix 3. Principal Component Analysis

eFigure 1. Flowchart Showing the Reasons for Excluding / Including Patients in the Present Study

eFigure 2. Twenty-four Hour Contact Lens Sensor Output

eFigure 3. Scree Plot Showing the Relationship Between Eigenvalues and the Number of Components

eTable 1. Factors Loadings From Principal Component Analysis With 14 Components

eTable 2. Spearman’s Correlation Coefficients (Top Row) and P-Values (Bottom Row)

eTable 3. Multivariable Linear Regression Analysis of Mean Goldmann Intraocular Pressure and Covariates

eTable 4. Univariable Linear Regression Analysis of Individual Principal Components (PCs) Derived From Contact Lens Sensor Parameters

eTable 5. Multivariable Linear Regression Analysis With Stepwise Backward Selection of Principal Components Derived From Contact Lens Parameters (P<0.20 in Univariable Models) and the Set of Covariates

eTable 6. Multivariable Linear Regression Analysis With Covariates Included as Confounders

eTable 7. Univariable Linear Regression Analysis of Individual Contact Lens Sensor Parameters (N=55)

eTable 8. Multivariable Logistic Regression Analysis With Stepwise Backward Selection of Contact Lens Parameters (P<0.20 in Univariable Models) and the Set of Covariates

eTable 9. Multivariable Logistic Regression Analysis With Mean Goldmann Intraocular Pressure and the Set of Covariates

eTable 10. Univariable Logistic Regression Analysis With Each Principal Component Derived From the Contact Lens Parameters

eTable 11. Multivariable logistic Regression Analysis With Stepwise Backward Selection of Principal Components Derived From the Contact Lens Parameters (P<0.20 in Univariable Models) and the Set of Covariates

Click here for additional data file.^{(321KB, pdf)}

References

1.Gordon MO, Beiser JA, Brandt JD, et al. . The Ocular Hypertension Treatment Study: baseline factors that predict the onset of primary open-angle glaucoma. Arch Ophthalmol. 2002;120(6):714-720. [DOI] [PubMed] [Google Scholar]
2.Leske MC, Heijl A, Hussein M, Bengtsson B, Hyman L, Komaroff E; Early Manifest Glaucoma Trial Group . Factors for glaucoma progression and the effect of treatment: the Early Manifest Glaucoma trial. Arch Ophthalmol. 2003;121(1):48-56. [DOI] [PubMed] [Google Scholar]
3.The AGIS Investigators The Advanced Glaucoma Intervention Study (AGIS)—7: the relationship between control of intraocular pressure and visual field deterioration. Am J Ophthalmol. 2000;130(4):429-440. [DOI] [PubMed] [Google Scholar]
4.Collaborative Normal-Tension Glaucoma Study Group The effectiveness of intraocular pressure reduction in the treatment of normal-tension glaucoma. Am J Ophthalmol. 1998;126(4):498-505. [DOI] [PubMed] [Google Scholar]
5.Musch DC, Gillespie BW, Niziol LM, Lichter PR, Varma R; CIGTS Study Group . Intraocular pressure control and long-term visual field loss in the Collaborative Initial Glaucoma Treatment Study. Ophthalmology. 2011;118(9):1766-1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Realini T, Weinreb RN, Wisniewski S. Short-term repeatability of diurnal intraocular pressure patterns in glaucomatous individuals. Ophthalmology. 2011;118(1):47-51. [DOI] [PubMed] [Google Scholar]
7.Barkana Y, Anis S, Liebmann J, Tello C, Ritch R. Clinical utility of intraocular pressure monitoring outside of normal office hours in patients with glaucoma. Arch Ophthalmol. 2006;124(6):793-797. [DOI] [PubMed] [Google Scholar]
8.Liu JH, Zhang X, Kripke DF, Weinreb RN. Twenty-four-hour intraocular pressure pattern associated with early glaucomatous changes. Invest Ophthalmol Vis Sci. 2003;44(4):1586-1590. [DOI] [PubMed] [Google Scholar]
9.Takagi D, Sawada A, Yamamoto T. Evaluation of a new rebound self-tonometer, Icare HOME: comparison with Goldmann applanation tonometer. J Glaucoma. 2017;26(7):613-618. [DOI] [PubMed] [Google Scholar]
10.Mudie LI, LaBarre S, Varadaraj V, et al. . The Icare HOME (TA022) study: performance of an intraocular pressure measuring device for self-tonometry by glaucoma patients. Ophthalmology. 2016;123(8):1675-1684. [DOI] [PubMed] [Google Scholar]
11.Mansouri K, Shaarawy T. Continuous intraocular pressure monitoring with a wireless ocular telemetry sensor: initial clinical experience in patients with open angle glaucoma. Br J Ophthalmol. 2011;95(5):627-629. [DOI] [PubMed] [Google Scholar]
12.Mansouri K, Weinreb RN, Liu JH. Efficacy of a contact lens sensor for monitoring 24-h intraocular pressure related patterns. PLoS One. 2015;10(5):e0125530. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.De Moraes CG, Jasien JV, Simon-Zoula S, Liebmann JM, Ritch R. Visual field change and 24-hour IOP-related profile with a contact lens sensor in treated glaucoma patients. Ophthalmology. 2016;123(4):744-753. [DOI] [PubMed] [Google Scholar]
14.World Medical Association World Medical Association Declaration of Helsinki: ethical principles for medical research involving human subjects. JAMA. 2013;310(20):2191-2194. [DOI] [PubMed] [Google Scholar]
15.Yohannan J, Wang J, Brown J, et al. . Evidence-based criteria for assessment of visual field reliability. Ophthalmology. 2017;124(11):1612-1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Leonardi M, Leuenberger P, Bertrand D, Bertsch A, Renaud P. First steps toward noninvasive intraocular pressure monitoring with a sensing contact lens. Invest Ophthalmol Vis Sci. 2004;45(9):3113-3117. [DOI] [PubMed] [Google Scholar]
17.Chauhan BC, Garway-Heath DF, Goñi FJ, et al. . Practical recommendations for measuring rates of visual field change in glaucoma. Br J Ophthalmol. 2008;92(4):569-573. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Cattell RB, Vogelmann S. A comprehensive trial of the scree and KG criteria for determining the number of factors. Multivariate Behav Res. 1977;12(3):289-325. [DOI] [PubMed] [Google Scholar]
19.Tojo N, Otsuka M, Miyakoshi A, Fujita K, Hayashi A. Improvement of fluctuations of intraocular pressure after cataract surgery in primary angle closure glaucoma patients. Graefes Arch Clin Exp Ophthalmol. 2014;252(9):1463-1468. [DOI] [PubMed] [Google Scholar]
20.De Moraes CG, Demirel S, Gardiner SK, et al. ; Ocular Hypertension Treatment Study Group . Effect of treatment on the rate of visual field change in the ocular hypertension treatment study observation group. Invest Ophthalmol Vis Sci. 2012;53(4):1704-1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Bengtsson B, Patella VM, Heijl A. Prediction of glaucomatous visual field loss by extrapolation of linear trends. Arch Ophthalmol. 2009;127(12):1610-1615. [DOI] [PubMed] [Google Scholar]
22.Chauhan BC, Malik R, Shuba LM, Rafuse PE, Nicolela MT, Artes PH. Rates of glaucomatous visual field change in a large clinical population. Invest Ophthalmol Vis Sci. 2014;55(7):4135-4143. [DOI] [PubMed] [Google Scholar]
23.Roberts MD, Sigal IA, Liang Y, Burgoyne CF, Downs JC. Changes in the biomechanical response of the optic nerve head in early experimental glaucoma. Invest Ophthalmol Vis Sci. 2010;51(11):5675-5684. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Girkin CA, Fazio MA, Yang H, et al. . Variation in the three-dimensional histomorphometry of the normal human optic nerve head with age and race: lamina cribrosa and peripapillary scleral thickness and position. Invest Ophthalmol Vis Sci. 2017;58(9):3759-3769. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Rhodes LA, Huisingh C, Johnstone J, et al. . Variation of laminar depth in normal eyes with age and race. Invest Ophthalmol Vis Sci. 2014;55(12):8123-8133. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Grytz R, Fazio MA, Libertiaux V, et al. . Age- and race-related differences in human scleral material properties. Invest Ophthalmol Vis Sci. 2014;55(12):8163-8172. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Fazio MA, Grytz R, Morris JS, Bruno L, Girkin CA, Downs JC. Human scleral structural stiffness increases more rapidly with age in donors of African descent compared to donors of European descent. Invest Ophthalmol Vis Sci. 2014;55(11):7189-7198. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials