PET and MRI image fusion based on combination of 2-D Hilbert transform and IHS method

Abstract

Background

The process of medical image fusion is combining two or more medical images such as Magnetic Resonance Image (MRI) and Positron Emission Tomography (PET) and mapping them to a single image as fused image. So purpose of our study is assisting physicians to diagnose and treat the diseases in the least of the time.

Methods

We used Magnetic Resonance Image (MRI) and Positron Emission Tomography (PET) as input images, so fused them based on combination of two dimensional Hilbert transform (2-D HT) and Intensity Hue Saturation (IHS) method. Evaluation metrics that we apply are Discrepancy (D_k) as an assessing spectral features and Average Gradient (AG_k) as an evaluating spatial features and also Overall Performance (O.P) to verify properly of the proposed method.

Results

In this paper we used three common evaluation metrics like Average Gradient (AG_k) and the lowest Discrepancy (D_k) and Overall Performance (O.P) to evaluate the performance of our method. Simulated and numerical results represent the desired performance of proposed method.

Conclusions

Since that the main purpose of medical image fusion is preserving both spatial and spectral features of input images, so based on numerical results of evaluation metrics such as Average Gradient (AG_k), Discrepancy (D_k) and Overall Performance (O.P) and also desired simulated results, it can be concluded that our proposed method can preserve both spatial and spectral features of input images.

At a glance commentary

Scientific background on the subject

The important goal of bringing up our proposed method based on combination of 2-D HT and IHS method to fuse PET and MRI images is highlighting the main and significant features and also ignoring the uncommon features in fused image.

What this study adds to the field

The advantage of this method is improving spatial information of fused image because of using IHS space and also improving spectral information due to applying 2-D HT transform. Our proposed method provides better results both in terms of visual and quantitative criteria than other fusion methods that mentioned in this paper.

Image fusion is the process of integrating two or more images in to a single image. The main purpose of image fusion is to preserve all significant, related and relevant information existing in each of the input images. Medical image fusion is one of the most important subcategory of image fusion. Generally the multi-modal medical image fusion is the process of combining the information from each of the input medical images that taken from specific organ of the body in to a single image, this resulted image is named fused image. Fused image is more useful than any of the input medical images. Nowadays medical imaging techniques, are used extensively in fields of diagnosis and treatment of diseases by doctors. Since each of the medical imaging modalities are not able to show all of the useful information of the specific organ under study, so employing the medical image fusion arises. Different medical images have different features, for example the origin of Magnetic Resonance Image (MRI) is very powerful magnetic source and radio waves. These images can represent the details of internal body structures and give useful information about soft tissues such as heart, brain tumors, lungs and livers. The main important advantages of MRI imaging system are non-invasive and does not use ionizing radiation and also create images that contain high spatial resolution. In addition it provides structural information of special organs. On the other hand the origin of PET images is based on positron emission. Also this imaging system can provide functional information and metabolisms of specific tissues in addition to anatomical information. This property gives the possibility to the physicians that early diagnose the diseases and progressive of tumors. PET images are colorful and have rather low spatial resolution [1], [2], therefore we need special fusion method to fuse PET and MRI images to find single fused image that contain both spatial and spectral useful information.

Material and methods

Medical image fusion methods commonly implemented in three important levels such as pixel level fusion, feature level fusion and decision level fusion [3], [4], [5]. In this paper we want to fuse PET and MRI images at pixel level. Also medical image fusion include the various fields such as image processing [6] computer vision [7], pattern recognition [8] and machine learning [1], [2], [9]. There are several different image methods such as the Brovey Transform (BT), Intensity Hue Saturation (IHS) [10] and Principal Component Analysis (PCA) [11], that provide the basis for many common image fusion techniques. These methods are commonly applied for fusing the RGB images. Each of the image fusion techniques that mentioned above have advantages and disadvantage. One of the benefits of these techniques is improving the spatial resolution of the fused image also on the other hand the main drawback of listed methods is the disability to preserve the original chromaticity of input images. Thus, using the transform domain techniques are usually used for fusing images. These transform methods are such as discrete wavelet transform (DWT) [12], curvelet transform (CVT) [13], [14], and contourlet transform (CT) [13]. Another part of image fusion techniques is pyramid methods like Gradient pyramid, Gaussian pyramid, FSD pyramid and Laplacian pyramid. In our paper we compare our proposed method with FSD pyramid technique and Gradient pyramid. Generally FSD pyramid technique is one of the computationally efficient version of Gaussian pyramid. This fusion method is similar to Laplacian pyramid method but one of the main differences between each other is omitting the upsampling step in FSD pyramid. Based on above mentioned reason we use FSD pyramid instead of Laplacian pyramid technique. Another pyramid fusion method is Gradient pyramid technique. Performance of Gradient pyramid in achieved by applying the 4 different filters such as horizontal, vertical and two diagonal filters [15]. Now in this section we want to explain briefly the Hilbert transform (HT) and the IHS method that form our proposed method.

The Hilbert Transform (HT) is one of the main and useful transform in signal processing. This transform provides a ±90° phase change to the input signal, this result implies that if the input signal is a cosine function after computing its Hilbert transform we will achieve sine function [16]. For applying Hilbert transform (HT) in signal processing, there are three steps:

• 1)Calculating the Fourier Transform to each of the input signal
• 2)Suppressing the negative frequencies
• 3)Applying inverse Fourier Transform to obtain the complex form function

Real part of the resulted signal is dealt with Analytic Signal (AS) and imaginary part is Hilbert transform (HT) of input signal. Based on explanation of calculating Hilbert Transform that stated above for input signal like S(t) we can write equations as follows [17], [18]:

$$S\underset{A}{\left(t\right)}=S\left(t\right)+iH\left\{S\left(t\right)\right\}$$ (1)

where $H\left\{S\left(t\right)\right\}$ is the HT of the signal S (t), and is calculated by the convolution:

$$S\underset{H}{\left(t\right)}=H\left\{S\left(t\right)\right\}=S\left(t\right)\ast \frac{1}{\pi t}=\frac{1}{\pi }\underset{-\infty }{\overset{+\infty }{\int }}\frac{S\left(t^{\prime }\right)}{t-t^{\prime }}d{t}^{\prime }$$ (2)

Three different mathematical methods for applying the Hilbert Transform (HT) are [19]:

• 1)Using the Cauchy integral in the complex plane
• 2)Using the Fourier Transform in the frequency domain
• 3)Looking at the ±90° phase-shift

In this paper we used the second method for applying the Hilbert Transform (HT). For real signal like f(t), if we apply the Fourier Transform, we will have the complex pair with real and imaginary part like following equations [19]:

$$Z_f\left(t\right)=f\left(t\right)+ig\left(t\right)$$ (3)

$$f\left(t\right)+ig\left(t\right)\stackrel{F}{\leftrightarrow }F\left(\omega \right)+Sgn\left(\omega \right)·F\left(\omega \right)$$ (4)

$$\text{Sgn}\left(\text{ω}\right)=\{\begin{array}{ll}1\hfill & \text{ω}>0\hfill \\ 0\hfill & \text{ω}=0\hfill \\ -1\hfill & \text{ω}<0\hfill \end{array}$$ (5)

$$\text{f}\left(\text{t}\right)\stackrel{\text{F}}{\leftrightarrow }\text{F}\left(\text{ω}\right)$$ (6)

$$\text{ig}\left(\text{t}\right)\stackrel{\text{F}}{\leftrightarrow }\text{Sgn}\left(\text{ω}\right)·\text{F}\left(\text{ω}\right)$$ (7)

Based on Eqs. (3), (4), (5), (6), (7) we can achieve the final equations for implementing of Hilbert Transform (HT) as follows:

$$\text{g}\left(\text{t}\right)\stackrel{\text{F}}{\leftrightarrow }\text{F}\left(\text{ω}\right)·\left(-\text{iSgn}\left(\text{ω}\right)\right)$$ (8)

$$\text{iSgn}\left(\text{ω}\right)\stackrel{{\text{F}}^{-1}}{\leftrightarrow }\frac{1}{\pi t}$$ (9)

And also implementation of 2-D Hilbert transform in spatial domain is given by Ref. [20]:

$$S_H\left(x\right)=S\left(x\right)\ast \frac{1}{{\pi }^{2}xy}$$ (10)

In the frequency domain, the corresponding association for the 2-D HT is:

$$S_H\left(u\right)=-\mathrm{sgn}\left(u\right)·\mathrm{sgn}\left(v\right)·S\left(u\right)$$ (11)

And the 2D-AS is given by:

$$S_A\left(u\right)=[1-\mathrm{sgn}\left(u\right)·\mathrm{sgn}\left(v\right)]·S\left(u\right)$$ (12)

Eqs. (11), (12) can be understood as the multiplication of the transformed image by a proper mask in the frequency domain. Two dimensional Hilbert transform (2-D HT) and Analytic Signal have important applications in different fields of image processing such as corner detection [16], [20]. AM-FM image models give a detailed description of localized two dimensional (2-D) frequency modulation (FM) and amplitude modulation (AM). Also these images are powerful tools for characterizing and processing textured images [21], [22], phase congruency calculations [23], edge detection [24] and operating images since the broadcast bandwidth is efficiently compact.

Image fusion based on IHS (Intensity-Hue-Saturation) technique is one of the most ordinarily used for sharpening. This color transform has become a standard method in image analysis for development of color, feature improvement and spatial resolution [25]. Also the IHS method is very simple and achieved by the matrices multiplication. For this purpose, it could be employed even for real-time systems [25]. One of the main features of IHS color space is reflecting the spectral information in to elements of Hue (H) and Saturation (S). This reason causes smaller changes of Intensity (I) component in visual system perception. The IHS space is deal with the human observation of colors. Many IHS transformation procedures are developed to convert the RGB values. Generally the instruction of IHS color space that commonly used can be summarized in three levels in bellow [25]:

• 1)Converting three components of the input image R, G and B into the IHS color space

$$\left[\begin{array}{c}1\\ {\text{V}}_1\\ {\text{V}}_2\end{array}\right]=\left[\begin{array}{ccc}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\\ -\raisebox{1ex}{$\sqrt{2}$}\!\left/ \!\raisebox{-1ex}{$6$}\right.& -\raisebox{1ex}{$\sqrt{2}$}\!\left/ \!\raisebox{-1ex}{$6$}\right.& 2\raisebox{1ex}{$\sqrt{2}$}\!\left/ \!\raisebox{-1ex}{$6$}\right.\\ \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.& -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.& 0\end{array}\right]·\left[\begin{array}{c}\text{R}\\ \text{G}\\ \text{B}\end{array}\right]$$ (13)

Where I is the intensity value. Variables V₁ and V₂ are used to represent the hue (H) and saturation (S):

$$\text{H}={\tan }^{-1}\left(\raisebox{1ex}{${\text{V}}_1$}\!\left/ \!\raisebox{-1ex}{${\text{V}}_2$}\right.\right)$$ (14)

$$\text{S}=\sqrt{{\text{V}}_1^2+{\text{V}}_2^2}$$ (15)

• 2)Replaying the intensity (I) element by the other image with higher spatial resolution after transformation
• 3)Getting back to RGB space with the original values of Hue (H) and Saturation (S).

$$\left[\begin{array}{c}{\text{R}}_{\text{new}}\\ {\text{G}}_{\text{new}}\\ {\text{B}}_{\text{new}}\end{array}\right]=\left[\begin{array}{ccc}1& -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.\\ 1& -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.& -\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.\\ 1& \sqrt{2}& 0\end{array}\right]·\left[\begin{array}{c}{\text{I}}_{\text{new}}\\ {\text{V}}_1\\ {\text{V}}_2\end{array}\right]$$ (16)

In Eq. (16) R_new, G_new and B_new show the red, green and blue components of the fused image. Fig. 1 shows the common cube model of IHS space that shows the how to transform RGB image in IHS space.

Fig. 1.

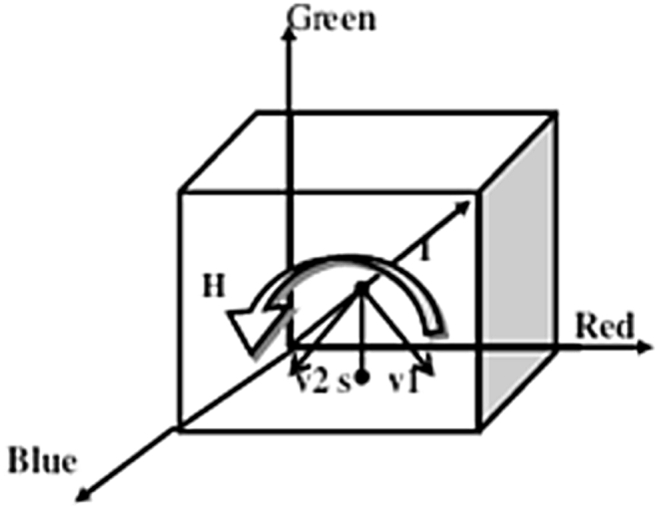
The color cube model of IHS space [25].

The IHS method is very simple and achieved by the matrices multiplication. For this purpose, it could be employed even for real-time systems [26].

In this study PET and MRI brain images used for applying proposed method. All of these input images are the same size 256×256. Preprocessing operations before the research was done to all of the input images and all of them have already been registered. There are several colormaps for representing color images like PET images such as RGB space, IHS space, HSV space and etc. Although our method apply to RGB and IHS colormaps but we have considered to display PET images in RGB space and use RGB space to IHS space algorithm in our proposed method. It is necessary to note that our proposed method has been implemented in MATLAB software. In order to apply this method to fuse PET and MRI input images, first we need to see how to apply two dimensional Hilbert transform (2-D HT) on MRI images. This process is summarized in few steps as follows:

Step 1. Applying two dimensional Hilbert transform to brain MRI images by use of Fourier transform that mentioned in section Material and methods and achieve series of coefficients related to the same transform.

Step 2. Employing multiplication of suitable mask and Fourier transform of input MRI image.

Step 3. Applying the appropriate fusion rules to combine the two dimensional Hilbert transform (2-D HT) coefficients of input images. Three common fusion rules to select the best rule is as follows:

$$H_F^K\left(i,j\right)=Max\left\{H_{MRI}^K\left(i,j\right),H_{PET}^K\left(i,j\right)\right\}$$ (17)

$$H_F^K\left(i,j\right)=Min\left\{H_{MRI}^K\left(i,j\right),H_{PET}^K\left(i,j\right)\right\}$$ (18)

$$H_F^K\left(i,j\right)=Average\left\{H_{MRI}^K\left(i,j\right),H_{PET}^K\left(i,j\right)\right\}$$ (19)

Which $H_{MRI}^K\left(i,j\right)$ is the two dimensional Hilbert transform (2-D HT) coefficients of MRI image. Also $H_{PET}^K\left(i,j\right)$ is the two dimensional Hilbert transform (2-D HT) coefficients of PET image. In this paper we use maximum fusion rule to fuse PET and MRI images based on combination of two dimensional Hilbert transform (2-D HT) and IHS method.

Step 4. Reconstructing fused image by applying inverse two dimensional Hilbert Transform (2-D HT) based on the combined coefficients that resulted in Step 3.

Also applying our proposed method to color image in RGB space like PET as input image abbreviated in 5 levels as follows:

Level 1. Using RGB to IHS algorithm to convert the color PET image from RGB space to HIS space.

Level 2. Separating the intensity component (I) of PET image in IHS domain. Hue (H) and saturation (S) of PET image in IHS space are kept the same.

Level 3. Applying two dimensional Hilbert transform (2-D HT) just for intensity component (I) of PET image. The process of applying (2-D HT) for intensity component (I) of PET is similar to applying this transform for MRI image that previously expressed.

Level 4. Using the inverse two dimensional Hilbert transform (2-D HT) to achieve the new intensity component as $\left(I_{new}\right)$.

Level 5. Representing the fused image in RGB space by using of IHS to RGB space algorithm.

Block diagram of PET and MRI image fusion based on combination of two dimensional Hilbert transform (2-D HT) and IHS method as our proposed method is shown in Fig. 2.

Fig. 2.

Block diagram of combination of proposed method (2-D HT and IHS).

Results

For evaluating our proposed method we use quantitative evaluation metrics like Average Gradient (AG_K) and Discrepancy (D_K). Also final results are achieved by calculating Overall Performance (O.P) as a trade-off between Average Gradient (AG_K) and Discrepancy (D_K) [27].

Average Gradient (AG_K) is a criteria to assess the ability of fused image to preserve the spatial quality of input images. And also the Average Gradient (AG_K) reflects the clarity of the fused image. A larger average gradient means a higher spatial resolution. The spatial quality of a M×N fused image can be measured by the Average Gradient (AG_K) at each band. The formula for calculating this measurement is computed as follows:

$$\begin{array}{l}A{G}_k=\frac{1}{(M-1)\mathrm{\cdot }(N-1)}\mathrm{\cdot }\sum _{i=1}^M\sum _{j=1}^N\sqrt{\frac{{\left(\frac{\partial f}{\partial x}\right)}^2+{\left(\frac{\partial f}{\partial y}\right)}^2}{2}}\end{array}$$ (20)

Also Discrepancy (D_K) is a measure for evaluating the ability of fused images to remain the spectral features of input images. A lower value of Discrepancy (D_K) represents a higher spectral resolution. Equation of this criteria is given by:

$$D_k=\frac{1}{M\ast N}\sum _{i=1}^M\sum _{j=1}^N\left|f_k(x,y)-f_{2k}(x,y)\right|$$ (21)

where F_k(x,y) and L_k(x,y) are the pixel values of the fused image at position (x,y). And M×N is the size of the both input images and fused image as 256×256.

At last, Overall Performance (O.P) is calculated by the difference between the Average Gradient (AG_K) and Discrepancy (D_K). Small amount of overall performance (O.P) means a higher overall fusion quality.

$$\text{O}.\text{P}=\frac{{\sum }_K\left|D_k-A{G}_k\right|}{3}\text{K}=\text{R}\left(\text{Red}\right),\text{G}\left(\text{Green}\right),\text{B}\left(\text{Blue}\right)$$ (22)

Numerical results based on Average Gradient (AG_K), Discrepancy (D_K) and Overall Performance (O.P) are given in Table 1.

Table 1.

Numerical results of comparing our proposed method (2-D HT and IHS method) based on Average Gradient (AG_K), Discrepancy (D_k) and Overall Performance (O.P).

Method	DK	AGK	O.P
IHS	14.773	5.171	9.61
Proposed method (2-D D HT and IHS)	12.826	5.227	7.568
Gradient pyramid	15.941	4.664	11.249
FSD pyramid	16.095	4.728	11.367
2-D HT	20.285	4.891	15.189
Haar wavelet	13.326	5.194	8.311

Also simulated results of our method are compared with 5 other fusion methods like IHS, FSD pyramid, Gradient pyramid, two dimensional Hilbert transform (2-D HT) and Haar wavelet in Fig. 3, Fig. 4.

Fig. 3.

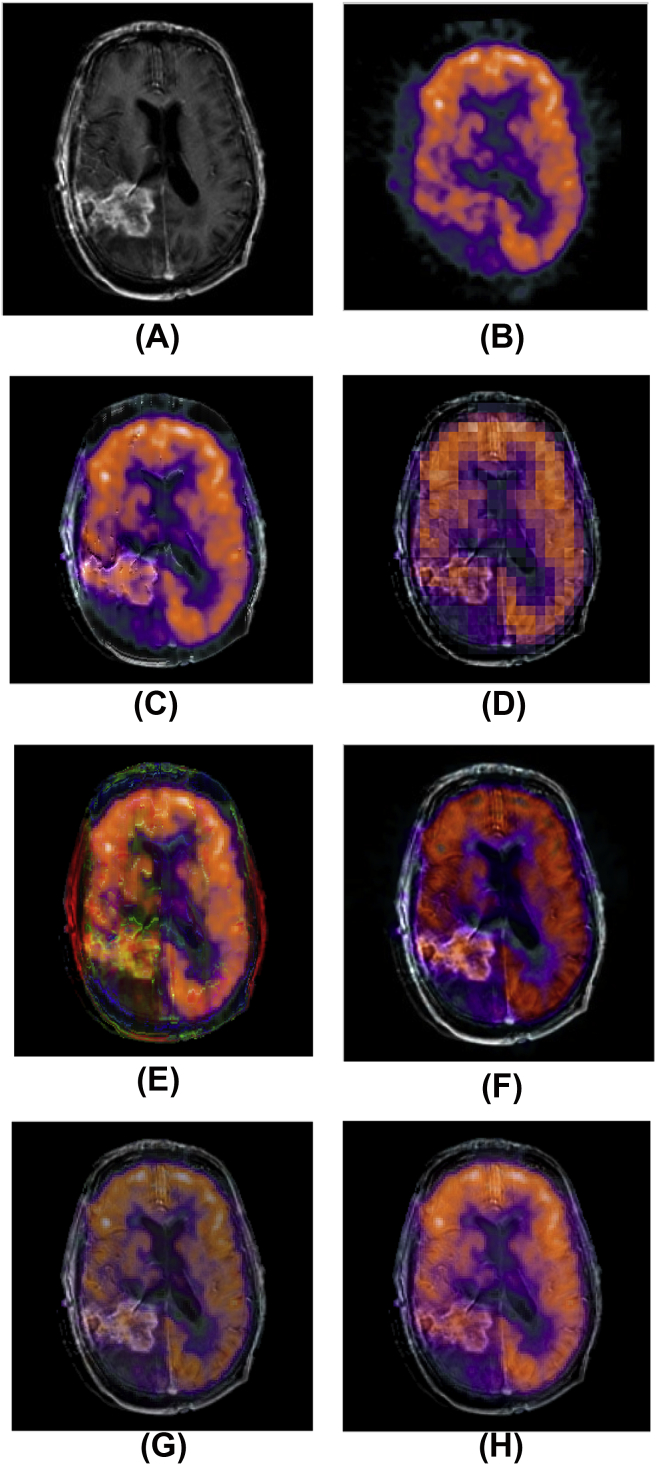
(A) Brain MRI image with tumor. (B) Brain PETimage with tumor. (C) Fused image using proposed method (2-D HT and IHS). (D) Fused image using Haar wavelet. (E) Fused image using 2-D HT. (F) Fused image using IHS (G) Fused image using FSD pyramid. (H) Fused image using Gradient pyramid.

Fig. 4.

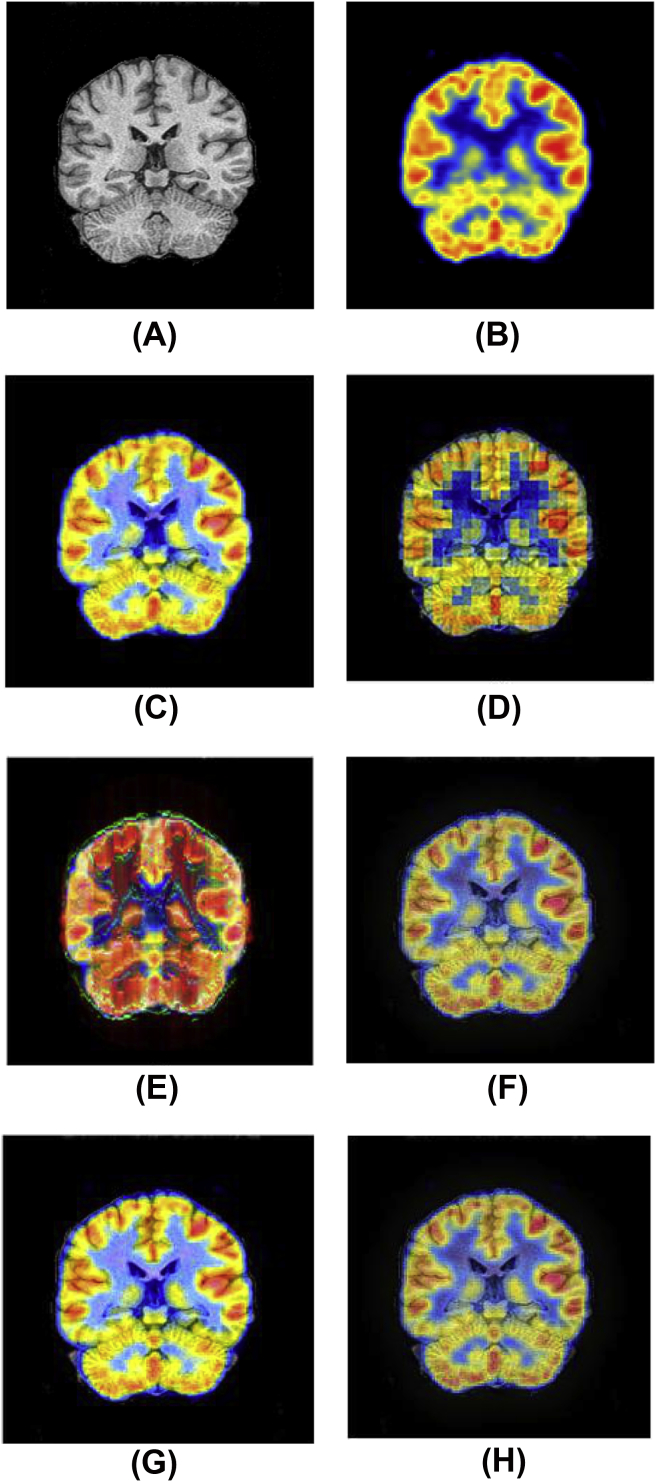
(A) Normal brain MRI image. (B) Normal PETimage. (C) Fused image using proposed method (2-D HT and IHS). (D) Fused image using Haar wavelet. (E) Fused image using 2-D HT. (F) Fused image using FSD pyramid (G) Fused image using IHS method. (H) Fused image using Gradient pyramid.

Fig. 3(A) and (B) are the MRI and PET brain images with tumor and Fig. 3(C–H) are respectively the resulted fused image based on proposed method (combination of 2-D HT and IHS), Haar wavelet, 2-D HT, FSD pyramid, IHS method and Gradient pyramid. And also Fig. 4(A) and (B) are the normal brain MRI and PET images Also Fig. 4(C–H) are respectively the resulted fused image based on proposed method (combination of 2-D HT and IHS), Haar wavelet, 2-D HT, FSD pyramid, IHS method and Gradient pyramid.

Discussion

In this paper we proposed new image fusion method based on combination of two dimensional Hilbert transform (2-D HT) and IHS method to fuse 9 series of PET and MRI normal brain images and also contain tumor. These simulated fused results are shown in Fig. 3, Fig. 4. Also for confirming the performance of our proposed method, we compared our method with 5 other common image fusion methods like IHS, FSD pyramid, Gradient pyramid, two dimensional Hilbert transform (2-D HT) and Haar wavelet. As we know there are two common evaluating analysis criteria for measuring the fusion algorithms such as qualitative and quantitative analysis [28]. Since in our work we used both normal brain PET and MRI images and brain images with tumor, so quality evaluations of the fused image plays very important role. So that whatever the quality of the fused image is high, doctors can easily recognize the location of the brain tumors and treat these disease in the least of the time. Due to the fusion results of our proposed method in Fig. 3, Fig. 4 obviously we can find out that our method's fusion results can preserve the spatial information of MRI image and also spectral features of PET image better than other fusion methods that mentioned above. Second of common evaluation metrics of fusion methods are quantitative analysis criteria. This evaluation metrics is based on mathematical equations. In this paper we used two cases of this evaluation metrics such as Average Gradient (AG_K) and Discrepancy (D_K) and Overall Performance as a connector between these mentioned metrics. Although the simulated fusion results of FSD pyramid in Fig. 3, Fig. 4 are similar to Gradient pyramid in Fig. 3, Fig. 4 and also the simulated fusion results of our proposed method and IHS method are partly similar to each other, but in case of quantitative numerical results are different. As we know, the best fusion method is the technique that presents the best qualitative and quantitative fusion results simultaneously. Since our proposed method consists of IHS method and two dimensional Hilbert transform (2-D HT) so we expect that this method has a better performance than IHS method and two dimensional Hilbert transform (2-D HT) alone in the field of preserving both quantitative and quality assessment criteria. Based on quantitative numerical results that are shown in Table 1, it can be realize that the performance of our proposed method is better than another fusion methods that we used in this paper; because of minimum Overall Performance (O.P), Discrepancy (D_k) and relatively high Average Gradient (AG_K).

Conclusion

In this paper we applied combination of IHS method and 2-D Hilbert transform to fuse 9 series of MRI and PET images. Based on values of quantitative assessment criteria that is listed in Table 1 and simulated results in Fig. 3, Fig. 4 we realized that our proposed method has minimum Discrepancy (D_K), this means that our method can preserve the spectral features and has good Average Gradient (AG_K) which means that spatial features has been preserved too. Also Overall Performance (O.P) of combination of two dimensional Hilbert transform (2-D HT) and IHS method is the lowest. Because O.P is the trade-off between spectral and spatial features, therefore desirable performance of our proposed method is proved.

Conflicts of interest

The authors declare no conflicts of interest.