Abstract
Pitch conveys critical information in speech, music, and other natural sounds, and is conventionally defined as the perceptual correlate of a sound's fundamental frequency (F0). Although pitch is widely assumed to be subserved by a single F0 estimation process, real-world pitch tasks vary enormously, raising the possibility of underlying mechanistic diversity. To probe pitch mechanisms we conducted a battery of pitch-related music and speech tasks using conventional harmonic sounds and inharmonic sounds whose frequencies lack a common F0. Some pitch-related abilities – those relying on musical interval or voice recognition – were strongly impaired by inharmonicity, suggesting a reliance on F0. However, other tasks, including those dependent on pitch contours in speech and music, were unaffected by inharmonicity, suggesting a mechanism that tracks the frequency spectrum rather than the F0. The results suggest that pitch perception is mediated by several different mechanisms, only some of which conform to traditional notions of pitch.
Introduction
Pitch is one of the most common terms used to describe sound. Although in lay terms pitch denotes any respect in which sounds vary from high to low, in scientific parlance pitch is the perceptual correlate of the rate of repetition of a periodic sound (Figure 1a). This repetition rate is known as the sound's fundamental frequency, or F0, and conveys information about the meaning and identity of sound sources. In music, F0 is varied to produce melodies and harmonies. In speech, F0 variation conveys emphasis and intent, as well as lexical content in tonal languages. Other everyday sounds (birdsongs, sirens, ringtones, etc.) are also identified in part by their F0. Pitch is thus believed to be a key intermediate perceptual feature, and has been a topic of intense interest throughout history1–3.
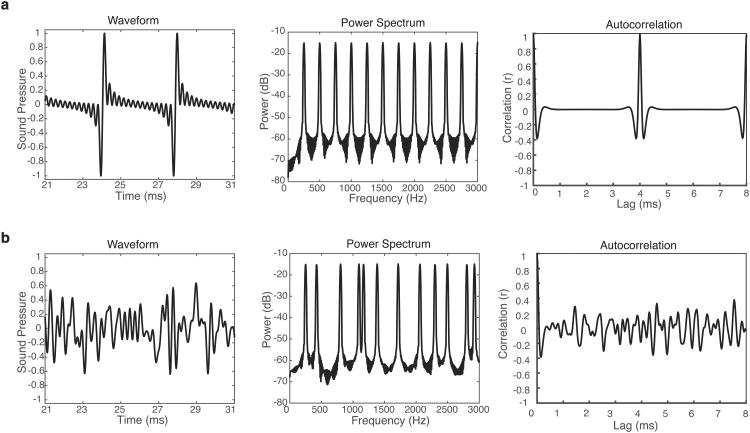
Figure 1. Example harmonic and inharmonic tones.
(A) Waveform, power spectrum and autocorrelation for a harmonic complex tone with a fundamental frequency (F0) of 250 Hz. The waveform is periodic (repeating in time), with a period corresponding to one cycle of the F0. The power spectrum contains discrete frequency components (harmonics) that are integer multiples of the F0. The harmonic tone yields an autocorrelation of 1 at a time lag corresponding to its period (1/F0).
(B) Waveform, power spectrum and autocorrelation for an inharmonic tone generated by randomly ‘jittering’ the harmonics of the tone in (a). The waveform is aperiodic, and the constituent frequency components are not integer multiples of a common F0 (evident in the irregular spacing in the frequency domain). Such inharmonic tones are thus inconsistent with any single F0. The inharmonic tone exhibits no clear peak in its autocorrelation, indicative of its aperiodicity.
The goal of pitch research has historically been to characterize the mechanism for estimating F04,5 from sound. Periodic sounds contain frequencies that are harmonically related, being multiples of the F0 (Figure 1a). The role of peripheral frequency cues, such as the place and timing of excitation in the cochlea, have thus been a focal point of pitch research6–10. The mechanisms for deriving F0 from these peripheral representations are also the subject of a rich research tradition6–14. Neurophysiological studies in non-human animals have revealed F0-tuned neurons in auditory cortex of one species (the marmoset)15,16, though as of yet there are not comparable findings in other species17,18. Functional imaging studies in humans suggest pitch-responsive regions in non-primary auditory cortex19–21. The role of these regions in pitch perception is an active area of research22,23. Despite considerable efforts to characterize the mechanisms for F0 estimation, there has been relatively little consideration of whether behaviors involving pitch might necessitate other sorts of computations24–27.
One reason to question the underlying basis of pitch perception is that our percepts of pitch support a wide variety of tasks. In some cases it seems likely that the F0 of a sound must be encoded, as when recognizing sounds with a characteristic F0, such as a person's voice28. But in many situations we instead judge the way that F0 changes over time – often referred to as relative pitch – as when recognizing a melody or speech intonation pattern29. Relative pitch could involve first estimating the F0 of different parts of a sound, and then registering how the F0 changes over time. However, pitch changes could also be registered by measuring a shift in the constituent frequencies of a sound, without first extracting F024–27. It thus seemed plausible that pitch perception in different stimulus and task contexts might involve different computations.
We probed pitch computations using inharmonic stimuli, randomly jittering each frequency component of a harmonic sound to make the stimulus aperiodic and inconsistent with any single F0 (Figure 1b)30. Rendering sounds inharmonic should disrupt F0-specific mechanisms and impair performance on pitch-related tasks that depend on such mechanisms. A handful of previous studies have manipulated harmonicity for this purpose, and found modest effects on pitch discrimination that varied somewhat across listeners and studies25–27. As we revisited this line of inquiry, it became clear that effects of inharmonicity differed substantially across pitch tasks, suggesting that pitch perception might partition into multiple mechanisms. The potential diversity of pitch mechanisms seemed important both for the basic understanding of the architecture of the auditory system and for understanding the origins of pitch deficits in listeners with hearing impairment or cochlear implants.
We thus examined the effect of inharmonicity on essentially every pitch-related task we could conceive and implement. These ranged from classic psychoacoustic assessments with pairs of notes to ethologically relevant melody and voice recognition tasks. Our results show that some pitch-related abilities – those relying on musical interval or voice perception – are strongly impaired by inharmonicity, suggesting a reliance on F0 estimation. However, tasks relying on the direction of pitch change, including those utilizing pitch contours in speech and music, were unaffected by inharmonicity. Such inharmonic sounds individually lack a well-defined pitch in the normal sense, but when played sequentially nonetheless elicit the sensation of pitch change. The results suggest that what has traditionally been couched as “pitch perception” is subserved by several distinct mechanisms, only some of which conform to the traditional F0-related notion of pitch.
Results
Experiment 1: Pitch discrimination with pairs of synthetic tones
We began by measuring pitch discrimination using a two-tone discrimination task standardly used to assess pitch perception31–33. Participants heard two tones and were asked whether the second tone was higher or lower than the first (Figure 2a). We compared performance for three conditions: a condition where the tones were harmonic, and two inharmonic conditions (Figure 2b). Here and elsewhere, stimuli were made inharmonic by adding a random amount of ‘jitter’ to the frequency of each partial of a harmonic tone (up to 50% of the original F0 in either direction) (Figure 1b). This manipulation was designed to severely disrupt the ability to recover the F0 of the stimuli. One measure of the integrity of the F0 is available in the autocorrelation peak height, which was greatly reduced in the inharmonic stimuli (Figure 1 Supplementary Figure 1).
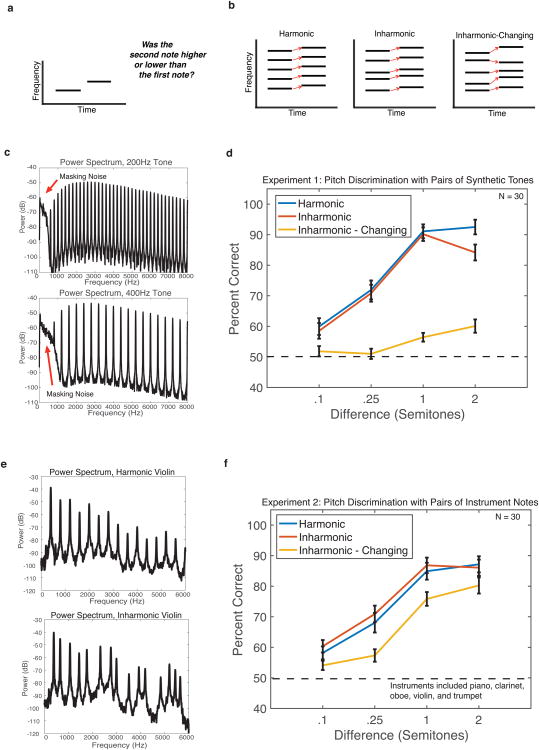
Figure 2. Task, example stimuli, and results for Experiments 1 and 2 – pitch discrimination with pairs of synthetic tones and pairs of instrument notes.
(A) Schematic of the trial structure for Experiment 1. During each trial, participants heard two tones and judged whether the second tone was higher or lower than the first tone.
(B) Schematic of the three conditions for Experiment 1. Harmonic trials consisted of two harmonic tones. Inharmonic trials contained two inharmonic tones, where each tone was made inharmonic by the same jitter pattern, such that the frequency ratios between components were preserved. This maintains a correspondence in the spectral pattern between the two tones, as for harmonic notes (indicated by red arrows). For Inharmonic-Changing trials, a different jitter pattern was applied to the harmonics of each tone, eliminating the correspondence in the spectral pattern.
(C) Power spectra of two examples tones from Experiment 1 (with F0s of 200 and 400 Hz, to convey the range of F0s used in the experiment). The fixed bandpass filter applied to each tone is evident in the envelope of the spectrum, as is the low-pass noise added to mask distortion products. The filter was intended to eliminate the spectral centroid or edge as a cue for pitch changes.
(D) Results from Experiment 1. Error bars denote standard error of the mean.
(E) Example power spectra of harmonic and inharmonic violin notes from Experiment 2.
(F) Results from Experiment 2. Error bars denote standard error of the mean.
For the “Inharmonic” condition (here and throughout all experiments), the same pattern of jitters was used within a given trial. In Experiment 1, this meant that the same pattern of jitters was applied to harmonics in both tones of the trial. This condition was intended to preserve the ability to detect F0 changes via shifts in the spectrum. For the “Inharmonic-Changing” condition, a different random jitter pattern was applied to the harmonics of each tone in the experiment. For example, for the first tone, the second harmonic could be shifted up by 30%, and in the second tone, the second harmonic could be shifted down by 10%. This lack of correspondence in the pattern of harmonics between the tones should impair the detection of shifts in the spectrum (Figure 2b) if the jitter were sufficiently large.
We hypothesized that if task performance was mediated by F0-based pitch, performance should be substantially worse for both Inharmonic conditions. If performance was instead mediated by detecting shifts in the spectrum without estimating F0, performance should be impaired for Inharmonic-Changing but similar for Harmonic and Inharmonic conditions. And if the jitter manipulation was insufficient to disrupt F0 estimation, performance should be similar for all three conditions.
In order to isolate effects of harmonic structure, a fixed bandpass filter was applied to each tone (Figure 2c). This filter was intended to approximately equate the spectral centroids (centers of mass) of the tones, which might otherwise be used to perform the task, and to prevent listeners from tracking the frequency component at the F0 (by filtering it out). This type of tone also mimics the acoustics of many musical instruments, in which a source that varies in F0 is passed through a fixed filter (e.g. the resonant body of the instrument). Here and in most other experiments, low pass noise was added to the stimuli to mask distortion products34,35, which might otherwise confer an advantage to harmonic stimuli. Demos of these and all other experimental stimuli from the paper are available as supplementary materials and at: http://mcdermottlab.mit.edu/McPhersonPitchPaper/InharmonicStimuli.html
Contrary to the idea that pitch discrimination depends on comparisons of F0, performance for Harmonic and Inharmonic tones was indistinguishable provided the pitch differences were small (a semitone or less; Figure 2d; F(1,29)=1.44, p=0.272). Thresholds were approximately 1% (.1-.25 of a semitone) in both conditions, which is similar to thresholds measured in previous studies using complex harmonic tones33. Performance for Harmonic and Inharmonic conditions differed slightly at 2 semitones (t(29)=5.22, p<0.001); this difference is explored further in Experiment 9. By contrast, the Inharmonic-Changing condition produced much worse performance (F(1,29)=92.198, p<0.001). This result suggests that the similar performance for Harmonic and Inharmonic conditions was not due to residual evidence of the F0.
To assess whether listeners might have determined the shift direction by tracking the lowest audible harmonic, we ran a control experiment in which the masking noise level was varied between the two tones within a trial, such that the lowest audible harmonic was never the same for both tones. Performance was unaffected by this manipulation (Supplementary Figure 2), suggesting that listeners are relying on the spectral pattern rather than any single frequency component. The results collectively suggest that task performance does not rely on estimating F0, and that participants instead track shifts in the spectrum, irrespective of whether the spectrum is harmonic or inharmonic.
Experiment 2: Pitch discrimination with pairs of instrument notes
To assess the extent to which the effects in Experiment 1 would replicate for real-world pitch differences, we repeated the experiment with actual instrument notes. We resynthesized recorded notes played on piano, clarinet, oboe, violin, and trumpet, preserving the spectrotemporal envelope of each note but altering the underlying frequencies as in Experiment 1 (Figure 2e; see Methods). As shown in Figure 2f, the results of these manipulations with actual instrument notes were similar to those for the synthetic tones of Experiment 1. Performance was indistinguishable for the Harmonic and Inharmonic conditions (F(1,29)=2.36, p=.136), but substantially worse in the Inharmonic-Changing condition, where different jitter patterns were again used for the two notes; (F(1,29)=41.88, p<.001). The results substantiate the notion that pitch changes are in many cases detected by tracking spectral shifts without estimating the F0s of the constituent sounds.
Experiment 3: Melodic contour discrimination
To examine whether the effects observed in standard two-tone pitch discrimination tasks would extend to multi-note melodies, we utilized a pitch contour discrimination task36. Participants heard two five-note melodies composed of semitone steps, with Harmonic, Inharmonic, or Inharmonic-Changing notes. The second melody was transposed up in pitch by half an octave, and had either an identical pitch contour to the first melody or one that differed in the sign of one step (e.g. a +1 semitone step was changed to -1 semitone). Participants judged whether the melodies were the same or different (Figure 3a).
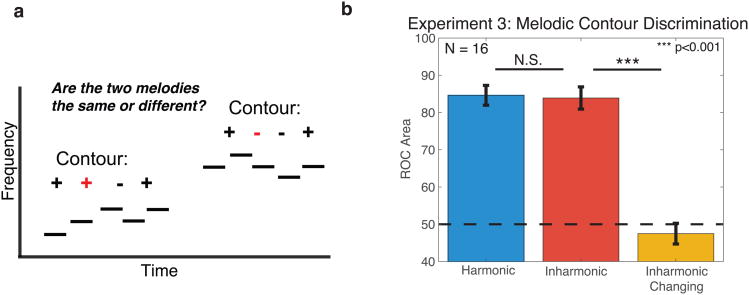
Figure 3. Task and results for Experiment 3 – melodic contour discrimination.
(A) Schematic of the trial structure for Experiment 3. Participants heard two melodies with note-to-note steps of +1 or -1 semitones, and judged whether the two melodies were the same or different. The second melody was always transposed up in pitch relative to the first melody.
(B) Results from Experiment 3. Performance was measured as the area under Receiver Operating Characteristic (ROC) curves. Error bars denote standard error of the mean.
We again observed indistinguishable performance for Harmonic and Inharmonic trials (Figure 3b; t(28)=.28, p=0.78); performance was well above chance in both conditions. By contrast, performance for the Inharmonic-Changing condition was at chance (t(28)=-0.21, p=0.84, single sample t-test vs. 0.5), suggesting that accurate contour estimation depends on the correspondence in the spectral pattern between notes. These results suggest that even for melodies of moderate length, pitch contour perception is not dependent on extracting F0, and instead can be accomplished by detecting shifts in the spectrum from note to note.
Experiment 4: Prosodic contour discrimination
To test whether the results would extend to pitch contours in speech we measured the effect of inharmonicity on prosodic contour discrimination. We used speech analysis/synthesis tools (a variant of STRAIGHT37–39) to manipulate the pitch contour and harmonicity of recorded speech excerpts. Speech excitation was sinusoidally modeled and then recombined with an estimated spectrotemporal filter following perturbations of individual frequency components.
During each trial, participants heard three variants of the same one-second speech token (Figure 4a&b). Either the first or last excerpt had a random frequency modulation (FM) added to its F0 contour, and participants were asked to identify the excerpt whose prosodic contour was different from that of the middle excerpt. The middle excerpt was “transposed” by shifting the F0 contour up by two semitones to force listeners to rely on the prosodic contour rather than some absolute feature of pitch. Stimuli were high-pass filtered to ensure that listeners could not simply track the F0 component (which would otherwise be present in both Harmonic and Inharmonic conditions), and noise was added to mask potential distortion products. Because voiced speech excitation is continuous, it was impractical to change the jitter pattern over time, and we thus included only Harmonic and Inharmonic conditions, the latter of which used the same jitter pattern throughout each trial.
Figure 4. Tasks and results for Experiments 4 and 5 – speech contour perception and Mandarin tone perception.
(A) Schematic of the trial structure for Experiment 4. Participants heard three one-second resynthesized speech utterances, the first or last of which had a random frequency modulation (1-2 Hz bandpass noise, with modulation depth varied across conditions) added to the F0 contour. Participants were asked whether the first or last speech excerpt differed from second speech excerpt. The second except was always shifted up in pitch to force listeners to make judgments about the prosodic contour rather than the absolute pitch of the stimuli.
(B) Example spectrograms of stimuli from harmonic and inharmonic trials in Experiment 4. Note the even and jittered spacing of frequency components in the two trial types. In these examples, the final excerpt in the trial contains the added frequency modulation.
(C) Results from Experiment 4. Error bars denote standard error of the mean.
(D) Schematic of trial structure for Experiment 5. Participants (fluent Mandarin speakers) heard a single resynthesized Mandarin word and were asked to type what they heard (in Pinyin, which assigns numbers to the 5 possible tones). Participants could, for example, hear the word wùlǐ, containing tones 4 and 3, and the correct response would be wu4li3.
(E) Results for Experiment 5. Error bars denote standard error of the mean.
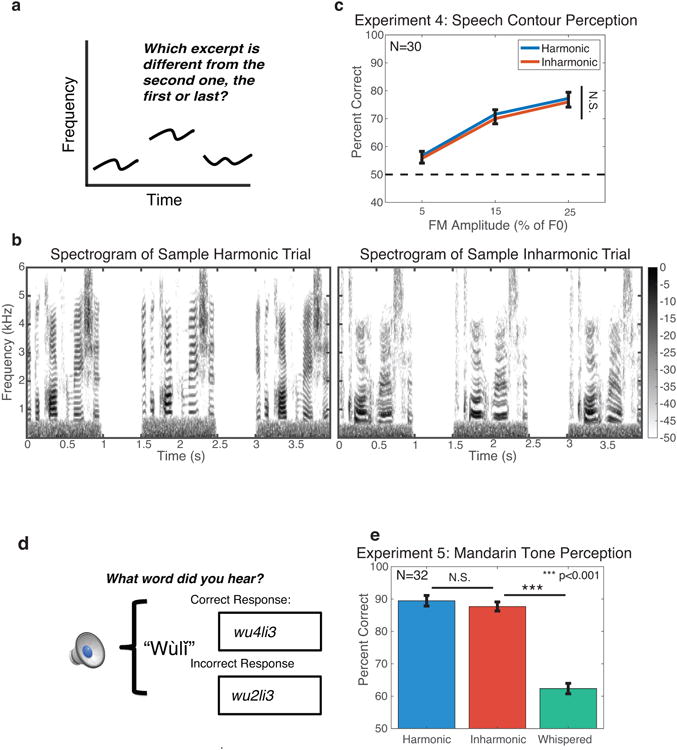
As the amplitude of the added FM increased, performance for Harmonic and Inharmonic conditions improved, as expected (Figure 4c). However, performance was not different for harmonic and inharmonic stimuli (F(1,29)=1.572, p=0.22), suggesting that the perception of speech prosody also does not rely on extracting F0. Similar results were obtained with FM tones synthesized from speech contours (Supplementary Figure 3).
Experiment 5: Mandarin tone perception
In languages such as Mandarin Chinese, pitch contours can carry lexical meaning in addition to signaling emphasis, emotion, and other indexical properties. To probe the pitch mechanisms underlying lexical tone perception, we performed an open-set word recognition task using Mandarin words that were resynthesized with harmonic, inharmonic, or noise carrier signals. The noise carrier simulated the acoustics of breath noise in whispered speech, and was intended as a control condition to determine whether lexical tone perception would depend on the frequency modulation introduced by the pitch contour. As in Experiment 4, the resynthesized words were filtered to ensure that listeners could not simply track the lower spectral edge provided by the F0 component, and noise was added to mask potential distortion products. Participants (fluent Mandarin speakers) were asked to identify single words by typing what they heard (Figure 4d).
As shown in Figure 4e, tone identification was comparable for harmonic and inharmonic speech (t(31)=1.99, p=0.06), but decreased substantially (p<0.001) for whispered speech (t(31)=22.14, p<0.001). These two results suggest that tone comprehension depends on the tone's pitch contour, as expected, but that its perception, like that of the prosodic contour, seems not to require F0 estimation. Listeners evidently track the frequency contours of the stimuli, irrespective of whether the frequencies are harmonic or inharmonic.
Experiment 6: Familiar melody recognition
Despite the lack of an effect of inharmonicity on tasks involving pitch contour discrimination, it seemed possible that F0-based pitch would be more important in complex and naturalistic musical settings. We thus measured listeners' ability to recognize familiar melodies (Figure 5a) that were rendered with harmonic or inharmonic notes. In addition to the Harmonic, Inharmonic, and Inharmonic-Changing conditions from previous experiments, we included Harmonic and Inharmonic conditions in which each interval of each melody (the size of note-to-note changes in pitch) was altered by 1 semitone while preserving the contour (directions of note-to-note changes) and rhythm (Figure 5a). These conditions were intended to test the extent to which any effect of inharmonicity would be mediated via an effect on pitch interval encoding, by reducing the extent to which intervals would be useful for the task.
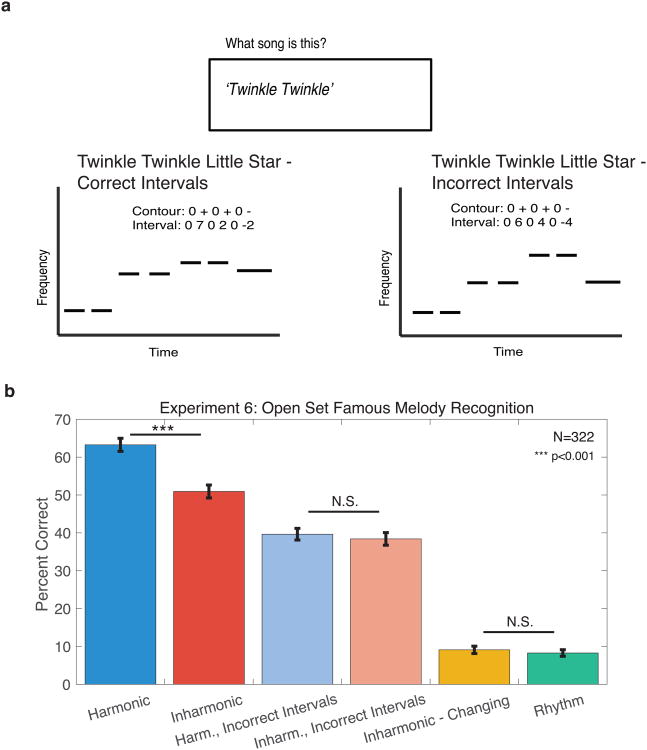
Figure 5. Task, results, schematic of incorrect interval trials from Experiment 6 – familiar melody recognition.
(A) Stimuli and task for Experiment 6. Participants on Amazon Mechanical Turk heard 24 melodies, modified in various ways, and were asked to identify each melody by typing identifying information into a computer interface. Three conditions (Harmonic, Inharmonic, and Inharmonic-Changing) preserved the pitch intervals between notes. Two additional conditions (Incorrect Intervals with harmonic or inharmonic notes) altered each interval between notes but preserved the contour (direction of pitch change between notes). The Rhythm condition preserved the rhythm of the melody, but used a flat pitch contour.
(B) Results from Experiment 6. Error bars denote standard deviations calculated via bootstrap.
Additionally, to evaluate the extent to which participants were using rhythmic cues to identify the melody, we included a condition where the rhythm was replicated with a flat pitch contour. Participants heard each of twenty-four melodies once (in one of the conditions, chosen at random), and typed the name of the song. Results were coded by the first author, blind to the condition. In order to obtain a large sample of participants, which was necessary given the small number of trials per listener, the experiment was crowd-sourced on Amazon Mechanical Turk.
As shown in Figure 5b, melody recognition was modestly impaired for Inharmonic compared to Harmonic melodies (p<0.001, via bootstrap). By contrast, performance was indistinguishable for Harmonic and Inharmonic conditions when melodic intervals were changed to incorrect values (p=0.50). The deficit in melody recognition with inharmonic notes thus seems plausibly related to impairments in encoding pitch intervals (the magnitude of pitch shifts), which are known to be important for familiar melody recognition36. Performance in the Inharmonic conditions was nonetheless far better than in the Inharmonic-Changing or Rhythm conditions (p<0.001 for both), consistent with the notion that the pitch contour contributes to familiar melody recognition, and is largely unaffected by inharmonicity.
Experiment 7: Sour note detection
To further examine whether pitch interval perception relies on F0, we assessed the effect of inharmonicity on the detection of an out of key (“sour”) note within a 16-note melody40,41. Sour notes fall outside of the set of notes used in the tonal context of a melody, and can be identified only by their interval relations with other notes of a melody. Melodies were randomly generated using a model of western tonal melodies42. On half of the trials, one of the notes in the melody was modified by 1 or 2 semitones to be out of key. Participants judged whether the melody contained a sour note (explained to participants as a “mistake” in the melody; Figure 6a). Notes were bandpass filtered and superimposed on masking noise as in the contour and two-tone discrimination tasks (to ensure that the task could not be performed by extracting pitch intervals from the F0 component alone; see Supplementary Figure 4c&d for comparable results with unfiltered notes). We again measured performance for Harmonic, Inharmonic, and Inharmonic-Changing conditions.
Figure 6. Task and results for Experiments 7 and 8 – sour note detection and interval pattern discrimination.
(A) Sample trial from Experiment 7. Participants judged whether a melody contained a ‘sour’ (out of key) note.
(B) Results for Experiment 7. Performance was measured as the area under Receiver Operating Characteristic (ROC) curves. Error bars denote standard error of the mean.
(C) Schematic of a sample trial from Experiment 8. Participants judged whether two melodies were the same or different. On ‘different’ trials (pictured) the two melodies had different intervals between notes, but retained the same contour. The second melody was always transposed up in pitch relative to the first.
(D) Results for Experiment 8. Performance was measured as the area under Receiver Operating Characteristic (ROC) curves. Error bars denote standard error of the mean.
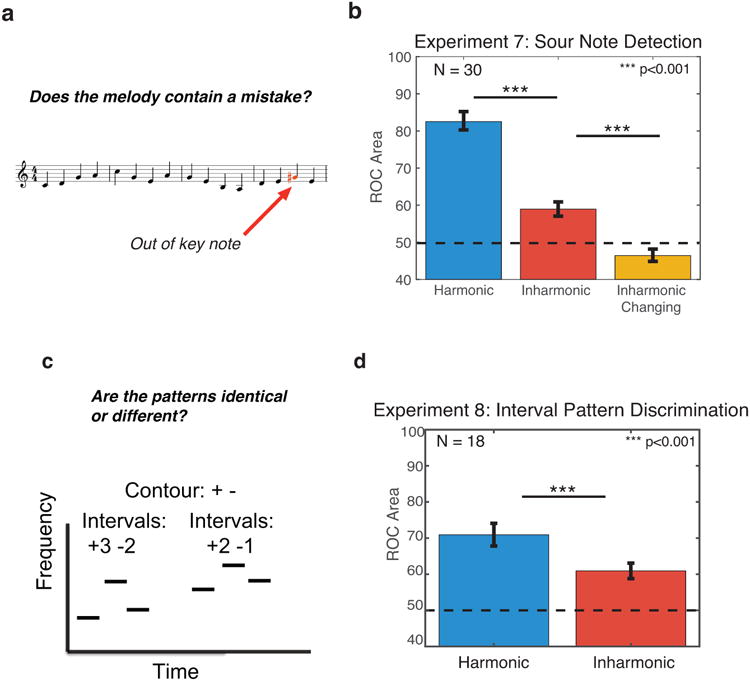
Consistent with the deficit observed for familiar melody recognition, and in contrast to the results for pitch contour discrimination (Experiment 3), sour note detection was substantially impaired for inharmonic compared to harmonic trials (Figure 6b; t(29)=4.67, p<0.001). This result is further consistent with the idea that disrupting F0 specifically impairs the estimation of pitch intervals in music.
Experiment 8: Interval pattern discrimination
It was not obvious a priori why inharmonicity would specifically prevent or impair the perception of pitch intervals. Listeners sometimes describe inharmonic tones as sounding like chords, appearing to contain more than one F0, which might introduce ambiguity in F0 comparisons between tones. But if the contour (direction of note-to-note changes) can be derived from inharmonic tones by detecting shifts of the spectrum, one might imagine that it should also be possible to detect the magnitude of that shift (the interval) between notes. A dissociation between effects of inharmonicity on pitch contour and interval representations thus seemed potentially diagnostic of distinct mechanisms subserving pitch-related functions. To more explicitly isolate the effects of inharmonicity on pitch interval perception, we conducted an experiment in which participants detected interval differences between two three-note melodies with harmonic or inharmonic notes (Figure 6c). On half of trials, the second note of the second melody was changed by one semitone so as to preserve the contour (sign of pitch changes), but alter both intervals in the melody. Tones were again bandpass filtered and superimposed on masking noise.
As shown in Figure 6d, this task was difficult (as expected – 1 semitone is close to previously reported pitch interval discrimination thresholds43), but performance was again better for harmonic than inharmonic notes (t(17)=4.59, p<0.001, t-test). Because this task, unlike those of Experiments 6 and 7, did not require comparisons to familiar pitch structures (known melodies or key signatures), it mitigates the potential concern that the deficits in Experiments 6 and 7 reflect a difficulty comparing intervals obtained from inharmonic notes to those learned from harmonic notes through experience with Western music. Instead, the results suggest that intervals are less accurately encoded (or retained) when notes are inharmonic, suggesting a role for F0-based pitch in encoding or representing the magnitude of pitch changes.
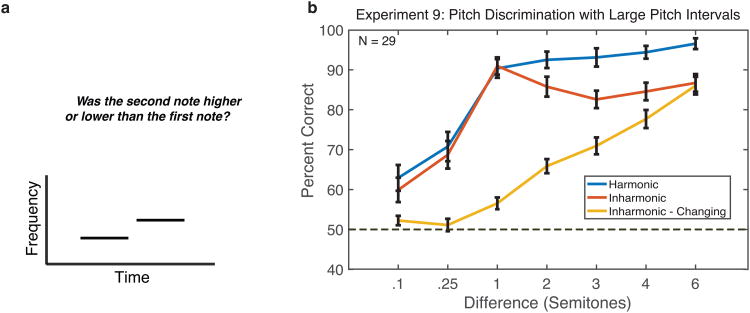
Experiment 9: Pitch discrimination with large pitch intervals
To better understand the relationship between deficits in interval perception (where pitch steps are often relatively large) and the lack of impairment for two-tone pitch discrimination (Experiment 1, where steps were small), we conducted a second pitch discrimination experiment with pitch steps covering a larger range (Figure 7a). As shown in Figure 7b, the results replicate those of Experiment 1, but reveal that performance for Harmonic and Inharmonic tones differs somewhat (by ∼10%) once pitch shifts exceed a semitone (producing an interaction between tone type and step size; F(1,27)=71.29, p<0.001). One explanation is that for larger steps, the match between the spectral pattern of successive tones is occasionally ambiguous, leading to a decrease in performance for Inharmonic tones (though participants were still above 85% on average). The lack of a similar decline for Harmonic conditions suggests that F0-based pitch may be used to boost performance in these conditions.
Figure 7. Task and results for Experiment 9 – pitch discrimination with large pitch intervals.
(A) Schematic of trial structure for Experiment 9. During each trial, participants heard two tones and judged whether the second tone was higher or lower than the first tone. The stimuli and task were identical to those of Experiment 1, except larger step sizes were included.
(B) Results from Experiment 9. Error bars denote standard error of the mean.
By contrast, performance on the Inharmonic-Changing condition progressively improved with the pitch difference (F(6,168)=80.30, p<0.001). This result suggests that participants were also able to detect pitch differences to some extent through the average density of harmonics (higher tones have greater average spacing than lower tones, irrespective of the jitter added). By six semitones, where Inharmonic and Inharmonic-Changing conditions produced equivalent performance (t(28)=.45, p=0.66), it seems likely that participants were relying primarily on harmonic density rather than spectral shifts, as there was no added benefit of a consistent spectral pattern. Overall, the results indicate that pitch changes between tones are conveyed by a variety of cues, and that listeners make use of all of them to some extent. However, pitch conveyed by the F0 appears to play a relatively weak role, and only in particular conditions.
The difference between Harmonic and Inharmonic performance for larger pitch steps nonetheless left us concerned that what appeared to be deficits in interval size estimation in Experiments 7 and 8 might somehow reflect a difficulty in recovering the direction of pitch change, because the intervals used in those two experiments were often greater than a semitone. To address this issue, we ran additional versions of both experiments in which the direction of pitch change between notes was rendered unambiguous– notes were not bandpass filtered, such that the F0 component moved up and down, as did the spectral centroid of the note (Supplementary Figure 4a). This stimulus produced up-down discrimination with tone pairs that was equally good irrespective of spectral composition (F(2,58)=.38, p=0.689; Supplementary Figure 4b), demonstrating that the manipulation had the desired effect of rendering direction unambiguous. Yet even with these alternative stimuli, performance differences for Inharmonic notes were evident in both the sour note detection and interval pattern discrimination tasks (t(18)=3.87, p<0.001, t(13)=4.54, p<0.001; Supplementary Figure 4c-f). The results provide additional evidence that the deficits on these tasks with inharmonic stimuli do, in fact, reflect a difficulty encoding pitch intervals between sounds that lack a coherent F0.
Experiment 10: Voice recognition
In addition to its role in conveying the meaning of spoken utterances, pitch is thought to be a cue to voice identity28. Voices can differ in both mean F0 and in the extent and manner of F0 variation, and we sought to explore the importance of F0 in this additional setting. We first established the role of pitch in voice recognition by measuring recognition of voices whose pitch was altered (Experiment 10a).
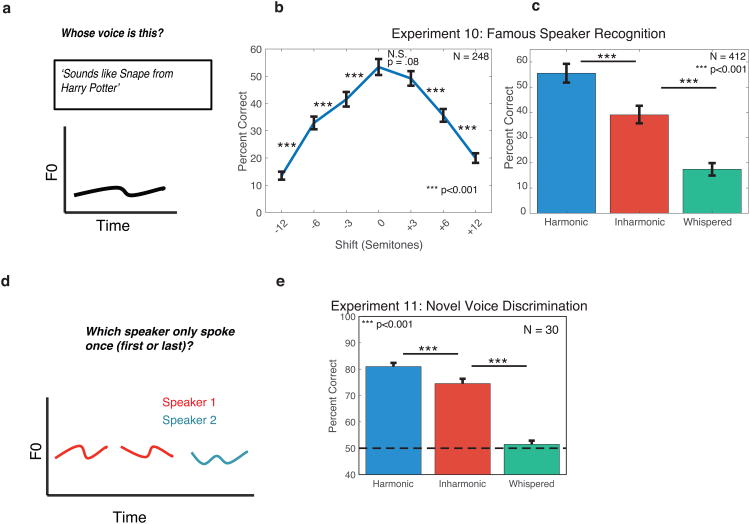
Participants were asked to identify celebrities from their speech, resynthesized in various ways (Figure 8a). The speakers included politicians, actors, comedians and singers. Participants typed their responses, which were scored after the fact by the first author, blind to the condition. Due to the small number of trials per listener, the experiments were crowd-sourced on Amazon Mechanical Turk in order to recruit sufficient sample sizes. The speech excerpts were pitch-shifted up and down, remaining harmonic in all cases. Voice recognition was best at the speaker's original F0, and decreased for each subsequent pitch shift away from the original F0 (Figure 8b). This result suggests that the average absolute pitch of a speaker's voice is an important cue to their identity and is used by human listeners for voice recognition.
Figure 8. Task and results for Experiments 10a, 10b, and 11 – famous speaker recognition and novel voice discrimination.
(A) Description of Experiments 10a and 10b. Participants on Mechanical Turk heard resynthesized excerpts of speech from recordings of celebrities, and were asked to identify each speaker by typing their guesses into an interface.
(B) Results from Experiment 10a, with harmonic speech pitch-shifted between -12 and +12 semitones. Here and in (c), error bars plot standard deviations calculated via bootstrap.
(C) Results from Experiment 10b. Stimuli in the Whispered condition were resynthesized with simulated breath noise, removing the carrier frequency contours.
(D) Schematic of trial structure for Experiment 11. Participants heard three one-second resynthesized speech utterances from unknown speakers, the first or last of which was spoken by a different speaker than the other two. Participants judged which speaker (first or last) only spoke once.
(E) Results from Experiment 11. Error bars denote standard error of the mean.
To probe the pitch mechanisms underlying this effect, we measured recognition for inharmonic celebrity voices (Experiment 10b). Participants heard speech excerpts that were harmonic or inharmonic at the original pitch, or resynthesized with simulated whispered excitation, and again identified the speaker. Recognition was substantially worse for Inharmonic speech (Figure 8c; p<0.001), suggesting that at least part of the pitch representations used for familiar voice recognition depends on estimating F0. Recognition was even worse for whispered speech (p<0.001), suggesting that aspects of the prosodic contour may also matter, independent of the integrity of the F0.
Experiment 11: Novel voice discrimination
As a further test of the pitch mechanisms involved in voice perception, we measured the effect of inharmonicity on the discrimination of unfamiliar voices. Participants were presented with three speech excerpts and had to identify which one was spoken by a different speaker than the other two (Figure 8d). Speech excerpts were taken from a large anonymized corpus44 and thus were unknown to participants.
As with celebrity voice recognition, we observed a significant deficit in performance for Inharmonic compared to Harmonic speech (t(29)=3.88, p<0.001, Figure 8e), and a larger impairment for whispered speech (t(29)=16.24, p<0.001). These results are further consistent with a role for F0 in the representation of voice identity, and show that voice-related deficits from inharmonicity do not only occur when matching an inharmonic stimulus to a stored representation of a normally harmonic voice (as in Experiment 10). Deficits occur even when comparing multiple stimuli that are all inharmonic, suggesting that voice representations depend in part on F0-based pitch. We note also that the inharmonicity manipulation that produced an effect here and in Experiment 10 is identical to the one that produced no effect on prosodic contour discrimination or Mandarin tone identification (Experiments 4 and 5). It thus serves as a positive control for those null results – the manipulation is sufficient to produce a large effect for tasks that depend on the F0.
To further test whether the performance decrements in voice recognition and discrimination reflect impairments in estimating F0, we conducted a control experiment. Participants performed an alternative version of the voice discrimination task of Experiment 11 in which the mean and variance of the F0 contours of each speech excerpt were equated, such that F0-based pitch was much less informative for the task. If the effect of inharmonicity were due to its effect on some other aspect of voice representations, such as vocal tract signatures extracted from the spectral envelope of speech, one would expect the deficit to persist even when F0 was rendered uninformative. Instead, this manipulation eliminated the advantage for harmonic over inharmonic speech (t(13)=0.43, p=0.67), suggesting that the deficit in Experiments 10 and 11 are in fact due to the effect of inharmonicity on pitch perception (Supplementary Figure 5a-b). This conclusion is also supported by findings that inharmonicity has minimal effects on speech intelligibility, which also depends on features of the spectral envelope resulting from vocal tract filtering. For example, Mandarin phoneme intelligibility (assessed from the responses for Experiment 5) was unaffected by inharmonicity (Supplementary Figure 5c-d).
Effects of musicianship
It is natural to wonder how the effects described here would vary with musicianship, which is known to produce improved performance on pitch-related tasks33,45,46. A comparison of musician and non-musician participants across all of our experiments (with the exception of Experiment 5, in which most participants identified as musicians) indeed revealed that musicians were overall better than non-musicians at most tasks– the only experiments in which this was not the case were those involving voice identification or discrimination (Supplementary Figures 6-8). However, the effects of inharmonicity were qualitatively similar for musicians and non-musicians. Tasks involving the direction of pitch changes (two-tone discrimination, melodic contour discrimination, and prosodic contour discrimination; Experiments 1-4) all showed similar performance for harmonic and inharmonic stimuli in both musicians and non-musicians (Supplementary Figure 6). Tasks involving pitch intervals or voice identity (Experiments 6-11) produced better performance for harmonic than inharmonic stimuli in both groups (Supplementary Figures 7&8). The lone exception was Experiment 8 (interval pattern discrimination), where most non-musicians performed close to chance in both conditions. The similarity in results across groups suggests that the differences we find in the effect of inharmonicity across tasks is a basic feature of hearing, and is present in listeners independent of extensive musical expertise.
Discussion
To probe the basis of pitch perception, we measured performance on a series of pitch-related music and speech tasks for both harmonic and inharmonic stimuli. Inharmonic stimuli should disrupt mechanisms for estimating F0, as are conventionally assumed to underlie pitch. We found different effects of this manipulation depending on the task. Tasks that involved detecting the direction of pitch changes, whether for melodic contour, spoken prosody, or single pitch steps, generally produced equivalent performance for harmonic and inharmonic stimuli. By contrast, tasks that required judgments of pitch intervals or voice identity showed substantially impaired performance for inharmonic stimuli. These results suggest that what has conventionally been considered “pitch perception” is mediated by several different mechanisms, not all of which involve estimating F0.
Tracking spectral patterns
Our results suggest a mechanism that registers the direction of pitch shifts (the contour) by tracking shifts in spectral patterns, irrespective of whether the pattern is harmonic or inharmonic. This mechanism appears to operate for both musical tones and for speech. When the correspondence in spectral pattern was eliminated in the Inharmonic-Changing conditions of Experiments 1-3, performance was severely impaired. These results provide evidence that the match in the spectral pattern between notes underlies the detection of the pitch change, and that in these conditions pitch changes need not be detected by first estimating the F0 of each note.
Previous results have shown that listeners hear changes in the overall spectrum of a sound47 (e.g. the centroid, believed to underlie the brightness dimension of timbre, or the edge), that these shifts can produce contour-like representations48, and that these shifts can interfere with the ability to discern changes in F047,49,50. Our findings are distinct from these prior results in suggesting that the substrate believed to underlie F0 estimation (the fine-grained pattern of harmonics) is often instead used to detect spectral shifts. Other prior results have provided evidence for “frequency shift detectors”, typically for shifts in individual frequency components51, though it has been noted that shifts can be heard between successive inharmonic tones52. Our results are distinct in showing that these shifts appear to dictate performance in conditions that have typically been assumed to rely on F0 estimation. Although we have not formally modeled the detection of such shifts, the cross-correlation of excitation patterns (perhaps filtered to accentuate fluctuations due to harmonics) between sounds is a candidate mechanism. By contrast, it is not obvious how one could account for detection of shifts in inharmonic spectra with an F0-estimation mechanism, particularly given that the same inharmonicity manipulation produces large deficits in some tasks, but not in tasks that rely on detecting the direction of pitch shifts, even when shifts are near threshold.
F0-based pitch
The consistently large effects of inharmonicity in some pitch-related tasks implicates an important role for F0-based pitch (historically referred to as “virtual” pitch, “residue” pitch, or “periodicity” pitch). F0-based pitch seems necessary for accurately estimating pitch intervals (the magnitude of pitch shifts; Experiments 6-8) and for identifying and discriminating voices (Experiments 10-11). These results provide a demonstration of the importance of F0-based pitch, and a delineation of its role in pitch-related behaviors such as interval perception and voice recognition.
Implications for relationship between F0 and pitch
Taken together, our data suggest that the classical view of pitch as the perceptual correlate of F0 is incomplete – F0 appears to be just one component of real-world pitch perception. The standard psychoacoustic assessment of pitch (two-tone up-down discrimination) does not seem to require the classical notion of pitch. At least for modest pitch differences and for the stimulus parameters we employed, it can be performed by tracking correspondence in the spectral pattern of sounds even when they are inharmonic.
Are the changes that are heard between inharmonic sounds really “pitch” changes? Listeners describe what they hear in the Inharmonic conditions of our experiments as a pitch change, but in typical real-world conditions the underlying mechanism presumably operates on sounds that are harmonic. The changes heard in sequences of inharmonic sounds thus appear to be a signature of a mechanism that normally serves to registers changes in F0, but that does so without computing F0.
Alternatively, could listeners have learned to employ a strategy to detect shifts in inharmonic spectra that they would not otherwise use for a pitch task? We consider this unlikely, both because listeners were not given practice on our tasks prior to the experiments, and because omitting feedback in pilot experiments did not alter the results. Moreover, the ability to hear “pitch” shifts in inharmonic tones is typically immediate for most listeners, as is apparent in the stimulus demonstrations that accompany our paper.
Several previous studies found effects of inharmonicity in two-tone pitch discrimination tasks. Although at face value these prior results might appear inconsistent with those reported here, the previously observed effects were typically modest, and were either variable across subjects25 or were most evident when the stimuli being compared had different spectral compositions26,27. In pilot experiments, we also found spectral variation between tones to cause performance decrements for inharmonic tones, as might be expected if the ability to compare successive spectra were impaired, forcing listeners to partially rely on F0-based pitch. Our results here are further consistent with this idea – effects of inharmonicity became apparent for large pitch shifts and a fixed spectral envelope, when spectral shifts were ostensibly somewhat ambiguous. It thus remains possible that F0-based pitch is important for extracting the pitch contour in conditions in which the spectrum varies, such as when intermittent background noise is present. But in many real-world contexts, where spectra are somewhat consistent across the sounds to be compared (as for the recorded instrument notes used in Experiment 2), F0 seems unlikely to be the means by which pitch changes are heard. The classic psychoacoustic notion of pitch is thus supported by our data, but primarily for particular tasks (interval perception and voice recognition/discrimination), and not in many contexts in which it has been assumed to be important (melodic contour, prosody etc.).
In addition to F0 and spectral pattern, there are other cues that could be used to track changes in pitch in real-world contexts, several of which were evident in our data. When tones were not passed through a fixed bandpass filter (Supplementary Figure 4), listeners could detect a pitch shift even when there was no F0 or consistent spectral pattern. This suggests that some aspect of the spectral envelope (the lower edge generated by the F0, or the centroid47,48,53) can be used to perform the task. We also found good up-down discrimination performance even when the spectral envelope was fixed and the spectral pattern was varied from note to note, provided the steps were sufficiently large (Inharmonic-Changing condition in Experiment 9). This result suggests that listeners can hear the changes in the density of harmonics that normally accompany pitch shifts. It thus appears that pitch perception is mediated by a relatively rich set of cues that vary in their importance depending on the circumstances.
Comparisons with previous models of pitch
Previous work on pitch has also implicated multiple mechanisms, but these mechanisms typically comprise different ways to estimate F0. Classical debates between temporal and place models of pitch have evolved into the modern view that different cues, plausibly via different mechanisms, underlie pitch derived from low- and high-numbered harmonics14,21,31,32,54. The pitch heard from low-numbered ‘resolved’ harmonics may depend on the individual harmonic frequencies, whereas that from high-numbered ‘unresolved’ harmonics is believed to depend on the combined pattern of periodic beating that they produce. But in both cases the mechanisms are thought to estimate F0 from a particular cue to periodicity. By contrast, we identify a mechanism for detecting changes in F0 that does not involve estimating F0 first, and that is thus unaffected by inharmonicity (a manipulation that eliminates periodicity). The pitch-direction mechanism implicated by our results is presumably dependent on resolved harmonics, though we did not explicitly test this. Resolved and unresolved harmonics may thus best be viewed as providing different peripheral cues that can then be used for different computations, including but not limited to F0-based pitch.
Previous work has also often noted differences in the representation of pitch contour and intervals29,36,55. However, the difference between contour and interval representations has conventionally been conceived as a difference in what is done with pitch once it is extracted (retaining the sign vs. the magnitude of the pitch change). By contrast, our results suggest that the difference between contour and interval representations may lie in what is extracted from the sound signal – pitch contours can be derived from spectral shifts without estimating F0, whereas intervals appear to require the initial estimation of the F0s of the constituent notes, from which the change in F0 between notes is measured.
Future directions
Our results suggest a diversity of mechanisms underlying pitch perception, but leave open the question of why multiple mechanisms exist. Real-world pitch processing occurs over a heterogeneous set of stimuli and tasks, and the underlying architecture may result from the demands of this diversity. Some tasks require knowledge of a sound's absolute F0 (voice identification being the clearest example) and the involvement of F0 estimation is perhaps unsurprising. Many other tasks only require knowledge of the direction of pitch changes. In such cases, detecting shifts in the underlying spectral pattern is evidently often sufficient, but it is not obvious why extracting the F0 and then measuring its change over time is not the solution of choice. It may be that measuring shifts in the spectrum is more accurate or reliable when shifts are small.
It is conversely not obvious why pitch interval tasks are more difficult with inharmonic spectra given that pitch direction tasks are not. Inharmonic tones often resemble multiple concurrent notes, which could in principle interfere with the extraction of note relationships, but no such interference occurs when determining the direction (provided the spectra shift coherently). The dependence on a coherent F0 could lie in the need to compress sound signals for the purposes of remembering them– pitch intervals must often be computed between notes separated by intervening notes, and without the F0 there may be no way to ‘summarize’ a pitch for comparison with a future sound. As discussed above, F0 may also be important for comparing sounds whose spectra vary, obscuring the correspondence in the spectral pattern of each sound. These ideas could be explored by optimizing auditory models for different pitch tasks and then probing their behavior.
One open question is whether a single pitch mechanism underlies performance in the two types of tasks in which we found strong effects of F0-based pitch. Voices and musical intervals are acoustically distinct and presumably require different functions of the F0 – e.g. the mean and variation of a continuously changing F0 for voice, vs. the difference in the static F0 of musical notes – such that it is not obvious that they would be optimally served by the same F0-related computation. A related question is whether the importance of harmonicity in musical consonance (the pleasantness of combinations of notes)56, and sound segregation57–59 reflects the same mechanism that uses harmonicity to estimate F0 for voice or musical intervals.
It remains to be seen how the distinct mechanisms suggested by our results are implemented in the brain, but the stimuli and tasks used here could be used toward this end. Our findings suggest that F0-tuned neurons15,16 are unlikely to exclusively form the brain basis of pitch, and that it could be fruitful to search for neural sensitivity to pitch-shift direction. Our results also indicate a functional segregation for the pitch mechanisms subserving contour (important for speech prosody as well as music) and interval (important primarily for music), suggesting that there could be some specialization for the role of pitch in music. We also found evidence that voice pitch (dependent on harmonicity) may be derived from mechanisms distinct from those for prosody (robust to inharmonicity). A related question is whether pitch in speech and music tap into distinct systems60–62. The diversity of pitch phenomena revealed by our results suggests that investigating their basis could reveal rich structure within the auditory system.
Methods and Materials
Participants
All experiments were approved by the Committee on the use of Humans as Experimental Subjects at the Massachusetts Institute of Technology, and were conducted with the informed consent of the participants. All participants were native English speakers.
30 participants (16 female, mean age of 32.97 years, SD=16.61) participated in Experiments 1, 3, 4, 7,8, 9, and 11, as well as the experiments detailed in Supplementary Figures 4b and 9d. These participants were run in the lab for three two-hour sessions each (except one participant, who was unable to return for her final 2-hour session). 15 of these participants had over 5 years of musical training, with an average of 13.75 years, SD=14.04 years. The sample size was over double the necessary size based on power analyses of pilot data; this ensured sufficient statistical power to separately analyze Musicians and Non-Musicians (Supplementary Figures 6-8).
Another set of 30 participants participated in Experiment 2, as well as the control experiment detailed in Supplementary Figure 2 (11 female, mean age of 37.15 years, SD=13.36). 15 of these participants had over five years of musical training, with an average of 17.94 years, SD = 14.04.
20 participants (8 female, mean age of 38.14 years, SD=15.75) participated in the two follow-up experiments detailed in Supplementary Figure 4c-f. 9 of these participants had over five years of musical training, with an average of 12.18 years, SD=13.64 years.
14 participants completed the control experiment described in Supplementary Figure 5a-b (5 female, mean age of 40 years, SD=13.41). 2 identified as musicians (average of 9.5 years, SD=0.71).
Between these four sets of experiments (combined N of 94), we tested 70 different individuals – 2 individuals completed all four sets of experiments, 3 completed 3 sets, and 12 completed 2 sets.
Participants in online experiments (Experiments 5, 6, and 10) were different for each experiment; their details are given below. For Mechanical Turk studies, sample sizes were chosen to obtain split-half correlations of at least .9.
Stimuli
Logic of Stimulus Filtering
Similar performance for harmonic and inharmonic sounds could in principle result from an ability to “hear out” the F0 frequency component in both cases. To prevent this from occurring, we filtered stimuli to remove the F0 component, and added noise to mask distortion products, which could otherwise re-instate a component at the F0 for harmonic stimuli (details of this filtering and masking noise are given below). The exceptions to this approach were the experiments on real instrument notes (Experiment 2), and voice identification or discrimination (Experiments 10-11). Filtering was not applied to the instrument tones because it seemed important to leave the spectral envelope of the notes intact (because the experiment was intended to test pitch discrimination for realistic sounds). We omitted filtering for the voice experiments because piloting indicated that both experiments would show worse performance for inharmonic stimuli, suggesting that participants were not exclusively relying on the F0 component. Given this, we opted to feature the version of the experiments with unfiltered voices given their greater ethological validity. Moreover, filtered speech showed qualitatively similar results, so in practice the filtering had little effect on the results (Supplementary Figure 9). All experiments for which filtered stimuli were used were likewise replicated with unfiltered stimuli, and in practice it had little effect on the results (Supplementary Figures 4 and 9).
Tasks with Synthetic Tones
Stimuli were composed of notes. Each note was a synthetic complex tone with an exponentially decaying temporal envelope (decay constant of 4 s-1) to which onset and offset ramps were applied (20 ms half-Hanning window). The sampling rate was 48,000 Hz. For Experiments 1, 3, 7, 8 and 9, notes were 400 ms in duration. For Experiment 6, note durations were varied in order to re-create familiar melodies; the mean note duration was 425 ms (SD=306 ms), and the range was 100 ms to 2 s. Harmonic notes included all harmonics up to the Nyquist limit, in sine phase.
In order to make notes inharmonic, the frequency of each harmonic, excluding the fundamental, was perturbed (jittered) by an amount chosen randomly from a uniform distribution, U(-.5, .5). This jitter value was chosen to maximally perturb F0 (lesser jitter values did not fully remove peaks in the autocorrelation for single notes, see Supplementary Figure 1). Jitter values were multiplied by the F0 of the tone, and added to the frequency of the respective harmonic. For example, if the F0 was 200 Hz and a jitter value of -0.39 was selected for the second harmonic; its frequency would be set to 322 Hz. To minimize salient differences in beating, jitter values were constrained (via rejection sampling) such that adjacent harmonics were always separated by at least 30 Hz. The same jitter pattern was applied to every note of the stimulus for a given trial, except for “Inharmonic-Changing” trials, for which a different random jitter pattern was generated for each note. Unlike the temporal jittering manipulations commonly applied to click train stimuli in neurophysiology experiments15, the frequency jittering manipulation employed here preserves the presence of discrete frequency components in the spectrum, allowing the possibility that spectral shifts could be detected even in the absence of an F0.
For all experiments with synthetic tones, each note was band-pass filtered in the frequency domain, with a Gaussian transfer function (in log frequency), centered at 2,500 Hz with a standard deviation of half an octave. This filter was applied to ensure that participants could not perform the tasks using changes in the spectral envelope. The filter parameters were chosen to ensure that the F0 was attenuated (to eliminate variation in a spectral edge at the F0) while preserving audibility of resolved harmonics (the 10th or lower, approximately). For supplementary experiments in which this filter was not applied, each note was unfiltered but harmonic amplitudes were set to decrease by 16 dB/octave.
To ensure that differences in performance for harmonic and inharmonic conditions could not be mediated by distortion products, we added masking noise to all bandpass filtered notes (all experiments described in the main text). We low-pass filtered pink noise using a sigmoidal transfer function in the frequency domain with an inflection point at the third harmonic of the highest note in the given sequence, and a slope yielding 40 dB of gain or attenuation per octave on the low and high sides of the inflection point, respectively. We scaled the noise so that it was 10 dB lower than the mean power of the three harmonics of the highest note of the trial that were closest to the 2,500 Hz peak of the Gaussian spectral envelope35. This filtered and scaled pink noise was added to each note, creating a consistent noise floor for each note sequence.
Speech Tasks
Speech was manipulated using the STRAIGHT analysis and synthesis method37–39. STRAIGHT decomposes a recording of speech into voiced and unvoiced vocal excitation and vocal tract filtering. If the voiced excitation is modeled sinusoidally, one can alter the frequencies of individual harmonics, and then recombine them with the unaltered unvoiced excitation and vocal tract filtering to generate inharmonic speech. This manipulation leaves the spectral shape of the speech largely intact, and supplementary experiments (Supplementary Figure 5) suggest that intelligibility of inharmonic speech is comparable to that of harmonic speech. The jitters for inharmonic speech were chosen in the same way as the jitters for inharmonic musical notes (described above). The same pattern of jitter was used throughout the entire speech utterance, and the entire trial for experiments 4 and 11. STRAIGHT was also used to perform pitch shifts, modify the F0 contour of speech utterances, and create “whispered speech” (the voiced vocal excitation is replaced with noise). Noise-excited stimuli were generated by substituting simulated breath noise for the tonal/noise excitation combination otherwise used in STRAIGHT. The breath noise was high-pass filtered white noise. The filter was a second-order high-pass Butterworth filter with a (3 dB) cutoff at 1,200 Hz whose zeros were moved towards the origin (in the z-plane) by 5%. The resulting filter produced noise that was 3 dB down at 1,600 Hz, 10 dB down at 1,000 Hz, and 40 dB down at 100 Hz, which to the authors sounded like a good approximation to whispering. Without the zero adjustment the filter removed too much energy at the very bottom of the spectrum. The stimuli were thus generated from the same spectrotemporal envelope used for harmonic and inharmonic speech, just with a different excitation signal. Speech was sampled at 12,000 Hz.
High-pass Filtering and Masking Noise
Unless otherwise noted, all speech (except “whispered” speech) was high-pass filtered to prevent participants from using the lowest harmonic as a proxy for the pitch contour, which a priori seemed like a plausible strategy for the inharmonic conditions. Filtering was accomplished by multiplying by a logistic (sigmoid-shaped) transfer function in the frequency domain. The transfer function was given an inflection point at twice the mean F0 (i.e., the average frequency of the second harmonic) of the utterance. The slope of the sigmoid function was set to achieve 40 dB of gain/attenuation per octave on either side of the inflection point (i.e., with the F0 40 dB below the second harmonic, and with the 4th harmonic 40 dB above the second harmonic). This meant that the F0 would be attenuated by 80 dB relative to the 4th harmonic.
In addition, masking noise was added to prevent potential distortion products from reinstating (for harmonic conditions) the F0 contour that had been filtered out. We low-pass filtered pink noise using a sigmoid function with an inflection point at the third harmonic (3*the mean F0 of the utterance) and the same slope as the low-pass filter described above but with opposite sign (such that the noise was attenuated by 40 dB at 3*F0 relative to 1.5*F0, and by 80 dB at 6*F0). The noise was then scaled so that its power in a gammatone filter centered at the F0 was 10 dB below the mean power of harmonics 3-8 in a pitch-flattened version of the utterance. Assuming any distortion products are at most 20 dB below the peak harmonics in the speech signal35, this added noise should render them inaudible. The filtered and scaled pink noise was added to the filtered speech signal to create the final stimuli.
Audio Presentation: In Lab
In all experiments, The Psychtoolbox for Matlab63 was used to play sound waveforms. Sounds were presented to participants at 70 dB over Sennheiser HD280 headphones (circumaural) in a soundproof booth (Industrial Acoustics).
Audio Presentation: Mechanical Turk
We used the crowdsourcing platform provided by Amazon Mechanical Turk to run experiments that necessitated small numbers of trials per participant. Each participant in these studies used a calibration sound to set a comfortable level, and then had to pass a “headphone check” experiment that helped ensure they were wearing headphones or earphones as instructed (described in Woods et. al)64 before they could complete the full experiment.
Feedback
For all in-lab experiments, conditions were randomly intermixed and participants received feedback (‘correct’/‘incorrect’) after each trial. Feedback was used to assure compliance with task instructions. However pilot results indicated that results without feedback were qualitatively similar across all tasks. Feedback was not given during Mechanical Turk experiments because they were open-set recognition tasks. Participants did not complete practice runs of the experiments.
Statistics
For Experiments 1, 2, 4, 5, 9 and 11, percent correct was calculated for each harmonicity condition and difficulty (if relevant). Paired t-tests were used to compare conditions, and for Experiments 1, 2, 4 and 9, the effects of harmonicity and difficulty (step size and modulation depth, respectively) were further examined using repeated measures ANOVAs. For Experiments 3, 7 and 8, hits and false alarms were converted into a receiver-operating characteristic (ROC) curve for each condition. The area under the ROC curve was the metric of performance; this area always lies between 0 and 1, and .5 corresponds to chance performance. Comparisons between conditions were made using paired t-tests.
For open set recognition tasks on Mechanical Turk (Experiments 5, 6 and 10), results were coded by the first author, blind to the condition. For example, in Experiment 10, a response such as “He plays Professor Snape in Harry Potter’, would be coded as ‘Alan Rickman’. Percent correct was calculated for each condition from the resulting scores. For experiments 6 and 10, confidence intervals were estimated using bootstrap (10,000 repetitions, with participants sampled randomly with replacement; data was nonGaussian due to the small number of trials per condition per participant), and p values were calculated using the cumulative distribution function of the means of the bootstrapped samples.
Experiment 1: Basic Discrimination with Pairs of Synthetic Tones
Procedure
Participants heard two notes and were asked whether the second note was higher or lower than the first note. There were three conditions: Harmonic (both notes were harmonic), Inharmonic (both notes had the same random jitter), and Inharmonic-Changing (the two notes had different random jitter patterns). After each trial, participants clicked a button to indicate their choice (‘down’ or ‘up’). Participants completed 40 trials for each step size in each condition in a single session. Here and in other in-lab experiments, participants were given short breaks throughout the session.
Stimuli
Each trial consisted of two notes, described above in Tasks with Synthetic Tones. We used the method of constant stimuli; the second note differed from the first by .1, .25, 1 or 2 semitones. The first note of each trial was randomly selected from a log uniform distribution spanning 200 to 400 Hz.
Experiment 2: Basic Discrimination with Pairs of Instrument Notes
Procedure
Procedure was identical to Experiment 1.
Stimuli
Each trial presented two instrument notes resynthesized from recordings. Notes were selected from the RWC Music Database of Musical Instrument Sounds. Only notes coded in the database as ‘Mezzo Forte’, and ‘Normal’ or ‘Non Vibrato’, were selected for the experiment. Five instruments were used: piano, violin, trumpet, oboe and clarinet. The first note of each trial was randomly selected from a uniform distribution over the notes in a Western classical chromatic scale between 196 and 392 Hz (G3 to G4). A recording of this note, from a randomly selected instrument, was chosen as the source for the first note in the trial. If the second note in the trial was higher, the note two semitones above (for 2 semitone trial), or 1 semitone above (for .1, .25 and 1 semitone trials) was selected to generate the second note (reversed if the second note of the trial was lower). The two notes were analyzed and modified using the STRAIGHT analysis and synthesis method37–39; the notes were pitch flattened to remove any vibrato, shifted to ensure that the pitch differences would be exactly .1, .25, 1, or 2 semitones, and resynthesized with harmonic or inharmonic excitation. Excitation frequencies were modified for the Inharmonic or Inharmonic-Changing conditions in the same way that the synthetic tones were modified in Experiment 1 (see Tasks with Synthetic Tones above). The resynthesized notes were truncated at 400 ms and windowed with a 20 ms half-Hanning window. Note onsets were always preserved, and notes were sampled at 12,000 Hz.
Experiment 3: Contour Perception
Procedure
The experimental design was inspired by the classic contour perception task of Dowling and Fujitani (1972)36. Participants heard two five-note melodies on each trial, and were asked to determine whether the melodies were the same or different. There were three conditions: Harmonic, Inharmonic or Inharmonic – Changing, as in Experiments 1 and 2. Following each trial, participants clicked a button to select one of four responses: “sure different,” “different,” “same,” “sure same”. Participants were instructed to attempt to use all four responses equally throughout the experiment. Participants completed 40 trials for each condition in a single session. Participants with performance >95% correct averaged across Harmonic and Inharmonic conditions (13 of 29 subjects) were removed from analysis to avoid ceiling effects; no participants were close to floor on this experiment.
Stimuli
Five-note melodies were randomly generated with steps of +1 or -1 semitone, randomly chosen. The tonic and starting note of each melody was set to 200, 211.89, or 224.49 Hz. On “same” trials, the second melody was identical to the first except for being transposed upwards by half an octave. On “different” trials, the second melody was altered to change the melodic contour (the sequence of signs of pitch changes). The alteration procedure randomly reversed the sign of the 2nd or 3rd interval in the melody (e.g. 1 became -1, in semitones).
Experiment 4: Speech Contour Perception
Procedure
Participants heard three, one-second speech utterances and were asked whether the first or the last was different from the other two. Following each trial, participants clicked a button to select one of two responses: ‘First Different’, ‘Last Different’. Percent correct for each condition was used as the metric of performance. Participants completed the two tasks in counterbalanced order. Participants completed 40 trials for each condition in a single session.
Stimuli
For each trial a single one-second speech excerpt was randomly chosen from the TIMIT training database44. For each participant, selections from TIMIT were balanced for gender and dialect region. The three speech signals used in a trial were resynthesized from this original speech excerpt. The ‘same’ utterance was resynthesized without altering the excitation parameters. To make the ‘different’ utterance, the speech was resynthesized with a random frequency modulation added to the original F0 contour. The frequency modulation was generated by bandpass filtering pink noise between 1 and 2 Hz, using a rectangular filter in the frequency domain. These bandlimits were chosen so that there would be at least one up-down modulation within the one-second speech segment. The added modulation was normalized to have RMS amplitude of 1, multiplied by the modulation depth (.05, .15, or .25, depending on the condition), then multiplied by the mean F0 of the speech segment, and then added to the original F0 contour of the speech segment. The second speech signal in each trial was shifted up in pitch by 2 semitones relative to the first and third, but otherwise unaltered. Stimuli were synthesized with either harmonic or jittered inharmonic excitation, using an extension of STRAIGHT37,38. The frequency jitter applied to harmonic components was constant within a trial. Each speech excerpt was high-pass filtered and masked as described above (in the section on High-pass Filtering and Masking Noise).
Experiment 5: Mandarin Tone Perception
Participants
32 self-reported native Mandarin speakers were tested using Amazon Mechanical Turk (17 female, mean age of 36.7 years, SD=10.99). 27 answered ‘Yes’ to the question, ‘have you ever known how to play a musical instrument?’
Procedure
Participants were instructed that they would hear 120 recordings of single words in Mandarin that had been manipulated in various ways. They could only hear each recording once. Their task was to identify as many words as possible. Responses were typed into a provided entry box using Hanyu Pinyin (the international standard for Romanization of Standard Chinese/Modern Standard Mandarin), which allows for the independent coding of tones (labeled 1-5) and phonemes. For example, if a participant heard the word ‘pō’, they could respond correctly with ‘po1’, have an incorrect tone response (ex. ‘po2’) or an incorrect phoneme/spelling, but correct tone, response (ex: ‘wo1’). Participants were given several example responses in Pinyin before they began the experiment. Participants heard each word once over the course of the experiment, and conditions were randomly intermixed.
Stimuli
In Mandarin Chinese, the same syllable can be pronounced with one of five different “tones” (1 – flat, 2 – rising, 3 – falling then rising, 4 – falling, 5 – neutral). The use of different tones can change the meaning of a syllable. For this experiment, 60 pairs of Mandarin word recordings spoken by a single female talker were chosen from the “Projet SHTOOKA” database (http://shtooka.net/). Each pair of recordings consisted of either two single syllables (characters) with the same phonemes but different tones, or two two-syllable words, with the same phonemes but different tones for only one of the syllables. For example, one pair was Wùlǐ/Wúlǐ: Wùlǐ, meaning “physics”, contains the 4th and 3rd tone, and is written in Pinyin as “Wu4li3”, whereas Wúlǐ, meaning “unreasonable”, contains the 2nd and 3rd tones, and is written in Pinyin as “Wu2li3”. All combinations of tone differences were represented with the exception of third tone vs. neutral tone. Only a few combinations involving the neutral tone could be found in the SHTOOKA database, which also reflects the relative scarcity of such pairings in the Mandarin language. In order to span the range of Mandarin vowels, the different tones within each word pair occurred on cardinal vowels (vowels at the edges of the vowel space), or diphthongs containing cardinal vowels. Additionally, to represent a range of consonant/vowel transitions, all voiced/unvoiced consonant pairs (ex. p/b, d/t) found in Mandarin and present in the source corpus were represented. Harmonic, Inharmonic and Whispered versions of each word were generated using STRAIGHT. A full list of words is available in the Supplementary Materials (Supplementary Table 1). Stimuli were high-pass filtered and masked as described above (in the section on High-pass Filtering and Masking Noise).
Experiment 6: Familiar Melody Recognition
Participants
322 participants passed the headphone quality check; 143 women, mean age of 36.49 years, SD=11.77 years. All reported normal hearing, and 204 answered ‘Yes’ to the question ‘Have you ever known how to play a musical instrument?’
Procedure
Participants were asked to identify twenty-four familiar melodies (see Supplementary Table 2, for a full list of melodies). There were five main conditions: Harmonic, Inharmonic, Inharmonic-Changing, and Harmonic and Inharmonic conditions in which the intervals were altered randomly by 1 semitone, with the constraint that the contours stayed intact. The experiments contained additional conditions not analyzed here. Participants were given the written instructions “You will hear 24 melodies. These melodies are well known. They come from movies, nursery rhymes, holidays, popular songs, etc. Some of the melodies have been manipulated in various ways. Your task is to identify as many of these melodies as you can. You will only be able to hear each melody once! Even if you don't know the name of the tune, but you recognize it, just describe how it is familiar to you. e.g., is it a nursery rhyme? What movie is it from? Who sings it?” Participants were allowed to type their responses freely into a provided space.
Stimuli
Harmonic (with either correct or incorrect intervals), Inharmonic (with either correct or incorrect intervals), and Inharmonic-Changing variants of 24 well-known melodies were generated by concatenating synthetic complex tones. The tonic was always set to an F0 of 200 Hz. A complete phrase of each melody was used (approximately four seconds of music per melody). For trials where the intervals were modified, +/- 1 semitone was randomly added to every note in the melody. Interval perturbations were iteratively sampled until they produced a new melody whose contour was the same as that of the original melody. For Rhythm conditions, the rhythm of the melody was played using a 200 Hz tone. Participants heard each melody once. Three melodies were assigned (randomly) to each condition (the experiment contained additional conditions not analyze here). This produced 966 trials per condition across all participants.
Experiment 7: Sour Note Detection
Procedure
Participants heard one sixteen-note melody per trial, and were asked whether this melody contained a “sour” note (a “mistake”)40,41. There were three conditions: Harmonic, Inharmonic and Inharmonic-Changing. Following each trial, participants clicked a button to select one of four responses: “sure mistake,” “maybe mistake,” “maybe no mistake,” “sure no mistake”. Participants were instructed to attempt to use all four responses equally throughout the experiment. Participants completed 42 trials for each condition in a single session.
Stimuli
Sixteen-note melodies were created using a modified version of a generative model outlined in Temperley (2008)42. This model uses a range profile (to restrict absolute range of a melody), a proximity profile (to restrict the size of note-to-note leaps), and a key profile (to maintain a consistent key within a melody), to generate melodies on a note-by-note basis. The Temperley (2008) range profile was modified to restrict the range of the five-note contours to 1.5 octaves, and the proximity profile was changed to allow a maximum leap of five semitones (a perfect fourth). Melodies were rejected if they contained a sequential note repetition (yielding a contour step of 0 semitones). Only major key profiles were used, and these were altered from the Temperley (2008) model so that there was no chance of notes outside the designated key. Melodies, initiated randomly on 200, 211.89, or 224.49 Hz, were generated and rejected until one was obtained with a specified scale degree (1, 3, or 5 – the tonic, median or dominant, randomly distributed over the course of the experiment, with 14 of each scale degree per harmonicity condition) in the 12th, 13th, 14th or 15th note position. For “sour” trials, the desired scale degree (1, 3, or 5) was changed: 1 was moved upwards by a semitone, 3 was moved upwards by two semitones, and 5 was moved upwards by one semitone. Melodies were rejected and a new melody was generated if the sour note altered the original contour. Only one note was altered in each “sour” trial. A fixed bandpass filter (described above) was applied to each note.
Experiment 8: Interval Pattern Discrimination
Procedure
Participants heard two three-note melodies that had identical contours, but in half of the trials, the interval relationship between the notes changed by one semitone41. Half the trials had Harmonic notes and the other half of the trials had Inharmonic notes. A fixed bandpass filter (described above) was applied to each note. Participants were asked whether the melodies were identical or different. There were four possible responses: ‘sure different’, ‘maybe different’, ‘maybe same’, and ‘sure same’. Participants were instructed to attempt to use all four responses equally throughout the experiment. Participants completed 40 trials per condition in a single session. This task was difficult, and participants with performance less than .55 across both conditions (12 of 30 participants) were excluded from analysis.
Stimuli
The two three-note contours were generated randomly using a uniform distribution and step sizes of +/- 1,2,3,4 and 5 semitones (5 semitones was the largest step size used in Experiment 7). The two melodies were separated by a .6 silent gap. ‘Different’ conditions were generated by randomly adding 1 or -1 to the middle note of the comparison melody, with the restriction that the original contour could not change (for example, creating a unison). The first melody started on 200 Hz, and the second melody was always transposed up by half an octave.
Experiment 9: Basic Discrimination with Larger Step Sizes
Stimuli and Procedure were identical to that of Experiment 1 except for the addition of 3, 4, and 6 semitones step sizes.
Experiment 10a and 10b: Famous Speaker Recognition
Participants 10a
248 participants, 123 female, with a mean age of 35.95 years, SD=9.89 years, completed experiment 10a. 133 answered ‘Yes’ to the question ‘have you ever known how to play a musical instrument?’
Participants 10b
412 participants, 212 female, with a mean age of 36.7 years, SD=10.99 years completed experiment 10b. 220 answered ‘Yes’ to the question ‘have you ever known how to play a musical instrument?’
Procedure (both)
Participants on Mechanical Turk were instructed that they would hear short recordings of people speaking: “These speakers are well-known. They are actors, politicians, singers, TV personalities, etc. Some of the voices have been manipulated in various ways. Your task is to identify as many of the speakers as you can. You will only be able to hear each audio sample once! If you don't know the name of the speaker, but you recognize their voice, just describe how it is familiar to you. e.g., What character does this actor play? What is this person's profession? etc.”. Participants typed their responses into a box provided on the screen.
Stimuli
For both experiments, overlapping subsets of 40 recognizable celebrity voices were chosen. 24 of the 40 voices were used for Experiment 10a and 39 of the 40 voices were used for Experiment 10b. The exact number of voices used in each experiment was determined by the number of conditions. The full list of celebrity voices used can be found in Supplementary Table 3. Clean recordings of these celebrities' voices were found using publically available videos, radio interviews, podcasts, etc. Four seconds of speech were selected for each celebrity. For experiment 10a, harmonic voices were resynthesized (using STRAIGHT) to have a shift in pitch of -12, -6, -3, 0, 3, 6, or 12 semitones. Participants heard each voice only once (in one of the seven conditions), and heard four examples of each pitch shift condition. For experiment 10b, there were 3 conditions: Harmonic, Inharmonic, and Whispered. The speech reported in the main results was not high-pass filtered (see Logic of Stimulus Filtering above), though an identical pattern of results was found for filtered speech (filtered using the same procedure described above, Supplementary Figure 9. This experiment contained additional conditions not analyzed here. Participants heard 3 trials for each condition. All voices recognized correctly on less than 10% of trials were excluded from the analysis to avoid floor effects – this removed 9 of 28 (32%) voices from Experiment 10a, and 17 of 39 (44%) voices from Experiment 10b. The excluded voices did not contribute to the scores for a participant in a condition. In some cases this eliminated all the voices in a condition for a participant, in which case that participant's score was excluded from the mean score for that condition. No participants were fully excluded from analysis as a consequence of this threshold. The inclusion of these poorly recognized voices in the analysis did not alter the qualitative pattern of results across conditions, though it lowered overall performance.
Experiment 11: Novel Voice Discrimination
Procedure
Participants heard three one-second samples of speech and were asked to identify the sample spoken by a different speaker than the other two (first or last). The two samples spoken by the same speaker were distinct (taken from different sentences). Following each trial, participants clicked a button to select one of two responses: ‘first different’, ‘last different’. Participants completed 48 trials for each condition in a single session.
Stimuli
For each trial, one-second speech excerpts were randomly chosen from the TIMIT training database. The excerpts were presented sequentially, with a half-second pause between each excerpt. Two excerpts were produced by the same speaker, and one was from another speaker of the same gender and from the same dialect region. There were three conditions: Harmonic, Inharmonic, and Whispered, the stimuli for which were all synthesized from STRAIGHT as described above, and was not high-pass filtered (see Logic of Stimulus Filtering above), though equivalent results were found for filtered speech (Supplementary Figure 9).
Data Availability
All data is available in Supplementary Table 4.
Code Availability
Custom code for synthesizing inharmonic versions of speech and other natural sounds is available at http://mcdermottlab.mit.edu/downloads.html
Supplementary Material
Acknowledgments
We thank C. Micheyl, K. Walker, B. Delgutte, and the McDermott lab for helpful comments on an earlier draft of this paper, D. Temperley for sharing code to generate melodies, C. Wang for assistance collecting data, V. Zhao for assistance selecting the Mandarin word pairs for Experiment 5, and K. Woods for help implementing Mechanical Turk paradigms. This work was supported by a McDonnell Foundation Scholar Award to J.H.M., NIH grant 1R01DC014739-01A1 to JHM, NIH-NIDCD training grant T32DC000038 in support of M.J.M., and a National Science Foundation Graduate Research Fellowship to M.J.M. The funding agencies were not otherwise involved in the research and any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the McDonnell Foundation, NIH, or NSF.
Footnotes
Author Contributions. M.J.M. designed the experiments, collected and analyzed data, and wrote the paper. J.H.M. designed the experiments and wrote the paper.
Competing Interests. The authors declare no competing interests.
References
- 1.Helmholtz HLF. On the sensations of tone. Longmans, Green, and Co; 1875. [Google Scholar]
- 2.Lord Rayleigh WS. London Macmillan, Repr 1945. Vol. 504. New York: Dover; 1896. Theory of sound. [Google Scholar]
- 3.Békésy G von. Experiments in hearing. McGraw-Hill; 1960. [Google Scholar]
- 4.Plack C, Oxenham A, Fay R, Popper A. Pitch: Neural Coding and Perception. Vol. 24. Springer; 2005. [Google Scholar]
- 5.DeCheveigné A. In: Pitch: Neural Coding and Perception. Plack CJ, Oxenham AJ, Fay R, Popper A, editors. Springer; 2005. pp. 169–233. [Google Scholar]
- 6.Licklider JCR. ‘Periodicity’ pitch and ‘place’ pitch. J Acoust Soc Am. 1954;26:945. [Google Scholar]
- 7.Schouten JF, Ritsma RJ, Cardozo BL. Pitch of the residue. J Acoust Soc Am. 1962;34:1418–1424. [Google Scholar]
- 8.Meddis R, Hewitt MJ. Virtual pitch and phase sensitivity of a computer model of the auditory periphery. I: pitch identification. J Acoust Soc Am. 1991;89:2866–2882. [Google Scholar]
- 9.Cariani P, Delgutte B. Neural correlates of the pitch of complex tones. I. Pitch and pitch salience. J Neurophysiol. 1996;76:1698–1716. doi: 10.1152/jn.1996.76.3.1698. [DOI] [PubMed] [Google Scholar]
- 10.Shamma S, Klein D. The case of the missing pitch templates: how harmonic templates emerge in the early auditory system. J Acoust Soc Am. 2000;107:2631–2644. doi: 10.1121/1.428649. [DOI] [PubMed] [Google Scholar]
- 11.Goldstein JL. An optimum processor theory for the central formation of the pitch of complex tones. J Acoust Soc Am. 1973;54:1496–1516. doi: 10.1121/1.1914448. [DOI] [PubMed] [Google Scholar]
- 12.Terhardt E. Calculating virtual pitch. Hear Res. 1979;1:155–182. doi: 10.1016/0378-5955(79)90025-x. [DOI] [PubMed] [Google Scholar]
- 13.Kaernbach C, Demany L. Psychophysical evidence against the autocorrelation theory of auditory temporal processing. J Acoust Soc Am. 1998;104:2298–2306. doi: 10.1121/1.423742. [DOI] [PubMed] [Google Scholar]
- 14.Bernstein JGW, Oxenham AJ. The relationship between frequency selectivity and pitch discrimination: sensorineural hearing loss. J Acoust Soc Am. 2006;120:3929–3945. doi: 10.1121/1.2372452. [DOI] [PubMed] [Google Scholar]
- 15.Bendor D, Wang X. The neuronal representation of pitch in primate auditory cortex. Nature. 2005;436:1161–1165. doi: 10.1038/nature03867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Feng L, Wang X. Harmonic template neurons in primate auditory cortex underlying complex sound processing. Proc Natl Acad Sci. 2017;201607519 doi: 10.1073/pnas.1607519114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fishman YI, Micheyl C, Steinschneider M. Neural representation of harmonic complex tones in primary auditory cortex of the awake monkey. J Neurosci. 2013;33:10312–10323. doi: 10.1523/JNEUROSCI.0020-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bizley JK, Walker KMM, King AJ, Schnupp JWH. Neural ensemble codes for stimulus periodicity in auditory cortex. J Neurosci. 2010;30:5078–91. doi: 10.1523/JNEUROSCI.5475-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Patterson RD, Uppenkamp S, Johnsrude IS, Griffiths TD. The processing of temporal pitch and melody information in auditory cortex. Neuron. 2002;36:767–776. doi: 10.1016/s0896-6273(02)01060-7. [DOI] [PubMed] [Google Scholar]
- 20.Penagos H, Melcher JR, Oxenham AJ. A neural representation of pitch salience in nonprimary human auditory cortex revealed with functional magnetic resonance imaging. J Neurosci. 2004;24:6810–6815. doi: 10.1523/JNEUROSCI.0383-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Norman-Haignere S, Kanwisher N, McDermott JH. Cortical pitch regions in humans respond primarily to resolved harmonics and are located in specific tonotopic regions of anterior auditory cortex. J Neurosci. 2013;33:19451–69. doi: 10.1523/JNEUROSCI.2880-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Allen EJ, Burton PC, Olman CA, Oxenham AJ. Representations of pitch and timbre variation in human auditory cortex. J Neurosci. 2017;37:1284–1293. doi: 10.1523/JNEUROSCI.2336-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tang C, Hamilton LS, Chang EF. Intonational speech prosody encoding in the human auditory cortex. Science (80-) 2017;801:797–801. doi: 10.1126/science.aam8577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Faulkner A. Pitch discrimination of harmonic complex signals: residue pitch or multiple component discriminations? J Acoust Soc Am. 1985;78:1993–2004. doi: 10.1121/1.392656. [DOI] [PubMed] [Google Scholar]
- 25.Moore BCJ, Glasberg BR. Frequency discrimination of complex tones with overlapping and non-overlapping harmonics. J Acoust Soc Am. 1990;87:2163–2177. doi: 10.1121/1.399184. [DOI] [PubMed] [Google Scholar]
- 26.Micheyl C, Divis K, Wrobleski DM, Oxenham AJ. Does fundamental-frequency discrimination measure virtual pitch discrimination? J Acoust Soc Am. 2010;128:1930–1942. doi: 10.1121/1.3478786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Micheyl C, Ryan CM, Oxenham AJ. Further evidence that fundamental-frequency difference limens measure pitch discrimination. J Acoust Soc Am. 2012;131:3989–4001. doi: 10.1121/1.3699253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Latinus M, Belin P. Human voice perception. Curr Biol. 2011;21 doi: 10.1016/j.cub.2010.12.033. [DOI] [PubMed] [Google Scholar]
- 29.McDermott JH, Oxenham AJ. Music perception, pitch, and the auditory system. Curr Opin Neurobiol. 2008;18:452–463. doi: 10.1016/j.conb.2008.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roberts B, Holmes SD. Grouping and the pitch of a mistuned fundamental component: Effects of applying simultaneous multiple mistunings to the other harmonics. Hear Res. 2006;222:79–88. doi: 10.1016/j.heares.2006.08.013. [DOI] [PubMed] [Google Scholar]
- 31.Houtsma aJM. Pitch identification and discrimination for complex tones with many harmonics. J Acoust Soc Am. 1990;87:304. [Google Scholar]
- 32.Shackleton TM, Carlyon RP. The role of resolved and unresolved harmonics in pitch perception and frequency modulation discrimination. J Acoust Soc …. 1994;95:3529–40. doi: 10.1121/1.409970. [DOI] [PubMed] [Google Scholar]
- 33.Micheyl C, Delhommeau K, Perrot X, Oxenham AJ. Influence of musical and psychoacoustical training on pitch discrimination. Hear Res. 2006;219:36–47. doi: 10.1016/j.heares.2006.05.004. [DOI] [PubMed] [Google Scholar]
- 34.Pressnitzer D, Patterson RD. Distortion products and the perceived pitch of harmonic complex tones. Physiol Psychophys Bases Audit Funct. 2001:97–104. [Google Scholar]
- 35.Norman-Haignere S, McDermott JH. Distortion products in auditory fMRI research: Measurements and solutions. NeuroImage. 2016;129:401–413. doi: 10.1016/j.neuroimage.2016.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dowling WJ, Fujitani DS. Contour, interval, and pitch recognition in memory for melodies. J Acoust Soc Am. 1971;49:524–531. doi: 10.1121/1.1912382. [DOI] [PubMed] [Google Scholar]
- 37.Kawahara H. STRAIGHT, exploitation of the other aspect of VOCODER: Perceptually isomorphic decomposition of speech sounds. Acoust Sci Technol. 2006;27:349–353. [Google Scholar]
- 38.Kawahara H, et al. TANDEM-STRAIGHT: A temporally stable power spectral representation for periodic signals and applications to interference-free spectrum, F0, and aperiodicity estimation. SADHANA. 2011;36:713–722. [Google Scholar]
- 39.McDermott JH, Ellis DP, Kawahara H. Inharmonic speech: a tool for the study of speech perception and separation. SAPA@ INTERSPEECH. 2012:114–117. [Google Scholar]
- 40.Sloboda JA. The musical mind: the cognitive psychology of music. Oxford University Press; 1985. [Google Scholar]
- 41.Peretz I, Champod AS, Hyde K. Varieties of musical disorders: The Montreal battery of evaluation of amusia. Annals of the New York Academy of Sciences. 2003;999:58–75. doi: 10.1196/annals.1284.006. [DOI] [PubMed] [Google Scholar]
- 42.Temperley D. A probabilistic model of melody perception. Cogn Sci. 2008;32:418–444. doi: 10.1080/03640210701864089. [DOI] [PubMed] [Google Scholar]
- 43.McDermott JH, Keebler MV, Micheyl C, Oxenham AJ. Musical intervals and relative pitch: frequency resolution, not interval resolution, is special. J Acoust Soc Am. 2010;128:1943–1951. doi: 10.1121/1.3478785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Garofolo JS, et al. TIMIT acoustic-phonetic continuous speech corpus. 1993 [Google Scholar]
- 45.Marques C, Moreno S, Castro SL, Besson M. Musicians detect pitch violation in a foreign language better than nonmusicians: behavioral and electrophysiological evidence. J Cogn Neurosci. 2007;19:1453–1463. doi: 10.1162/jocn.2007.19.9.1453. [DOI] [PubMed] [Google Scholar]
- 46.Tervaniemi M, Just V, Koelsch S, Widmann A, Schröger E. Pitch discrimination accuracy in musicians vs nonmusicians: An event-related potential and behavioral study. Exp Brain Res. 2005;161:1–10. doi: 10.1007/s00221-004-2044-5. [DOI] [PubMed] [Google Scholar]
- 47.Schneider P, et al. Structural and functional asymmetry of lateral Heschl's gyrus reflects pitch perception preference. Nat Neurosci. 2005;8:1241–1247. doi: 10.1038/nn1530. [DOI] [PubMed] [Google Scholar]
- 48.McDermott JH, Lehr AJ, Oxenham AJ. Is relative pitch specific to pitch? Psychol Sci. 2008;19:1263–1271. doi: 10.1111/j.1467-9280.2008.02235.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Borchert EMO, Micheyl C, Oxenham AJ. Perceptual grouping affects pitch judgments across time and frequency. J Exp Psychol Hum Percept Perform. 2011;37:257–269. doi: 10.1037/a0020670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Warrier CM, Zatorre RJ. Influence of tonal context and timbral variation on perception of pitch. Percept Psychophys. 2002;64:198–207. doi: 10.3758/bf03195786. [DOI] [PubMed] [Google Scholar]
- 51.Demany L, Pressnitzer D, Semal C. Tuning properties of the auditory frequency-shift detectors. J Acoust Soc Am. 2009;126:1342–1348. doi: 10.1121/1.3179675. [DOI] [PubMed] [Google Scholar]
- 52.Chambers C, et al. Prior context in audition informs binding and shapes simple features. Nat Commun. 2017;8 doi: 10.1038/ncomms15027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bregman MR, Patel AD, Gentner TQ. Songbirds use spectral shape, not pitch, for sound pattern recognition. Proc Natl Acad Sci. 2016;113:1–6. doi: 10.1073/pnas.1515380113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gockel HE, Carlyon R, Plack C. Across-frequency interference effects in fundamental frequency discrimination: questioning evidence for two pitch mechanisms. J Acoust Soc Am. 2004;116:1092–1104. doi: 10.1121/1.1766021. [DOI] [PubMed] [Google Scholar]
- 55.Trainor LJ, Desjardins RN, Rockel C. A comparison of contour and interval processing in musicians and nonmusicians using event-related potentials. Australian Journal of Psychology. 1999;51:147–153. [Google Scholar]
- 56.McDermott JH, Lehr AJ, Oxenham AJ. Individual differences reveal the basis of consonance. Curr Biol. 2010;20:1035–1041. doi: 10.1016/j.cub.2010.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Moore BC, Glasberg BR, Peters RW. Thresholds for hearing mistuned partials as separate tones in harmonic complexes. J Acoust Soc Am. 1986;80:479–83. doi: 10.1121/1.394043. [DOI] [PubMed] [Google Scholar]
- 58.Hartmann WM, McAdams S, Smith BK. Hearing a mistuned harmonic in an otherwise periodic complex tone. J Acoust Soc Am. 1990;88:1712–1724. doi: 10.1121/1.400246. [DOI] [PubMed] [Google Scholar]
- 59.Roberts B, Bailey PJ. Spectral regularity as a factor distinct from harmonic relations in auditory grouping. J Exp Psychol Hum Percept Perform. 1996;22:604–14. doi: 10.1037//0096-1523.22.3.604. [DOI] [PubMed] [Google Scholar]
- 60.Schön D, Magne C, M B. The music of speech: music training facilitates pitch processing in both music and language - Schön - 2004 - Psychophysiology - Wiley Online Library. Psychophysiology. 2004;41:341–349. doi: 10.1111/1469-8986.00172.x. [DOI] [PubMed] [Google Scholar]
- 61.Norman-Haignere S, Kanwisher NG, McDermott JH. Distinct cortical pathways for music and speech pevealed by hypothesis-free voxel decomposition. Neuron. 2015;88:1281–1296. doi: 10.1016/j.neuron.2015.11.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Patel AD. Can nonlinguistic musical training change the way the brain processes speech? The expanded OPERA hypothesis. Hearing Research. 2014;308:98–108. doi: 10.1016/j.heares.2013.08.011. [DOI] [PubMed] [Google Scholar]
- 63.Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
- 64.Woods KJP, Siegel MH, Traer J, McDermott J. Headphone screening to facilitate web-based auditory experiments. Atten Percept Psychophys. 2017;79:2064–2072. doi: 10.3758/s13414-017-1361-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data is available in Supplementary Table 4.