Task and Distribution Sampling Affect Auditory Category Learning

Abstract

There is substantial evidence that two distinct learning systems are engaged in category learning. One is principally engaged when learning requires selective attention to a single dimension (rule-based) and the other is drawn online by categories requiring integration across two or more dimensions (information-integration). This distinction has been largely drawn from studies of visual categories learned via overt category decisions and explicit feedback. Recent research has extended this model to auditory categories, the nature of which introduces new questions for research. The current experiment addresses the influence of incidental versus overt training and category distribution sampling on learning information-integration and rule-based auditory categories. The results demonstrate that training task influences category learning, with overt feedback generally outperforming incidental feedback. Additionally, distribution sampling (probabilistic or deterministic) and category type (information-integration or rule-based) affects how well participants are able to learn. Specifically, rule-based categories are learned equivalently regardless of distribution sampling, whereas information-integration categories are learned better with deterministic sampling than probabilistic sampling. The interactions of distribution sampling, category type, and kind of feedback impacted category learning performance, but these interactions have not yet been integrated into existing category learning models. These results suggest new dimensions for understanding category learning, inspired by real-world properties of auditory categories.

Everyday decisions depend on well-learned category representations, whereby perceptually discriminable experiences are treated as functionally equivalent. For example, one must be able to categorize an animal encountered on the street as “friendly” or “dangerous” to decide whether to approach or avoid it. Speech perception can be considered an example of categorization (Holt & Lotto, 2010) in the sense that perceptually discriminable and acoustically variable utterances come to be mapped to phonetic categories. Speech presents a challenging case of auditory perceptual category learning because phonetic categories are defined by multiple acoustic dimensions that may not be perceptually separable or easily verbalized, the distributions of which are highly overlapping (Hillenbrand, Getty, Clark, & Wheeler, 1995; Holt & Lotto, 2008, 2010; Jongman, Wayland, & Wong, 2000; Lisker, 1986; Vallabha, McClelland, Pons, Werker, & Amano, 2007).

An influential cognitive neuroscience framework of category learning developed in the visual category learning literature (Ashby, Alfonso-Reese, Turken, & Waldron, 1998) has recently been applied to auditory and speech category learning (Chandrasekaran, Koslov, & Maddox, 2014; Chandrasekaran, Yi, & Maddox, 2014; Maddox, Chandrasekaran, Smayda, & Yi, 2013; Yi, Maddox, Mumford, & Chandrasekaran, 2014). The COmpetition of Verbal and Implicit Systems (COVIS) “dual systems” model of category learning posits two distinct learning systems mediated by the striatum: an explicit system that involves the frontal cortex and the head of the caudate nucleus and an implicit system that recruits the putamen and the tail of the caudate. These dual systems are differentially engaged by distinct distributions of category exemplars (Ashby & Maddox, 2011). Rule-based category distributions—which are thought to engage an explicit, reflective, hypothesis-testing system that relies upon working memory and attention—can be distinguished by a single, simple verbalizable rule (Ashby et al., 1998). Conversely, information-integration category distributions— proposed to engage an implicit, reflexive system that uses procedural learning—can only be distinguished if information from multiple dimensions is integrated at a pre-decisional stage (Ashby & Gott, 1988). Because this integration is pre-decisional, the relationship between information-integration categories is often non-verbalizable. In the dual systems theory, the distribution structure of category exemplars is thought to be the primary determinant of which of the two category-learning systems drives the motor response.

Research on auditory category learning in the context of the dual systems model has focused mostly on non-native speech category learning of Mandarin lexical tones via overt training (Chandrasekaran, Koslov, et al., 2014; Maddox & Chandrasekaran, 2014; Yi et al., 2014). In overt training, participants are aware that they are performing a categorization task, make explicit categorization decisions, and are given explicit feedback about these decisions after each trial. Additionally, with overt training participants are sometimes explicitly informed of the dimensions on which the stimuli vary. Under these conditions, Mandarin tone speech categories are learned best when participants used a reflexive strategy that relies upon the implicit system that learns information-integration categories (Chandrasekaran, Koslov, et al., 2014; Maddox & Chandrasekaran, 2014; Yi et al., 2014). The reasoning is that speech categories—like information-integration categories—are defined by highly variable exemplars signaled by multiple acoustic dimensions in a manner that is difficult to verbalize (Chandrasekaran, Koslov, et al., 2014) and thus are learned better via the implicit, reflexive learning system. In support of this, functional neuroimaging reveals that the patterns of corticostriatal activation during speech category learning are more consistent with the involvement of implicit, reflexive system posited by COVIS (Yi et al., 2014).

These recent results suggest the promise of dual systems theory in understanding auditory, and in particular, speech, category learning. However, the categorization challenges presented by auditory (and speech) signals are somewhat different from those invited by the visual categories that have served as the principle testing ground for dual systems theory (Holt & Lotto, 2010). There remain important open questions about how well auditory category learning aligns with the predictions of dual systems theory. In the present research, we examine the predictions of dual systems theory in the context of how manipulations of task, distribution sampling, and the category type affect auditory category learning.

We test these questions using novel, artificial nonspeech auditory categories. Although nonspeech categories have not been used as frequently in the context of examining dual systems theory as non-native speech categories (but see Chandrasekaran, Koslov, et al., 2014), they provide us with the control to precisely define and manipulate category distributions, distribution sampling, and the course of learning as a function of different learning tasks. Thus, in the same way that very simple visual dimensions have been used productively to understand the learning systems available to categorizing more complex objects in the natural world, we employ nonspeech sounds to understand the processes available to support learning more complex speech categories. We next describe the rationale for focusing on task, category distributions, and distribution sampling in the present research.

Task

Nearly all studies of visual or auditory category learning from a dual systems perspective have used an overt training task (Ashby, Maddox, & Bohil, 2002; Chandrasekaran, Yi, et al., 2014; Dunn, Newell, & Kalish, 2012; Ell, Ing, & Maddox, 2009; Maddox, Filoteo, Hejl, & Ing, 2004; Maddox, Love, Glass, & Filoteo, 2008; c.f. for a discussion about unsupervised learning see Ashby, Queller, & Berretty, 1999). Participants are told how many categories exist, they are instructed that the goal is to categorize the stimuli, and they are provided with corrective trial-by-trial feedback on category decisions. In an exception that used an unsupervised category training paradigm without overt feedback, Ashby et al. (1999) found that rule-based (RB) categories distinguished by a single, simple verbalizable rule could be learned without feedback, but that information integration (II) categories requiring information from multiple dimensions to be integrated at a pre-decisional stage could not. The researchers concluded that learning II categories is critically dependent on feedback, whereas learning RB categories can occur without feedback. Thus, due to the inability of participants to learn II categories without feedback, the majority of research from the dual systems literature has utilized supervised learning tasks with overt feedback.

Yet, recent research in auditory category learning suggests an alternative approach that is neither wholly explicit nor unsupervised. Incidental learning occurs without instructions to categorize, overt category decisions, or explicit feedback. Instead, sound categories are learned incidentally by virtue of their relationship to success in performing a primary task distinct from auditory category learning (Gabay, Dick, Zevin, & Holt, 2015; Lim & Holt, 2011; Lim, Lacerda, & Holt, 2015; Liu & Holt, 2011; Vlahou, Protopapas, & Seitz, 2012; Wade & Holt, 2005). For example, when auditory categories’ exemplars are presented in a manner that correlates with where a visual ‘x’ will next appear on the screen in a visual detection task, participants incidentally learn complex auditory categories, including speech, in the course of performing the visual detection task (Gabay et al., 2015; Liu, 2014). Incidental auditory category learning is also apparent across more challenging primary tasks, such as navigating a videogame environment in which sound categories are correlated with aspects of the input that support success in the primary, game navigation, task (Gabay et al., 2015; Lim & Holt, 2011; Lim et al., 2015; Liu & Holt, 2011; Wade & Holt, 2005). Inasmuch as this incidental category learning proceeds even without instructions about the importance of the sounds, knowledge of the existence of auditory categories, overt category decisions, or explicit feedback about categorization, it may better model aspects of category learning in natural environments whereby correlated objects, events and actions across modalities are available as structure that may guide learning (Gabay et al., 2015; Wade & Holt, 2005).

Although prior studies of category learning in a dual systems theory framework have relied nearly exclusively on overt training, there is extensive evidence to demonstrate the importance of task variables on category learning. Investigations of the distinction between II and RB category learning have emphasized the significance of feedback timing (Dunn et al., 2012; Ell et al., 2009; Maddox, Ashby, & Bohil, 2003; Maddox, Ashby, Ing, & Pickering, 2004; Maddox & Ing, 2005; Smith et al., 2014; Worthy, Markman, & Maddox, 2013), amount of feedback and feedback type (Ashby et al., 2002, 1999; Ashby & O’Brien, 2007; Dunn et al., 2012; Goudbeek, Cutler, & Smits, 2008; Goudbeek, Swingley, & Smits, 2009; Maddox et al., 2008), and changing instructions to participants (Chandrasekaran, Yi, Smayda, & Maddox, 2016; Grimm & Maddox, 2013) However, the question of whether category learning for II and RB categories differs across overt training compared to incidental training has yet to been investigated.

We hypothesize that II categories—which are difficult to verbalize and require predecisional integration—may benefit more from incidental training tasks in which attention is directed toward a primary task, and away from decisions about category exemplars. In contrast, consistent with the dual systems theory, RB categories may benefit more from an overt training task in which attention can be directed toward the stimuli and features that distinguish categories. The overt task may encourage more explicit, verbalizable hypothesis testing to support learning RB categories. Since this kind of explicit strategizing can be detrimental for II category learning (Grimm & Maddox, 2013), incidental training may be beneficial for learning II categories.

Category Distribution Sampling

The categorization challenges presented by speech – and, indeed, most natural categories – almost always involve complex, probabilistic category exemplar distributions that overlap in acoustic space (Kuhl et al., 1997; Lotto, Sato, & Diehl, 2004; McMurray & Jongman, 2011; Peterson & Barney, 1952). Yet, many studies of speech and nonspeech auditory category learning have examined learning across non-overlapping, deterministic distributions well differentiated in acoustic space and characterized by a small number of exemplars experienced repeatedly across training (Holt & Lotto, 2006; Kluender, Lotto, Holt, & Bloedel, 1998; Kuhl, 1991; Lim & Holt, 2011; Mirman, Holt, & McClelland, 2004; Wade & Holt, 2005). Even when more probabilistic distributions of natural speech productions have been used to study category learning among non-native listeners (Bradlow, Pisoni, Akahane-Yamada, & Tohkura, 1997; Lively, Logan, & Pisoni, 1993; Logan, Lively, & Pisoni, 1991; Yi et al., 2014), the impact of distribution sampling on learning has not been a focus of investigation.

The approaches using probabilistic and deterministic distributions differ on several dimensions. However, each approach is meant to approximate some sampling that is similar to real-world categories, such as speech. Deterministic distributions are highly stylized, the categories do not overlap, and there are relatively few exemplars. Probabilistic distributions are randomly sampled, the categories are often overlapping, and there are many possible exemplars. It is important to understand what, if any, effect sampling from these different kinds of distributions has on category learning. To the extent that each effectively approximates sampling from naturalistic categories, then approach to distribution sampling should not have an impact on learning. However, it is entirely possible that sparser, non-overlapping, more stylistically sampled distributions may be learned in a different manner than denser, overlapping, randomly sampled distributions.

This issue has not been investigated thoroughly even with the artificially constructed visual categories upon which the dual systems model of categorization is based. To our knowledge only one study has addressed something similar to the issue of probabilistic versus deterministic category distribution sampling in the visual domain. Ell and Ashby (2006) examined the impact of category overlap on learning. The degree to which exemplars from different categories were drawn from overlapping versus entirely distinct regions of stimulus space impacted learning of visual II categories, but not visual RB categories. Specifically, when categories’ exemplars were moderately overlapping across II distributions, participants were able to use optimal II strategies in category learning; however, with too much or too little overlap of II distributions, participants relied on suboptimal, RB strategies. This indicates that at least some aspects of the sampling distribution, specifically overlap, may influence the course of learning. Thus, it is important to examine the potential learning differences between carefully sampled deterministic distributions and randomly sampled probabilistic distributions, especially in light of the fact that the auditory category learning literature has employed them somewhat interchangeably.

In the present study, we manipulate whether the II and RB category distributions are sampled probabilistically or deterministically in acoustic space. Examining the interaction of category distribution type (II versus RB) and task (incidental versus overt) and distribution sampling (deterministic, non-overlapping versus probabilistic, overlapping) is important given the ubiquity of probabilistic, overlapping category distributions in speech and other natural categories, including visual categories (e.g. Nosofsky, Sanders, Meagher, & Douglas, 2017).

In the present study, we investigate learning across highly stylized, deterministic distributions of sound category exemplars like those that have characterized most auditory category learning studies to date. We also examine learning across categories defined more probabilistically. There is not a large literature to support strong predictions about the effect of these different sampling distributions on learning. Drawing from Ell and Ashby’s (2006) results, one might predict that category overlap in deterministic compared to probabilistic sampling will impact learning of II categories, but not RB categories. Participants learning categories sampled deterministically may be biased toward explicit strategies thereby impeding II learning and benefitting RB learning. To the extent that explicit strategies influence the learning, there may also be an interaction between task type (incidental, overt) and distribution sampling. Compared to probabilistic distributions learned through incidental training, learning via overt training may be better across deterministic, non-overlapping category distributions that are easy to learn with verbalizable rules and for which the feedback is perfectly consistent with optimal strategies.

Summary

In the present experiment, we examined the impact of task and category distribution sampling on learning four auditory categories defined by either II or RB stimulus distributions. We trained separate groups of participants with either a traditional, overt categorization paradigm with explicit feedback on every trial or with an incidental paradigm in which neither categorization decisions nor feedback were explicit task demands. Finally, we varied the nature of distribution sampling to examine the influence of the probabilistic or deterministic nature of the category distributions on learning. We directly examined the influence of category type, task, and distribution sampling on auditory category learning using within-training metrics, as well as a common overt labeling task administered post-training to assess generalization of learning to novel category exemplars.

Methods

Participants

One hundred and sixty-six adults ages 18-25 (89 females, 77 males) affiliated with Carnegie Mellon University participated for partial course credit or a small payment ($10). All participants had normal or corrected-to-normal vision and reported normal hearing. There was a total of eight conditions that varied by training task, category distribution, and distribution sampling (Table 1). Participants were trained on either an incidental task or an overt task, learned either to categorize rule-based or information-integration category distributions, and the distributions were either probabilistic or deterministic in their sampling. An additional five participants were run but excluded from all analyses because of equipment failure.

Table 1.

Number of Participants in Each Condition

Deterministic Sampling
Task	Information-Integration	Rule-Based
Incidental task	21	20
Overt task	21	21
Probabilistic Sampling
Task	Information-Integration	Rule-Based
Incidental task	20	21
Overt task	21	21

Stimuli

The learning challenge differed across four conditions defined by the category input distributions. Each condition had four categories separated by optimal decision boundaries, as shown in Figure 1. Participants trained on either information-integration (II) distributions (Figure 1b, 1d) distributions or rule-based (RB) distributions (Figure 1a, 1c) that were sampled deterministically in acoustic space (Figure 1a, 1b) or probabilistically (Figure 1c, 1d). For the deterministic distributions, it is possible to define optimal decision boundaries that classify exemplars with perfect accuracy because there is no overlap between the categories. However, no decision boundary results in 100% accuracy for the probabilistic distributions because exemplars can probabilistically belong to more than one category due to category overlap. Optimal performance for the probabilistic RB and II conditions was 90.5% and 90.25%, respectively. We used these moderate levels of overlap to reflect similar levels of overlap in Ell and Ashby (2006), who found that moderate levels of overlap did not hinder learning for either II or RB categories.

Figure 1.

Stimulus distributions. a) Rule-Based, Deterministic b) Information-Integration, Deterministic. c) Rule-Based, Probabilistic d) Information-Integration Probabilistic.

The two-dimensional acoustic space from which stimulus exemplars were sampled was defined by two dimensions: center, or carrier, frequency (CF) and modulation frequency (MF). CF can be described approximately as the pitch of the tone and MF as the warble of the tone. We chose these particular acoustic dimensions because they were used in an existing auditory category learning study (Holt & Lotto, 2006), demonstrating that listeners are able to learn categories defined across these acoustic dimensions. Additionally in this previous study, these dimensions were psychoacoustically matched for discriminability across the approximate range used in the present study (Holt & Lotto, 2006). Further, manipulation of sounds across these dimensions creates highly artificial exemplars that participants are unlikely to have heard previously. In the same manner that Gabor patches provide a simple stimulus to manipulate parametrically in the visual domain, these simple acoustic stimuli provide us with a testbed for auditory category learning. Each 300-ms stimulus was defined by a CF modulated with a depth of 100 Hz at the corresponding MF, with overall energy RMS matched across exemplars and all synthesis accomplished using MATLAB R2014a (The MathWorks, Inc., Natick, Massachusetts).

The stimulus distributions for the Deterministic, RB categories were adapted from Holt and Lotto (2006). The stimulus distributions for the Deterministic II categories were generated by rotating the RB stimuli counterclockwise in acoustic space by 45 degrees. The Deterministic categories were highly stylized, in the manner of previous auditory studies (Holt & Lotto, 2006; Kluender et al., 1998; Kuhl, 1991). The Deterministic categories also did not overlap and had a relatively small number of exemplars per category. For the Deterministic categories (Figure 1a, 1b), there were 48 exemplars per category plus the centroid of each category. Half of the exemplars were used during the training phase (24 exemplars/category, 96 total stimuli) and half of the exemplars plus the centroid were reserved for the generalization test phase (100 stimuli).

To create the Probabilistic stimulus distributions, we defined the underlying distributions to have the same means in CFxMF acoustic space as each of the Deterministic category distributions. We increased the number of exemplars and the variance of the category distributions to manipulate sampling. We then sampled randomly from the defined distribution; the random sampling resulted in means, variance, and covariance that varied somewhat from those defining in the underlying distribution (Appendix A). The probabilistic distributions were created with MATLAB R2012. The Probabilistic distributions (Figure 1c, 1d) had 100 exemplars per category. Half of the exemplars were used during the training phase (50 stimuli/category, 200 total stimuli) and half of the exemplars were reserved for the generalization test phase (200 stimuli). Unlike the Deterministic conditions, not all of the exemplars from the Probabilistic distributions were played in the test phase. Rather, they were randomly sampled for each participant for a total of 100 trials.

Task

Participants were trained on one of two training tasks: incidental or overt (see Figure 2). After training, all participants were tested on an overt generalization post-test, which included exemplars not experienced during training. By adding an overt generalization post-test, we were able to compare learning between the Incidental and Overt training tasks and to better understand learning that extends beyond individual exemplars experienced in training, to include generalization to novel exemplars consistent with the category distribution.

Figure 2.

Outline of tasks used in the current experiment. a) Incidental training task b) Overt training task.

Training Task: Incidental.

Research in our laboratory has demonstrated the effectiveness of a simple incidental learning task, the SMART task, in training listeners to categorize sounds (Gabay et al., 2015; Liu, 2014; Liu & Holt, n.d.). This paradigm was adapted as a highly simplified version of a videogame training paradigm successful in training speech and nonspeech categories incidentally, without overt training or feedback (e.g., Lim & Holt, 2011; Wade & Holt, 2005). In the SMART task, the primary objective is to rapidly detect the appearance of a visual target in one of four possible screen locations by pressing a key corresponding to the screen location.

Within-trial category-exemplar variability.

On each trial, five unique exemplars drawn from one of the four sound categories preceded the appearance of the visual target. For the Deterministic categories, the sound categories perfectly predict the location of the upcoming visual target and, consequently, the action required to complete the visual detection task. The overlap of the Probabilistic categories makes it such that the exemplars played on a single trial may not be equally representative exemplars of the category based on the optimal boundary between the categories. However, the exemplars played on each trial were always drawn from a single category, so the sound category was predictive of the visual target location. Prior research demonstrates that participants learn auditory categories incidentally in the SMART task and generalize learning to labeling novel exemplars in an overt, post-training labeling task (Gabay et al., 2015). The generalization to novel sound category exemplars underscores the important point that this learning is not a simple sound-to-location mapping. The inherent variability in sound category exemplars encourages participants to learn sound categories that robustly generalize to guide subsequent responses to novel, unfamiliar exemplars (Gabay et al., 2015).

In the present experiment, we used the SMART task to assess incidental auditory category learning and generalization across deterministic and probabilistic II and RB category distributions with a covert reaction-time measure during online learning and an overt, post-training category labeling task.

Covert reaction time measure of learning.

Participants were instructed that their task was to indicate where a visual target (a red X) appeared on the screen by responding with the corresponding keyboard button (responses were U, I, O, and P buttons; see Figure 2). They were told that sounds would precede the X, but no mention was made about the relationship between the sounds and the location of the X.

Participants experienced three Training Blocks (96 trials/block) in which each of the four sound categories predicted the appearance of the visual target in one specific location. Subsequently, they completed a brief Random Test Block (48 trials), in which the mapping of sound categories to visual target locations was fully random; any sound category exemplar could precede the presentation of the visual target in any position with equal probability. Following the approach of Gabay et al. (2015), this block was shorter to avoid extensive exposure to a random mapping that may erode category learning across the Training Blocks. The final block was one last Training Block. This block was included to reinstate category learning prior to the post-training Generalization Post-Test.

On each trial, the sound category was chosen pseudo-randomly (random shuffle of a fixed number of trials for each category per block). Then five exemplars were randomly selected from the pool of category exemplars. The 300-ms exemplars were each presented once, with a 50 ms inter-stimulus silent interval. The final exemplar was followed by a 500 ms silence, after which a red X appeared in the location is associated with the sound category. The trial structure was identical for the Random Test Block, except that the red X appeared in a randomly-selected location as opposed to the location associated with the sound category in training blocks. Participants responded to indicate the location of the red X by pressing the associated button as quickly as possible. Reaction times were measured as the time lapsed from the onset of the visual detection target to the press of the response key. After each experimental block, participants were encouraged to rest briefly.

The Random Test Block provides for a covert measure of incidental category learning to be collected online during training. If participants have incidentally learned sound categories in service of guiding visual detection behavior, then eliminating the consistent relationship between category and location in the Random Test Block should slow response to the visual target. As evident in prior studies (Gabay et al., 2015; Liu, 2014), learning should be apparent in a reaction time (RT) Cost (RT_{block 4} – RT_{block 3}) between Block 4 (random) and Block 3 (consistent). This RT Cost serves as our covert reaction time measure of learning across incidental training conditions.

Overt measures of learning and generalization.

An overt labeling task immediately followed the SMART task. Before the start of the Generalization Post-Test, participants were informed that, the location of the X had been associated with the sounds that preceded it in the SMART task and that they should respond with a key press to guess the location the visual target would be most likely to appear. On each of 100 trials (25 trials/category), five novel sound category exemplars not experienced in the SMART task were randomly selected from the pool of generalization stimuli and presented with the same timing characteristics as in training. As in training, the Generalization Post-Test had within-trial variability. But, no visual targets appear in this task, thereby providing no feedback. This overt labeling task provides an explicit test of category learning and its generalization to novel exemplars not experienced in training.

Training Task: Overt.

The overt task modeled the training approach taken in most studies of category learning (Ashby et al., 2002; Yi et al., 2014), while aligning closely with many of the task details of the incidental SMART task (Gabay et al., 2015). In the Overt task, participants experienced the same kind of multi-modal location-to-sound category mapping as the Incidental (SMART) task participants, but were explicitly informed of the relationship between sounds and visuomotor targets, made explicit categorization decisions, and were given overt corrective feedback following each categorization decision.

As in the Incidental training task, participants first experienced three Training Blocks (96 trials/block) in which sound categories predicted the position of the visual target. However, unlike the Incidental task, participants did not receive a Random Test Block because such a block played no role in covert assessment of learning in this overt feedback version of the paradigm. In sum, the Overt task involved four Training Blocks followed by the Generalization Post-Test.

For each trial, the sound category was first chosen pseudo-randomly (random shuffle of a fixed number of trials for each category per block). As with the Incidental task, there was within-trial variability in the Overt task. Five category exemplars were then randomly selected from the pool of exemplars for that category. The 300-ms exemplars were sequentially presented at the onset of the trial, with 50-ms silent intervals. Participants pressed a button (U, I, O, or P) to indicate which visual location they believed to be associated with the sound. A 500-ms silence followed the response, after which a red X appeared in the visual location associated with the sound category presented on that trial as feedback about category identity.

After each block, participants were encouraged to rest briefly. Button presses were considered correct if they corresponded to the correct visual location mapped to the trial’s sound category, providing a measure of accuracy across blocks.

Overt generalization post-test.

Immediately after the last block of training, participants engaged in an overt categorization test with within-trial variability that was identical to the Generalization Post-Test described for Incidental training.

Results

We describe the results separately for the Incidental and Overt training conditions because some measures were task-specific. The Incidental training task provided covert online measures of learning via reaction time (Figure 3), whereas the Overt task did not. For the Overt task, the relevant behavior is accuracy across training blocks (Figure 4). Across Incidental and Overt conditions, there was a common post-training overt labeling task to assess generalization of learning (Figure 5).

Figure 3.

Average reaction time during the Incidental training task. Ribbon error bars represent the standard error of the mean. Individual points represent individual participant averages. Participants in the II condition are shown as blue circles and participants in the RB condition are shown as red squares.

Figure 4.

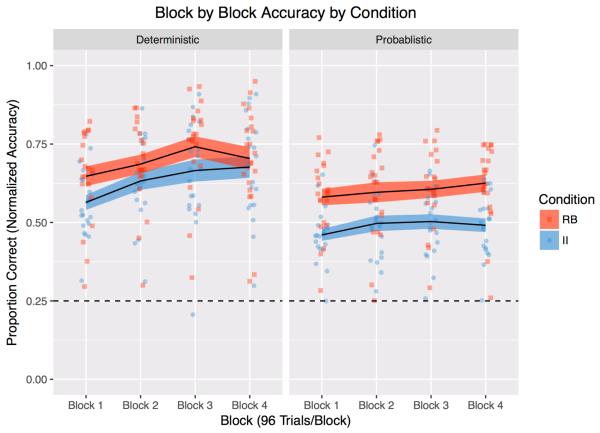
Block-by-block performance during the Overt training task. The dotted line denotes chance performance (25%). Ribbon error bars represent the standard error of the mean. Individual points represent individual participant averages. Performance for participants in the II condition is shown in blue circles and performance for the RB condition is shown in red squares.

Figure 5.

Generalization test performance for all conditions. The dotted line denotes chance performance (25%). Error bars represent the standard error of the mean. Individual points represent individual participant average.

Training Task: Incidental

Reaction time filtering.

We filtered the reaction times to include only trials on which participants were accurate in responding to the X on the screen and for which reaction times were less than 1500 ms or greater than 100 ms. A total of 3.77% of trials were excluded across all conditions (2.74% of trials were excluded for II-Probabilistic, 3.74% for RB-Probabilistic, 4.46% for II-Deterministic, 4.11% for RB-Deterministic).

Covert reaction time measure of learning.

The covert measure of learning, Reaction Time Cost (RT Cost), provided an online measure of incidental category learning. We predicted that eliminating the consistent relationship between the sound category and the upcoming location of the visual target established across Blocks 1-3 would slow reaction times to detect the visual target in Block 4, compared to Block 3, as expressed by a positive RT Cost (RT_Block4 – RT_Block3). Since exemplars vary on a trial-by-trial basis, this is indicative of sound category learning.

Figure 3 shows the average reaction times for each condition. Following the approach of prior research (Gabay et al., 2015), we first examined the RT Cost by conducting paired-samples t-tests comparing Block 4 and Block 3 reaction times for each condition. There were significant RT Costs, indicative of incidental auditory category learning, for both Deterministic II (M=33.7 ms, t(20) = 3.39, p = .003, Cohen’s d = .56) and RB (M=22.3ms, t(19) = 2.79, p = .012, Cohen’s d = .38) distributions. For the Probabilistic distributions, only the RB condition resulted in a significant RT Cost indicative of incidental auditory category learning (M=31.2 ms, t(20) = 3.39, p = .003, Cohen’s d =.45). The RT Cost for the Probabilistic II condition was not significant (M=12.3 ms, t(19) = 1.10, p = .29, Cohen’s d = .10). Thus, with the exception of the Probabilistic II condition, each group exhibited significant incidental auditory category learning, as indexed by the covert, online RT Cost measure.

We next asked whether the magnitude of the RT Cost varied as a function of the learning challenges presented by the different conditions. It did not. A 2 (Category Distribution) × 2 (Distribution Sampling) between-subjects ANOVA revealed that the magnitude of the RT Cost did not depend on either Category Distribution (II vs. RB; F(1, 78) = 0.15, p = .70, η_p² = .002) or Sampling (Deterministic vs. Probabilistic; F(1, 78) = 0.42, p = .52, η_p² = .005), and there was no interaction (F(1, 78) = 2.48, p = .12, η_p² = .031). Although all conditions except for Probabilistic II demonstrated evidence of incidental category learning by the RT Cost measure, the magnitude of the RT Cost was not dependent on either Category Distribution or Sampling.

Average Reaction Time.

We also compared average RTs across all training blocks as a function of condition. Participants learning Deterministic category distributions were marginally faster (M=381 ms, SE=11.4) to respond to the visual targets than participants in learning Probabilistic category distributions (M=413 ms, SE=11.4, F(1, 78) = 4.06, p = .047, η_p² = .049). It appears that the more highly overlapping Probabilistic category distributions slowed visual target detection somewhat relative to simpler, more coherent Deterministic category distributions. One possibility is that participants may be sensitive to the deterministic versus probabilistic structure of the category input distributions. However, group differences cannot be ruled out in this between-subjects design. There was no effect of Category Distribution (II, RB) on the average RT (F(1, 78) = 0.56, p = .46, η_p² = .007) and only a marginal interaction between Category Distribution and Sampling (F(1, 78) = 3.63, p = .060, η_p² = .045).

We note that we did not have any a priori predictions that the conditions would differ by average reaction time. Thus, examining average reaction time serves as a manipulation check to make sure that the different conditions did not differ on RT. However, there is one subject in the Probabilistic II condition who was consistently slower than the other participants. We also ran the analyses excluding this subject, who was more than three standard deviations above the mean on four out of five blocks. No other subject was more than three standard deviations above the mean on any individual block. Examining the reaction time data without this subject had largely the same results, except for on the average RT. Excluding the outlier from the Probabilistic II condition, the effect of Sampling distribution on average RT disappears, such that there were no significant differences between the Probabilistic and Deterministic average RT (Probabilistic M=404 ms, SE=9.6; Deterministic M=381 ms, SE=11.4; F(1, 77) = 2.94, p = .090, η_p² = .037). Similar to the results including the outlier, the effect of Category Distribution and interaction were not significant after excluding the outlier from the Probabilistic II condition (Category Distribution: F(1, 77) = .042, p = .84, η_p² = .001; Interaction: F(1,77) = 2.52, p = .12, η_p² = .032). After excluding the outlier in the Probabilistic II condition, there were no differences between the groups on average RT, indicating that any differences in learning are not tied to differences in reaction time.

Training Task: Overt

Normalization.

Recall that an optimal observer would achieve 100% accuracy in the Deterministic conditions, but only 90.25% or 90.5% accuracy in the Probabilistic conditions. To account for this difference, we first computed normalized accuracy values for data from the Probabilistic learning conditions as (Normalized Accuracy = Raw Accuracy / Optimal Accuracy) with optimal accuracy (.9025 and .905, for Probabilistic II and RB, respectively). All comparisons were conducted with these normalized accuracy values. We note that none of the qualitative patterns of results changed as a result of normalization; it simply provides for equitable cross-condition comparison.

Accuracy across blocks.

In the Overt training task, (normalized) accuracy across blocks is the principle measure of category learning; Figure 4 plots these results. Examining performance across blocks with a 2 × 2 × 4 repeated-measures ANOVA [Category Distribution (II, RB) × Sampling (Deterministic, Probabilistic) × Block], we found that independent of Category Distribution or Sampling, participants generally improved with training across Blocks (F(2.6, 209.2)¹ = 15.42, p < .001, η_p² = .162). Participants in the Deterministic condition learned more across blocks than participants in the Probabilistic condition (F(2.6, 209.2) = 3.25, p = .029, η_p² = .039). Performance across blocks was not impacted by the interaction of Category Distribution (II, RB) and Sampling (F(2.6, 209.2) = 1.40, p = .25, η_p² = .017) and there was no advantage in learning II versus RB Category Distributions across training, (F(2.6, 209.2) = 0.54, p = .63, η_p² = .007). Generally, this may indicate that Sampling – whether categories are sampled Deterministically, or Probabilistically – is the main driver of the difference in improvement across conditions, rather than Category Distribution or the interaction between Category Distribution and Sampling. Deterministic auditory categories were more readily learned than probabilistic auditory categories. The overall pattern of learning was differentiated by the distribution Sampling, not Category Distribution.

In examining overall accuracy, rather than performance across blocks, we found that participants learning RB categories had higher average accuracy than participants learning II categories (F(1, 80) = 11.58, p = .001, η_p² = .13). Deterministic category input distributions were more easily learned than Probabilistic category input distributions (F(1, 80) = 21.87, p < .001, η_p² = .22). There was no interaction between Category Distribution and Sampling (F(1, 80) = 1.12, p = .30, η_p² = .014), indicating that RB conditions were learned better than II conditions for both Deterministic and Probabilistic category distributions. Moreover, Deterministic distributions were better learned than Probabilistic distributions for both II and RB categories. These results support the prediction that overt training should benefit RB category learning. We also predicted that RB might not be affected by sampling distribution. In contrast to our predictions, the sampling distribution affected learning for both II and RB categories such that Deterministic sampling led to better overall category learning than Probabilistic sampling.

We also note that learning was quite rapid. Significant learning was evident in the first 96-trial block of training in each of the conditions (chance = 25%; Deterministic II: t(20) = 13.15, p < .001, M=56.4%, Cohen’s d = 5.88, Deterministic RB: t(20) = 12.62, p < .001, M=64.7%, Cohen’s d = 5.64, Probabilistic II: t(20) = 12.41, p < .001, M=51.0%, Cohen’s d = 4.97, Probabilistic RB: t(20) = 13.57, p < .001, M=64.2%, Cohen’s d = 5.66).

Generalization Post-Test: Incidental and Overt Training

Both Incidental and Overt training results in auditory category learning, as assessed by the task-specific measures during training. Here, we examine the post-training measure of generalization of category learning assessed using a common task across the groups trained incidentally and overtly. Performance during the Generalization Post-Test is shown in Figure 5.

Normalization.

As for the Overt training task, we normalized generalization test accuracies. We computed normalized accuracy values for data from the Probabilistic learning conditions as (Normalized Accuracy = Raw Accuracy / Optimal Accuracy) with optimal accuracy (.9025 and .905, for Probabilistic II and RB, respectively). We did not compute normalized accuracies for the Deterministic conditions because the optimal accuracy was 100%. We note that none of the qualitative patterns of results changed as a result of normalization; it simply provides for a fair cross-condition comparison.

To compare learning in all conditions, we ran a 2 × 2 × 2 ANOVA of Training Task (Incidental vs. Overt) × Category Distribution (II vs. RB) × Sampling (Deterministic vs. Probabilistic). This allowed us to determine the aspects of the training task and/or stimulus components that drive the differences among conditions. The COVIS model predicts that the main driver of differences in performance will be Category Distribution because II and RB categories are learned by distinct neural systems. Additionally, we examined the impact of Training Task and distribution Sampling on performance. We predicted that learning differences would depend on Category Distribution, but also on Training Task and Sampling. In comparing generalization test performance, we found a marginally significant three-way interaction among Training Task, Category Distribution, and Sampling (F(1,158) = 3.75, p = .055, η_p² = .023). To understand the causes of this marginal interaction, we looked more closely at the two-way interactions.

We predicted that performance on II and RB Category Distributions would depend on Training Task, such that Overt training would better support learning RB categories and Incidental training would support learning II categories. We did not find support for this hypothesis; the interaction was not significant (F(1,158) = 0.002, p = .96, η_p² = .000). Instead, we found significantly better generalization of category learning for Overt training compared to Incidental training, irrespective of whether the categories were RB or II. Ignoring distribution Sampling, for both II and RB, Overt training resulted in significantly greater generalization of category learning than Incidental training (RB: t(81) = 3.78, p < .001, Cohen’s d = .84 ; II: t(81) = 3.41, p = .001, Cohen’s d = .76).

We also predicted that Incidental and Overt training tasks might have different effects on Probabilistic and Deterministic category learning. We predicted that Overt training would lead to better performance for Deterministic categories than Probabilistic, but that Incidental training would lead to better performance for Probabilistic categories than Deterministic. We found that performance for Probabilistic and Deterministic distributions did depend on Training Task (F(1,158) = 5.18, p = .024, η_p² = .032). In line with our predictions, Overt training led to better generalization of category learning for Deterministic category distributions than Probabilistic distributions (t(82) = 2.37, p = .020, Cohen’s d = .52). Ignoring category type for Overt training, the Deterministic conditions had an average test accuracy of 68.2% and Probabilistic conditions had an average test accuracy of 54.1%. However, Incidental training did not result in significant differences in generalization across learning Deterministic and Probabilistic distributions (t(80) = 0.75, p = .46, Cohen’s d = .17). Ignoring category type for Incidental training, the Deterministic conditions had an average test accuracy of 49.4% and the Probabilistic conditions had an average test accuracy of 47.4.6%. These findings cannot be accounted for directly by the differences in difficulty between Deterministic and Probabilistic distributions because we used normalized accuracies in these analyses. In line with our predictions, Overt training led to better learning for Deterministic relative to Probabilistic categories. However, we predicted that Probabilistic categories would be learned better during Incidental training and we found that Deterministic and Probabilistic categories were learned equivalently during Incidental training.

Our third prediction was that performance of participants learning RB categories, Deterministic and Probabilistic sampling might not affect performance, but for II categories, the Deterministic sampling would be learned better than the Probabilistic sampling. We found an interaction between Category Distributions (II, RB) and the Distribution Sampling on generalization of category learning, (F(1,158) = 13.31, p < .001, η_p² = .078). In support of our prediction, generalization of RB categories did not differ for Deterministic and Probabilistic distributions (t(64.1) = 1.56, p = .13, Cohen’s d = .39 , corrected for inequality of variances). We also note that this is different than what we found during overt training, where Deterministic was learned better than Probabilistic. After Incidental and Overt training, generalization of RB categories did not differ between Deterministic and Probabilistic distributions. Also in support of our prediction, for II categories, the Deterministic distributions resulted in significantly higher generalization accuracy than the Probabilistic distributions (t(76.3) = 3.00, p = .004, Cohen’s d = .69, corrected for inequality of variances). The ability to generalize RB categories is not affected by differences in sampling distributions, but generalization of II categories is worse with Probabilistic distributions than Deterministic.

Though overall generalization accuracy can give us some clues as to what participants were able to learn about these categories through overt or incidental training, this does not allow for a full understanding of the category representations that participants learned. To gain a better understanding of these representations, we constructed confusion matrices for each condition learning II (Figure 6) and RB (Figure 7) categories. These confusion matrices demonstrate participants’ response behavior in the generalization test based on the actual category that was presented to them. For correct responses, the actual category on a trial (columns) and the category of the participant’s response (rows) converge (Figures 6 and 7 on the positive diagonal). For incorrect responses, we can observe a clear pattern of confusion among multiple categories or a random confusion across all categories. Confusion matrices allow us to quantify similarities and differences among categories based on categorization errors during the generalization test.

Figure 6.

Confusion matrices for information-integration conditions in the generalization test. Each column represents the actual category identity of the exemplars played on a trial and each row represents the category response that the participant made. The shading gradient and percentages within each cell represent how frequently participants gave a particular response for each category. Columns sum to 100%. To the right is a schematic diagram of the information-integration category structures (also shown in Figure 2).

Figure 7.

Confusion matrices for rule-based conditions in the generalization test. Each column represents the actual category identity of the exemplars played on a trial and each row represents the category response that the participant made. The shading gradient and percentages within each cell represent how frequently participants gave a particular response for each category. Columns sum to 100%. To the right is a schematic diagram of the rule-based category structures (also shown in Figure 2).

The pattern of results in the confusion matrices for II categories demonstrates a tendency for participants in all four conditions to respond in a way that groups categories A and B together and groups categories C and D together (Figure 6). The confusable categories are not distinguished easily by either dimension used to construct the categories. Instead, this particular pattern of response is consistent with responses informed by integration along the positive correlation between the two dimensions. Note that this pattern of responses was similar across II conditions, despite quantitatively different levels of overall performance.

The pattern of results in the confusion matrices for RB categories demonstrates a different tendency (Figure 7). Participants in the RB Overt Deterministic condition were the most consistent in their responses across the four categories. These participants did not demonstrate a clear pattern of confusion among any of the categories in the generalization test, which may have stemmed from their higher accuracy in the generalization test. Participants in the other three RB conditions demonstrated varying levels of confusion between categories B and C. Participants demonstrated clear response patterns that distinguished categories A and D from the other categories and there was some confusion between categories B and C. Categories B and C differ on both stimulus dimensions used to construct the categories, just as the distinct categories of A and D. In these three RB conditions, participants did not appear to be using simple unidimensional rules to separate the four categories into two groups. Instead, there is a more complex pattern of responses that even includes confusion of two categories that differ on both acoustic dimensions. The pattern of responses--and particularly of the errors--in the generalization test provides us some information about how participants represent the categories and the relations between the categories as a function of task and distribution sampling.

General Discussion

We examined learning and generalization of auditory categories across incidental and overt training tasks, likewise assessing the influence of probabilistic versus deterministic sampling of category distributions defined by a simple rule or requiring integration across dimensions. To our knowledge, this study is the first to compare dual-systems category learning across II and RB stimulus distributions in an incidental training task and an overt training task and the first to systematically examine the effect of the sampling distribution of the categories and the interaction with training task type. We aimed to understand the extent to which category learning generalizes to novel exemplars since generalization is a central characteristic of categorization. This further served to provide a common measure across the incidental and overt training tasks, which we focus on in discussing the results.

Incidental versus Overt Training.

The results demonstrate that artificial nonspeech auditory categories can be learned incidentally under conditions in which participants to not overtly make categorization decisions and are not informed that categories of sound relate to the primary (visual detection) task. Participants were engaged in a simple visual detection task and were not told that the sounds were important or related to the task, that the sounds were drawn from different categories, or that the sounds would later be central in an overt generalization task. The incidental category learning was apparent in overt labeling of novel generalization sounds at post-test, which requires a transfer of incidentally-acquired category knowledge to an explicit category labeling task. Across conditions, incidental training led to successful generalization of category learning across both II and RB stimulus distributions defined deterministically and probabilistically. This tells us that explicit awareness of the relevance of the feedback or even the goal of the task to learn and generalize their category knowledge is not necessary for category learning. This is notable because prior studies have almost exclusively examined learning with training tasks that involve explicit feedback following each overt categorization decision (Ashby et al., 2002; Chandrasekaran, Yi, et al., 2014; Dunn et al., 2012; Ell et al., 2009; Maddox, Filoteo, et al., 2004; Maddox et al., 2008; c.f. for a discussion about unsupervised learning see Ashby et al., 1999).

The COVIS model emphasizes the importance of feedback in driving learning, particularly in the case of learning II stimulus distributions. In this context, it may seem surprising that there was such robust incidental learning of II stimulus distributions. However, although the incidental training paradigm does not utilize feedback in the traditional manner of overt training tasks it should not be considered to lack feedback entirely. The consistent correlation of category exemplars with the location of visual targets presents a situation for which auditory categorization supports predictions regarding the primary visual detection task. These predictions are either correct or incorrect, as indicated by the ultimate appearance of the visual target. In this way, categorization is incidentally associated with outcomes via the primary visual detection task. We have argued previously that this form of feedback may relate more closely to how sound categories are used in the world; they allow listeners to use variable sensory input to make predictions that support behavior in the larger environment, which sometimes lead to positive outcomes (Gabay et al., 2015; Lim & Holt, 2011). The present results demonstrate that this alternative, less overt, form of feedback is sufficient to support category acquisition across both RB and II stimulus distributions when they are sampled either probabilistically or deterministically. Even for II distributions, which COVIS posits to rely more heavily on feedback, neither overt awareness about the category learning task nor explicit feedback appear to be necessary for category learning.

There are important implications for theory. Based on the prior literature on visual and auditory category learning and the COVIS model, we predicted that categories defined by II stimulus distributions would be better learned via Incidental training than Overt training and, conversely, that categories defined by RB stimulus distributions would be better learned under Overt training, relative to Incidental training. Specifically, since the incidental task is speeded visual detection and not auditory categorization it directs attention away from overt categorization decisions. Thus, we hypothesized that learning II stimulus distributions would benefit from incidental training because overt reasoning is thought to hinder II learning (Ashby & Maddox, 2011). The data do not support the prediction; there was no interaction of training task and category stimulus distribution. Both RB and II stimulus distributions were learned better in the Overt, relative to the Incidental training task.

Overt training lead to better performance than Incidental training regardless of category type. One factor possibly contributing to this finding is that in the Incidental training task involved a brief block in which the relationship between sound category and visual location as randomized (to covertly assess learning online). This short block may have been enough to differentiate the Incidental training condition from Overt training to influence generalization performance. Another possible explanation for the Overt training advantage is that the simple visual detection of the SMART incidental training task may not be fully tapping into the procedural learning system that best learns II categories. Therefore, caution is warranted in concluding that learning via overt training is necessarily always superior to learning via incidental training.

Category Distribution Sampling.

The sampling distributions defining the categories impacted learning and generalization performance. This finding is critical because many speech and nonspeech auditory category learning studies have used highly stylized, deterministic distributions, whereas natural categories, including speech, are defined by more variable and probabilistic distributions. We predicted, based on the visual category learning results of Ell and Ashby (2006), that Sampling might affect learning of II categories, but not RB categories. Our generalization test results were consistent with Ell and Ashby’s (2006) findings that overlap affected learning of II categories, but not RB categories. We found poorer category generalization accuracy for II stimulus distributions defined Probabilistically compared to Deterministically. In contrast, category generalization accuracy was equivalent across Probabilistic and Deterministic RB stimulus distributions. While our results are consistent with the general premise from Ell and Ashby (2006)—that RB category learning is unaffected by differences in overlap and II category learning is affected—our finding that generalization for Deterministic distributions was better than generalization for Probabilistic distributions is inconsistent with their findings. Ell and Ashby (2006) found that moderately overlapping categories, such as our Probabilistic distributions led to better II learning than categories that did not overlap, such as our Deterministic distributions. Of course, the sampling manipulation in the current study involved more than just overlap, which may account for the differences between our study and Ell & Ashby’s (2006). Additionally, this difference may have been driven by the stimuli themselves. It is possible that simple, verbalizable visual dimensions may be used differently by participants during learning than the auditory dimensions used in the current study. Further research is needed to disentangle the effects of overlap or sampling distribution on auditory II category learning.

Our results provide further evidence of the applicability of COVIS to auditory category learning and the instantiation of the multiple systems theory for auditory category learning. Although Ell and Ashby (2006) did not test generalization of learning to novel category exemplars, this finding is in accord with their conclusion that category overlap, one of the differences between our sampling distributions, affects II, but not RB, category learning.

In future research, it will be necessary to disentangle the potentially interacting effects of the factors defining Deterministic and Probabilistic category distributions, including overlap, number of exemplars, and stylistically sampled versus randomly sampled distributions. The Deterministic distributions mirroring those used in many nonspeech and speech category learning studies have fewer exemplars and less exemplar overlap both between and within categories compared to our Probabilistic distributions that were meant to more closely approximate natural category distributions. The differences in learning that were explained by the Sampling distributions underscores the significance of this factor in category learning. If our goal is to understand natural category learning, whether it is visual or auditory, it is critical to best approximate the natural structure of those categories in future experimental studies.

These results caution that reliance on simple, carefully designed deterministic input distributions may not capture the learning challenges involved in acquiring speech categories characterized by highly overlapping distributions across complex and multidimensional input dimensions (Hillenbrand et al., 1995; Swingley, 2009). If we are to generalize the conclusions about II categories and the mechanisms that are used to learn them, we also must carefully consider differences in distributions that can define different existing real-world speech categories (see Wanrooij & Boersma, 2013 for a similar argument about frequency distributional learning).

Interaction of Sampling and Task.

We predicted that Sampling distribution may also interact with training task such that Incidental training might be better across Probabilistic distributions, whereas Overt training might be better across Deterministic distributions. In line with our predictions, Overt training led to better generalization of category learning for Deterministic, compared to Probabilistic, stimulus distributions. In contrast to our predictions, Incidental training resulted in equivalent generalization of category learning across Deterministic and Probabilistic stimulus distributions. This interacted with the type of stimulus distribution sampling, as well. For II stimulus distributions, the learning advantage of Overt training over Incidental training held for both Probabilistic and Deterministic distributions. For RB stimulus distributions with Deterministic sampling, there was an Overt training advantage. However, this advantage was not apparent for Probabilistic RB stimulus distributions. This highlights that important differences in category learning occur with different distribution sampling, training, and category types.

For the Probabilistic distributions, participants are receiving information about the category boundaries that is inherently less consistent, compared to feedback given for the Deterministic distributions. All category exemplars in the Deterministic distributions fall perfectly within the hypothetical boundaries within acoustic space defining the respective categories. For the Probabilistic categories, there are a minority of exemplars from each category that cross these hypothetical boundaries, leading to category overlap. This means that the category-consistent feedback (incidental or overt) available in training is not as well-aligned with exemplar similarity in the Probabilistic, compared to Deterministic, conditions. The ambiguous nature of the alignment of the feedback signal with acoustic similarity may lead to less clear category representations, especially around the category boundary. Thus, this leads to a specific benefit of Deterministic over Probabilistic distributions in the Overt task when information is available to explicitly process feedback and incorporate it in future category decisions. On the hypothesis that feedback given in a deterministic manner depends more on explicit memory systems (Seger & Cincotta, 2005), the poorer alignment of exemplar similarity and feedback associated with the Probabilistic distributions may be less impactful during learning in the Incidental task if it draws from learning via more implicit procedural learning systems. The nature of the category distributions and the complexity of category sampling are important aspects to consider because they can greatly impact learning outcomes.

Within-trial variability.

A key difference between the current study and previous studies investigating the dual systems of category learning is that we used within-trial variability in our training and testing paradigms. On each trial, participants heard five unique exemplars from within a single category. In typical dual system experiments, whether visual or auditory, participants encounter a single exemplar on each trial. This methodology allows experimenters to model the decision bound strategy response based on how a participant responds to each exemplar.

Previous research with auditory category learning, including speech, has demonstrate an overall benefit in generalization performance following training with high within-category variability (Bradlow et al., 1997; Iverson, Hazan, & Bannister, 2005; Liu & Holt, n.d.; Logan et al., 1991). This appears to be particularly potent when within-category variability is aligned with trial-level feedback. Using the same incidental training task as the present study, Gabay et al. (2015) found superior learning when participants experienced category exemplar variability within a trial, and therefore tightly coupled with task-driven predictions and feedback. Participants who experienced the same overall exemplar variability across individual trials in the experiment learned less. However, whereas within-trial variability is likely to have promoted learning and generalization in the present study, it also precluded the use of decision bound modeling to assess individual participant response strategies during learning. Current iterations of decision bound models map an individual’s decision boundary based on the location of a single exemplar in the stimulus space given their response. In future work, it will be useful to build decision bound models that can incorporate within-trial variability.

Strategy use during category learning across within-trial exemplar variability remains an open question for future research. Among many possible strategies, for example, it could be the case that participants use only one exemplar out of five that they experience on a trial to make their decision, or that the average similarity space of exemplars experienced within a trial influences decisions. Since distributional sampling had an influence on learning in the present research it will be informative to direct future research toward understanding how trial-level distributional statistics and longer-term distributional statistics that must be accumulated across an experiment interact to influence category learning.

To take a step in this direction, we examined the patterns of responses in the generalization test to obtain a broad sense of participant strategy. Participants’ category confusions across the generalization test provide a window through which to approximate the kinds of representations learned. The confusion matrices make clear that similar overall performance in the generalization test can be arrived at via distinct paths. For the II categories, the pattern of confusability implies that listeners tended to group categories in a way that suggests integration across the dimensions, particularly in a positive-going direction. Intriguingly, this same pattern may be evident in the confusion matrices for RB categories. Rather than confuse RB categories distinguished by a single dimension in the stimulus space, listeners tended to make errors consistent with dimension integration across the positive-going dimension correlation. The apparent pattern of reliance on a positive-going integration strategy is consistent with recent results demonstrating a learning advantage for categories defined by a positive-going, compared to a negative-going, slope in this same stimulus space (Roark & Holt, submitted).

Implications.

Although dual systems theory has been largely developed in the context of empirical data regarding visual category learning, recent work has very successfully applied it to auditory and speech categorization and yielded important insights (Chandrasekaran, Koslov, et al., 2014; Chandrasekaran, Yi, et al., 2014; Maddox & Chandrasekaran, 2014). Because the categorization challenges presented by auditory (and speech) signals are somewhat different from those of visual categories (Holt & Lotto, 2010), this also presents the opportunity to examine first-principles of the model in greater detail through the lens of auditory category learning. We view the present research as a necessary bridge between the auditory category learning research that has focused on the representations acquired in category learning and the highly influential COVIS approach that is beginning to influence auditory category learning research. Our results highlight that small differences in task demands result in quite different patterns of learning that interact with the sampling of category exemplars in acoustic space. Overt categorization decisions and explicit awareness of the category-learning task were not necessary for learning II or RB categories. In the present work, the most effective training approach involved overt training across deterministic category distributions. Since the majority of studies informing theoretical development have relied on just such category learning challenges, it is important to consider that laboratory-based studies may tend to overestimate the ease of category learning under more natural conditions that involve probabilistically-defined categories learned across incidental conditions. This is true for both auditory and visual studies. While we have used a specific pair of acoustic dimensions here, future work should examine the effect of these aspects of the training stimuli on learning with other acoustic dimensions and visual dimensions. The dual systems approach has not yet investigated the effect of these aspects of distributions and training task with either auditory or visual dimensions. Next-generation models of category learning will need to consider the nature of the complexity and overlap of sampling distributions, along with their interaction under more incidental learning situations, to better characterize how the system reacts to real-world category learning challenges.

Appendix A. Category Distribution Means, Variances, and Covariances

Deterministic Category Distribution Information

Category	Mean (CF, MF)	Variance (CF, MF)	Covariance
II: Category A	(674, 197)	(3377.5, 1213.3)	0
II: Category B	(865, 312)	(3377.5, 1213.3)	0
II: Category C	(1056, 197)	(3377.5, 1213.3)	0
II: Category D	(865, 82)	(3377.5, 1213.3)	0
RB: Category A	(730, 278)	(3377.5, 1213.3)	0
RB: Category B	(1000, 278)	(3377.5, 1213.3)	0
RB: Category C	(730, 116)	(3377.5, 1213.3)	0
RB: Category D	(1000, 116)	(3377.5, 1213.3)	0

Probabilistic Category Distribution Information

Category	Mean (CF, MF)	Variance (CF, MF)	Covariance
II: Category A	(701.1, 199.4)	(6306.0, 1629.8)	−15.5
II: Category B	(853.1, 310.7)	(7032.6, 2281.8)	494.9
II: Category C	(1059.0, 196.5)	(6677.8, 2207.2)	−36.7
II: Category D	(863.1, 86.8)	(6156.6, 2123.3)	119.8
RB: Category A	(735.8, 277.1)	(7198.3, 2600.3)	−201.7
RB: Category B	(922.4, 279.8)	(7496.4, 2082.0)	−804.6
RB: Category C	(749.0, 116.7)	(5081.2, 2251.4)	156.3
RB: Category D	(1007.8, 114.3)	(5102.4, 1891.0)	367.6

The Probabilistic category distributions were created by defining a two-dimensional Gaussian distribution with the same means and increased variances relative to the Deterministic category distributions. Then, 100 random samples from that underlying distribution were taken to form the Probabilistic category distributions. Thus, the means, variances, and covariances between categories in the Probabilistic category distributions vary relative to the underlying multidimensional Gaussian distributions.