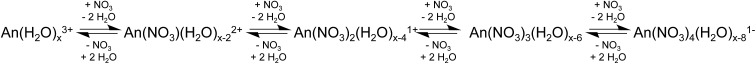The coordination chemistry of Cm^III, Am^III, and Ac^III in nitrate solutions: an actinide L₃-edge EXAFS study

Cm^III, Am^III, and Ac^III have been characterized by solution L₃-edge X-ray absorption spectroscopy as a function of nitric acid concentration. This enabled the first experimental determination of Cm and Ac nitrate distances.

Abstract

Understanding actinide(iii) (An^III = Cm^III, Am^III, Ac^III) solution-phase speciation is critical for controlling many actinide processing schemes, ranging from medical applications to reprocessing of spent nuclear fuel. Unfortunately, in comparison to most elements in the periodic table, An^III speciation is often poorly defined in complexing aqueous solutions and in organic media. This neglect – in large part – is a direct result of the radioactive properties of these elements, which make them difficult to handle and acquire. Herein, we surmounted some of the handling challenges associated with these exotic 5f-elements and characterized Cm^III, Am^III, and Ac^III using An^III L₃-edge X-ray absorption spectroscopy (XAS) as a function of increasing nitric acid (HNO₃) concentration. Our results revealed that actinide aquo ions, An(H₂O)_x³⁺ (x = 9.6 ± 0.7, 8.9 ± 0.8, and 10.0 ± 0.9 for Cm^III, Am^III, and Ac^III), were the dominant species in dilute HNO₃ (0.05 M). In concentrated HNO₃ (16 M), shell-by-shell fitting of the extended X-ray fine structure (EXAFS) data showed the nitrate complexation increased, such that the average stoichiometries of Cm(NO₃)_4.1±0.7(H₂O)_5.7±1.3^{(1.1±0.2)–}, Am(NO₃)_3.4±0.7(H₂O)_5.4±0.5^{(0.4±0.1)–}, and Ac(NO₃)_2.3±1.7(H₂O)_8.3±5.2^(0.7±0.5)+ were observed. Data obtained at the intermediate HNO₃ concentration (4 M) were modeled as a linear combination of the 0.05 and 16 M spectra. For all three metals, the intermediate models showed larger contributions from the 0.05 M HNO₃ spectra than from the 16 M HNO₃ spectra. Additionally, these efforts enabled the Cm–NO₃ and Ac–NO₃ distances to be measured for the first time. Moreover, the An^III L₃-edge EXAFS results, contribute to the growing body of knowledge associated with Cm^III, Am^III, and Ac^III coordination chemistry, in particular toward advancing understanding of An^III solution phase speciation.

Introduction

The actinide(iii) (An^III) cations of Cm^III, Am^III, and Ac^III occupy central roles in numerous nuclear technologies important to society. These range from the medical applications in the targeted alpha therapeutic treatment of disease (Ac^III)1–3 to being critical components in advanced nuclear fuel cycles (Am^III and Cm^III).4–9 Solving technical problems in these areas require detailed understanding of fundamental +3 f-element chemistry. Unfortunately, aside from a limited number of experimental and computational studies,10–21 the chemistry of Cm^III, Am^III, and Ac^III is underdeveloped in comparison to the d-block, main group, and many other 4f- and 5f-elements. This discrepancy – in large part – is related to the rarity of these elements combined with handling difficulties that accompany the radioactive Cm, Am, and Ac isotopes.

This manuscript documents our latest effort to address needs for advancing fundamental Cm^III, Am^III, and Ac^III chemistry. We focused on characterizing the coordination chemistry of these elements in an aqueous environment that contained actinide complexation agents, namely within nitric acid (HNO₃) solutions. These results are of particular relevance, given the importance of HNO₃ matrices in An^III separation processing. For Cm^III and Am^III, HNO₃ solutions find widespread application in almost every advanced nuclear fuel processing flow chart.4,22–24 Additionally, HNO₃ is widely used in the production of ²²⁵Ac for medical purposes (targeted alpha therapy), both in terms of purifying ²²⁵Ac from ²³²Th targets irradiated with high energy protons25–27 and when isolating ²²⁵Ac from ²²⁹Th generators.28–30 Towards these ends, we contribute an An^III L₃-edge X-ray absorption spectroscopy (XAS) study focused on characterizing Cm^III, Am^III, and Ac^III solution-phase coordination chemistry as a function of increasing HNO₃ concentration. Our data provided the first An^III–NO₃ bond distance measurements for Cm^III and Ac^III of any kind (i.e. solid or solution) and represented the first Am^III–NO₃ measurement made in HNO₃ solutions. We observed that at low HNO₃ concentrations (0.05 M), Cm^III, Am^III, and Ac^III existed as aquo ions. The propensity of NO₃^– to complex the An^III cations increased with increasing HNO₃ concentration, such that in HNO₃ (16 M) solutions there were 2 to 4 bound NO₃^– ligands. The results have been presented in the context of the limited number of HNO₃ speciation studies reported previously.

Results and discussion

Sample preparation

Samples were generated by first preparing chemically pure Cm^III, Am^III and Ac^III stock solutions, as previously described.12,20,31 Next, aliquots that contained Cm^III (0.5 mg in 0.5 mL, 4.0 mM), Am^III (0.5 mg in 0.5 mL, 4.1 mM), and Ac^III (28 μg in 0.3 mL, 0.4 mM) were heated to soft dryness. The resulting residues were dissolved in the desired concentration of nitric acid (HNO₃; 0.05, 4, or 16 M). This process was repeated for a total of three times to ensure that the final HNO₃ concentrations were as close to 0.05, 4 and 16 M as possible. Samples were then loaded into XAS holders equipped with three layers of containment to guard against release of radiological material during shipment and data acquisition. Next, the holders were shipped to the Stanford Synchrotron Radiation Lightsource (SSRL) for XAS analysis at the An^III L₃-edge on beam line 11-2.

An^III L₃-edge X-ray absorption near edge spectroscopy (XANES)

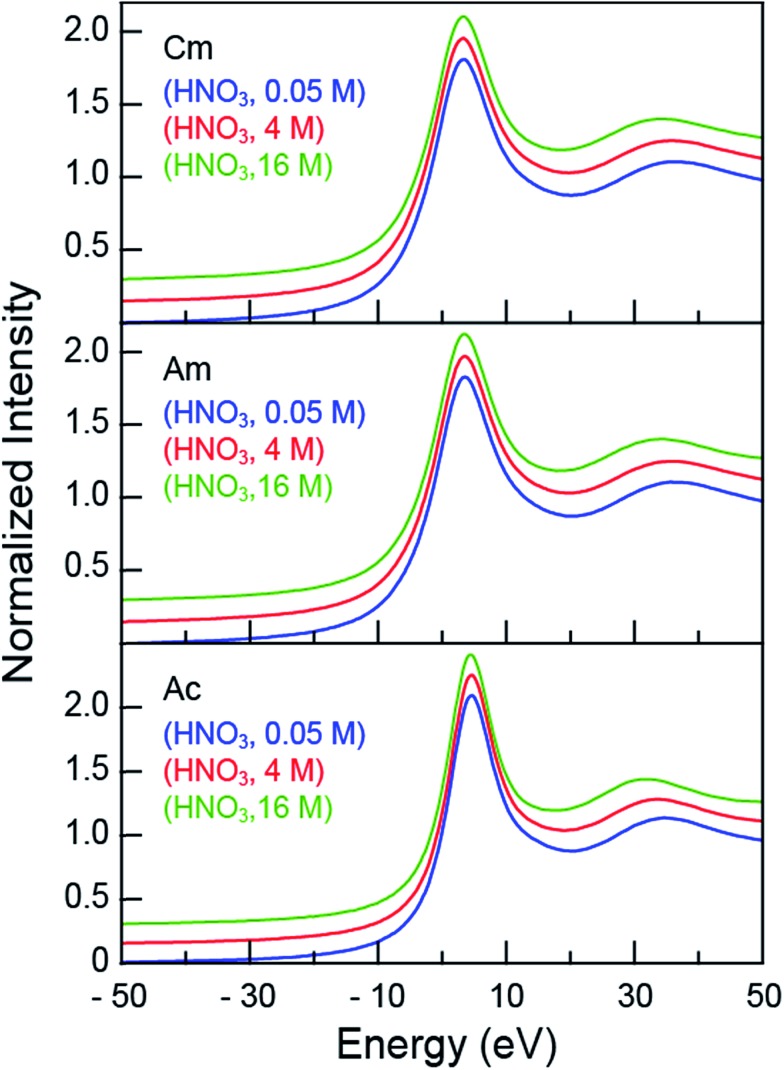
The room temperature Cm^III, Am^III and Ac^III L₃-edge XANES spectra obtained from aqueous solutions that contained increasing amounts of nitric acid (HNO₃; 0.05, 4, 16 M) were background subtracted and normalized (Fig. 1). Each spectrum contained a pronounced absorption peak superimposed on an ionization threshold. From the perspective of the free ion, the edge-feature could be crudely described as originating from electric-dipole allowed transitions from the actinide 2p-orbitals to unoccupied states that contained actinide 6d-character, i.e. for Ac^III 2p⁶···5f⁰ 6d⁰ → 2p⁵···5f⁰ 6d¹.32,33 The inflection points and peak maxima were determined graphically where the second derivatives (inflection point) and first derivatives (peak maxima) of the data equaled zero (Table 1). These values were impacted marginally by changes in HNO₃ concentration: the inflection points for Cm^III were centered around 18 976 eV, for Am^III near 18 514 eV, and for Ac^III close to 15 875 eV. Based on our previous experience in reproducing actinide L₃-edge features,12,21,34–41 uncertainties in edge and peak positions were estimated to be on the order of 0.2 eV. Hence, for a given element (Cm^III, Am^III, or Ac^III), the 0.05, 4, and 16 M absorption edges and peak positions were nearly equivalent.

Fig. 1. The background subtracted and normalized room temperature solution-phase An^III L₃-edge XANES spectra of An^III (An = Cm^III, top; Am^III, middle; Ac^III, bottom) cations dissolved in HNO₃ (0.05 M, blue trace; 4 M, red trace; and 16 M, green trace). Spectra are displayed with a slight y-offset for clarity.

Table 1. Inflection points and peak positions (eV) of the room-temperature Cm^III, Am^III, and Ac^III L₃-edge solution-phase XANES spectra of An^III dissolved in HNO₃ (0.05, 4 and 16 M). The Cm^III and Am^III spectra were calibrated to the peak maximum of a Zr foil (18 013.3 eV) while the Ac^III spectra were calibrated to the first inflection point of a RbCl pellet (15 203.8 eV).

	Inflection point (eV)	Peak position (eV)	2nd peak position (eV)
Cm aquo (1 M HClO4),47 a	18 973.0	—	—
Cm (HNO3, 0.05 M)	18 976.4	18 980.3	19 013.5
Cm (HNO3, 4 M)	18 976.3	18 980.2	19 012.9
Cm (HNO3, 16 M)	18 976.3	18 980.2	19 011.4
Am (0.11 M HO3SCF3),21	18 514.3	18 517.9
Am (HNO3, 0.05 M)	18 514.0	18 517.5	18 550.6
Am (HNO3, 4 M)	18 513.8	18 517.4	18 549.9
Am (HNO3, 16 M)	18 513.8	18 517.4	18 547.1
Ac (0.11 M HO3SCF3),12	15 874.3	15 876.9
Ac (HNO3, 0.05 M)	15 874.7	15 877.6	15 908.1
Ac (HNO3, 4 M)	15 874.6	15 877.5	15 906.7
Ac (HNO3, 16 M)	15 874.6	15 877.5	15 905.0

^aThe Cm aquo complex in 1 M HClO₄ was calibrated with Nb foil (18 986 eV).

Although the absorption peak position showed essentially no dependence on the HNO₃ concentration, changing the HNO₃ concentration from 0.05 M to 16 M had a marked impact on the energy of the post-edge feature approximately 30 to 40 eV above the inflection point (Fig. 1). This peak marks the first extended X-ray absorption fine structure (EXAFS) oscillation. Increasing the HNO₃ concentration systematically lowered the energy for the oscillation maximum (Table 1). For Cm^III, moving from 0.05 M to 4 M HNO₃ caused a 0.6 eV oscillation maximum decrease. Similarly, moving from 4 M to 16 M HNO₃ caused a –2.1 eV energy shift. Similar trends were observed for Am^III and Ac^III, albeit the 3.5 (Am^III) and 3.1 (Ac^III) energy shifts were larger. Dependence of the post-edge line-shape on the HNO₃ concentration foreshadowed structural changes that accompanied coordination of An^III cations by NO₃^– ligands, which were revealed when the EXAFS spectra were rigorously analyzed.

An^III L₃-edge extended X-ray absorption fine structure (EXAFS) spectroscopy

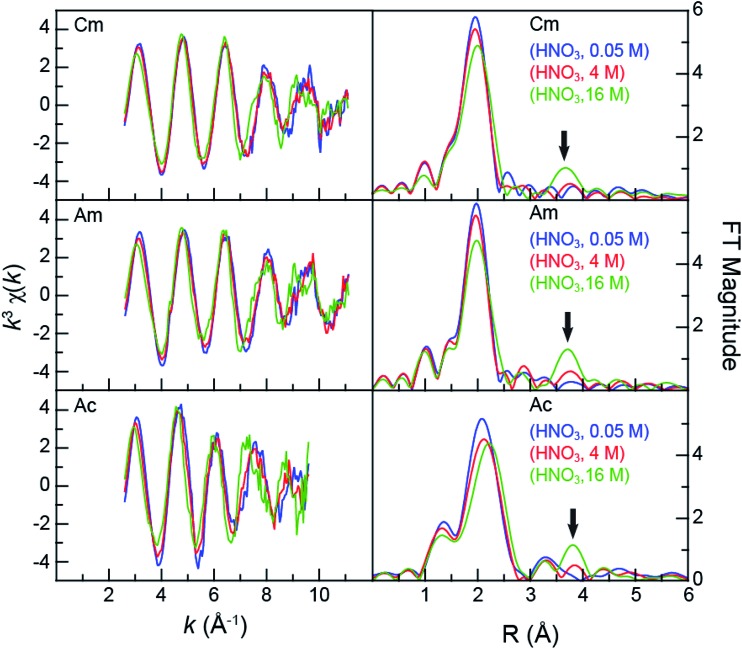
Speciation metrics (i.e. coordination numbers and bond distances) for solution-phase samples were extracted from the k³χ(k) solution-phase measurements (Fig. 2). For Cm^III and Am^III – present in relatively high concentrations (0.5 mg in 0.5 mL per sample) – high quality data were obtained from 2.7 to 11 Å^–1 (in k-space). This energy range provided shell-by-shell resolution in the Cm^III and Am^III measurements to be approximately 0.19 Å (resolution = π/2Δk; in R-space). The Cm^III and Am^III L₃-edge k³χ(k) spectra were quite similar and changed uniformly with increasing HNO₃ concentration (Fig. 2). The first three oscillations were nearly superimposable despite the changes in HNO₃ concentration. Upon reaching the fourth and fifth oscillations, some dependence on the HNO₃ concentration became apparent. For example, moving from 0.05 M to 4 M HNO₃ caused a subtle shoulder to emerge in the fifth oscillation (ca. 9 Å^–1). Changing to concentrated HNO₃ (16 M) increased the magnitude of this shoulder and caused a second shoulder to emerge on the low energy side of the fourth oscillation (ca. 7.5 Å^–1). These line shape changes suggested that some of the scattering pathways were moving out of phase.

Fig. 2. Left – the room temperature An^III L₃-edge EXAFS function k³χ(k) from An^III (An = Cm^III, top; Am^III, middle; Ac^III, bottom) cations dissolved in HNO₃ (0.05 M, blue trace; 4 M, red trace; and 16 M, green trace). Right – the Fourier Transform of k³-EXAFS spectra. The black arrow emphasizes the growing nitrate contribution to the spectra.

In general, the Ac^III spectra were similar to those of Cm^III and Am^III. For example, increased HNO₃ concentrations had little impact on the first three oscillations and showed evidence of out-of-phase scattering pathways for the fourth and fifth oscillations. The Ac^III L₃-edge data differed in two notable ways. First, the signal-to-noise ratio was smaller, on account of the smaller quantity of Ac^III (28 μg). This restricted the energy range over which high quality data were available; from 2.7 to 9.5 in k-space (resolution = 0.23 Å in R-space). Second, the EXAFS oscillation frequency increased in comparison to those of Cm^III and Am^III. This frequency increase was somewhat expected. For example, the frequency in k-space (left, Fig. 2) is inversely related to the interatomic distance. Higher frequencies result from longer bonds. As shown in Fig. 2, the large Ac^III ionic radius42 should provide longer bond distances (higher oscillation frequencies) than those for Cm^III and Am^III, as long as the analytes have similar chemical compositions. Given the observed change in frequency upon moving from Cm^III and Am^III to Ac^III and the similar interference pattern, these data suggested – superficially – that the Ac^III speciation was similar to that of Am^III and Cm^III.

Closer examination of the Cm^III, Am^III, and Ac^III L₃-edge EXAFS spectra supported the proposition that chemical speciation was similar for these three compounds, revealing only subtle differences in Cm^III, Am^III, and Ac^III coordination environments. The experimental data were analyzed using well-established shell-by-shell curve fitting techniques.43 Interpretations of the data were guided by identifying scattering pathways using FEFF8 (ref. 44 and 45) and DFT geometry optimized An^III structures that contained a combination of water molecules and bidentate nitrate ligands, An(H₂O)_9–2x(NO₃)_x^3–x (An = Cm^III, Am^III, Ac^III; x = 0, 1, 2, 3). The coordination numbers (CN), bond lengths (R), Debye–Waller factors (σ²), and energy shifts (E₀) were allowed to converge to reasonable values. The amplitude reduction factor was set to 0.9. The fitting results have been summarized and compared with other relevant EXAFS studies in Table 2.12,21,46,47 For the sake of discussion, we begin by reporting on spectra collected in dilute HNO₃ (0.05 M), then move to concentrated HNO₃ (16 M), and conclude at the intermediate HNO₃ concentration (4 M).

Table 2. The energy shift (ΔE₀), bond distance (R), coordination number (CN), and Debye–Waller factor (σ²) fitting parameters used to model the room-temperature An^III L₃-edge solution-phase EXAFS spectra from An^III cations (An^III = Cm^III, Am^III, Ac^III) dissolved in HNO₃ (0.05, 4, and 16 M). Data were additionally compared with the previously measured An^III aquo complexes.12,21,46,47 In each of our models, the structural amplitude reduction factors (S₀²) were set to 0.9 ^a .

	ΔE0 (eV)	R M–O (Å)	CNbound oxygen	σ bound oxygen 2	R M···N (Å)	CNnitrogen	R M···O terminal oxygen	σ terminal oxygen 2
Cm aquo (0.25 M HCl),46,*	–13.0	2.450 ± 0.002	10.2 ± 0.3	0.009 (fixed)	—	—	—	—
Cm aquo (1 M HClO4),47,* fit 1	–2.0 ± 0.9	2.469 ± 0.007	7.0 ± 0.4	0.0071(8)	—	—	—	—
Cm aquo (1 M HClO4),47,* fit 2	–0.7 ± 0.7	2.470 ± 0.006	6 (fixed)	0.0053(2)	—	—	—	—
		2.63 ± 0.02	3 (fixed)	0.009 (2)
Cm (HNO3, 0.05 M)	–5.5 ± 0.8	2.47 ± 0.01	9.6 ± 0.7	0.009(1)	—	—	—	—
Cm (HNO3, 4 M)	1.5 ± 1.3	2.45 ± 0.01	7 (fixed)	0.007(3)	2.93 ± 0.07	1 fixed	4.25 ± 0.03	0.006 (4)
		2.54 ± 0.05	2 (fixed)
		2.63 ± 0.04	2 (fixed)
Cm (HNO3, 16 M)	3.4 ± 1.1	2.49 ± 0.02	8.9 ± 2.2	0.009(2)	2.95 ± 0.02	4.1 ± 0.7	4.25 ± 0.02	0.010(3)
		2.64 ± 0.03	5.7 ± 1.3
Am (0.25 M HCl),46,*	–8.7	2.480 ± 0.002	10.3 ± 0.3	0.009 (fixed)	—	—	—	—
Am (0.11 M HO3SCF3),21	–4.7 ± 0.9	2.48 ± 0.01	9.5 ± 0.9	0.0088(9)	—	—	—	—
Am (HNO3, 0.05 M)	–5.0 ± 1.0	2.47 ± 0.01	8.9 ± 0.8	0.008(1)	—	—	—	—
Am (HNO3, 4 M)	2.1 ± 1.3	2.46 ± 0.01	6 (fixed)	0.003(1)	2.98 ± 0.04	1 (fixed)	4.27 ± 0.04	0.003 (2)
		2.57 ± 0.03	2 (fixed)
		2.67 ± 0.02	2 (fixed)
Am (HNO3, 16 M)	3.3 ± 0.8	2.50 ± 0.01	7.7 ± 0.8	0.005(1)	2.97 ± 0.01	3.4 ± 0.7	4.26 ± 0.01	0.006(2)
		2.67 ± 0.01	5.4 ± 0.5
Ac (0.11 M HO3SCF3),12	–3.9 ± 1.0	2.63 ± 0.01	10.9 ± 0.5	0.009 (fixed)	—	—	—	—
Ac (HNO3, 0.05 M)	–2.9 ± 1.6	2.63 ± 0.02	10.0 ± 0.9	0.009 (fixed)	—	—	—	—
Ac (HNO3, 4 M)	3.9 ± 2.0	2.61 ± 0.02	6 (fixed)	0.006(4)	3.24 ± 0.11	1 (fixed)	4.42 ± 0.05	0.003 (5)
		2.75 ± 0.04	2 (fixed)
Ac (HNO3, 16 M)	4.4 ± 2.1	2.70 ± 0.02	12.9 ± 4.0	0.012(4)	3.20 ± 0.12	2.3 ± 1.7	4.42 ± 0.03	0.003(6)

^aAdditionally, σ_N² was fixed to σ_O² and CN_{terminal oxygen} set to CN_nitrogen. Data found in the literature and marked with an asterisk (*) had S₀² values set to 1.

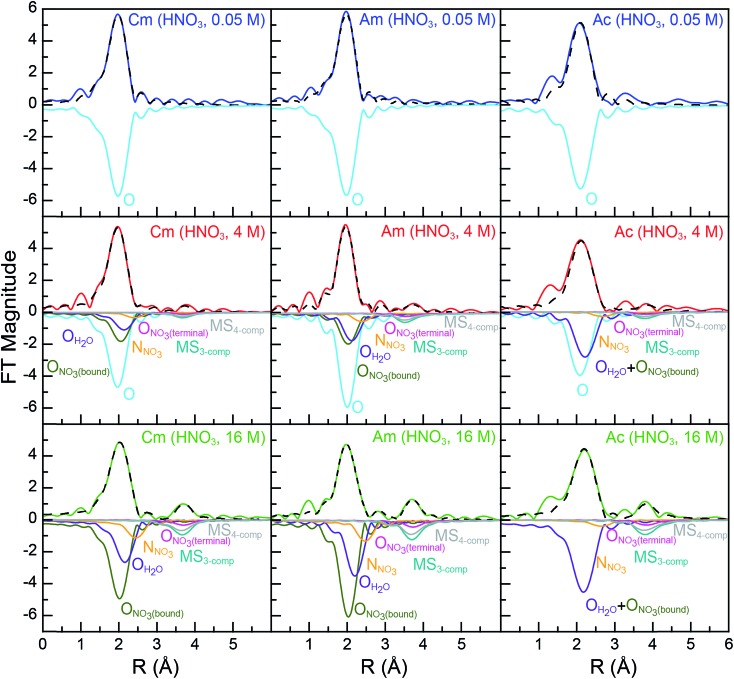
As shown in Fig. 2, all spectra collected from dilute HNO₃ (0.05 M) solutions were best described by a single frequency whose amplitude in k-space (left, Fig. 2) dampened with increased energy. Best fits for the data (top, Fig. 3; Table 2) – those with the smallest residuals and lowest reduced chi-squared values – confirmed this superficial interpretation. The histogram of frequencies shown in the Fourier transform spectra (right, Fig. 2; top, Fig. 3) contained a single peak near R = 2 Å. As the frequency resolution ranged from 0.19 to 0.23 Å for Cm^III, Am^III, and Ac^III, we refrained from attempting to resolve multiple M–O_H2O scattering pathways within this first water shell. Furthermore, the data quality was not sufficient for observing H₂O molecules at longer distances, i.e. in the second and third hydration shells. Fitting the data with a single H₂O shell revealed approximately nine water molecules for Cm^III (9.6 ± 0.7) and Am^III (8.9 ± 0.8) with equivalent M–O_H2O distances of 2.47(1) Å. These results agreed well with the literature values for Cm^III and Am^III aquo ions. The single crystal structure of the Cm^III aquo ion showed nine H₂O ligands with an average Cm–O_H2O distance of 2.51(8) Å.48 Previous EXAFS measurements obtained from the Cm^III aquo ion in dilute HCl (0.25 M)46 and dilute HClO₄ (1 M)47 showed 10.2 ± 0.3 oxygen atoms at 2.450(2) Å and 7.0 ± 0.4 oxygen atoms at 2.469(7) Å, respectively. Similarly, recent EXAFS studies characterized the Am^III aquo ion as having 9.5 ± 0.9 oxygen atoms at 2.48(1) Å (HO₃SCF₃; 0.11 M)21 and 10.3 ± 0.3 oxygen atoms at 2.480(2) Å (HCl; 0.25 M).46 A single crystal structure for the Am^III aquo ion has also been reported, showing nine H₂O ligands with a 2.52(8) Å average Am–O_H2O distance.48

Fig. 3. Fourier transform of room temperature solution-phase An^III L₃-edge k³-EXAFS spectra of An^III (An = Cm^III, left; Am^III, middle; Ac^III, right) cations dissolved in HNO₃ (0.05 M, top, blue trace; 4 M, middle, red trace; 16 M, bottom, green trace). Fits to the data are shown as dashed black traces and scattering pathway contributions to the fit have been plotted inversely. The dilute HNO₃ system (0.05 M) was modeled with a single H₂O scattering pathway (cyan trace). The concentrated HNO₃ system (16 M) was modeled with scattering pathways from O_H2O (purple trace), O_NO3(bound) (olive trace), N_NO3 (orange trace), and O_{NO3(terminal)} (pink trace). Additionally, two multiple scattering paths were included, a three competent pathway labeled MS_3-comp (An^III → O_{NO3(terminal)} → N_NO3 → An^III; blue-green traces) and a four component pathway labeled MS_4-comp (An^III → N_NO3 → O_{NO3(terminal)} → N_NO3 → An^III, grey trace). The intermediate HNO₃ (4 M) data were modeled using a combination of fits for dilute HNO₃ (0.05 M, cyan scattering pathway) and concentrated HNO₃ (16 M; purple, olive, pink, orange, blue-green, and grey scattering pathways) spectra.

For the larger Ac^III cation, a longer Ac–O_H2O distance of 2.63(2) Å was observed. In comparison to the Cm^III and Am^III aquo ions described above, the larger Ac–O_H2O bond distance was statistically relevant. The Ac^III coordination number also seemed larger than those from Cm^III and Am^III with 10.0 ± 0.9 inner sphere H₂O ligands. However, these values were equivalent when the measurement uncertainties were considered. The Ac–O_H2O bond distance and H₂O coordination numbers were consistent with the only other data obtained on an Ac^III aquo ion,12 despite differences in the solution matrices; HNO₃ (0.05 M) vs. HO₃SCF₃ (0.11 M). This previous analysis showed 10.9 ± 0.5 oxygen atoms at 2.63(1) Å. Additional confidence in these Ac–O_H2O distances was provided by comparison with previous Ac^III L₃-edge EXAFS measurements made in HCl (11.7 M) solutions, which gave a 2.59(3) Å Ac–O_H2O distance.21 Overall, all of our An–O_H2O (An = Cm^III, Am^III, Ac^III) distances were in agreement with the Shannon ionic radii.42 For example, subtracting the six coordinate ionic radii from the experimental M–O_H2O distances gave 1.50, 1.50, and 1.51 Å for Cm^III, Am^III, and Ac^III, respectively. These values were bracketed by the calculated (1.67 Å) and crystallographically measured (1.38 Å) H₂O ionic radii.49 In all of the An^III aquo spectra (HNO₃, 0.05 M for Cm^III, Am^III, and Ac^III; HO₃SCF₃, 0.11 M for Am^III and Ac^III), there was no evidence of An^III aquo ion dimerization. No An^III···An^III scattering pathways were detected nor was there evidence for short An^III–OH interactions, which would result from hydrolysis. Hence, these data were consistent with previous EXAFS studies on An^III and Ln^III aquo ions,12,50–54 suggesting that Cm^III, Am^III, and Ac^III aquo ions existed primarily as discrete An^III(H₂O)_x³⁺ species. However, EXAFS spectroscopy is relatively insensitive to dilute impurities, and dimeric species present at less than 10% of the total sample would be difficult to detect.43

Consistent with the Ac^III aquo L₃-edge EXAFS spectra reported previously in dilute HO₃SCF₃, the data reported here contained a feature near 3.2 Å in the Fourier transform. To date, we have been unable to identify physically realistic models to explain these high-frequency oscillations. Given the instability of these features in various k ranges (7, 8, 9, 10 Å^–1), at this time we believe their origin is not related to the Ac^III coordination chemistry and likely results from systematic artifacts related to the data quality. While not conclusive, this proposition was supported by the absence of this mysterious peak in the higher quality Cm^III and Am^III spectra, as long as one assumes analogous coordination chemistry exists for all three cations.

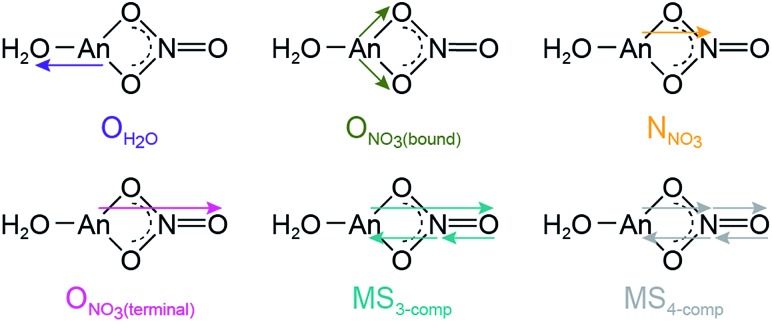
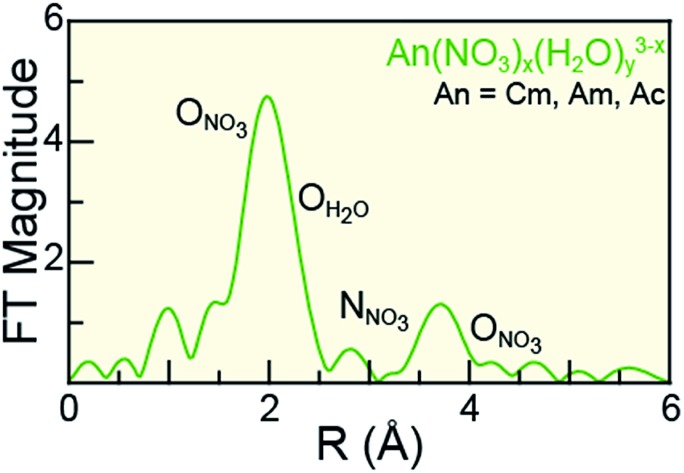
Comparison between 0.05 and 16 M HNO₃ offered the highest probability to identify differences in An^III speciation. Our approach to modeling these EXAFS data was consistent with previous models used to explain spectra from Ln^III and An^III cations dissolved in HNO₃ (6.8 M,55 13 M) (Scheme 1; bottom, Fig. 3). For Cm^III and Am^III, there were two short oxygen scattering pathways. The shorter path was assigned to metal bound oxygen atoms from NO₃^– ligands (O_NO3(bound), olive trace); meanwhile the other was attributed to a shell of oxygen atoms from the H₂O ligands (O_H2O, purple trace, Fig. 3; Scheme 1). However, because these designations resulted from calculations on static actinide nitrate molecules, we do not have high confidence in the rigidity of these assignments. For example, in solution, NO₃^– and H₂O ligand exchange could likely occur. For Ac^III, the data were not sufficient to resolve the two O_H2O and O_NO3(bound) scattering pathways. Hence, in the Ac^III model, the O_H2O and O_NO3(bound) shells were combined (purple trace, bottom right, Fig. 3).

Scheme 1. Scattering pathways deployed in fitting An L₃-edge EXAFS data from An^III cations dissolved in 16 M HNO₃.

Consistent with An^III–NO₃^– binding was the presence of four higher frequency scattering pathways, characteristic of inner-sphere NO₃^– ligands.55 There was a pathway at intermediate distances associated with the central nitrogen of the NO₃^– anion, referred to as N_NO3 (orange trace, Fig. 3; ca. R = 2.5 Å). This shell was followed by the NO₃^– terminal oxygen (O_{NO3(terminal)}; pink trace, ca. R = 3 Å). Subsequently, between ca. 3 < R < 4.5 Å there were two linear multiple scattering pathways. There was the three component An^III → O_{NO3(terminal)} → N_NO3 → An^III (MS_3-comp; blue-green trace) pathway and the four component An^III → N_NO3 → O_{NO3(terminal)} → N_NO3 → An^III (MS_4-comp; grey trace) pathway (Scheme 1). Our attempts to model the data with bent multiple scattering pathways (i.e. An^III → O_NO3(bound) → N_NO3 → An^III) or as dimers and oligomers (with An···An scattering paths) were unsuccessful. Best fits for the data contained η²-NO₃^– (bidentate) ligands and were modeled using the following constraints. The O_{NO3(terminal)} amplitude (coordination number) was fixed to N_NO3, which in turn was allowed to converge. In addition, the N_NO3 and O_NO3(bound) Debye–Waller factors (σ²) were fixed to that associated with O_H2O, as all three scattering pathways had similar frequencies and because these three scattering pathways combined to form a single peak in the Fourier transform. This constraint additionally minimized the number of free fitting parameters.

For Cm^III, refinement of the model to experimental data showed 8.9 ± 2.2 O_NO3(bound) atoms at 2.49(2) Å. There were also 5.7 ± 1.3 O_H2O at 2.64(3) Å and 4.1 ± 0.7 N_NO3 atoms at 2.95(2) Å. The Cm^III–O_{NO3(terminal)} distance was 4.25(2) Å (Table 2, Fig. 3). To determine the number of NO₃^– ligands, two options existed involving either the N_NO3 coordination number or the O_NO3(bound) coordination number. Although, similar stoichiometries were obtained for both scenarios, reported here is a chemical formula based on N_NO3(bound) to facilitate comparison with the Ac^III data below. Overall, these data indicated that the average Cm^III species present in concentrated HNO₃ (16 M) had a stoichiometry of Cm(NO₃)_4.1±0.7(H₂O)_5.7±1.3^{(1.1±0.2)–} with an overall coordination number of 13.9 ± 1.9. Stoichiometric self-consistency associated with the coordination number ratio for N_NO3, O_NO3(bound), O_{NO3(terminal)} (2 : 1 : 1) – as well as the magnitude of the multiple scattering pathways – provided additional confidence in our model.

The Am^III data in 16 M HNO₃ resembled that from Cm^III (Table 2), albeit with slightly smaller uncertainties. For instance, this analysis showed that the average coordination numbers for all of the Am^III species present in concentrated HNO₃ had 7.7 ± 0.8 O_NO3(bound) atoms at 2.50(1) Å, 5.4 ± 0.5 O_H2O atoms at 2.67(1) Å, 3.4 ± 0.7 N_NO3 atoms at 2.97(1) Å, and an Am–O_{NO3(terminal)} distance of 4.26(1) Å (Table 2, Fig. 3). Based on the N_NO3 and O_H2O values, the analysis suggested an average stoichiometry of Am(NO₃)_3.4±0.7(H₂O)_5.4±0.5^{(0.4±0.1)–} (mean coordination number of 12.2 ± 1.5). Again, the O_NO3(bound), N_NO3, and O_{NO3(terminal)} coordination numbers and magnitudes from the multiple scattering pathways were all self-consistent with this average stoichiometry.

Moving to the larger Ac^III ion had little effect on the overall coordination number, showing 12.9 ± 4 inner-sphere oxygen atoms. The average Ac(NO₃)_2.3±1.7(H₂O)_8.3±5.2^(0.7±0.5)+ solution phase stoichiometry was (essentially) equivalent to that from Cm^III and Am^III; however, the uncertainties associated with the Ac^III L₃-edge measurements were larger. The presence of 2.3 ± 1.7 N_NO3 atoms at 3.20(12) Å and Ac^III–O_{NO3(terminal)} atoms at 4.42(3) Å confirmed the presence of inner-sphere NO₃^– ligands in HNO₃ (16 M; Table 2, Fig. 3). The largest differences between the Cm^III, Am^III, and Ac^III L₃-edge EXAFS data were associated with the Ac^III interatomic distances. As expected based on the ∼0.15 Å increase in Ac^III six coordinate ionic radii, the An^III–O_H2O and An^III–O_NO3(bound) distances increased by approximately 0.2 Å from Cm^III and Am^III to Ac^III.

Because EXAFS spectroscopy probes all species in solution, it does not exclude An^III access to other stoichiometric ratios of NO₃^– and H₂O, Scheme 2. Instead, it provides an average signal from all of the molecules in the sample. In this context, good models of the data were only obtained with η²-NO₃^– ligands (bidentate), which were consistent with many models previously reported for lanthanide and actinide EXAFS data.50,56–58 One notable exception was identified by Antonio and coworkers. These authors successfully identified monodentate η¹-NO₃^– binding for Ce^III in 3 M HNO₃, a notably lower concentration than the 16 M HNO₃ discussed here.59 Our attempts to introduce η¹-NO₃^– (monodentate) binding increased the An^III → N_NO3 and An^III → O_{NO3(terminal)} distances into unrealistic regions of the spectra where no intensity was present. Additionally, η¹-NO₃^– diminished the amplitude for linear multiple scattering pathways, giving an appreciable misfit between 3 < R < 4.5 Å in the Fourier transform. We interpret these results as suggesting that in 16 M HNO₃ An^III–η²-NO₃ binding was preferred for Cm^III, Am^III, and Ac^III over monodentate modes, likely due to the chelation effect.60 Consistent with this observation were quantum calculations on M(NO₃)_x(H₂O)_y^3–x (M = Am^III, Eu^III) reported by Xi and coworkers.61 Their calculations predicted that η²-NO₃ binding was preferred energetically in aqueous solutions, especially when the first coordination shell was sterically saturated. Xi's calculated 2.45 Å Am–[η²-O_NO3(bound)] bond distance is in excellent agreement with our EXAFS results, lending confidence to our η²-NO₃ binding model. As pointed out to us privately by Antonio, the larger An–NO₃^– stability constants62 may be responsible for Cm^III, Am^III, and Ac^III preference for η²-NO₃^– binding.59,63

Scheme 2. Various actinide nitrate speciation possibilities.

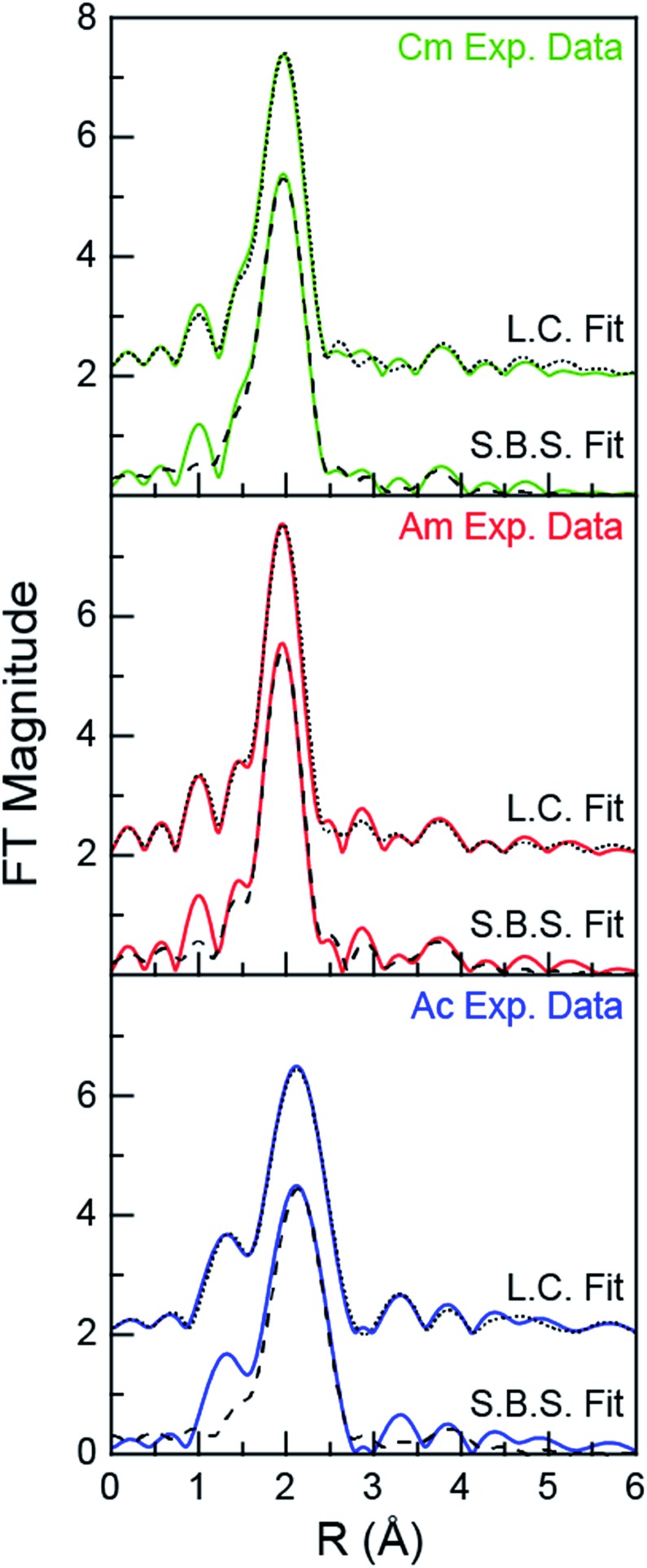
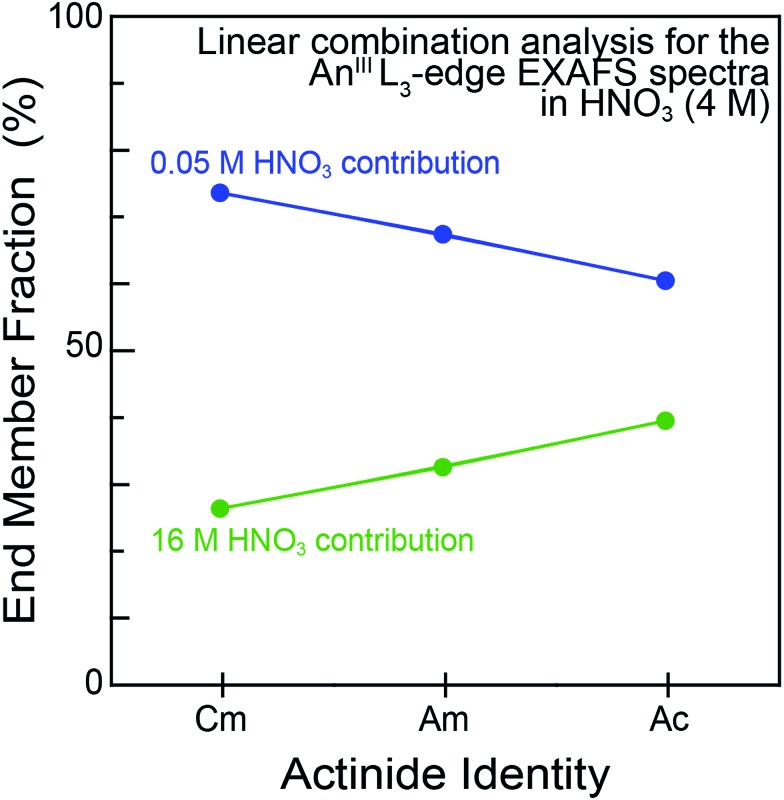
For experiments conducted at the intermediate HNO₃ concentration (4 M), an alternative fitting method was pursued. The initial model was generated from a linear combination of the two end members, namely An^III dissolved in 0.05 and 16 M HNO₃. This fit (Fig. 4) suggested that the 4 M HNO₃ Cm^III speciation could be described as containing 73.6(1.8)% of the Cm^III aquo ion and 26.4(1.8)% of the Cm(NO₃)_4.1±0.7(H₂O)_5.7±1.3^{(1.1±0.2)–} (Fig. 5). The slightly larger Am^III cation gave a similar ratio; 67.4(1.4)% of the Am^III aquo and 32.6(1.4)% Am(NO₃)_3.4±0.7(H₂O)_5.4±0.5^{(0.4±0.1)–}. More substantial differences were observed when moving to the much bigger Ac^III ion. The analysis showed 60.5(1.4)% of the Ac^III aquo and 39.5(1.4)% of the Ac(NO₃)_2.3±1.7(H₂O)_8.3±5.2^(0.7±0.5)+. These analyses assisted subsequent modeling efforts that used shell-by-shell methods, similar to those described above to fit the 0.05 and 16 M HNO₃ spectra. The fitting routine for the HNO₃ (4 M) data differed in that it included all of the scattering pathways used in the 0.05 and 16 M models. To keep the number of fitted parameters less than half of the total number of independent variables,64 the coordination numbers were fixed in accordance with the percentages determined from the linear combination analyses (Fig. 4 and 5). Under these conditions, variables associated with the interatomic distance (R) and Debye–Waller factors (σ²) were allowed to converge to reasonable values, as shown in Table 2. The good agreement of these shell-by-shell fits with the experimental data validated conclusions from the linear combination analyses, suggesting that the H₂O and NO₃^– coordination numbers were between those of the 0.05 and 16 M end-members.

Fig. 4. Fourier transform of the An^III L₃-edge k³-EXAFS spectra of An^III dissolved in 4 M HNO₃ (An = Cm^III, top; Am^III, middle; Ac^III, bottom). Experimental data are shown as green, red and blue traces (for Cm^III, Am^III, and Ac^III, respectively), linear combination fitting (L.C. Fit) results are shown as a dotted black trace, and shell-by-shell fitting (S.B.S. Fit) results are shown as a dashed black trace.

Fig. 5. Linear combination analyses of the An^III L-edge EXAFS spectra of An^III cations dissolved in HNO₃ (4 M; An^III = Cm^III, Am^III and Ac^III). The end member identities were obtained from fits to the Ac^III L₃-edge EXAFS spectra from dilute (0.05 M; blue trace) vs. concentrated (16 M; green trace) HNO₃ solutions.

Outlook

The An^III L₃-edge XAS results described herein represent a humble contribution to the growing body of knowledge associated with Cm^III, Am^III, and Ac^III coordination chemistry, aqueous speciation, and chemical reactivity.10–21,65–69 To most effectively communicate the significance of these results, we find it instructive to present the data within the context of some relevant studies reported for NO₃^– binding of Cm^III, Am^III, and Ac^III. For example, in the solid state, there are only two single crystal X-ray structures reported that contain Am–NO₃ bonds. In these complexes the Am–O_NO3 distances ranged from 2.514 to 2.635(12) Å,70,71 which was in good agreement with our Am–O_NO3 results, 2.50(1) and 2.57(3). To date, we have been unaware of any Cm single crystal structures that contain Cm–NO₃ bonds and no single crystal data of any kind have been reported for Ac. Solution-phase characterization using EXAFS spectroscopy is equally sparse. There is a report from Den Auwer on the Am(NO₃)₃(TEMA)₂ complex,72 another by Girnt on Am(NO₃)_x(dmpbipy)_x,73 one by Bremer involving Am(NO₃)_x(C5-BPP)_x,74 and finally Ekberg investigated [Am(NO₃)(CyMe₄-BTBP)₂]²⁺.75 These studies showed an average Am–O_NO3 distance of 2.49 ± 0.01 Å. For Cm, numerous measurements have been made on NO₃^– species. These include (but are not limited to) time resolved laser fluorescence and luminescence measurements made on Cm^III in nitrate containing solutions,11,76,77 numerous studies documenting the extraction of Cm^III from HNO₃ solutions,78–81 as well as thermal decomposition of Cm^III(NO₃)₃.82,83 For Cm we are unaware of EXAFS measurements made in HNO₃ solutions and for Ac the Ac–NO₃^– interaction has not been characterized previously.

In the context of what is understood regarding complexation of Cm^III, Am^III, and Ac^III by NO₃^– in aqueous media, the EXAFS results reported herein provide hard data that can be used broadly to assist applied and fundamental efforts that require An^III cations to be dissolved in HNO_3(aq). Our data suggested that Cm^III, Am^III, and Ac^III existed as aquo ions in dilute HNO₃ matrices (0.05 M). These results agreed with the small An^III–NO₃ stability constants: ([An^III–NO₃]/[An^III][NO₃^–]; log K, ionic strength = 1 M, 25 °C) 0.34 (Cm^III),84 0.25 ± 0.02 (Am^III),85 and 0.1 (Ac^III).85 Along these lines, Choppin and coworkers used Cm^III fluorescence to evaluate NO₃^– complexation in aqueous solutions with varied HNO₃ concentrations. In this study, moving from 0.1 to 13 M HNO₃ decreased the number of bound H₂O molecules, presumably accompanied by NO₃^– complexation. A total of four H₂O molecules were reportedly removed in 13 M HNO₃, suggesting that a bis-nitrato [M(NO₃)₂(H₂O)₅]¹⁺ complex had formed.86 Consistent with Choppin and coworkers' results,86 our EXAFS data showed that nitrate complexation for Cm^III, Am^III, and Ac^III increased with increasing HNO₃ concentration. In 4 M HNO₃, we observed approximately one inner sphere NO₃^–. Moving past Choppin and Coworkers' 13 M HNO₃ to concentrated HNO₃ (16 M), increased the number of coordinated NO₃^– ligands, ranging from 4.1 ± 0.7 for Cm^III, to 3.4 ± 0.7 for Am^III, and 2.3 ± 1.7 for Ac^III. It is interesting that the NO₃^– coordination numbers seemed to decrease with increasing metal ionic radius. While tempting to correlate these results with the stability constants referenced above and with the Lewis acidity for the An^III cations, we refrain since the NO₃^– coordination numbers were equivalent when the uncertainties for the measurements were considered.

In terms of structural characterization, the Ac^III–O_H2O and Ac^III–O_NO3(bound) bond distance measurements represent another impactful component of this manuscript. Prior to these experiments, there were two reported Ac–O_H2O bond distances, both measured by solution-phase Ac^III L₃-edge EXAFS spectroscopy. One was in concentrated HCl (11 M) solutions (2.59 ± 0.03 Å)21 and the other in dilute HO₃SCF₃ (0.11 M; 2.63 ± 0.01 Å).12 Contributed here are three additional Ac–O_H2O measurements; 2.63 ± 0.02 (0.05 M HNO₃), 2.61 ± 0.02 (4 M HNO₃), and 2.70 ± 0.02 (16 M HNO₃). This brings the total number of reported Ac–O_H2O bond distances to five, averaging 2.63 ± 0.04 Å (error reported as the standard deviation of the mean, 1 σ). Their consistency provides confidence in the accuracy of these Ac^III L₃-edge EXAFS measurements. In terms of NO₃^– complexation, these results are also exciting as they represent the first Ac^III–NO₃^– interaction observed spectroscopically. Although the Ac^III–O_NO3 distance was not resolved from the inner-sphere Ac^III–O_H2O interaction, the Ac^III–O_NO3 bond length can be indirectly inferred based on the measured Ac^III–N_NO3 distance. For example, the Ac–O_NO3(bound) distance can be calculated using the cosine rule; assuming an average N–O distance of 1.31 Å and an average Ac–N–O angle of 113°.57 This analysis gives an Ac^III–O_NO3 distance of 2.70 ± 0.10 Å.

In terms of fundamental exploratory science, the chemistry of Cm^III, Am^III, and Ac^III presents uncharted landscapes in comparison to many other elements in the periodic table. Unique safety hazards and limited access to sizable quantities of material represent significant technical challenges faced during experimental studies of these elements. Even interactions with common ligands – such as the An–H₂O and An–NO₃ bonds – are poorly defined. On top of scientific curiosity is the need to support innovation for An^III processing. This need includes developing advanced nuclear fuel cycles, medical isotope production, and targeted alpha therapy. It seems likely that our approach for characterizing An–NO₃ and An–H₂O (An = Cm^III, Am^III, Ac^III) interactions using An^III L₃-edge EXAFS can be broadly applied to other An^III–ligands interactions, which are equally relevant for nuclear processing and medical applications. We hope that the results presented herein will provide insight aiding our current efforts – as well as those associated with other researchers embarking on their own fundamental and applied scientific campaigns – to solve complicated technical problems associated with Cm^III, Am^III, and Ac^III.

Experimental section

General consideration

Caution! The ^246/248Cm [t_1/2 = 4706(40) years/3.48(6) × 10⁵ years],87²⁴³Am [t_1/2 = 7364(22) years],87 and ²²⁷Ac [t_1/2 = 21.772(3) years]87 isotopes present serious health threats due to their (as well as their daughters) direct neutron-, α-, β-, and γ- emissions of their radioactive daughters. Hence, all studies that involved uncontained manipulations were conducted in a radiation laboratory equipped with HEPA filtered hoods, continuous air monitors, negative pressure gloveboxes, and monitored equipment appropriate neutron-, α-, β-, and γ-particle detection. All free-flowing solids were handled within negative pressure gloveboxes equipped with HEPA filters. The ^246/248Cm, ²⁴³Am, and ²²⁷Ac isotopes were supplied by the United States Department of Energy Office of Science Isotope Program in the Office of Nuclear Physics. Chemically pure Cm^III, Am^III, and Ac^III stock solutions were prepared as previously described.12,20,31 Optima grade nitric acid was obtained commercially (Fisher Scientific). Water was purified to 18.2 MΩ cm^–1 resistivity using Thermo-Scientific Barnstead Nanopure or Millipore Nanopure water purification systems. For Ac^III, the water was further purified by using a Teflon distilling apparatus.

Sample preparation

Three solution-phase XAS samples were prepared for each element. The first was prepared in 0.05 M HNO₃, the second in 4 M HNO₃ and the third in 16 M (concentrated) HNO₃. To prepare the samples, aliquots from purified Cm^III (0.5 mg; 2.02 μmol), Am^III (0.5 mg; 2.06 μmol), and Ac^III (28 μg; 0.123 μmol) stock solutions were transferred to conical glass vials. The aqueous solution was removed by heating the samples on a hot plate at around 110 °C under a flow of argon gas until soft dryness was achieved. The residue was dissolved in aqueous nitric acid of desired molarity. Each sample was boiled and dissolved three times to ensure that the HNO₃ concentration was actually 0.05, 4, or 16 M. The solution volumes for each sample were 0.5 mL (Am), 0.5 mL (Cm), and 0.3 (Ac). The resulting solutions were transferred to an XAS holder.

Radiological containment for XAS samples

The XAS holders and handling procedures provided adequate containment (three layers) and administrative/engineering controls that guarded against release of radiological material during shipment and during data acquisition. The holder consisted of a plastic body with a 5 mm well for Cm^III and Am^III and a 2 mm well for Ac^III equipped with a set of Teflon windows (1 mil) and a Kapton window (1 mil). Solutions were introduced into the holder through an injection hole sealed with a Teflon gasket that was held in place by an aluminum plate. This primary holder was then held within a secondary container, which in turn was held within the tertiary container. The secondary and tertiary containers are best described as a set of nested aluminum holders equipped with Kapton windows (2 mil) and rubber gaskets.

XAS data acquisition

The actinide L₃-edge XANES and EXAFS measurements were made at the Stanford Synchrotron Radiation Lightsource (SSRL) under dedicated operating conditions (3.0 GeV, 5%, 500 mA) on end station 11-2. This beamline was equipped with a 26-pole and a 2.0 tesla wiggler. Using a liquid nitrogen-cooled double-crystal Si(220) (Φ = 0° for Cm^III; Φ = 90° for Am^III and Ac^III) monochromator and employing collimating and focusing mirrors, a single energy was selected from the incident white beam. Vertical acceptance was controlled by slits positioned before the monochromator. For Cm^III, the monochromator crystals were 35% detuned. Meanwhile, Am^III and Ac^III L₃-edge measurements were conducted with the monochromator crystals fully-tuned. For these experiments, higher harmonics from the monochromatic light were removed using a 370 mm Rh coated harmonic rejection mirror. The Rh coating was 50 nm with a 20 nm seed coating and the substrate was Zerodur. The harmonic rejection cut-off was set by the mirror angle, controlling which photons experience total external reflection. The samples were attached to the beamline 11-2 XAS rail. The rail was equipped with three ionization chambers through which nitrogen gas was continually flowed. One chamber was positioned before the sample holder to monitor the incident radiation (I₀, 10 cm). The second chamber was positioned after the sample holder, such that sample transmission (I₁, 30 cm) could be evaluated against I₀, while a third chamber (I₂, 30 cm) was positioned downstream from I₁ so that the XANES of a calibration foil could be measured in situ during the XAS experiments against I₁. All actinide L₃-edge XAS spectra were measured by monitoring sample fluorescence against the incident radiation (I₀). The detector was positioned 90° to the incident radiation (I₀). For Cm^III and Am^III a Lytle detector, equipped with Soller slits and Sr (3 absorption lengths) filters were used. For Ac^III measurements, a solid-state 100-element Ge detector was used. This detector was windowed on the Ac^III Lα₁-emission line (12.652 keV). High-energy contributions to the fluorescence signal were removed using a bromine filter (6 absorption lengths). Using a Se filter, detector dead time was characterized approximately 400 eV above the Se K-edge by defining the detector response from 0 to ∼70% dead (windowed counts of the emission line versus the total of incoming counts in the solid-state detector).

XAS data analysis

Data manipulation and analysis was conducted as previously described.21,43 All calibration spectra were measured in situ. The Cm^III and Am^III spectra were calibrated to the energy of the absorption peak maximum of a Zr foil (18 013.3 eV (ref. 88)). The actinium sample data were dead time corrected and calibrated to the energy of the first inflection point of a rubidium(ii) chloride, RbCl, pellet diluted with boron nitride (BN) to a 1 absorption length thickness. The energy for the first inflection point for RbCl was determined in comparison to the Bi L₂-edge of a bismuth foil (15 711 eV) to be 15 203.8 eV.

The XAS data were analyzed by fitting a line to the pre-edge region, which removed the background from experimental data in the spectra. Then a third order polynomial fit was chosen for the post-edge region. The difference between pre and post edge lines was set to unity at the first inflection point, normalizing the absorption jump to 1.0. Samples were measured for several hours resulting in the collection of multiple scans. The EXAFS data were analyzed by either shell-by-shell fitting methods using IFEFFIT software88 and FEFF8 calculations44,45 or linear combination analyses (IFEFFIT).88 Atomic coordinates for the FEFF8 calculations were obtained by geometry optimizations generated from DFT calculations (see below). Data were fit over the following ranges; for curium and americium 2.7 < k < 11 Å^–1 and 1.1 < R < 4.5 Å (to 3 Å for 0.05 M) and for actinium 2.7 < k < 9.5 Å^–1 and 1.25 < R < 4.5 Å.

DFT calculations

All DFT calculations were performed with ORCA version 4.0.1.89 Calculations utilized the PBE functional,90 the SARC-ZORA-TZVP91,92 and def2 (ref. 93) basis sets, and the D3 dispersion corrections.94,95 Coordinates of the DFT optimized structures are given in the ESI.†

Conflicts of interest

There are no conflicts to declare.