Machine learning meets volcano plots: computational discovery of cross-coupling catalysts

The application of modern machine learning to challenges in atomistic simulation is gaining attraction.

Abstract

The application of modern machine learning to challenges in atomistic simulation is gaining attraction. We present new machine learning models that can predict the energy of the oxidative addition process between a transition metal complex and a substrate for C–C cross-coupling reactions. In turn, this quantity can be used as a descriptor to estimate the activity of homogeneous catalysts using molecular volcano plots. The versatility of this approach is illustrated for vast libraries of organometallic catalysts based on Pt, Pd, Ni, Cu, Ag, and Au combined with 91 ligands. Out-of-sample machine learning predictions were made on a total of 18 062 compounds leading to 557 catalyst candidates falling into the ideal thermodynamic window. This number was further refined by searching for candidates with an estimated price lower than 10 US$ per mmol. The 37 catalyst finalists are dominated by palladium phosphine ligand combinations but also include the earth abundant transition metal (Cu) with less common ligands. Our results indicate that modern statistical learning techniques can be applied to the computational discovery of readily available and promising catalyst candidates.

1. Introduction

Chemists constantly pursue new molecular systems that provide increasingly higher yields and better control of selectivity. Rather than blindly searching for promising catalysts to meet their needs, numerous tools that aid in identifying the most appropriate species have been developed. These range from high-throughput screening1,2 (including combinatorial methods3,4), which quickly evaluates reaction conditions and the structures of catalysts, to multidimensional modeling based on a design of experiments (DoE),5 that relates steric and structural descriptors (e.g., Charton values and Sterimol parameters) to enantioselectivity. Such methods have found broad application in asymmetric homogeneous catalysis.6–14 On the other hand, the tremendous increase in computer power accompanied by methodological advancements has also made computational studies of catalytic processes commonplace.15 While virtually any catalytic system can be subjected to computational analysis, often the conclusions reached are not transferable and provide little insight into the best way to develop more active and selective catalysts. Thus, a tool that assesses the properties of untested catalysts based on a simple energetic or structural criterion would rapidly accelerate the discovery pace of new species. Indeed, similar concepts involving the mapping of a difficult to determine quantity onto an easily obtained variable have been a central pillar of catalysis and physical organic chemistry for more than 80 years, and are at the core of familiar concepts such as the Bell–Evans–Polanyi principle,16,17 the Hammett equation,18–21 or the Brønsted catalysis equation.22 Today, volcano plots,23,24 which relate easily accessible descriptor variables directly to catalytic performance, accomplish this objective and find regular use in the fields of heterogeneous catalysis25–27 and electrocatalysis.28–34

Based on knowledge of a chosen descriptor variable, volcano plots function by discriminating catalytic performance using Sabatier's principle.35 Sabatier conceived the notion of an ideal catalyst that should not bind a substrate too strongly or too weakly. The unique volcano shape facilitates rapid discrimination of catalytic activity. Species positioned highest on the plot (generally on or near the volcano plateau or peak) have the best profiles and fulfill Sabatier's principle. Species located along the left- and right-slopes have less ideal profiles and can be characterized as having either overly strong (left) or overly weak (right) substrate/catalyst interactions. While being commonly used in heterogeneous and electrocatalysis, and frequently invoked for homogeneous systems,36–38 only recently have these appealing tools been concretely realized for molecular catalysts.39 Corminboeuf and co-workers have pioneered the use of molecular volcano plots to study various aspects of prototypical C–C cross-coupling reactions in order to gauge the feasibility of using these tools to identify attractive homogeneous catalysts.39–42 Subsequent work has also focused on adapting volcano plots for applications in homogeneous catalysis via the inclusion of kinetics (as opposed to the typically used thermodynamic based criteria) of the catalytic cycle.43

The use of molecular volcano plots involves establishing linear scaling relationships that relate the quantitative value of a descriptor to the thermodynamic or kinetic performance of the catalyst. As such, this tool has clear utility in high-throughput screening applications that search for prospective catalysts by computing the value of this descriptor for any species desired. However, currently both the geometries and energies associated with multiple forms of each catalysts must be determined through a relatively slow process involving density functional theory computations. Clearly, increasing the speed at which the descriptor variable can be determined would result in an overall increase in the discovery pace of new catalysts because prospective species could be screened more rapidly. One route with the potential to provide virtually instantaneous access to the descriptor involves the application of quantum machine learning (ML) models, i.e., ML models which can be trained on, and used to predict, quantum properties.44–46 The application of ML models to estimate volcano plot energy descriptors offers increased speed for two reasons: first, the energy based value can be immediately accessed for any desired species, and second, the need to establish a precise geometry of the catalyst can be circumvented by also including this task into the ML model, as already demonstrated within the Δ-ML approach.47 As such, the ML model can predict an accurate descriptor value from an approximated 3D structure of a catalyst.

While, generally speaking, applications of machine learning methods in chemistry are still in their infancy, their use has begun to appear in the fields of materials science48–53 and catalysis.54–61 For example, a gradient-boosting regression method62 has been used to predict the d-band center of mono and bimetallic surfaces63 and to estimate CO adsorption energies on Pt nanoparticles,64 while a local similarity kernel could predict the catalytic activity of nanoparticles.65 Moreover, applications of support vector machines (SVMs)66 were able to anticipate CO₂ uptake in metal organic frameworks (MOFs)67 by developing an atomic property-weighted radial distribution function (AP-RDF) based descriptor68 that captures geometric and chemical features of periodic systems. Predictive structure–reactivity models have identified promising Pt-based electrocatalysts for the oxygen reduction reaction,69 while artificial neural networks (ANNs) have recognized multimetallic alloys possessing high selectivity for electrochemical CO₂ reduction to C₂ species.70,71 Recently, Nørskov investigated various machine learning based approaches72 to systematically search for the active sites of bimetallic (nickel gallium) nanoparticles,73 to construct Pourbaix surface phase diagrams,74 and to identify probable mechanisms of hydrocarbon–syngas reactions on rhodium(111).75 Rappe and co-workers also exploited the regularized random forest machine learning algorithm,76 and discovered the key role played by structure and charge descriptors (namely the Ni–Ni bond length and the Ni residual charge) in the hydrogen evolution reaction activity of Ni₂P(0001).

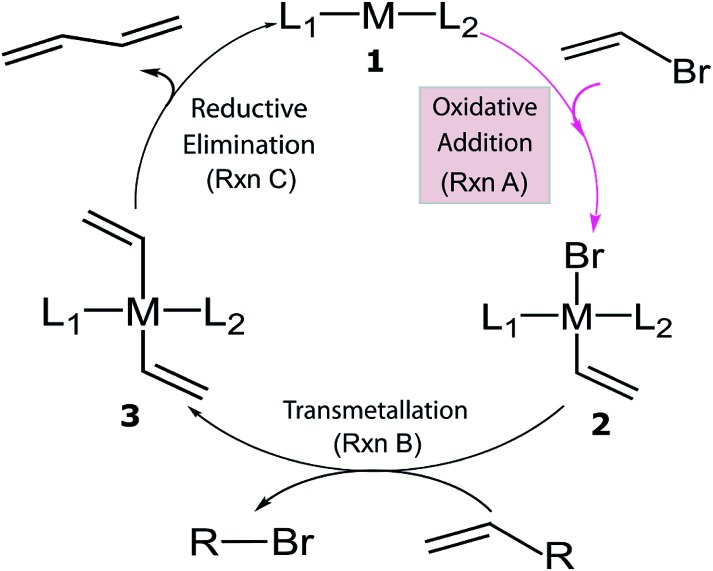
Despite the considerable amount of progress in applying ML models to chemical problems, each of the aforementioned contributions tackled issues surrounding heterogeneous catalysis, while ML applications to homogeneous catalysis remain exceedingly rare.54,77 Significant advances with ML models to obtain fundamental molecular electronic properties (e.g., atomization or total energies of molecules) have been made,78–85 however, the prediction of catalytic cycle intermediates energies has never been attempted to the best of our knowledge. The purpose of this work is to demonstrate how ML models can be used to accelerate the screening of prospective homogeneous catalyst candidates, thereby enabling the computational discovery of novel catalytic materials. To this end, we selected the problem of finding catalysts for the Suzuki–Miyaura C–C cross-coupling reaction (Fig. 1).86–88 Specifically, we trained and applied ML models using the reaction energy associated with oxidative addition (eqn (1)), which has previously been shown to be a descriptor variable for analyzing the catalytic cycle thermodynamics using volcano plots.39 Although kinetic profiles are obviously important for obtaining a full and accurate description of catalytic performance, here we rely on a simplified thermodynamic picture (Fig. 1), which can be exploited to rapidly discriminate between catalysts with promising or inadequate energy profiles.39–42

L₁ML₂ + (C C)Br → L₁M(Br) (C C)L₂, ΔE_{Rxn A} 1

Fig. 1. General catalytic cycle for C–C cross-coupling reactions. Coupling partners (R) depend on specific cross-coupling reactions. Suzuki coupling undergoes a ligand exchange step replacing Br by an alkoxy group before transmetallation (Rxn B). The dissociated compound in Rxn B is alkoxy–R instead of Br–R and R is [B(OH)₂(O^tBu)]^– for the Suzuki reaction.39,40 .

Using machine learning models of this quantity, along with previously constructed molecular volcano plots, it is possible to screen thousands of potential catalysts with controlled accuracy (by virtue of learning curves) and at a negligible computational overhead.

2. Computational details

The initial set of Cartesian coordinates for each catalyst was obtained by converting Simplified Molecular Input Line Entry System (SMILES) formats (i.e., a line notation for entering and representing molecules and reactions)89,90 into three-dimensional structures with the 3D structure generator operation (i.e., gen3d operation) of the OpenBabel software (see the ESI† for details).91 To generate target energy values for the training and test complexes, we proceeded as follows: computations involving geometry optimization and electronic energies were generated and executed via the AiiDA automated platform.92 Gas phase geometry optimizations were computed at the B3LYP93–95-D3 (ref. 96 and 97) with 3-21G (for Ni, Pd, Cu and Ag complexes)98–101 and a def2-SVP102 basis set (for Pt and Au complexes) in Gaussian09.103 Single point energies were computed at the B3LYP-D3/def2-TZVP level.104 The oxidation states of the catalysts were adjusted to comply with the dominant 14e^–/16e^– nature of the complexes in the Suzuki cross-coupling reaction. The reaction electronic energies (eqn (1)) were computed and used as a descriptor (see a volcano plot in Fig. 2) for training the machine learning models. The ML models were trained and applied using the Quantum Machine Learning toolkit QMLcode.105

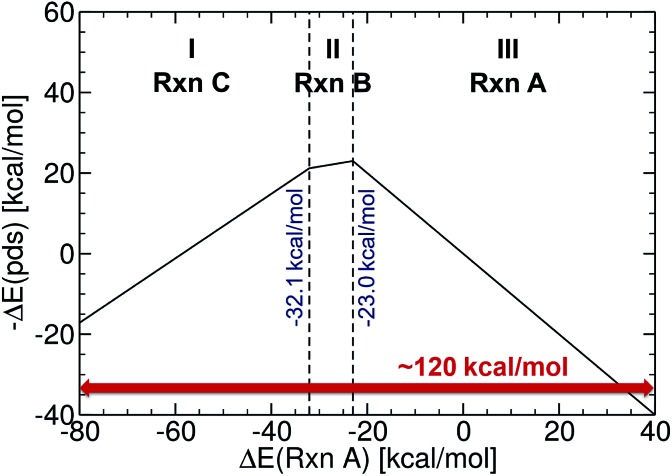
Fig. 2. Reference volcano plot for the Suzuki cross-coupling reaction. Region (I) corresponds to reductive elimination, (II) to transmetallation, and (III) to oxidative addition. Acceptable catalysts should fall into the mid region (in between –32.1 and –23.0 kcal mol^–1).

The reference volcano plot associated with the catalytic cycle of Fig. 1 was constructed according to the procedure outlined in our previous work39,43 (detailed description of the procedure can be found in the ESI†) using the same theory level as for the descriptors of the machine learning training set. Note that despite the relatively modest level of theory used herein (engendered by the large computational effort associated with generating the training set for the ML model), the geometries and key energetic properties are in line with those previously computed (see Table S1†).39,40 Similarly, we previously demonstrated that the same set of linear free-energy scaling relationships capably describe variations in the number of coordinated ligands (i.e., bis vs. monoligated), as well as different oxidation or spin states of the catalyst.39,42,43 Rather than predicting the entire volcano plot, the most essential property is the descriptor [ΔE(Rxn A)] (eqn (1)), which can be machine learned, as well as knowledge about its target value, i.e., the energy range corresponding to the ideal plateau region (extending from –32.1 to –23.0 kcal mol^–1, Fig. 2).

3. Methods

3.1. Database

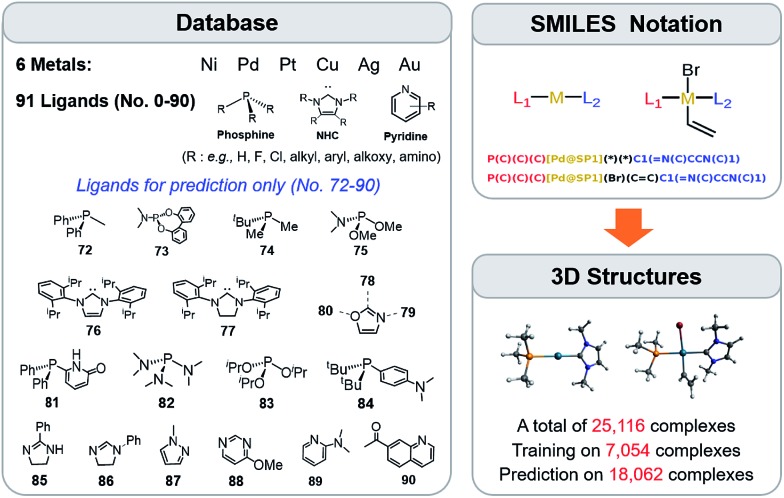
The training procedure relies upon constructing a large database of catalysts that are obtained through combining various ligands and metals. These species are then used for training and testing the ML models which, in turn, are used to predict descriptor values so rapidly and with such accuracy that large libraries can be scanned in order to identify acceptable catalyst candidates. Ninety-one ligands including CO, phosphines, N-heterocyclic carbenes and pyridines were combined with six transition metals (Ni, Pd, Pt, Cu, Ag, and Au) to form the database. All possible metal/ligand combinations (i.e., L₁ and L₂, where L₁ML₂ is equivalent to L₂ML₁) of catalytic cycle intermediates 1 and 2 (Fig. 1) lead to a total library consisting of 25 116 species for each intermediate (see the ESI† for a complete list of ligands used). Rather than providing the optimized structures for each ligand to build the catalysts, the geometries of catalytic cycle intermediates 1 and 2 for each database entry were created by converting SMILES strings (Fig. 3)89,90,106 to Cartesian coordinates using the OpenBabel implementation91 of the Merck Molecular Force Field method (MMFF94).107–111 This database was divided into two subsets: (i) the training/test set used within cross-validated learning curves (see details on the cross-validation procedure in Section 3.2) for which the computed descriptor values [ΔE(Rxn A)] were used as a reference and (ii) the prediction set on which the model was applied to screen candidates based on their ML predicted descriptor values. Since collecting reference data for the training and test sets involves costly DFT geometry relaxations, we proceeded in two steps:112 first, an initial training set made of complexes involving a diverse set of ligands (72 in total) with Pd (2595 complexes).113 Secondly, a small subset of illustrative ligands (12) with each of five other metals (Pt, Au, Ag, Cu, Ni) (390 complexes) was created. The final set consisted of a total of 7054 reaction energy values corresponding to our descriptor. All DFT optimized geometries and computed electronic energies of each intermediate 1 and 2 as well as the associated ΔE(Rxn A) values are provided in the ESI.† ML models were trained on this set (vide infra), and out-of-sample predictions were then made on the prediction set that consisted of all the other complexes (18 062 in total). Note that included in this set are 19 realistic ligands that have already been employed in experimental settings (i.e., ligand no. 72–90 in Fig. 3).114–116

Fig. 3. A database of 25 116 molecular transition-metal catalyst candidates. Each complex consists of one out of six transition metals and a combination of two out of 91 ligands (left) (see the ESI† for details). Each ligand was written as the SMILES notation and all possible L₁–M–L₂ combinations were constructed (top right-hand corner). SMILES strings were then converted into Cartesian coordinates through the 3D structure generator of the OpenBabel software (bottom right-hand corner). DFT reference results for training and testing of ML models were obtained for a sub-set of 7054 candidates. Those structures were exploited for computing binding energies and for training the ML models.

3.2. Training

To begin the machine learning process, information intrinsically contained within each three-dimensional structure must be transformed into a suitable representation. The approach selected to represent a molecule has a crucial impact on the learning curve (for a recent example of a study discussing the role of the representation, see ref. 83). It is of particular importance to construct a meaningful relationship between the representation and the catalyst candidate, that will be learned by the machine learning algorithm. For this reason, all the relevant variables for computing the target properties (in our case ΔE(Rxn A)) should be represented in the chosen machine learning representation of the molecule. Over the last few years, increasingly improved representations44,78,82,117,118 that progressively encode increasing amounts of physical information have been proposed. Here, we focus on the sorted Coulomb Matrix (CM), the first representation introduced for ML models trained throughout chemical space and used to predict quantum properties,44 a two-body bagged variant of the CM with superior performance, the Bag of Bonds (BoB),78 and the recently proposed Spectrum of London and Axilrod–Teller–Muto potential (SLATM).119 The CM representation consists of a square atom by atom matrix, where the diagonal elements model the potential energies of free atoms while the off-diagonal elements correspond to the Coulomb nuclear repulsion between atom pairs. In the BoB representation, CM elements are bagged (e.g., C–C, C–N, C–H, etc. are accounted for in separate bags.). SLATM is based on the dissociative limits of intermolecular dispersion contributions between unpolarized moieties. They account for interatomic two-body terms through London's dispersion curve (rather than Coulomb), and for the three-body terms according to Axilrod–Teller–Muto.120,121

We stress that our principal objective is to describe the oxidative addition step directly from rough-coordinate estimates obtained from the SMILES structure (i.e., without providing accurate geometry as an input). After conversion from SMILES to coordinates, we map our input representation onto the corresponding continuous label value (here ΔE(Rxn A)) using kernel ridge regression (KRR),122 which solves nonlinear problems by mapping data from the input space into a high-dimensional linear feature space (kernel trick). A Laplacian kernel function is used for the CM and BoB representations, and a Gaussian kernel for the SLATM representation (more details in the ESI†). The quality of the models is evaluated by reporting test errors, which can be obtained by separating the dataset into training and test frames and calculating the average error (typically a mean absolute error (MAE)) for the predictions on the out-of-sample test set. This random sub-sampling cross-validation procedure46 was used to shuffle the dataset randomly into different training sets. For every shuffling step the MAE for the model was calculated and the procedure repeated ten times for every training set size N. Afterwards, the errors for the different models were averaged into a single cross-validated error. Note that this error remains a random variable that is dependent on the initial splitting of the training/test datasets. When plotted on a log–log scale, successful learning is indicated by linearly decaying behavior for large training set sizes, as already suggested by Vapnik and others in the nineties.123,124

4. Results and discussion

4.1. Machine learning

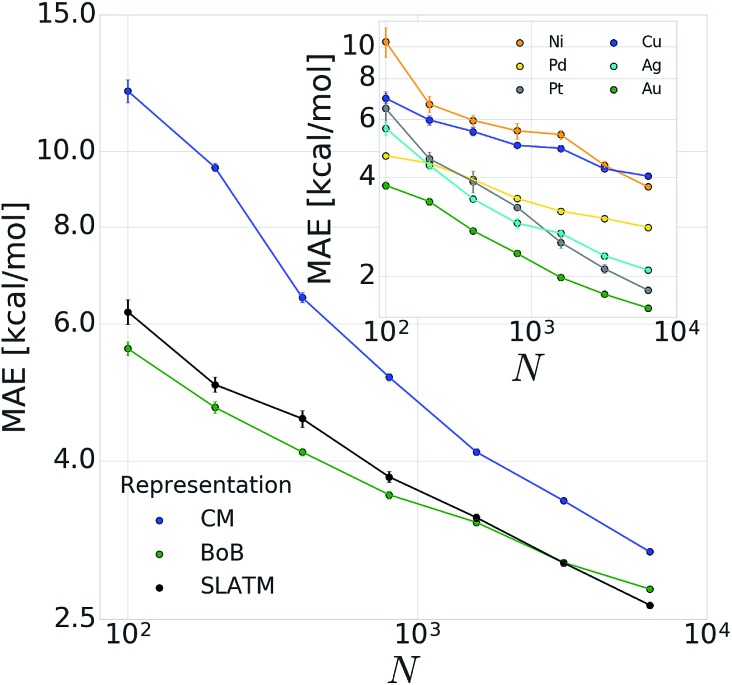
In order to verify the performance and validity of our ansatz, we have trained and tested machine learning models for various training set sizes. The resulting learning curves, depicted in Fig. 4, demonstrate the efficiency and accuracy of the learning process in terms of a near-linear decay of test error with training set size. While learning is observed for all representations, the learning curves illustrate the impact of the molecular representation on the off-set and slope. Overall, the performances of the ML models based on the SLATM and BoB are very similar (for the largest training set, the MAE is 2.61 kcal mol^–1 and 2.73 kcal mol^–1 respectively) and superior to CM (largest training set MAE = 3.05 kcal mol^–1). Despite these small variations, it is obvious that efficient learning is achieved by all three representations. This result contrasts with findings in ref. 51 where the CM was claimed to be of little use when constructing ML models for transition metal complexes. The poor performance of CM is more likely due to inappropriate choice of properties (electronic spin-states) than to the molecular systems themselves. It seems intuitive that any purely structure and composition based representation will struggle to account for various electronic states. When it comes to simple electronic ground state properties, such as the oxidative addition step studied here, Fig. 4 clearly demonstrates that the CM is very applicable to the machine learning modeling of properties of transition metal complexes. We also note that the BoB representation performs surprisingly well for this problem. We ascribe this behavior to the bagging which allows the model to place appropriate weights to bonds involving the transition metal.

Fig. 4. Learning curves (test error of catalytic descriptor values as a function of training set size (N)) for oxidative addition of vinyl bromide. Error bars correspond to standard deviation in cross validation. Inset: corresponding learning curves for individual metals for BoB.

The energy range for the descriptors of the training set (corresponding to the x-axis of the molecular volcano plot) is ≈120 kcal mol^–1 (Fig. 2). We therefore considered the ML model to be sufficiently well converged for the task of picking catalysts, once the learning curve dropped to less than 3 kcal mol^–1 (i.e., 2% of the descriptor range). The most efficient representations, SLATM and BoB, reached this threshold with a training set of 7054 binding energies. The following discussion will thus be based on the less sophisticated representation, BoB. All the predictions associated with the other two representations are presented in the ESI.† It is important to reiterate that while the machine learning models were trained on DFT reaction energies obtained for DFT optimized geometries, the molecular representations in the test set were constructed solely from the coordinates directly obtained from SMILES conversion.

The heterogeneity of the training set112 (i.e., unequal representation of the six transition metals) has been looked into by evaluating the individual predictions of the BoB based machine learning model on each metal separately. The resulting learning curves depicted in the inset of Fig. 4 demonstrate that learning is attained for all metals. For the largest training set size, the target MAE of 3 kcal mol^–1 is achieved for Pd, Pt, Ag and Au, while the Ni and Cu metal complexes are less accurately described (best MAE = 3.74 and 4.04 kcal mol^–1, respectively). These larger errors certainly originate from the smaller sample of Ni complexes and from copper-ligand combinations featuring ligands that are less frequent in the rest of the training set. This leads to a larger energy range in the descriptor variables which can be seen as a broader distribution/width (see the histograms (Fig. S2 and S3) in the ESI†). Overall, however, the ML performance for Ni and Cu-based complexes is still useful as it is not more than 5% of the descriptor's energy range (i.e., inferior to 5 kcal mol^–1).

4.2. Catalyst prediction

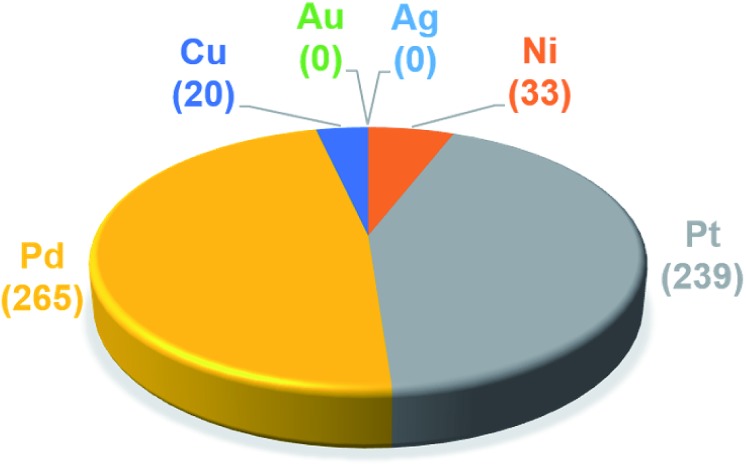
The trained ML models were subsequently exploited to predict the energy based descriptor of 18 062 potential out-of-sample catalysts with negligible computational cost (vide supra). At this point, it is worth noting that out-of-sample predictions that involve ligands not previously seen by the models should be considered with more care. Additionally, the predictive power of the model would be limited for catalysts that would suffer from a convergence problem in an actual computation.113 Because we are interested only in the catalysts predicted to have the best thermodynamic profile for the Suzuki–Miyaura reaction, emphasis was placed on a narrow range of descriptor energy values (from –32.1 to –23.0 kcal mol^–1) corresponding roughly to the plateau of the volcano. However, the same ML models would be relevant to the analysis of other cross-coupling reaction variants differing only by the width of the plateau region.40 Using the BoB model, 557 catalysts were identified that fell into this region. A brief examination of the metal distribution (Fig. 5) yields expected results, namely that catalysts incorporating group 10 metals (Ni, Pd, Pt) appear more frequently than their group 11 (Cu, Ag, Au) counterparts. This finding is in line with our earlier DFT-based molecular volcano plot analysis of the same reaction.39–41

Fig. 5. Occurrence of the six metal complexes in the selected range of –32.1/–23.0 kcal mol^–1 predicted by the machine learning model using the BoB representation.

A prevalent metal identified by the ML model is palladium, which has 265 species that appear on or near the volcano plateau (Fig. 5). The large number of Pd catalysts attests to the accuracy of the ML models, as these species have a rich history in catalyzing cross-coupling reactions.125–128 On the other hand, Pt catalysts are virtually experimentally unknown129 and those that have been tested tend to show only moderate catalytic ability.130 Nonetheless, their significant presence on the volcano plateau does align with our earlier DFT-based evaluations.39–41 Indeed, we previously postulated that the presence of Pt based catalysts on top of the volcano may indicate that the problem with these species is less thermodynamic and more kinetic in nature.40 In addition, others have speculated that an enhanced M–R bond strength causes transmetallation in these species to be sluggish.131 Despite being well-known cross-coupling catalysts,132 only a handful of Ni based species are predicted by the ML model to appear near the volcano plateau. However, in its current state, the ML models consider only a single oxidation state, that for Ni corresponds to a Ni(0)/Ni(ii) based catalytic cycle. Thus, the more catalytically active Ni(i) oxidation state, which is accessed via a one-electron redox process133 and generally shifts Ni catalysts from the strong-binding side of the volcano onto the plateau,42 is currently not assessed by the ML models (vide supra) but incorporation of alternative catalytic oxidation states represents an appealing future improvement of the current model. The volcano plot also reveals the influence of ligand type on the thermodynamics of the catalytic cycle. For example, Fig. 6 clearly indicates that phosphine ligands generally outperform N-heterocyclic carbene and pyridine ligands when combined with group 10 metal (Ni, Pd, and Pt) complexes. More interesting is the presence of oxazole ligands for Pd metals. While the use of the monodentate variant (e.g., ligands no. 78–80) appears elusive in the literature, the chemistry associated with the use of bidentate bis(oxazole) ligands for cross-coupling reactions is relatively well established.134

Fig. 6. Histogram ranking of the five most identified ligands that appear on the volcano plateau (i.e., with descriptor values between –32.1 and –23.0 kcal mol^–1) by metal type as predicted by the machine learning model using the BoB representation. The histogram is scaled relative to the Pd/oxazole ligand combination, which has the highest metal/ligand occurrence appearing 38 times on the volcano plateau.

By far, the vast majority of the coinage metal (group 11) catalysts have very weak binding energies and, correspondingly, lie on the right (weak-binding) slope of the volcano. Indeed, no Au or Ag based catalyst has sufficiently strong binding energy to appear on the volcano plateau (Fig. 5). This finding directly agrees with experimental and computational studies that have found Ag and Au catalysts to have unfavorable free energies associated with oxidative addition.135 On the other hand, a handful (20) of Cu based catalysts are found to have nearly ideal thermodynamic profiles. While instances of Cu-based Suzuki coupling have appeared in the literature,136,137 these catalysts tend to employ bidentate acetylacetone (acac) or acetate/triflate ligands.138,139 Thus, it is interesting to note that each of the thermodynamically most appealing Cu catalysts involves either a tris(dimethylamino)phosphine or bulky N-heterocyclic carbene (Fig. 6). These findings represent a potentially interesting research direction that should be explored in more depth and that has been revealed solely through the application of ML models coupled with molecular volcano plots.

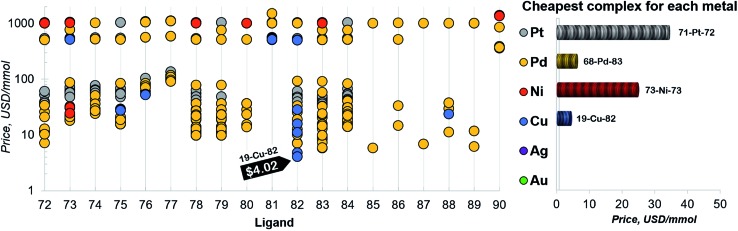
Finally, a more refined selection of catalysts was obtained based on their estimated price per mmol (Fig. 7). Among the 557 catalysts with promising thermodynamic profiles, 37 complexes have an estimated price less than 10 US$ per mmol. These species include earth abundant metals (copper with tris(dimethylamino)phosphine) and a multitude of more standard palladium phosphine combinations.

Fig. 7. Estimated price (for one mmol in US dollars) of the catalysts in the selected range of –32.1/–23.0 kcal mol^–1 (for ligand no. 72–90). The price is calculated as a summation of the commercial price of transition metal precursors (one mmol) and one mmol of each ligand. The cheapest complex for each metal is shown on the right. The estimated price of all the 557 catalysts is detailed in the ESI.† .

5. Conclusions

We have trained and used machine learning models to dramatically accelerate the descriptor screening of 18 062 homogeneous catalysts for the Suzuki–Miyaura C–C cross-coupling reaction. The model was based on the capability of molecular volcano plots to identify thermodynamically attractive candidates with respect to a simple energy descriptor. Overall, we have identified 37 promising low-cost complexes featuring palladium and copper combined with both standard and less expected ligands. Our findings also indicate that machine learning can be used to screen thousands of catalysts, and that previously introduced machine learning representations can be used for property predictions of transition-metal complexes. Exploitation of a Δ-machine learning approach represents an appealing future improvement of the proposed ML models.47,117

Conflicts of interest

There are no conflicts to declare.