Single-exposure optical focusing inside scattering media using binarized time-reversed adapted perturbation

Abstract

Light scattering inhibits high-resolution optical imaging, manipulation and therapy deep inside biological tissue by preventing focusing. To form deep foci, wavefront shaping techniques that break the optical diffusion limit have been developed. For in vivo applications, such focusing must provide high gain, high speed, and a high focal peak-to-background ratio. However, none of the previous techniques meet these requirements simultaneously. Here, we overcome this challenge by rapidly measuring the perturbed optical field within a single camera exposure followed by adaptively time-reversing the phase-binarized perturbation. Consequently, a phase-conjugated wavefront is synthesized within a millisecond, two orders of magnitude shorter than the digitally achieved record. We demonstrated real-time focusing in dynamic scattering media, and extended laser speckle contrast imaging to new depths. The unprecedented combination of fast response, high gain, and high focusing contrast makes this work a major stride toward in vivo deep tissue optical imaging, manipulation, and therapy.

1. INTRODUCTION

Visible and near-infrared photons occupy a unique portion of the electromagnetic spectrum: Through non-carcinogenic molecular interaction with biological tissue and exogenous agents, they provide rich structural and physiological information [1] and noninvasive solutions for manipulation [2], control [3], and therapy [4]. However, these photons undergo severe scattering in tissue, rendering traditional control over their propagation completely ineffective beyond the optical diffusion limit — about 1 mm in biological tissue [5,6]. Such scattering shuts the door to important diagnostic and therapeutic applications at depths.

In recent years, the optical diffusion limit has been conquered by two categories of wavefront shaping (WFS) techniques: iterative WFS and optical time reversal. In iterative WFS [7–13], a subset of the transmission matrix [14] of the scattering medium is measured iteratively. Subsequently, the phase of the light is controlled spatially to compensate for the inhomogeneous delays due to random scattering, generating a focus through constructive interference. In optical time reversal, the optical wavefront from a real [15–17] or virtual guide star [18–20] is detected, and its phase-conjugated copy is converged back to the origin. A feasible approach to achieving time reversal is through optical phase conjugation (OPC) [21–23].

Due to the highly dynamic and scattering nature of living tissue, it is important that the focusing be sufficiently fast (ideally with a response time of ~1 ms [24,25]) and have high quality (i.e., having a large number of independent control elements for high focal peak-to-background ratio (PBR) [14]). Consequently, an important figure of merit is the average mode time (i.e., the average operation time per spatial mode [7, 8, 14]), which should ideally approach 1 ps/mode (for a 1 ms response time with a billion modes).

However, the average mode times achieved by existing techniques are orders-of-magnitude greater than 1 ps/mode, preventing any practical applications in biological tissue. For example, iterative WFS achieved an average mode time of 145 μs/mode (37 ms for 256 spatial modes [12]) in the fastest implementation of this technique. Ultimately, when data transfer and processing times are assumed negligible, iterative WFS can achieve an average mode time of 18 μs/mode by employing a digital micromirror device (DMD) for wavefront control [8,12,13]. In contrast, because OPC measures the desired wavefront at once, it is potentially faster. Analog OPC [18,21,22,25] approaches based on nonlinear optical crystals have demonstrated a short average mode time (≈100 ps/mode, a 10 ms response time for 10⁷ modes [25]), but suffered from an energy gain (defined as the ratio of the focal light energy in the reading phase to that in the probing phase) well below unity, which is a drawback detrimental to wide-spread applications. In comparison, digital OPC (DOPC) [15,19,20] provides inherently large gains and reasonably fast response, with 2 μs/mode being recently realized for focusing inside scattering media [26] (100 ms response time with 50,000 spatial modes). The lowest possible average mode time (≈ 60 ns/mode) for previous DOPC techniques is dictated by the phase modulation speed (assuming a 30 ms settling time and 5×10⁵ spatial modes), and it is still four orders of magnitude longer than the goal of 1 ps/mode. To break through this limit, the slow phase modulation must be replaced by faster binary amplitude or phase modulation [27], which could potentially reach 36 ps/mode using a DMD (assuming an 18 μs settling time [13] and 5×10⁵ spatial modes). To date, none of the existing DOPC technologies for focusing inside scattering media have been demonstrated using binary modulation.

Here we address this challenge by demonstrating light focusing inside scattering media using binary phase modulation. The technology, named binarized time-reversed adapted-perturbation optical focusing (b-TRAP), has achieved the shortest average mode time to date (≈ 300 ns/mode) among all methods developed for focusing inside scattering media with high energy gain. Compared with the binary-amplitude WFS technology [13] that finds and utilizes the same binary mask, our technology uses an adaptive mask, enhances the speed by 10⁵ times, and doubles the focusing quality at no additional cost. More strikingly, we show that by using b-TRAP, the formation time of the binary mask is determined only by the laser pulse interval, which is highly tunable and can be less than 1 μs. These features not only facilitate fast light focusing, but also enable us to acquire detailed information about tissue dynamics (such as blood flow speed). The demonstrated capabilities pave the way toward in vivo deep tissue biophotonics.

2. METHODS

A. Basic principle

Time reversal by analysis of changing wavefronts from kinetic targets (TRACK) and time-reversed adapted-perturbation (TRAP) optical focusing [26,28] employ intrinsic tissue dynamics as guide stars for completely noninvasive and non-contact light focusing inside scattering media. In short, if the scattered fields at two instants are recorded in the presence of internal dynamic perturbations (e.g., absorption or refractive index changes), subtracting the two fields generates a differential field, whose conjugate copy enables focusing at the perturbed sites by cancelling the scattering contribution originating from the static portion of the medium.

The original TRAP focusing [28] relied on phase-shifting holography [29] to record the complex amplitude of the scattered electromagnetic fields, which took multiple intensity measurements to accomplish and was impractically slow for many applications. In comparison, b-TRAP measures each field indirectly within the time duration of a single laser pulse. As shown in Fig. 1(a), at instant t₁, a short laser pulse probes the scattering medium in which the permittivity of the target (i.e., the guide star) is ε(t₁). The exterior scattered light field, termed the “sample beam”, whose complex amplitude is expressed as E_s(t₁), is combined with a planar reference beam E_R on an amplitude-only spatial light modulator (SLM). The SLM surface is imaged onto a scientific complementary metal oxide semiconductor camera (sCMOS) to generate a time-averaged intensity pattern

$$I(t_1)=|E_{\mathrm{s}}(t_1){|}^2+|E_{\mathrm{R}}{|}^2+E_{\mathrm{s}}^{\ast }(t_1)E_{\mathrm{R}}+E_{\mathrm{s}}(t_1)E_{\mathrm{R}}^{\ast }.$$ (1)

Fig. 1.

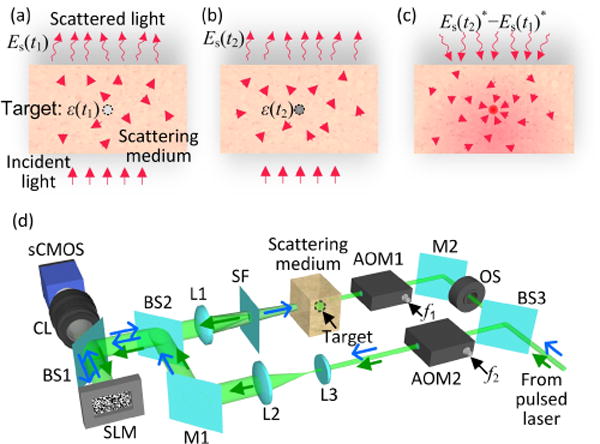
Principle and schematic of b-TRAP focusing. (a)-(c) Principle of b-TRAP focusing (details see text). (d) Schematic of the focusing method. Green (solid) arrows represent light path in the probing process; blue (slim) arrows show light path in the time reversal process. AOM, acousto-optic modulator; BS, beam-splitter; CL, camera lens; L, lens; M, mirror; OS, optical shutter; sCMOS, scientific complementary metal oxide semiconductor camera; SF, spatial filter; SLM, spatial light modulator.

As shown in Fig. 1(b), at a later instant t₂, the above process is repeated, at which time the target permittivity has changed to ε(t₂) either from naturally occurring event, such as movement, or from externally induced perturbation. The result is a different intensity pattern:

$$I(t_2)=|E_{\mathrm{s}}(t_2){|}^2+|E_{\mathrm{R}}{|}^2+E_{\mathrm{s}}^{\ast }(t_2)E_{\mathrm{R}}+E_{\mathrm{s}}(t_2)E_{\mathrm{R}}^{\ast }.$$ (2)

Subtracting the two patterns (Eqs. (1) and (2)) generates multiple terms:

$$\mathrm{\Delta }I=I(t_2)-I(t_1)=\mathrm{\Delta }|E_s{|}^2+\mathrm{\Delta }{E}_{\mathrm{s}}^{\ast }{E}_{\mathrm{R}}+\mathrm{\Delta }{E}_{\mathrm{s}}{E}_{\mathrm{R}}^{\ast },$$ (3)

where Δ|E_s|² = |E_s(t₂)|² − |E_s(t₁)|², and ΔE_s = E_s(t₂) − E_s(t₁). The second term on the right-hand side of Eq. (3) encodes the TRAP field $\mathrm{\Delta }{E}_{\mathrm{s}}^{\ast }$, which can be reconstructed upon reading an amplitude hologram ΔI with a conjugate reference (reading) beam $E_{\mathrm{R}}^{\ast }$ (Fig. 1(c)). It should be noted that b-TRAP focusing dramatically simplifies the complicated task of complex amplitude measurement, and allows indirect, single laser-shot electric field recording. The advantages of the new technology will be discussed in detail in the next section.

The above focusing procedure can be implemented using the schematic shown in Fig. 1(d). The system employs a Mach-Zehnder interferometric structure where the scattering medium resides in one arm and the planar reference/reading beam is generated in the other. Intensity patterns I(t₁) and I(t₂) are recorded via an sCMOS camera. The SLM, along with the camera, forms a DOPC system [23]. Adjusting the driving frequencies (f₁ and f₂) of the two acousto-optic modulators (AOMs) allows the system to work under different operation modes, as detailed in the next section. For a more detailed description of the system setup, see Supplementary Method A of Supplement 1.

B. Operation modes

TRAP relies on embedded novelties [30] to guide light focusing, meaning that the target’s permittivity must be time-variant. Accordingly, the light field scattered by the target continuously decorrelates over time [31]. In real practice, the background medium (e.g., biological tissue) also generates time-variant scattering, resulting in a continuously decorrelating background field. The focusing quality sensitively hinges on the background field decorrelation during the entire time-reversal process [25,32]. Hence, TRAP focusing is valid only if the field from the target decorrelates faster than the field from the surrounding medium. The time interval between the field measurements must be properly chosen to allow for detectable target decorrelation yet a highly correlated background. The above condition is illustrated in Fig. 2(a)–(c). The curves drawn on the upper rows depict distinct correlation decays derived from the target’s and the background’s scattering. During the process, the difference between the two field measurements exposes the target decorrelation against a relatively stable background. For example, the correlation time of flowing blood is on the order of milliseconds, while that of the surrounding tissue varies, but is at least 10 times slower [22,25,33] with proper stabilization.

Fig. 2.

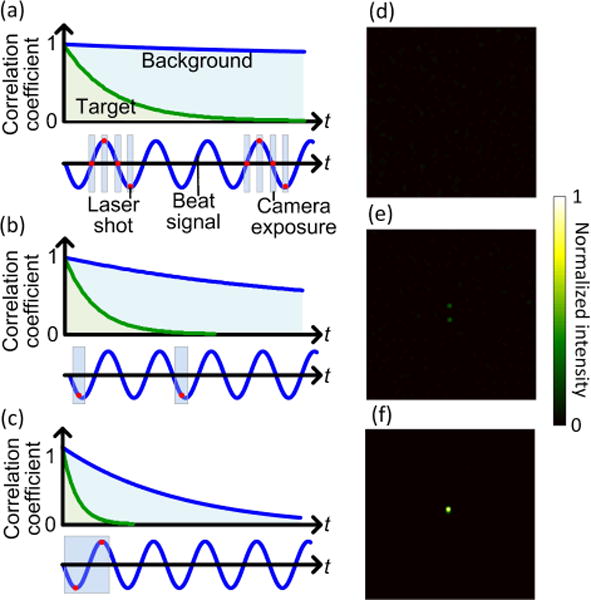
Influence of field sampling scheme on the focusing quality under both target and medium decorrelations. (a)-(c) Time-dependent correlation coefficients of the scattered electromagnetic fields due to the target and the background (upper rows), and the field sampling schemes (lower rows). (a) Full-field (amplitude and phase) sampling using a phase-shifting scheme. (b) Amplitude-only sampling with double camera exposures and digital subtraction. (c) Amplitude-only sampling with single camera exposure and automatic analog subtraction. (d)-(f) Simulated focal light intensity distributions corresponding to the sampling schemes in (a)-(c), normalized by the peak intensity in (f).

Note that the duration of each field measurement must be shorter than the target decorrelation time to avoid significant reduction of focal PBR. As shown in Fig. 2(a), the original TRAP focusing scheme relied on digital phase shifting holography, which required at least four laser shots synchronized with four camera exposures to complete a single field measurement. The speed of the method was primarily restricted by the camera frame-rate. For example, if the camera ran at 50 Hz, the minimum duration of four exposures was ~ 60 ms. Consequently, the target needed to be stable within 60 ms, which is impractically long for many applications. Moreover, the second field measurement had to be significantly delayed (e.g., to after 1 s) due to the slow target decorrelation, making the method applicable only to a nearly stable background.

To remove such limitations, the field measurement time must be shortened. As shown in Fig. 2(b), b-TRAP records each of the two fields with a single laser shot, which is accomplished on a time scale defined by the laser pulse width. By using a laser with 6 ns pulse width, the original constraint on the target correlation time is relaxed by 7 orders of magnitude (from 60 ms to 6 ns [28]). Such a fast field measurement makes b-TRAP applicable to almost any biological targets. The phase differences between the reference beam and the static portion of the sample beam are kept constant for the two measurements, and thus digitally subtracting the two intensity patterns directly generates the TRAP field (Eq. (3)). The response speed of the scheme is limited only by the camera frame rate and SLM refresh time. Because it requires two camera exposures, the scheme is named double-exposure b-TRAP focusing.

b-TRAP focusing has been made even more powerful by the single camera-exposure scheme described below (referred to as single-exposure b-TRAP hereafter), which can reduce the hologram formation time by two orders of magnitude in comparison to the state of the art [26]. As shown in Fig. 2(c), in this mode, one camera exposure records two consecutive laser shots, with a π phase shift introduced between the sample and reference beams in the second shot. The intensities of the first and second light pulses are $I_1=|E_{\mathrm{s}}(t_1){|}^2+|E_{\mathrm{R}}{|}^2+E_{\mathrm{s}}^{\ast }(t_1)E_{\mathrm{R}}+E_{\mathrm{s}}(t_1)E_{\mathrm{R}}^{\ast }$ and $I_2=|E_{\mathrm{s}}(t_2){|}^2+|E_{\mathrm{R}}{|}^2-E_{\mathrm{s}}^{\ast }(t_2)E_{\mathrm{R}}-E_{\mathrm{s}}(t_2)E_{\mathrm{R}}^{\ast }$, respectively. In a single exposure, the two intensities are added automatically by the camera sensor, resulting in a total intensity of

$$I=\sum |E_{\mathrm{s}}{|}^2+2|E_{\mathrm{R}}{|}^2+\mathrm{\Delta }{E}_{\mathrm{s}}^{\ast }{E}_{\mathrm{R}}+\mathrm{\Delta }{E}_{\mathrm{s}}{E}_{\mathrm{R}}^{\ast },$$ (4)

where Σ|E_s|² = |E_s(t₁)|² + |E_s(t₂)|², and the TRAP field is encoded in the third term. By reading the hologram using a planar reading beam, the TRAP field $\mathrm{\Delta }{E}_{\mathrm{s}}^{\ast }$ is reconstructed. In this focusing mode, the time interval between the two field measurements is determined by the laser repetition rate, making the procedure independent of the camera frame rate. Thus, a hologram can be formed within less than 1 μs for operation at a >1 MHz laser repetition rate (e.g., by using a mode-locked laser). The ultimate speed is determined only by the image transfer and SLM refresh rates.

The advantage of b-TRAP focusing is demonstrated by the simulation results shown in Fig. 2(d)–(f). In these simulations, a point target moves (downward) inside a dynamic scattering medium. The original TRAP scheme (Fig. 2(a)) fails to focus (Fig. 2(d)) due to its low speed. In vivid contrast, b-TRAP focusing successfully captures the target movement and focuses into the time-variant scattering media with double exposures (Fig. 2(e)) and a single exposure (Fig. 2(f)). However, single-exposure b-TRAP shows the strongest background suppression (Fig. 2(f)), thanks to its higher speed and greater tolerance to medium decorrelation: For TRAP to work, the medium should be stable when E_s(t₁) and E_s(t₂) are measured—a requirement most easily fulfilled by the single-exposure scheme. In the simulation, the single-exposure approach yields the highest PBR since the background decorrelates 10 times less than that in double-exposure b-TRAP, and 70 times less than that in traditional TRAP focusing. See Supplementary Method B of Supplement 1 for detailed simulation method.

In the experiment, for double-exposure b-TRAP focusing, the modulation frequencies of AOM1 and AOM2 are set to f₁ = 50 MHz (50 MHz is the central frequency of the device) and f₂ = −f₁ + Δf. The frequency difference is Δf = Nf_c, where f_c is the frame-rate of the camera and N is a non-negative integer. The laser repetition rate is f_L = Mf_c, where M is a positive integer. In the single-exposure scheme, the sign of the beat between the sample and reference beams flips from shot to shot, requiring Δf = (N+1/2) f_L, where N is a non-negative integer. Laser shots are synchronized with camera exposures, with f_L = Mf_c (M > 2) and 1/f_L < t_exp < 2/f_L, where t_exp is the camera exposure time.

C. Hologram binarization

Spatial light modulators with binary modulation, such as DMDs, provide much faster actuation in comparison to their continuous-modulation counterparts. As such, the intensity holograms shown in Eqs. (3) and (4) are binarized to facilitate the implementation of b-TRAP focusing on such devices. The binarization process is straightforward: The mean intensity of the hologram is used as a threshold. Pixel values exceeding the threshold are set to unity, otherwise they are set to zero. We used a zero-order block to double the focal PBR by converting binary amplitude to binary phase modulation [27].

The binarization process is subject to contamination from the speckle background (Δ|E_s|² in Eq. (3) and Σ|E_s|² in Eq. (4)), which causes error in the hologram and consequently reduces the focal PBR. In order for the binarization to work properly, the reference beam intensity should be sufficiently large, so that the TRAP term (ΔE_s*E_R in Eqs. (3) and (4)) dominates. A theoretical model is provided in Supplement 1 Section 2C to show the relationship between the beam ratio I_s/I_R and the focal PBR. Computer simulations were performed to verify the theory. Simulation and analytical results are co-plotted in Fig. 3 for both the double- and single-exposure sampling schemes. As is evident from the figure, the PBRs undergo continuous reduction when the beam ratio increases.

Fig. 3.

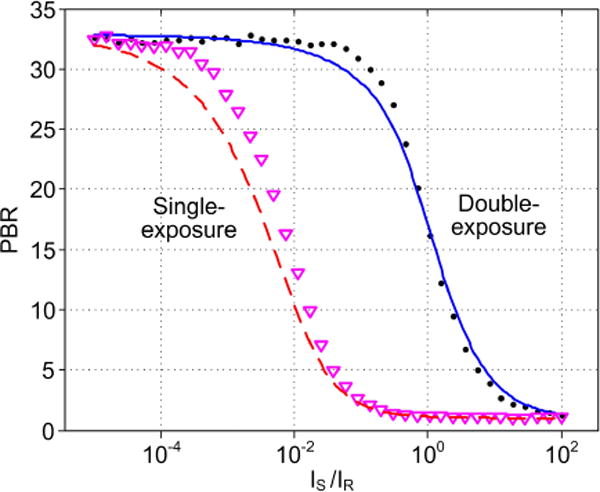
Influence of the beam ratio I_s/I_R on the PBR of b-TRAP focusing. Discrete points are from numerical simulations, lines are from analytical model. The total number of control is 100.

In b-TRAP focusing, we used an on-axis spatial sampling scheme. It is also possible to use off-axis sampling scheme for both double- and single-exposure TRAP hologram measurement [26]. The advantage of using an off-axis scheme is apparent: By using a sufficiently high carrier spatial-frequency, the TRAP term can be separated from the speckle background in the spatial frequency domain. However, this comes at the expense of reduced spatial bandwidth, resulting in 16 times fewer number of controls in the off-axis scheme compared to the on-axis scheme at the same spatial sampling capacity (i.e., camera pixel count; see Supplement 1 Section 2A for a detailed analysis). Equivalently, the focal PBR will be 16 times lower. According to Fig. 3, as long as the beam ratio is below 6% for single-exposure, and 10 for double-exposure schemes, the on-axis schemes yield higher PBR than their off-axis counterparts. Moreover, to calculate the binary hologram, the off-axis scheme has much higher computational complexity in comparison to the on-axis scheme (see, e.g., Ref. [32]), giving rise to much slower response. Considering all the above factors, we used on-axis sampling scheme, in conjunction with hologram binarization for the subsequent experiments.

3. RESULTS

A. Moving object tracking

Real-time tracking of moving objects has extensive applications [34,35], and TRAP (and TRACK) focusing is the only known optical method that tracks moving objects inside scattering media. A robust tracking system must meet two criteria. First, the time it spends on field measurement must be sufficiently short. Since there is no external control over the objects’ movement speeds, it is essential that the field measurement be accomplished sufficiently fast to accommodate potentially fast field decorrelations. Second, the entire focusing procedure, including measurement, calculation, and display of the hologram, must be finished within a short time span so as to minimize the spatial lag of the focus, and to robustly adapt to any potential host medium decorrelation.

In a demonstration of the original TRAP focusing, the target moved slowly, with an estimated decorrelation time of ~6 s. With the new b-TRAP focusing system, we shortened the field measurement time from 60 ms down to 6 ns, and reduced the repetition period from ~2 s to 140 ms. These speed improvements allowed us to optically track fast moving objects inside scattering media. A simplified experimental setting is depicted in Fig. 4(a), where a black human hair target (~50 μm in diameter), vertically positioned between two optical diffusers (DG10-600, Thorlabs, USA), was mounted onto a motorized stage. The target was moved back and forth in the x direction at a speed of 0.78 mm/s (with an estimated decorrelation time of <60 ms), while b-TRAP focusing was performed at a repetition rate of 7 Hz. A detailed explanation of the timing of the focusing procedure, including key steps and their execution times, are provided in Supplementary Method C of Supplement 1. The focal light intensity distribution was sampled using a beamsplitter onto the detection plane of a CMOS camera (Firefly MV, Point Grey, Canada) to monitor the focusing process in real time. The two-dimensional (2D) light intensity distribution was then averaged along y, condensed into a 1D intensity map, and stacked in time to form an intensity distribution time-trace, as shown in Fig. 4(b). The movement of the target was clearly revealed by the tracking focus. Most of the focusing patterns comprised two foci, typical of TRAP focusing patterns induced by a moving object [28]. As shown in the inset of Fig. 4(b), the twin foci were contributed by the old and the new target positions.

Fig. 4.

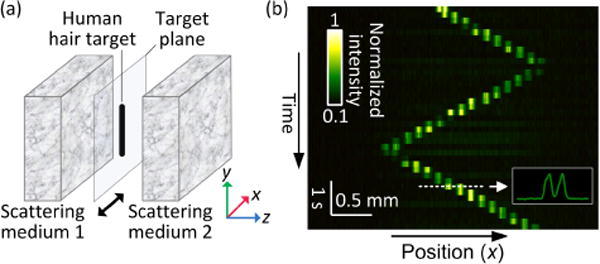
Tracking a moving target inside scattering media. (a) Experimental scheme. The hair target between two scattering media moves back and forth on a motorized stage. (b) Measured time trace of the focal light intensity distribution. Each row depicts the light intensity distribution (integrated along y) at a fixed time point. Each column shows the temporal evolution of the intensity at a fixed position. Process repetition rate, 7 Hz. Insets: Intensity profile along the dashed line.

B. Tissue-mimicking phantom experiment

One unique feature of TRAP focusing is its ability to concentrate light onto endogenous contrast agents, such as moving red blood cells (RBCs). As RBCs are exclusively confined within blood vessels, TRAP focusing selectively deposits time-reversed photons onto the vasculature. This feature is potentially useful in applications such as photoacoustic tomography of blood vessels [36] and treatment of port-wine stains [37]. It is important to note that living tissue is associated with two distinct correlation times: A fast decorrelation due to blood flow, and a slow one from the relatively stationary background [25,32]. The TRAP focusing procedure must be able to capture the fast changing information, and to adapt to the slow background evolution.

We demonstrated the above capability in the tissue-mimicking phantom experiment shown in Fig. 5(a). The phantom was composed of two ground-glass diffusers (DG10-600, Thorlabs, USA) as scattering media with a tube (300 μm inner diameter, silicone) containing flowing blood placed vertically in between. The mimic blood vessel was completely invisible outside of the ground glass. To mimic tissue decorrelation with controlled correlation time, the scattering layers were mounted onto a motorized stage with adjustable movement speed. The speckle correlation time [25] of the scattered light was measured as a function of the media’s movement speed, and subsequently fitted according to

$$t_{\mathrm{c}}[\mathrm{s}]=1.2[\text{μm}]\times {\{v[\text{μm}/\mathrm{s}]\}}^{-1},$$ (5)

as shown in Fig. 5(c). From Eq. (5), we were able to pre-set the tissue correlation time by controlling the media’s movement speed. During the focusing demonstration, diluted bovine blood (1 (blood):8 (PBS solution) by volume) was pumped through the silicone tube at a constant flow rate. The moving RBCs perturbed the scattered field, forming targets for time-reversed focusing of the entire vessel. While the focusing procedure was performed at a repetition rate of 7 Hz, the scattering media were translated at various speeds to set the background correlation time to +∞, 0.81 s, 0.41 s, and 0.28 s; the corresponding 2D focal light intensity distributions and 1D cross-sectional intensity profile along x are plotted in Fig. 5 (b) and (d) in subplots (i)–(iv), respectively. Despite an intensity drop, the focus was well preserved, even when the background medium decorrelated within as short as 0.28 s. Such demonstrated capabilities take a quantum leap from an earlier demonstration [28], where the slow response of the system forced us to temporarily stop the blood flow to facilitate field measurements, and required absolutely stationary background media.

Fig. 5.

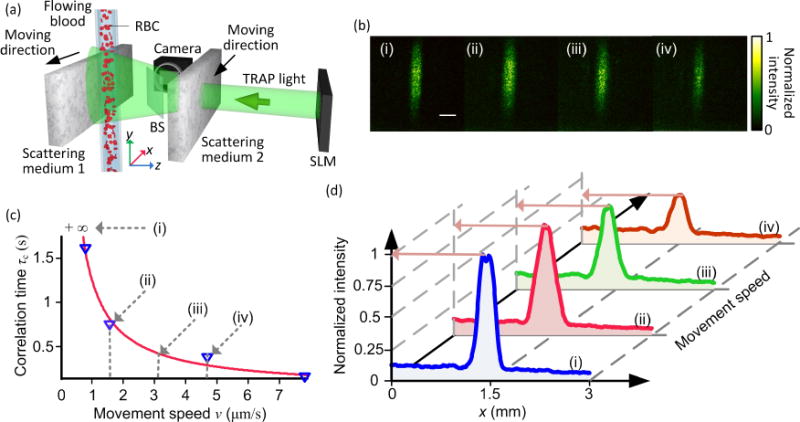
Tissue-mimicking phantom experiment. (a) Experimental arrangement. RBC, red blood cell; BS, beam-splitter. (b) Focal light intensity distribution, each averaged over 100 speckle realizations, measured at different movement speeds of the media. (c) Medium’s correlation time as a function of its movement speed. Triangles are measured data, solid line is the fitted curve. (d) Evolution of the focal intensity profile with increasing media decorrelation rate. Indices (i) through (iv) in (b)-(d) label different medium’s correlation times as shown in (c). Scale bar, 500 μm.

C. Deep flow measurement

As shown in the preceding section, blood flow perturbs the scattered light field, which enables time-reversed focusing: The field decorrelation associated with the RBC movement is captured externally and converted to a differential field, the conjugate copy of which ultimately leads to the time-reversed focusing. Two consecutive laser pulses “see” two sets of spatially shifted RBC positions, as illustrated in Fig. 6(a). The displacement d = v × Δt, where v is the flow speed and Δt is the pulse interval. A larger displacement results in greater decorrelation (Fig. 6(d)), creating a stronger differential field (Fig. 6(b)) and a brighter focus (Fig. 6(c)). The focusing power (P_TRAP) is a function of RBC displacement:

$$P_{\text{TRAP}}=P_{max}\{1-\{\xi -\sin \xi \}/\pi \},$$ (6)

where $\xi =2{\cos }^{-1}\left(\frac{d}{D}\right)$, D is the average diameter of the moving particle and P_max is the maximum power, see Supplementary Method D of Supplement 1 for detailed analysis.

Fig. 6.

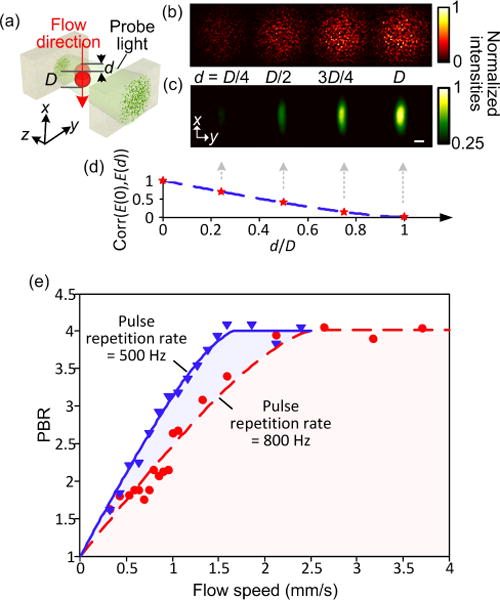
Deep flow measurement with single-exposure b-TRAP focusing. (a) Simplified schematic. d, displacement; D, size of the moving particle. (b) Intensity maps of the exterior differential field (upper row, simulation) and interior focal field (lower row, experimental) at various target displacements. (c) Correlation of the scattered fields at different target displacements. Stars, simulation; dashed curve, theory. (d) Flow measurement results showing focal peak-to-background ratio (PBR) as a function of flow speed, obtained at 500 Hz and 800 Hz laser repetition rates, respectively. Discrete points are experimental data, curves are theoretical fittings. Scale bar, 500 μm.

At fixed Δt, d was adjusted by varying v, giving rise to dramatically different focal PBR. Blood flow speed was controlled by a motorized syringe pump during the measurement. We used a hybrid scheme to generate the digital hologram for the best focal PBR. Two laser repetition rates were employed during the test: f_L = 500 Hz and f_L = 800 Hz. For f_L = 500 Hz, f_c = 12.5 Hz, Δf= 250 Hz, and t_exp= 3 ms. For f_L = 800 Hz, f_C = 12.5 Hz, Δf= 400 Hz, and t_exp = 2 ms. At a fixed flow speed, 51 single-exposure b-TRAP holograms were recorded, and the hybrid holograms were calculated using H_H,i = H_SE,i+1 − H_SE,i (i = 1,…,50), where H_H,i represents the i-th hybrid hologram, and H_SE,i denotes the i-th single-exposure hologram. The focal PBR was then characterized using a CMOS camera (Firefly MV, Point Gray, Canada) by averaging over the 50 corresponding focal light patterns. Repeating the above procedure at various flow speeds produced the experimental results shown in Fig. 6(e). To finalize the characterization process, the results were then fitted using a nonlinear least-squares model to Eq. (6), with P_max and D as unknown parameters. Experimental results are compared with theoretical ones for Δt = 2 ms (500 Hz laser repetition rate) and Δt = 1.25 ms (800 Hz laser repetition rate) in Fig. 6(e). The theoretical curves were plotted based on Eq. (6), with P_max and D fitted to the experimental data. The effective RBC diameters were found to be 3.4 μm and 3.2 μm for Δt = 2 ms and 1.25 ms, respectively; the difference is attributed to measurement noise. For flow measurement, the laser repetition rate can be swept to scan d, and v is then readily obtained by fitting. The focal PBR and location can be acquired photoacoustically [38].

In the experiment, the interval between the two field measurements must be precisely adjustable and can be squeezed below the target decorrelation time. Among all technologies developed to date, only single-exposure b-TRAP focusing has this unique capability. It is important to note that in such working mode, the time to generate a hologram is entirely dependent on the laser pulse interval (as opposed to the camera frame-rate), which is short and highly adjustable. Consequently, the finely and broadly tunable Δt makes the method extremely appealing due to its large dynamic range: It can measure both slow [39] and fast [40] flow, and extends laser speckle contrast imaging of blood flow [31] into the diffusive regime.

4. DISCUSSION AND CONCLUSION

We discovered that the b-TRAP mask is equivalent to the hologram generated by the binary amplitude iterative WFS technique [13], but we doubled the PBR by employing a zero-order block for binary phase modulation [27] (see Supplementary Discussion C of Supplement 1 for details). Using a DMD, the binary amplitude iterative WFS technique took several minutes to find the mask with 3228 degrees of freedom (DOF; i.e., controlled number of spatial modes); the limited speed was attributed to the iterative algorithm and data transfer between a personal computer and the DMD. In comparison, b-TRAP focuses in 143 ms with a DOF of 5×10⁵, equivalently 10⁵ faster than the iterative WFS approach on a per mode basis.

In OPC, two types of systems were developed. The analog systems perform optical phase conjugation using nonlinear crystals. The response of such systems can be fast, ranging from milliseconds [25] to microseconds [41]. The DOF of the analog systems are large [25], and can exceed 10⁷. Nevertheless, the gain of the systems is low. Despite a large power gain recently demonstrated using pulsed hologram readout [42], the achievable energy gain is still well below unity. Without large energy gains, many applications are still infeasible.

In digital systems, optical phase conjugation is accomplished by digital spatial light modulators, which can provide high gains [20]. However, the low camera frame rates significantly limit the field measurement times and the overall speeds. A single-shot off-axis holographic scheme has been employed to reduce the field measurement time and accelerate focusing [32]. However, the speed improvement compromises spatial resolution and reduces the total number of DOF significantly (see Supplementary Discussion A of Supplement 1). In contrast, b-TRAP focusing achieves a similar field measurement time (enabled by single-shot holographic recording) while preserving the number of DOF; thus, the technology has the shortest average mode time among all digital systems developed to date (We have demonstrated an average mode time of ~0.3 μs/mode, using a focusing repetition rate of 7 Hz and 5×10⁵ spatial modes). Moreover, for double-exposure b-TRAP focusing, the computational load is significantly reduced compared to other digital approaches. It took ~30 ms on a computer with 3.6 GHz quad-core i7 CPU (Intel, USA) and 1600 MHz memory frequency for Matlab to generate a binary mask with 1920×1080 resolution. The single-exposure scheme further improves the focusing speed by automatically forming the TRAP hologram within one camera exposure, thereby decoupling the speed from the camera frame-rate and hologram computation time, leaving the ultimate speed defined by the rates of data transfer and SLM actuation. In deep flow measurements, we have achieved a hologram formation time of 1.25 ms, which is nearly two orders of magnitude shorter than that of the state-of-the-art technique [26]. By using a pulsed laser with >1 MHz repetition rate, the hologram formation time can be further reduced to below 1 μs, sufficiently fast for most biological applications. Moreover, this unique capability allows us to not only detect, but also quantify target decorrelation during time-reversal (which is the key to deep flow measurement).

The demonstrated binary modulation makes b-TRAP focusing implementable on DMDs with minimal system modification, which can potentially further improve light focusing speed and make in vivo applications possible. Currently, besides low speed, the number of DOF supported by the liquid-crystal-based SLM is insufficient for most real applications, since the resultant low focal PBR in deep tissue is unsuitable for applications such as imaging, therapy or control. On the other hand, the DMD has recently emerged as an attractive solution for optical time reversal thanks to its high speed [8,12,13,27,43–48], and its relatively low price makes the use of multiple devices in parallel affordable, which can potentially increase the total number of DOF dramatically. The method invented herein can be integrated with other time-reversal based approaches, such as ultrasonically encoded focusing (TRUE) [18–20], to improve their speeds and efficiencies.

Single-exposure b-TRAP focusing has a smaller diffraction efficiency than the double-exposure approach because the ratio of the TRAP component in the hologram is lower. As dictated by the nature of amplitude modulation, b-TRAP schemes have weaker diffraction compared to those focusing methods implementing phase modulations; the focusing efficiency is about 10 times lower (see Supplementary Discussion B of Supplement 1). It is important to note that lower diffraction efficiency does not necessarily lead to lower PBR (which determines the focusing quality). The light reflected as the zeroorder component can be effectively blocked by a spatial filter, leading to binary phase modulation with a focal PBR ~40% of that attainable using a phase-only approach (see Supplementary Discussion C of Supplement 1). To compensate for the lower reflectivity, stronger input light can be used as long as damage to the SLM is avoided. Multiple DMDs can work in parallel to further enhance the energy gain.

In sum, optical time reversal techniques promise to revolutionize biomedical optics by dramatically extending the depth of optical focusing inside tissue. However, several key factors, including gain, speed, and focal PBR, must be simultaneously improved to implement these techniques in vivo. b-TRAP focusing has shown great potential in fulfilling all these criteria and in bridging the gap between laboratory explorations and real-world applications of deep tissue biophotonics. The technology has anticipated applications in deep-tissue molecular imaging [49], flow measurement and cytometry [26], photodynamic therapy [50], optogenetics [51], micro-surgery [4], and more.