Abstract
Topographic regularity of axonal connections is commonly understood as the preservation of spatial relationships between nearby neurons and is a fundamental structural property of the brain. In particular the retinotopic mapping of the visual pathway can even be quantitatively computed. Inspired from this previously untapped anatomical knowledge, we propose a novel tractography method that preserves both topographic and geometric regularity. We make use of parameterized curves with Frenet-Serret frame and introduce a highly flexible mechanism for controlling geometric regularity. At the same time, we incorporate a novel local data support term in order to account for topographic organization. Unifying geometry with topographic regularity, we develop a Bayesian framework for generating highly organized streamlines that accurately follow neuroanatomy. We additionally propose two novel validation techniques to quantify topographic regularity. In our experiments, we studied the results of our approach with respect to connectivity, reproducibility and topographic regularity aspects. We present both qualitative and quantitative comparisons of our technique against three algorithms from MRtrix3. We show that our method successfully generates highly organized fiber tracks while capturing bundle anatomy that are geometrically challenging for other approaches.
Keywords: connectome, dMRI, retinotopy, corticospinal tract
1. Introduction
Tractography is an exciting technique that enables extraction of the brain connectome, in-vivo, using diffusion MRI (dMRI) (Wandell, 2016). However validation of tractograms is challenging due to lack of ground truth (Côté et al., 2013). On the other hand, the regular topographic organization of many fiber systems in human brains provide a surprisingly untapped anatomical knowledge for the improvement and validation of tractography techniques. Some of the well-known examples include the retinotopic organization of the visual pathway (Engel et al., 1997), the somatotopic organization of the somatosensory pathway (Ruben et al., 2001), and the tonotopic organization of the auditory pathway (Morosan et al., 2001). In this study, we leverage this anatomical knowledge to develop a novel probabilistic tractography algorithm as well as quantitative techniques to validate tractograms.
There has been a plethora of tractography algorithms proposed in the literature during the last two decades. Initial tractography algorithms were based on the diffusion tensor model and propagation along the direction of the principal eigenvalue (Conturo et al., 1999; Jones et al., 1999; Mori et al., 1999; Basser et al., 2000; Mori and van Zijl, 2002; Lazar et al., 2003). Acknowledging the limitations of the noisy, low resolution dMRI data, there has been a shift towards addressing the uncertainty. This lead to several propagation or walker based solutions including techniques based on (i) front evolution and marching methods (Parker et al., 2002; Tournier et al., 2003; Kang et al., 2005; Pichon et al., 2005; Jackowski et al., 2005; Prados et al., 2006; Li et al., 2014), (ii) probabilistic and combinatorial techniques based on random walks and various sampling schemes (Bjrnemo et al., 2002; Behrens et al., 2003; Hagmann et al., 2003; Parker et al., 2003; Lu et al., 2006; Friman et al., 2006; Behrens et al., 2007; Lifshits et al., 2009; Descoteaux et al., 2009; Tournier et al., 2012; Jeurissen et al., 2014), (iii) Kalman filtering (Gössl et al., 2002; Malcolm et al., 2009, 2010), (iv) bootstrap methods (Lazar and Alexander, 2005; Jones, 2008; Jeurissen et al., 2011; Vorburger et al., 2013; Campbell et al., 2014; Jeurissen et al., 2011), (v) graph theoretical techniques (Iturria-Medina et al., 2007; Sotiropoulos et al., 2010) and (vi) particle filtering (Zhang et al., 2009; Savadjiev et al., 2010; Pontabry et al., 2013; Stamm et al., 2013; Rowe et al., 2013). Simultaneous to these efforts, there have been several creative approaches proposed for a global solution using (i) fast marching methods and geodesics (Parker et al., 2002; O’Donnell et al, 2002; Campbell et al., 2005; Jbabdi et al., 2007a; Zalesky, 2008; Péchaud et al., 2009; Hageman et al., 2009; Lenglet et al., 2009) (ii) spin glass models (Mangin et al., 2002; Fillard et al., 2009) (iii) Bayesian model (Jbabdi et al., 2007b) (iv) Gibbs sampling (Kreher et al., 2008; Reisert et al., 2011) (v) Hough transform (Aganj et al., 2011) and (vi) ant colony optimization (Feng and Wang, 2011).
With the advances in multi-band and parallel imaging techniques (Feinberg et al., 2010; Moeller et al., 2010; Setsompop et al., 2012), leading to the availability of HARDI (Tuch et al., 2002; Jansons and Alexander, 2003; Porter and Heidemann, 2009) and multi-shell diffusion imaging data (Sotiropoulos et al., 2013; Ugurbil et al., 2013), representation and modeling of signals have improved from tensors and multi-tensors to Q-ball (Tuch, 2004) and constrained spherical deconvolution (Tournier et al., 2004, 2007). With the increasing efforts on analyzing tissue microstructure and compartment modeling that provide even more accurate local uncertainty models for fiber orientation densities (FODs) (Tran and Shi, 2015; Novikov et al., 2016; Panagiotaki et al., 2012; Ferizi et al., 2014), the community has been pushing towards obtaining quantitative tractograms (Girard et al., 2014; Jbabdi and Johansen-Berg, 2011). Majority of the efforts aiming for this goal mainly start with a large set of precomputed streamlines and filter or weight them so they best match the underlaying diffusion signal (Sherbondy et al., 2008, 2010; Smith et al., 2013, 2015; Takemura et al., 2016; Pestilli et al., 2014; Daducci et al., 2015; Lemkaddem et al., 2014). It is worth mentioning that there are also tractography algorithms proposed to solve the local microstructure problem together with the global tractogram (Reisert et al., 2014).
Despite the vast amount of efforts spent on obtaining reproducible and reliable results, recent validation studies and reviews (Besseling et al., 2012; Thomas et al., 2014; Donahue et al., 2016; Daducci et al., 2016; Yeh et al., 2016) caution for the limitations of tractography. In addition to false negatives results (Aydogan et al., 2018), algorithms generating large amounts of false positives (Maier-Hein et al., 2017) are recently reported to be significantly detrimental in the analysis of connectomes (Zalesky et al., 2016), indicating a need for novel tractography algorithms towards quantitative tractograms and connectomes.
Previous tractography techniques do not take into account the topographic organization that is commonly encountered in the brain. To the best of our knowledge, there is no tractography algorithm in the literature that makes use of this precious neuroanatomic property of the axonal connections of the brain. Additionally, conventional tractography methods mostly rely only on step size and curvature parameters to control the geometric regularity of streamlines (Fillard et al., 2011) which can be improved with a more general representation of curves using differential geometry, enabling flexible mechanisms to reliably reconstruct pathways that have sharply bending segments such as the Meyer’s loop of the optic radiation.
In this work, we propose a novel propagation based probabilistic technique that incorporates mechanisms to address both topographic and geometric regularities of brain’s connections. We use a general parametric representation for each segment of streamlines using the Frenet-Serret frame that enables geometrically very regular tracking of pathways while allowing the tracker to handle very sharp turns. In order to take into account the topographic regularity, we developed a novel algorithm to measure the data support that tests the match of parallel curves to the FODs in the neighborhood of each point. Taking geometry and topography together, we use a Bayesian approach with rejection sampling for propagation and reconstruct highly organized tractograms.
In addition to lack of reliable tractography algorithms, the validation of results is another challenge towards quantitative tractography. Phantom based validation approaches were proposed in various earlier studies (Bach et al., 2014; Campbell et al., 2006; Fieremans et al., 2008; Pullens et al., 2010). However the translation of artificial phantoms to biological tissues is not clear. As an anatomically and histologically more reliable approach, tracer injections have been used in several studies (Calabrese et al., 2015; Chen et al., 2015). Injection experiments on the other hand are very costly, difficult and conducting tests on human or monkey are extremely challenging (Dauguet et al., 2007; Jbabdi et al., 2013a; Schmahmann et al., 2007; van den Heuvel et al., 2015). Alternatively, synthetic phantoms have been used in the literature for the validation of tractograms (Leemans et al., 2005; Neher et al., 2014); which are cheap and easy to use, but computer simulated and do not truly reflect the real tissue. Recent developments for 3D histology such as 3D polarized light imaging (Axer et al., 2011) and CLARITY (Chung and Deisseroth, 2013) also provide promising tools and opportunities for tractography validation.
The second contribution of our work is the novel in-vivo tractography validation framework that we used. In contrast to previous techniques, we propose to use the already known anatomical information based on the topographically organized connections in the brain. To achieve this, we developed two independent techniques. Our first approach is based on the visual pathway that is retinotopically organized (Engel et al., 1997). The second approach is based on a mathematical formulation of the neuroscientific understanding of topographic regularity, which implies the preservation of the spatial relationships between the end points of axonal projections. In our literature review, we were not able to find any other example of a validation approach for topographic regularity of tractograms.
We tested our technique with four sets of experiments that address the “connectivity”, “reproducibility” and “topographic regularity” aspects. The FiberCup phantom that was featured in the MICCAI 2009 tractography challenge and the Traced dataset that was collected for the ISMRMR 2017 tractography challenge were used respectively to study connectivity and reproducibility performances of our approach. For topographic regularity tests, we conducted experiments on the visual and motor pathways using the multi-shell dMRI data of the Human Connectome Project (HCP) (Van Essen et al., 2012). Using tractograms of 56 subjects for visual and 10 subjects for motor pathway reconstructions, we compared our method with three tractography algorithms of the MRtrix package (J-D Tournier, Brain Research Institute, Melbourne, Australia, http://github.com/MRtrix3/mrtrix3).
In a precursory study (Aydogan and Shi, 2016), we presented the motivation of our work with limited technical information and demonstrated preliminary results. The current work not only provides all the details of the algorithm and its implementation, it also introduces a completely new technique to assess topographic regularity. Lastly, in this study, we provide extensive qualitative and quantitative evaluations of our technique.
Our results show that the proposed method is able to generate highly organized streamlines while capturing challenging pathways such as the Meyer’s loop of the visual radiation. We also quantitatively show with two independent techniques that our method performs very well in preserving the topographic alignment for both visual and motor pathways. Overall, the proposed tractography method and the measurement techniques offer novel tools to study and understand the structural and topographic organization of the brain which is largely unexplored.
2. Methods
We divided the explanation of our methods into two parts. In section 2.1, we explain our tractography approach. In section 2.2, we propose validation approaches for topographic regularity.
2.1. Geometric and topographic regularity preserving probabilistic tractography
Our tractography approach is based on preserving geometric and topographic regularity of streamlines. Before explaining our technique in detail, we first outline our mathematical notation, definitions and give an overview of our approach.
Definition 1 (Streamline). A streamline is a finite sequence of points that is used to represent a connection in the brain obtained using dMRI based tractography. Following the sequence notation, we denote a streamline as Γ = (p0, p1, p2, ··· ) where pt ∈ ℝ3.
The tractography technique we propose is a propagation based probabilistic approach. These techniques typically start from a user provided point that is commonly called the seed. Initiating from the seed, a series of computations are done to determine a direction to propagate. At each time step, a new propagation direction is computed and a step is taken towards this direction. Evidently these techniques are also called walker approaches in the literature.
Due to the time evolving nature of walker based streamline reconstruction, we will use the notation pt for the point at time step t. Therefore the seed point is p0. Let’s assume that at t − 1 and point pt-1, the direction to propagate is computed as Tt-1. Then 1st order integration based walker tractography techniques set Pt = Pt-1 + Tt-1Δs where Δs is a step size for propagation. This assignment assumes that the tangent, , of the streamline between pt-1 and pt is constant. Using Tt-1, a streamline can be expressed as a sequence of points along piecewise arc length parameterized curves:
| (1) |
here γt (s) is used to denote a parameterized curve with its arc length, s, initialized at point, pt. At each time step, t, shown in the subscript, a different curve parametrizes the points for the propagation of the streamline starting from pt. Figure 1 shows a visual representation of our notation for clarification. Notice that γt (−s) = γt-1(Δs — s) only at s = 0.
Figure 1:
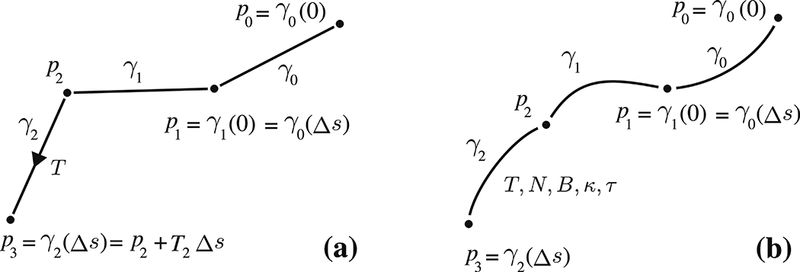
(a) Typical propagation based techniques walk along straight line segments (b) Our approach generalizes the propagation with segments parametrized by any smooth curve.
Almost all tractography techniques have mechanisms to preserve the geometric regularity of streamlines since it is common to consider that the axonal connections in the brain project along smoothly varying curves. However, because of the very definition of the parameterization shown in Equation 1, there are limited ways to achieve this during propagation. As a result, most tractography approaches, including the global techniques, almost always control the geometric regularity of streamlines by constraining the maximum angle between consecutive tangents which is not a sufficient solution as pointed out in earlier studies (Tournier et al., 2002, 2012). The problem is well-known and from the early years of tractography, numerical solutions such as higher order Runge-Kutta integrations (Basser et al., 2000) and later 2nd order propagations were proposed to introduce stronger geometric regularity and preventing overshoots (Tournier et al., 2010).
In contrast to other approaches, we propose to use a Bayesian framework to preserve geometric and topographic regularity of streamlines while tracking. Given a seed point p0, at time t = 0, our tractography algorithm initializes by finding the first curve γ0(s), p0 = γ0(0) . Then it moves by taking a step of Δs which gives, p1 = γ0(Δs) . Given a previous curve parametrization, γt-1 the probability of picking the next curve, γt for t > 0 can be expressed as:
| (2) |
Here the prior term relates the previous curve to the next, thus, can be used to control geometric regularity. On the other hand, the likelihood term relates the data, , to the next curve which we use to control topographic regularity. As the data term, our algorithm uses FODs that are represented with spherical harmonic coefficients which can be estimated from dMRI using various techniques (Tournier et al., 2007; Tran and Shi, 2015) and software packages (Tournier et al., 2012; Garyfallidis et al., 2014). Figure 2 explains our propagation technique. In the next sections, we describe our approach to compute the prior and likelihood terms.
Figure 2:
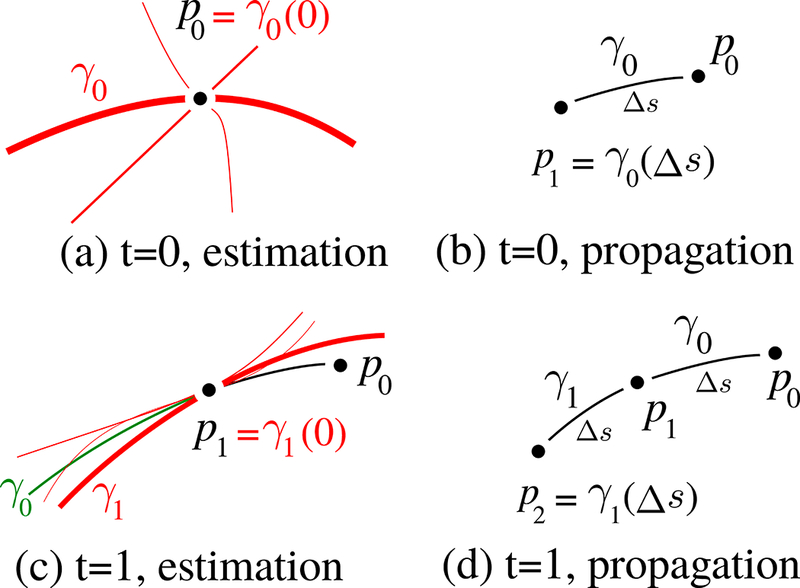
(a) For initialization, we randomly select a curve among red candidates. (b) After the selection of the first curve, we take a step, Δs. (c) For the next time point, posterior probabilities are estimated using the geometrical prior and topographical likelihood terms. For the computation of prior we look at the difference between the candidate curves and the previous curve, γ0, that is shown in green. (d) Propagate to p2 and iterate.
2.1.1. Preservation of geometric regularity
Equation 1 shows that each segment between consecutive points of a streamline lay on a parameterized curve. In order to preserve geometric regularity, we propose to use a generalized parametrization. For that purpose, we use the Frenet-Serret frame and formulas to represent segments of streamlines.
Frenet-Serret frame is composed of three orthonormal vectors: tangent (T), normal (N) and binormal (B). Given a non-degenerate curve γ (s) : ℝ → ℝ3 that is parameterized by its arc length s, T = dγ / ds, N = (dT / d/s) / | dT / ds | and B = T × N . The T, N, B vectors control the 3D positioning of curves which we will shortly denote as ℱ = {T,N,B}. Frenet-Serret formulas express the derivatives of T, N and B with a system of first order ODEs: dT / ds = κN , dN / ds = −κΤ + τΒ and dB / ds = ‒τΝ. Here κ is the curvature and τ is the torsion of the curve. Our method parameterizes each segment with constant κ and τ. Given the initial condition, i.e.: γ (0) , Τ (0) , N (0) and B (0), Frenet-Serret ODE system can be solved as shown in Appendix A. During the propagation of γt-1(s) from pt-1 = γt-1(0) to point pt = γt-1(Δs), the Frenet-Serret frame is subjected to rotation as a function of s due to non-zero curvature and torsion. We will use ℱt-1(s) = {Tt-1(s), Nt-1(s), Bt-1(s)} to denote the arc length dependence of the Frenet-Serret frame as shown in Figure 3(a). The constant curvature and torsion for this segment are denoted as κt-1 and τt-1 respectively.
Figure 3:
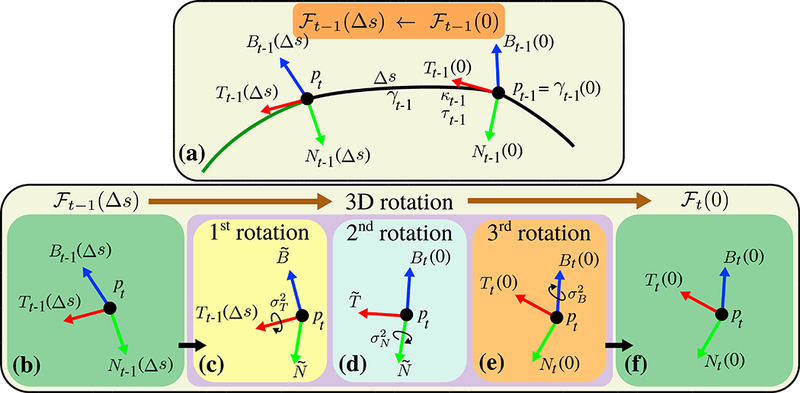
(a) Frenet-Serret frame rotates as a function of arc length, s. The frame at pt-1, ℱt-1(0), gradually changes into the frame at pt-1, ℱt-1(Δs), during propagation. At pt, based on ℱt-1(Δs), the Frenet-Serret frame of a candidate curve, ℱt (0), is randomly generated using 3 consecutive rotations. (b-c) ℱt-1(Δs) is first rotated around Tt-1(Δs) with a random angle picked from a zero mean Gaussian distribution with user defined variance , creating and vectors. (d-e) Second and third rotations are done around and Bt(0) with random angles picked from zero mean Gaussian distributions with user defined variances and respectively. Notice that the Frenet-Serret frame is always orthonormal during the propagation and after each rotation.
At the end of each propagation, pt = γt-1(Δs), in order to propagate to the next point, pt+1, we need to pick a new curve parametrization and solve γt(s). By definition, γt(0) = pt, thus ℱt(0), κt and τt need to be known to solve γt(s). In order to determine these parameters, we generate and consider random candidate curve parameterizations that resemble the previous parametrization that is ℱt-1(Δs), κt-l and τt-1. For this purpose, random κt and τt are picked from Gaussian distributions with mean κt-1 and τt-1 with user defined variances and respectively. A random ℱt(0) on the other hand is obtained by rotating the previous Frenet-Serret frame, ℱt-1(Δs), following the intrinsic Tait-Bryan rotation (x- y’ -z”) around Τ, N and B axes as shown in Figure 3(b-f). The angles for the rotations are randomly picked from zero mean Gaussian distributions with user defined variances , and .
Prior term can be thought as a weight for the likelihood. It lowers the (posterior) probability of selecting a candidate parameterization that has a very large data support (likelihood), if it is geometrically very different than the current segment. On the other hand, if a candidate is geometrically similar to the current parameterization, prior increases its chances to be picked even it is poorly supported by the data. In our current implementation, we use the prior term shown in Equation 3 as a measure of the geometrical transition between the two curves. The expression has its highest value when the curve parameterizations at pt are identical, and it decreases with the increase in parameter differences between the two curves.
| (3) |
The functions used to compute the prior are given in Equation 4.
| (4) |
where 〈 , 〉 is the dot product. , and are the vectors shown in Figure 3(c-d). Because all vectors in Equation 4 have unit norm, acos (〈 , 〉) gives the angle between the two inputs. If a rotation dramatically changes a vector, then is low, which is the desired functionality of the prior term. Similarly, if randomly picked κt and τt are largely different than κt-1 and τt-1,. prior w ill be low. In Equation 4, Ψ(κ) = asin(κ) is used to linearly vary the curvature which is explained in detail in Appendix C. The terms of the Gaussian functions are not used since they are same for all the candidates.
2.1.2. Preservation of topographic regularity
We showed with Equation 2 that the likelihood term is used to quantify how well the local FOD field supports topographically aligned streamlines. Note that the field of FODs over an image volume can be expressed as a spherical function Ɗ(p,T) : ℝ3 ×S2 → ℝ , where p∈ℝ3 is the location of a point in the dMRI and T ⊰S2 is a unit vector. In order to calculate the likelihood using FOD data, we use the parallel curve definition which are also known as offset curves in computer graphics and computer aided design:
Definition 2 (Parallel curves). Let γ and γt be two curves. If γ (0) lies on the normal plane of γt at γt(0) and ℱ(0) = ℱt(ο), κ = κt. τ = τ, then γ and γt are parallel curves which is denoted as γ ║ γt . Here ℱ , κ and τ are the Frenet-Serret frame, curvature and torsion of γ respectively. For a curve γt at pt = γt(0), we use the following function to quantify how well topographical organization is supported by the FOD data:
| (5`) |
where r is the radius of the integration sphere that has the center point pt. By integrating the contributions of FODs belonging to parallel curves, we measure the data support for the candidate γt.
The constant term in front of Equation 5 normalizes the expression which is written here for completeness but not computed in our implementation. In order to estimate the likelihood expression, we discretize the integration domain using evenly spaced 27 points and add the individual contributions of FODs for each point as illustrated in Figure 4. For this visualization, we picked a center point that is located in the corpus callosum of one of the HCP subjects. For clarity, parallel curves are shown on 4 of the 27 points. We analytically obtain the tangents of parallel curves at each point as shown in Appendix B and linearly interpolate the FODs at the integration points. The final likelihood is the average data support for the parallel curves obtained using the amplitude of interpolated FODs along the directions of the tangents.
Figure 4:
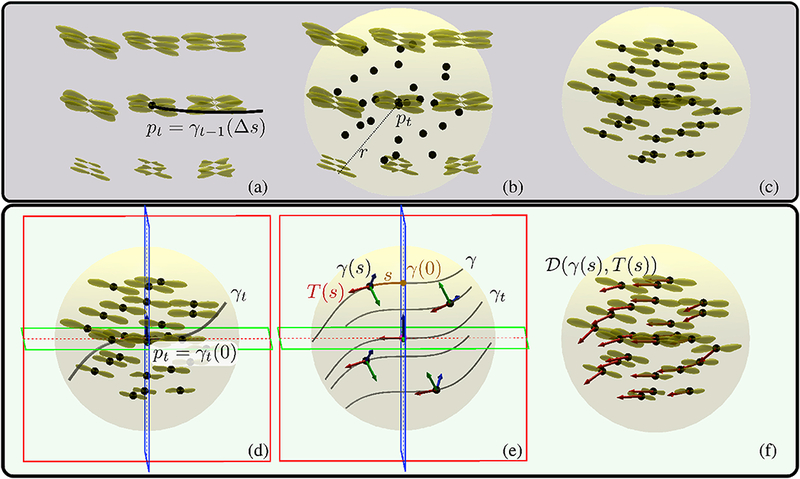
(a) Yellow glyphs on a regular grid show the FOD data, . pt is determined by taking a step along the previous curve γt-1(Δs). (b) Likelihoods are estimated using 27 points in the integration sphere shown as black dots. The integration sphere is centered at pt and has a user defined radius of r. (c) To start, we obtain FODs at the integration points using trilinear interpolation. (d) Then candidate curves resembling the previous curve at γt-1(Δs) are generated. An example candidate curve, γt, is shown with red, green and blue frames indicating the rectifying (TB), osculating ( TN ) and normal ( NB ) planes respectively. (e) To estimate the data support for the candidate curve, parallel curves passing through the integration points are computed. These are shown at few selected integration points in order to keep the visualization clean. A parallel curve, γ, at point γ (0) has the identical Frenet-Serret frame of γt at pt. At integration points, the rotated Frenet-Serret frames and s are computed as shown in Appendix B. Red, green and blue arrows indicate Τ, N and B respectively. (f) Likelihood is assigned as the average of the FOD amplitudes at the integration points along the computed parallel curve tangents, . In order to speed up the likelihood computations for different candidate curves, all likelihoods are computed using the same integration points and interpolated FODs.
2.1.3. Implementation details and the algorithm
Algorithm 1 shows the pseudo code for the proposed method. At time t = 0, candidate curves are randomly generated. For t > 0, candidate curves are generated as explained in section 2.1.1.
For propagation, a single curve is randomly sampled from the candidate curve space using rejection sampling (lines 5–19 in Alg 1). For that we use an estimate of the maximum posterior probability for the space of candidate curves. Notice that a close estimate is not theoretically required, but it speeds up the sampling. One common way for the estimation is to compute the maximum posterior probability of a number of candidates and multiply it with a constant ( > 1 ) in order to compensate for possible underestimation. In our implementation, we compute the maximum of 100 candidates’ posterior probabilities and multiply it with 2. A random candidate is finally picked if its posterior probability divided by the estimated maximum is bigger than a random number selected from the uniform distribution (lines 16–18 in Alg 1). The same rejection sampling approach is found effective for other probabilistic techniques as well and it is used for example in MRtrix’s iFOD1 and iFOD2 algorithms.
Because our technique takes steps along smooth curves, we typically use very small steps, ~1/1000 of a voxel size. Since the posterior maximum depends on the data which does not noticeably change at the scale of our algorithm’s step size, we compute an estimate for the posterior probability maximum at each 100 steps in order to speed up the propagation (lines 3–4 in Alg 1). Also in order to save hard-drive space, we write segments after each 100 steps (line 22 in Alg 1). For the initial likelihood computation we use the whole sphere around the seed point. However during the propagation, we compute the likelihood on half the sphere that is along the propagation direction. As stopping conditions, the propagation is terminated if a candidate with a likelihood above a user defined cut-off threshold can not be found or a suitable candidate can not be picked by rejection sampling after 1000 trials. Additionally, propagation can be stopped by user defined ROI constraints.
Algorithm 1: Tractography algorithm
2.2. Quantitative validation of topographic regularity
Quantitative validation of tractography is a very challenging and a standing problem. In this section we present two different ways to achieve this. The first approach that is presented in section 2.2.1 shows a technique based on prior anatomical knowledge. In particular the well known topographic organization of the visual pathway. However this precise anatomical knowledge is not yet known for other topographically regular fiber systems of the brain. For that reason we developed another approach that measures the intrinsic topographic regularity (ITR) without the need of anatomical ground truth. This is presented in section 2.2.2.
2.2.1. Quantitative validation using retinotopic organization
The projections of the optic radiation that connect the lateral geniculate nucleus (LGN) and the primary visual cortex (V1) are long known to be topographically regular, following the retinotopical organization (Holmes, 1918) that implies a mapping between the visual field and the visual cortex (Figure 5).
Figure 5:
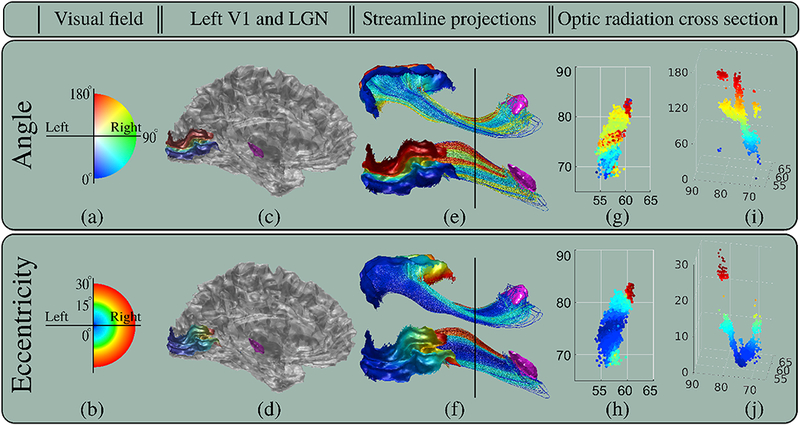
Retinotopic organization shown using the HCP subject #100307. (a-b) show the angle and eccentricity coordinates of the visual field. (c-d) show LGN in purple and the mappings of angle and eccentricity coordinates on V1. (e-f) show streamlines between LGN and V1 obtained using the proposed technique with parameters shown in Table 4. Streamlines are colored using the corresponding angle and eccentricity values on V1. For clarity, visualizations from inferior and lateral point of views are provided. (g-h) show the angle and eccentricity values on the cross sections of the optic radiation that are marked with black lines in (e-f). (i-j) show the 3D scatter plots of angle and eccentricity. Both coordinates smoothly vary, however variation of angle is mathematically more complicated than the U-shaped eccentricity. All angle and eccentricity values are to the scale and shown using the corresponding color maps on the left.
Early studies based on electrophysiological and electrical stimulation in the monkey brain proposed quantitative models to map the points in the visual field defined with angle and eccentricity coordinates to the superior colliculus (Ottes et al., 1986). Similarly, in (Arcaro et al., 2015), authors showed the topographic organization of the retinotopic coordinates inside the human LGN using fMRI. Angle and eccentricity coordinates were also mapped on the visual cortex. In (Tootell et al., 1988), authors conducted experiments on the monkey brain showing excellent topographic mapping between the visual field and the cup shaped occipital pole. Similar results were obtained using fMRI on the human brain as well (Engel et al., 1997).
More recently in (Benson et al., 2012, 2014), authors proposed an approach to compute the retinotopic mapping on V1 by using only the geometrical properties of the cortical surface. With this approach, angle and eccentricity coordinates can be mapped on V1 as shown in Figure 5 using only structure MRI (T1). This provides an opportunity for in-vivo validation of tractograms in terms of how well they preserve the retinotopic mapping between LGN and V1.
Although the exact functions are still subject to research, smooth variations of angle and eccentricity values are expected on the cross sections of the optic radiation when traced back from V1 towards LGN. In particular, based on the previous works summarized above, we expect the eccentricity component to preserve its cup shape organization around the occipital pole. The U-shaped eccentricity function can be approximated with a quadratic expression along the cross sections of the optic radiation. As a result, we propose the quality of fit measures such as mean square error (MSE) and coefficient of determination ( R2 ) to quantify how well tractograms preserve topographic regularity.
In addition to its intriguing topographic organization, optic radiation has also an alluring geometric property. The inferior bundle of the optic radiation has an unconventional trajectory which first courses anteriorly and then sharply turns posteriorly towards the visual cortex forming the elusive Meyer’s loop (Meyer, 1907). Because of the quantitative coordinates provided by the retinotopic map and the challenges in reconstructing the Meyer’s loop, we believe the optic radiation is one of the ideal test benches to study and validate tractograms.
2.2.2. Quantitative validation using intrinsic topographic regularity (ITR)
In neuroscience, topographic regularity although does not have a precise definition, it is commonly understood as point-to-point axonal connections among neurons which preserve certain spatial relationships (Thivierge and Marcus, 2007; Patel et al., 2014). In this section, we translate this definition into a mathematical form and propose a measure to quantify topographic regularity.
Let and be two 2-manifolds with elements . And let . And let be a set of streamlines, e. : a tractogram. Consider the case that , and where Γi = (xi, · · ·, yi) that is xi and yi are the first and last points of Γi. respectively. Resultantly, is a one-to-one mapping that maps the set of points to . Figure 6 is used to clarify our notation.
Figure 6:
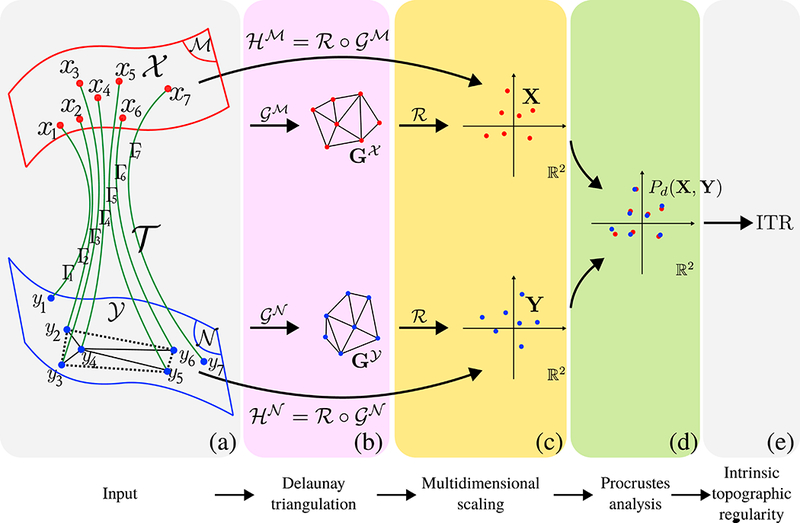
Computation of ITR. (a) Input is a tractogram that can be expressed as a mapping between two 2-manifolds, . (b) We first compute the Delaunay triangulations, and , using the end points of the tractogram, and respectively. The unweighted graphs reduce spatial relationships to ordinal relationships. Notice that regardless of y4 ‘s distance from its neighbors, as long as it is within the dashed area, the triangulation will not chance and the ITR value will remain the same which is consistent with the neuroscientific interpretation of topographic regularity. This would not have been the case if geodesic distances on manifolds and were compared. (c) We then use MDS to map the ordinal relationships in the unweighted and graphs onto ℝ2. (d) Procrustes analysis is done to find the best rotational match between the point sets X and Y . (e) ITR is assigned as the procrustes dissimilarity, ITR = Pd(X, Y).
The neuroscientific understanding of topographic regularity implies that certain spatial relationships among the points in are preserved among . In order to compare and that are on different manifolds, we propose to use the composite mappings that are in the form of and , which map and onto ℝ2. Figure 6 provides visualizations for the mappings that are used.
The Voronoi cell on associated with point is by definition the set of all points whose distance to xi is not greater than the distance to any other , i. e.: . Therefore by Voronoi partitioning the whole manifold , a complete representation of the spatial relationships of the neighboring points can be obtained. Using the identified neighbors, we can form Delaunay triangulations that are the dual graphs of Voronoi diagrams, which further establish ordinal relationships, i.e. : two points have a second order relationship if one of them is a neighbor of a neighbor of the other point.
We define as the Delaunay triangulation on , obtained using all points in . Similarly is the Delaunay triangulation on , obtained using all points in . The unweighted graphs, and , reduce the spatial relationships between points, to ordinal relationships. The reason behind this reduction can be explained using the example shown in Figure 6(a). As long as y4 is within the dashed region, its ordinal relationships with other points will be the same, indicating that all such cases have the same topographic regularity. This is consistent with the neuroscientific interpretation of topographic organization that implies the projections from to do not mix nor tangle. On the other hand, when y4 moves within the dashed area pairwise geodesic distances between y4 and its neighbors do change. Therefore direct comparison of pairwise distances between and is not an adequate choice to measure topographic regularity. Pair-wise distance relationships are only preserved when end points , can be expressed as a rigid transform of end points . Topographically regular projections on the other hand, involve a larger set of transformations, including non-linear deformations as well. This makes comparison of ordinal relationships a suitable choice to quantify preservation of topographic regularity.
In order to compare ordinal relationships, we compute the shortest distances between the vertices of graphs and use the classical multidimensional scaling (MDS), ℛ : 𝒢 → ℝ2, and map and onto ℝ2. The resultant point sets are: and . For point sets with identical pairwise ordinal relationships, MDS produces projections on ℝ2 that are identical with unknown 2D rotation. Therefore the procrustes dissimilarity measure between X and Y , Pd(X, Y), that considers only rotational changes provides a measure to the loss of topographic regularity. As a result, the intrinsic topographic regularity (ITR) measure, ITR = Pd(X, Y) = 0 for perfectly topographically regular mappings and increases with the loss of regularity.
ITR does not require any parameters. ITR is unitless since it is computed based on distances on unweighted graphs. ITR measures the loss of neighborhood integrity of streamlines and it is always ≥0 . We demonstrate the properties of ITR on toy examples shown in Figure 7. Here we did not draw the tractograms since only the end points are used to compute ITR. For simplicity we considered cases where tractograms project from one plane, , to another, , and showed the graphs on the planes. Examples demonstrate why ITR does not change with identity, rotation, translation, scaling transforms and also some non-linear deformations.
Figure 7:
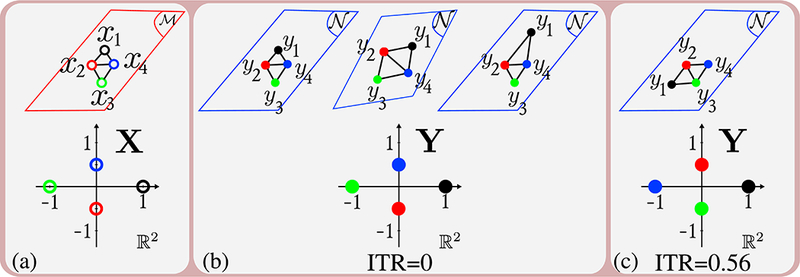
Toy examples demonstrating properties of ITR. Top row shows the end points of tractograms. Bottom row shows the coordinates on X and Y after MDS. (a) shows the end points of 4 streamlines on and X . (b) shows cases where ITR = 0 which include identity, rotation, translation, scaling transforms and also some non-linear deformations which do not change the graphs. (c) shows the case where ITR is non-zero since there is dissimilarity between the graphs and the points on X and Y
3. Test data and experimental setup
We conducted four different experiments in our study and evaluated the performance of our approach from various aspects. For all experiments we provided results for qualitative and quantitative comparisons. A summary of our experiments are given in Table 1.
Table 1:
Summary of experimental setup. Experiments 1 and 2 are conducted on datasets used in international challenges. Our results can be compared with independent evaluations which are listed in the last row. (*) Traced website: https://www.synapse.org/#!Synapse:syn8457617/wiki/415854.
| Experiment 1 | Experiment 2 | Experiment 3 | Experiment 4 | |
|---|---|---|---|---|
| Test aspect | connectivity | reproducibility | Topographic regularity | Topographic regularity |
| Test metric | Tractometer (Côté et al., 2013) | Dice and ICC | MSE, R2, ITR | ITR |
| Tested algorithms | proposed, iFOD1, iFOD2, SD_STREAM | proposed | proposed, iFOD1, iFOD2, SD_STREAM | proposed, iFOD1, iFOD2, SD_STREAM |
| Dataset | FiberCup (MICCAI 2009 challenge data) | Traced (ISMRM 2017 challenge data) | 56 HCP subjects (3T dMRI) | 10 HCP subjects (3T dMRI) |
| Fiber bundle | whole phantom | 16 different bundles | visual pathway | motor pathway (CST) |
| Independent evaluations | (Côté et al., 2013), (Neher et al., 2014), (Fillard et al., 2011) | Traced website * | - | - |
For all datasets, we used our recent algorithm (Tran and Shi, 2015) to compute the FODs that are represented with 8th, 10th, 16th and 16th order spherical harmonics respectively for experiments 1 to 4, that are fully compatible with MRtrix.
We compared our technique against MRtrix’s iFOD1, iFOD2 and SD_STREAM algorithms. iFOD1 and iFOD2 algorithms are probabilistic techniques whereas SD_STREAM is a deterministic tractography algorithm.
3.1. Experiment 1: FiberCup
The FiberCup phantom was built based on the procedure introduced in (Poupon et al., 2008) and it was used in the MICCAI2009 tractography challenge (Fillard et al, 2011). The data is extensively studied and tested in several tractography papers for benchmarking purposes (Côté et al., 2013). The dMRI data for the FiberCup can be freely downloaded from http://www.tractometer.org/original_fibercup/data/. In our tests we used the average data with b-value 1500.
parameters are carefully chosen such that all techniques can successfully capture all the 7 bundles of the FiberCup phantom with low amount of false connections. However parameters are not optimized for any of the approaches. Because the elimination of the short streamlines can drastically change the results, we conducted two sets of evaluations addressing this issue. In one set, we did not remove any short tracks as adopted in (Côté et al., 2013). In another set, we removed the streamlines shorter than 20mm which was adopted in (Neher et ah, 2014). For the reconstruction of tractograms, we used the white matter mask provided with the phantom and uniformly seeded it to obtain 100 thousand streamlines for each technique.
Table 2:
Tractography parameters used for FiberCup experiments, vs is voxel size, ° is degree.
| Step (vs) | Angle | Cut-off | σT | σN | σB | σκ (1 / mm) | στ (1 / mm) | r(vs) | |
|---|---|---|---|---|---|---|---|---|---|
| Our Method | 0.0003 | 0.004 | 30° | 0.05° | 0.05° | 0.25 | 0.01 | 2 | |
| MRtrix3 iFOD2 | 0.1 | 25° | 0.0075 | ||||||
| MRtrix3 iFODl | 0.033 | 9° | 0.0075 | ||||||
| MRtrix3 SD_STREAM | 0.1 | 40° | 0.0075 |
Figure 8 shows the manually marked labels that are used to identify the 7 bundles shown with arrows in different colors. For visual evaluations on the crossings, we focused on the ~ 90° and ~ 70° crossing regions shown with green and red boxes respectively. For quantitative comparisons, we used the Tractometer evaluation (Côté et al., 2013) and reported the fraction of valid connections (VC), fraction of invalid connections (IC), fraction of no connections (NC) and bundle overlap (OL).
Figure 8:
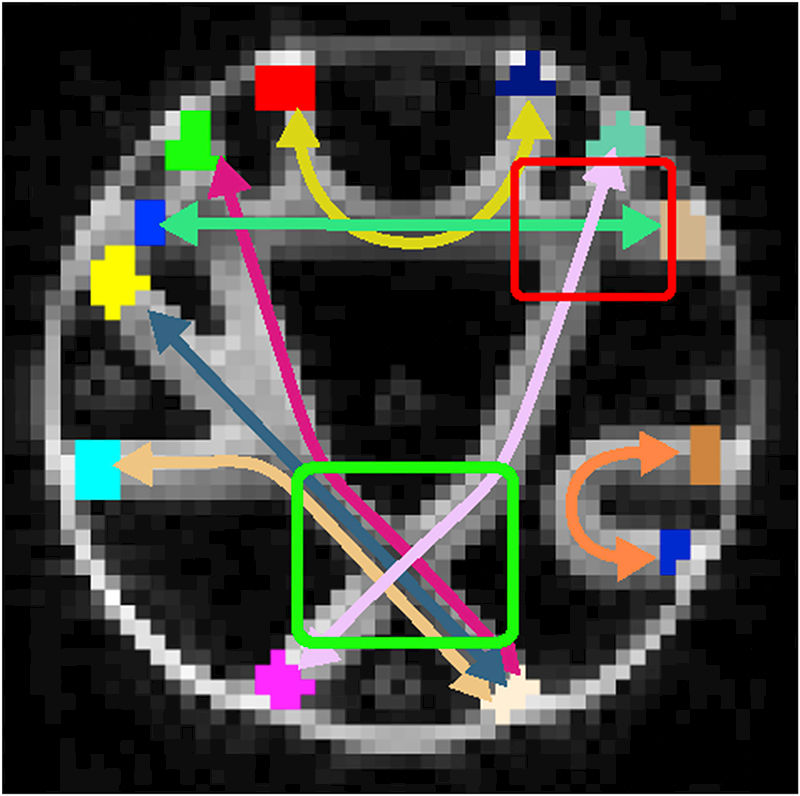
Arrows show the 7 different bundles of the FiberCup phantom. The manually marked labels are shown at the end of each arrow and they are used to identify the connections. For visual evaluations, we used the ~ 90° and ~ 70° crossings marked in green and red boxed respectively.
3.2. Experiment 2: Traced
In order to study the reproducibility of tractograms obtained using our approach, we conducted experiments on the Traced dataset which is used in the ISMRM 2017 tractography challenge. Traced contains 20 dMRI images of the same human subject. Images are collected using 2 scanners (Philips 3T) during 2 different sessions per scanner where 5 separate acquisitions are done in each session. A detailed description of the images as well as the dataset can be accessed through the challenge website (https://my.vanderbilt.edu/ismrmtraced2017/).
For all images, we obtained whole brain tractograms consisting of 1.25 million streamlines. All tractograms are obtained using the same parameters shown in Table 3.
Table 3:
Tractography parameters used for Traced experiments, vs is voxel size, ° is degree.
| Step (vs) | Cut-off | σT | σN | σB | σκ (1 / mm) | στ (1 / mm) | r(vs) | |
|---|---|---|---|---|---|---|---|---|
| Our Method | 0.002 | 0.04 | 60° | 0.8° | 0.8° | 0.5 | 0.25 | 1.5 |
In accordance with the challenge specifications, we extracted 16 fiber bundles from whole brain tractograms using manually drawn included and/or excluded ROIs (same ROIs are used for all images). The extracted bundles are left and right cingulum, fornix, inferior fronto-occipital fasciculus (IFO), inferior longitudinal fasciculus (IFL), superior longitudinal fasciculus (IFL), uncinate fasciculus and corticospinal tract (CST). Additionally forceps major and minor are extracted.
We used tract density images (TDI) (Calamante et al, 2010) of fiber bundles to assess the reproducibility of results. For quantitative tests, we obtained the intra-class correlation coefficient (ICC) and Dice similarity scores using the challenge submission system. ICC values are computed using the continuous TDI values, Dice scores are computed using the binary fiber bundle masks.
3.3. Experiment 3: Visual pathway
We studied the left visual pathways of 56 subjects from the HCP dataset (3T dMRI). We obtained the tractograms using unidirectional tracking starting from the LGN that is the seed and V1 that is the included ROI. The tractography parameters used to extract the visual pathways are given in Table 4. None of the parameter combinations are optimized. However, for each technique, separate adjustments are done so that Meyer’s loop can be captured. To achieve this, compared to the default MRtrix parameters, we used increased angle values. For the same purpose, we used a lower cut-off value for the SD_STREAM approach compared to the other techniques. 2000 streamlines were reconstructed by each technique.
Table 4:
Tractography parameters used for the visual pathway, vs is voxel size, ° is degree.
| Step(vs) | Angle | Cut-off | σT | σN | σΒ | σκ (1 / mm) | στ (1 / mm) | r(vs) | |
|---|---|---|---|---|---|---|---|---|---|
| Our Method | 0.001 | 0.04 | 60° | 1.25° | 1.25° | 0.25 | 0.25 | 2 | |
| MRtrix3 iFOD2 | 0.2 | 22° | 0.04 | ||||||
| MRtrix3 iFODl | 0.1 | 11° | 0.04 | ||||||
| MRtrix3 SD_STREAM | 0.1 | 60° | 0.02 |
LGN, V1 and the eccentricity values on V1 are computed using our previous technique proposed in (Kammen et al., 2016). This approach is based on (Benson et al., 2012, 2014) that is mentioned in section 2.2.1 and was used earlier to identify the sub bundles of the optic radiation (Kammen et al., 2016).
3.4. Experiment 4: Motor pathway
We studied the left and right motor pathways of 10 subjects from the HCP dataset (3T dMRI). We focused on the extraction of corticospinal tract (CST), in particular the part from the internal capsule (IC) to precentral gyrus (PCG). This part of the CST is topographically regular and it follows the somatotopic organization (Ruben et al, 2001). We obtained CST by unidirectionally tracking streamlines starting from IC to PCG. Figure 9 shows the location of the manually marked IC region. The PCG labels are obtained using Freesurfer (Fischl et al, 2002). The tractography parameters used to obtain the CST are given in Table 5. The parameters are not optimized for any of the techniques. They are adjusted such that each algorithm can capture a large portion of PCG while keeping their geometric regularity. For quantitative comparisons based on ITR, we used the end points of 2000 streamlines.
Figure 9:
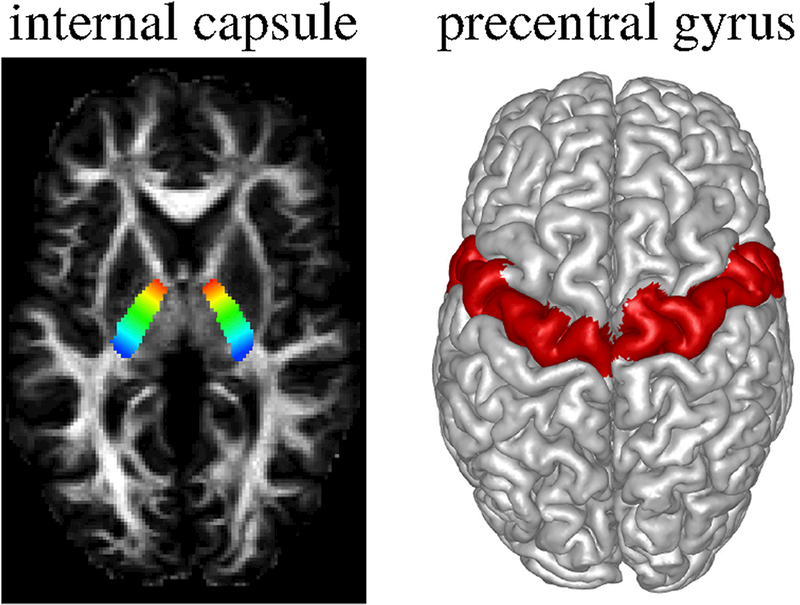
We focused on the CST, in particular the part from internal capsule (IC) to precentral gyrus (PCG). Left shows the manually marked seed region on IC. The ROI is shown with a color gradient from blue to red that is used to color code streamlines for clearer visualization. Right shows the PCG labels obtained using Freesurfer.
Table 5:
Tractography parameters used for the motor pathway, vs is voxel size, ° is degree.
| Step(vs) | Angle | Cut-off | σT | σN | σΒ | σκ (1 / mm) | στ (1 / mm) | r(vs) | |
|---|---|---|---|---|---|---|---|---|---|
| Our Method | 0.001 | 0.04 | 60° | 0.5° | 0.5° | 0.5 | 0.25 | 2 | |
| MRtrix3 iFOD2 | 0.5 | 45° | 0.04 | ||||||
| MRtrix3 iFODl | 0.1 | 9° | 0.04 | ||||||
| MRtrix3 SD_STREAM | 0.1 | 60° | 0.04 |
4. Results
4.1. Experiment 1: FiberCup
Figure 10 shows visual comparisons of iFODl, iFOD2 and the SDSTREAM techniques with the proposed approach on the FiberCup phantom. Tractograms are obtained using the parameters in Table 2. In order to keep the visualizations clear, approximately 600 random streamlines are shown using TrackVis (Wang et ah, 2007a). Short streamlines are not filtered for fair comparison. Each streamline segment is colored using the helix angle coloring for clear highlighting of cross sections.
Figure 10:
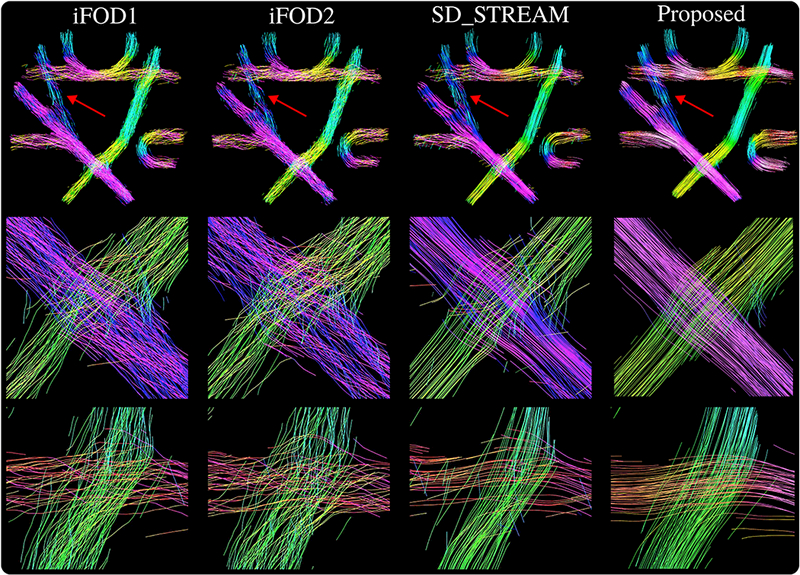
Visualizations of the streamlines reconstructed for the FiberCup data. Segments are colored using the helix angle coloring option of TrackVis. Each column shows results obtained using the technique indicated on top. Streamlines reconstructed with the proposed method visually look very well organized, even on noisy and challenging areas of the phantom shown with red arrows. While other techniques lose bundle organization, our approach successfully propagates through crossings as shown on the second and third rows.
In order to demonstrate that the geometrically and topographically organized bundles obtained with our approach is not due to the small step size, in Figure 11, we show iFODl results obtained with the same step size parameter used for our technique. For a fair comparison, to generate our results in Figure 11(c-d), we edited and recompiled our code so that each segment is saved instead of every 100th
Figure 11:
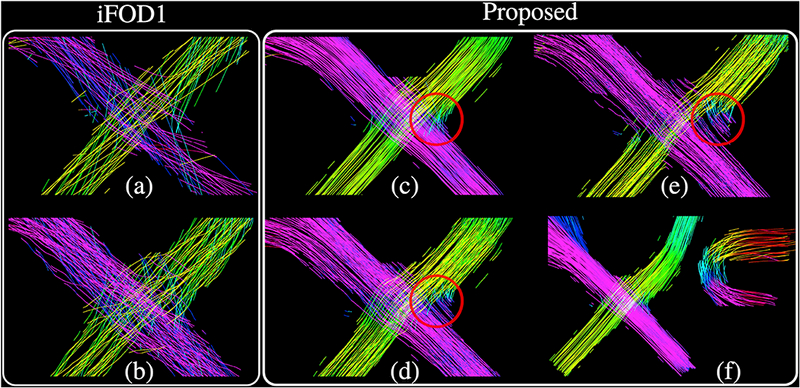
(a-b) show the iFODl results obtained with the same step size used for our approach (Table 2). For (a), an angle constraint of 0.058° is used ( 0.05° was not possible with MRtrix), that is comparable to the rotation of the tangent axis of the Frenet-Serret frame for our approach since we used σΝ = σΒ = 0.05°. For (b), an angle constraint of 0.5° is used, below which iFODl fails to capture all the bundles of the phantom. Notice that for both (a-b) a cut-off value of 0.0075 is used which is higher than the one used in our approach that is 0.004. (c-d) show the results obtained using the proposed approach after recompiling the code in order to write each segment instead of every 100th. (c) shows the results obtained using the parameters in Table 2. (d) shows the result when σΝ = σΒ = 0–5° for which the bundle organization starts to get lost in the circled areas, (e) Our approach is no more successful for increased σΝ =<σB = 2°. (f) shows the case when σΝ =<JB =0°. in which propagations are made mainly due to curvature and torsion variations. Although we obtain the most organized streamlines using this setting, our method fails to make the sharp turns. For (c,d,e,f), all other parameters are kept the same as shown in Table 2.
Overall iFOD1 and iFOD2 approaches visually are not found to reconstruct as well aligned streamlines as the SD_STREAM and the proposed approach. The deterministic SD_STREAM approach produces visually pleasing results; however the organization of the bundles are not as well preserved as the proposed approach which visually performed the best in FiberCup experiments. Quantitative comparisons of the algorithms are shown in Table 6. The deterministic SD STREAM approach performed remarkably better than the other approaches in IC ratio. The proposed approach on the other hand yielded exceptional values for the NC and VC ratios. The IC ratio for our approach is similar to iFODl’s. Best OL ratio was obtained by iFOD2 which also yielded the highest IC. Quantitative evaluations on the FiberCup data point out that the proposed approach brings the favorable aspects of deterministic and probabilistic techniques together.
Table 6:
Results of the FiberCup experiments. Best results are shown in bold. Columns show values for the fraction of no connections (NC), fraction of valid connections (VC), fraction of invalid connections (IC) and the overlap (OL) as proposed by the Tractometer evaluation protocol (Côté et al., 2013).
| NC (%) | VC (%) | IC (%) | OL (%) | |
|---|---|---|---|---|
| Results without removing the short streamlines | ||||
| iFODl | 89.9 | 8.6 | 1.5 | 94.7 |
| iFOD2 | 91.4 | 6.5 | 2 | 96.3 |
| SD_STREAM | 86.3 | 13.4 | 0.3 | 85.4 |
| Proposed | 77.1 | 21.3 | 1.6 | 89.8 |
| Results after removing the streamlines smaller than 20mm | ||||
| iFODl | 87.6 | 10.6 | 1.8 | 94.7 |
| iFOD2 | 89.3 | 8.2 | 2.5 | 96.3 |
| SD_STREAM | 82.4 | 17.3 | 0.3 | 85.4 |
| Proposed | 73.9 | 24.2 | 1.9 | 89.8 |
4.2. Experiment 2: Traced
Figure 12 shows example fiber bundles obtained using the Traced dataset. For visual evaluations, examples from both scanners are shown. In Figure 12, we visualized the results obtained using the first acquisition of the first session for both scanners.
Figure 12:
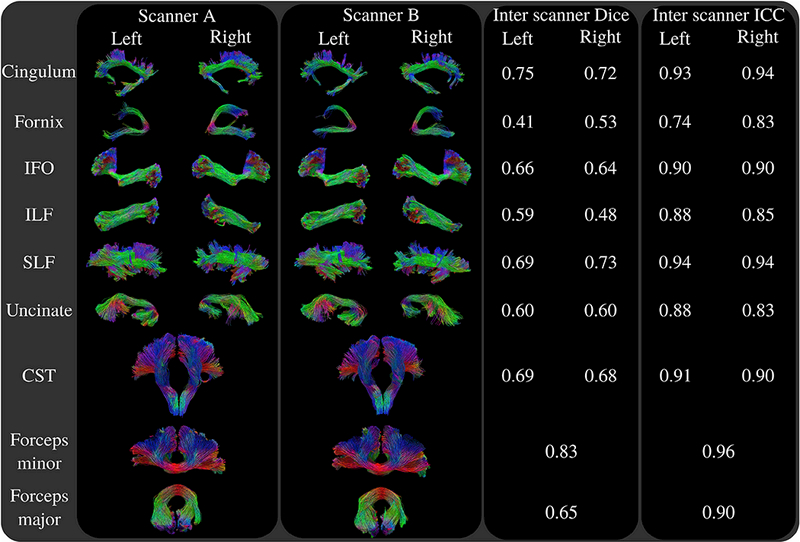
Results of the reproducibility tests using the Traced dataset. Visualizations of the fiber bundles in the first two columns show the results obtained with the first acquisition of the first sessionfor both scanners. Third and forth columns show the inter scanner Dice and ICC measures. Resultss how that our algorithm can successfully track challenging white matter connections and resolve fiber crossings for example in the frontal parts of SLF. While our technique is capable of tracking sharp turns as in the case of cingulum, fornix, uncinate and CST, it could also densely sample the fanning frontal parts of IFO, lateral projections of CST and forceps minor. On average, our technique obtained a Dice score of 0.64 and ICC of 0.89, ranking 2nd among 46 entries during the ISMRM 2017 tractography challenge.
The visualizations show that our technique is capable of tracking challenging white matter connections. Our approach successfully tracks sharp turns that are present in cingulum, fornix, uncinate and CST. Also fanning connections such as the frontal part of IFO and lateral projections of CST and forceps minor are densely sampled, and they are clearly observable in our results. Covering a large portion of the brain, many of the fiber bundles shown in the results have projections through crossing regions which were resolved by our algorithm. While our approach was able to track intricate white matter connections of the brain, the streamlines generated by our technique also visually look well organized which is important for studying topographic regularity.
On the other hand, nearly for all bundles, some differences are observable between the two scanners. Based on visual evaluation, fomix seems to be the most challenging fiber bundle in our tests. Also the streamlines extracted for uncinate fasciculus visually do not look as consistent as most other tested fiber bundles.
The inter scanner Dice and ICC values are written on the third and forth columns of Figure 12. Consistent with our visual evaluations, we obtained the poorest reproducibility for fomix whereas forceps minor, cingulum and SLF scored high Dice and ICC measures. The presented results obtained an average Dice score of 0.64 and ICC of 0.89 in the ISMRM 2017 tractography challenge, which ranked 2nd among 46 submissions.
4.3. Experiment 3: Visual pathway
Figure 13 shows the tractograms of the left optic radiation for four HCP subjects. Our approach successfully captures the Meyer’s loop while preserving highly organized trajectories. Meyer’s loop is not obtained well enough with other techniques. Especially, we were not able to clearly obtain the Meyer’s loop using the deterministic tractography algorithm SD_STREAM. Also as the streamlines approach V1, we observe that the probabilistic results from iFODl and iFOD2 start to lose their topographical organization.
Figure 13:
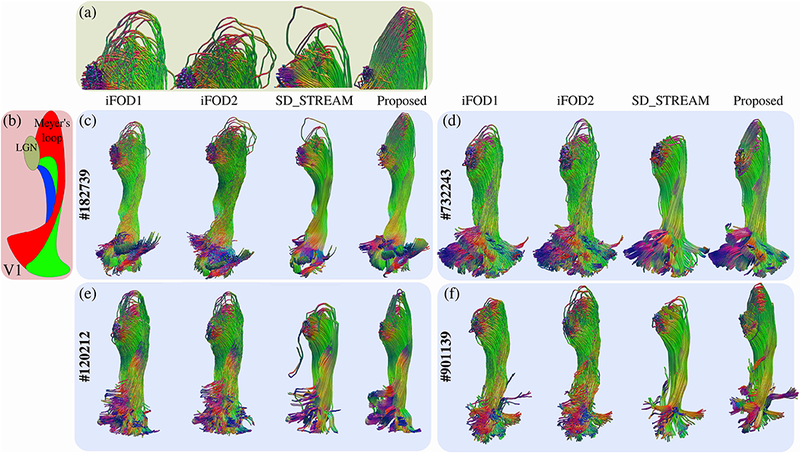
Optical pathways obtained for four of the subjects. The HCP subject ids are indicated on the left of each case in (c-f). A schematic based on the dissection study in (Párraga et al., 2012) is shown in (b) in order to point the approximate locations of LGN, Meyer’s loop and V1. Red, green and blue colors show the anterior, central and dorsal bundles respectively, (a) shows close-up images for the Meyer’s loop of subject #182739. The corresponding algorithm for each tractogram is indicated on top of each example. For all subjects, SDSTREAM fails to properly capture the Meyer’s loops. iFODl and iFOD2 while partially capturing the Meyer’s loops, lose their topographic organization during their propagation towards V1. Our technique successfully captures the Meyer’s loops for all subjects, at the same time, it preserves the topographic alignment. Tractograms are colored based on segment orientations. Red, green and blue tones are used for left-right, anterior-posterior and inferior-superior directions respectively.
Figure 14 (a) shows visualizations and quantitative measures for topographic organization assessed using the quality of fit measures of eccentricity as explained in section 2.2.1. Results show very organized eccentricity values associated with streamlines obtained using our technique. Visually iFODl and iFOD2 produce similar results with similar quantitative measures. SD STREAM approach, although yields better R2 and ITR values, its MSE is higher and visually the eccentricity values do not look well organized. All the quantitative measures obtained for our technique are consistent with the visual quality of the organization of the eccentricity values.
Figure 14:
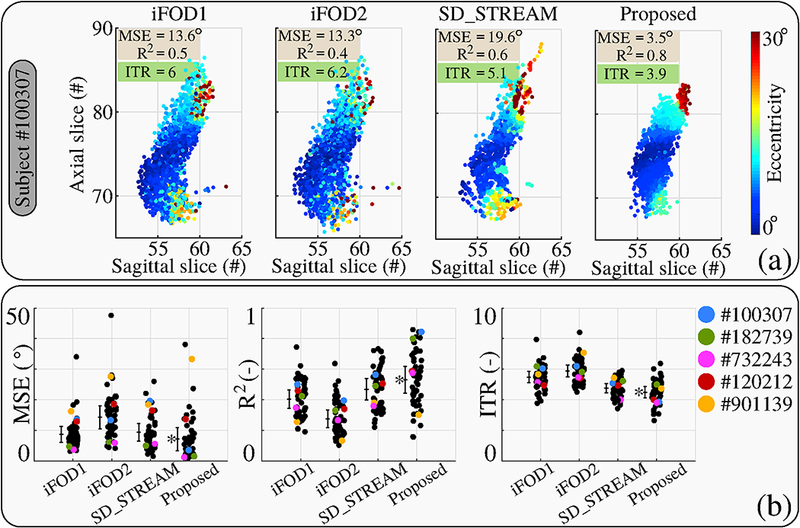
(a) Eccentricity values along the cut plane (explained in Figure 5) are shown for each technique for HCP subject #100307. The quality of quadratic fit measures (MSE and R2 ) along with the ITR are written on upper left comers. Color coded eccentricity values are most organized for the tractogram obtained by our technique, all quantitative measures are also consistent with this visual observation, (b) shows the results for all the subjects. Subject #100307 is shown with blue color. Four subjects whose optical pathways are visualized in Figure 13 are also shown in different colors. Lengths of bars for each technique show the standard deviation. The middle lines of the bars indicate the mean value. Best results are shown with a (*).
Figure 14 (b) shows the results for all 56 subjects. The dots above each technique represent different subjects. HCP subject #100307 is shown separately with blue color since this subject is used to explain our quantitative evaluation approach. Subjects #182739, #732243, #120212, #901139 are also shown in different colors since the optical pathways belonging to these subjects are visualized in Figure 13. The lengths of bars shown for each technique indicate the standard deviation among subjects. The lines in the middle of the bars show the mean value. The technique with the best score is marked with a (*) next to its bar.
Based on all three quantitative measures, the proposed approach performs the best in preserving the topographic regularity of the visual pathway. iFOD2 algorithm performs the poorest among the four techniques that were tested. The quantitative results obtained using ITR measure are consisted with MSE and R2.
4.4. Experiment 4: Motor pathway
Figure 15 shows side by side visual comparisons of the CST tractograms obtained using iFODl, iFOD2, SDSTREAM and our technique. Each streamline is assigned a color that matches their projection on the internal capsule as shown in Figure 9. We observe that except the SD_STREAM algorithm, all tested techniques are able to generate streamlines projecting to a large part of PCG. Compared to iFODl and iFOD2 algorithms, SD STREAM and our algorithm generate more organized streamlines.
Figure 15:
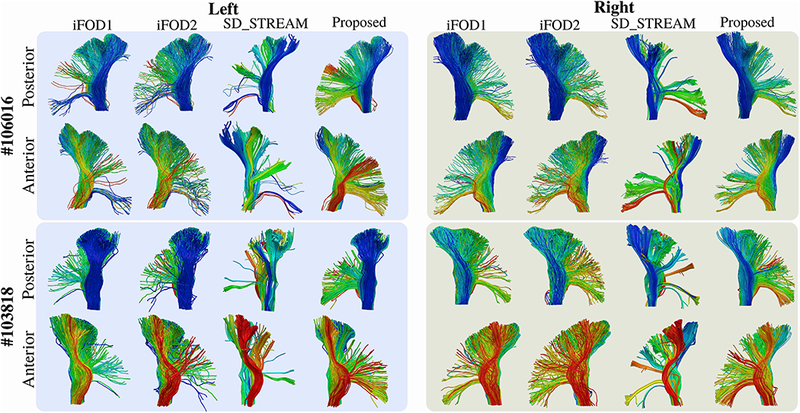
The extracted left and right CST tractograms for HCP subjects #106016 and #103818 are shown from anterior and posterior views. For all tractograms, the corresponding algorithm is indicated on top. SD_STREAM results visually look organized, however they fail to generate streamlines for a large portion of PCGs. Tractograms computed by iFODl and iFOD2 techniques do not look organized. Our approach was capable of generating organized streamlines which also project to large areas of PCGs.
In Figure 6 we graphically showed how ITR is computed. Figure 16 (a) shows the actual results for each step obtained for the left CST of subject #106016. Figure 16 (b) shows the ITR values computed for all the left and right CST tractograms. Each dot indicate a different subject. The values for subjects #106016 and #103818 are shown in different colors since the CSTs for these subjects are visualized in Figure 15. The lengths of the bars indicate the standard deviation and the middle lines on the bars show the mean values. The best average ITR scores for left and right are shown with a (*).
Figure 16:
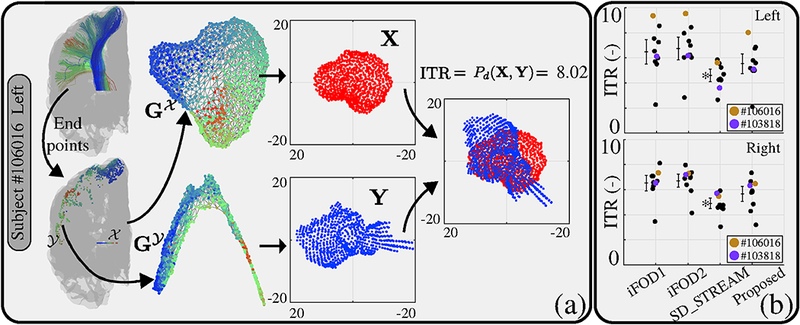
(a) Demonstration of each step of ITR explained in section 2.2.2. Given atractogram, the end points of each streamline, and , on two 2-manifolds are marked. The Delaunay triangulations, and are obtained. After MDS, procrustes distance is assigned as ITR. (b) ITR values for all individuals are shown separately with dots. Bars indicate standard deviations and the middle lines on the bars show the mean values. The best scoring technique is marked with a (*).
Quantitatively our method scored between the deterministic and the probabilistic approaches. While SD STREAM yielded the highest ITR score, qualitative results on Figure 15 show that this approach is not successful in reconstructing a large amount of the projections on PCG. Similar to the results obtained for the visual pathway experiments, iFOD2 performed the poorest in our CST tests as well.
5. Discussions and Conclusion
Topographic organization of the brain’s connections is a fundamental structural property (Patel et al, 2014). This intriguing structural organization of the brain has been studied in numerous earlier studies using dMRI and tractography (Wedeen et al, 2012; Jbabdi et al., 2013b; Lee et al, 2015). However, it has not been utilized well for extracting streamlines. Our goal in this study is to leverage this very underused feature of the brain and formulate a new tractography technique that respects the integral structural properties of the connections.
The recent trend towards quantitative tractography aims to solve the local microstructure problem while generating consistent streamlines globally forthe whole brain (Daducci et al, 2016). Unlike recent solutions such as (Reisert et al, 2014), our technique decouples these two problems. Similar to earlier techniques, we start with the already analyzed microstructure which provides FODs (Tran and Shi, 2015). Although we did not study in this work, methods like SIFT2 (Smith et al, 2015), COMMIT (Daducci et al, 2015) and LiFE (Pestilli et al, 2014; Takemura et al, 2016) can also be used with the streamlines generated by our technique for quantitative tractography.
Our technique employs two independent mechanisms for propagation. The first mechanism ensures that the streamlines are geometrically regular. Tractography techniques although typically employ constraints for geometric regularity, a significant majority of the algorithms achieve this by limiting the angle between consecutive steps and optionally adding Euler’s or Runge-Kutta’s method for additional regularity (Basser et ah, 2000). This approach is applied in almost all of the commonly used propagation based deterministic and probabilistic techniques such as the algorithms in popular tractography softwares like MRtrix (Tournier et al, 2012, 2010), ExploreDTI (Leemans et ah, 2009), DSI Studio (Yeh et al., 2013), Camino (Seunarine et al., 2007; Whitcher et al., 2008), TrackVis (Wang et al., 2007b), 3DSlicer (Malcolm et al., 2010) as well as the global techniques like the Gibbs tracker (Reisert et al., 2011). Many other newer algorithms have also adopted similar strategies (Feng and Wang, 2011; Vorburger et al, 2013; Ye et al, 2016; Ye and Prince, 2017). Our approach radically differs from these techniques because it does not assume that streamlines are locally straight. To the best of our knowledge, Frenet-Serret frame is used for the first time in the core of the tracking algorithm to ensure geometric regularity. Arc length parameterized streamlines have been previously used in a Hough transform based tractography algorithm (Aganj et al., 2011). Similar to our approach, this technique is also capable of generating geometrically very regular streamlines. However, in this study authors used a parameterization based on polynomial approximations whereas we used a more general parameterization based on a first order system of ODE. The five independent variance parameters in our technique that are used to control streamline geometry allow a much higher degree of freedom for propagation compared to other approaches.
In our technique, additional to ensuring geometric regularity, a second mechanism is used to propagate along topographically regular pathways by incorporating neighborhood information. It was shown earlier in (Savadjiev et al., 2008) that neighborhood information can be used to identify bundle architectures. Using the data support for helical curves, (Savadjiev et al., 2006) devised a technique to distinguish curving or fanning structures. In (Rowe et al., 2013), authors proposed a tractography technique based on particle filtering that weighs candidate streamlines according to local data support and neighborhood informed fODFs from the local dispersion estimates. In this approach, neighborhoods are explored with streamlines along varying trajectories. In contrast, we evaluate the data support for a set of parallel curves, that is inspired from the underlaying topographically regular nature of fiber bundles. Our technique also differs from approaches that aim for directional smoothing or regularization using neighborhood information, such as (Reisert and Kiselev, 2011). Unlike our approach, these techniques assume that neuronal fibers are locally straight and they do not take into account local curvature and torsion. Our technique on the other hand only assumes that connections are locally smooth. This takes into account different curves with varying curvatures and torsions which share the same direction or tangent.
Curves can be parametrized in many ways. For our work we chose to work with the Frenet-Serret frame since this parametrization supports parallel curves without the need to introduce any other additional mathematical concepts. More critically, the tangents necessary to compute the likelihood expression can be analytically obtained using a Frenet-Serret frame representation as shown in Appendix B. The analytical solution allows us to use the same integration points to compute likelihoods of candidates. With this benefit, Frenet-Serret frame requires the costly FOD interpolations to be done only once at each step. Therefore, although simpler parameterizations such as splines can have advantages for tracking geometrically regular streamlines, their extension to support topographic regularity is not as trivial as the Frenet-Serret frame’s.
For the rotation of the Frenet-Serret frame, we chose the Tait-Bryan approach because the angular deviations that are required from the user are simple and intuitive to set, i.e: first, second and third rotations are done around , and respectively, which are the same as roll, pitch and yaw maneuvers used in aircrafts. Because the rotations are done intrinsically, i.e.: axes of rotations are bound to the moving body, our 3D rotation does not suffer from gimbal locks. The three elementary rotations shown in Figure 3 are implemented using quaternions.
An additional goal of our work was to devise techniques to quantify topographic regularity. For that purpose, we proposed two different approaches, the first one is based on the known retinotopic mapping of the visual pathway. The other approach, ITR, is purely based on the geometric properties of the streamlines. The two approaches are fundamentally different. Both techniques showed that our tractograms are more topographically regular compared to the other two probabilistic techniques. We could not find any other method in the literature that is developed to quantify topographic regularity of tractograms. Because it is a fundamental property of the brain’s connections, we believe it is important to have quantitative measures for topographic regularity which we will work on more in the future.
In an earlier work, we had proposed an approach to quantify topographic regularity of individual streamlines using spectral graph theory and tensor decomposition (Wang et al, 2017). This approach takes into the account the propagation of streamlines together with their neighbors which are obtained based on a distance parameter. We proposed to use this technique to filter out topographically irregular streamlines. In contrast, the ITR measure quantifies the topographic regularity of a tractogram (set of streamlines) that connects two surfaces (2-manifolds). It is important to note that ITR also does not suffer from any parameter biases since it does not require any inputs other than the corresponding end points of the tractogram on the two connected surfaces. From Figure 14(b), we observe that ITR provides consistent topographic organization information with MSE and R2 which are obtained using retinotopic mapping.
We compared our tractography algorithm against popular deterministic and probabilistic techniques that are included in the MRtrix3 suite. Extensive benchmarking of our results against other techniques such as global tractography is not within the scope of our current work, however, are planned to be done in the future.
In our experiments, we tested our algorithm with respect to “connectivity”, “reproducibility” and “topographical regularity”. In order to evaluate the connectivity aspect, we chose to work with the original FiberCup phantom since it is very well known and used in several other previous studies. Both qualitative and quantitative evaluations show very promising results favoring our approach. (Côté et al., 2013) conducted extensive studies on the FiberCup data featuring over 50 thousand experiments. The results shown on the upper part of Table 6 are obtained using the same approach and are comparable to the values obtained by these authors. As (Côté et al., 2013) demonstrated, with different parameter combinations, individual scores for NC, VC, IC and OL can be optimized. Our goal in this study was to obtain adequate results for each measure rather than focusing on one of them. An extensive study on the determination of the best parameter combination for each measure is not in the scope of our work. Overall our approach performed the best in NC and VC measures while scoring similar to the other probabilistic approaches with respect to the IC measure. Additionally many authors such as (Neher et al, 2014) prefer to remove the short streamlines when studying the FiberCup phantom. In order to provide our results for this case, we provided the lower half of Table 6 for interested readers.
We studied the ISMRM 2017 tractography challenge dataset in order to test the reproducibility of our approach. Notice that this challenge compared images that contain probabilities of fiber bundles for each voxel. Streamlines themselves were not submitted nor qualitatively compared during the challenge. The fiber bundles in Figure 12 visualize the streamlines from our submission which were not shown prior to this study. With average Dice score of 0.64 and ICC of 0.89, our results quantitatively ranked 2 nd during the challenge among 46 submissions.
We conducted two sets of experiments in order to study topographic regularity, one using the visual and the other using the motor pathway. The seed and included ROIs were obtained automatically for the visual pathway experiments. The seed ROIs for the motor pathway however were manually marked. Therefore we used a limited number of subjects for these experiments. For quantitative comparisons, we took a different approach than the one chosen for the FiberCup and Traced studies. This is because we focused only on the reconstruction of individual bundles and their topographic regularity. All quantitative results for the visual pathway favored our technique. Although SDSTREAM quantitatively performed better in motor pathway experiments, this approach was not able to generate streamlines that cover large portions of PCGs unlike all the other techniques. We believe this highlights the importance of visual inspection while evaluating the quality of tractograms.
Overall our experiments point out some interesting properties of our technique. For the FiberCup experiments, our approach yielded an overlap ratio (OL) that is between the probabilistic and deterministic techniques. Coincidentally, we visually observe in Figure 14 that the end points obtained with our approach look tighter compared to probabilistic techniques and they also seem more clustered similar to the deterministic SD STREAM approach. Previous studies show that deterministic techniques tend to cover limited parts of fiber bundles resulting in high ratios of false negatives (Côté et al., 2013). We believe this is partly because deterministic approaches mainly follow peaks and do not address local uncertainty during propagation. On the other hand, while probabilistic techniques are able to sample challenging pathways, they tend to oversample and generate large numbers of false positives (Maier-Hein et al., 2017). Our experiments show that the proposed approach provides a balanced compromise between deterministic (SD_STREAM) and probabilistic techniques (iFOD1, iFOD2) when addressing the uncertainty. The results show that our method not only can generate highly organized streamlines similar to deterministic techniques but it can also sample challenging ones akin to probabilistic methods.
Our tracker geometrically has a very large degree of freedom for maneuverability since each segment is parametrized using three orthonormal vectors, together with a curvature and torsion value. This however comes with the downside of increased number of input parameters. We believe the flexibility during propagation enables our tracker to make very sharp turns and sample intricate connections. At the same time, by taking into account large neighborhoods during propagation, we think our approach mitigates noise effects that enables tracking of smooth looking curves. This can be visually observed in Figure 10 plotted for the FiberCup experiments. We believe this also has a role in decreasing NC and increasing VC that are shown in Table 6. The relatively low OL obtained with our technique (in comparison to probabilistic approaches) might be due to the noise in the dataset which locally reduces topographic regularity thus our likelihood function. Although for our approach OL could be increased by decreasing the neighborhood dimension or the cut-off parameter, we expect this to come with a cost of increased NC, increased FP and decreased VC. Based on our experiments, we observe that a neighborhood size of one to two times the voxel dimension produces robust and adequate results. Although using small values is possible with our algorithm, this would reduce the benefit of leveraging topographic regularity. On the other hand, very large values may hinder tracking of intricate connections since neighboring larger bundles can dominate the likelihood function. Although we have not observed any clear problems at fiber crossing, fanning or diverging regions, we believe a large neighborhood dimension may lead to early termination of streamlines close to grey-white matter interface where data support for propagation is lower.
Our current implementation is written in MATLAB and C++. Our code is not yet optimized. It generally takes several hours to populate a few thousands streamlines, which we are working on, by improving our implementation and the algorithm. Although our technique uses more parameters compared to conventional algorithms, they are intuitive and their effects are easy to anticipate.
In summary, a novel probabilistic tractography technique that captures the topographic organization of fiber bundles is developed in this study. We used parallel curves to examine the local fitting of streamlines to the underlaying field of FODs while preserving geometric regularity using parameterized curves with a Bayesian framework. Using tractograms obtained with datasets featured in international tractography challenges, we studied our technique with respect to connectivity and reproducibility aspects. Additionally, we performed experiments with the visual and motor pathways of subjects from the HCP dataset. We conducted qualitative and quantitative evaluations and showed that our method is able to generate very organized streamlines while capturing geometrically challenging connections.
Acknowledgment
This work was in part supported by the National Institute of Health (NIH) under grants R01EB022744, U01EY025864, P41EB015922, P50AG005142, U01AG051218, R01AG025340.
Appendix
A. Solution to Frenet-Serret equations
The Frenet-Serret equations are a first order ODE system given as:
| (A.1) |
The eigenvalues and eigenvectors of matrix A are as follows:
| (A.2) |
where . Note that in this case the duplicate eigenvalue λ3 = λ4 = 0 is defective thus we set v4 as:
| (A.3) |
Then the solution for the ODE system is:
| (A.4) |
Given the initial condition, x(x = 0), the coefficients (C1. C2, C3 and C4, can be computed as follows:
| (A.5) |
Notice that λ, v1 and ( C1 are complex conjugates of λ2. v2 and C2 respectively. From the basic identity that (a+ib)eix+(a−ib)e−ix = 2acos(x)−2bsin(x), it follows that:
| (A.6) |
7. Finding tangents at integration points
All integration points lay along parallel curves. Let y be a random parameterized curve and γ‖ be the parallel curve that the integration point p = γ‖(s) lays on. By definition, y and γ‖ have the same T, N, B, K, τ, , and C4. However their C3 are not same. Because γ‖(0) = γ(0) + aB + bN (by the definition of parallel curves), C3 for γ‖ is aB + bN more than of γ’s. Then using Equations F.5 and F.6, γ‖ can be expressed as:
| (B.1) |
This is a non-linear system of 3 equations with 3 unknowns, s, a and b; which can be expanded into:
| (B.2) |
where the x, y and z components are separated. After expressing a and b in terms of Fx (.s), Fz (.s) and Fz (.v) (steps are not shown since it is lengthy and straightforward), the following can be obtained:
| (B.3) |
using Equations A.5 and B.l this further reduces to:
| (B.4) |
where D = d1(C3x − px) + d2(C3y − py) + d3(C3z − pz). For Equation B.4 we obtain a fast estimate to sβ by using a 3rd order polynomial approximation of sin ( sβ) . Fastly we compute the tangents by plugging sβ in Equation A.6.
8. Contribution of curvature to prior probability
In our algorithm, we mapped curvatures, κ, to angles using the function ψ(κ) = asin (κ). With this mapping, curvature contributes to prior probability using the following expression, , instead of . Notice that the latter produces close results and it is also a valid choice. We however preferred to use Ψ (κ), because the curve with curvature κ = sin (α), intersects a circle with radius 2mm (currently hard-coded in our implementation) at a radians, i.e: evenly spaced angles, yield evenly spaced intersection points that are comparable, thereby linearizing the affect of varying curvature. This is not the case when curvature itself is linearly varied which is explained graphically in Figure 17. Notice that the effect of torsion is incorporated separately in the prior term and not included here.
Figure 17:
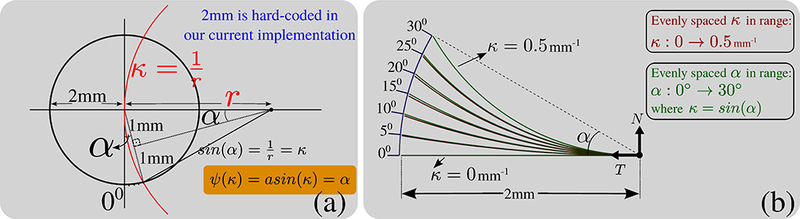
Graphical explanation of the function ψ (κ). (a) shows the relationship between κ and a using a red curve with radius of curvature r. (b) Curves in red color show the case for evenly spaced κ. Curves in green show when α = ψ (κ) is evenly spaced. Notice that green curves exactly intersect at corresponding angles whereas red ones are close but do not exactly match the angles.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aganj I, Lenglet C, Jahanshad N, Yacoub E, Harel N, Thompson PM, Sapiro G, 2011. A Hough transform global probabilistic approach to multiple-subject diffusion MRI tractography. Medical Image Analysis 15, 414–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arcaro MJ, Pinsk MA, Kästner S, 2015. The Anatomical and Functional Organization of the Human Visual Pulvinar. Journal of Neuroscience 35, 9848–9871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axer M, Amunts K, Grssel D, Palm C, Dämmers J, Axer H, Pietrzyk U, Zilles K, 2011. A novel approach to the human connectome: Ultra-high resolution mapping of fiber tracts in the brain. Neuroimage 54, 1091–1101. [DOI] [PubMed] [Google Scholar]
- Aydogan DB, Jacobs R, Dulawa S, Thompson SL, Francois MC, Toga AW, Dong H, Knowles JA, Shi Y, 2018. When tractography meets tracer injections: a systematic study of trends and variation sources of diffusion-based connectivity. Brain Structure and Function , 1–18URL: https://link.springer.com/article/10.1007/s00429-018-1663-8, doi: 10.1007/s00429-018-1663-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aydogan DB, Shi Y, 2016. Probabilistic Tractography for Topographically Organized Connectomes, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer International Publishing, pp. 201–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bach M, Fritzsche KH, Stieltjes B, Laun FB, 2014. Investigation of resolution effects using a specialized diffusion tensor phantom. Magnetic Resonance in Medicine 71,1108–1116. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A, 2000. In vivo fiber tractography using DT-MRI data. Magnetic Resonance in Medicine 44, 625–632. [DOI] [PubMed] [Google Scholar]
- Behrens T, Woolrich M, Jenkinson M, Johansen-Berg H, Nunes R, Clare S, Matthews P, Brady J, Smith S, 2003. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magnetic Resonance in Medicine 50, 1077–1088. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Berg HJ, Jbabdi S, Rushworth MFS, Woolrich MW, 2007. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage 34, 144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Brainard DH, Aguirre GK, 2014. Correction of Distortion in Flattened Representations of the Cortical Surface Allows Prediction of Vl-V3 Functional Organization from Anatomy. PFOS Computational Biology 10, el003538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Datta R, Radoeva PD, Brainard DH, Aguirre GK, 2012. The retinotopic organization of striate cortex is well predicted by surface topology. Current biology: CB 22,2081–2085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besseling R, Jansen J, Overvliet G, Vaessen M, Braakman H, Hofman P, Aldenkamp A, Backes W, 2012. Tract specific reproducibility of tractography based morphology and diffusion metrics. PLoS ONE 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjrnemo M, Brun A, Kikinis R, Westin CF, 2002. Regularized Stochastic White Matter Tractography Using Diffusion Tensor MRI, in: Medical Image Computing and Computer-Assisted Intervention MICCAI 2002, Springer, Berlin, Heidelberg: pp. 435–442. [Google Scholar]
- Calabrese E, Badea A, Cofer G, Qi Y, Johnson GA, 2015. A Diffusion MRI Tractography Connectome of the Mouse Brain and Comparison with Neuronal Tracer Data. Cerebral Cortex 25, 4628–4637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calamante F, Tournier JD, Jackson GD, Connelly A, 2010. Track-density imaging (TDI): Super-resolution white matter imaging using whole-brain track-density mapping. Neuroimage 53, 1233–1243. URF:http://linkinghub.elsevier.com/retrieve/pii/S1053811910009766, doi: 10.1016/j.neuroimage.2010.07.024. [DOI] [PubMed] [Google Scholar]
- Campbell JSW, Momayyez Siahkal P, Savadjiev P, Feppert IR, Siddiqi K, Pike GB, 2014. Beyond crossing fibers: bootstrap probabilistic tractography using complex subvoxel fiber geometries. Brain Imaging Methods 5, 216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell JSW, Savadjiev P, Siddiqi K, Pike GB, 2006. Validation and regularization in diffusion MRI tractography, in: 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro, 2006, pp. 351–354. [Google Scholar]
- Campbell JSW, Siddiqi K, Rymar VV, Sadikot AF, Pike GB, 2005. Flow-based fiber tracking with diffusion tensor and q-ball data: Validation and comparison to principal diffusion direction techniques. Neuroimage 27, 725–736. [DOI] [PubMed] [Google Scholar]
- Chen H, Liu T, Zhao Y, Zhang T, Li Y, Li M, Zhang H, Kuang H, Guo L, Tsien JZ, Liu T, 2015. Optimization of large-scale mouse brain connectome via joint evaluation of DTI and neuron tracing data. Neuroimage 115, 202–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung K, Deisseroth K, 2013. CLARITY for mapping the nervous system. Nature Methods 10, 508–513. [DOI] [PubMed] [Google Scholar]
- Conturo TE, Lori NF, Cull TS, Akbudak E, Snyder AZ, Shimony JS, McKinstry RC, Burton H, Raichle ME, 1999. Tracking neuronal fiber pathways in the living human brain. Proceedings of the National Academy of Sciences 96, 10422–10427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Côté MA, Girard G, Bor A, Garyfallidis E, Houde JC, Descoteaux M, 2013. Tractometer: Towards validation of tractography pipelines. Medical Image Analysis 17, 844–857. [DOI] [PubMed] [Google Scholar]
- Daducci A, Dal Pal A, Descoteaux M, Thiran JP, 2016. Microstructure informed tractography: pitfalls and open challenges. Brain Imaging Methods 10, 247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daducci A, Dal Palu A, Lemkaddem A, Thiran JP, 2015. COMMIT: Convex Optimization Modeling for Microstructure Informed Tractography. IEEE Transactions on Medical Imaging 34, 246–257. [DOI] [PubMed] [Google Scholar]
- Dauguet L, Peled S, Berezovskii V, Delzescaux T, Warfield SK, Bom R, Westin CF, 2007. Comparison of fiber tracts derived from in-vivo DTI tractography with 3d histological neural tract tracer reconstruction on a macaque brain. Neuroimage 37, 530–538. [DOI] [PubMed] [Google Scholar]
- Descoteaux M, Deriche R, Knosche TR, Anwander A, 2009. Deterministic and Probabilistic Tractography Based on Complex Fibre Orientation Distributions. IEEE Transactions on Medical Imaging 28, 269–286. [DOI] [PubMed] [Google Scholar]
- Donahue CJ, Sotiropoulos SN, Jbabdi S, Hernandez-Femandez M, Behrens TE, Dyrby TB, Coalson T, Kennedy H, Knoblauch K, Essen DCV, Glasser MF, 2016. Using Diffusion Tractography to Predict Cortical Connection Strength and Distance: A Quantitative Comparison with Tracers in the Monkey. The Journal of Neuroscience 36, 6758–6770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel SA, Glover GH, Wandell BA, 1997. Retinotopic organization in human visual cortex and the spatial precision of functional MRI. Cerebral Cortex 7, 181–192. [DOI] [PubMed] [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E, 2010. Multiplexed Echo Planar Imaging for Sub-Second Whole Brain FMRI and Fast Diffusion Imaging. PLoS ONE 5, e15710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Y, Wang Z, 2011. Ant Colony Optimization for Global White Matter Fiber Tracking, in: Tan Y, Shi Y, Chai Y, Wang G (Eds.), Advances in Swarm Intelligence. Springer; Berlin Heidelberg: number 6728 in Lecture Notes in Computer Science, pp. 267–276. [Google Scholar]
- Ferizi U, Schneider T, Panagiotaki E, Nedjati-Gilani G, Zhang H, Wheeler-Kingshott CAM, Alexander DC, 2014. A ranking of diffusion MRI compartment models with in vivo human brain data. Magnetic Resonance in Medicine 72, 1785–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fieremans E, Deene YD, Delputte S, zdemir MS, Achten E, Lemahieu I, 2008. The design of anisotropic diffusion phantoms for the validation of diffusion weighted magnetic resonance imaging. Physics in Medicine and Biology 53, 5405. [DOI] [PubMed] [Google Scholar]
- Fillard P, Descoteaux M, Goh A, Gouttard S, Jeurissen B, Malcolm J, Ramirez-Manzanares A, Reisert M, Sakaie K, Tensaouti F, Yo T, Mangin JF, Poupon C, 2011. Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom. Neuroimage 56, 220– 234. [DOI] [PubMed] [Google Scholar]
- Fillard P, Poupon C, Mangin JF, 2009. A Novel Global Tractography Algorithm Based on an Adaptive Spin Glass Model, in: Yang GZ, Hawkes D, Rueckert D, Noble A, Taylor C (Eds.), Medical Image Computing and Computer-Assisted Intervention MICCAI 2009. Springer; Berlin Heidelberg, number 5761 in Lecture Notes in Computer Science, pp. 927–934. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM, 2002. Whole Brain Segmentation: Automated Labeling of Neuroanatomical Structures in the Human Brain. Neuron 33,341–355. [DOI] [PubMed] [Google Scholar]
- Friman O, Farneback G, Westin CF, 2006. A Bayesian approach for stochastic white matter tractography. IEEE Transactions on Medical Imaging 25, 965–978. [DOI] [PubMed] [Google Scholar]
- Garyfallidis E, Brett M, Amirbekian B, Rokem A, Van Der Walt S, Descoteaux M, Nimmo- Smith I, 2014. Dipy, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics 8 URL: http://journal.frontiersin.org/article/10.3389/fninf.2014.00008/full , doi: 10.3389/fninf.2014.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard G, Whittingstall K, Deriche R, Descoteaux M, 2014. Towards quantitative connectivity analysis: reducing tractography biases. Neuroimage 98, 266–278. [DOI] [PubMed] [Google Scholar]
- Gössl C, Fahrmeir L, Ptz B, Auer LM, Auer DP, 2002. Fiber Tracking from DTI Using Linear State Space Models: Detectability of the Pyramidal Tract. Neuroimage 16, 378–388. [DOI] [PubMed] [Google Scholar]
- Hageman NS, Toga AW, Narr KL, Shattuck DW, 2009. A Diffusion Tensor Imaging Tractography Algorithm Based on Navier Stokes Fluid Mechanics. IEEE Transactions on Medical Imaging 28, 348–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagmann P, Thiran JP, Jonasson L, Vandergheynst P, Clarke S, Maeder P, Meuli R, 2003. DTI mapping of human brain connectivity: statistical fibre tracking and virtual dissection. Neuroimage 19, 545–554. [DOI] [PubMed] [Google Scholar]
- van den Heuvel MP, de Reus MA, Feldman Barrett L, Scholiens LH, Coopmans FM, Schmidt R, Preuss TM, Rilling JK, Li L, 2015. Comparison of diffusion tractography and tracttracing measures of connectivity strength in rhesus macaque connectome. Human Brain Mapping 36, 3064–3075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes G, 1918. Disturbances of vision by cerebral lesions. Br. J. Ophthalmol 2, 353–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iturria-Medina Y, Canales-Rodrguez EJ, Melie-Garca L, Valds-Hernndez PA, Martnez- Montes E, Alemn-Gmez Y, Snchez-Bomot JM, 2007. Characterizing brain anatomical connections using diffusion weighted MRI and graph theory. NeuroImage 36, 645–660. [DOI] [PubMed] [Google Scholar]
- Jackowski M, Kao CY, Qiu M, Constable RT, Staib LH, 2005. White matter tractography by anisotropic wavefront evolution and diffusion tensor imaging. Medical Image Analysis 9, 427–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansons KM, Alexander DC, 2003. Persistent angular structure: new insights from diffusion magnetic resonance imaging data. Inverse Problems 19, 1031. [DOI] [PubMed] [Google Scholar]
- Jbabdi S, Bellec P, Toro R, Daunizeau J, Pélégrini-Issac M, Benali H, 2007a. Accurate Anisotropic Fast Marching for Diffusion-Based Geodesic Tractography. International Journal of Biomedical Imaging 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Johansen-Berg H, 2011. Tractography: Where Do We Go from Here? Brain Connectivity 1, 169–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Lehman JF, Haber SN, Behrens TE, 2013a. Human and Monkey Ventral Prefrontal Fibers Use the Same Organizational Principles to Reach Their Targets: Tracing versus Tractography. The Journal of Neuroscience 33, 3190–3201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Behrens TE, 2013b. The topographic connectome. Current Opinion in Neurobiology 23, 207–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Woolrich MW, Andersson JLR, Behrens TEJ, 2007b. A Bayesian framework for global tractography. Neuroimage 37, 116–129. [DOI] [PubMed] [Google Scholar]
- Jeurissen B, Leemans A, Jones DK, Tournier JD, Sijbers J, 2011. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution. Human Brain Mapping 32, 461–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeurissen B, Tournier JD, Dhollander T, Connelly A, Sijbers J, 2014. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. Neuroimage 103, 411–426. [DOI] [PubMed] [Google Scholar]
- Jones DK, 2008. Tractography Gone Wild: Probabilistic Fibre Tracking Using the Wild Bootstrap With Diffusion Tensor MRI. IEEE Transactions on Medical Imaging 27, 1268–1274. [DOI] [PubMed] [Google Scholar]
- Jones DK, Simmons A, Williams SC, Horsfield MA, 1999. Non-invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI. Magnetic Resonance in Medicine 42, 37–41. [DOI] [PubMed] [Google Scholar]
- Kammen A, Law M, Tjan BS, Toga AW, Shi Y, 2016. Automated retinofugal visual pathway reconstruction with multi-shell HARDI and FOD-based analysis. Neuroimage 125, 767–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang N, Zhang J, Carlson ES, Gembris D, 2005. White matter fiber tractography via anisotropic diffusion simulation in the human brain. IEEE Transactions on Medical Imaging 24, 1127–1137. [DOI] [PubMed] [Google Scholar]
- Kreher B, Mader I, Kiselev V, 2008. Gibbs tracking: A novel approach for the reconstruction of neuronal pathways. Magnetic Resonance in Medicine 60, 953–963. [DOI] [PubMed] [Google Scholar]
- Lazar M, Alexander AL, 2005. Bootstrap white matter tractography (BOOT-TRAC). NeuroImage 24,524–532. [DOI] [PubMed] [Google Scholar]
- Lazar M, Weinstein DM, Tsuruda JS, Hasan KM, Arfanakis K, Meyerand ME, Badie B, Rowley HA, Haughton V, Field A, Alexander AL, 2003. White matter tractography using diffusion tensor deflection. Human Brain Mapping 18, 306–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee DH, Lee DW, Han BS, 2015. Topographic organization of motor fibre tracts in the human brain: findings in multiple locations using magnetic resonance diffusion tensor tractography. European Radiology 26, 1751–1759. [DOI] [PubMed] [Google Scholar]
- Leemans A, Jeurissen B, Sijbers J, Jones D, 2009. ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data, p. 3537. [Google Scholar]
- Leemans A, Sijbers J, Verhoye M, Van der Linden A, Van Dyck D, 2005. Mathematical framework for simulating diffusion tensor MR neural fiber bundles. Magnetic Resonance in Medicine 53, 944–953. [DOI] [PubMed] [Google Scholar]
- Lemkaddem A, Skildebrand D, Dal Pal A, Thiran JP, Daducci A, 2014. Global Tractography with Embedded Anatomical Priors for Quantitative Connectivity Analysis. Frontiers in Neurology 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenglet C, Prados E, Pons J, Deriche R, Faugeras O, 2009. Brain Connectivity Mapping Using Riemannian Geometry, Control Theory, and PDEs. SIAM Journal on Imaging Sciences 2, 285–322. [Google Scholar]
- Li M, Ratnanather JT, Miller MI, Mori S, 2014. Knowledge-based automated reconstruction of human brain white matter tracts using a path-finding approach with dynamic programming. Neuroimage 88, 271–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lifshits S, Tamir A, Assaf Y, 2009. Combinatorial fiber-tracking of the human brain. Neuroimage 48, 532–540. [DOI] [PubMed] [Google Scholar]
- Lu Y, Aldroubi A, Gore JC, Anderson AW, Ding Z, 2006. Improved fiber tractography with Bayesian tensor regularization. Neuroimage 31, 1061–1074. [DOI] [PubMed] [Google Scholar]
- Maier-Hein KH, Neher PF, Houde JC, Ct MA, Garyfallidis E, Zhong L, Chamberland M, Yeh FC, Lin YC, Ji Q, Reddick WE, Glass JO, Chen DQ, Feng Y, Gao C, Wu Y, Ma L, Renjie H, Li Q, Westin CF, Deslauriers-Gauthier S, Gonzlez JOO, Paquette M, St-Jean S, Girard G, Rheault F, Sidhu J, Tax CMW, Guo F, Mesri HY, Dvid S, Froeling M, Heemskerk AM, Leemans A, Bor A, Pinsard B, Bedetti C, Desrosiers M, Brambati S, Doyon J, Sarica A, Vasta R, Cerasa A, Quattrone A, Yeatman J, Khan AR, Hodges W, Alexander S, Romascano D, Barakovic M, Aura A, Esteban O, Lemkaddem A, Thiran JP, Cetingul HE, Odry BL, Mailhe B, Nadar MS, Pizzagalli F, Prasad G, Villalon-Reina JE, Galvis J, Thompson PM, Requejo FDS, Laguna PL, Lacerda LM, Barrett R, DellAcqua F, Catani M, Petit L, Caruyer E, Daducci A, Dyrby TB, Holland-Letz T, Hilgetag CC, Stieltjes B, Descoteaux M, 2017. The challenge of mapping the human connectome based on diffusion tractography. Nature Communications 8, 1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malcolm JG, Michailovich O, Bouix S, Westin CF, Shenton ME, Rathi Y, 2010. A filtered approach to neural tractography using the Watson directional function. Medical Image Analysis 14, 58–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malcolm JG, Shenton ME, Rathi Y, 2009. Neural Tractography Using An Unscented Kalman Filter. Information Processing in Medical Imaging 21, 126–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangin JF, Poupon C, Cointepas Y, Rivire D, Papadopoulos-Orfanos D, Clark CA, Rgis J, Le Bihan D, 2002. A framework based on spin glass models for the inference of anatomical connectivity from diffusion-weighted MR data a technical review. NMR in Biomedicine 15, 481–492. [DOI] [PubMed] [Google Scholar]
- Meyer A, 1907. The connections of the occipital lobes and the present status of the cerebral visual affections. Trans Assoc Am Physicians 22, 7–16. [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K, 2010. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magnetic Resonance in Medicine 63, 1144–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, Van Zijl PCM, 1999. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Annals of Neurology 45, 265–269. [DOI] [PubMed] [Google Scholar]
- Mori S, van Zijl PCM, 2002. Fiber tracking: principles and strategies a technical review. NMR in Biomedicine 15, 468–480. [DOI] [PubMed] [Google Scholar]
- Morosan P, Rademacher J, Schleicher A, Amunts K, Schormann T, Zilles K, 2001. Human Primary Auditory Cortex: Cytoarchitectonie Subdivisions and Mapping into a Spatial Reference System. Neuroimage 13, 684–701. [DOI] [PubMed] [Google Scholar]
- Neher PF, Laun FB, Stieltjes B, Maier-Hein KH, 2014. Fiberfox: Facilitating the creation of realistic white matter software phantoms. Magnetic Resonance in Medicine 72, 1460–1470. [DOI] [PubMed] [Google Scholar]
- Novikov DS, Jespersen SN, Kiselev VG, Fieremans E, 2016. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. arXiv: 1612.02059 [physics] ArXiv: 1612.02059. [DOI] [PMC free article] [PubMed]
- O’Donnell L, Haker S, Westin CF, 2002. New Approaches to Estimation of White Matter Connectivity in Diffusion Tensor MRI: Elliptic PDEs and Geodesics in a Tensor-Warped Space, in: Medical Image Computing and Computer-Assisted Intervention MICCAI 2002, Springer, Berlin, Heidelberg, pp. 459–466. [Google Scholar]
- Ottes FP, Van Gisbergen JAM, Eggermont JJ, 1986. Visuomotor fields of the superior colliculus: A quantitative model. Vision Research 26, 857–873. [DOI] [PubMed] [Google Scholar]
- Panagiotaki E, Schneider T, Siow B, Hall MG, Lythgoe MF, Alexander DC, 2012. Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison. Neuroimage 59, 2241–2254. [DOI] [PubMed] [Google Scholar]
- Parker G, Wheeler-Kingshott C, Barker G, 2002. Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging. IEEE Transactions on Medical Imaging 21, 505–512. [DOI] [PubMed] [Google Scholar]
- Parker GJ, Haroon HA, Wheeler-Kingshott CA, 2003. A framework for a streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. Journal of Magnetic Resonance Imaging 18, 242–254. [DOI] [PubMed] [Google Scholar]
- Párraga RG, Ribas GC, Welling LC, Alves RV, de Oliveira E, 2012. Microsurgical Anatomy of the Optic Radiation and Related Fibers in 3-Dimensional Images. Operative Neurosurgery 71, 160–172. [DOI] [PubMed] [Google Scholar]
- Patel GH, Kaplan DM, Snyder LH, 2014. Topographic organization in the brain: searching for general principles. Trends in Cognitive Sciences 18, 351–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Péchaud M, Descoteaux M, Keriven R, 2009. Brain Connectivity Using Geodesics in HARDI, in: Yang GZ, Hawkes D, Rueckert D, Noble A, Taylor C (Eds.), Medical Image Computing and Computer-Assisted Intervention MICCAI 2009. Springer; Berlin Heidelberg, number 5762 in Lecture Notes in Computer Science, pp. 482–489. [DOI] [PubMed] [Google Scholar]
- Pestilli F, Yeatman J, Rokem A, Kay K, Wandeil B, 2014. Evaluation and statistical inference for living connectomes. Nature methods 11, 1058–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pichon E, Westin CF, Tannenbaum AR, 2005. A Hamilton-Jacobi-Bellman Approach to High Angular Resolution Diffusion Tractography, in: Medical Image Computing and Computer-Assisted Intervention MICCAI 2005, Springer, Berlin, Heidelberg: pp. 180–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pontabry J, Rousseau F, Oubel E, Studholme C, Koob M, Dietemann JL, 2013. Probabilistic tractography using Q-ball imaging and particle filtering: Application to adult and in-utero fetal brain studies. Medical Image Analysis 17, 297–310. [DOI] [PubMed] [Google Scholar]
- Porter DA, Heidemann RM, 2009. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magnetic Resonance in Medicine 62, 468–475. [DOI] [PubMed] [Google Scholar]
- Poupon C, Rieul B, Kezele I, Perrin M, Poupon F, Mangin JF, 2008. New diffusion phantoms dedicated to the study and validation of high-angular-resolution diffusion imaging (HARDI) models. Magnetic Resonance in Medicine 60, 1276–1283. [DOI] [PubMed] [Google Scholar]
- Prados E, Lenglet C, Pons JP, Wotawa N, Deriche R, Faugeras O, Soatto S, 2006. Control Theory and Fast Marching Methods for Brain Connectivity Mapping. Research Report RR-5845. INRIA. [Google Scholar]
- Pullens P, Roebroeck A, Goebel R, 2010. Ground truth hardware phantoms for validation of diffusion-weighted MRI applications. Journal of Magnetic Resonance Imaging 32, 482–488. [DOI] [PubMed] [Google Scholar]
- Reisert M, Kiselev VG, 2011. Fiber Continuity: An Anisotropic Prior for ODF Estimation. IEEE Transactions on Medical Imaging 30, 1274–1283. doi: 10.1109/TMI.2011.2112769. [DOI] [PubMed] [Google Scholar]
- Reisert M, Kiselev VG, Dihtal B, Kellner E, Novikov DS, 2014. MesoFT: Unifying Diffusion Modelling and Fiber Tracking, in: Golland P, Hata N, Barillot C, Homegger J, Howe R (Eds.), Medical Image Computing and Computer-Assisted Intervention MICCAI 2014. Springer International Publishing, number 8675 in Lecture Notes in Computer Science, pp. 201–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisert M, Mader I, Anastasopoulos C, Weigel M, Schnell S, Kiselev V, 2011. Global fiber reconstruction becomes practical. Neuroimage 54, 955–962. [DOI] [PubMed] [Google Scholar]
- Rowe M, Zhang HG, Oxtoby N, Alexander DC, 2013. Beyond Crossing Fibers: Tractography Exploiting Sub-voxel Fibre Dispersion and Neighbourhood Structure, in: Gee JC, Joshi S, Pohl KM, Wells WM, Zllei L (Eds.), Information Processing in Medical Imaging. Springer; Berlin Heidelberg: number 7917 in Lecture Notes in Computer Science, pp. 402–413. [DOI] [PubMed] [Google Scholar]
- Ruben J, Schwiemann J, Deuchert M, Meyer R, Krause T, Curio G, Villringer K, Kurth R, Villringer A, 2001. Somatotopic Organization of Human Secondary Somatosensory Cortex. Cerebral Cortex 11,463–473. [DOI] [PubMed] [Google Scholar]
- Savadjiev P, Campbell JSW, Descoteaux M, Deriche R, Pike GB, Siddiqi K, 2008. Labeling of ambiguous subvoxel fibre bundle configurations in high angular resolution diffusion MRI. Neuroimage 41, 58–68. [DOI] [PubMed] [Google Scholar]
- Savadjiev P, Campbell JSW, Pike GB, Siddiqi K, 2006. 3d curve inference for diffusion MRI regularization and fibre tractography. Medical Image Analysis 10, 799–813. [DOI] [PubMed] [Google Scholar]
- Savadjiev P, Rathi Y, Malcolm JG, Shenton ME, Westin CF, 2010. A Geometry-Based Particle filtering Approach to White Matter Tractography, in: Jiang T, Navab N, Pluim JPW, Viergever MA (Eds.), Medical Image Computing and Computer-Assisted Intervention MICCAI 2010. Springer; Berlin Heidelberg: number 6362 in Lecture Notes in Computer Science, pp. 233–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmahmann JD, Pandya DN, Wang R, Dai G, D’Arceuil HE, Crespigny A.J.d., Wedeen VJ, 2007. Association fibre pathways of the brain: parallel observations from diffusion spectrum imaging and autoradiography. Brain 130, 630–653. [DOI] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzei T, Wedeen VJ, Wald LL, 2012. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magnetic Resonance in Medicine 67, 1210–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seunarine KK, Cook PA, Hall MG, Embleton KV, Parker GJM, Alexander DC, 2007. Exploiting peak anisotropy for tracking through complex structures, in: pp. 1–8. [Google Scholar]
- Sherbondy AJ, Dougherty RF, Ben-Shachar M, Napel S, Wandeil BA, 2008. ConTrack: Finding the most likely pathways between brain regions using diffusion tractography. Journal of Vision 8, 15–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherbondy AJ, Rowe MC, Alexander DC, 2010. MicroTrack: An Algorithm for Concurrent Projectome and Microstructure Estimation, in: Jiang T, Navab N, Pluim JPW, Viergever MA (Eds.), Medical Image Computing and Computer-Assisted Intervention MICCAI 2010. Springer; Berlin Heidelberg, number 6361 in Lecture Notes in Computer Science, pp. 183–190. [DOI] [PubMed] [Google Scholar]
- Smith RE, Tournier JD, Calamante F, Connelly A, 2013. SIFT: Spherical-deconvolution informed filtering of tractograms. Neuroimage 67, 298–312. [DOI] [PubMed] [Google Scholar]
- Smith RE, Tournier JD, Calamante F, Connelly A, 2015. SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. Neuroimage 119, 338–351. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos SN, Bai L, Morgan PS, Constantinescu CS, Tench CR, 2010. Brain tractography using Q-ball imaging and graph theory: Improved connectivities through fibre crossings via a model-based approach. Neuroimage 49, 2444–2456. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, Feinberg DA, Yacoub E, Lenglet C, Van Essen DC, Ugurbil K, Behrens TEJ, 2013. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage 80, 125–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamm A, Commowick O, Barillot C, Prez P, 2013. Adaptive Multi-modal Particle Filtering for Probabilistic White Matter Tractography, in: Gee JC, Joshi S, Pohl KM, Wells WM, Zllei L (Eds.), Information Processing in Medical Imaging. Springer; Berlin Heidelberg, number 7917 in Lecture Notes in Computer Science, pp. 594–606. [DOI] [PubMed] [Google Scholar]
- Takemura H, Caiafa CF, Wandell BA, Pestilli F, 2016. Ensemble Tractography. PLOS Computational Biology 12, e1004692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thivierge JP, Marcus GF, 2007. The topographic brain: from neural connectivity to cognition. Trends in Neurosciences 30, 251–259. [DOI] [PubMed] [Google Scholar]
- Thomas C, Ye FQ, Irfanoglu MO, Modi P, Saleem KS, Leopold DA, Pierpaoli C, 2014. Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proceedings of the National Academy of Sciences 111, 16574–16579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tootell RB, Switkes E, Silverman MS, Hamilton SL, 1988. Functional anatomy of macaque striate cortex. II. Retinotopic organization. Journal of Neuroscience 8, 1531–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A, 2007. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. Neuroimage 35, 1459–1472. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A, 2010. Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions. Proc. 18th Annual Meeting of the Intl. Soc. Mag. Reson. Med.(ISMRM), 1670. [Google Scholar]
- Tournier JD, Calamante F, Connelly A, 2012. MRtrix: Diffusion tractography in crossing fiber regions. International Journal of Imaging Systems and Technology 22, 53–66. [Google Scholar]
- Tournier JD, Calamante F, Gadian DG, Connelly A, 2003. Diffusion-weighted magnetic resonance imaging fibre tracking using a front evolution algorithm. Neuroimage 20, 276–288. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Gadian DG, Connelly A, 2004. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage 23, 1176–1185. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, King M, Gadian D, Connelly A, 2002. Limitations and requirements of diffusion tensor fiber tracking: An assessment using simulations. Magnetic Resonance in Medicine 47, 701–708. [DOI] [PubMed] [Google Scholar]
- Tran G, Shi Y, 2015. Fiber Orientation and Compartment Parameter Estimation From Multi-Shell Diffusion Imaging. IEEE Transactions on Medical Imaging 34, 2320–2332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch DS, 2004. Q-ball imaging. Magnetic Resonance in Medicine 52, 1358–1372. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ, 2002. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic Resonance in Medicine 48, 577–582. [DOI] [PubMed] [Google Scholar]
- Ugurbil K, Xu L, Auerbach EJ, Moeller S, Vu AT, Duarte-Carvajalino JM, Lenglet C, Wu X, Schmitter S, Van de Moortele PF, Strupp J, Sapiro G, De Martino F, Wang D, Harel N, Garwood M, Chen L, Feinberg DA, Smith SM, Miller KL, Sotiropoulos SN, Jbabdi S, Andersson JLR, Behrens TEJ, Glasser MF, Van Essen DC, Yacoub E, 2013. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. Neuroimage 80, 80–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens TEJ, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, Della Penna S, Feinberg D, Glasser MF, Harel N, Heath AC, Larson-Prior L, Marcus D, Michalareas G, Moeller S, Oostenveld R, Petersen SE, Prior F, Schlaggar BL, Smith SM, Snyder AZ, Xu L, Yacoub E, 2012. The Human Connectome Project: A data acquisition perspective. Neuroimage 62, 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vorburger RS, Reischauer C, Boesiger P, 2013. BootGraph: Probabilistic fiber tractography using bootstrap algorithms and graph theory. Neuroimage 66, 426–435. [DOI] [PubMed] [Google Scholar]
- Wandell BA, 2016. Clarifying Human White Matter. Annual Review of Neuroscience 39, 103–128. [DOI] [PubMed] [Google Scholar]
- Wang J, Aydogan DB, Varma R, Toga AW, Shi Y, 2017. Topographic Regularity for Tract Filtering in Brain Connectivity, in: Information Processing in Medical Imaging, Springer, Cham; pp. 263–274. URL: https://link.springer.com/chapter/10.1007/978-3-319-59050-9_21, doi: 10.1007/978-3-319-59050-9_21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Benner T, Sorensen A, Wedeen V, 2007a. Diffusion Toolkit: A Software Package for Diffusion Imaging Data Processing and Tractography. Proc. 15th Annual Meeting of the Intl. Soc. Mag. Reson. Med.(ISMRM), 3720. [Google Scholar]
- Wang R, Benner T, Sorensen AG, Wedeen VJ, 2007b. Diffusion toolkit: a software package for diffusion imaging data processing and tractography, in: Proc Intl Soc Mag Reson Med, Berlin. [Google Scholar]
- Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng WYI, 2012. The Geometrie Structure of the Brain Fiber Pathways. Science 335, 1628–1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitcher B, Tuch DS, Wisco JJ, Sorensen AG, Wang L, 2008. Using the wild bootstrap to quantify uncertainty in diffusion tensor imaging. Human Brain Mapping 29, 346–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye C, Prince JL, 2017. Probabilistic tractography using Lasso bootstrap. Medical Image Analysis 35,544–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye C, Zhuo J, Gullapalli RP, Prince JL, 2016. Estimation of fiber orientations using neighborhood information. Medical Image Analysis 32, 243–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh CH, Smith RE, Liang X, Calamante F, Connelly A, 2016. Correction for diffusion MRI fibre tracking biases: The consequences for structural connectomic metrics. Neuroimage 142, 150–162. [DOI] [PubMed] [Google Scholar]
- Yeh FC, Verstynen TD, Wang Y, Fernndez-Miranda JC, Tseng WYI, 2013. Deterministic Diffusion Fiber Tracking Improved by Quantitative Anisotropy. PLOS ONE 8, e80713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, 2008. DT-MRI Fiber Tracking: A Shortest Paths Approach. IEEE Transactions on Medical Imaging 27, 1458–1471. [DOI] [PubMed] [Google Scholar]
- Zalesky A, Fomito A, Cocchi L, Gollo LL, van den Heuvel MP, Breakspear M, 2016. Connectome sensitivity or specificity: which is more important? NeuroImage 142, 407–420. [DOI] [PubMed] [Google Scholar]
- Zhang F, Hancock ER, Goodlett C, Gerig G, 2009. Probabilistic white matter fiber tracking using particle filtering and von MisesFisher sampling. Medical Image Analysis 13, 5–18. [DOI] [PMC free article] [PubMed] [Google Scholar]


