Abstract
The study on the polymerization of fibrinogen molecules into fibrin monomers and eventually a stable, mechanically robust fibrin clot is a persistent and enduring topic in the field of thrombosis and hemostasis. Despite many research advances in fibrin polymerization, the change in structure of fibrin clots and its influence on the formation of a fibrous protein network is still poorly understood. In this paper, we develop a new computational method to simulate fibrin clot polymerization using dissipative particle dynamics simulations. With an effective combination of reactive molecular dynamics formularies and many body dissipative particle dynamics (MDPD) principles, we constructed the reactive dissipative particle dynamics (RDPD) model to predict the complex network formation of fibrin clots and branching of the fibrin network. The 340 kDa fibrinogen molecule is converted into a spring-bead coarse grain system with 11 beads using a topology representing network (TRN) algorithm, and using RDPD, we simulated polymerization and formation of the fibrin clot. The final polymerized structure of the fibrin clot qualitatively agrees with experimental results from the literature, and to the best of our knowledge this is the first molecular based study that simulates polymerization and structure of fibrin clots.
Keywords: Reactive dissipative particle dynamics, Fibrinogen, Molecular dynamics, Fibrin clot, Force field
Graphical Abstract
1. Introduction
Fibrinogen is a large, soluble glycoprotein which plays a critical role in the formation of a blood clot, by forming a robust network of fibrin polymers that provides the mechanical stability of a blood clot. Over 50 years of research was necessary to obtain the accurate structural representation of the fibrinogen molecule (Kollman et al. 2009), where previously, the trinodular structure of the fibrinogen molecule was determined by various methods including electron micrographs (Hall and Slayter 1959). Using the molecular models of fibrinogen and thrombin, an enzyme which cleaves the fibrinopeptides of fibrinogen and thereby initiating polymerization, studies were conducted to understand their interactions (Rose and Di Cera 2002). Toward the simulation of the formation of a blood clot and blood flow, there exists a few studies with discrete particles (Boryczko et al. 2004) and multiscale models (Averett et al. 2012; Moiseyev and Bar-Yoseph 2013; Wang and King 2012; Yamaguchi et al. 2010). There exists studies focused on understanding the adsorption behavior of fibrinogen with different substrates (Bajpai 2008) that can be helpful in understanding immunological response (Castner and Ratner 2002). In addition, prior work has been conducted on fibrin networks to understand lateral aggregation and fibril formation (Weisel 1986) and fiber branching (Baradet et al. 1995).
Fibrin clots have been implicated in numerous disease states, both arterial and venous, and the formation and structure of fibrin clots in disease states is still poorly understood. Studies suggest that patients with deep vein thrombosis and diabetes often possess hyper-coagulable blood plasma conditions leading to higher risks of thrombotic disorders by the formation of blood clots. Deep vein thrombosis is the formation of a blood clot (thrombus) within a deep vein most commonly in the legs, which can lead to a wide range of complications (Kyrle and Eichinger 2005). In the event of thrombus rupture, a fragment of the clot may travel to the lungs and can cause a pulmonary embolism to develop, which can be fatal (Collins et al. 1988; Kakkar and De Lorenzo 1998) if left untreated. Vascular endothelial damage, stasis of blood flow, and hypercoagulability of blood is found to be directly related to the risk factors of deep vein thrombosis (Jiang et al. 2015; Liu et al. 2014; Michetti et al. 2015; Zhang et al. 2017) and pulmonary embolisms (Anderson and Spencer 2003; Li et al. 2014; Ma and Wen 2017; Wang et al. 2016). The venous thromboembolism is considered an epidemic (Dowling et al. 2003; Kearon 2003; Kroegel and Reissig 2003; Lee 2003; White 2003) and various thrombolytic therapies have been suggested by clinicians to control formation after a typical surgery (Agnelli 2004; Aronow 2004; Brambilla et al. 2004; Cimminiello et al. 2004; Davison et al. 2004; Eriksson and Dahl 2004; Geerts et al. 2004; Greer 2004; Iorio 2004; Minnema et al. 2004; Mismetti et al. 2004). In addition, platelets interact with fibrin matrices and cause mechanical retraction, specifically in hypercoagulable states (Lam et al. 2011; Qiu et al. 2015). The characterization of the mechanical properties of thromboemboli also plays an important role in developing thrombolytic therapies (Chueh et al. 2011), and a number of studies has been conducted recently (Chueh et al. 2013; Gounis et al. 2013; Luo et al. 2012; Moftakhar et al. 2013). Fibrin clot network structure, fibrin composition, and degree of retraction are known to have specific effects on the degree of thrombolysis, where it has been shown previously that unretracted clots and clots with a loose fibrin network and loose erythrocyte aggregates promote an enhancement of thrombolysis (Sutton et al. 2013; Tomaru et al. 1987).
Despite all developments in the field to understand the complexity of fibrin network formation, computational modeling of fibrin polymerization has not been well developed. An accurate computational model based on molecular information will be helpful in predicting the mechanical behavior of fibrin clots in various pathogenic states and can also be useful for designing thrombolytic therapies. Currently, there exists no computational models which can accurately predict the polymerization and formation of fibrin clots, based on molecular level information. Prior computational studies are mainly based on the empirical rate of clot formation information modeled as first order partial differential equations. Studies suggest that multiscale models that can leverage molecular information to the mesoscale and macroscale can be used to elucidate fibrin network formation and can be used to develop new thrombotic and thrombolytic therapies. In this research, we developed a coarse grain model of fibrinogen in conjunction with modified reactive DPD potentials to simulate fibrin clot polymerization at the macro scale. The force field parameters were optimized by matching the self-diffusion coefficient and we have compared the simulation results using conventional DPD and solvent free many body DPD. We have observed some critical events in fibrin clot formation such as continuous long strand formation, fibrin fiber branching, and cross-linking and also the length of the fibers were in agreement with the scanning electron microscopy (SEM) results found in the literature.
2. Coarse Grain Model Development
An ideal coarse grain model possesses a minimal number of beads, and still can mechanically represent the structural properties of fibrinogen. This minimizes computational cost, while still possessing enough beads and springs to maintain the flexibility and extensibility of the fibrinogen molecule. To achieve this, we used a shape based coarse graining approach (Arkhipov et al. 2006) implemented in NAMD (Phillips et al. 2005) and divided the human fibrinogen (RCSB 3GHG (Kollman et al. 2009)) molecule into eleven fragments and estimated their molecular mass and positions based on a topology representing network algorithm (Martinetz and Schulten 1994). The coarse grain beads are connected by bonds modeled as harmonic springs. Figure 1a shows the molecular model of human fibrinogen (Kollman et al. 2009) with α, β, and γ-chains along with the D-region, E-region and the coiled region (C-region). The mass partitioning procedure based on the topology representing network algorithm was used (Fig. 1b) to assign the appropriate molecular weights to the various segments of the fibrinogen molecule. The same methodology was used to estimate the partial charges in the beads (Fig. 1c).
Figure 1.
Coarse graining of the fibrinogen molecule. (a) Atomic model of human fibrinogen with α-chain, β-chain and γ-chain in representation using VMD (Humphrey et al. 1996). (b) Partitioning of the fibrinogen molecule based on the TRN algorithm. The spheres represent the beads and background shades represent the atomic cloud of the fibrinogen molecule. (c) Partial charges and molecular mass of the beads. Bead numbering: 1 to 11 (left to right). (d) Coefficient of spring stiffness for bond and angle potentials between the beads (Bond and angle numbering is from left to right. Subscript AA represents the target value of the spring constants based on all atomic simulations and subscript Iter #1 represents the spring coefficients after a coarse grain simulation iteration.) (e) Equilibrium bond distance value and angle value for various bonds and angles.
The beads of the fibrinogen model (Fig. 1b) are represented as 1 to 11 (left to right). Bead type 1 and type 11 are represented as type-D beads, type 6 beads are represented as type-E beads and remaining beads (2–5 and 7–10) are represented as type-C beads. Other coagulation factors which play a role in the coagulation cascade such as thrombin (RCSB 1PPB (Bode et al. 1989)) and Factor XIII (RCSB 1GGU (Fox et al. 1999)) are not modeled in the system and their effects are considered indirectly through a polymerization potential (explained in a later section).
The bonds in the coarse grain model were modeled using a harmonic bond potential (Eqn. 1) which connects the beads and maintains the average equilibrium distance at a constant value for a long period of time.
| (1) |
Here, 2kb is the spring stiffness, r0 is the equilibrium distance of the bonds, and r is the instantaneous spacing between the beads in the bond.
For maintaining the shape and to avoid worm-like chain behavior of the fibrinogen molecule during polymerization, we applied an angle harmonic potential (Eq. 2) between the bonds consecutively.
| (2) |
Here, 2ka is the stiffness potential, which controls the flexibility of the bonds and θ0 is the equilibrium angle.
2.1. Characterization of CG model parameters
An important problem to address pertains to the values of the spring parameters. The objective of a shape based coarse graining approach is to develop the coarse grain (CG) model and perform the molecular dynamics simulations with both an all-atomic (AA) model and a CG model. The resulting trajectory is then analyzed and compared and the spring parameters are optimized until they correspond with a maximum average error of 25%. A detailed explanation of this method and its usage is explained in the literature (Freddolino et al. 2008).
With the first iteration of the process, we obtained the parameters of the CG fibrinogen model. The resulting values of the spring constants of bond potential and angle potential were calculated (Fig. 1d) as well as the equilibrium distances (Fig. 1e). A tabular format of the parameters is also provided (Table 1).
Table 1.
List of CG model parameters of fibrinogen
| Number | Beads | Bonds | Angles | |||
|---|---|---|---|---|---|---|
| Mass | Charge | Kbond | d0 | Kangle | θ0 | |
| (kDa) | (e) | (kcal/mol/A2) | (A) | (kcal/mol/rad2) | (deg) | |
| 1 | 23907.3 | −5.77 | 2.096 | 27.9 | 623.446 | 151.7 |
| 2 | 18300.6 | 2.71 | 1.931 | 27.9 | 474.766 | 153.25 |
| 3 | 27129.2 | −0.62 | 2.573 | 42.9 | 250.468 | 150.28 |
| 4 | 15964.3 | −0.65 | 0.987 | 55.1 | 501.023 | 166.35 |
| 5 | 14568.1 | −0.01 | 3.102 | 62.9 | 1300.543 | 172.42 |
| 6 | 22788.7 | −2.3 | 3.723 | 55.9 | 382.519 | 168.72 |
| 7 | 13740.4 | −0.37 | 2.877 | 57.2 | 463.528 | 158.76 |
| 8 | 15540.5 | −2.44 | 3.133 | 47.5 | 1525.552 | 173.23 |
| 9 | 26815.7 | 3.68 | 7.39 | 28.1 | 1479.259 | 150.68 |
| 10 | 20332.8 | −2 | 6.806 | 32 | ||
| 11 | 26357.2 | −2.21 | ||||
After obtaining the parameters of the CG model, the next step was to develop a force field for inter- molecular interaction. One option was to use coarse grain water models to represent the plasma of the blood stream. However, the currently available CG water models can represent a small number of water molecules, which would make the computation very expensive. Another option was to develop a solvent-free model. Our attempts with solvent free model construction (not published) shows that the parameterization of these force fields will make them phenomenological models and thus an alternative solution is needed. One feasible alternative is the dissipative particle dynamics (DPD) method (Groot and Warren 1997), which is widely used in mesoscopic simulations and is a robust modeling method used in all fields of science and engineering.
2.2. Dissipative Particle Dynamics (DPD)
DPD is a stochastic simulation technique for simulating the dynamic and rheological properties of simple and complex fluids, which can be used for simulating the fluidic properties of water at different length and time scales. The forces (F) acting on a DPD particle represent a combination of a conservative force (FC), a dissipative force (FD) and a random force (FR).
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Here, r is the distance between the beads, w is the interpolation function, α is a Gaussian random number with zero mean and unit variance, rc is the cutoff radius, and rij and vij are the relative displacement and velocities of the two beads. The unknown parameters to be evaluated in a new DPD simulation are A, γ, Δt and rc.
Typical values of these parameters used for simulations are A = 1, γ = 4.5, Δt = 0.02 and rc = 1. However, for our simulations it was necessary to re-parameterize these values to correspond with the thermodynamic properties of water. The average distance between the beads was considered as 5 nm. This provides geometric space for beads with 2.5 nm radius. The spherical volume of this radius allows for 2,187 water molecules. Utilizing the mass conservation relationship of DPD and molecular dynamics (MD) simulations, it is shown that: . This leads to: rc = 6.8943 nm, where Nm = 2,187.
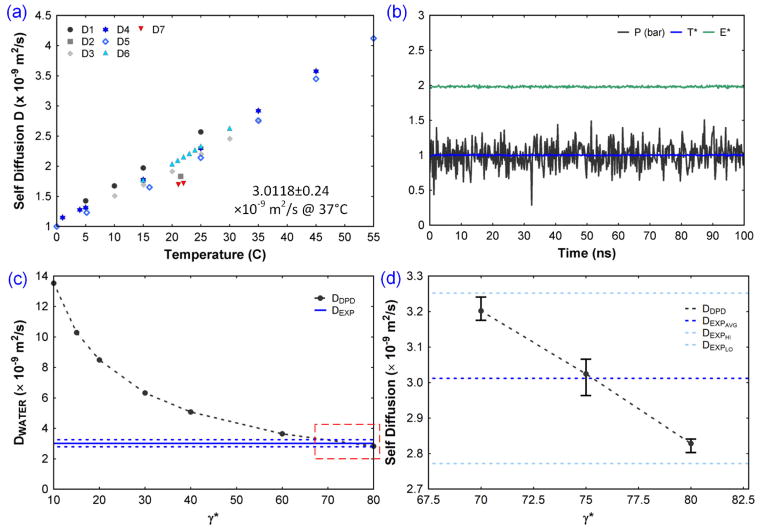
The DPD simulation was then performed with the typical DPD force field parameter values and the pressure, temperature, energy and self-diffusion coefficient were estimated. The variation of pressure, temperature (in LJ units) and energy (LJ units) is shown for a DPD simulation (Fig. 2b). The self-diffusion coefficient was estimated from the Einstein relation (Eq. 9).
Figure 2.
Parameterization of the DPD force field. (a) Self diffusion coefficients of water from D1 (Wang 1965), D2 (Baranowska and Olszewski 1996), D3 (Tanaka 1975), D4 (Mills 1973), D5 (Wang 1951), D6 (Tofts et al. 2000), D7 (Murday and Cotts 1970). The average self-diffusion coefficient of water at 37°C from these experiments was computed as 3.0118 ± 0.24 × 10−9 m2/s. (b) Pressure, temperature, and energy during the DPD simulation. (c) Self diffusion coefficient of water and its sensitivity with DPD parameter, γ. (d) Estimation of the value of γ corresponding to the selected bead size, which matches the experimental self-diffusion coefficient.
| (9) |
2.3. DPD Simulation Model
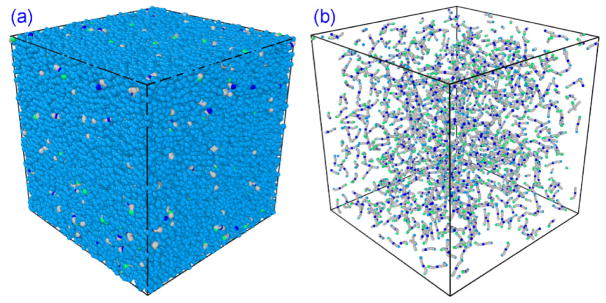
In a typical DPD simulation, the number density of water molecules per bead ranges from 3 to 5. In the present study, the number density is 2,187 and hence it was necessary to recalibrate the DPD force field parameters to account for the size effect. To achieve this, a system with only DPD water beads in a 100 nm3 was created (Fig. 3c). Numerical integration was performed using the velocity Verlet scheme (Verlet 1967), and the temperature of the system was controlled using a Nose-Hoover thermostat (Hoover 1985; Nosé 1984). All DPD simulations were performed using the open source software LAMMPS (Plimpton et al. 2007). Visualization of the molecular models and the corresponding trajectories was achieved using OVITO software (Stukowski 2010) and the molecular models were created using MATLAB (MathWorks 2012) codes. DPD simulations were conducted in LJ units (dimensionless units) and the conversion factors and units are provided in Table 2.
Figure 3.
(a) A 500 nm × 500 nm × 500 nm water-fibrinogen DPD system used for characterization of inter bead potential parameters. (b) The same system is shown with fibrinogens highlighted and water beads hidden.
Table 2.
SI unit to LJ unit conversion
| Quantity | SI unit | LJ unit | Conversion factor | |
|---|---|---|---|---|
| Distance (r) | m | r* | rc | |
| Boltzmann constant (kB) | J/k | 1 | 1.38064852 e-23 | |
| Temperature (T) | K | 1 | 310 | |
| Cutoff radius (rc) | m | 1 | 6.8943 e-9 | |
| Reference mass (mref) | Kg | 1 | 6.535 e-23 | |
| Time (t) | s | τ | 8.51904 e-10 | |
| Energy (E) | J | kBT | E = E*kBT | |
| Stiffness (k) | N/m | k* |
|
|
| Charge (q) | e |
|
q* = 2.796q |
2.4. Validation of the DPD force field
To validate the DPD force field parameters, we utilized this DPD water system and performed the simulation for more than 100 ns to obtain the time evolution of pressure, temperature, and energy (Fig. 2b). The average values of pressure (1 bar), temperature (310 K), and energy shows good stability over time. The self-diffusion coefficient of water as a function of temperature was computed using 7 different experiments from the literature (Fig. 2a). From these experimental values, the self-diffusion coefficient of water (DW–EXP) was obtained by computing the average at 37°C and obtained as 3.0118 ± 0.24 × 10−9(m2/s). From the DPD simulation, the self-diffusion coefficient (DDPD) was estimated as 13.5 × 10−9(m2/s), which is a high value compared with the experimental value, DW–EXP. The factor that controls pressure in the system is the conservative force parameter A, (value of 1) and gives P = 1bar. Correspondingly, the dissipative force parameter γ controls the DDPD.
γ was changed from 10 to 80, a set of DPD simulations was conducted, and the DDPD relationship was computed (Fig. 2c). The experimental average value and DPD simulation value of the self-diffusion coefficient intersects between γ = 70 and 80. Because the DPD simulations include the random force component which changes the dynamics at every run, five simulations were performed at γ = 70,75 and 80, totaling 15 simulations. The average values of DDPD were compared with DW–EXP (Fig. 2d). The data shows that the experimental and computational values intersect at γ = 75 and this was employed as the DPD parameter for all simulations.
With the parameterization and validation of the DPD force field, the next step was to introduce fibrinogen into the system and perform DPD simulations. A physiological fibrinogen concentration of 4 g/l was chosen for the initial studies and an equivalent number of fibrinogen molecules were inserted to the water DPD system (Fig. 3). The mass and spring constants of the DPD model were obtained from the previously characterized CG model. The bead size is chosen as 17 nm to minimize the large number of water beads, leading to a 125107 beads in a 500 nm cubic box. Due to the size difference between the solvent beads and the fibrinogen beads, it is impossible for using a same DPD parameter γ for both. Hence we changed them independently to arrive at a desired value. The experimental diffusion coefficient of fibrinogen in water varies as 2.04 × 10−11 m2/s (Palmer et al. 1979), 1.73 × 10−11 m2/s (Muller and Burchard 1981), 1.95 × 10−11 m2/s (Wiltzius et al. 1982) and a consolidated value of 2.0 × 10−11 m2/s based on both experiments and theory (Martinez et al. 1984).
The simulation results show that the diffusion coefficient of fibrinogen is less than the water self-diffusion coefficient and the outcome of various trials are shown in the table 3. Due to the big size difference between the water and fibrinogen beads, gamma couldn’t be increased beyond 300 as it will lead to unstable simulation. Hence, the best of the results from the trials, yet closer to the experimental values were chosen as the values for simulation. Therefore for fibrinogen γFF = 12, and for water γFW = 100 is chosen with A = 2.5 for further simulations.
Table 3.
Estimation of the parameter gamma for fibrinogen system
| γWW | Dwat(m2/s) | γFW, γFF | Dfib(m2/s) | A |
|---|---|---|---|---|
| 0.1 | 8.29E-08 | 0.1 | 1.83E-08 | 1 |
| 1 | 4.05E-08 | 1 | 6.60E-09 | 1 |
| 10 | 7.83E-09 | 10 | 2.18E-09 | 1 |
| 100 | 9.87E-10 | 100 | 5.02E-10 | 1 |
| 15 | 1.96E-09 | 100 | 6.21E-10 | 1 |
| 12 | 2.24E-09 | 200 | 4.95E-10 | 1 |
| 12 | 2.69E-09 | 300 | 1.37E-09 | 1 |
| 12 | 5.00E-09 | 100 | 8.52E-10 | 1.5 |
| 12 | 5.71E-09 | 100 | 9.85E-10 | 2.5 |
3. Polymerization Force Field Development
3.1. Mechanism of fibrin polymerization
It is well established that fibrinogen is converted to fibrin monomer upon the cleavage of fibrinopeptides in the E-region by activated thrombin (factor IIa), and thrombin remains bound to the fibrinogen molecule (Liu 1981; Liu et al. 1979; Pechik et al. 2004). These fibrin monomers initially form dimers and oligomers with two or three fibrin monomers (Fig. 4), which polymerize into long double stranded protofibrils. These long protofibrils aggregate laterally and longitudinally, eventually forming a stable fibrin clot. Factor XIIIa also binds and infuses into the fibrin clot (Fukue et al. 1992; Greenberg et al. 1985) and completes the coagulation cascade (Brown and Barker 2014). The various stages involved in the polymerization process has been detailed (Fig. 4) and a thorough description of the chain of events and various stages of the coagulation cascade are provided in the literature (Brown and Barker 2014; Doolittle 1984). An exact molecular simulation of this biochemical reaction at the atomic scale is very challenging to simulate, and hence we utilized the power of the DPD technique, combined with distance based bond formation potentials to simulate the fibrin polymerization process.
Figure 4.
Conceptual representation of various stages of fibrin polymerization. Initially, fibrin monomers form a dimeric structure. The dimers axially connect to other dimers to form oligomers. Eventually long double stranded oligomers form and these double stranded oligomers laterally aggregate to form fibrin fibers (not shown).
3.2. Bond formation using distance based criteria
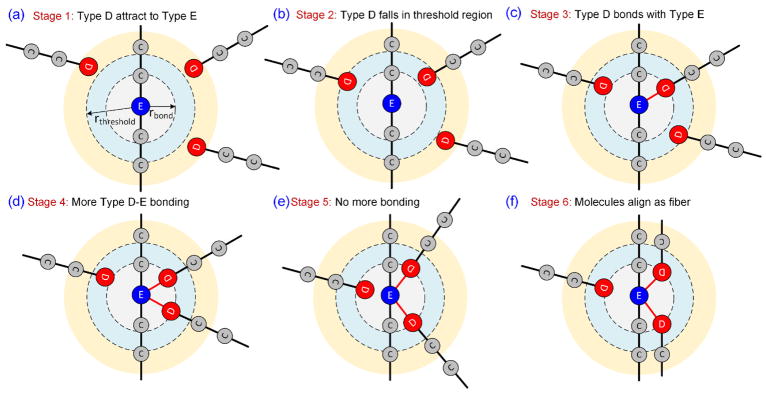
A plethora of techniques are available for the polymerization of chain molecules. Some include multibody potentials, Coulomb potential, Lennard jones potential, and Morse potential. Based on the experimental literature and our knowledge of the fibrin polymerization process, there are certain characteristics that these potentials should adhere to. The potential should be capable of simulating the hydrophobic effect which attracts the D-region to the E-region of the fibrinogen molecules. Once they are close enough, they should bind together and retain this structure. A typical situation during this process is shown graphically in Fig. 5. We define a threshold region around type-E beads (rthreshold) which detects the presence of type-D beads (Fig. 5a). If any type-D beads migrate into the threshold region, a harmonic bond with equilibrium distance (rbond) is created between the type-E and type-D beads (Fig. 5b–c). This bonding process continues until a maximum of two type-D beads are bonded to a type-E bead (Fig. 5d).
Figure 5.
Reactive DPD potential logic diagram. Various stages of polymerization of two DPD fibrinogen molecules are represented here. (a) All neighboring type-D beads attracted to type-E beads through modified attractive Coulombic potential. (b) If any of the type-D beads fall inside threshold region, then (c) a harmonic bond is created between type-D and type-E beads. (d) One type-E bead can accommodate two type-D beads, and leads to bonding. (e) Once the maximum number of bonds is reached, further bonding is not possible. (f) After sufficient time, the bonded molecules eventually align as a double strand.
The repulsive parameter (A) of the DPD potential is kept as 1 for all types of beads during the equilibration phase. After equilibration, when the polymerization logic is applied the repulsive parameter between water and all other beads is kept as 1, and the same between type-C, type-D and type-E beads are reduced to 0.01. This will effectively simulate hydrophobicity and the fibrin molecules tend to have a weak attraction. Once the maximum number of bonds are achieved, the bond formation stops and eventually the attached molecules align together due to the hydrophobic attraction of type-C with type-C beads (Fig. 5e–f). The average bond distance between the beads near the ends of fibrinogen CG model is 2.8 nm. The bond distance selection of the type-D-type-E bond should be in this range and it was selected as 2.5 nm = 0.363rc. It is necessary for the threshold radius to be greater than rbond; in addition, it must be close to rthreshold, otherwise during bond formation of the type-D bead and type-E bead, a singularity occurs toward attaining the bond radius that causes abnormal spikes in energy and dynamics and often crashes the simulation. Hence the selection of rthreshold = 2.75 nm was selected for the simulations.
3.3. Challenges during polymerization simulation
The DPD technique employs potentials that are repulsive and random in nature. Using the DPD potential, an efficient way to mimic experimental attraction between the beads is to reduce the repulsive computational parameter (A) between them. Using the developed fibrinogen-water system, long simulation times are necessary due to the low diffusivity of the fibrinogen molecule. Thus to more accurately represent the experimental behavior of the polymerization process, additional attractive potentials were employed to simulate the polymerization process. Challenges related to employing traditional attractive potentials such as Lennard-Jones and Coulomb potentials relate to spikes in energy and dynamics near singular positions (singularities). This will lead to beads “bouncing off” and unnecessary oscillations near the bond formation locations. However, among all, the Coulomb potential is suitable in this context since the strength attraction is not negligible when the beads are far away. However, care should be taken to avoid the singular point behavior. To address this concern, we used a modified soft version of the Coulomb potential (Eq. 10) (Beutler et al. 1994).
| (10) |
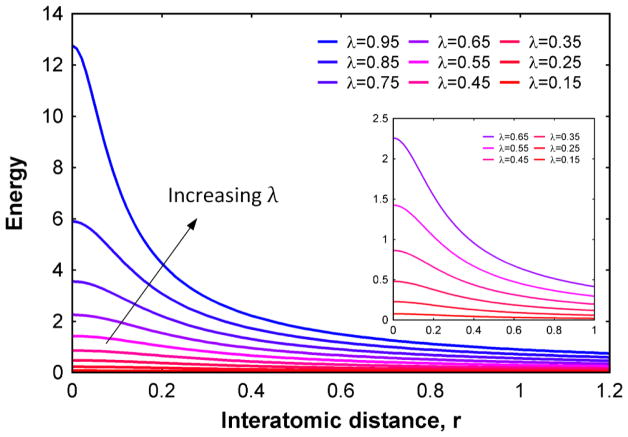
Here, C = 1/4πε0, q is the partial charge of beads, ε the dielectric constant, r is the inter bead distance, and αC is a scaling factor which can be used to reduce the intensity of the potential. Standard values of αC is 10 A2 and n = 1 were used. λ is a tuning parameter which controls the degree of softness of the potential. The change in potential energy with increasing λ value is shown in (Fig. 6). When λ = 1, the potential is representative of the regular Coulomb potential and in other cases, it possesses a finite value at a singular point (r = 0).
Figure 6.
Modified smooth coulomb potential function plotted for various values of λ. As the value of λ becomes closer to 1, the potential will tend to the normal Coulomb potential behavior. For any other value, the energy value will be finite at inter bead spacing of zero. (The inset diagram shows a zoomed in variation of the modified coulomb potential.)
To use this attractive soft potential, partial charges of the fibrinogen molecule are necessary. From the developed CG model of fibrinogen, the partial charges vary inconsistently (Table 1). This is due to two reasons – 1) the net charge in the system was not neutral and 2) the location based bead selection leads to undesirable partial charges. If these charges are used, then polymerization may never happen due to the repulsion between type-D and type-E beads and this does not represent the experimental polymerization behavior of the system. Hence, we assigned bead #1 and #11 with −0.66., bead #2 and #10 with −0.34., bead #6 with +2e., and the remaining beads as zero, leading to a charge-neutral system. In addition, this allows the type-D and type-E beads to attract. We have used λ = 0.15 for our simulations.
4. Results and Discussion
The developed DPD system with validated force field parameters was used to study the polymerization process of the fibrin monomers, with an effective combination of distance based bonding criteria and soft Coulomb potential. The cubic DPD system with sides 500 nm (Fig. 3) was considered for the simulations. The water DPD beads and fibrinogen beads were arranged initially in a random configuration preserving mass density using a random molecular filling algorithm written in MATLAB (MathWorks 2012). The systems were equilibrated for 50,000 steps using an NVT ensemble prior to polymerization simulation.
Dissipative particle dynamics simulations were performed for more than 1 μs (766,500 steps) to understand the mesoscale polymerization details of the aforementioned fibrin system. The time step of integration is chosen as 0.002τ (1703 fs), instead of the standard value of 0.05τ used in a typical DPD simulation. This is due to the presence of the strong (stiff) bonds between DPD beads in the fibrinogen model, which is uncommon in standard DPD simulations. 96 hours of real CPU time was needed to simulate a 1.306 μs study of 500 nm × 500 nm × 500 nm system in 28 CPUs using our cluster computing facility (GACRC, UGA). After 1.306 μs simulation, the system was analyzed with OVITO (Stukowski 2010) to detect the presence of oligomers, protofibrils, individual fibers etc. Figure 7a shows the molecular arrangement of the system after 1.306 μs simulation time, and Fig. 7b shows the same with only bonds displayed. The simulations show that the fibrin monomers polymerized and assembled into long continuous chains and formed an interconnected, complex fibrillar network. Branching, cross-linking of the fibrin polymers with a maximum two branches at intersections are observed from the simulations. With the current system, we could observe only the oligomer formation as shown in the Fig. 7c. The expected long protofibrils formation, lateral aggregation into fibrin fibers were not observed in this set of simulations.
Figure 7.
(a) Resulting fibrin system after 1.306 μs simulation in a 500 nm × 500 nm × 500 nm DPD system. (b) Beads are hidden and only bonds are shown (green) for visualizing fibrin structure. (c) Oligomer formation and bonding of fibrin monomers are observed.
Despite the attempts to mimic the physiological process of fibrin polymerization, the results at this point are not in great agreement with the SEM and confocal experiments. One main challenge is the length scale of the system that we chose for study which is 0.5 μm cubic box, which is very small compared with the actual experiments, due to the computational power consumption. The fibrin polymerization mechanism is a complex cascade of events, and this process is difficult to simulate with exact molecular and mesoscale details. Especially the simulation of formation of oligomers, protofibrils, lateral aggregation and branching etc, are challenging to mimic with simple hybrid simulations.
The level of coarse graining is very high in our system (2,187 water molecules per bead) compared to a typical DPD simulation (3 to 11 molecules per bead). Still, a small sized box system with 500 nm sides is computationally expensive to conduct long simulations and improvised polymerization logic testing etc. This is due to the presence of large number of beads in the system, of which only 1% are fibrinogen beads, making 99% of the model with water. Hence an approach with solvent free models can significantly reduce the computational power requirement.
5. Extended Studies with Many body DPD
Recently the use of solvent free DPD potentials like many body DPD (MDPD) potential is being used in many applications (Ghoufi et al. 2013). The main difference between the conventional DPD potential and MDPD is the conservative force term.
| (11) |
The first term represents an attractive interaction (Aij < 0) and second many body term a repulsive interaction. The weight functions ωC and ωd are chosen as,
| (12) |
| (13) |
The average local density at the position of the ith bead is given by,
| (14) |
The generic values of the MDPD parameters are rc = 1, rd = 0.75, A = −40 and B = 25 (Cupelli et al. 2008; Li et al. 2013).
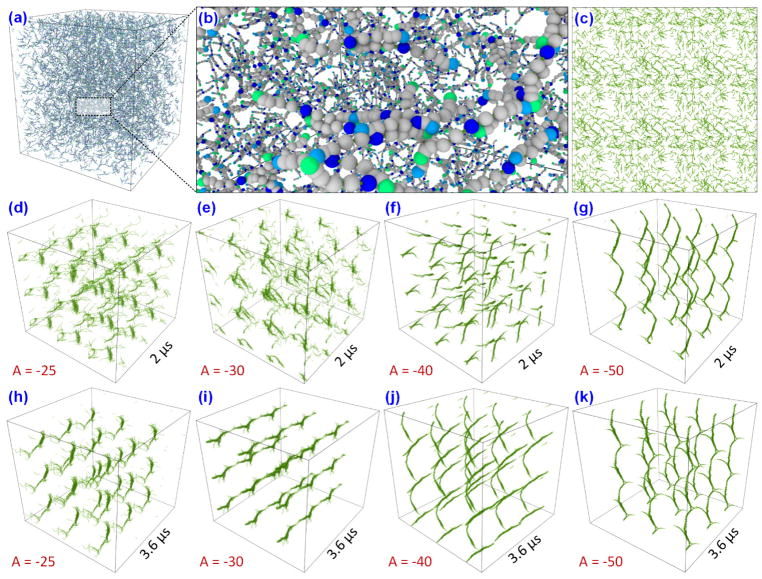
To study fibrin polymerization, we have used this MDPD potential and constructed two cubic systems of sides 400 nm and 1 μm with a fibrinogen concentration of 3g/l. The 400 nm system is used to test the influence of the attractive component of the MDPD potential in the formation of the fibrin polymers. The 3-D view of the 400 nm system with one layer of periodic images around it is shown in the Fig. 8a and its close-up view with details of the individual fibrinogens in Fig. 8b. The system is equilibrated for 500000 steps (0.5 μs) with a time step of integration 0.0024τ (1ps) and with A = −0.0001 for mixing the system to the desired temperature of 1 (310 K). All other parameters are kept as the same from the previous DPD simulations. The system after equilibration with bonds (beads hidden for clarity) are shown in Fig. 8c. After equilibration, four separate simulations are done with A = −25, −30, −40, and −50 to understand the effect of attraction parameter on polymerization. The results of the simulation at 2 μs and 3.6 μs is shown in Fig. 8d–g and Fig. 8h–k respectively. The results show that the increasing attractive strength can lead to faster or earlier clot formation, most importantly the standard parameters A = −40 and B = 25 can simulate the clot formation. In these simulations the bonding algorithm is used at every 50 steps (50 ps).
Figure 8.
(a) A 400 nm cubic box of fibrinogen MDPD model with one layer of periodic boxes around it. (b) A close-up view of the fibrinogen system. (c) The beads of the system are hidden to show only the bonds. The simulations are performed for varying factor B (attractive component of MDPD) from −25 to 50, to check its influence on structural formation. The system snapshot at 50 ns is shown from (d–g) and at 110 ns is shown from (h–k). B = −40 gives sharper clot formation compared to B = −30 and B = −25.
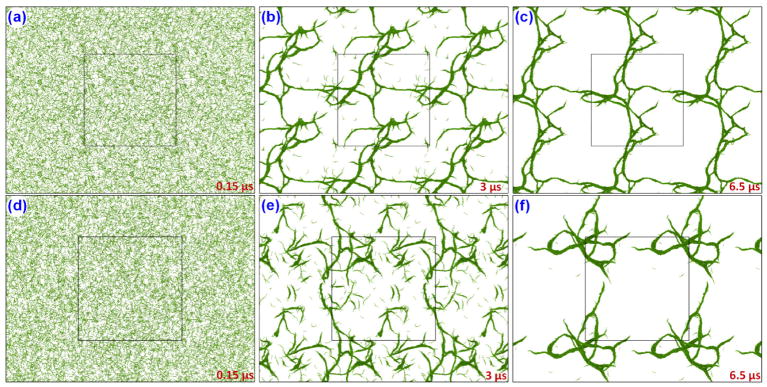
In the next step of the simulations, we have considered A = −40 and B = 25 and 1 μm cubic system for studying polymerization at micro scale. The equilibrated (for 0.5 μs) system with periodic images around it is shown in Fig. 9a and 9d. In the first set of simulations (fast bonding case) the bonding algorithm is applied at every 10 steps (10 ps) and for the second set of simulations (slow bonding case) the same is applied at every 1000 steps (1 ns). The results of these simulations at 3 μs and 6.5 μs is shown in Fig. 9b,e and Fig. 9c,f for fast and slow bonding cases respectively. In the fast bonding case, the bond formation makes it difficult to move around and make further connections and it thus leaner in nature. But in the case of slow bonding case, the fiber like structures tend to attract to each other forming clusters of fibrin polymers. These studies show how the interaction strength and bonding plays important role in the formation of fibrin clots.
Figure 9.
Fibrin polymerization in a 1 μm cubic system for fast bonding (first row) and slow bonding (second row) cases. The screenshots are taken with periodic images (master cell is shown in the center). The time evolution of the fibrin clot formation is shown at (a) 0.15 μs, (b) 3 μs, (c) 6.5 μs for fast bonding case and at (d–f) for slow bonding case.
To simulate a more physiologically similar case, we have made a case study in which the fibrin monomers were kept very low initially. The total number of fibrinogens in the 1 μm cubic system is divided into 15 groups. In the beginning only 1 group is turned into fibrin monomers, which participates in bonding and the rest won’t. At every 250000 steps (0.25 μs) another group of fibrinogens are converted to fibrin monomers. Once all groups are converted to fibrins the simulation will be continued for another 2,500,000 steps (2.5 μs). This strategy can mimic the conversion of fibrinogen to fibrin in the presence of thrombin to an extent. The converted fibrin monomers will interact each other and will start forming oligomers and protofibrils which eventually form fibrin fibers.
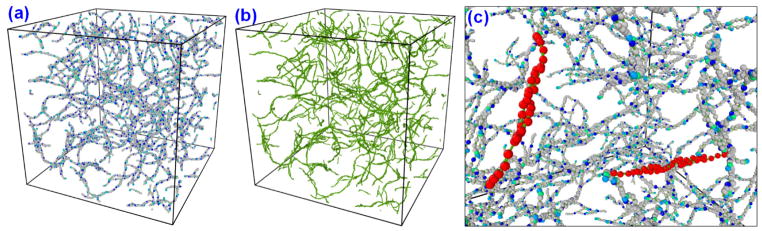
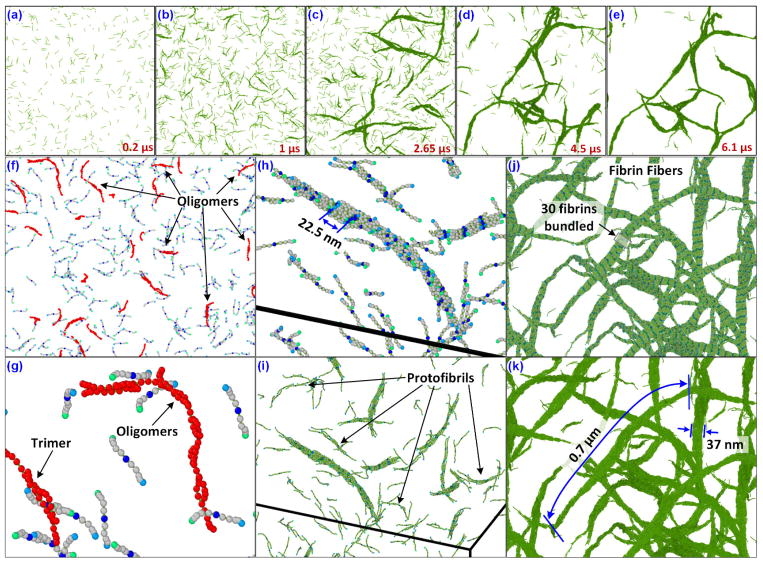
A time elapsed screenshot of the system at various stages of the simulation is shown in the Fig. 10a–e. Initially the number of fibrin monomers were small in number and gradually as the numbers started increasing, they formed into oligomers, protofibrils and eventually as fibrin-fiber like complex structures. The formation of trimers, oligomers are shown in the Fig. 10f,g. This is consistent with the confocal and scanning electron microscope experiments (Baradet et al. 1995; Weisel 2004). In addition, some important characteristics of the fibrin fibers, to include periodicity of the fibrin monomers as 22.5 nm, and bundling of fibrin monomers to form thicker fibers etc. are observed from our simulations (Fig. 10h–k). The length of the fibrin fibers formed is estimated with a maximum of 0.7 μm which is of the same order of magnitude observed in experiments (Baradet et al. 1995; Ryan et al. 1999).
Figure 10.
Presence of the fibrin monomers (in green, beads and fibrinogens hidden for clarity) is shown at (a) 0.2 μs, (b) 1 μs, (c) 2.65 μs, (d) 4.5 μs and (e) 6.1 μs. (f) Formation of fibrin oligomers and trimers are shown with a close-up view (g). The formation of the protofibrils are marked in (i) and the pitch length of the fibrils are estimated as 22.5 nm (h). (j) The cross sections of the fiber-like structures consisted of 30 fibrins with a diameter of 37 nm, and (k) the maximum length of the fibers before branching is 0.7 μm.
The fibrin length and diameters deduced from experiments vary based on a number of factors like concentration of fibrinogen, concentration of salts, presence of pH stabilizers, concentration of thrombin etc. This makes the values of fiber lengths between the junctions of the clot structures varying between 0.9 μm and 1.7 μm in the SEM results (Baradet et al. 1995; Ryan et al. 1999).
Limitations and possible improvements
The MDPD modeling of the fibrin system has successfully simulated the major steps of the polymerization process. Also, the results are in direct corroboration with the experimentally observed data. The improvised solvent free method has enabled us to simulate micro length scales and time scales with 12 CPUs in a week’s time. This study can be the starting point of fibrin polymerization studies, which can find applications in modeling of fibrin clot formation under cardiovascular disease conditions.
Some of the improvements in the model can be the estimation of the attraction parameter based on physiological data. Our current understanding of the time scales of thrombin activation can be utilized to perform this. Another improvement can be the simulation of large systems and varying concentrations of fibrinogens in the system. One shortcoming of the current studies is that the diameter of the fibrin fibers are not matching exactly with the experiments. Effect of presence of free fibrins available for clotting has to be investigated to rectify this. Another improvement area is the consideration of the blood factors. Currently our system doesn’t capture the effects of FXIIIa and others explicitly, but they are simulated instead using the attractive part of the many body DPD potential.
6. Conclusions
We developed a reactive many body dissipative particle dynamics (RDPD) method to simulate fibrin polymerization into a fibrillary network structure. The coarse grain model of fibrinogen with 11 beads interconnected through springs was developed from atomic model using Boltzmann Inversion method. Intra molecular parameters were characterized using the shape based coarse grain method. We have utilized the conventional DPD and the MDPD for simulating the polymerization. In conventional DPD, the coarse grain model was used in conjunction with distance based bonding criteria and a soft attractive Coulombic potential to simulate the polymerization. The force field parameters of this new method were characterized by validating the pressure, temperature and self-diffusion coefficient from experimental values from the literature. In the second approach, using many body DPD (MDPD), the coarse grain model was combined with bonding criteria and applied to micrometer scale systems and performed simulations for several micro seconds. The results from our simulations are in agreement with the experiments including the length of the fibrin fibers and branching of the fibers. We could simulate the important stages of the clot formation like trimer formation, oligomer formation, protofibrils formation, lateral aggregation towards the formation of fibrin fibers. To our knowledge, this is the first successful attempt on the polymerization of the fibrin clot using simple force fields and without using multiscale coupling, and this research can serve as the example to perform polymerization studies of chain molecules using RDPD. Also, this study weighs the use of MDPD method over conventional DPD method for simulating polymerization of long chain molecules.
Acknowledgments
Research reported in this publication was supported by the National Heart, Lung, and Blood Institute of the National Institutes of Health under Award Number K01HL115486. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This study was also supported in part by resources and technical expertise from the Georgia Advanced Computing Resource Center (GACRC), a partnership between the University of Georgia’s Office of the Vice President for Research and Office of the Vice President for Information Technology.
Footnotes
Conflict of Interest
The authors declare that they have no conflict of interest.
Supplementary material
A movie is available showing the formation of the fibrin clot using the reactive many body dissipative particle dynamics method.
References
- Agnelli G. Prevention of venous thromboembolism in surgical patients. Circulation. 2004;110:IV4–12. doi: 10.1161/01.CIR.0000150639.98514.6c. [DOI] [PubMed] [Google Scholar]
- Anderson FA, Jr, Spencer FA. Risk factors for venous thromboembolism. Circulation. 2003;107:I9–16. doi: 10.1161/01.CIR.0000078469.07362.E6. [DOI] [PubMed] [Google Scholar]
- Arkhipov A, Freddolino PL, Schulten K. Stability and dynamics of virus capsids described by coarse-grained modeling. Structure. 2006;14:1767–1777. doi: 10.1016/j.str.2006.10.003. [DOI] [PubMed] [Google Scholar]
- Aronow WS. The prevention of venous thromboembolism in older adults: guidelines. The journals of gerontology Series A, Biological sciences and medical sciences. 2004;59:42–47. doi: 10.1093/gerona/59.1.m42. [DOI] [PubMed] [Google Scholar]
- Averett RD, Menn B, Lee EH, Helms CC, Barker T, Guthold M. A Modular Fibrinogen Model that Captures the Stress-Strain Behavior of Fibrin Fibers. Biophysical Journal. 2012;103:1537–1544. doi: 10.1016/j.bpj.2012.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajpai AK. Fibrinogen adsorption onto macroporous polymeric surfaces: correlation with biocompatibility aspects Journal of materials science. Materials in medicine. 2008;19:343–357. doi: 10.1007/s10856-006-0024-y. [DOI] [PubMed] [Google Scholar]
- Baradet TC, Haselgrove JC, Weisel JW. Three-dimensional reconstruction of fibrin clot networks from stereoscopic intermediate voltage electron microscope images and analysis of branching. Biophysical journal. 1995;68:1551–1560. doi: 10.1016/S0006-3495(95)80327-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baranowska HM, Olszewski KJ. The hydration of proteins in solutions by self-diffusion coefficients NMR study. Bba-Gen Subjects. 1996;1289:312–314. doi: 10.1016/0304-4165(95)00141-7. [DOI] [PubMed] [Google Scholar]
- Beutler TC, Mark AE, van Schaik RC, Gerber PR, van Gunsteren WF. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem Phys Lett. 1994;222:529–539. [Google Scholar]
- Bode W, Mayr I, Baumann U, Huber R, Stone SR, Hofsteenge J. The refined 1.9 A crystal structure of human alpha-thrombin: interaction with D-Phe-Pro-Arg chloromethylketone and significance of the Tyr-Pro-Pro-Trp insertion segment. The EMBO journal. 1989;8:3467–3475. doi: 10.1002/j.1460-2075.1989.tb08511.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boryczko K, Dzwinel W, Yuen DA. Modeling fibrin aggregation in blood flow with discrete-particles. Computer methods and programs in biomedicine. 2004;75:181–194. doi: 10.1016/j.cmpb.2004.02.001. [DOI] [PubMed] [Google Scholar]
- Brambilla S, Ruosi C, La Maida GA, Caserta S. Prevention of venous thromboembolism in spinal surgery. European spine journal: official publication of the European Spine Society, the European Spinal Deformity Society, and the European Section of the Cervical Spine Research Society. 2004;13:1–8. doi: 10.1007/s00586-003-0538-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown AC, Barker TH. Fibrin-based biomaterials: Modulation of macroscopic properties through rational design at the molecular level. Acta Biomater. 2014;10:1502–1514. doi: 10.1016/j.actbio.2013.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castner DG, Ratner BD. Biomedical surface science: Foundations to frontiers. Surf Sci. 2002;500:28–60. doi: 10.1016/S0039-6028(01)01587-4. Pii S0039-6028(01)01587-4. [DOI] [Google Scholar]
- Chueh JY, Kuhn AL, Puri AS, Wilson SD, Wakhloo AK, Gounis MJ. Reduction in distal emboli with proximal flow control during mechanical thrombectomy: a quantitative in vitro study. Stroke. 2013;44:1396–1401. doi: 10.1161/STROKEAHA.111.670463. [DOI] [PubMed] [Google Scholar]
- Chueh JY, Wakhloo AK, Hendricks GH, Silva CF, Weaver JP, Gounis MJ. Mechanical characterization of thromboemboli in acute ischemic stroke and laboratory embolus analogs. AJNR American journal of neuroradiology. 2011;32:1237–1244. doi: 10.3174/ajnr.A2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cimminiello C, Planes A, Samama MM. Prevention of venous thromboembolism after orthopedic surgery: the EXPRESS study. Journal of thrombosis and haemostasis: JTH. 2004;2:2036–2040. doi: 10.1111/j.1538-7836.2004.01006.x. [DOI] [PubMed] [Google Scholar]
- Collins R, Scrimgeour A, Yusuf S, Peto R. Reduction in fatal pulmonary embolism and venous thrombosis by perioperative administration of subcutaneous heparin. Overview of results of randomized trials in general, orthopedic, and urologic surgery. The New England journal of medicine. 1988;318:1162–1173. doi: 10.1056/NEJM198805053181805. [DOI] [PubMed] [Google Scholar]
- Cupelli C, Henrich B, Glatzel T, Zengerle R, Moseler M, Santer M. Dynamic capillary wetting studied with dissipative particle dynamics. New J Phys. 2008;10 doi: 10.1088/1367-2630/10/4/043009. Artn 043009. [DOI] [Google Scholar]
- Davison SP, Venturi ML, Attinger CE, Baker SB, Spear SL. Prevention of venous thromboembolism in the plastic surgery patient. Plastic and reconstructive surgery. 2004;114:43E–51E. doi: 10.1097/01.prs.0000131276.48992.ee. [DOI] [PubMed] [Google Scholar]
- Doolittle RF. Fibrinogen and Fibrin. Annu Rev Biochem. 1984;53:195–229. doi: 10.1146/annurev.bi.53.070184.001211. [DOI] [PubMed] [Google Scholar]
- Dowling NF, Austin H, Dilley A, Whitsett C, Evatt BL, Hooper WC. The epidemiology of venous thromboembolism in Caucasians and African-Americans: the GATE Study. Journal of thrombosis and haemostasis: JTH. 2003;1:80–87. doi: 10.1046/j.1538-7836.2003.00031.x. [DOI] [PubMed] [Google Scholar]
- Eriksson BI, Dahl OE. Prevention of venous thromboembolism following orthopaedic surgery: clinical potential of direct thrombin inhibitors. Drugs. 2004;64:577–595. doi: 10.2165/00003495-200464060-00002. [DOI] [PubMed] [Google Scholar]
- Fox BA, Yee VC, Pedersen LC, Le Trong I, Bishop PD, Stenkamp RE, Teller DC. Identification of the calcium binding site and a novel ytterbium site in blood coagulation factor XIII by x-ray crystallography. The Journal of biological chemistry. 1999;274:4917–4923. doi: 10.1074/jbc.274.8.4917. [DOI] [PubMed] [Google Scholar]
- Freddolino PL, Arkhipov A, Shih AY, Yin Y, Chen Z, Schulten K. Application of residue-based and shape-based coarse graining to biomolecular simulations. Coarse-graining of condensed phase and biomolecular systems. 2008:299–315. [Google Scholar]
- Fukue H, Anderson K, McPhedran P, Clyne L, McDonagh J. A unique factor XIII inhibitor to a fibrin-binding site on factor XIIIA. Blood. 1992;79:65–74. [PubMed] [Google Scholar]
- Geerts WH, Pineo GF, Heit JA, Bergqvist D, Lassen MR, Colwell CW, Ray JG. Prevention of venous thromboembolism: the Seventh ACCP Conference on Antithrombotic and Thrombolytic Therapy. Chest. 2004;126:338S–400S. doi: 10.1378/chest.126.3_suppl.338S. [DOI] [PubMed] [Google Scholar]
- Ghoufi A, Emile J, Malfreyt P. Recent advances in Many Body Dissipative Particles Dynamics simulations of liquid-vapor interfaces. Eur Phys J E. 2013;36 doi: 10.1140/Epje/I2013-13010-7. Artn 10. [DOI] [PubMed] [Google Scholar]
- Gounis MJ, Nogueira RG, Mehra M, Chueh J, Wakhloo AK. A thromboembolic model for the efficacy and safety evaluation of combined mechanical and pharmacologic revascularization strategies. Journal of neurointerventional surgery. 2013;5(Suppl 1):i85–89. doi: 10.1136/neurintsurg-2012-010435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg CS, Dobson JV, Miraglia CC. Regulation of plasma factor XIII binding to fibrin in vitro. Blood. 1985;66:1028–1034. [PubMed] [Google Scholar]
- Greer IA. Prevention of venous thromboembolism in pregnancy. European journal of medical research. 2004;9:135–145. [PubMed] [Google Scholar]
- Groot RD, Warren PB. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. The Journal of chemical physics. 1997;107:4423–4435. [Google Scholar]
- Hall CE, Slayter HS. The fibrinogen molecule: its size, shape, and mode of polymerization. The Journal of biophysical and biochemical cytology. 1959;5:11–16. doi: 10.1083/jcb.5.1.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoover WG. Canonical Dynamics: Equilibrium Phase-Space Distributions. Physical Review A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. Journal of molecular graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Iorio A. Prevention of venous thromboembolism after major orthopedic surgery: summing up evidence about old and new antithrombotic agents. Journal of thrombosis and haemostasis: JTH. 2004;2:1055–1057. doi: 10.1111/j.1538-7836.2004.00753.x. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Li J, Liu Y, Li YC, Zhang WG. Risk factors for deep vein thrombosis after orthopedic surgery and the diagnostic value of D-dimer. Annals of vascular surgery. 2015;29:675–681. doi: 10.1016/j.avsg.2014.12.022. [DOI] [PubMed] [Google Scholar]
- Kakkar VV, De Lorenzo F. Prevention of venous thromboembolism in general surgery. Bailliere’s clinical haematology. 1998;11:605–619. doi: 10.1016/s0950-3536(98)80085-1. [DOI] [PubMed] [Google Scholar]
- Kearon C. Epidemiology of postoperative venous thromboembolism: lessons from an administrative data base. Thrombosis and haemostasis. 2003;90:367–368. [PubMed] [Google Scholar]
- Kollman JM, Pandi L, Sawaya MR, Riley M, Doolittle RF. Crystal structure of human fibrinogen. Biochemistry. 2009;48:3877–3886. doi: 10.1021/bi802205g. [DOI] [PubMed] [Google Scholar]
- Kroegel C, Reissig A. Principle mechanisms underlying venous thromboembolism: epidemiology, risk factors, pathophysiology and pathogenesis. Respiration; international review of thoracic diseases. 2003;70:7–30. doi: 10.1159/000068427. 68427. [DOI] [PubMed] [Google Scholar]
- Kyrle PA, Eichinger S. Deep vein thrombosis. Lancet. 2005;365:1163–1174. doi: 10.1016/S0140-6736(05)71880-8. [DOI] [PubMed] [Google Scholar]
- Lam WA, et al. Mechanics and contraction dynamics of single platelets and implications for clot stiffening. Nature materials. 2011;10:61–66. doi: 10.1038/nmat2903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AY. Epidemiology and management of venous thromboembolism in patients with cancer. Thrombosis research. 2003;110:167–172. doi: 10.1016/s0049-3848(03)00347-5. [DOI] [PubMed] [Google Scholar]
- Li F, Wang X, Huang W, Ren W, Cheng J, Zhang M, Zhao Y. Risk factors associated with the occurrence of silent pulmonary embolism in patients with deep venous thrombosis of the lower limb. Phlebology. 2014;29:442–446. doi: 10.1177/0268355513487331. [DOI] [PubMed] [Google Scholar]
- Li Z, Hu GH, Wang ZL, Ma YB, Zhou ZW. Three dimensional flow structures in a moving droplet on substrate: A dissipative particle dynamics study. Phys Fluids. (25) 2013 doi: 10.1063/1.4812366. Artn 072103. [DOI] [Google Scholar]
- Liu CY. Mechanism of thrombin binding by fibrin. Annals of the New York Academy of Sciences. 1981;370:545–550. doi: 10.1111/j.1749-6632.1981.tb29762.x. [DOI] [PubMed] [Google Scholar]
- Liu CY, Nossel HL, Kaplan KL. The binding of thrombin by fibrin. The Journal of biological chemistry. 1979;254:10421–10425. [PubMed] [Google Scholar]
- Liu LP, et al. Risk assessment of deep-vein thrombosis after acute stroke: a prospective study using clinical factors. CNS neuroscience & therapeutics. 2014;20:403–410. doi: 10.1111/cns.12227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo ZH, et al. Creation of fibrinogen-enhanced experimental blood clots to evaluate mechanical thrombectomy devices for treatment of acute stroke: an in vitro study. Journal of vascular and interventional radiology: JVIR. 2012;23:1077–1083. doi: 10.1016/j.jvir.2012.04.031. [DOI] [PubMed] [Google Scholar]
- Ma L, Wen Z. Risk factors and prognosis of pulmonary embolism in patients with lung cancer. Medicine. 2017;96:e6638. doi: 10.1097/MD.0000000000006638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinetz T, Schulten K. Topology Representing Networks. Neural Networks. 1994;7:507–522. doi: 10.1016/0893-6080(94)90109-0. [DOI] [Google Scholar]
- Martinez MCL, Rodes V, Delatorre JG. Estimation of the Shape and Size of Fibrinogen in Solution from Its Hydrodynamic Properties Using Theories for Bead Models and Cylinders. International journal of biological macromolecules. 1984;6:261–265. doi: 10.1016/0141-8130(84)90005-9. [DOI] [Google Scholar]
- MathWorks I. MATLAB and Statistics Toolbox Release. Natick, MA: The MathWorks; 2012. [Google Scholar]
- Michetti CP, Franco E, Coleman J, Bradford A, Trickey AW. Deep vein thrombosis screening and risk factors in a high-risk trauma population. The Journal of surgical research. 2015;199:545–551. doi: 10.1016/j.jss.2015.04.069. [DOI] [PubMed] [Google Scholar]
- Mills R. Self-diffusion in normal and heavy water in the range 1–45. deg. The Journal of Physical Chemistry. 1973;77:685–688. [Google Scholar]
- Minnema MC, et al. Prevention of venous thromboembolism with low molecular-weight heparin in patients with multiple myeloma treated with thalidomide and chemotherapy. Leukemia. 2004;18:2044–2046. doi: 10.1038/sj.leu.2403533. [DOI] [PubMed] [Google Scholar]
- Mismetti P, Laporte S, Zufferey P, Epinat M, Decousus H, Cucherat M. Prevention of venous thromboembolism in orthopedic surgery with vitamin K antagonists: a meta-analysis. Journal of thrombosis and haemostasis: JTH. 2004;2:1058–1070. doi: 10.1111/j.1538-7836.2004.00757.x. [DOI] [PubMed] [Google Scholar]
- Moftakhar P, et al. Density of thrombus on admission CT predicts revascularization efficacy in large vessel occlusion acute ischemic stroke. Stroke. 2013;44:243–245. doi: 10.1161/STROKEAHA.112.674127. [DOI] [PubMed] [Google Scholar]
- Moiseyev G, Bar-Yoseph PZ. Computational modeling of thrombosis as a tool in the design and optimization of vascular implants. J Biomech. 2013;46:248–252. doi: 10.1016/j.jbiomech.2012.11.002. [DOI] [PubMed] [Google Scholar]
- Muller M, Burchard W. Quasi-Elastic Light-Scattering from Fibrinogen and Fibrin Intermediate Structures. International journal of biological macromolecules. 1981;3:71–76. doi: 10.1016/0141-8130(81)90070-2. [DOI] [Google Scholar]
- Murday J, Cotts R. Self-Diffusion in Liquids: H2O, D2O, and Na. The Journal of Chemical Physics. 1970;53:4724–4725. [Google Scholar]
- Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Molecular physics. 1984;52:255–268. [Google Scholar]
- Palmer G, Fritz O, Hallett F. Quasielastic light-scattering studies on human fibrinogen and fibrin. I. Fibrinogen Biopolymers. 1979;18:1647–1658. [Google Scholar]
- Pechik I, Madrazo J, Mosesson MW, Hernandez I, Gilliland GL, Medved L. Crystal structure of the complex between thrombin and the central “E” region of fibrin P. Natl Acad Sci USA. 2004;101:2718–2723. doi: 10.1073/pnas.0303440101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips JC, et al. Scalable molecular dynamics with NAMD. Journal of computational chemistry. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plimpton S, Crozier P, Thompson A. LAMMPS-large-scale atomic/molecular massively parallel simulator. Sandia National Laboratories; 2007. p. 18. [Google Scholar]
- Qiu Y, Ciciliano J, Myers DR, Tran R, Lam WA. Platelets and physics: How platelets “feel” and respond to their mechanical microenvironment. Blood reviews. 2015;29:377–386. doi: 10.1016/j.blre.2015.05.002. [DOI] [PubMed] [Google Scholar]
- Rose T, Di Cera E. Three-dimensional modeling of thrombin-fibrinogen interaction. The Journal of biological chemistry. 2002;277:18875–18880. doi: 10.1074/jbc.M110977200. [DOI] [PubMed] [Google Scholar]
- Ryan EA, Mockros LF, Weisel JW, Lorand L. Structural origins of fibrin clot rheology. Biophysical Journal. 1999;77:2813–2826. doi: 10.1016/s0006-3495(99)77113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool Model. Simul Mater Sc. 2010;18 doi: 10.1088/0965-0393/18/1/015012. Artn 015012. [DOI] [Google Scholar]
- Sutton JT, Ivancevich NM, Perrin SR, Jr, Vela DC, Holland CK. Clot Retraction Affects the Extent of Ultrasound-Enhanced Thrombolysis in an Ex Vivo Porcine Thrombosis Model. Ultrasound in Medicine & Biology. 2013;39:813–824. doi: 10.1016/j.ultrasmedbio.2012.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka K. Measurements of Self-Diffusion Coefficients of Water in Pure Water and in Aqueous-Electrolyte Solutions. J Chem Soc Farad T 1. 1975;71:1127–1131. doi: 10.1039/F19757101127. [DOI] [Google Scholar]
- Tofts P, et al. Test liquids for quantitative MRI measurements of self-diffusion coefficient in vivo. Magnetic resonance in medicine. 2000;43:368–374. doi: 10.1002/(sici)1522-2594(200003)43:3<368::aid-mrm8>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- Tomaru T, Uchida Y, Masuo M, kato A, Sugimoto T. Experimental canine arterial thrombus formation and thrombolysis: A fiberoptic study. American Heart Journal. 1987;114:63–69. doi: 10.1016/0002-8703(87)90308-5. [DOI] [PubMed] [Google Scholar]
- Verlet L. Computer Experiments on Classical Fluids .I. Thermodynamical Properties of Lennard-Jones. Molecules Phys Rev. 1967;159:98. doi: 10.1103/Physrev.159.98. [DOI] [Google Scholar]
- Wang CY, et al. Risk factors and clinical features of acute pulmonary embolism in children from the community. Thrombosis research. 2016;138:86–90. doi: 10.1016/j.thromres.2015.12.005. [DOI] [PubMed] [Google Scholar]
- Wang J. Self-diffusion and structure of liquid water. I. Measurement of self-diffusion of liquid water with deuterium as tracer. Journal of the American Chemical Society. 1951;73:510–513. [Google Scholar]
- Wang JH. Self-Diffusion Coefficients of Water. Journal of Physical Chemistry. 1965;69:4412. doi: 10.1021/J100782a510. [DOI] [Google Scholar]
- Wang WW, King MR. Multiscale Modeling of Platelet Adhesion and Thrombus Growth. Annals of biomedical engineering. 2012;40:2345–2354. doi: 10.1007/s10439-012-0558-8. [DOI] [PubMed] [Google Scholar]
- Weisel JW. Fibrin assembly. Lateral aggregation and the role of the two pairs of fibrinopeptides. Biophys J. 1986;50:1079–1093. doi: 10.1016/S0006-3495(86)83552-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisel JW. The mechanical properties of fibrin for basic scientists and clinicians. Biophysical Chemistry. 2004;112:267–276. doi: 10.1016/j.bpc.2004.07.029. [DOI] [PubMed] [Google Scholar]
- White RH. The epidemiology of venous thromboembolism. Circulation. 2003;107:I4–8. doi: 10.1161/01.CIR.0000078468.11849.66. [DOI] [PubMed] [Google Scholar]
- Wiltzius P, Dietler G, Kanzig W, Haberli A, Straub PW. Fibrin polymerization studied by static and dynamic light-scattering as a function of fibrinopeptide A release. Biopolymers. 1982;21:2205–2223. doi: 10.1002/bip.360211109. [DOI] [PubMed] [Google Scholar]
- Yamaguchi T, Ishikawa T, Imai Y, Matsuki N, Xenos M, Deng Y, Bluestein D. Particle-based methods for multiscale modeling of blood flow in the circulation and in devices: challenges and future directions. Sixth International Bio-Fluid Mechanics Symposium and Workshop March 28–30, 2008 Pasadena, California. Annals of biomedical engineering. 2010;38:1225–1235. doi: 10.1007/s10439-010-9904-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, et al. Incidence and risk factors of deep vein thrombosis (DVT) after total hip or knee arthroplasty: a retrospective study with routinely applied venography. Blood coagulation & fibrinolysis: an international journal in haemostasis and thrombosis. 2017;28:126–133. doi: 10.1097/MBC.0000000000000556. [DOI] [PubMed] [Google Scholar]