Efficient Injection and Detection of Out-of-Plane Spins via the Anomalous Spin Hall Effect in Permalloy Nanowires

Abstract

We report a novel mechanism for the electrical injection and detection of out-of-plane spin accumulation via the anomalous spin Hall effect (ASHE), where the direction of the spin accumulation can be controlled by manipulating the magnetization of the ferromagnet. This mechanism is distinct from the spin Hall effect (SHE), where the spin accumulation is created along a fixed direction parallel to an interface. We demonstrate this unique property of the ASHE in nanowires made of permalloy (Py) to inject and detect out-of-plane spin accumulation in a magnetic insulator, yttrium iron garnet (YIG). We show that the efficiency for the injection/detection of out-of-plane spins can be up to 50% of that of in-plane spins. We further report the possibility to detect spin currents parallel to the Py/YIG interface for spins fully oriented in the out-of-plane direction, resulting in a sign reversal of the nonlocal magnon spin signal. The new mechanisms that we have demonstrated are highly relevant for spin torque devices and applications.

Electrical injection and detection of spin currents play an essential role for the technological implementation of spintronics. The conventional way of electrical spin injection is by driving a spin-polarized current from a ferromagnet into a normal metal.¹ This method, however, is limited in the scalability and direction of the injected spin current, which is parallel to the charge current and has motivated the study of alternative methods based on the spin Hall effect (SHE) present in heavy nonmagnetic metals.^2,3 The SHE generates a spin current perpendicular to a charge current, which is particularly significant for spin torque applications⁴⁻⁸ and for spin injection into magnetic insulators.⁹⁻¹¹

However, the spin direction of the spin accumulation generated via the SHE is fixed, parallel to the interface, depending only on the direction of the charge current through the heavy nonmagnetic metal [Figure 1a]. Alternatively, the anomalous Hall effect¹² in ferromagnetic metals can be used as a tunable source of transverse spin current, as has been theoretically predicted¹³⁻¹⁵ and recently demonstrated experimentally.¹⁶⁻¹⁹ We call this phenomenon the anomalous spin Hall effect (ASHE), which generates a spin accumulation oriented parallel to the ferromagnet’s magnetization [Figure 1b–d]. In principle, the ASHE provides a novel way of electrically injecting and detecting a spin accumulation with out-of-plane components, which can be controlled by manipulating the ferromagnet’s magnetization.

Figure 1.

Schematic illustration of (a) the spin Hall effect (SHE) in a metal with high spin–orbit coupling, and (b–d) the anomalous spin Hall effect (ASHE) in a ferromagnetic metal for three different orientations of the ferromagnet’s magnetization (M) and a fixed charge current (I). The magnitude and the direction of the spin current generated due to the ASHE is given by M × I, with the spin accumulation direction parallel to M. Spin accumulation with both in-plane and out-of-plane components is generated at the bottom interface when M tilts out of the plane, as shown in (c). The contribution of the out-of-plane component of the spin accumulation at the bottom interface is given by sin θ cos θ and reaches a maximum of 50% when θ = 45°, compared to the contribution of the in-plane spin component at the bottom interface when θ = 0°. Spin accumulation exclusively oriented perpendicular to the top/bottom interface is achieved at the edges when M is oriented completely in the out-of-plane direction, as shown in (d). The dashed arrows indicate the directions of the spin current.

Here, we experimentally demonstrate the versatility of the ASHE for electrically injecting and detecting spin accumulation oriented in arbitrary directions, parallel to the ferromagnet’s magnetization, in a proof-of-concept device geometry. We utilize the ASHE in a nanowire made of a ferromagnetic metal, permalloy (Ni₈₀Fe₂₀, Py), to inject a magnon spin accumulation in a magnetic insulator, yttrium iron garnet (Y₃Fe₅O₁₂, YIG). The injected magnon spins are electrically detected at a second Py nanowire. This nonlocal geometry, shown in Figure 2a, and the insulating property of the YIG film ensure that we exclusively address spin-dependent effects, free from magnetoresistance due to the magnetization of the Py nanowire (M_Py). Moreover, the YIG film serves as a selector of the spin components from the Py injector because only the spin component parallel to the YIG magnetization (M_YIG) will result in the generation of magnon spin accumulation in the YIG film.⁹ We apply an external magnetic field (B) at different out-of-plane angles for the distinct manipulation of the magnetizations M_Py and M_YIG. Therefore, we control both the direction of the injected and detected spin accumulation generated by the ASHE (parallel to M_Py) and the efficiency of the magnon injection and detection process (via the projection of M_Py on M_YIG). Furthermore, we detect a finite nonlocal signal with a negative sign when both M_Py and M_YIG are oriented fully perpendicular to the sample (xy) plane. We attribute this to a second mechanism of generation and detection of horizontal spin currents, parallel to the Py/YIG interface. The efficiency of this injection/detection mechanism is maximum when the spins are fully oriented in the out-of-plane direction. Besides its possible use for magnon transistor and magnon-based logic operations,²⁰⁻²² this model system is also highly relevant for spin torque applications.⁴⁻⁸

Figure 2.

(a) Schematic illustration of the experimental geometry. The ASHE and its reciprocal effect in Py are used to inject and detect magnons in the YIG film. An external magnetic field (B) is applied in the xz-plane at an angle ϕ with respect to the x-axis to manipulate the magnetizations of Py (M_Py) and YIG (M_YIG). (b) SEM image of a representative device illustrating the electrical connections. An alternating current (I) is sourced through the injector (middle Py nanowire). The corresponding nonlocal voltages across the left Py detector (V_Py) and the right Pt detector (V_Pt) are measured simultaneously. (c,d) The first harmonic response of the nonlocal resistance (R_NL^1f) is plotted as a function of B applied at different angles (ϕ, measured by the Py detector (c) and the Pt detector (d). Symbols represent experimental data, while solid black lines are modeled curves following eq 1 and eq 2 for the Py and the Pt detectors, respectively.

The devices were patterned using electron beam lithography on a 210 nm thick YIG film, grown on a GGG (Gd₃Ga₅O₁₂) substrate by liquid-phase epitaxy. A scanning electron microscope (SEM) image of a representative device is shown in Figure 2b. The devices consist of two Py nanowires (left and middle) and one Pt nanowire (right) with thicknesses of 9 nm (Py) and 7 nm (Pt), respectively. The Py and the Pt nanowires were deposited by dc sputtering in Ar⁺ plasma. Electron beam evaporation was used to deposit the Ti/Au leads and bonding pads following the final lithography step (see Supporting Information Section 4 for additional details on device fabrication). The middle Py nanowire is used as the spin injector, while the outer Py and Pt nanowires are used as detectors. The width of the middle Py injector is 200 nm and that of the outer Py and Pt detectors is 400 nm. The edge-to-edge distance between the injector and the detectors is 500 nm. The electrical connections are also depicted in Figure 2b. An alternating current (I) with an rms amplitude of 310 μA and frequency of 5.5 Hz is sourced through the middle Py injector. The nonlocal voltages across the left Py detector (V_Py) and the right Pt detector (V_Pt) are simultaneously recorded by a phase-sensitive lock-in detection technique. The first harmonic response (1f) of the nonlocal voltage corresponds to the linear-regime electrical spin injection and detection via the (A)SHE and their reciprocal processes. The second harmonic (2f) response, driven by Joule heating at the injector and proportional to I², corresponds to the thermally generated magnons near the injector via the spin Seebeck effect (SSE)^9,23 which travel to the detector. At the Py detector, a lateral temperature gradient along the x-axis also contributes to an electrical signal via the anomalous Nernst effect (ANE).^24,25 The nonlocal voltage [V^1(2)f] measured across the detectors has been normalized by the injection current (I) for the first harmonic response (R_NL^1f = V^1f/I) and by I² for the second harmonic response (R_NL = V^2f/I²). The experiments have been conducted in a low vacuum atmosphere at 293 K.

To explore the injection/detection of out-of-plane spins, we performed magnetic field (B) sweeps within the xz-plane at different angles ϕ with respect to the x-axis [see Figure 2a]. The first harmonic responses (R_NL^1f) measured by the Py and the Pt detectors are plotted as a function of B in Figure 2c,d, respectively. R_NL comprises of magnon spin injection and detection due to two different mechanisms: (i) SHE (independent of M_Py) and (ii) ASHE (maximum contribution when M_Py is perpendicular to I).¹⁶ The SHE results in a constant spin accumulation oriented along the x-axis at the bottom interface of the injector, which leads to a maximum magnon spin injection when M_YIG is also oriented parallel to the x-axis. Because the YIG film has a small in-plane coercivity of less than 1 mT, M_YIG will be oriented along the x-axis at low magnetic fields. This gives rise to a signal of 0.35 mΩ at the Py detector [Figure 2c] and 1.30 mΩ at the Pt detector [Figure 2d] for B ∼ 0. At such low fields, M_Py is oriented along the Py nanowire (y-axis) due to shape anisotropy, thus only the SHE contributes to the magnon injection and detection processes. The ASHE starts to contribute when M_Py has a component oriented perpendicular to I, and becomes maximum when M_Py is parallel to the x-axis [see Figure 1b]. Therefore, the maximum nonlocal signal is attained for ϕ = 0° when B > 50 mT, corresponding to M_Py oriented along the x-axis.¹⁶

As the angle ϕ is increased, the z-components of M_Py (M_Py^z) and M_YIG (M_YIG) increase, while the x-components (M_Py^x and M_YIG) decrease. The schematic shown in Figure 1c depicts the case when M_Py is oriented at an angle θ with respect to the positive x-axis, such that 0° < θ < 90°. The contribution of the out-of-plane spin component to the spin accumulation at the bottom interface is given by sin θ cos θ and reaches a maximum of 50% when θ = 45°, compared to that of the in-plane spin component (given by cos² θ) when θ = 0°. When M_Py is oriented fully perpendicular to the bottom interface [Figure 1d], spin accumulation with only out-of-plane components are created at the left and right edges of the Py nanowire. In this case, the spin injection and detection efficiency through the bottom interface is expected to be zero.

However, when B is applied almost perpendicular to the plane of the sample (ϕ = 89°) the first harmonic response R_NL^1f measured by the Py detector changes sign and becomes negative. This result cannot be explained within the standard framework of (SHE driven) transport dominated by in-plane spins, where a vanishing signal is expected.⁹⁻¹¹ We therefore argue that such a negative signal can only be understood by the injection/detection mechanism of spin currents parallel to the x-axis via the ASHE, the efficiency of which is maximized for spins oriented fully along the z-axis [see Figure 1d]. This is consistent with R_NL measured by the Pt detector, which is zero, as expected from the lack of the ASHE detection in the Pt nanowire. Furthermore, we have unambiguously established the linearity (see Supporting Information Section 7 on the absence of any third harmonic response) and the reciprocity (see Supporting Information Section 8 for measurements using a Pt injector and a Py detector) of the nonlocal signal. Thus, a spin accumulation with an exclusively out-of-plane component can only be injected and detected via the ASHE and in our sample geometry results in a distinct negative polarity of the nonlocal signal.

Further understanding is achieved by studying the second harmonic response measured by the Py and Pt detectors, shown in Figure 3a,b, respectively. The temperature gradient generated due to Joule heating at the injector drives the spin Seebeck effect (SSE), and the generated magnons are detected by the Pt nanowire via the inverse spin Hall effect (ISHE) and by the Py detector as a combination of the ISHE and the inverse ASHE. In addition to these spin detection processes, at the Py detector the ANE also contributes to R_NL^2f. Starting with the case ϕ = 0°, when M_Py is oriented along the x-axis, only the SSE contributes to R_NL measured by the Py detector with a negligible ANE contribution due to the small temperature gradient along the z-axis within the Py detector. However, when ϕ ≠ 0° and the z-component of M_Py increases, the ANE starts to dominate and is maximized for ϕ = 90°, whereas the contribution due to the SSE goes down as the x-component of M_YIG decreases. We therefore consider ANE ∝M_Py^z and SSE ∝M_YIG and employ the Stoner–Wohlfarth model²⁶ to extract from R_NL^2f the magnetization behavior of the Py nanowire and the YIG film (see Supporting Information Section 1). From these second harmonic measurements, we conclude the absence of any significant interfacial exchange interaction, which if present would lead to effective exchange fields below 1 mT (see Supporting Information Section 5), in agreement with our previous experimental results.¹⁶ The extracted M_Py and M_YIG^z are plotted as a function of B for different angles ϕ in Figure 3c,d, respectively. The different mechanisms contributing to the second harmonic response have been summarized in the Supporting Information Section 9.

Figure 3.

(a) The second harmonic response of the nonlocal resistance (R_NL^2f) measured by the Py detector has two contributions: the anomalous Nernst effect (ANE) (proportional to M_Py) and the spin Seebeck effect (SSE) (proportional to M_YIG^x). (b) The R_NL measured by the Pt detector is only due to the SSE, which decreases as M_YIG^z increases. M_Py (c) and M_YIG^z (d) are plotted against B for the different out-of-plane angles (ϕ). The magnetizations are extracted from the Stoner–Wohlfarth model by fitting the second harmonic responses (discussed in the Supporting Information).

We use the extracted magnetization behavior of the Py nanowires and the YIG film to model the first harmonic response via the following expressions

1

2

where (M_YIG·M_Py) = (M_YIG^xM_Py + M_YIG^yM_Py + M_YIG^zM_Py) with M_YIG and M_Py being unitary vectors. The coefficients a, b and c can be expressed as 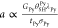, 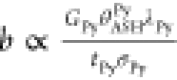and 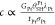.¹⁶ Here, G_Py(Pt), θ_SH^Py(Pt), λ_Py(Pt), t_Py(Pt), and σ_Py(Pt) represent the effective spin mixing conductance for the Py(Pt)/YIG interface, the spin Hall angle, the spin relaxation length, the thickness and the charge conductivity of the Py (Pt) nanowire, respectively. θ_ASH is the anomalous spin Hall angle of Py. For the simulations, we use a = 0.58 (mΩ)^1/2, b = 0.72 (mΩ)^1/2, and c = 2.37 (mΩ)^1/2, which are extracted by fitting the experimental data at ϕ = 0°. This fitting procedure leads to an uncertainty below 10% in determining the values of these parameters, which are consistent with the previously reported values.¹⁶

The first part of eq 1 within the first set of square brackets accounts for the spin current directed perpendicular to the Py/YIG interface, as depicted in Figure 4a. The term with the coefficient a is related to the (constant) spin accumulation along the x-axis due to the SHE in Py, which is independent of M_Py. This term only depends on M_YIG^x since the generation of magnons is proportional to the projection of M_YIG on the spin accumulation direction. The term with the coefficient b is related to the ASHE in Py, which is maximized when M_Py is parallel to the x-axis. The ASHE generates a spin accumulation parallel to M_Py, thus the magnon generation is also proportional to the projection of M_Py on M_YIG. This term includes both the in-plane and the out-of-plane components of the spin accumulation. Since the injection and detection processes are reciprocal, the term within the square brackets is squared.

Figure 4.

(a) Mechanism for spin current injection and detection along the −z and the +z directions, respectively, resulting in a positive nonlocal signal (V_NL). This mechanism has the maximum contribution to V_NL for in-plane spins. (b) Mechanism for spin current injection and the detection along the x-direction, parallel to the Py/YIG interface, resulting in a negative V_NL. This mechanism has the maximum contribution to V_NL for out-of-plane spins. The individual contribution of the two different mechanisms to the nonlocal resistance (R_NL) measured by the Py detector, following eq 1, has been plotted in (c) for the injection and detection of vertical spin current and in (d) for the injection and detection of horizontal spin current.

The second part of eq 1, within the second set of square brackets and preceded by a negative sign, accounts for the spin current parallel to the Py/YIG interface, as depicted in Figure 4b. The contribution of this part to the magnon injection and detection processes is maximum for out-of-plane spins. It is clear from the symmetry of the ASHE and our measurement geometry that the detection of such in-plane spin currents with spins oriented in the out-of-plane direction, will result in a negative nonlocal signal measured by the Py detector [Figure 4a,b]. Moreover, the parameter η tells us the efficiency of detecting spin currents parallel to the interface for out-of-plane spins as compared to that of detecting spin currents perpendicular to the interface for in-plane spins. By fitting the experimental data, we obtain η = 61%. Note that the detection of the spin current parallel to the interface is achieved exclusively via the ASHE. This is evident in the lack of a negative signal while using the Pt nanowire as a detector, where the only detection mechanism is via the ISHE. Thus, the Pt nanowire is only sensitive to the spin current perpendicular to the Pt/YIG interface for in-plane spins. Equation 2 describes the spin injection by the Py injector (following eq 1) and the detection via the ISHE in the Pt nanowire.

The simulated curves, following eq 1 and eq 2, are shown as solid black lines in Figure 2c,d, respectively. This modeling for all tilt angles (ϕ) employs the same values for the parameters a, b, and c as those extracted from the in-plane measurements at ϕ = 0°. The satisfactory agreement with the experimental data, both in terms of magnitude and line shape, demonstrates that our model captures the dominant physics of the out-of-plane spin injection and detection processes. To achieve further insight, we separate the modeled contributions of the spin current perpendicular to the interface and the spin current parallel to the interface to the nonlocal signal at the Py detector, following eq 1. The results, shown in Figure 4c,d, present in an explicit manner the contribution of the two different mechanisms of detecting the spin current oriented along the z-axis and that along the x-axis, respectively, with increasing ϕ.

Note that, although we understand the different symmetries of the injection/detection mechanisms depicted in Figure 4a,b, we do not fully understand why these mechanisms have comparable efficiencies, given the specific cross sections of the nanowires. Although at ϕ = 89°, an equal and opposite out-of-plane spin accumulation is generated at the two lateral edges of the Py injector [Figure 1d], we can still measure a finite signal with the Py detector. This is because the contribution from the closest edges of the injector and the detector is expected to dominate the nonlocal signal in this case (see Supporting Information Section 10). The minor disagreement between model and experiment, observed at intermediate values of B, can be attributed either to the extraction method of the magnetization behavior of the Py nanowires and the YIG film, shown in Figure 3c,d, or could hint to a subtle effect not present in our description. To explore the latter, we have considered a second set of fitting curves with a nonconstant b parameter, motivated by recent studies on spin rotation symmetry and dephasing.²⁷ The apparent variation of the spin injection and detection processes due to a tilted M_Py is of only up to ∼20% (see Supporting Information Section 2). Note that another possible mechanism for the injection of out-of-plane spins is the anisotropic magnetoresistance (the planar Hall effect).¹³ However, the expected contribution of the planar Hall effect is inconsistent with our experimental observations and it does not affect our quantitative analysis of the ASHE microscopic parameters nor our main conclusions (see Supporting Information Section 6). Finally, control experiments and modeling with a different architecture using a Pt injector and a Pt detector have been performed, confirming the absence of injection and detection of out-of-plane spins via the SHE alone (see Supporting Information Section 3).

The present demonstration of electrical injection and detection of spin accumulation in arbitrary directions is highly desirable in spintronics. We envision that the use of out-of-plane spins within transverse spin currents in a common ferromagnetic metal-like permalloy has the potential to impact spintronic-based technologies like spin-transfer-torque memories⁴⁻⁸ and logic devices.²⁰⁻²² Further remains both on the fundamental understanding, and on the possible implications for previous SHE studies, where the control of spin transport efficiency and directionality enabled by the ASHE¹⁶⁻¹⁹ has not been hitherto considered.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b02114.

• Additional details on the determination of M_Py and M_YIG, modeling results with an angle-dependent b-parameter, a control device with a Pt injector and a Pt detector, device fabrication methods, ruling out interfacial exchange interaction, contribution due to the anisotropic magnetoresistance/the planar Hall effect in the Py nanowire, linearity and reciprocity checks, mechanisms contributing to the second harmonic response, and the finite nonlocal signal at ϕ = 89° measured by the Py detector (PDF)

The authors declare no competing financial interest.