The Common Time Course of Memory Processes Revealed

Abstract

Magnetoencephalography (MEG) was used to compare memory processes in two experiments, one involving recognition of word pairs and the other involving recall of newly learned arithmetic facts. A combination of hidden semi-Markov models and multivariate pattern analysis was used to locate brief “bumps” in the sensor data that marked the onset of different stages of cognitive processing. These bumps identified a separation between a retrieval stage that identified relevant information in memory and a decision stage that determined what response was implied by that information. The encoding, retrieval, decision, and response stages displayed striking similarities across the two experiments in their duration and brain activation patterns. Retrieval and decision processes involve distinct brain activation patterns. We conclude that memory processes for two different tasks, associative recognition versus arithmetic retrieval, follow a common spatiotemporal neural pattern and that both tasks have distinct retrieval and decision stages.

The goal of this research was to investigate the cognitive processing that occurs during the brief period when someone retrieves a well-known fact. To take a current example, most people would have no problem answering the question “Who won the 2016 U.S. election?” They are unlikely to introspect on how they answer this question, nor would they come up with much insight if they did (they would be much more likely to report on how they felt about the answer they retrieved). Answers to such questions seem to come effortlessly, but they do not come instantaneously. The goal of this research was to identify the stages in generating such answers, what brain regions they involve, how the stage durations vary on a trial-by-trial basis, and especially how these processes generalize across tasks. We found that tasks with rather different memory contents—word pairs versus arithmetic facts—show surprisingly similar stage structures.

The first stage in answering such a question must involve encoding the terms in question, and the last stage must involve programming and executing the answer. While the identities of these two stages are fairly certain, there is still uncertainty as to their durations. There is much greater uncertainty about what happens in between. One class of models (e.g., Shiffrin & Steyvers, 1997; Starns & Ratcliff, 2014; Wixted & Stretch, 2004) implies a continuous growth of evidence for an answer. When a threshold is met, that answer is converted into a response. A second class of models, often applied to neuroimaging data (e.g., Badre & Wagner, 2007; Thompson-Schill, D’Esposito, & Kan, 1999), proposes two stages: an initial access to some relevant knowledge in memory and then a postretrieval process that determines an answer from what is retrieved. An instance of such a two-stage model is the adaptive control of thought–rational (ACT-R) model of recognition memory and recall (e.g., Schneider & Anderson, 2012; Sohn et al., 2005), which involves separate retrieval and decision stages. In this article, we provide neural imaging evidence that at least two distinct stages intervene between encoding and response in associative memory tasks.

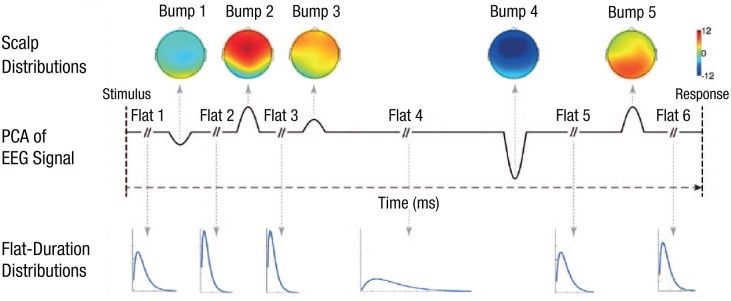
In recent work (Anderson, Zhang, Borst, & Walsh, 2016; Zhang, Walsh, & Anderson, 2017), we have used the temporal resolution of electroencephalography (EEG) to identify the stages and when they were occurring in single trials. To cope with the trial-by-trial variability in the onset latencies of event-related-potential (ERP) components, we developed a novel method that involves applying hidden semi-Markov models (HSMMs) and multivariate pattern analysis (MVPA) to EEG data. Transitions from one cognitive stage to the next are signaled by bumps that are added to the task-irrelevant oscillatory activity in the EEG signal (see Fig. 1). The bumps have finite durations, amplitudes, and topographical distributions. The bumps are separated by variable duration flat regions (or flats) in which the signal is treated as sinusoidal noise around 0. The postulation that processing stages are signaled by such bumps is consistent with theories of ERP generation in EEG data (Makeig et al., 2002; Yeung, Bogacz, Holroyd, & Cohen, 2004), which corresponds closely to event-related-field (ERF) generation in magnetoencephalography (MEG) data. The HSMM-MVPA attempts to recover the number, timing, and topographical distributions of these bumps.

Fig. 1.

Illustration of the bumps and distribution of flat durations. The scalp distributions show electrical potential (in microvolts) associated with each bump between one cognitive stage and the next. The middle row shows the bumps and flat regions across the first dimension of a principal component analysis (PCA) of the electroencephalogram (EEG) signal. The bottom row shows probability density functions for the duration of each flat region. Figure reprinted from Anderson, Zhang, Borst, and Walsh (2016).

Previous EEG experiments (Anderson et al., 2016; Zhang, Walsh, & Anderson, 2017) applied these methods to associative memory tasks and found evidence for an encoding phase associated with a number of early bumps (Bumps 1–3 in Fig. 1), a retrieval phase ending with another bump (Bump 4 in Fig. 1), a decision phase ending with a final bump (Bump 5 in Fig. 1), and then a response phase. In this research, we extended the HSMM-MVPA methodology to two MEG studies with two goals. First, the greater precision in localization that can be obtained with MEG facilitates studying activity during these stages in different brain regions. Second, to assess the generality of the memory processes, we compared two tasks that might seem rather different in the processes and memory content they engaged. One experiment was a pair-recognition task (Borst, Ghuman, & Anderson, 2016) in which subjects had to judge whether they had studied a pair of words together. The other was a recall task in which subjects had to retrieve the value of a newly learned arithmetic relationship (Tenison, 2017). Despite their differences, both tasks required retrieving associative information and acting on it. Moreover, both had a similar input-output structure in that two terms were encoded, and subjects had to hit a single key in response (see Fig. 2).

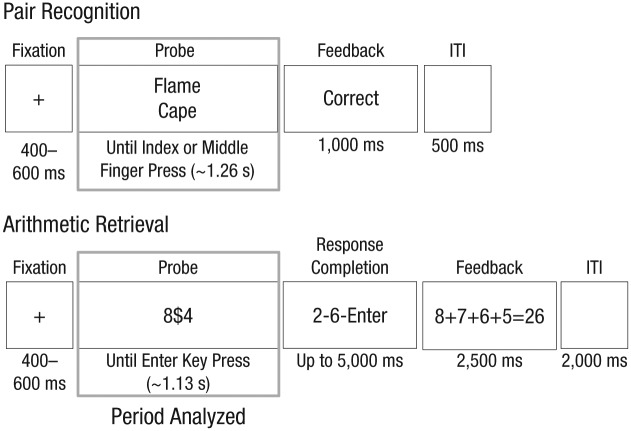
Fig. 2.

Timeline of a single trial in the pair-recognition task and in the arithmetic-retrieval task. During the encoding period (highlighted here with a rectangle), subjects made a binary choice (target or foil) in the recognition task and an indication that they were ready to enter an answer in the retrieval task. Only this period was analyzed in the present experiments. ITI = intertrial interval.

We expected to identify again encoding, retrieval, decision, and response stages. Finding a distinction between retrieval and decision in two different tasks with another imaging modality would add further support to the separation of retrieval and decision. To test whether the retrieval and decision stages are focused on memory processing, we partitioned the trials from the two experiments according to factors known to affect memory: a manipulation of associative interference in the recognition task and a manipulation of practice in the arithmetic-retrieval task. These should affect only the durations of the retrieval and decision stages. Beyond these tests of stage structure, the use of MEG allows critical additional tests of our understanding of memory access: If there are a common set of stages in these two rather different tasks, then they should evoke a common profile of brain activity and there should be distinct activity patterns for the retrieval and decision stages.

Method

Detailed information about the two experiments is available in Borst et al. (2016) and Tenison (2017). Here, we focus on providing the information necessary for understanding the two experiments and the new methods unique to this article, for processing the imaging data, and for performing the HSMM-MVPAs.

Subjects

All subjects were right-handed. There were 18 subjects in the pair-recognition experiment (6 males, 12 females; age: M = 23.6 years, range = 18–35) and 28 subjects in the arithmetic-retrieval experiment (15 males, 13 females; age: M = 20.1 years, range = 19–27). We have found that approximately 20 subjects with over 100 trials per subject are required for a robust application of HSMM-MVPA.

Procedure

The pair-recognition experiment consisted of two phases: a training phase in which subjects learned word pairs and a test phase in which subjects were asked to recognize pairs. The test phase was scheduled the day after the training phase and took place in the MEG scanner. During the test phase, subjects had to distinguish between targets (trained word pairs) and re-paired foils (rearranged pairs). A critical manipulation was whether the words in the probe appeared uniquely in one pair or appeared in two pairs. This is referred to as a fan manipulation. Each word used in the fan condition appeared in two study items (A-B, A-C, D-B, D-C, E-F, E-G, H-F, H-G), whereas each word in the no-fan condition uniquely appeared in a single study item (W-X, Y-Z). Foils were created by re-pairing words from the fan condition (A-F, D-G) or from the no-fan condition (W-Z). Subjects completed a total of 14 blocks (7 left-handed, 7 right-handed) with 64 trials per block. To ensure that data corresponded to the arithmetic-retrieval experiment, we used only the blocks with right-hand responses. Hand did not have a significant effect on response time but did have a major effect on activity patterns.

Tenison (2017) performed a MEG study of the learning of new arithmetic facts involving the pyramid relation. Pyramid problems (presented with a dollar symbol as the operator, e.g., 8$4 = X) involve a base (8) that is the first term in an additive sequence and a height (4) that determines the number of terms to add. Each term in the sequence is one less than the previous (e.g., 8$4 = 8 + 7 + 6 + 5 = 26). The bases vary from 4 to 11, and the heights vary from 3 to 5. Subjects solved a subset of these problems 54 times over the course of the experiment. As shown in earlier functional MRI (fMRI) studies (Tenison & Anderson, 2016; Tenison, Fincham, & Anderson, 2016), subjects quickly transition to just retrieving these facts instead of calculating the answers. We used a threshold of 2.4 s to identify retrieved facts and compared retrievals with relatively little practice (30 or fewer practice opportunities, an average of 21 prior trials of practice) with retrievals with more practice (greater than 30 practice opportunities, an average of 45 trials of prior practice).

Although these are two rather different tasks, they were quite similar in terms of what the subject saw and the physical response. Figure 2 compares the sequence of events for the two experiments. Each trial began with a variable fixation period of 400 to 600 ms. While the probes were different (words versus numeric expression), in both cases two things needed to be encoded (the two words or two numbers). The data to be analyzed for each trial ended with a key press. The key press in the recognition task was a binary choice providing the answer (target or foil), whereas in the arithmetic-retrieval task it was a signal indicating the subject was ready to enter the answer. The sequence of events diverged after this key press and was not analyzed: The pair-recognition experiment ended with feedback as to correctness and an intertrial interval (ITI). In the arithmetic-retrieval task, the subject had to then enter the answer and was shown more elaborate feedback explaining the answer, followed by an ITI.

MEG recording and processing

In both experiments, MEG data were recorded with the same 306-channel Elekta Neuromag (Elekta Oy, Helsinki, Finland) whole-head scanner. The 306 channels are distributed into 102 sensor triplets, each containing one magnetometer and two orthogonal planar gradiometers. Data were digitized at 1 kHz. As part of standard MEG testing, four head-position indicator coils were attached to the subject’s scalp to track the position of the head in the MEG helmet. In addition, we obtained anatomical MRIs for source localization. In the pair-recognition experiment, subjects responded with a response glove, and in the arithmetic-retrieval experiment, they responded with a numerical keyboard. The stimuli were projected onto a screen about 1 m in front of the subject. Stimulus onset was measured by a photodiode that was directly connected to the MEG recording system.

Only trials with correct responses and only trials lasting between 600 and 2,400 ms (60–240 samples after down-sampling to 100 Hz) were used. The two resulting normed data sets involved 6,461 trials (781,900 samples of 10 ms) for pair recognition and 3,005 trials (332,889 samples) for arithmetic retrieval. For each trial and each sensor, the activity was referenced to a standard baseline by subtracting the mean activity in the 200 ms prior to trial onset. To normalize the variance among the three types of sensors (magnetometer, planar gradiometer, axial gradiometer), we divided the activity of all sensors of a particular type by the standard deviation for that type of sensors.

As a step of dimensionality reduction and to deal with the fact that individual sensors do not necessarily correspond across subjects, we performed a multiset canonical correlation analysis (MCCA) on the data (Zhang, Borst, et al., 2017). This analysis compresses the data from the 306 sensors into a reduced number (10 in our case) of uncorrelated dimensions that are common across subjects. The details of the MCCA are explained in the Supplemental Material available online. The output of the MCCAs applied to the data from the two experiments was a 1,114,789 × 10 matrix representing 9,466 trials and 46 subjects. The HSMM-MVPAs will estimate parameters that maximize the probability of these data.

Bump analysis of the MEG data

On a trial-by-trial basis, the HSMM-MVPA identified the location of bumps that mark various stages of processing. This analysis assumes that stage boundaries are marked by 50-ms half-sine bumps added to task-irrelevant oscillatory activity. In between these 50-ms periods are flats (see Fig. 1) where the activity is modeled as sinusoidal noise with a mean of 0. Bounded by trial onset and the finger press, the placement of N bumps results in N + 1 intervening flats, and stage duration is the time between these bounds.

The assumptions, mathematics, and computations underlying the HSMM-MVPA that estimates the bump parameters (see Anderson et al., 2016, for detailed mathematical development) can be summarized in six points. First, the estimation process finds a set of parameters that will maximize the likelihood of the data from all the trials, given some description of the structure of those trials. Second, the description of a trial is anchored by the placement of N bumps during the trials. The number of ways of placing N bumps in a trial of S samples is (S + N)!/(S! × N!) (a very large number, given trials averaging more than 100 samples). Every possible placement has a probability, and the probability of the trial is the sum of all these probabilities. The essential power of the HSMM algorithms is that they can efficiently compute these sums. Third, any placement of the N bumps results in a partition of the trial into N bump regions and N + 1 flats marked off by these bumps. The probability of such a partition is the product of the probabilities of the N bumps and the probabilities of the N + 1 flats. Fourth, the probability of a flat varies with its duration. This variation is modeled as a simple latency-like distribution for these flats—gamma distributions with shape 2 and scale parameters to be estimated. Fifth, the probability of a bump is determined by how well it matches the profile for that bump on each of the 10 MCCA dimensions. Because MCCA produces orthogonal dimensions, the probability of a bump is the product of the probabilities on each dimension. Thus, each bump can be characterized by a set of 10 magnitudes that represent the mean values on that dimension. Sixth, for any dimension, the 50 ms (five samples) that constitute the bump define a half-sine pattern that starts at 0 at the onset of the bump, reaches a maximum at 25 ms, and comes back down to 0 at 50 ms. The probability of the bump of that dimension is determined by how much variability in the sample can be explained by the assumption of such a bump.

Thus, an N-bump model requires estimating N + 1 scale parameters to describe the durations of the flats and 10N magnitude parameters to describe the magnitudes of bumps. The scale parameters reflect the temporal pattern of the bump locations, and the magnitude parameters reflect the multivariate pattern of the bumps. These parameters are estimated iteratively using the expectation maximization algorithm associated with an HSMM (Yu, 2010).

A single cognitive event can result in a train of bumps with highly correlated scalp profiles and little temporal separation. This can occur because of alpha ringing, where ERPs give lasting oscillations that are fit to more than one bump, or because the underlying width of the bump is much wider than the assumed 50 ms. To identify only bumps signaling distinct cognitive processes, we constrained how strongly correlated adjacent bumps could be according to how close they were: If T ms was the mean duration of the intervening flat, the maximum correlation allowed between adjacent bumps was (T – 50)/150. This constrains nearby bumps to be uncorrelated and eliminates any constraints on the profiles of adjacent bumps more than 200 ms apart. In the Supplemental Material, we compare this constrained solution with an unconstrained solution and show that the only difference is elimination of highly correlated adjacent bumps.

Results

In all, 64.1% of the arithmetic-retrieval trials fell between 600 and 2,400 ms (35.6% were longer than 2,400 and may have reflected calculation; 0.3% were briefer), and 96.3% of these were correctly answered. There were 1,467 correct early trials averaging 1.21 s, and 1,538 correct late trials averaging 1.01 s. In the pair-recognition experiment, 2% of the no-fan trials were errors, and 6% of the fan trials were errors. Of the correct trials, 96.0% fell in the interval between 600 and 2,400 ms, with almost all remaining trials longer. There were 3,477 no-fan trials averaging 1.11 s and 2,984 fan trials averaging 1.33 s.

We estimated models of one to eight bumps for the two experiments. The estimation procedure for each experiment was entirely independent of the estimation for the other experiment. The estimation process produces parameters that describe the topographies of the bumps and the durations of the flats. We then used these parameters estimated from one experiment to calculate the likelihood of the data from the other experiment. In essence, we used one experiment to predict the other. Figure 3 shows how well the parameters from one experiment can predict the data from the other. In both directions, the likelihood of data increases up to six bumps. The increase in log-likelihood up to five bumps is quite decisive: Data from 25 of the 28 arithmetic subjects are better predicted by the five-bump model than by any model with fewer bumps. Data from all 18 of the pair-recognition subjects are better predicted by the five-bump model. The improvement to six bumps continues to be quite clear for the arithmetic-retrieval experiment (better than five bumps for 25 of 28 subjects). The effect is less strong for the pair-recognition experiment but is still better for 14 of the 18 subjects (p < .05 by a sign test).

Fig. 3.

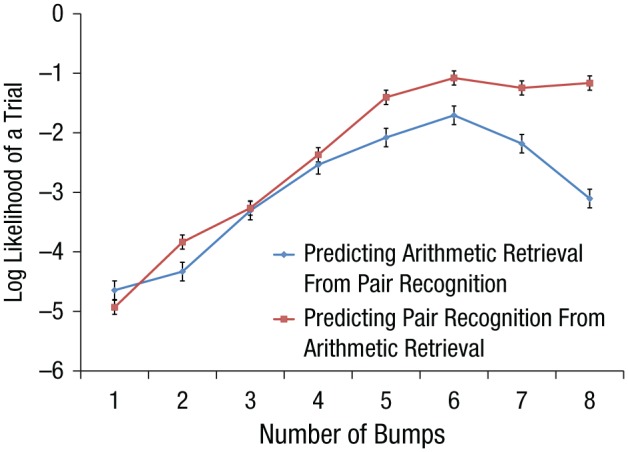
Average likelihood of a trial from one experiment given an N-bump model estimated from the other experiment. Error bars represent standard errors of the mean.

The corresponding bumps for the two fits of the five-bump model were strongly correlated in terms of their magnitudes on the 10 MCCA dimensions (r = .939) but less so for the six-bump model (r = .784)—see the Supplemental Material for all individual correlations. The six flat durations estimated for the two experiments under the five-bump model were very consistent (r = .995), whereas the seven flat durations for the six-bump model were less correlated (r = .926). The high correlation for the five-bump model is quite remarkable given that the two fits were entirely independent. Because of this consistency and because it corresponds to the five-bump results from our prior EEG study (Fig. 1), we focus on this model in the article. In the Supplemental Material, we describe the six-bump solution and compare it with the five-bump solution.

The HSMM-MVPA estimation produced an estimate of how long each stage took on each trial. Figure 4 shows the averages of these estimates for each condition from the separate models fit to the two experiments. This displays the striking similarity in the stage durations for the two experiments. As in Anderson et al. (2016), our interpretation is that the first stage reflects a preattentive period before the stimulus reaches the brain and is attended, the second and third stages reflect processing of the two terms, the fourth stage is retrieval, the fifth stage is decision, and the last stage is motor execution.

Fig. 4.

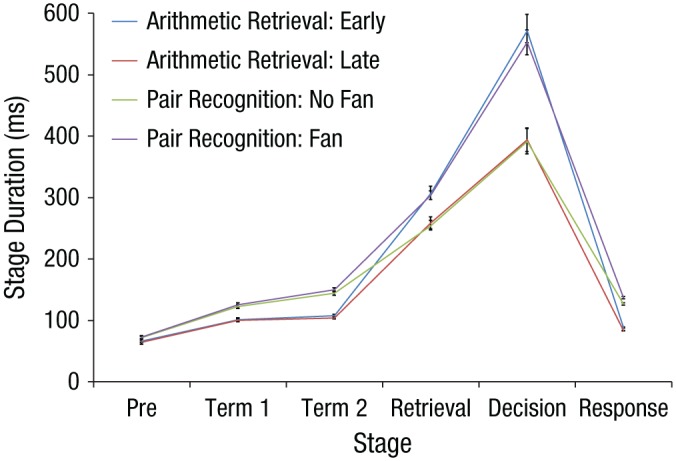
Estimated duration of the six stages for the two conditions in each experiments. Error bars represent standard errors of the mean.

The large effect of condition appears to be on duration of the decision stage but small differences appear in other stages. One complication in interpreting any differences in stage duration is that the five bumps, while very similar, are not identical in the fits to the two experiments. Thus, the stage durations measure slightly different things for the two experiments. However, almost the same pattern of data appears when we fitted one model with a common set of bumps to both experiments.

Another problem in interpreting stage durations is that to the degree that the bumps in the data are not strong, the estimation of bump location is imprecise and biases can appear in the estimation of stage durations. In particular, there is a tendency for the estimation process to distribute any effect of condition duration across all of the stages (see discussion in the Supplemental Material). To determine which differences in stage durations are strongly supported, we allowed the HSMM to estimate different duration for a flat in different conditions.¹ We fit 2⁶ = 64 models, which represented all possible ways of allowing a flat to vary with condition or not. The goal was to identify the model that had the fewest flats varying that could characterize the data. We both predicted the data of the odd subjects using flat durations estimated from the even subjects and vice versa, keeping constant the bump magnitudes of the overall five-bump model. Of the models that had just one flat varying, letting the fifth flat vary had the largest improvement over having no flats (improved 21 of 23 odd subjects, p < .001; mean gain in log likelihood of 9.62; 18 of 23 even subjects, p < .01, with a mean gain of 6.65). Allowing the fourth flat to vary had the second largest effect for the odd subjects (18 of 23 subjects, p < .01, mean gain of 6.13) but was not significant for the even subjects (12 of 23 subjects, mean gain of 1.78). Varying any other flat duration did not lead to significant improvement for either odd or even subjects. Allowing both the fourth and fifth flat to vary led to a significant improvement over just the fifth for the odd subjects (17 of 23 subjects, p < .05, mean gain of 5.02) but actually slightly decreased the mean fit for the even subjects (12 of 23, mean gain of −1.0). None of the other models were significantly superior to the model with just flat 5 varying for either the odd or even subjects. While we cannot reject the possibility of an effect on some other stage (particularly the retrieval stage given the significant effects for the odd subjects), the only strongly supported effect of condition is on the decision stage, as Figure 4 suggests.

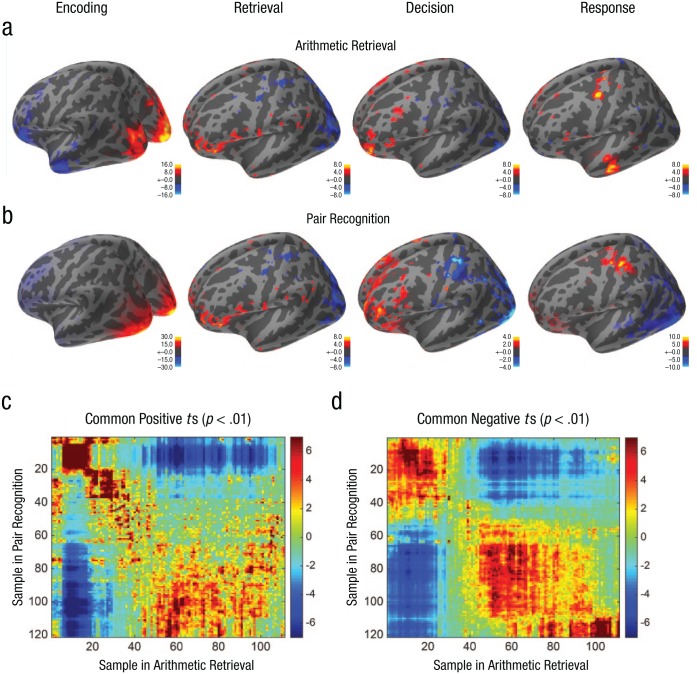
As described in the Supplemental Material, we used sample-by-sample sensor activity to infer patterns of activity in 5,124 sources placed on the cortical surface. To see whether the two experiments were showing similar patterns, we warped the trial data to fit a common template for that experiment. This involves identifying the maximum-likelihood bump locations for each trial and placing these bumps at the average bump locations for that experiment. The flat data between the bumps on each trial were then stretched or shrunk to have the same duration as the average flat durations. We calculated how much activity in a region was above or below the global activity at each of the warped time points. Because the average trial was 1.11 s in arithmetic retrieval and 1.21 s for pair recognition, this resulted in 111 and 121 samples of 10 ms per trial, which we averaged for each subject. Figures 5a and 5b illustrate areas that were significant (p < .05, two-tailed) at time points during the encoding (120 ms), retrieval (500 ms), decision (720 ms in arithmetic retrieval, 770 ms in pair recognition), and response (1,050 ms during arithmetic retrieval, 1,150 ms during pair recognition) periods. There appeared to be overlap between the two experiments at different stages: Visual areas were active during encoding, prefrontal areas during retrieval and decision, and motor areas during response.

Fig. 5.

Significant source activity at various time points in the experiment. The brain scans illustrate significant activations in the (a) arithmetic-retrieval and (b) pair-recognition experiment. The heat maps show (c) the overlap of positive ts (p < .01) between the two experiments and (d) the overlap of negative ts (p < .01) between the two experiments. The lines in (c) and (d) mark the boundaries between the encoding, retrieval, decision, and response periods.

Figures 5c and 5d examine whether the same sources tend to be significant for pairs of time samples, one sample from the arithmetic-retrieval experiment and the other from the pair-recognition experiment. On average, for any of 111 × 121 sample pairs, 10.4 source pairs share significantly positive ts (p < .01, one-tailed), and 30.1 share significantly negative ts. However, the number of jointly significant source pairs varies from 0 to many hundreds for different sample pairs. In part, this variation reflects that different sample points in each experiment have different numbers of significant sources, but we were interested in whether some sample pairs shared more significant sources that would be expected because of these marginal frequencies. Figures 5c and 5d show how significantly the number of significant sources at sample pair deviates from what would be predicted from the marginal counts for each experiment. Table 1 summarizes Figures 5c and 5d, with the average values of all the ts in pairs of periods, one from each experiment. It shows evidence for common overlap between periods (positive main diagonal), but in some cases there is overlap in adjacent periods. In particular, the retrieval period for arithmetic retrieval overlaps in terms of shared activity with the decision period for pair recognition. Similarly, the decision period for arithmetic retrieval overlaps with the response period for pair recognition.

Table 1.

Mean ts Measuring the Number of Common Periods for Sample Pairs

Pair-recognition period	Arithmetic-retrieval period
	Encoding	Retrieval	Decision	Response
Pairs in Figure 5c
Encoding	4.93 (0.21)	−1.18 (0.08)	−3.30 (0.05)	−0.89 (0.07)
Retrieval	−0.18 (0.09)	1.59 (0.11)	0.01 (0.04)	0.89 (0.25)
Decision	−3.50 (0.08)	0.84 (0.06)	2.50 (0.05)	0.69 (0.10)
Response	−3.73 (0.20)	0.54 (0.16)	2.22 (0.11)	0.73 (0.32)
Pairs in Figure 5d
Encoding	4.05 (0.07)	−1.90 (0.07)	−2.88 (0.03)	−0.70 (0.12)
Retrieval	−0.30 (0.09)	0.94 (0.07)	−0.04 (0.05)	−0.46 (0.11)
Decision	−4.19 (0.03)	2.05 (0.07)	2.85 (0.04)	0.03 (0.06)
Response	−3.81 (0.07)	−0.21 (0.06)	3.95 (0.13)	4.62 (0.51)

Note: Standard errors are given in parentheses.

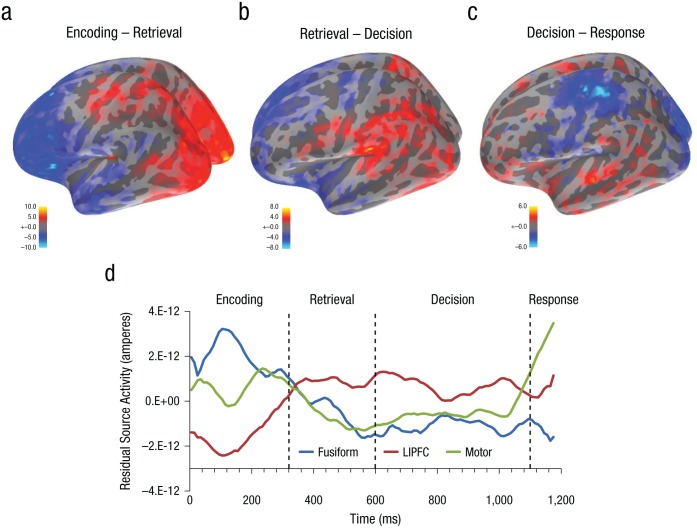
While Figure 5 gives evidence for the common activity that produces the same stage structure for the two experiments, it does not provide evidence about the nature of the differences among the periods. To test this, we fitted one model to the data from both experiments and looked for contrasts between periods. Figures 6a to 6c show the results of t tests comparing source activity in adjacent time periods. The encoding-minus-retrieval contrast shows that the encoding period had greater activity in visual areas, whereas the retrieval period had greater activity in prefrontal regions. The retrieval-minus-decision contrast shows that the retrieval period had greater activity at the temporoparietal junction, whereas the decision period had greater activity in prefrontal regions. The decision-minus-response contrast showed that the decision period had greater activity at the right temporoparietal junction (not shown), whereas the response period has greater activity in left motor areas (shown).

Fig. 6.

Contrasts of source activity during different stages. The brain scans show t values for contrasts between mean activity in adjacent periods, separately for the (a) encoding-minus-retrieval, (b) retrieval-minus-decision, and (c) decision-minus-response contrasts. The graph (d) shows average residual source activity for the pair-recognition experiment and arithmetic-retrieval experiment after warping every trial, separately for the fusiform (Talairach coordinates: x = −42, y = −60, z = −8), left lateral inferior prefrontal cortex (LIPFC; Talairach coordinates: x = −43, y = 23, z = 24), and motor (Talairach coordinates: x = −42, y = 19, z = 50) regions.

These effects in Figures 6a to 6c were generally in the direction we would expect, given our understanding of the function of the stages. However, we did not have a priori predictions about most of the sources in such a brainwide analysis. We examined three a priori regions that past fMRI research (e.g., Anderson, Carter, Fincham, Ravizza, & Rosenberg-Lee, 2008; Borst & Anderson, 2013) has associated with relevant modules in ACT-R: the left fusiform as an index of encoding activity, the left motor region as an index of response activity, and the left lateral inferior prefrontal cortex (LIPFC) as an index of retrieval. Figure 6d displays the activity in these regions over the course of the two experiments. It has been warped to overall average time of 1,180 ms, and the figure plots the 118 resulting samples for each region.

Table 2 gives the results of pairwise t tests for differences between different periods, and the results are quite clear: The fusiform was more active in the encoding period than any other periods, whereas none of the other pairwise contrasts of periods was significant. The LIPFC shows the opposite effect: All the later periods were significantly more active than the encoding period, whereas there were no significant differences among these later periods. The motor region was significantly more active in the response period than any other and was more active in the encoding period than either the retrieval or decision period. With the exception that the motor region starts high in the encoding period (but not as high as in the response period), these are the effects we would predict. We should note that while condition had a large effect on the duration of the decision stage (Fig. 4), there were no significant differences between the conditions in either experiment for any stage for any of these three regions.

Table 2.

Results of Pairwise t Tests

Region and period	Retrieval	Decision	Response
Fusiform
Encoding	4.66****	5.90****	5.16****
Retrieval		1.87	1.37
Decision			0.49
Left lateral inferior prefrontal cortex
Encoding	−7.34****	−6.30****	−3.70**
Retrieval		0.64	0.77
Decision			0.48
Motor
Encoding	3.11**	2.78*	−2.16*
Retrieval		−0.24	−4.03***
Decision			−4.31***

Note: Each cell shows results for the contrast between the period identified in the row label minus the period identified in the column label. The significance levels are for two-tailed tests with 45 degrees of freedom.

^*p < .05. **p < .005. ***p < .0005. ****p < .00005.

Conclusions and Discussion

Even though the memory judgments in these experiments averaged only a little longer than a second, the HSMM-MVPA methodology was able to parse individual trials into periods associated with encoding, retrieval, decision, and response. Sensibly, the encoding and response times were not affected by condition, and the decision time was. We expected to see the retrieval time also affected by condition, and there was evidence for that but it was much weaker (only significant for odd subjects). In past experiments, we have seen different-sized effects of variables intended to manipulate memory difficulty on the retrieval and decision stages, with the effect of retrieval being sometimes quite strong (Anderson et al., 2016; Zhang, Walsh, & Anderson, 2017). In the Supplemental Material, we show that if there is an effect on the duration of two adjacent stages, HSMM-MVPA has a bias to overestimate the effect on the longer stage and underestimate the effect on the shorter stage. This would be consistent with the pattern of results we have seen across experiments.

Over and above confirming the stage structure found in past EEG experiments, our use of MEG allowed us to identify the brain regions engaged during these stages. The results provide striking evidence for similarity of the processing involved in a pair-recognition task and a task that involved retrieval of newly learned arithmetic facts. Independent HSMM-MVPA fits found similar bumps occurring in the two tasks at similar intervals (Fig. 4). As a consequence, a model fit to one task could successfully predict the data from the other task (Fig. 3). These models worked on the results of an MCCA performed on sensor data, and there was no guarantee that the same brain regions were involved in the two tasks. Nonetheless, when the bump analysis was used to temporally align the source data, the two tasks did show a common pattern of brain activity (Fig. 5) during each period. Moreover, each period showed a pattern of activity distinct from the other periods (Figs. 6a–6c).

While these data provide strong evidence for at least two distinct stages intervening between encoding a probe and generating a response, their identities are less certain. Our characterization of these as retrieval and decision follows from the ACT-R process model and a detailed analysis of previous stage-discovery results (Borst & Anderson, 2015, p. 70); other neuroimaging models (e.g., Badre & Wagner, 2007; Thompson-Schill et al., 1999) reference a similar distinction between retrieval and postretrieval stages. In a study of a task very similar to the arithmetic-retrieval task (Paynter, Reder, & Kieffaber, 2009; Reder & Ritter, 1992), it has been suggested that there is an initial familiarity stage followed by a recollection stage. Similarly, in Cox and Shiffrin’s (2017) model of associative recognition, item information becomes available before associative information. This reflects the general idea behind a class of theories known as dual-process theories, which have linked specific EEG components to these different processes (e.g., Diana, Reder, Arndt, & Park, 2006; Rugg & Curran, 2007). Thus, one could view what we have called the retrieval stage as a familiarity/item stage and what we have called the decision stage as a recollection/associative stage. Portoles, Borst, and van Vugt (2017), who used HSMM-MVPA to analyze EEG data of associative recognition, found evidence for an early familiarity process by inspecting connectivity patterns during the stages.

It is noteworthy that we found a sustained increase in LIPFC activation throughout the two stages that we call retrieval and decision. It has been argued (e.g., Barredo, Öztekin, & Badre, 2015) that there is a need to exert control on the retrieval process to ensure that task-relevant information is obtained and on the postretrieval process to select the appropriate action on the basis of the retrieved information. While it remains to be determined just what is happening between encoding and response, our research indicates that associative memory tasks involve more than a single process accumulating evidence.

There are ways of reconciling the current evidence with single-stage decision-accumulation models. One could argue that single-stage models are appropriate only to nonassociative tasks such as item recognition. Such tasks may be based on familiarity and do not have an associative retrieval stage. While single-stage models have mainly been applied to nonassociative tasks, they have also been applied to associative memory tasks. For instance, as Voskuilen and Ratcliff (2016) describe their model of associative memory,

Reaction time distributions are obtained by combining the decision time (the time taken for one of the evidence accumulators to reach a decision boundary) with a uniformly distributed non-decision component. The non-decision component . . . encompasses both encoding and response output processes. (p. 64)

The experiments to which these models have been applied typically have much less well-learned material than our two experiments (and so analysis of errors becomes critical). One might argue that only experiments with high degrees of practice have a distinct retrieval stage.² However, a better tack might be to include the retrieval phase in the nondecision component, which is assumed to be constant across conditions. The fact that there is not strong evidence for an effect of memory difficulty on the retrieval stage in these experiments would be consistent with that, although Anderson et al. (2016) and Zhang, Walsh, and Anderson (2017) have found clear effects on the retrieval stage.

However one interprets and treats the retrieval stage, one can view the decision stage as an evidence-accumulation process that could be described with a variety of models. Some sort of evidence-accumulation process seems natural for both of the memory tasks. For instance, Zhang, Walsh, and Anderson (2017) manipulated foil similarity and described a process by which the words in the probe are compared one by one with the words in the retrieved memory. One could propose a similar comparison process for arithmetic-memory tasks in which the elements of numbers in the probe are compared with the probe (as suggested by Sohn et al., 2005, for a different recall task). Alternatively, one could characterize the decision phase as involving a continuous accumulation of evidence as in Voskuilen and Ratcliff (2016).

In summary, while there remain questions to answer about the exact nature of the stages and their implications for different theories of memory, we have provided strong evidence for two distinct stages between encoding and retrieval. We have shown that similar stages are found in two rather different memory tasks, although questions remain as to just what the boundaries are of tasks that have these two stages. We have shown that it is possible to identify the durations of individual stages and their distinct brain activity. We think continued use of such trial-by-trial methods will bring further resolution to the outstanding questions.