Optimal Hydrophobicity and Reorientation of Amphiphilic Peptides Translocating through Membrane

Abstract

Cell-penetrating and some antimicrobial peptides can translocate across lipid bilayers without disrupting the membrane structure. However, the molecular properties required for efficient translocation are not fully understood. We employed the Metropolis Monte Carlo method together with coarse-grained models to systematically investigate free-energy landscapes associated with the translocation of secondary amphiphilic peptides. We studied α-helical peptides with different length, amphiphilicity, and distribution of hydrophobic content and found a common translocation path consisting of adsorption, tilting, and insertion. In the adsorbed state, the peptides are parallel to the membrane plane, whereas, in the inserted state, the peptides are perpendicular to the membrane. Our simulations demonstrate that, for all tested peptides, there is an optimal ratio of hydrophilic/hydrophobic content at which the peptides cross the membrane the easiest. Moreover, we show that the hydrophobicity of peptide termini has an important effect on the translocation barrier. These results provide general guidance to optimize peptides for use as carriers of molecular cargos or as therapeutics themselves.

Introduction

Peptides with specific properties possess the ability to cross biological membranes without the help of cellular machinery. Many of them can be classified as cell-penetrating peptides and/or antimicrobial peptides (AMPs), which are vital components of the innate immune system (1). AMPs are believed to selectively target bacterial membranes based on their physicochemical properties (2, 3, 4). One of the best-studied translocating peptides is Buforin II, a histone-derived peptide isolated from Asian toad Bufo gargarizans (3, 5). Its mechanism of action involves crossing bacterial membrane and interacting with its genome (6). However, for most peptides, comprehensive understanding of their selectivity, let alone their mechanism of action, is lacking (7). Elucidating the key properties necessary for activity would help to move from large-scale screening and trial-and-error approaches to the rational design of novel therapeutics. The translocating peptides could be used as therapeutics directly or as carriers for selective and efficient transport of covalently bound (8, 9) or complexed (10) cargo into targeted cells.

The most widely used model to estimate the peptide translocation is based on the free-energy difference between the peptide adsorbed state and inserted state in the membrane (11). Using the fluorescence experiments with dye efflux kinetics (12), the helical peptides were observed to translocate when their free-energy difference is ≤20 kcal mol⁻¹ (11). In this model, the adsorption energy is calculated via the Wimley-White interfacial hydrophobicity scale derived for 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (13), in which the inserted state is approximated by full immersion of the peptide in octanol. It is intriguing that the middle of the membrane hydrophobic core can be mimicked by octanol and that the translocation is usually determined independent of the lipid type. To advance the model, more details about the translocation process and the involved inserted state are necessary.

It is challenging to experimentally capture the translocation event occurring on a small scale of membrane thickness (∼5 nm). In contrast, computer simulations can capture such events with molecular or higher resolution. Translocation across phospholipid membranes has already been investigated for many small molecules (14, 15, 16), polymers (17), and nanoparticles (18). Nanoparticles are typically much larger than peptides, and their membrane crossing is associated with the formation of a large membrane pore or defect (19). Polymers of a size comparable to peptides can be less disruptive than large nanoparticles and can translocate without inducing large membrane defect. Indeed, coarse-grained simulations showed that polymers with optimal hydrophobicity could cross the membrane without large free-energy changes (17). Such polymers change their conformation from expanded to compact upon membrane insertion and remain unstructured. In contrast, peptides are known to become more folded and typically α-helical on membrane because of the backbone hydrogen bond formation in the hydrophobic environment.

A limited number of simulations also investigated peptide translocation. However, most of them actually focused on the insertion of transmembrane helices (20, 21, 22, 23). The insertion of a peptide in the membrane is half of the translocation process. Therefore, these results are very relevant. However, the transmembrane helices are mostly hydrophobic with hydrophilic ends. As a result, it is not surprising to find such peptides in transmembrane orientation while inserted in the membrane. Amphiphilic peptides could behave differently because amphiphilic molecules such as cholesterol and other lipids follow a different translocation path, with the inserted state being parallel to the membrane (24, 25). Nevertheless, two recent studies on translocation of a few specific AMPs suggest that the path could be similar to transmembrane helices (26, 27).

Here, we used general coarse-grained models to investigate peptide properties for efficient translocation. We focused on secondary amphiphilic peptides, i.e., peptides forming both hydrophobic and hydrophilic surfaces after adopting a secondary structure rather than having a hydrophobic and a hydrophilic segment within the sequence (28). We studied the effects of the peptide length and hydrophobic content, which are believed to determine the ability to translocate (29). To quantify the translocation efficacy, we calculated the free-energy profiles of peptide passing through the membrane. Because the change of the orientation during the translocation of molecules was demonstrated to be important (14, 15), we calculated the free energy as a function of peptide distance from the membrane center and its orientation. Our results show consistent insertion and translocation pathway for all combinations of peptide parameters. From the free-energy profiles, we derive optimal hydrophobic content for peptides of a given length. The observed preference of transmembrane not parallel orientation inside the hydrophobic core is validated by all-atom simulations.

Methods

Coarse-grained simulations

Simulations were performed using the Monte Carlo method with Metropolis scheme using in-house spherocylinder software (freely available at https://github.com/robertvacha/SC). For computational efficiency, implicit-solvent coarse-grained models were employed to systematically investigate peptide parameters required for translocation. By comparison of the model dimensions with respect to their biological counterparts, the coarse-grained units of σ can be roughly translated to nanometers, and this conversion will be used henceforth.

The employed lipid model was developed by Cooke et al. (30) and describes each lipid by three particles. The hydrophilic lipid headgroup is represented by one purely repulsive particle with the diameter of 0.95 nm. Both lipid tails are coalesced together and modeled by two particles with the diameter of 1 nm. Overall, the lipid has a roughly cylindrical shape, suitable for forming planar bilayers with elastic properties and phase transitions matching common lipid membranes (30).

A phenomenological model for amphiphilic peptides, the so-called patchy spherocylinder (PSC) model, was used to describe the peptides (31). The whole peptide is described as a single particle with a diameter of 1 nm to roughly match the size of an ideal α-helix. Each particle can have one or more interacting patches with tunable interaction (31). The attractive patch represents the peptide hydrophobic content and is defined by the dihedral angle of cylinder wedge. The patch is either confined to the cylindrical part of the particle, denoted as PSC-NE (PSC-nonattractive endcaps). Or it can stretch toward the hemispherical ends, denoted as PSC-AE (PSC-attractive endcaps). At either side of the patch, there is a switching range to linearly scale the interaction potential to zero over the selected angle. The remaining surface is purely repulsive and thus considered to be hydrophilic. The NE represent hydrophilic residues at both peptide termini.

The repulsive interactions were modeled by Weeks-Chandler-Andersen (shifted and truncated Lennard-Jones) potential. The attractive potential had a cos² profile. The employed PSCs have a switching range (distance from the potential minimum to zero) at 1.0 nm. As described in Cooke et al. (30), the switching range of lipids is extended to 1.6 nm to keep the membrane in the fluid phase. The depth of the attractive potential well is 1 kT for lipid tail particles and 1 kT per unit length of PSC line segment.

The model system was composed of 200 lipid molecules inside a rectangular box with dimensions of roughly 11 × 11 × 50 nm. For a peptide of length 8 nm, the membrane was composed of 500 lipids with box dimensions 17 × 17 × 50 nm. Using small membrane patches is computationally efficient and mitigates the effects of undulation. A single peptide (represented by either PSC-AE or PSC-NE) was placed close to the membrane surface. The patch sizes were 90, 170, and 255° with a switching range of 5° on each side. The peptide length was selected to be 4 nm, matching the membrane thickness, and 6 and 8 nm to evaluate the effect of hydrophobic mismatch. In addition, fully hydrophobic peptides of length 1, 2, 3, 4, and 6 nm were investigated for comparison. Based on our all-atom simulation, the lengths of 1, 2, 3, 4, 6, and 8 nm peptides roughly correspond to the peptides with 5, 10, 15, 20, 30, and 40 residues, respectively.

Free-energy calculations

The Wang-Landau method (32) was employed for the free-energy calculations. To fully describe peptide translocation, two collective variables (CVs) were used. The first CV is the z-distance (distance along the membrane normal) between peptide and membrane centers of mass in the range of −5.7 to 5.7 nm with bin width 0.1 nm. The second CV is the cosine of the angle between the main peptide axis and the membrane normal in the range of 0–1 with bin width 0.125. To facilitate the comparison, the Boltzmann average of the peptide orientation was calculated.

The starting modification factor was set to 1.0e⁻⁵ kT. The following two convergence criteria have to be met before the modification factor is decreased by half: 1) each histogram bin has to contain at least 1000 samples, and 2) the maximal roughness, defined as kT × ln(H_max/H_min), must be lower than 1.0e⁻⁴ kT. T is the simulation temperature, k is the Boltzmann constant, and H is the number of samples in a histogram bin of the CV. Once the modification factor is below the 1.0e⁻⁷ kT threshold, the free-energy surface modifications are stopped. This means the peptides translocated across the membrane many times before the convergence was reached. Subsequently, the obtained free-energy surface is used as an external bias, and a simulation, complying with detailed balance (without adding any bias), is performed. The roughness of the obtained histogram represented the calculation inaccuracies and was used to further improve the calculated free-energy surface. Because translocation is calculated from one side of the membrane to the other, the asymmetry of the surface provides information to estimate the calculation error being below 1 kT.

All-atom simulations

All-atom molecular dynamics simulations were performed using GROMACS (Groningen Machine for Chemical Simulations) version 5.1.4 (33, 34). To test the influence of force field parameterization, simulations were performed with 1) Amberff99SB-ILDN (35, 36) + Slipids (37, 38) and 2) CHARMM36 (39, 40). The simulation time step was set to 2 fs. A Nosé-Hoover thermostat (41, 42, 43) was used for temperature control with protein-lipid and solvent atoms assigned to two separate coupling groups. The temperature was kept at 310 K with a coupling constant 0.5 ps. A Parrinello-Rahman barostat (44, 45) with a semi-isotropic coupling scheme was employed for pressure control at 1 bar using coupling constant 1 ps. Long-ranged electrostatic interactions were treated with the particle mesh Ewald method (46) with the real-space cutoff set to 1.2 nm. Lennard-Jones interactions were cut off at 1.2 nm. For Slipids all-atom simulations, all bonds were constrained using the LINCS (Linear Constraint Solver algorithm); long-range dispersion corrections for both energy and pressure (47) were applied. For CHARMM36, constraints were used only for covalent bonds with hydrogen atoms; dispersion correction was turned off, and Lennard-Jones forces were smoothly switched to zero between 1.0 nm and the cutoff distance.

The 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid bilayer was assembled in the xy plane using the CHARMM-GUI (Chemistry at HARvard Macromolecular Mechanics graphical user interface) (48). The bilayer was composed of 128 lipids and more than 50 water molecules per lipid were added. NaCl ions were added at the physiological concentration of 150 mM. The exact system compositions are in the Supporting Materials and Methods. Fully hydrophobic peptides, composed of varying numbers (5, 8, 11, 21) of isoleucine residues, were prepared in α-helical conformation with acetyl and N-methyl groups added at N- and C-terminal ends, respectively. To test the effect of starting conditions, peptides were placed in the membrane center and aligned either parallel or perpendicular with respect to the membrane normal. Lipids overlapping with parallel-oriented peptides were removed while keeping the same number of lipids in both leaflets. The initial box dimensions were 6.5 × 6.5 × 8.6 nm, and three-dimensional periodic boundary conditions were applied.

Membrane excess

The membrane excess of the peptide is given by the Mayer integral ${\int }_{-l/2}^{l/2}\left[\text{exp}\left(-dG\left(z\right)/kT\right)-1\right]dz$, where l is the membrane thickness, dG(z) is the free-energy difference between solvent and z position in the membrane, k is the Boltzmann constant, and T is the temperature. The membrane excess is somewhat related to the permeability coefficient, $P={\int }_{-l/2}^{l/2}\text{exp}\left(dG/kT\right)/D\left(z\right)dz$, assuming a constant diffusion coefficient, D(z). Another calculated value is apparent free energy of the peptide in the membrane,

$$d{G}_{app}=-kT\ln \left[\frac{{\int }_{-l/2}^{l/2}\text{exp}\left(-dG\left(z\right)/kT\right)dz}{{\int }_{-l/2}^{l/2}dz}\right],$$

which approximates the membrane with a single state.

Results

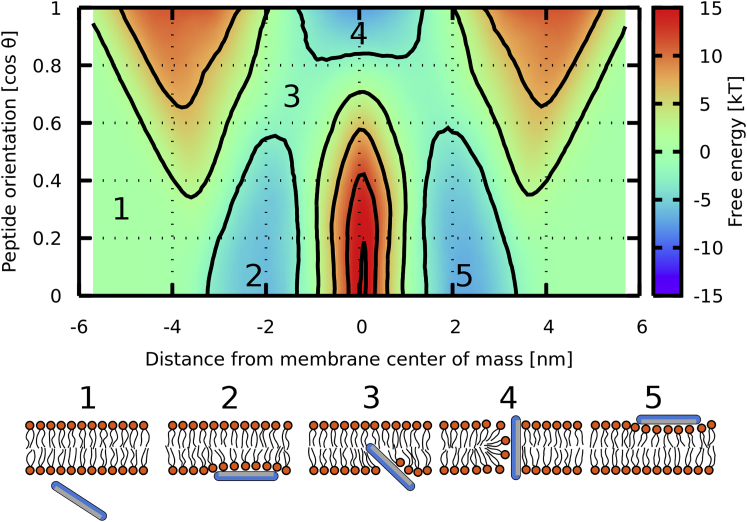
The free-energy surface of peptide translocation across the phospholipid membrane was calculated as a function of 1) the z-distance between peptide and membrane centers of mass and 2) peptide orientation with respect to the membrane normal. Fig. 1 shows a representative free-energy surface for a peptide of length 6 nm with the hydrophobic patch width of 170° and NEs. Initially, the peptide binds in the membrane headgroup region perpendicular with respect to the membrane normal. Subsequently, the peptide starts tilting while inserting deeper inside the hydrophobic core. In the inserted state, the peptide is oriented along the membrane normal. This translocation pathway is consistent for all simulated peptide parameters. All free-energy surfaces are included in the Supporting Materials and Methods. For peptides of length 4, 6, and 8 nm, see Figs. S1–S3, respectively.

Figure 1.

A typical example of calculated free-energy surface of peptide translocation across the lipid bilayer with five important positions of peptide: 1) in solution, 2) adsorbed at the membrane interface, 3) partially inserted, 4) inserted state with transmembrane orientation, and 5) adsorbed on the second leaflet. This particular surface is for a peptide of length 6 nm with hydrophobic patch width 170° and NE. Contours are drawn at every 5 kT. θ is the angle between the peptide main axis and the membrane normal. To see this figure in color, go online.

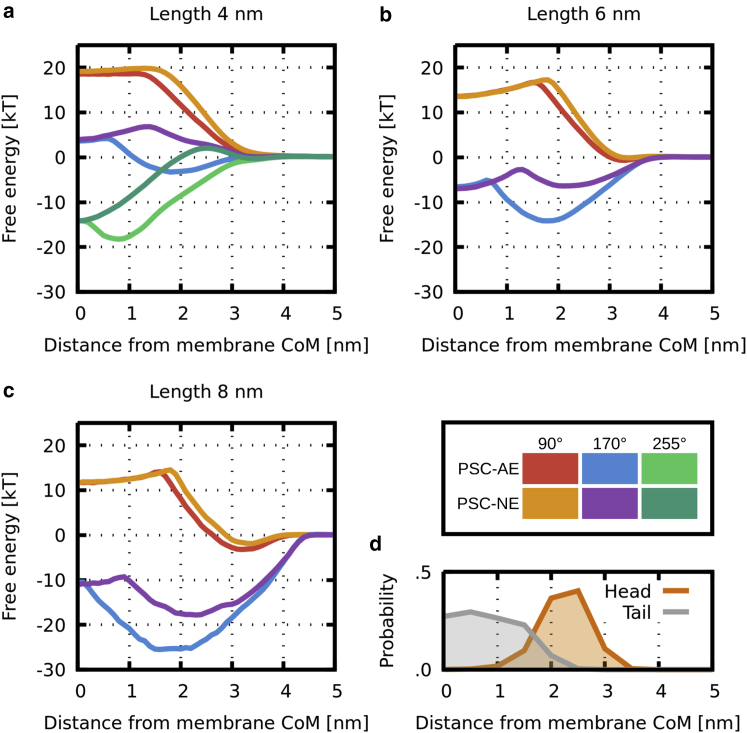
Fig. 2 shows free-energy profiles of translocation only as functions of distance between the peptide and membrane centers of mass. The orientation of peptides was averaged out using the Boltzmann weights. The strength and depth of peptide adsorption depend on both hydrophobic content as well as peptide capping. Short peptides with low hydrophobic content remain in the solution and do not significantly adsorb on the membrane. Longer peptides are adsorbed at the membrane interface, where PSC-AEs generally adsorb more strongly and deeply compared to PSC-NEs. The difference in adsorption is caused by the slightly smaller hydrophobic surface of PSC-NEs and local membrane perturbation caused by hydrophilic endcaps in contact with the hydrophobic core.

Figure 2.

(a–c) Calculated free-energy profiles of peptide translocation across the lipid bilayer as a function of distance between peptide and membrane centers of mass. In each graph, there are peptides of the same length whereas the hydrophobic content (patch width 90, 170, or 255°) and its distribution (AE, NE) are varied. (d) The probability density distribution of lipid head and tail beads showing the membrane thickness is shown. CoM, center of mass. To see this figure in color, go online.

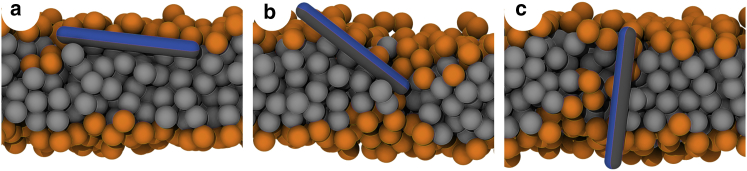
When the peptide free-energy differences along the profiles are sufficiently small (below a few kT), the translocation can become spontaneous. Indeed, we observed such translocation in unbiased simulations for 6-nm-long peptides with NE. Fig. 3 shows simulation snapshots along the translocation pathway. Upon the adsorption, perturbations in the lipid packing with local changes in membrane thickness around the hydrophilic ends of the peptide can be observed. As the peptide inserts, such local perturbations to membrane structure become more pronounced, and membrane thickness can be severely affected at this point. Considering the locally increased rate of lipid exchange between the membrane leaflets, it can be concluded that the peptide in the inserted state decreases the barrier for lipid flip-flop. Possibly, the peptide could be able to stabilize small transient pores.

Figure 3.

Snapshots from an unbiased simulation of peptide translocation. A peptide of length 6 nm with hydrophobic patch width 170° and NE is shown. The following three stages of peptide translocation are shown: (a) adsorption, (b) tilting, and (c) insertion. To see this figure in color, go online.

There are several important features on the profiles (see Fig. 1: points 2 and 5, adsorbed state with the peptide orientation roughly perpendicular to the membrane normal; point 3, barrier at local maximum; and point 4, inserted state with peptide orientation along the membrane normal). Related free-energy differences are ΔG_A, the free energy at the headgroup region, commonly a local minimum on the profile. ΔG_D is the largest free-energy difference on the profile, i.e., the difference between maximum (ΔG_max) and minimum (ΔG_min). ΔG_I corresponds to the free-energy difference between the bulk solution and center of the hydrophobic core (inserted state). All free-energy differences are summarized in Table 1.

Table 1.

Summary of Free-Energy Differences

Peptide	La	Pb	ΔGmin	ΔGmax	ΔGD	ΔGA	ΔGI
PSC-AE	4	90	0.0	18.7	18.7	0.0	18.5
	4	170	−3.3	4.2	7.5	−3.3	3.6
	4	255	−18.3	0.2	18.4	−18.3	−14.1
	6	90	−0.7	16.7	17.4	−0.7	13.6
	6	170	−14.2	0.1	14.3	−14.2	−6.6
	8	90	−3.2	14.1	17.3	−3.2	11.7
	8	170	−25.5	0.2	25.7	−25.5	−10.5
PSC-NE	4	90	0.0	19.8	19.8	0.0	19.1
	4	170	0.0	6.8	6.8	0.0	3.9
	4	255	−14.2	2.1	16.2	−0.3	−14.2
	6	90	−0.1	17.3	17.4	−0.1	13.5
	6	170	−7.0	0.1	7.1	−6.4	−7.0
	8	90	−1.9	14.5	16.4	−1.9	11.6
	8	170	−17.8	0.1	17.9	−17.8	−11.1

Estimated error for the free-energy differences is below 1 kT.

^aPeptide length in nanometers.

^bWidth of the hydrophobic patch in degrees.

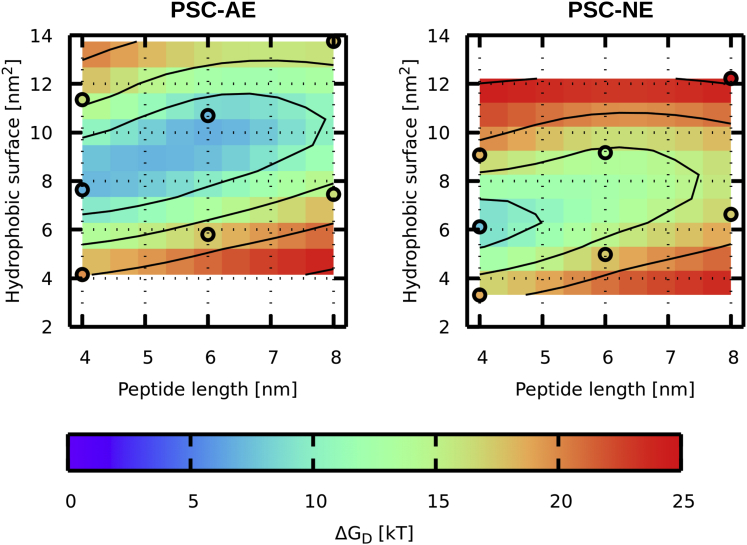
ΔG_D is the most important free-energy difference for the estimation of the peptide translocation. Fig. 4 and Table 1 show ΔG_D does not change monotonically with peptide hydrophobicity. Nonmonotonic behavior is caused by the position of the maximum, which changes from the local barrier (due to peptide tilt) to the water bulk values once the peptide becomes very hydrophobic. In contrast, ΔG_min and ΔG_I are monotonically decreasing with the higher hydrophobic content. In the inserted state, the peptide adopts transmembrane orientation with ends located at the headgroup region of the opposite leaflets. As a result, ΔG_I is very similar for both PSC-AE and PSC-NE peptides. The presence of the local barrier determines the metastability of the inserted state. The barrier originates in the unfavorable disruption of lipid packing induced by the partially inserted tilting peptide and favorable hydrophobic interactions. Hydrophobicity can also modify the barrier position with more hydrophobic peptides having the barrier closer to the membrane center.

Figure 4.

The largest free-energy differences on the profiles, ΔG_D, for PSC-AE (left figure) and PSC-NE (right figure) peptides. Individual data points from the simulations are shown in circles. The surface is created by interpolation, and contours are drawn every 5 kT. To see this figure in color, go online.

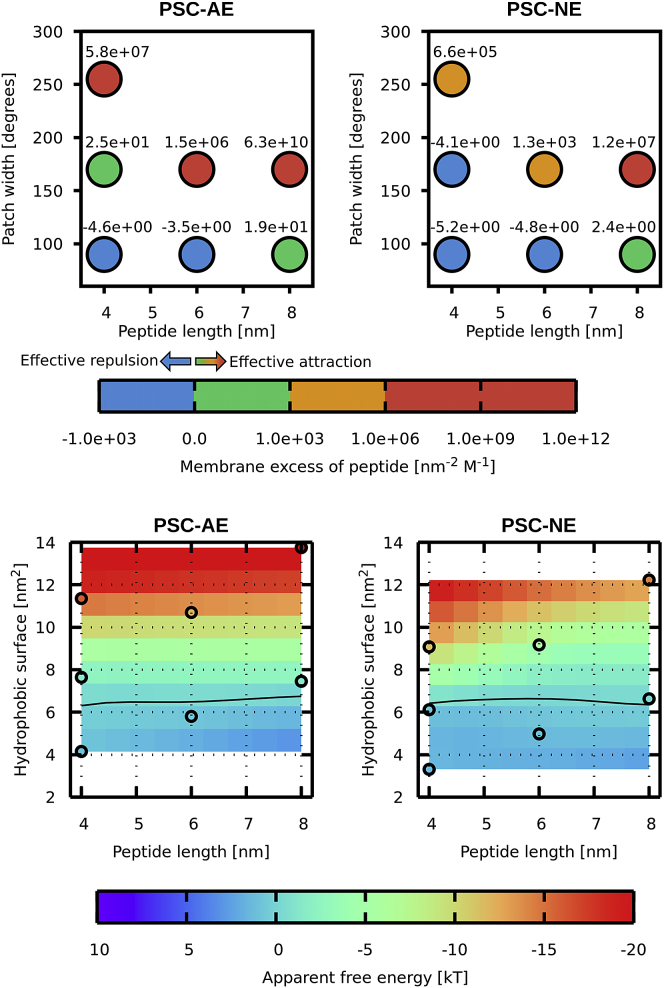
The peptide preference for membrane can be evaluated by calculating the membrane excess and apparent free energy (for definition and comparison to permeability coefficient, see the Methods). The membrane excess and the apparent free energy should be as close to zero as possible to balance the amount of peptides on the membrane and in solution. We have calculated both values for all studied peptides, and Fig. 5 provides guidance for the optimal length-to-hydrophobicity relationship. The values of apparent free energy differ less and were easier to interpolate. The optimal hydrophobic area of the peptide seems to be roughly constant with the peptide length, i.e., the optimal patch angle decreases with 1/peptide length.

Figure 5.

Membrane excess (top) and apparent membrane free energy (bottom) of peptide for PSC-AE (left figure) and PSC-NE (right figure) peptides. Individual data points from the simulations are shown in circles. The excess values are placed above the points and expressed in the units of nm⁻² M⁻¹. The free-energy surface is created by interpolation with the zero value depicted by the black line. To see this figure in color, go online.

In all our simulations, we have observed the model amphiphilic peptides to orient along the membrane normal in the inserted (transmembrane) state. This behavior, however, could still depend on the peptide hydrophobic content. Therefore, we have calculated the free energy surfaces for fully hydrophobic model peptides of length 4 and 6 nm, as shown in Fig. S4. The 4-nm peptide, which roughly spans the membrane, orients along the membrane normal. The longer, fully hydrophobic peptide has two minima inside the membrane: 1) tilted by 75° (cosθ = 0.26) with respect to the z axis and 2) slightly deeper minimum with peptide oriented along the membrane normal. The free-energy difference is less than 1 kT; however, these two minima are separated by a barrier of ∼5 kT. The tilted minimum corresponds to the peptide matching the membrane thickness (i.e., so-called hydrophobic mismatch) (49, 50). A graph showing the free energy to change the peptide orientation in the center of the membrane is shown in Fig. S5.

Unbiased simulations were performed for shorter (length 1-, 2-, and 3-nm) peptides. To diminish the effect of the initial conditions, each simulation was run twice, starting from 1) parallel or 2) perpendicular orientation with respect to the membrane normal. The 2- and 3- nm peptides remained in the membrane oriented along the normal. Although fully hydrophobic, the shortest peptide (1 nm in length) did not have peptide-solvent interactions strong enough to be adsorbed at the membrane, and the peptide remained in the solution. The results are shown in Fig. S6.

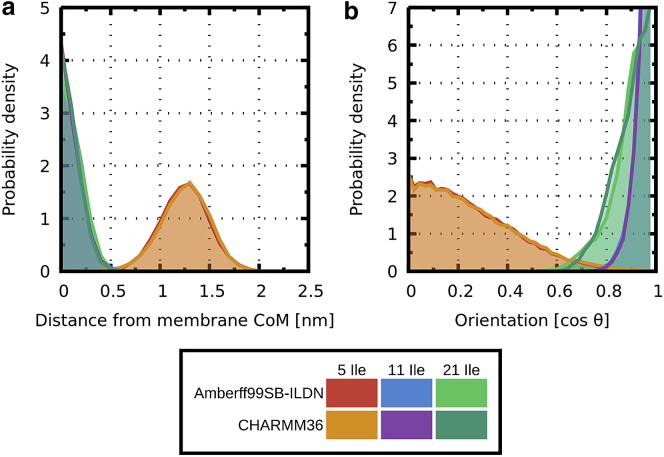
To validate the behavior of coarse-grained models, we have performed simulations using common all-atom force fields as follows: 1) Amber99SB-ILDN + Slipids and 2) CHARMM36. Simulations started from both parallel and perpendicular orientations with respect to the membrane normal. Probability densities of 1) peptide position with respect to the membrane center of mass and 2) orientation with respect to the membrane normal were calculated to assess the convergence of simulations. After equilibration, peptides (of length 5, 11, and 21 residues), despite differences in starting conditions and force fields, adopted the same position and orientation, suggesting converged results. Fig. 6 shows the probability distribution of peptide position and orientation averaged from 500-ns-long simulations.

Figure 6.

Probability densities of peptide (a) position (with respect to the membrane center of mass) and (b) orientation (with respect to the membrane normal) are shown. Poly-isoleucine peptides of length 11 and 21 residues are positioned in the membrane center and orient along the membrane normal. However, the shortest five-residue peptide remains in the interface region. In this case, a broader range of orientation is sampled, with a preference for perpendicular orientation to the membrane normal. A color-coded legend is below the graphs. The area below each curve is highlighted with corresponding color for clarity. CoM, center of mass. To see this figure in color, go online.

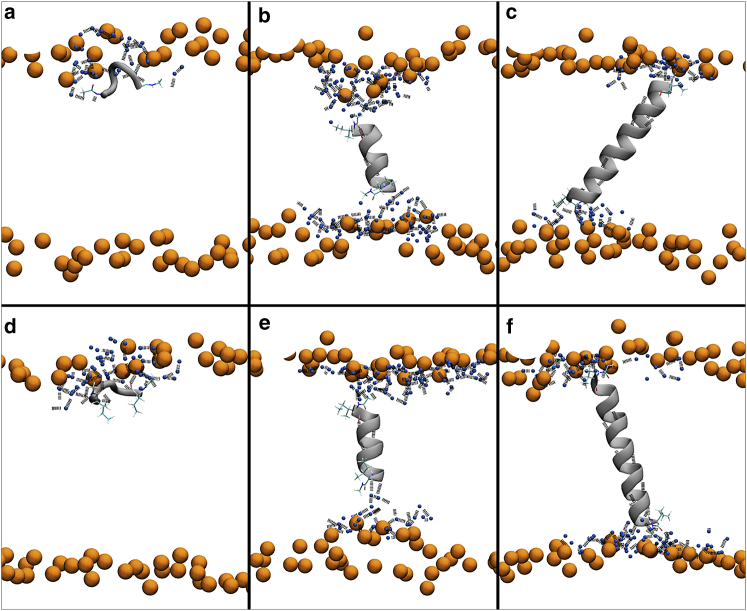
Fig. 7 shows the simulation snapshots from the end of the 500-ns-long molecular dynamics simulation. The poly-isoleucine peptides interact with water molecules via their termini. Both termini are not charged, and the interaction with water molecules is mediated via hydrogen bonds with the backbone. In all simulations, the five-residues-long peptide positions itself below the headgroup region. However, the transmembrane state (with peptide oriented along the membrane normal or slightly tilted) is metastable for 11-residues-long peptide, which is still not long enough to fully span the hydrophobic core. Because of the mismatch, membrane thinning and formation of water-filled membrane defects can be observed. The longest 21-residues-long peptide has to tilt to remain in the hydrophobic core following the hydrophobic mismatch.

Figure 7.

Snapshots from the end of 500-ns-long unbiased simulations of poly-isoleucine peptides with terminal capping. (a–c) Amberff99SB-ILDN + Slipids snapshots and (d–f) snapshots of CHARMM36 force fields. Peptides of length 5 (a and d), 11 (b and e), and 21 (c and f) residues are shown. Lipid phosphates are displayed in orange, water oxygens in the peptide proximity are colored in blue, peptide terminal residues are highlighted by sticks, and black dashed lines represent hydrogen bonds. To see this figure in color, go online.

We also investigated eight-residues-long peptide, for which its behavior is close to the peptide with 11 residues. However, in one out of four simulations, the peptide moved below the headgroup region oriented along the membrane surface, making the metastability of transmembrane state uncertain (see Fig. S7). Moreover, the stability of the peptides in the transmembrane orientation is likely affected by the composition of the membrane and the hydrophobic mismatch.

Discussion

Using coarse-grained simulations, we showed that the general translocation of secondary amphiphilic peptides with various lengths and hydrophobicity consists of three main steps: 1) adsorption on membrane surface (parallel to the membrane), 2) tilting, and 3) full insertion of the peptide with transmembrane orientation (see Fig. 1). This pathway is in agreement with previously observed translocation of a few specific peptides studied with coarse-grained Martini simulations (21) and also with microsecond-long all-atom simulations of PGLa peptide (26). However, not all amphiphilic molecules follow the same path. For example, cholesterol is known to be perpendicular to the membrane normal in the inserted state (24, 25). Therefore, we speculate that primary amphiphilic peptides would be different from secondary amphiphilic peptides and translocate similar to cholesterol.

In the inserted state, which can be metastable, all our amphiphilic peptides were found in the parallel orientation with respect to the membrane normal. In such orientation, the peptide ends are in contact with water molecules and lipid headgroups. The central part of the peptide is in contact with the hydrophobic core of the membrane. However, membrane defects can form along the hydrophilic part of the peptide (see Fig. 3). Fully hydrophobic peptides were observed in both transmembrane and tilted orientations, as described by hydrophobic mismatch theory used for transmembrane peptides/proteins (49).

We verified the observed transmembrane orientation of peptides by all-atom simulations. To make the peptides fully hydrophobic, we prepared poly-isoleucine peptides capped at both ends. Isoleucine was selected based on the Wimley-White hydrophobicity scale (13), in which isoleucine has the highest preference for membrane interior. Using different initial conditions and two different force fields (CHARMM36 and Amber99sb-ILDN + Slipids), we demonstrated that peptides longer than 10 residues have a metastable inserted state with transmembrane orientation (Figs. 7 and S7). The orientation follows hydrophobic mismatch orientation, which is stabilized with hydrogen bonds between the ends of the peptide backbone and water molecules.

Experimentally, the peptide orientation can be detected, but the comparison to our results is not straightforward. In the pioneering study, orientational circular dichroism was used to determine the orientation of alamethicin in the membrane (51). However, the exact tilt angle might not be possible to determine because the measured orientational circular dichroism curve could arise from, e.g., an average of two populations (52). Another common method to determine peptide orientation is solid-state nuclear magnetic resonance (53), but the samples typically have a low amount of water between the bilayers, which was shown to able to affect the peptide orientation (51). Moreover, if the inserted state is only metastable and its population is small compared to the other states, e.g., the adsorbed state being perpendicular to the membrane normal, it might not be detected at all. Yet, our findings are consistent with previous results on polyleucine peptides with hydrophilic ends, which spontaneously insert and orient parallel to the membrane normal for more than 10 leucines (54). Change of the orientation from perpendicular to parallel to the membrane normal was also reported for increasing length of leucine-serine peptides (55).

In the partially inserted state, a peptide end is inserted into the hydrophobic core of the membrane, and there is a barrier on the free-energy profile. By comparing the results of peptides with hydrophilic and hydrophobic ends, we conclude that hydrophobicity of the peptide termini has an important effect on the barrier and related metastability of the inserted state. Interestingly, many AMPs, including translocating peptide Buforin II, tend to have the charged residues positioned toward the peptide ends. In addition, LAK peptides were found in the transmembrane configuration for sequences with less than three lysines, but sequences with more lysines were observed adsorbed at the membrane in equilibrium (56). This suggests that electrostatic interactions could not only be responsible for membrane selectivity but can also increase the translocation barrier and modify the stability of the inserted state. The (de)stabilization of the inserted state is likely to depend on the position of charged residues within the peptide sequence.

We simulated the whole range of peptides from fully hydrophobic to very hydrophilic, and the calculated free-energy profiles are depicted in Fig. 2. From the free-energy profiles, we calculated the membrane excess of the peptide and the membrane apparent free energy, which are related to the peptide distribution. For insertion, fully hydrophobic peptides with hydrophilic ends are most suitable because they stabilize the transmembrane orientation. However, for translocation, the peptide should not be fully hydrophobic in order to have the distribution in membrane similar to bulk, i.e., the peptides are neither accumulated nor repelled from the membrane. Intuitively, increasing the hydrophobic content of peptide should facilitate its insertion into the membrane. However, excessively enhancing the insertion into the membrane would prevent it from membrane dissociation. Peptide with high hydrophobic content thus remains either on the membrane surface or inside the hydrophobic core. Peptide with low hydrophobic content remains in solution. The effectivity of such peptides as cargo transporters would be very limited.

The membrane apparent free energy and the membrane excess are single-value simplifications of the peptide distribution across the membrane (see the Methods). The value is zero for both the apparent free energy and the membrane excess when the peptide concentration in the membrane is the same as in the bulk. However, two very different free-energy profiles can produce similar values of apparent free energy, e.g., PSC-NE of length 4 nm and 170° patch and PSC-NE of length 8 nm and 90° patch (see Figs. 2 and 5). In the latter case, the apparent free energy has a significant contribution originating from the adsorbed states, balancing the concentration in the bulk. Thus, for translocation, it is important to further ensure that there are not large differences within the profile, i.e., the difference between the minimum and maximum (ΔG_D) on the free-energy profile should be as small as possible. Generally, ΔG_D is affected by hydrophobicity at the peptide termini, and it seems to be smaller for shorter peptides (Fig. 4). Coincidentally, many (currently 159 out of 437 in the antimicrobial peptide database (57)) helical AMPs are amidated on the C-terminus (58), possibly decreasing the barrier for insertion. These clues could be utilized during the design of more effective translocating peptides, in which the strength of adsorption and translocation barrier height should be minimized.

We can compare our results for peptide translocation to a previous study that focused on translocation of polymers (17). Significant differences were found. Namely, constant hydrophobicity per unit length is optimal for translocation of a polymer (17), whereas in the case of peptides, it only balances the concentration of peptides in the membrane and in the bulk. Moreover, the translocation path is different because peptides have a transmembrane orientation (parallel to membrane normal) that can be metastable; in contrast, the polymers had no metastable inserted states (17). The differences seem to originate from the structures of molecules. The studied polymers were unstructured in both membrane and solution (with decreasing size in the membrane) (17), whereas our peptides had a constant helical structure in the employed coarse-grained model, justified by increased helicity upon membrane adsorption. The peptide unfolding in solution could shift the free energy of the solution state. We can approximate the folding contribution by 0.4 kcal mol⁻¹ per residue, which was estimated for Melittin peptide (59); however, the value is likely to significantly depend on the peptide sequence.

Conclusions

Using computer simulations with coarse-grained models, we systematically investigated free-energy landscapes associated with the translocation of secondary amphiphilic and fully hydrophobic helical peptides. The translocation was described using both position and orientation of the peptide with respect to the membrane. We found a common translocation pathway consisting of adsorption, tilting, and insertion for all investigated amphiphilic peptides irrespective of their length, hydrophobic content, and hydrophilicity of peptide ends. If present, the adsorbed state is characterized by peptides bound perpendicular to the membrane normal. The depth of adsorption is determined by hydrophobic content including the peptide ends. The tilted state is characterized by partial peptide insertion with one peptide end in the hydrophobic core. Such a state typically corresponds to the free-energy barrier of the translocation. In the inserted state, all the peptides were found to be in transmembrane orientation with peptide ends at opposing leaflets. The inserted state is usually metastable, but the height of the barrier varies significantly. The characteristics of the inserted state were further verified with fully hydrophobic peptides of various lengths. The behavior of these peptides complies with the hydrophobic mismatch. Moreover, the transmembrane orientation of the peptide and its metastability was confirmed with all-atom simulations of poly-isoleucine peptides using two different force fields. From the free-energy profiles of peptide translocation, we calculated the membrane apparent free energy and membrane excess of the peptides. When the excess and the apparent free energy are zero, the concentration of peptide in the membrane and in the bulk is balanced. However, the translocation of the peptide is not ensured. Translocating peptides should have the free-energy profile as flat as possible (i.e., minimize the difference between the free-energy minimum (typically adsorption) and maximum (barrier or bulk state)). The provided translocation path and clues to optimize hydrophobicity are expected to be of broad interest in the development of new peptides with antimicrobial, cell-penetrating, or drug-delivery properties.

Author Contributions

R.V. designed the research. I.K. carried out all simulations and analyzed the data. Both R.V. and I.K. wrote the article.

Editor: D. Peter Tieleman.