Computational Model of Chimeric Antigen Receptors Explains Site-Specific Phosphorylation Kinetics

Abstract

Chimeric antigen receptors (CARs) have recently been approved for the treatment of hematological malignancies, but our lack of understanding of the basic mechanisms that activate these proteins has made it difficult to optimize and control CAR-based therapies. In this study, we use phosphoproteomic mass spectrometry and mechanistic computational modeling to quantify the in vitro kinetics of individual tyrosine phosphorylation on a variety of CARs. We show that each of the 10 tyrosine sites on the CD28-CD3ζ CAR is phosphorylated by lymphocyte-specific protein-tyrosine kinase (LCK) with distinct kinetics. The addition of CD28 at the N-terminal of CD3ζ increases the overall rate of CD3ζ phosphorylation. Our computational model identifies that LCK phosphorylates CD3ζ through a mechanism of competitive inhibition. This model agrees with previously published data in the literature and predicts that phosphatases in this system interact with CD3ζ through a similar mechanism of competitive inhibition. This quantitative modeling framework can be used to better understand CAR signaling and T cell activation.

Introduction

One of the most widely used methods for engineering a patient’s T cells to fight cancer is through the expression of chimeric antigen receptors (CARs). CARs are proteins that combine an extracellular antibody-derived targeting domain with intracellular T-cell-activating domains derived from the endogenous T cell receptor (1). These engineered T cells have emerged as promising treatments for hematopoietic cancers (2, 3); however, not all patients respond to treatment, and it has been difficult to expand these therapies to solid tumors (4, 5, 6, 7). Significantly, it has been shown that CARs are less effective at activating T cells than engineered T cell receptors (TCRs) (8). More work needs to be done to better understand the mechanisms through which CAR-engineered T cells become activated so that they can be more optimally designed and expanded to a wider patient population. In this study, we use quantitative phosphoproteomic mass spectrometry and computational modeling to explore the mechanisms that lead to the phosphorylation of CAR proteins. Computational models, like the one developed here, provide a unique method to use basic engineering principles to better understand and optimize the signaling pathways that activate CAR-engineered T cells.

The CAR-T-cell therapy Yescarta was approved by the Food and Drug Administration in October 2017 and contains signaling domains derived from the CD3ζ domain of the TCR and the CD28 costimulatory domain (3). These T-cell-signaling domains are phosphorylated by the Src family kinases, the most important of which in endogenous T cells is lymphocyte-specific protein-tyrosine kinase (LCK) (9, 10, 11). CD3ζ contains six tyrosine phosphorylation sites arranged in pairs on three immunoreceptor tyrosine-based activation motifs (ITAMs) (Fig. 1 A) (12). When doubly phosphorylated, these ITAMs can bind to the adaptor protein ZAP-70, perpetuating downstream signaling and also protecting the CD3ζ ITAMs from dephosphorylation (13, 14). Importantly, in addition to this main form of activation through ZAP-70, the three ITAMs can also bind other signaling proteins. Literature data indicate that the ITAMs have different binding capabilities and, therefore, can induce different downstream signaling events (15); however, more work needs to be done to specifically enumerate how the individual ITAMs differ in both their activation and, subsequently, their downstream signaling.

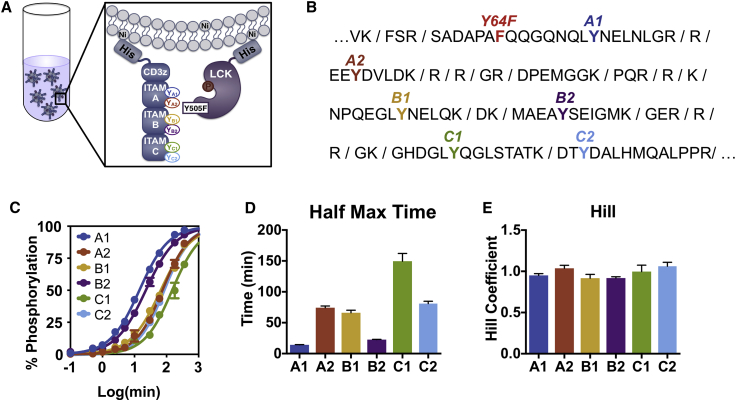
Figure 1.

CD3ζ sites are phosphorylated by LCK with different kinetics. (A) A schematic of the experimental liposomal system is shown. CD3ζ and LCK His-tagged proteins were purified and allowed to bind to large unilamellar liposomes bearing nickel-chelated lipids. Once proteins were bound, ATP was added, and the proteins were allowed to interact for various times before being subjected to phosphoproteomic mass spectrometry for quantification. (B) A sequence of CD3ζ intracellular domain is shown, with trypsin cut sites denoted. Individual ITAM tyrosine sites are labeled in different colors. Y64F indicates a tyrosine-to-phenylalanine mutation to ensure that each peptide only has one tyrosine phosphorylation site. This mutation does not influence overall phosphorylation kinetics (see Fig. S3). (C) Experimental data (circles) and sigmoidal fit (lines) for CD3ζ ITAM phosphorylation on liposomes containing 10% acidic POPS lipids are shown. Error bars represent the SD of two technical replicates normalized by site-specific standard curves. (D) The half-maximal time for each CD3ζ ITAM site is shown. Data represent mean and mean ± standard error of the fit to a four-parameter sigmoidal curve. (E) The Hill coefficient for each CD3ζ ITAM site is shown. Data represent mean and mean ± standard error of the fit to a four-parameter sigmoidal curve. To see this figure in color, go online.

Previous studies have attempted to qualitatively define the order of CD3ζ phosphorylation using CD3ζ phosphotyrosine-specific antibodies (16), but the similarity between ITAM sites limited the antibody specificity, preventing reliable conclusions regarding the phosphorylation order. In 2003, Housden et al. (17) used synthetic peptides that each contained one ITAM tyrosine to measure the preference of LCK for each site through radioactive phosphate incorporation. Although they did find differences in the rates of tyrosine peptide phosphorylation, their experiments were performed in solution, and each single tyrosine-bearing peptide was phosphorylated independently. Therefore, this study did not account for conformational, steric, and competitive factors that may influence the phosphorylation rates at different sites.

A study from Mukhopadhyay et al. (18, 19) proposed a mechanism for CD3ζ phosphorylation and dephosphorylation based on experimental measurements of total protein phosphorylation for CD3ζ with individual ITAM mutations. In this work, wild-type or ITAM mutant CD3ζ was coexpressed with LCK and phosphatase CD148 in human embryonic kidney 293 (HEK293) cells. Total CD3ζ phosphorylation was measured as a function of phosphatase inhibition, and it was found that there is no significant difference between the individual ITAMs; however, increasing the number of ITAMs decreased the half maximal effective concentration (EC50) value of the phosphorylation curve without changing the Hill coefficient. Mukhopadhyay and colleagues (18) hypothesized that the addition of phosphate groups on the CD3ζ intracellular domain could increase the rigidity of the CD3ζ tertiary structure, making unphosphorylated sites more accessible. They modeled this as an exponential increase in the association rate of the kinase and phosphatase toward CD3ζ; however, this mechanism is not fully validated without site-specific phosphorylation data.

Combining the CD3ζ activating domain and a costimulatory domain on the same protein adds additional complexity to the CAR. The CD28 costimulatory domain has four tyrosine sites, which can be phosphorylated by LCK (20) and may also influence the catalytic activity of LCK (21, 22). Once phosphorylated, CD28 tyrosine sites bind to various adaptor proteins that are also phosphorylated downstream of CD3ζ (23). Thus, CD28 can tune the response to CD3ζ activation. Additionally, the recruitment and competition by CD28 for LCK may alter the phosphorylation of CD3ζ.

All 10 of the tyrosine sites on CD3ζ and CD28 work together, in different ways, to affect the downstream signaling that controls T-cell-activation responses such as cytotoxicity, cytokine production, proliferation, and survival (24, 25, 26, 27, 28). By better understanding how these chimeric proteins are phosphorylated, we can identify ways to tune them to create more optimal CAR therapies. In this study, we have explored the kinetics of CD3ζ and CD28 phosphorylation in detail. We paired a recombinant protein system with phosphoproteomic mass spectrometry to measure the site-specific phosphorylation of CAR proteins by LCK over time. To our knowledge, this is the first study to quantify phosphorylation at individual sites on the intact intracellular domain of a CAR protein. We then fit these data using a computational model to robustly quantify the differences between the phosphorylation kinetics of the 10 tyrosine sites. We used the computational model to generate new predictions regarding the mechanism with which LCK phosphorylates the CD3ζ ITAMs. We can use the insights from this study to continue expanding our understanding of CAR-mediated T cell activation and better engineer future CAR therapies.

Materials and Methods

Recombinant protein expression and purification

His₁₀-KKCK-CD3ζ in the pET28a vector and HIS₁₀-LCK-G2A in the pFastBacHTA vector were a kind gift from Dr. Ronald Vale (29). To make the HIS₁₀-CD28-CD3ζ recombinant protein, the DNA sequence for the intracellular domain of CD28 (aa 180–220) was codon optimized and constructed by Integrated DNA Technologies. This sequence was then cloned directly upstream of CD3ζ in the pET28a vector using Gibson Assembly (Gibson Assembly Master Mix, New England BioLabs, Ipswitch, MA). All individual point mutations in the CAR vectors were introduced by the QuikChange XL site-directed mutagenesis kit (Agilent, Santa Clara, CA).

The sequence for HIS₁₀-LCK-G2A was amplified out of the pFastBacHTA vector by PCR (polymerase chain reaction) and cloned into the FUW vector through Gibson assembly. LCK is able to undergo autophosphorylation at both activating and inhibitory tyrosine sites (Y394 and Y505, respectively). We previously showed that when LCK is phosphorylated at these tyrosine residues, it has differential catalytic activity (30). Therefore, to exclude any confounding effects due to changes in enzymatic efficiency, we used a constitutively active form of LCK containing a tyrosine-to-phenylalanine mutation at the inhibitory site (Y505F). This point mutation was introduced by the QuikChange XL site-directed mutagenesis kit (Agilent).

All CAR proteins were expressed in the BL28(DE3) strain of Escherichia coli cells. E. coli cells were lysed as described in (31). His₁₀-LCK-G2A-Y505F was transiently expressed in HEK293T cells through a standard calcium phosphate precipitation protocol (32). 48 h after transfection, HEK293T cells were lysed in buffer containing 20 mM Tris·HCl (pH 7.5), 600 mM NaCl, 2 mM MgCl₂, 5 mM immidazole, 10% glycerol, 1% nonidet P-40, 1 mM Na₃VO₄, 10 mM NaF, and 1× complete protease inhibitor (Roche, Basel, Switzerland). All HIS₁₀ proteins were purified using fast protein liquid chromatography, first on a Ni-NTA agarose column followed by gel purification using the HiPrep 16/60 Sephacryl S-200 HR column (both columns are from General Electric Life Sciences, Marlborough, MA) in HEPES-buffered saline solution containing 50 mM HEPES-NaOH (pH 7.5), 150 mM NaCl, and 10% glycerol, as described in (29). Protein monomer fractions were concentrated, snap frozen in liquid nitrogen, and stored at −80°C. All purified recombinant proteins were quantified by sodium dodecyl sulfate polyacrylamide gel electrophoresis and Coomassie brilliant blue staining using bovine serum albumin as a standard.

Mass spectrometry confirmed that nearly 100% of the purified LCK-Y505 is phosphorylated at the activating Y394 site, whereas 100% of the CAR proteins were unphosphorylated after purification.

Liposome preparation

Synthetic 1,2-dioleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-l-serine (POPS), and 1,2-dioleoyl-sn-glycero-3-[(N-(5-amino-1-carboxypentyl)iminodiacetic acid)succinyl] (nickel salt, DGS-NTA-Ni) were purchased from Avanti Polar Lipids (Alabaster, AL) and resuspended in chloroform. Liposomes were prepared as described in (29). Briefly, phospholipids (80% POPC, 10% POPS, 10% 1,2-dioleoyl-sn-glycero-3-[(N-(5-amino-1-carboxypentyl)iminodiacetic acid)succinyl] (nickel salt)) were dried as thin films under Ar gas and desiccated overnight. The lipids were then resuspended in 1× kinase buffer (50 mM HEPES-NaOH (pH 7.5), 150 mM NaCl, 10 mM MgCl₂, 1 mM tris(2-carboxyethyl)phosphine), and subjected to 5× freeze thaw cycles. The lipid mixture was then extruded through 200-nm pore-size polycarbonate filters to produce large unilamellar liposomes. As such, we assume that the liposomes have an outer diameter of roughly 200 nm (29). For liposomes with varying POPS concentration, the amount was compensated for by adjusting the POPC concentration.

Protein phosphorylation time courses

His-tagged LCK and CAR proteins were mixed with Ni-bearing liposomes for 1 h to allow for the proteins to attach to nickel-bearing lipids on the surface of the liposome, as calculated and described in (29). We used 20,000 molecules/μm² CAR proteins and titrated down LCK to a very low concentration to allow us to distinguish the differences between the CD3ζ site phosphorylation kinetics. The low LCK concentration allows us to measure the rapid phosphorylation kinetics of CAR tyrosine sites. Estimation of the final LCK concentration is described in the Comparison of Model Structures. Once the proteins attached to the liposomes, 10× ATP in kinase buffer was added to a final concentration of 1 M. Samples were taken at various times, and the reaction was stopped by adding urea to 8 M and boiling for 5 min. Time samples were then frozen at −20°C until they were prepared for phosphoproteomic mass spectrometry.

Standard curve preparation

Because differing ionization efficiencies for each peptide result in different intensities for the same amount of peptide on a mass spectrometer (MS), a standard curve is necessary to compare between peptide MS intensities in a sample. We constructed our standard curves based on a known ratio of phosphorylated/unphosphorylated peptide. For each CAR protein, we quantified the amount of protein and aliquoted the same volume from a given sample into two vials. To one vial, we added LCK and ATP and let LCK phosphorylate the CAR overnight at room termperature. To the other vial, we added equal volumes of HEPES-buffered saline buffer, so that the phosphorylated and unphosphorylated CAR proteins would remain at the same concentration. The next morning, urea was added to both vials to a final concentration of 8 M. We then combined various volume ratios of the two solutions to create a standard curve with known ratios of phosphorylated/unphosphorylated peptides. The standard curve samples were stored at −20°C until they were ready to be prepared for analysis by mass spectrometry.

Phosphoproteomic sample preparation

The time course and standard curve samples were thawed to room temperature and reduced by the addition of dithiothreitol to a final concentration of 5 mM for 1 h at 37°C. Samples were next alkylated with iodoacetamide at a final concentration of 25 mM for 1 h at room temperature in the dark. This reaction was quenched by the addition of dithiothreitol to a final concentration of 10 mM for 30 min. Samples were then diluted to a final urea concentration of 2 M with 100 mM Tris (pH 8) and trypsin digested overnight at 37°C. The next morning, samples were acidified to a pH < 4 with 5% trifluoroacetic acid, purified by C18 zip-tip (Millipore, Burlington, MA) according to the manufacturer’s instructions, and eluted into 50% acetonitrile solution. Purified samples were then dried and stored at −80°C until they were ready to be analyzed.

Phosphoproteomic data collection

All data samples were run in technical duplicates. Data were collected in three sets, each with their own standard curve, shown in Fig. S1: 1) the first biological replicate of the wild-type ITAM phosphorylation on 10% POPS liposomes, the wild-type ITAM phosphorylation on 0 and 45% POPS liposomes, and a CD3ζ standard curve; 2) the second biological replicate of the wild-type ITAM phosphorylation on 10% POPS liposomes, the individual tyrosine-to-phenylalanine CD3ζ ITAM point mutants, and a CD3ζ standard curve; and 3) all 28ζ proteins, including the Y206F and Y209F mutants, and a standard curve for 28ζ, CD28-Y206F-CD3ζ, and CD28-Y209F-CD3ζ. Desalted samples were reconstituted in buffer A (0.1% formic acid). The samples were injected into an Easy 1200 nanoLC ultrahigh-pressure liquid chromatography coupled to a Q-Exactive Plus MS (ThermoFisher Scientific). Peptides were separated by reversed-phase chromatography (PepMap RSLC C18, 2 μm, 100 Å, 75 μm × 15 cm; ThermoFisher Scientific, Waltham, MA). The flow rate was set to 300 nL/min at a gradient starting with 6% buffer B (0.1% FA, 80% acetonitrile) to 55% B in 25 min, followed by an 8-min washing step to 100% B. The maximal pressure was set to 1180 bar, and the column temperature was held constant at 50°C.

Peptides separated by the column were ionized at 2.0 kV in positive mode. Mass spectrometry analyzer 1 survey scans were acquired at A resolution of 70 k from 275 to 1500 m/z, with a maximal injection time of 80 ms and automatic gain control target of 10⁶. MS/MS fragmentation of the 10 most abundant ions was analyzed at a resolution of 35 k, automatic gain control target 10⁵, maximal injection time 100 ms, and normalized collision energy 25. Dynamic exclusion was set to 10 s, and ions with a charge of 1, 7, or >7 were excluded.

Mass spectrometry data analysis and normalization

MS/MS fragmentation spectra were searched with Proteome Discoverer SEQUEST (version 1.4; ThermoFisher Scientific) against the recombinant protein sequences (17 entries) used in this study. The maximal missed cleavages was set to 2. Dynamic modifications were set to oxidation on methionine, phosphorylation on serine, threonine, and tyrosine, and acetylation on protein N-terminus. Fixed modification was set to carbamidomethylation on cysteine residues. The maximal parental mass error was set to 10 ppm, and the MS/MS mass tolerance was set to 0.02 daltons. The false discovery threshold was set to 0.01 using Percolator node validated by q-value. Phosphosite localization was confirmed using PhosphoRS (all sites >75% probability).

MS1 peak quantification was performed manually in Skyline (version 3.7) for each phosphorylated/unphosphorylated peptide pair. We analyzed only peptides with no missed cleavages and no modifications other than tyrosine phosphorylation, which were consistently the largest peaks. One exception was made for the CD28 peptide containing tyrosine site Y218. The unphosphorylated form of this peptide was smaller than the cutoff mass/charge ratio used in our data collection. Therefore, we analyzed this site using the peptide with one N-terminal missed cleavage.

To create our peptide standard curves, we calculated the ratio of each phosphorylated/unphosphorylated peptide, plotted them against the known ratios, and fitted the resulting linear plots (Fig. S1). Technical replicates of each peptide were combined together to fit the standard curves so that one standard curve was used to normalize the phosphorylated/unphosphorylated peptide intensity ratios for each set of peptide time course technical replicates. We then used the normalized ratios to calculate the percent phosphorylation over time for each time course technical replicate and used the two sets to calculate the mean and SD of the data. Time courses were only normalized to the standard curve data collected at the same time.

Statistical analysis

All statistical analyses were done using a one-way analysis of variance followed by multiple pairwise comparisons using the Tukey t-test in Prism (version 7; GraphPad, La Jolla, CA).

Sigmoidal parameter calculations

Data were fitted in Prism to a standard sigmoidal curve with plateaus at 0 and 100%:

$$y=\frac{100}{1+{10}^{\left(\log \left(t_{half}\right)-x\right)\ast Hill}},$$ (1)

where x is the time on a log scale, y is the output, t_half is the half-maximal time, and Hill is the Hill coefficient. For the comparison of t_half and Hill for the random and sequential models, the models were first fitted to data using MATLAB (The MathWorks, Natick, MA), as described in Comparison of Model Structures below. The model responses were then entered into Prism as data sets and fitted to Eq. 1.

Model implementations

The four models used in this work are briefly described below, along with an explanation of the equations used to implement the models. Detailed model definitions and mechanistic descriptions are presented in Results, Mechanism of CD3ζ phosphorylation by LCK.

Overview of models

The sequential-order model assumes LCK phosphorylates the six CD3ζ sites in a specified order determined by the ordering of the sites’ half-maximal times (shortest to longest). The random-order model allows the CD3ζ sites to be phosphorylated in any order needed to fit our experimental data. In the phosphate priming model, proposed by Mukhopadhyay et al. (18), the rate of phosphorylation at one CD3ζ site is enhanced because of the presence of other phosphate groups. Lastly, we introduce the competitive inhibition model to account for competition between unphosphorylated and phosphorylated sites on CD3ζ.

Model equations

For the sequential- and random-order models, the ordinary differential equations were written using standard Michaelis-Menten kinetics, as shown in Eq. 2:

$$\frac{d\left[p{Y}_i\right]}{dt}=\frac{k_{cat}\ast LCK\ast Y_i}{K_{M,i}+Y_i},$$ (2)

where Y_i and pY_i represent the unphosphorylated and phosphorylated species, respectively, for ITAM tyrosine site i. Here, i can be A1, A2, B1, B2, C1, or C2. LCK represents the concentration of the kinase LCK, k_cat is the catalytic rate, and K_M,i is the Michaelis-Menten constant for each ITAM site i.

For the phosphate priming model, we also used random-order Michaelis-Menten kinetics. However, the Michaelis-Menten constant for each ITAM site, K_M,i, was scaled by a constant, λ, raised to the power of the number of phosphate groups on the indicated CD3ζ molecule, p, resulting in, $K_{M,i}^p$, as shown in Eq. 3:

$$K_{M,i}^p=\frac{K_{M,i}}{{\lambda }^p}.$$ (3)

We started with a λ-value of three, as estimated by Mukhopadhyay et al. (18), and fitted the k_cat, six K_M,i-values, and the total amount of LCK kinase to the data. We then expanded our parameter space to explore other values of λ. We found that λ-values less than one were able to significantly improve the fit. However, this inversion of the λ parameter resulted in a mechanism that was deemed physiologically irrelevant based on previous work in the literature (18); therefore, λ was kept at a value of three.

The competitive inhibition model also relied upon Michaelis-Menten kinetics. The equation describing the rate of each ITAM phosphorylation is shown in Eq 4:

$$\frac{dp{Y}_i}{dt}=\frac{\left(\raisebox{1ex}{$k_{cat}$}\!\left/ \!\raisebox{-1ex}{$K_{M,i}$}\right.\right)\left(Y_i\right)\left(LCK\right)}{1+\frac{Y_{A1}}{K_{M,A1}}+\frac{Y_{A2}}{K_{M,A2}}+\frac{Y_{B1}}{K_{M,B1}}+\frac{Y_{B2}}{K_{M,B2}}+\frac{Y_{C1}}{K_{M,C1}}+\frac{Y_{C2}}{K_{M,C2}}+\frac{p{Y}_{A1}}{K_{I,A1}}+\frac{p{Y}_{A2}}{K_{I,A2}}+\frac{p{Y}_{B1}}{K_{I,B1}}+\frac{p{Y}_{B2}}{K_{I,B2}}+\frac{p{Y}_{C1}}{K_{I,C1}}+\frac{p{Y}_{C2}}{K_{I,C2}}},$$ (4)

where all variables are the same as described for Eq. 1 and K_I,i is the inhibitory constant for each ITAM site, i.

In our preliminary exploration of the model parameter space, we identified the following several groups of parameters in this model structure that were correlated: the Michaelis-Menten constants, the inhibition constants, and the total LCK concentration and catalytic rate. Therefore, to better constrain this system, we made a series of assumptions. First, the addition of six inhibition constants greatly overparameterizes the model. To reduce this number, we assume that adding a phosphate group will affect all of the ITAM sites the same way. Therefore, we simplified the inhibition constants to a single factor (X_I) that could be used to scale the Michaelis-Menten constant for each site, as shown in Eq. 5:

$$K_{I,i}=K_{M,i}\ast X_I.$$ (5)

Second, we fixed the catalytic rate of LCK. The initial conditions for the CAR proteins were based on the measured protein densities used in our experiments, 20,000 molecules/μm². To distinguish between the rapid phosphorylation kinetics of CAR tyrosine sites, low concentrations of LCK were used in the experiments. This experimental condition also agrees with the assumption of Michaelis-Menten kinetics that the enzyme concentration is much less than the substrate concentration. However, this low level of LCK made it very difficult to measure the exact concentration relative to the experimental errors. Therefore, we held the catalytic rate constant based on the average rate of CD3ζ phosphorylation by constitutively active LCK, calculated in (29), and fitted the initial concentration of LCK.

Third, because all of the K_M-values varied together in a correlated manner, we chose to hold the K_M-value for site B1, K_M,B1, which is phosphorylated at an intermediate rate relative to the other sites, equal to the estimated K_M-value from (29). Through many simulations, we confirmed that these parameter assumptions did not significantly affect the model fitted to the data.

Comparison of model structures

Our mechanistic computational models were written as a set of rules in BioNetGen (33) and implemented in MATLAB (Data S1–S5). We used Michaelis-Menten kinetics to describe the reaction rate of LCK toward each of the six ITAM sites, as described in the previous section. Parameter fitting was performed in an iterative manner. For the different model structures, starting values for Michaelis-Menten constants were first identified by manually performing parameter sweeps across a wide range. For this step, the catalytic rate was held at 360 min⁻¹, based on literature values (29), and the total LCK concentration was 60 molecules/μm², as estimated in the experimental setup. Once a suitable order of magnitude was identified for the K_M-values, all of the parameters were allowed to vary twofold up and down, and the parameters were fitted to all of the data together (wild-type CD3ζ, mutant CD3ζ, and liposome concentration data) using particle swarm optimization (PSO) (34). Each data set was fitted a minimum of 10 times. The error between the model fits and experimental data (calculated as the sum of the squared error, SSE) were used to characterize the goodness of fit to select the best parameter sets.

For model structures that did not fit the data well, we further explored the parameter space to see if changing the range of parameters could improve the fit. To do this, we manually altered the parameters for which the physiological range is not well defined (i.e., the two-dimensional Michaelis-Menten constants and any scaling factors). If we identified a parameter space that better represented the data, we performed another round of 10-parameter-set fits using PSO. For the final parameter estimation, all of the parameters that were not fixed were allowed to vary two orders of magnitude up and down from their baseline values (LCK = 60 molecules/μm², K_M,i = 270 molecules/μm², and X_I = 1). The model was fitted 100 times using PSO, and the 50 best fits were taken as the final parameter ranges. For all models, the parameter set with the best fit was used for model comparison.

The best fit to each model was compared using Akaike information criterion (AIC) (35). AIC measures the quality of a model to represent a given set of data while accounting for the number of parameters fitted to that data. Therefore, the AIC allows us to compare between model structures with different numbers of parameters. To calculate AIC, we used an approximation that incorporates the error between model fit and experimental data (36). This approximation is based on the assumption that the residuals between the model and data are normally distributed. Although the residuals for the four candidate models have a slightly wider distribution than normal (Fig. S2), the residuals are not skewed, and all distributions are centered around zero. Equation 6 shows the calculation of AIC used to compare the models:

$$AIC=n\times \log \left(\frac{SSE}{n}\right)+2k,$$ (6)

where n is the number of data points, SSE is the sum of the squared error between the data and the model predictions, and k is the number of parameters used to fit the model. The model with the smallest AIC is assumed to be the best model. The difference in the AIC for each model compared to the model with the lowest AIC is an indication of the plausibility of a model. A model with an AIC difference greater than 10 may be omitted from further consideration compared to the model with the lowest AIC (36).

Phosphatase model

To explore the mechanism of phosphatase activity on the model, we implemented phosphatase mechanisms with a random order, a phosphate-priming mechanism, or a competitive inhibition mechanism. For the phosphate-priming model, we held the phosphate-dependent scaling factor, λ, equal to three, as estimated by Mukhopadhyay et al. (18). In the competitive inhibition model, both phosphorylated and unphosphorylated ITAM sites provide competitive inhibition. For each of these mechanisms, we manually explored ranges of parameter space within one order of magnitude above or below the value that was estimated for the LCK phosphorylation parameters. We particularly focused on variations in the parameters for which all of the phosphatase Michaelis-Menten kinetics were 1) all the same between the ITAM sites and 2) scaled so that they maintained the same relative differences as were identified for the LCK parameters. Once a mechanism and parameter space with the correct trends for EC50 and Hill coefficients were identified, we then further tuned the phosphatase Michaelis-Menten constants to better fit the data.

Results

The six tyrosine sites on CD3ζ are phosphorylated by LCK with different kinetics

We first sought to explore how LCK phosphorylates the six tyrosine sites on CD3ζ. To do this, we utilized a liposome-based recombinant protein system developed by Hui and Vale (29). In this system, His-tagged proteins are bound to nickel-chelating lipids on the surface of large unilamellar liposomes, as shown in Fig. 1 A. Because the CAR and LCK proteins are largely membrane bound in T cells, this system allows us to mimic the two-dimensional protein arrangement and more accurately capture the true kinetics of the interactions between these proteins.

The liposome-bound proteins were allowed to react in the presence of ATP, and we performed phosphoproteomic mass spectrometry to specifically measure the phosphorylation at each ITAM site over time. To quantify the site-specific phosphorylation, we needed to directly compare the mass spectrometry intensity of phosphorylated and unphosphorylated peptide pairs. To do this, we used a standard curve with a known ratio of phosphorylated/unphosphorylated peptide (Fig. S1) (37). Additionally, we needed to ensure that there is only one tyrosine site on each tryptic peptide. This is true for all CD3ζ ITAM tyrosine sites except A1 (Fig. 1 B). The peptide containing site A1 also contains a tyrosine at position 64, which is not part of an ITAM and is not predicted to play a significant role in CD3ζ phosphorylation based on known LCK-binding motifs and computational predictions (38, 39, 40, 41). Therefore, we added a Y64F mutation in the CD3ζ recombinant protein and validated that it does not influence the overall phosphorylation kinetics within this system (Fig. S3). In this way, we were able to normalize the phosphorylated/unphosphorylated intensity ratios for each ITAM site in our time courses by the standard curves, thus calculating the percent phosphorylation over time for each tyrosine site of interest.

Fig. 1 C (dots) shows the percent phosphorylation of each of the six ITAM sites over time on liposomes that contain 10% acidic phosphatidylserine (POPS) lipids, which is similar to the concentration of phosphatidylserine on the inner leaflet of the T-cell plasma membrane (29). Our measurements show that the sites are not phosphorylated at the same rate. To quantify the differences, we fitted these data to a four-parameter sigmoidal curve (Fig. 1 C, lines), estimating the half-maximal time (Fig. 1 D) and the Hill coefficient (Fig. 1 E) for each site. The half-maximal times show that the six sites are phosphorylated with different kinetics (A1 > B2 > B1 ≥ A2 ≥ C2 > C1). In comparison, the Hill coefficients for all tyrosine phosphorylation sites are close to one.

CD3ζ ITAM mutations

We next wanted to explore the influence that individual tyrosine sites have over the phosphorylated kinetics of other sites. Specifically, we wanted to identify if there are any binding or competitive effects that influence the kinetics at distant sites. Therefore, we individually mutated each tyrosine site to a phenylalanine and measured the percent phosphorylation of the other sites over time.

We also investigated the effect of the liposome membrane acidity. Several TCR proteins, including the closely related CD3ε and CD28 proteins, have been shown to have basic residues in their intracellular domains that can interact with acidic lipids on the inner leaflet of the T-cell membrane (42, 43, 44). These interactions are thought to help limit tyrosine accessibility, thus controlling aberrant phosphorylation in unstimulated cells. Therefore, we also tested if CD3ζ interactions with the acidic POPS lipids in the liposome membrane were contributing to the different rates of phosphorylation seen in the site-specific data.

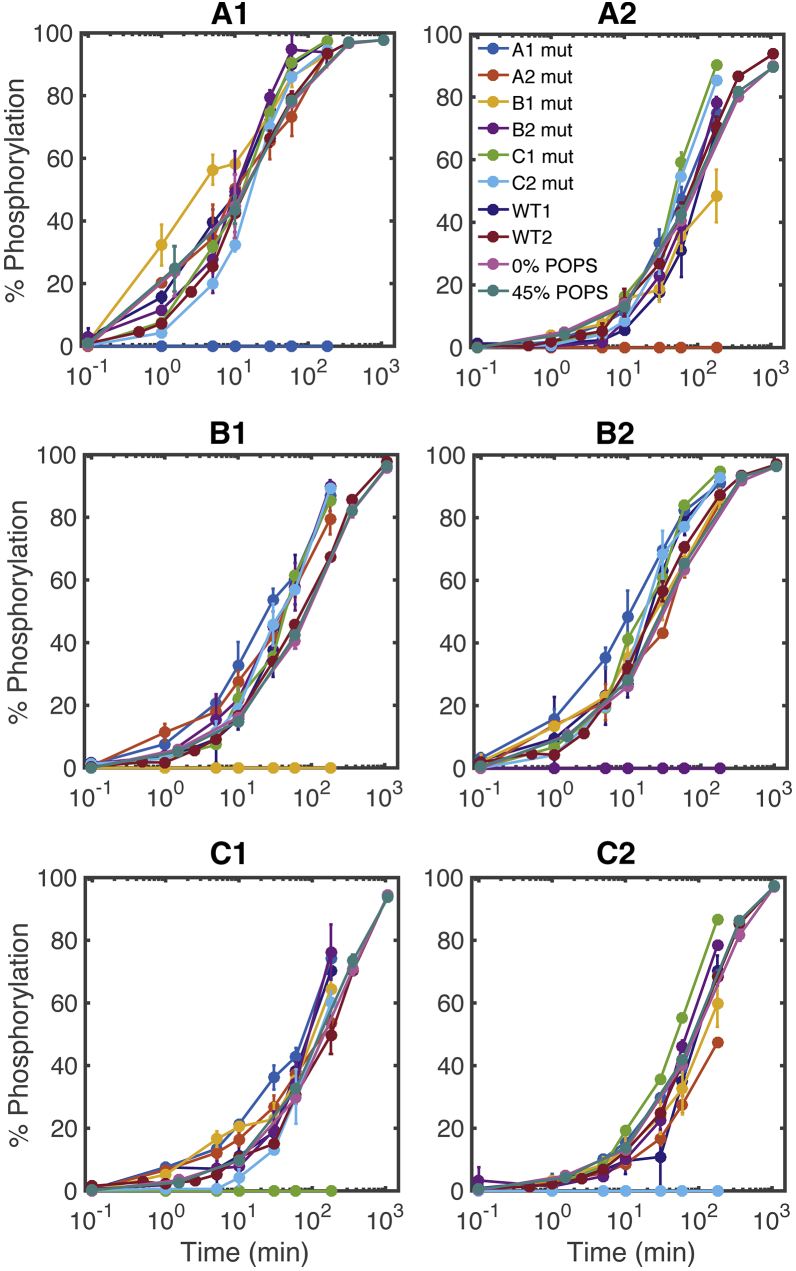
Fig. 2 shows the overlay of all of the phosphorylation time course experiments (six individual CD3ζ Y to F point mutations, wild-type CD3ζ stimulated on 0 and 45% POPS liposomes, and two biological replicates of wild-type CD3ζ stimulated on 10% POPS liposomes) for each site. Although there is some variability in the phosphorylation time courses between the mutations, the trends for all of the site-specific time courses are very similar. Additionally, individual site mutations and changes to the acidic lipid microenvironment do not significantly affect the order of the phosphorylation kinetics of CD3ζ tyrosine sites.

Figure 2.

A comparison of individual tyrosine site mutations and lipid concentrations on phosphorylation kinetics. Experimental data for each CD3ζ ITAM site for different experimental conditions are shown: wild-type (WT) 1 and 2 (biological replicates of CD3ζ with unmutated ITAMs on liposomes containing 10% POPS), XX mutant (mut) (where XX represents the tyrosine-to-phenylalanine ITAM mutation site for CD3ζ stimulated on 10% POPS liposomes), and X% POPS (where X represents the POPS concentration for liposomes bearing CD3ζ with wild-type ITAMs). Error bars represent the SD of two technical replicates normalized by site-specific standard curves. To see this figure in color, go online.

To further compare between the sites, we grouped the time course responses together for all of the experimental conditions and used the pairwise Tukey t-test to identify which ITAM site phosphorylation levels were significantly different from the others (Fig. S4). We compared the data sets at two different time points of 10 min (blue), which is close to the half-maximal time of the quickly phosphorylated ITAM sites A1 and B2, and 60 min (orange), which is close to the half-maximal time of the majority of the other sites. The 10-min comparison shows that A2, C1, and C2 are not significantly different from each other, whereas site B1 is significantly different from A2 and C1 but not C2. From both the 10- and 60-min comparisons, we see that sites A1 and B2 are both significantly different from all other sites.

Mechanism of CD3ζ phosphorylation by LCK

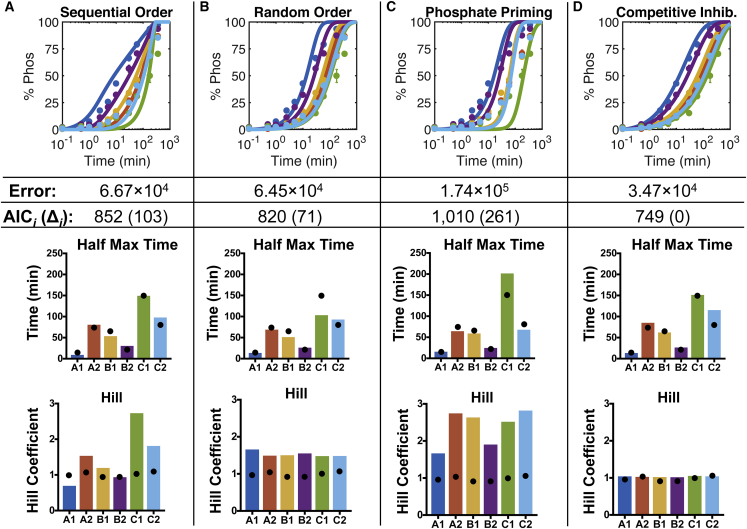
These data show us key features of the kinetics of CD3ζ site-specific activation. To determine a specific mechanism of interaction between LCK and CD3ζ, we turned to computational mechanistic modeling. We explored a variety of different mechanisms described in the literature or indicated by the data themselves (see Materials and Methods for further explanation). We fitted each of these various models to all of our data (wild-type CD3ζ, tyrosine-to-phenylalanine mutant CD3ζ, and changes to the liposome composition) and analyzed the results to make a hypothesis about which mechanism best represents the system. To quantitatively assess the characteristics of each model in relation to our data, we calculated the half-maximal time and Hill coefficient of each model-predicted phosphorylation time course. Note that the time is plotted on the log scale to display the full time course and the early kinetics of phosphorylation. The model mechanisms were compared, and the most suitable model was chosen based on the overall fit to the data (SSE) and AIC.

Sequential order

The first mechanism we tested was a sequential phosphorylation order, in which LCK can phosphorylate the six CD3ζ in a specified order defined by the order of the half-maximal time from the sigmoidal fit to the data (Fig. 1 D). These reactions are modeled using Michaelis-Menten interactions (best fit parameters are listed in the BioNetGen Data S1). As shown in Fig. 3 A, this model is able to capture the differences in half-maximal time well, but it leads to a consistent increase in the Hill coefficient for each subsequent tyrosine site in the sequence (A1, B2, B1, A2, C2, and C1). This increase in slope has been previously described as a characteristic of sequential multisite phosphorylation (19, 45, 46). However, this steep slope does not match our raw data, which show a consistent Hill coefficient for all sites (Fig. 1 E), or other data of CD3ζ phosphorylation in the literature (18). Additionally, the shape of the model fits does not qualitatively match the experimental data. Overall, the modeling results indicate that LCK does not phosphorylate CD3ζ sequentially.

Figure 3.

A comparison of CD3ζ phosphorylation mechanisms. A model analysis for mechanisms of (A) sequential-order phosphorylation, (B) random-order phosphorylation, (C) phosphate-priming phosphorylation (Phos) rates, and (D) competitive inhibition (Inhib) by unphosphorylated and phosphorylated CD3ζ ITAM sites is shown. (Top) The model was fitted to experimental data. Error represents the residual error between the model and the data for all data sets, including wild-type, individual tyrosine-to-phenylalanine mutants, and different liposome concentrations. AIC represents the Akaike information criterion calculation for each model (AIC_i). We also report the AIC difference (Δ_i) between each model and the model with the lowest AIC, as a means of model comparison. (Middle) Half-maximal times of the model predictions are shown. (Bottom) Hill coefficients of the model predictions are shown. Black dots indicate the mean values from the sigmoidal fit to the data shown in Fig. 1, D and F. To see this figure in color, go online.

Random order

We next tried a simple mechanism of a random phosphorylation order. In this random-order model, each of the six ITAM sites interacts with LCK independently using Michaelis-Menten kinetics (Fig. 3 B, best fit parameters are listed in the BioNetGen Data S2). With this model structure, each of the sites has the same Hill coefficient, which is similar to the experimental data, although the model Hill coefficient is slightly higher than that estimated for the data themselves. Additionally, the random-order model has a lower residual error and lower AIC and thus fits the data better than the sequential model. Upon visual inspection, we can see that the random-order model better captures the overall trends of the data. However, it consistently underestimates the level of phosphorylation at early time points and overestimates the gradual approach to saturation seen at later time points in the data. Therefore, we continued to explore other, more complex models of random phosphorylation to find a mechanism that could better represent our data.

Phosphate priming

We, therefore, turned to a previously proposed mechanisms in the literature, one given by Mukhopadhyay and colleagues (18) and described in the Introduction. In this mechanism, the addition of phosphate groups to CD3ζ causes an increase in the accessibility of unphosphorylated sites (18). In this model, a phosphate-dependent scaling factor, λ, is used to adjust the Michaelis-Menten constant for each ITAM site, K_M,i (see Materials and Methods). For phosphate groups to increase binding in our model, λ must be greater than one. Using a constant λ equal to three, predicted by Mukhopadhyay and colleagues (18), the model is not able to fit our data well (Fig. 3 C; best fit parameters are listed in the BioNetGen Data S3). Although the predicted response is able to capture differences in the half-maximal time between the sites, it does not fit the early or late phosphorylation time courses well. Additionally, the Hill coefficients are much higher than those of the data themselves, and they show site-specific differences. This is because the sites that are phosphorylated later start with higher effective Michaelis-Menten constants because of the scaling from sites that are already phosphorylated. Upon a wider parameter search, we find that having a λ-value less than one will result in a significantly better fit to the data (residual error = 3.72 × 10⁴) because this will increase the K_M-value for high levels of CD3ζ phosphorylation, allowing for the system to slow down at later time points. However, this inversion of the λ-value would contradict the biological hypothesis proposed by Mukhopadhyay and colleagues (18) and is, therefore, not feasible.

Competitive inhibition

Because the previously described models in the literature do not accurately reflect our site-specific data, we sought to identify a new mechanism that could more accurately fit our experimental data while still agreeing with published data, including work by Mukhopadhyay et al. (18). Using the random-order Michaelis-Menten model as a starting point, we modified the equations to address the overestimation at later time points. We implemented a mechanism of competitive inhibition, in which the unphosphorylated and phosphorylated tyrosine sites could interact to compete with each other. Competitive inhibition and product inhibition have been shown to play a role in other systems with multiple phosphorylation sites (45, 47), indicating that it may play a role in CD3ζ phosphorylation.

The competitive inhibition model is able to fit the data with the lowest error and lowest AIC of all the mechanisms we explored (Fig. 3 D; best fit parameters are listed in the BioNetGen Data S4). Additionally, it is able to capture the differences between the half-maximal phosphorylation times while maintaining the same Hill coefficient throughout the system, matching our experimental data (Fig. 1 E). We also implemented two additional variations of the competitive inhibition model, in which only phosphorylated or unphosphorylated CD3ζ tyrosine sites compete for LCK activity. The model that only allowed competitive inhibition between the unphosphorylated sites was not able to fit the data well (residual error = 1.32 × 10⁵). On the other hand, only having inhibition from the phosphorylated species was better able to fit the data (residual error = 4.02 × 10⁴), indicating that product inhibition plays a more significant role in this system. Ultimately, the best fit to the data was given by a mechanism including both competitive inhibition from the unphosphorylated ITAM sites and product inhibition from phosphorylated sites (residual error = 3.47 × 10⁴; AIC = 749). Although the effect of competitive inhibition from the unphosphorylated sites is less significant than that of the product, physiologically, because the sites are in such close proximity, it is clear that all of these sites are interacting with LCK together, and this model accounts for that interaction.

To further validate that the competitive inhibition model mechanism gives a better fit than the phosphate-priming model, we tested a model structure that combines both of these features. This model mechanism did not give a significantly better fit to the data than the competitive inhibition model alone. Additionally, the effect of the phosphatase inhibition was negligible compared to the competitive inhibition effect, as evidenced by the fact that increasing the value of λ two orders of magnitude did not significantly influence the model. Ultimately, we conclude that a model of competitive inhibition by both phosphorylated and unphosphorylated sites on CD3ζ is the mechanism that best represents the data.

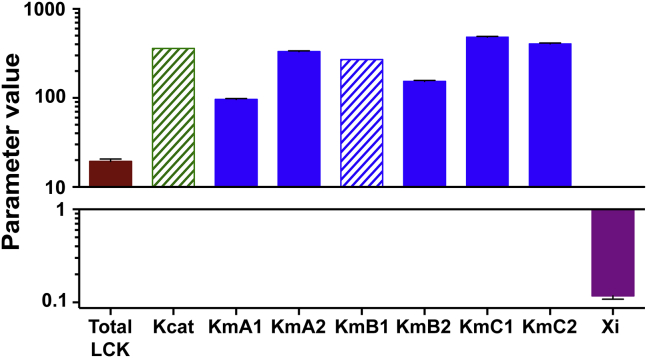
To estimate a final set of physiologically relevant parameter values, the LCK catalytic rate and K_M-value for ITAM site B1, K_M,B1, were held constant based on values in the literature (29). Additionally, a single scaling factor was used to estimate the inhibitory constants such that all of the parameters estimated were identifiable (see Materials and Methods). The final parameter distributions for the 50 best sets are shown in Fig. 4. From the SD, we can see that the model consistently estimates parameter values within a narrow range. The estimated K_M-values correspond directly with the differences in half-maximal time between the individual sites. These various parameter sets are able to fit all of the data, including CD3ζ mutant and liposome concentration data sets, similarly well (Fig. S5), indicating that the slight variation in the phosphorylation rates due to the individual site mutations can be accounted for by the competitive inhibition between sites. The same fits can be achieved by estimating different catalytic rates for each ITAM site and keeping the same K_M-values between the ITAM sites as long as the competitive inhibition is still present (data not shown). Altogether, the modeling results provide confidence that the mechanism of competitive inhibition described here can accurately reflect the way in which LCK is able to phosphorylate CD3ζ.

Figure 4.

Estimated parameter sets. Solid bars show the mean and SD of the 50 best fitted parameter sets. Shaded bars show the value of parameters that were held constant during fitting. To see this figure in color, go online.

Effects of ITAM mutations can be explained by differences in LCK and phosphatase K_M parameter values

For this competitive inhibition mechanism of CD3ζ phosphorylation to be validated, it must be consistent with other experimental data of CD3ζ phosphorylation. To test this, we explored how this new model mechanism is able to reproduce experimental data from (18). Because the experimental data from that study indicated that there was no significant difference between the phosphorylation states of individual ITAMs, we first explored how CD3ζ ITAM mutations affect phosphorylation in the competitive inhibition model.

To test this effect, we used the median values of the best fit parameter sets from Fig. 4 and simulated LCK phosphorylation of CD3ζ with single or double ITAM mutations. The time course phosphorylation results for the competitive inhibition model are shown in Fig. S6 A, whereas the results of the random-order model are shown in Fig. S6 B. In comparing these two figures, we see that there is a much smaller difference between the individual ITAMs in the competitive inhibition model compared to the random-order model. This is particularly evident when comparing the results of ITAM C to ITAMs A and B in the single ITAM phosphorylation curves (xxC compared to Axx and xBx). These small differences in the half-maximal time predicted by the competitive inhibition model are consistent with the data from (18).

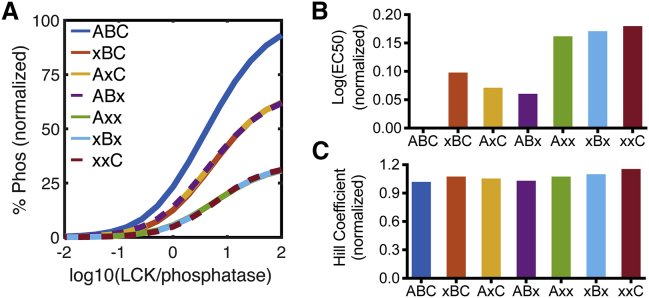
Interestingly, although the competitive inhibition model does show a similar Hill coefficient between all of the CD3ζ ITAM mutant curves (Fig. S6 C), there is a difference in the half-maximal time, with fewer ITAMs resulting in a faster half-maximal time (Fig. S6 D). This is a similar effect shown by the experimental data from (18) in the presence of the phosphatase CD148. In these data, fewer ITAMs showed a higher EC50 for phosphatase inhibition. We, therefore, wanted to explore which mechanisms of phosphatase activity could allow the model to reproduce these results.

Keeping the same mechanism of LCK phosphorylation with competitive inhibition, we tried various mechanisms of dephosphorylation using parameters on the same order of magnitude as those for LCK phosphorylation. Specifically, we implemented a random-order and phosphate-priming model for dephosphorylation. Although a few parameter sets for the random-order dephosphorylation mechanism or phosphate-priming dephosphorylation mechanism allowed for the Hill coefficients to be the same between all of the CD3ζ mutants, neither gave a clear increase in EC50 for increasing ITAM mutations.

On the other hand, with the competitive inhibition dephosphorylation mechanism, we were able to identify a defined parameter space that shows the same trends as seen in the experimental data for ITAM mutants in the presence of phosphatase inhibition (Fig. 5; model BioNetGen Data S5 and equations and parameters listed in Data S6). This parameter space is characterized by phosphatase K_M-values that are lower than those of LCK but follow the same trends in terms of the differences between tyrosine sites. A representative parameter set is shown in Data S6. This parameter space does not significantly depend on the catalytic rate of dephosphorylation (within an order of magnitude up or down from the baseline value) but does require that the competitive inhibition constant of the phosphatase (X_I) be significantly less than one. Thus, we predict that CD3ζ is phosphorylated and dephosphorylated through a mechanism of competitive inhibition in which the phosphatase has a stronger binding preference for its substrates than LCK and more significant competitive inhibition.

Figure 5.

A model comparison to literature data of CD3ζ phosphorylation and dephosphorylation. (A) Predicted phosphorylation profiles for wild-type, single, and double ITAM mutant CD3ζ are shown. Mutated ITAMs are indicated by (x). The model was implemented using initial conditions described in the model from (18): 1 CD3z/μm², 1000 LCK/μm², and phosphatase concentrations between 10 and 100,000 molecules/μm². (B) The Hill coefficient of the predicted phosphorylation response for each CD3ζ mutant is shown. (C) EC50 of the predicted phosphorylation response for each CD3ζ mutant is shown. To see this figure in color, go online.

CD28 tyrosine sites are phosphorylated more slowly than CD3ζ tyrosine sites

Next, we investigated how the addition of a costimulatory domain, like CD28, could influence CAR phosphorylation. To test this, we inserted the intracellular domain of CD28 at the N-terminal of CD3ζ (28ζ), the same configuration typically used in the CAR constructs evaluated in preclinical studies and clinical trials (Fig. 6 A). CD28 has four tyrosine sites, each of which can be phosphorylated by LCK. We again used phosphoproteomic mass spectrometry to quantify the site-specific phosphorylation levels of 28ζ. Fig. S7 A shows the sequence and trypsin cut sites of the CD28 intracellular domain, in which the second and third tyrosine sites in CD28 (Y206 and Y209) are both on the same peptide after trypsin digestion. Therefore, to individually measure the phosphorylation rates of these two sites, we made two more proteins with a tyrosine-to-phenylalanine mutation at each of these sites (28ζ-Y206F and 28ζ-Y209F).

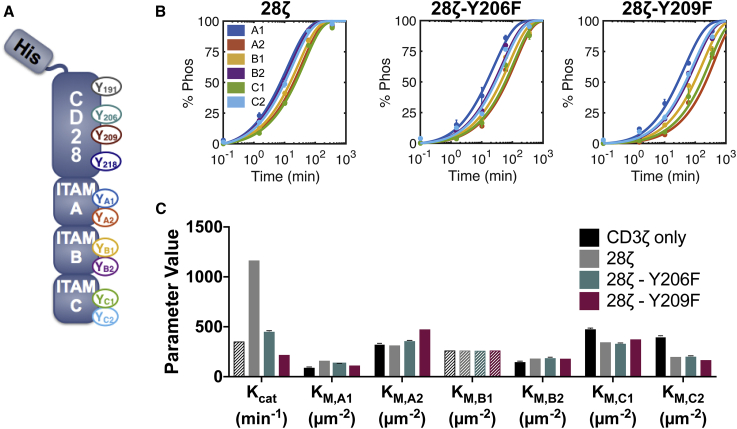
Figure 6.

CD28 influences CD3ζ phosphorylation (Phos) kinetics. (A) A schematic of the His-tagged CD28-CD3ζ recombinant protein is shown. (B) Experimental data (circles) and model fit (lines) for CD3z ITAM phosphorylation on wild-type CD28-CD3ζ, CD28-Y206F-CD3ζ, and CD28-Y209F-CD3ζ are shown. Error bars represent the SD of two technical replicates normalized by site-specific standard curves. (C) Estimated parameter sets are shown. Solid bars show the mean and SD of the 50 best fitted parameter sets. Shaded bars show the value of parameters that were held constant during fitting. For all model fits, the value of X_I was held constant at 0.115, based on the best fitted value from the CD3ζ-only model fits. To see this figure in color, go online.

Interestingly, our measurements indicate that Y209 phosphorylation is required for the phosphorylation of Y206. Fig. S7 B shows the individual CD28 tyrosine site phosphorylation time courses for each of the three CD28-CD3ζ recombinant proteins. From these graphs, we can see that there is no significant phosphorylation of the Y206 site without previous phosphorylation of Y209 (teal lines). In agreement with the literature (48), all tyrosine sites on CD28 are phosphorylated more slowly than the CD3ζ tyrosine sites. From the Y206F and Y209F mutants, we can see that mutating these sites reduces the overall phosphorylation rates of the CD28 protein, with almost no detectable CD28 phosphorylation in the Y209F mutant. This indicates that Y209, and to a lesser extent Y206, plays a significant role in either the recruitment or phosphorylation activity of LCK toward CD28.

CD28 increases the phosphorylation rate of CD3ζ

CD28 influences the overall phosphorylation rate of CD3ζ as well as the individual phosphorylation rate of site C2. Fig. 6 B (dots) shows the phosphorylation time courses of CD3ζ ITAM sites on the three CD28-CD3ζ recombinant proteins. Wild-type CD28 increases the overall phosphorylation rate of all CD3ζ tyrosine sites, making it difficult to distinguish a specific order of phosphorylation in the 28ζ recombinant protein. To explore the mechanism of CD3ζ phosphorylation in the presence of CD28, we returned to our model of competitive inhibition. As each of the CD28 mutants show a clear change in the kinetics, we fitted each of the data sets separately. To gain more mechanistic insight into the way that CD28 influences the phosphorylation, we attempted to independently fit the following three types of parameters: the 1) catalytic rate, 2) Michaelis-Menten constants, and 3) inhibition constant scaling factor. None of the parameter types were able to provide an adequate fit on their own; however, fitting the catalytic rate and Michaelis-Menten constants together provided a good fit to the data (Fig. 6 B, lines). This fit was not improved by fitting all three parameter types together or by fitting pairwise combinations including the inhibition constant scaling factor.

The presence of CD28 results in a robust increase in the apparent catalytic rate of LCK phosphorylation (Fig. 6 C). This change in the catalytic rate is reduced for the CD28 mutants. Physiologically, this apparent catalytic rate likely represents a change in the local concentration of LCK because of recruitment by CD28. Comparing the changes in catalytic rate to those of the K_M-values, we can see that the change in catalytic rate is much more significant, whereas there are only slight differences in the estimated K_M-values. K_M,C2 shows the clearest difference, which accounts for its change in order of C2 now being phosphorylated before C1. These parameter-fitting data confirm that the main mechanism of CD28 on CD3ζ is to increase the catalytic rate of LCK.

Discussion

In this study, we used phosphoproteomic mass spectrometry and computational modeling to quantitatively assess the mechanism of CD3ζ and CD28 intracellular phosphorylation in a CAR construct. By measuring the phosphorylation of individual tyrosine sites on CD3ζ and CD28 over time, we showed that the six sites on CD3ζ and four sites on CD28 are phosphorylated at different rates. Individual CD3ζ point mutations showed that there is only a small amount of interaction between the CD3ζ ITAM sites because removing one site does not greatly influence phosphorylation at any of the other sites. Additionally, attaching CD28 to the N-terminal of CD3ζ increased the overall phosphorylation rate of the protein and particularly increased the relative rate of phosphorylation at the C2 ITAM site.

Interestingly, we did not see any effect of acidic lipid concentration on the phosphorylation rates of CD3ζ tyrosine sites. Previous studies have reported different effects of acidic lipids on CD3-family protein phosphorylation. Several studies have indicated that acidic lipids in the plasma membrane can control aberrant phosphorylation of CD3ε and CD28 in unstimulated cells through the binding of basic residues in the protein to acidic lipids in the plasma membrane (42, 43, 44). In addition, Hui and Vale (29) saw that ZAP-70 tandem Src homology 2 domains were able to bind more quickly as CD3ζ became phosphorylated in a system containing 10% acidic POPS lipids compared to 0% POPS lipids. In our system, changing the concentration of acidic POPS lipids on the liposome surface (even up to 45% POPS) did not change the rate of phosphorylation of the protein as a whole or the relative phosphorylation rate order of the individual sites. Therefore, we believe that the acidic lipid concentration does not directly affect the phosphorylation of CD3ζ; but, as Hui and Vale showed, it may influence the binding kinetics of downstream proteins like ZAP-70 by more readily recruiting these proteins to membrane regions with acidic lipids.

We constructed a computational model to further investigate the mechanisms that lead to CD3ζ phosphorylation. With the model, we were able to identify a robust mechanism that accurately reflects the experimental data and calculate site-specific phosphorylation parameters, which are difficult to distinguish experimentally. Interestingly, previous work to attempt to determine an order for LCK phosphorylation of CD3ζ identified orders that differ from each other and from the order indicated by our measurements (16, 17). These previous studies were performed in solution and with individual tyrosine peptides using techniques that limited their physiological relevance. However, in one study, the authors did use mass spectrometry to measure full length recombinant protein CD3ζ phosphorylation and found that, at intermediate time points, ITAM site A1 was significantly more phosphorylated than the other sites, which is consistent with our data (17).

To our knowledge, our work is the first study to specifically quantify the individual phosphorylation kinetics and phosphorylation mechanism of all six CD3ζ ITAM tyrosine sites on the same protein in a two-dimensional lipid-bound setting. We note that this recombinant protein system does make some modifications to the endogenous protein structure. In this study, we mutated out the CD3ζ tyrosine at site 64, which was shown to have no influence on the overall phosphorylation rate on the protein as a whole (Fig. S3). As such, it is unlikely that this mutation significantly changes the individual rates in such a way as to keep the total phosphorylation rate constant. One change to the protein that may play a more significant role is that the CAR proteins used in this liposomal system are not anchored by a transmembrane domain. Interactions within the extracellular or transmembrane domains of CAR proteins may play a role in the intracellular arrangement of CARs and their accessibility to LCK, thus influencing the phosphorylation rates. Despite these limitations, our work provides, to our knowledge, new mechanistic insights into the interplay among CD3ζ ITAM sites and between CD3ζ and CD28.

Our model provides, to our knowledge, novel insights into the effects of LCK-CD3ζ interactions. Our modeling results confirm a random order of LCK phosphorylation of CD3ζ, which validates previous studies in the literature based on average CD3ζ protein phosphorylation (18). The model also indicates that phosphorylated and unphosphorylated tyrosine sites on CD3ζ provide competitive feedback on one another and predicts that a similar mechanism is used by phosphatases in this system. This is significant as it provides an alternative mechanism to that of phosphate dependence, described by (18). Our competitive inhibition model is more robust and is able to reproduce a wider set of data. We believe that these two mechanisms are not entirely incompatible, as demonstrated by the modeling results including both of these effects together, although, in this system, the effects of the phosphate priming model were masked by the significantly stronger effects of competitive inhibition. Additionally, the insights from this modeling work could help inform other hypothesized models of LCK interaction with CD3ζ in the literature (14).

CD28 also plays an important role in the CAR structure, both by adding its costimulatory signaling and modulating the phosphorylation rates of CD3ζ. We showed that adding CD28 to the N-terminal of CD3ζ increases the overall phosphorylation of CD3ζ, and this is largely dependent on CD28–Y209. Our computational modeling work indicates that this is due to an increase in the effective catalytic rate of LCK. In the model, this parameter has the same effect as an increase in the local concentration of LCK. Importantly, our predictions agree with published experimental observations in which the Y206/Y209 region of CD28 has been implicated in the recruitment of LCK to the immunological synapse in endogenous T cells through binding of the Src homology 2 domain on LCK (49). Here, we validate the importance of this site as a strong recruiter of LCK and its potential role in the strong activation of CD28-bearing CAR proteins.

Interestingly, CD28–Y209 is phosphorylated much more slowly than any of the sites on CD3ζ. In fact, when all of the CD3ζ sites are 100% phosphorylated, only ∼25% of the CD28–Y209 sites are phosphorylated. This leads us to further hypothesize that unphosphorylated Y209 plays a role in recruiting LCK to the system. The CD28 Y206/Y209 sites are surrounded by multiple proline residues, and this proline-rich binding domain is likely responsible for LCK recruitment when CD28, Y206, and Y209 are unphosphorylated (39). A similar proline-rich region is also thought to help recruit LCK to CD3ε and CD2 (38, 40). Perhaps this proline-rich Y206/Y209 site on CD28 is able to bind and recruit the Src homology 3 domain of LCK more readily than other sites, but given its lower affinity for the catalytic pocket of LCK, it can be outcompeted by other sites on the same protein.

We also used our experimental system to explore the effects of the CD28-dependent reordering of CD3ζ ITAM phosphorylation. The data show that CD28 increases the relative rate of site C2. This effect appears to be independent of phosphorylation at CD28 site Y209, indicating that another mechanism, such as the folding of the CD3ζ protein chain, must contribute to the increased phosphorylation at this particular site. More work needs to be done to decouple the binding preferences that lead to LCK recruitment from the catalytic activity of the protein-substrate pairs, to better understand how CD28 influences the relative order of CD3ζ phosphorylation.

Taken together, this work provides new, to our knowledge, insights into the activation of CAR-T-cells through quantitative phosphoproteomic experiments and computational modeling. Our model predicts a single mechanism for LCK phosphorylation of CD3ζ ITAMs. In addition to producing novel measurements and a modeling framework that explains experimental observations, our work generates, to our knowledge, novel hypotheses regarding protein phosphorylation that can inform new experiments. In the future, this mechanistic insight about the CAR phosphorylation levels could be applied to better engineer CARs that are phosphorylated more quickly and to a greater extent and hence more optimally activate T cells for therapeutic purposes.

Author Contributions

J.A.R., P.W., and S.D.F. conceived and designed the project. J.A.R. performed the experiments, advised by P.W. D.Z. acquired the phosphor proteomic data, advised by N.A.G. J.A.R. analyzed the proteomic data, advised by N.A.G. J.A.R. performed the computational modeling, advised by S.D.F. J.A.R. wrote the original draft. All coauthors contributed to reviewing and editing the manuscript. J.A.R, N.A.G., P.W., and S.D.F. provided funding and resources to support the project.

Editor: Kevin Janes.

Supporting Material

Data S1. Sequential Order

BioNetGen file of CD3ζ LCK sequential order phosphorylation model. Mean optimal parameter sets are listed.

Data S2. Random Order

BioNetGen file of CD3ζ LCK random order phosphorylation model. Mean optimal parameter sets are listed.

Data S3. Phosphate Priming

BioNetGen file of CD3ζ LCK phosphate priming phosphorylation model. Mean optimal parameter sets are listed.

Data S4. Competitive Inhibition

BioNetGen file of CD3ζ LCK competitive inhibition phosphorylation model. Mean optimal parameter sets are listed.

Data S5. Phosphatase Competitive Inhibition

BioNetGen file of CD3ζ LCK phosphatase competitive inhibition model. Mean optimal parameter sets are listed.

Data S6. LCK-Phosphatase Competitive Inhibition Model

List of the model parameters and equations used to simulate the competitive inhibition mechanism of LCK and phosphatase interaction with CD3ζ.