Co-Entangled Actin-Microtubule Composites Exhibit Tunable Stiffness and Power-Law Stress Relaxation

Abstract

We use optical tweezers microrheology and fluorescence microscopy to characterize the nonlinear mesoscale mechanics and mobility of in vitro co-entangled actin-microtubule composites. We create a suite of randomly oriented, well-mixed networks of actin and microtubules by co-polymerizing varying ratios of actin and tubulin in situ. To perturb each composite far from equilibrium, we use optical tweezers to displace an embedded microsphere a distance greater than the lengths of the filaments at a speed much faster than their intrinsic relaxation rates. We simultaneously measure the force the filaments exert on the bead and the subsequent force relaxation. We find that the presence of a large fraction of microtubules (>0.7) is needed to substantially increase the measured force, which is accompanied by large heterogeneities in force response. Actin minimizes these heterogeneities by reducing the mesh size of the composites and supporting microtubules against buckling. Composites also undergo a sharp transition from strain softening to stiffening when the fraction of microtubules (ϕ_T) exceeds 0.5, which we show arises from faster poroelastic relaxation and suppressed actin bending fluctuations. The force after bead displacement relaxes via power-law decay after an initial period of minimal relaxation. The short-time relaxation profiles (t < 0.06 s) arise from poroelastic and bending contributions, whereas the long-time power-law relaxation is indicative of filaments reptating out of deformed entanglement constraints. The scaling exponents for the long-time relaxation exhibit a nonmonotonic dependence on ϕ_T, reaching a maximum for equimolar composites (ϕ_T = 0.5), suggesting that reptation is fastest in ϕ_T = 0.5 composites. Corresponding mobility measurements of steady-state actin and microtubules show that both filaments are indeed the most mobile in ϕ_T = 0.5 composites. This nonmonotonic dependence of mobility on ϕ_T demonstrates the important interplay between mesh size and filament rigidity in polymer networks and highlights the surprising emergent properties that can arise in composites.

Introduction

The cytoskeleton is a complex network of protein filaments that gives eukaryotic cells structural integrity and shape while enabling cell motility, division, and morphogenesis. Such multifunctional mechanics and processes are possible because of the varying structural properties of cytoskeletal proteins, as well as the interactions between them (1, 2, 3, 4). Actin and tubulin are two such proteins that form filaments with very different stiffnesses. Tubulin dimers (∼110 kDa) polymerize into 25-nm-wide hollow, rigid microtubules with persistence lengths of l_p ≈ 1 mm, whereas actin monomers (∼42 kDa) polymerize into ∼7-nm-wide semiflexible filaments (F-actin) with l_p ≈ 10 μm (5, 6, 7). At high concentrations, both actin filaments and microtubules form sterically interacting entangled networks with filament dynamics that can be described by the reptation or tube model. Within this framework, each filament is confined to a tube-like region formed by surrounding constraining filaments, and is forced to relax stress by diffusing curvilinearly (i.e. reptating) out of its deformed tube (8, 9). The timescale for this process, often termed disengagement, is on the order of minutes to hours for actin and microtubules (10, 11, 12). Entangled actin can also partially relax via faster mechanisms such as bending fluctuations (13, 14, 15). The entanglement density in networks of actin and microtubules can be characterized by their respective mesh sizes, ξ_A = 0.3/c_A^1/2 and ξ_M = 0.89/c_T^1/2, where c_A and c_T are the corresponding protein concentrations in units of mg/mL and the resulting mesh sizes are in units of microns (16, 17, 18). As can be seen from these equations, because of the differences in molar mass and filament structure of the two proteins, the mesh size for a microtubule network of a given molarity is ∼2× larger than that for actin.

Steric interactions between actin and microtubules within cells directly influence cell shape and mechanics by regulating filament mobility and providing coordinated reinforcement to the cytoskeleton (6, 19). Processes such as cell motility and cytokinesis also rely on the physical interactions between these filaments (6, 20). Further, although individual microtubules buckle under substantial compressive forces (21, 22, 23, 24), steric interactions with the elastic actin network allow microtubules to bear larger compressive loads within the cell (6, 11, 21, 25, 26). Studies of composite networks of actin and microtubules are further motivated by materials engineering, in which soft elastic networks are often reinforced with stiff fibers or rigid rods. By tuning the concentration of rigid rods relative to the flexible filaments, bulk properties of composites can be optimized to create lightweight materials with high strength and stiffness (20, 27). Such composites also offer enhanced control over large-scale mechanics and increased failure limits tuned by the mechanical differences of the two composite constituents. Finally, composites both in nature and in industry often exhibit emergent properties in which the resulting mechanical properties are not a simple sum of the single-component network mechanics.

In vitro studies of cytoskeleton networks have largely focused on single-component systems of either actin or microtubules (16, 18, 24, 26, 28, 29, 30, 31, 32). One previous passive microrheology study of an equimolar composite of actin and microtubules showed that although entangled actin solutions appeared incompressible, the composite displayed a finite compressibility resulting from the high stiffness of microtubules (11, 33). A previous nonlinear bulk rheology study of cross-linked actin networks doped with low concentrations of microtubules showed that the addition of microtubules led to nonlinear strain stiffening as compared to the signature strain-softening behavior of entangled and weakly cross-linked actin networks (20, 34, 35). The authors explained this shift as due to stiff microtubules suppressing actin bending modes and local fluctuations, leading to enhanced stretching and affine deformation. Although these few studies revealed important emergent properties in actin-microtubule composites, they were limited in the parameter space of composite makeup. Thus, the question remains as to how the relative concentrations of actin and microtubules impact the mechanical properties of composites. Further, these studies probed the bulk response resulting from large-scale nonlinear strains and the microscopic linear response due to passively diffusing microspheres. Yet, the relevant length scales in actin-microtubule composites are in between these two scales, with persistence lengths of ∼10 μm–1 mm, filament lengths of ∼5–20 μm, and mesh sizes on the order of a micron. Finally, in these prior studies, composites were created by adding pre-polymerized microtubules to actin rather than polymerizing both proteins together. This method often induces flow alignment of filaments, shearing of microtubules, and bundling of actin filaments, preventing the formation of truly isotropic, well-integrated, co-entangled composites.

Here, we create co-polymerized, co-entangled actin-microtubule composites with systematically varying molar ratios of actin to tubulin. We characterize the nonlinear mesoscale mechanics of composites by pulling optically trapped microspheres a distance of 30 μm through the composites at a rate much faster than the system relaxation rates while measuring the force locally applied to the bead by the composites. These measurements perturb the composites far from equilibrium and are uniquely able to probe possible buckling, rupture, and rearrangement events, as well as micro- and mesoscale spatial heterogeneities. We complement these nonlinear measurements with steady-state image analysis of composites.

Methods

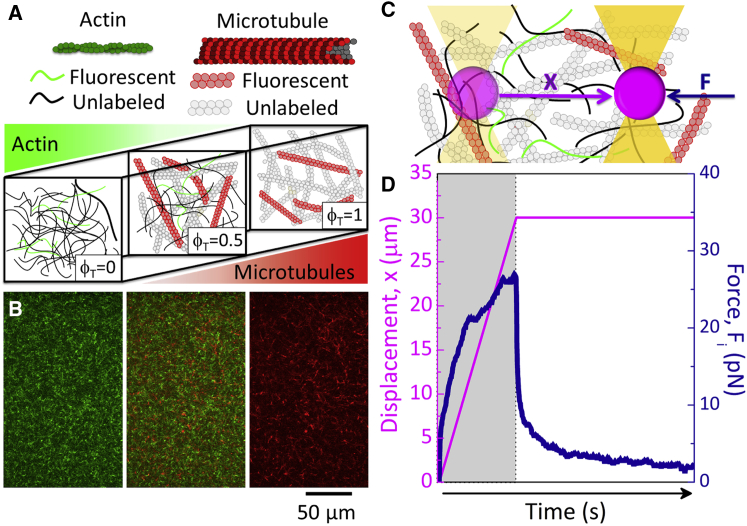
Rabbit skeletal actin, porcine brain tubulin, and rhodamine-labeled tubulin were purchased from Cytoskeleton (AKL99, T240, TL590M; St. Denver, CO), and Alexa-488-labeled actin was purchased from Thermo Fisher Scientific (A12373; Waltham, MA). To form actin-microtubule composites, varying ratios of unlabeled actin monomers and tubulin dimers were suspended in an aqueous buffer containing 100 mM piperazine-N,N′-bis(ethanesulfonic acid) (pH 6.8), 2 mM MgCl₂, 2 mM glycol ether diamine tetraacetic acid, 2 mM ATP, 1 mM GTP, and 5 μM Taxol to a final total protein concentration of 11.3 μM (Fig. 1 A). ATP and GTP are required for polymerization of actin and tubulin, respectively. Taxol is used to stabilize microtubules against depolymerization (29). Co-polymerization of both proteins was achieved by incubating the sample for 1 h at 37°C, resulting in well-integrated and stable co-entangled composites (Figs. 1 B, S1, and S2). To image composites, 0.13 μM of pre-assembled Alexa-488-labeled actin filaments at a 1:1 labeled:unlabeled monomer ratio and 0.19 μM pre-assembled rhodamine-labeled microtubules at a 1:5 labeling ratio were also added to the solution as tracer filaments (Figs. 1 B and S1–S3). Only ∼1% of filaments are labeled so as to be able to resolve single filaments within the concentrated three-dimensional (3D) networks. Oxygen scavenging agents (4.5 mg/mL glucose, 0.5% β-mercaptoethanol, 4.3 mg/mL glucose oxidase, 0.7 mg/mL catalase) were added to inhibit photobleaching during imaging (36).

Figure 1.

Schematic of experimental approach. (A) A cartoon of molecular components used in actin-microtubule composites is shown. The tubulin molar fraction, ϕ_T= [tubulin]/([actin] + [tubulin]), is varied from 0 to 1, with total protein concentration fixed at 11.6 μM. (B) To display network architecture, 0.13 μM of actin and 0.19 μM of microtubules are labeled with Alexa-488 (green) and rhodamine (red), respectively. The images shown are two-color laser scanning confocal micrographs of the actin channel (green, left), the microtubule channel (red, right), and an overlay of the two (middle) for the ϕ_T = 0.5 composite. (C) For microrheology measurements, an optically trapped microsphere (4.5 μm diameter, not drawn to scale) embedded in the composite is displaced 30 μm (x, magenta) at a speed of 20 μm/s while the restoring force F_i(x,t) applied to the bead by the composite is measured (F, blue). (D) Sample microrheology data showing the measured Force (blue) and bead Displacement (magenta) during (gray region) and after (white region) displacement are depicted. Data shown are for the ϕ_T = 0.5 composite. To see this figure in color, go online.

The molar fraction of tubulin in composites, ϕ_T = [tubulin]/([actin] + [tubulin]) where [actin] and [tubulin] are the molar concentrations of each protein, was varied from 0 to 1. The lengths of actin and microtubules in composites were measured to be 8.7 ± 2.8 and 18.8 ± 9.7 μm, respectively, independent of ϕ_T (Fig. S3). Buffer and incubation conditions were optimized through independent tuning of buffering agents, pH, and nucleotide concentrations as well as incubation time and temperature. Criteria used to assess optimization were 1) both proteins polymerize into filaments ∼2–30 μm in length; and 2) networks are isotropic and well-mixed with no visible bundling, aggregation, phase separation, or nematic structure formation. The structure and force response of single-component actin and microtubule networks created using our optimized hybrid conditions are comparable to those formed using standard conditions (Fig. S4). Further details and characterization of optimization methods are described in the Supporting Materials and Methods.

For microrheology measurements (Fig. 1, C and D), a sparse number of microspheres (beads; Polysciences, Warrington, PA) with diameter a = 4.5 μm were added to composites. Before polymerization, the protein and bead mixture was pipetted into a sample chamber made from a glass slide and coverslip, separated by ∼100 μm with double-sided tape to accommodate ∼20 μL, and sealed with epoxy. Beads were coated with Alexa-488 BSA (ThermoFisher), following previously described methods (13, 37), to inhibit binding interactions with the filaments and visualize beads during measurements. The diameter of the bead was chosen to be large compared to the mesh size of the composites such that the measured force response is reflective of the network rather than the solvent (38, 39, 40, 41, 42, 43). In this limit, one can assume that the bead is continuously in contact with a roughly equal number of filaments and does not move through voids in the networks. Specifically, the bead diameter is ∼6× larger than the largest mesh size of our composites (0.79 μm, Fig. S5). Thus, at every point during the perturbation, the bead is in contact with ≥12 filaments (∼6 filaments each in y and z directions), assuming the bead encounters a roughly constant y-z grid of crossing filaments as it moves along x, so even at very small bead displacements, our measurements reflect the response of the network rather than individual filaments.

The optical trap used in microrheology measurements was formed using an IX71 fluorescence microscope (Olympus, Shinjuku, Tokyo) outfitted with a 1064 nm Nd:YAG fiber laser (RPMC Lasers, O’Fallon, MO) focused with a 60× 1.4 NA objective (Olympus). A position-sensing detector (First Sensor, Mansfield, MA) measured the deflection of the trapping laser, which is proportional to the force acting on the trapped bead. Trap stiffness was calibrated using the Stokes drag method (44, 45, 46). During force measurements, a bead embedded in the composite was trapped and moved a displacement x of 30 μm at a constant speed of v = 20 μm/s relative to the sample chamber using a nanopositioning piezoelectric stage (Nano-PDQ; Mad City Labs, Madison, WI) (Fig. 1, C and D). In comparison to macrorheology experiments, the displacement and speed correspond to a strain of γ = x/a = 6.7 and strain rate of $\dot{\gamma }$ = 18^1/2(v/a) = 18.9 s⁻¹ (38, 47). Laser deflection and stage position during and after bead displacement were recorded at a rate of 20 kHz using custom-written Labview code. Post-measurement data analysis was done using custom-written MATLAB software. The response frequency of the stage is 4 kHz, so during the first 0.25 ms, there is some acceleration from 0 to 20 μm/s. Therefore, the initial data points that we evaluate and present in Figs. 1, 2, 3, and 4 occur at t = 0.25 ms. For this reason, we measure a nonzero initial force, as the bead has already moved 5 nm (encountering ≥12 filaments). Displayed force curves in Figs. 2 and 4 are averages over an ensemble of 25 different trials, i, with each i^th trial located in a different region of the network separated by >100 μm. All 25 trials for each composite (shown in Figs. 3 A and S6) were carried out in a single sample. However, for each composite, 2–3 different samples were tested to ensure reproducibility of ensemble-averaged quantities. Ensemble-averaged force curves <F_i(x)> are smoothed using a sliding Gaussian blur with a window of 20 data points (1 ms). This smoothing does not result in any detectable change in <F_i(x)> curves but is needed for reducing noise that becomes amplified by computing the numerical derivative of <F_i(x)>, K(x) = d<F_i(x)>/dx (Fig. 2, C and D). Because of the small smoothing window compared to the dynamical timescales of the system, this level of smoothing only serves to reduce electrical and Brownian noise while maintaining the relevant features of each curve (Fig. S7).

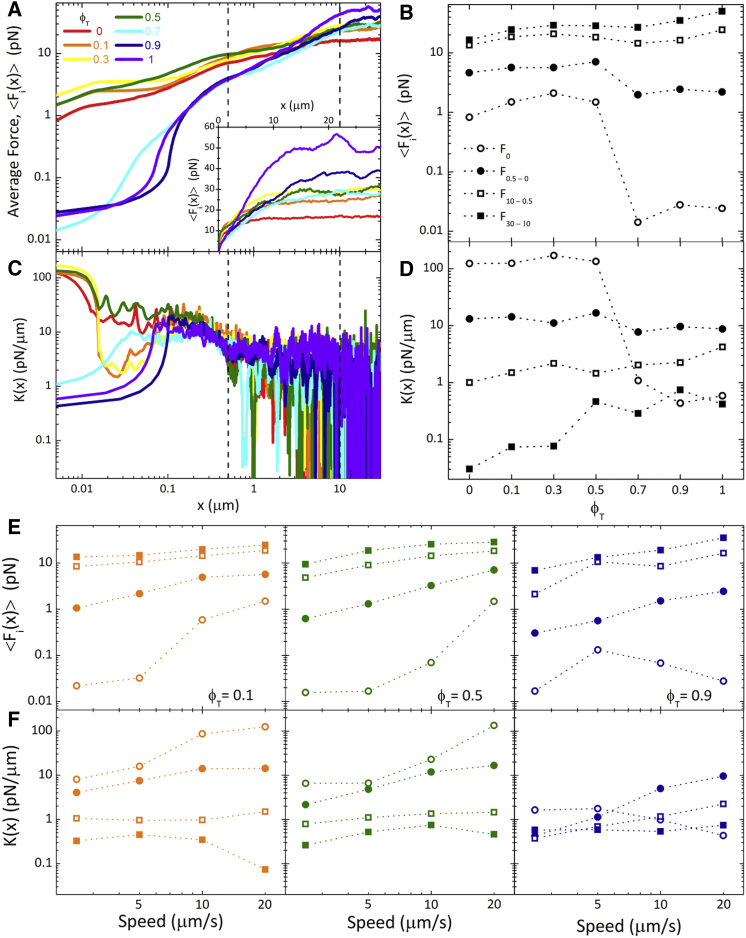
Figure 2.

Mesoscale force response of actin-microtubule composites display a ϕ_T-dependent crossover from strain-softening to strain-stiffening. (A) The ensemble-averaged force <F_i(x)> applied to the moving bead by actin-microtubule composites of varying tubulin molar fraction ϕ_T (listed in legend) is plotted. Data shown are an average over 25 individual (i) measurements. Dotted vertical lines denote the displacements over which <F_i(x)> and K(x) are averaged in (B) and (D). Inset shows <F_i(x)> on a linear scale. (B) The initial <F_i(x)> value, F₀ (open circles), and the average of <F_i(x)> values plotted over different bead displacements, x_f − x_i, denoted as F_xf−xi. Displacements of x_f − x_i = 0.5 − 0 μm (F_{0.5 − 0}, closed circles), 10 – 0.5 (F_10−0.5, open squares), and 30 – 10 (F₃₀₋₁₀, closed squares) are shown. (C) Stiffness, K(x), is calculated as the derivative of the average force with respect to bead displacement (K(x) = d<F_i(x)>/dx). (D) The initial K value, K₀, and the average of K(x) values plotted over different displacements (K_0.5−0, K_10−0.5, K₃₀₋₁₀). Displacements and symbol scheme are the same as in (B). (E and F) The dependence of force and stiffness on the speed of the bead displacement for ϕ_T = 0.1 (orange, left), 0.5 (green, middle), and 0.9 (purple, right) composites is presented. F₀, F_0.5−0, F_10−0.5, and F₃₀₋₁₀ (E) and K₀, K_0.5−0, K_10−0.5, and K₃₀₋₁₀ (F) are shown as a function of bead speed, with the symbol scheme the same as in (B) and (D). To see this figure in color, go online.

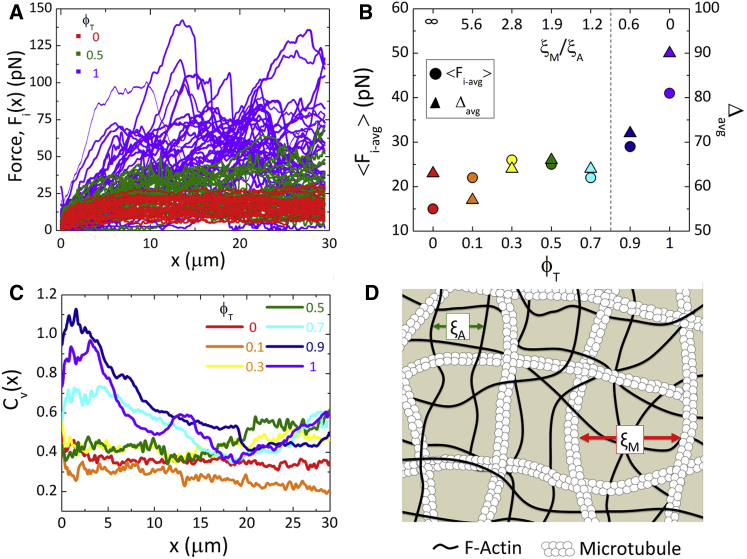
Figure 3.

Microtubules increase average resistive force and heterogeneity of force response. (A) Force curves are shown for all 25 measurements, i, of composites with tubulin molar fractions of ϕ_T = 0 (red), 0.5 (green), and 1 (purple). (B) Average force during strain, <F_i-avg>, for each composite (circles, left axis), as well as the corresponding percent range, Δ_avg = 100^∗(F_{i-avg_max} − F_{i -avg_min})/(2<F_i-avg>) (triangles, right axis) are shown as a function of ϕ_T (bottom axis) and ratio of microtubule mesh size to actin mesh size ξ_M/ξ_A (top axis). The dotted vertical line shows when the mesh sizes for both filaments are equal (ξ_M = ξ_A). (C) The coefficient of variation, C_V(x) = σ_F/<F_i(x)>, for each ϕ_T as a function of x, shows increasing microscale heterogeneity in the force response with more microtubules. (D) An illustration of an equimolar actin-microtubule composite (ϕ_T = 0.5) is shown. As depicted, the actin mesh size is ∼2× smaller than the microtubule mesh, with ξ_A = 0.6 μm and ξ_M = 1.1 μm. To see this figure in color, go online.

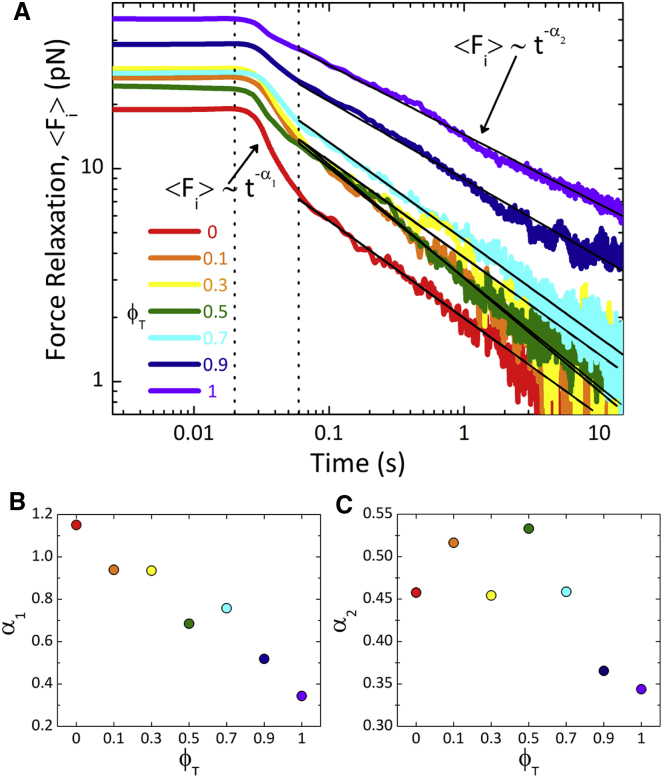
Figure 4.

Force relaxation of actin-microtubule composites exhibits two-phase power-law decay. (A) Relaxation of ensemble-averaged resistive force after bead displacement is shown as a function of time for composites of varying tubulin fractions ϕ_T. The color scheme is the same as in Figs. 2 and 3. Force curves exhibit an initial plateau phase until t₁ ≈ 0.02 s, after which composites relax via two distinct power-law decays: an initial fast decay (<F_i> ∼ t^−α₁) until t₂ ≈ 0.06 s, followed by a slow decay (<F_i> ∼ t^−α₂). Vertical dotted lines indicate the crossover timescales t₁ and t₂. Solid black lines are fits of the data to power laws with exponents α₂. (B) Estimated scaling exponents α₁ for the fast decay, which decrease proportionally with increasing ϕ_T and become indistinguishable from α₂ when ϕ_T = 1, are shown. (C) Scaling exponents α₂ measured for the second decay phase are shown. Exponents exhibit a nonmonotonic dependence on ϕ_T reaching a maximum value of ∼0.53 for ϕ_T = 0.5. To see this figure in color, go online.

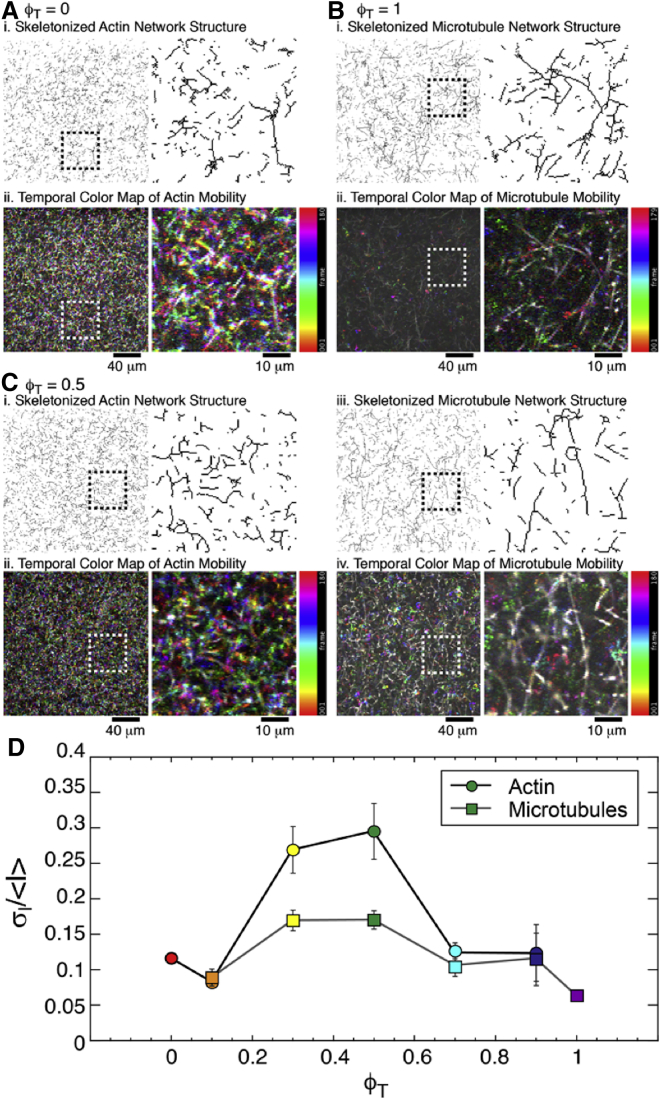
To visualize network mobility (Figs. 5, S9, and S10) and architecture (Figs. 1 B, S1, and S2), we used a Nikon A1R laser scanning confocal microscope with 60× objective (Nikon, Tokyo, Japan) and QImaging QICAM CCD camera (Surrey, Canada) to collect two-dimensional (2D) images, 2D time series, and 3D images of composites. The microscope has 488 and 532 nm lasers to alternately record separate images in green and red channels to visualize 488-actin and rhodamine-tubulin, respectively. To characterize filament mobility within composites, 512 × 512 pixel time series with a pixel size of 0.41 μm were recorded at 30 fps for 3 min in green and red channels. Post-imaging analysis was carried out using ImageJ/Fiji. Color channels were separated upon import and analyzed separately. To reduce noise, each time series was averaged over every 30 frames, resulting in a 1-fps time series of 180 frames. We computed the standard deviation (σ_I) and mean (<I>) of intensity values over all pixels and all frames of each time series. We then computed the coefficient of variation of intensity, σ_I/<I>, to quantify the mobility of actin and microtubules in each composite while accounting for any systematic intensity differences between movies. We performed this measurement on 3–5 movies from a single sample for each network composition (ϕ_T) and plotted σ_I/<I> and the corresponding standard error for the actin and the microtubule channels separately (Fig. 5). To visualize filament mobility, we also created temporal color maps for each movie in which the different colors represent different times during the movie. Color maps in which structures appear mostly white indicate that filaments are largely immobile, whereas the presence of many different colors signifies fluctuations and motion. We compare color maps to 2D images from each movie, which we skeletonize to show the planar network structure (Fig. 5). 2D images also demonstrate that actin and microtubules are well-mixed and co-entangled such that the structural images for both actin and microtubules span the network and are homogeneously distributed. The sparseness of the 2D structure images are a result of having only ∼1% of filaments labeled.

Figure 5.

Mobility of both actin and microtubules in composites exhibits a nonmonotonic dependence on tubulin fraction. (A–C) 2 × 2 images show binary skeletonization of a single frame (top row) and temporal color maps (bottom row) of movies for (A) ϕ_T = 0, (B) ϕ_T = 1, and (C) ϕ_T = 0.5 networks. Full 512 × 512 images (left) as well as zoomed-in images (right, corresponding to box in left-hand images) are shown. The different colors in temporal color maps correspond to different times during each 180 s movie. Colors go from red at 0 to magenta at 180 s, as shown in the scale bar to the right of each map. (D) The standard deviation of intensity values, σ_I, over all pixels and all frames of each time series, normalized by the corresponding mean, <I>, versus tubulin fraction ϕ_T, is shown. σ_I/<I> is calculated separately for actin and microtubule channels to determine the mobility of each filament in composites. Error bars are the standard error from averaging over 512 × 512 pixels in 3–5 images for each ϕ_T. As shown, the mobility of both actin (circles) and microtubules (squares) increases as ϕ_T increases to 0.5, followed by a subsequent drop. Color coding represents the different ϕ_T values, as in Figs 2, 3, and 4. To see this figure in color, go online.

Results and Discussion

Although actin and microtubules coexist in cells, the standard in vitro polymerization and network formation conditions for the two proteins are incompatible. The few previous studies that have investigated actin-microtubule networks have pre-polymerized and stabilized microtubules with Taxol before adding them to actin monomers to polymerize (3, 11), which can lead to flow alignment and rupturing of microtubules upon pipetting into actin monomer solutions and/or the experimental sample chamber. We instead sought to assemble unperturbed co-polymerized networks of actin and microtubules entangled with one another within an experimental sample chamber. To do so, we designed hybrid buffers and polymerization methods detailed in the Methods and Supporting Materials and Methods. Our system includes both ATP and GTP to polymerize actin and tubulin, respectively, as well as the widely used microtubule-stabilization agent Taxol to stabilize microtubules once they polymerize. Although the addition of Taxol likely reduces the stiffness of microtubules compared to those in cells, the reported difference is less than a factor of 10 (29, 48), which is well below the ∼100-fold difference between the stiffness of microtubules compared to actin. So, we expect our results to also translate to composites without Taxol and to bear physiological relevance. Our methods result in isotropic, well-integrated composite networks of co-entangled actin and microtubules (Figs. 1 B, S1, and S2).

We use active microrheology to measure the local nonlinear force response of actin-microtubule composites with varying tubulin molar fractions, ϕ_T. Fig. 2 A shows the ensemble-averaged force, <F_i(x)>, exerted on optically trapped microspheres as they are pulled a distance x through each composite. We further quantify the length-scale dependence of the force response by averaging <F_i(x)> over different bead displacements x_f−x_i, which we denote as F_xf−xi, and comparing to the value measured at x = 0, F₀ (Fig. 2 B). As shown, composites comprised of mostly actin (ϕ_T ≤ 0.5) exert a ∼100× higher initial force, F₀, on the bead than networks comprised of mostly microtubules (ϕ_T > 0.5). However, the rise in force with x is steeper for ϕ_T > 0.5 networks such that at ∼5 μm, <F_i(x)> becomes larger for ϕ_T > 0.5 composites compared to ϕ_T ≤ 0.5 (Fig. 2, A and B). We also evaluate the stiffness of composites, which we quantify by K(x) = d<F_i(x)>/dx, in analogy to macrorheology measurements that define the differential modulus K as the derivative of stress with respective to strain (49, 50, 51). Increasing and decreasing K(x) values during bead displacement signify strain stiffening and softening, respectively. As shown in Fig. 2 C, composites comprised of mostly actin (ϕ_T ≤ 0.5) are initially relatively stiff but quickly soften, whereas ϕ_T > 0.5 composites display an initially soft/viscous force response followed quickly by strain stiffening. We quantify the length-scale dependence of stiffening/softening by computing x-averaged K(x) values analogous to the force values shown in Fig. 2 B (i.e., K₀, K_0.5−0, K_10−0.5, K₃₀₋₁₀). As shown in Fig. 2 D, from 0 to 0.5 μm, the average stiffness increases by an order of magnitude from its initial value for microtubule-rich composites (ϕ_T > 0.5), whereas it drops by an order of magnitude for ϕ_T ≤ 0.5 composites. For x > 0.5 μm, all composites exhibit softening (K_0.5−0 > K_10−0.5 > K₃₀₋₁₀) as the force response approaches a more viscous regime. However, although actin-rich composites exhibit much more initial stiffness (∼100× higher K₀), microtubule-rich composites exhibit an order of magnitude higher stiffness at the end of the strain (∼10× higher K₃₀₋₁₀). We note that the actin-rich composites actually display two types of behavior for a very brief period of the displacement (∼0.02–0.06 μm), with the ϕ_T = 0 and 0.5 composites exhibiting purely softening behavior, whereas the ϕ_T = 0.1 and 0.3 composites soften more dramatically but then stiffen, such that all ϕ_T ≤ 0.5 composites exhibit similar K values after ∼0.06 μm. In future work, we plan to directly focus on the nanoscale response of actin-microtubule composites rather than the mesoscale response to further explore this interesting behavior.

The ϕ_T-dependent stiffening we measure is qualitatively in line with previous bulk rheology results for cross-linked actin networks doped with microtubules. The authors attribute this ϕ_T-dependent stiffening to microtubules suppressing actin bending modes (16, 20, 52). However, the strain at which stiffening occurs in these studies is ∼0.5, which corresponds to a bead displacement of ∼2.25 μm in our setup, whereas the stiffening we measure occurs at much smaller strains. At the same time, the strain rate used in these experiments was 0.1 s⁻¹ compared to our rate of ∼19 s⁻¹. Our comparatively high strain rate could very likely give rise to the stiffening phenomena occurring at much shorter length scales. Further, although stiffening occurs over smaller length scales in our measurements, the stiffness of ϕ_T > 0.5 composites does not actually become larger than that of ϕ_T ≤ 0.5 composites until ∼0.5 μm, with the most pronounced difference occurring for x > 10 μm (Fig. 2 D). Given that these strains are comparable to those in the macrorheology studies, it is likely suppression of bending modes that gives rise to this increased stiffness at large displacements (K₃₀₋₁₀) for microtubule-rich composites. However, our studies show a unique feature not seen in macrorheology measurements—actin-rich composites are initially much stiffer and exert a much higher force on the bead than those with more microtubules (Fig. 2)—which suggests that we need to consider the differences in the nature of the perturbation in our experiments compared to macrorheology.

In our measurements, the bead is forced to displace water as it moves so it experiences a hydrodynamic drag force as well as the force from the filament network. Especially at very early times, when the filaments have not yet had time to relax or respond to stress, the movement of water through the mesh likely plays an important role in the stress response. In fact, poroelastic models, which consider the dynamics of the mesh as well as the pervading fluid, have been used to accurately describe the stress relaxation of cytoplasm as well as cross-linked polymer hydrogels (53, 54, 55). In these models, the faster the timescale for water to drain from the compressed/deformed mesh, the faster the system can relax, such that it will exert a smaller initial force on the bead. The poroelastic timescale is t_p = axη/2Gξ², where a is the bead diameter, x is the bead displacement, η is the solvent viscosity, and G is the elastic modulus of the network. The elastic modulus of microtubule networks comparable to ours has been measured to be ∼1 Pa compared to ∼0.1 Pa for comparable actin networks (16, 56, 57). Further, as described above, the mesh size of microtubule networks is ∼2× larger than for actin networks (Fig. S5). Thus, comparison of t_p for actin and microtubule networks gives t_p(ϕ_T = 0)/t_p(ϕ_T = 1) = (G_M/G_A)(ξ_M²/ξ_A²) ≈ 40. So, water will drain from actin networks ∼40× more slowly than from microtubule networks, suggesting that the initial force and stiffness may be comparably higher for actin-rich compared to microtubule-rich composites (Fig. 2). However, this difference will only arise if t_p for actin-rich composites is greater than or comparable to the timescale of the bead displacement, whereas t_p for microtubule-rich composites is shorter than the displacement timescale. For a displacement of x = 0.01 μm, we calculate t_p(ϕ_T = 0) ≈ 1.2 ms compared to t_p(ϕ_T = 1) ≈ 0.04 ms. The corresponding timescale for the bead to travel 0.01 μm is 0.5 ms, >12× faster than t_p(ϕ_T = 1) and >2× slower than t_p(ϕ_T = 0), confirming the important role that poroelasticity plays in the initial force response. The faster draining ability of microtubule networks also enables microtubules to confer compressibility into otherwise nearly incompressible actin networks, as previously reported (27, 58).

To further verify this interpretation, we repeated measurements at three slower speeds (2.5, 5, and 10 μm/s) for three of the composites (ϕ_T = 0.1, 0.5, and 0.9) (Figs. 2, E and F and S8). Slower bead displacements would allow more time for water to drain from composites, so we should expect to see the initial force and stiffness of actin-rich composites reduced as speed is reduced. On the other hand, we should expect to see minimal difference in F₀ and K₀ values for microtubule-rich networks, as the water has already effectively drained on the timescale of the original perturbation. This effect is exactly what we see for measurements performed at slower speeds (Fig. 2, E and F). For ϕ_T = 0.1 and 0.5, composites F₀ and K₀ decrease ∼100-fold and >10-fold, respectively, with decreasing speed. For ϕ_T = 0.9, on the other hand, there is much less change in F₀ and K₀ with no discernible dependence on speed. As we describe below, we find further evidence of poroelasticity in our force relaxation data (Fig. 4).

Previous micro-indentation experiments on cytoplasm have shown that poroelasticity only plays a role in the force response at very short times, after which the filament mesh dominates (55). This effect arises from the fast draining timescale of water compared to the relaxation timescales of the mesh. So, to understand the subsequent ϕ_T-dependent stiffening and softening, we turn to the varying responses of actin compared to microtubules. Actin filaments can bend in response to strain, deforming nonaffinely and sliding off of the moving bead, which can lead to softening after the initial stiff response. Microtubules, on the other hand, cannot readily bend and are instead compressed in the direction of the displacement, building up in front of the bead and increasing the force and stiffness of the response (Fig. 2, B and D). Further, the amount of stiffening (K_0.5−0/K₀) for the ϕ_T = 0.9 composite decreases with decreasing speed, and only exhibits softening for speeds ≤5 μm/s. At slower speeds, the microtubules have more time to reorient themselves in response to strain to alleviate stress, further indicating that stiffening is a result of suppressed nonaffine deformations.

As shown in Fig. 3, we also find that increasing the fraction of tubulin in composites increases the heterogeneities in force response. Microscale heterogeneities are displayed by increased noise or “bumpiness” in the individual force curves (Fig. 3 A), whereas large-scale heterogeneities can be seen by comparing the force curves for all i trials measured in different regions of the sample (separated by >100 μm) (Figs. 3 A and S6). Fig. 3 A, which shows the individual force curves, F_i(x), for all i measurements for actin networks (ϕ_T = 0), microtubule networks (ϕ_T = 1), and ϕ_T = 0.5 composites, clearly shows that increasing the fraction of microtubules increases heterogeneity at both scales.

This heterogeneity could indicate that the ensemble-averaged quantities presented in Figs. 2 and 4 may misrepresent or mask the system dynamics. However, despite the fact that we see broad distributions of force curves for composites with high ϕ_T, we do not see multiple distinct clusters or distributions of curves (Fig. S6). Rather, all curves appear to be part of a single distribution such that the ensemble average should be a meaningful representation of the data. Nonetheless, to determine how faithfully the ensemble average represents small subsets of the data, we have carried out the analysis shown in Fig. 2 B for three randomly chosen trials for ϕ_T = 0, 0.5, and 1. Although the values calculated from each trial do vary because of the increased noise in the individual curves compared to the ensemble average, the average of the three values is remarkably close to the value determined from the full ensemble-averaged curve (Fig. S6). Thus, the presented ensemble averages appear to be robust quantities that not rely on the full spectrum of curves and meaningfully represent the system dynamics. However, the ϕ_T-dependent breadth of the distributions and noise in individual curves is an important result in and of itself and merits quantitative analysis.

To evaluate the heterogeneity, we first average each F_i(x) over the bead displacement x, which we signify as F_i-avg, and calculate the ensemble average, <F_i-avg>, as well as the corresponding percent range, Δ_avg = 100^∗(F_{i-avg_max} − F_{i-avg_min})/(2<F_i-avg>). As shown in Fig. 3 B, we find that the average force (<F_i-avg>) is ∼3× larger for microtubule networks than that for actin networks, and the corresponding percent range (Δ_avg) is doubled. However, surprisingly, the resistive force and heterogeneities do not increase smoothly as ϕ_T increases. Rather, they remain relatively unchanged until the tubulin fraction exceeds 0.7. The large peaks and dips in force curves, partly responsible for the increased Δ_avg in microtubule-dominated composites, are suggestive of microtubule buckling events. Previous studies have shown that microtubules buckle under large compressive loads (23, 24), except when they are integrated within the cytoskeletal matrix (21, 25, 33, 59). In line with these results, we interpret the displayed reduced Δ_avg and elimination of large dips in the force for ϕ_T < 0.7 composites as due to the elastic actin network providing reinforcement to microtubules against buckling. Another possibility for the observed dips and peaks is the unbinding of transient filament cross-links, which have been shown to lead to large heterogeneities in force curves (60). We have no cross-linking proteins present in our composites, but divalent cations can cause transient cross-bridges between filaments (61). Although we cannot rule out this possibility, the strong dependence on ϕ_T suggests that the heterogeneities arise solely from microtubules, whereas we would expect cation cross-linking to impact both actin and microtubules (61, 62, 63).

To determine if the forces that we impose are sufficient to buckle microtubules at high ϕ_T while preventing them from buckling at low ϕ_T, we calculate the predicted critical force to buckle isolated microtubules, f_c1, compared to that for microtubules embedded in an elastic network f_cN (25). Isolated microtubules are predicted to buckle at a force f_c1 ≈ 10 κ/L², where κ is the bending rigidity and L is the length of microtubules, whereas microtubules embedded in a network are predicted to buckle at a force f_cN ≈ 4(κG)^1/2, where G is the elastic modulus of the network. Using previously published values for κ (2 × 10⁻²⁴ Nm (2, 48)), our measured L value (∼19 μm, Fig. S3), and reported G values for comparable actin networks (∼0.1 Pa (57)), we calculate the critical buckling forces to be f_c1 ≈ 0.05 pN and f_cN ≈ 2 pN. As described in Methods, we can estimate that the bead is in contact with at least ∼12 filaments at each x position along its path, so a minimal force of F_b ≈ 24 pN would be needed to induce measurable buckling of microtubules in the network. As shown in Fig. 3 B, the force at which heterogeneities (Δ_avg) begin to increase substantially is ∼25 pN, demonstrating that buckling events likely play a principle role in the increased heterogeneity. Further, only above F_b are large dips and peaks observable in force curves. Finally, we find that <F_i-avg> does not increase with increasing ϕ_T for ϕ_T = 0.3–0.7. In this range, <F_i-avg> values are all close to F_b, suggesting that intermittent buckling events could be occurring in these composites and releasing some of the network stress. In other words, as ϕ_T increases, the number of buckling events may increase, which in turn would release some resistive force and keep the force from rising appreciably.

The relative mesh sizes of the actin and microtubule networks comprising the composites, as well as the overall “effective” mesh size of the composite, are changing with ϕ_T and could also play a role in the nonlinear dependence of <F_i-avg> on ϕ_T. Larger mesh sizes, or a mesh dominated by rigid rods rather than soft filaments, should result in more heterogeneities, particularly at small length scales. As the number of mesh sizes the bead moves through increases (i.e. as x reaches mesoscopic scales) the differences in the microscale environment should play less of a role in the force response. To quantify the length-scale dependence of our observed heterogeneities, we calculate the standard deviation of F_i(x), σ_F(x), as well as the ensemble mean, <F_i(x)>, over all i trials for each ϕ_T as function of the bead displacement x. Fig. 3 C shows the coefficient of variation, C_V(x) = σ_F/<F_i(x)>, for each ϕ_T as a function of x. As shown, C_V generally increases with increasing ϕ_T, but only for ϕ_T > 0.5 is there a substantial increase in C_V. This discrete jump in C_V is most apparent for x < 10 μm and becomes negligible for x > 20 μm.

The reduced variation in C_V values occurs at nearly the same displacement at which all composites approach a primarily viscous regime (x ≈ 20 μm) in which F is no longer increasing significantly with x. In this regime, the polymers can flow and deform in response to straining, and stress-induced buckling of microtubules can facilitate rearrangement and flow to release stress. These dynamics likely contribute to reduced heterogeneities. To understand the origin of the microscale heterogeneities causing the increased C_V values at small x, we calculate the predicted mesh size for single-species actin and microtubule networks, ξ_A and ξ_M, at each concentration present in composites. As displayed in the top axis of Fig. 3 B, ξ_M/ξ_A remains larger than 1 up to ϕ_T ≈ 0.8, with the actin mesh size ranging from ∼6 to 1.25× smaller than that for microtubules. Only at tubulin molar fractions of ϕ_T > 0.7 do we see a marked increase in <F_i-avg>, Δ_avg, and C_V as the microtubule mesh size becomes smaller than that for actin (ξ_M/ξ_A < 1). Up to ϕ_T ≈ 0.8, a tighter, more entangled actin network pervades the system, which could suppress the heterogeneities caused by larger, more rigid microtubules (Fig. 3 D). We can also quantify an “effective” composite mesh size ξ_C by considering the density of mesh-sized volumes in each composite, ξ_C = (ξ_M⁻³ + ξ_A⁻³)^−1/3 (Fig. S5). We find that ξ_C increases from 0.42 to 0.79 μm with increasing ϕ_T, with the value remaining close to ξ_A until ϕ_T ≈ 0.8. So, although semiflexible actin filaments are being replaced by rigid microtubules, the decrease in the density of entanglements offsets the increase in filament rigidity such that the resistive force and heterogeneities remain relatively unchanged until ϕ_T > 0.7.

We also characterize the relaxation of the applied force on the bead after the displacement. As shown in Fig. 4 A, the force relaxations for all composites display power-law relaxation in time (<F_i> ∼ t^−α) after an initial time-independent plateau. The initial plateau, in which no force dissipates, persists until t₁ ≈ 0.02 s, after which all networks with actin present undergo a very brief ϕ_T-dependent decay phase that lasts until t₂ ≈ 0.06 s. Although the small timescale of this phase prohibits accurate quantification of its functional form (64), if we estimate as power law, we can extract approximate scaling exponents that we find decrease roughly linearly with increasing fractions of tubulin (Fig. 4 B). At t₂ ≈ 0.06 s, the relaxations for all networks transition to slower power-law decay with exponents of α₂ ≈ 0.34–0.53 that display a nonmonotonic dependence on ϕ_T, reaching a maximum at ϕ_T = 0.5 (Fig. 4 C).

These unique relaxation characteristics are in opposition to the expected dynamics for entangled polymer systems, in which force relaxation is typically described by a sum of exponential decays due to distinct relaxation mechanisms with well-separated timescales (13, 65). Power-law relaxation suggests that there is a wide spectrum of relaxation times that are not well separated (66). Such spectra can arise from a distribution of filament lengths, stiffnesses, and mesh sizes; or from temporal evolution of relaxation mechanisms such that the corresponding timescales are changing in time (67). Our composites indeed have a distribution of macromolecular properties and responses to applied force (Fig. S6), so power-law relaxation is not entirely surprising. Yet, the initial plateau, the ϕ_T-independent crossover times, and the ϕ_T-dependent scaling exponents all warrant further discussion.

The initial plateau, in which there is no force dissipation, suggests that there are no available relaxation mechanisms that the filaments can undergo on these timescales. Previous micro-indentation experiments on cytoplasm found that force relaxation also exhibited an initial plateau followed by power-law relaxation. Authors showed that the short-time plateau behavior could be fit to a poroelastic model but that this model failed for longer times in which the relaxation was distinctly power law as opposed to a stretched exponential (55). The agreement between our early-time relaxation and that of poroelastic cytoplasm is not only further evidence that our short-timescale stress response described above (Fig. 2) can be described in terms of poroelasticity, but also suggests that our composites can indeed be used to shed light on cellular mechanics.

Once the timescale has become longer than that of the fastest relaxation mode of the network, filament relaxation should dominate the response over poroelastic fluid draining. We can estimate the fastest relaxation time of our composites as that of the fastest predicted actin relaxation mode, which is the time for length scales comparable to the mesh size to relax (68, 69). This actin mesh time, τ_m,A ≈ βζξ_Α⁴l_p⁻¹, where β = 1/k_BT and ζ is the translational friction coefficient (10, 70), can be understood as the time it takes for hydrodynamic interactions between filaments to become important. For ϕ_T = 0 networks, τ_m,A ≈ 0.01 s, which is quite close to the time at which power-law relaxation begins (t₁). Our measurements carried out at slower speeds all show the same initial plateau and timescale t₁ for relaxation to ensue, demonstrating that t₁ is an intrinsic timescale of the system rather than an artifact of the loading rate.

To understand the fast relaxation that occurs at t₁ < t < t₂, we evaluate the next relevant relaxation timescale in the system, which is the actin entanglement time τ_e,A ≈ βζξ_Α^3.2l_p^−0.2 (10). This is the time at which each actin filament begins to “feel” its entanglement tube and undergo reptation to relax stress. For t < τ_e,A, entangled semiflexible actin can relax stress via bending fluctuations, which are less accessible to more rigid microtubules (13, 15). For ϕ_T = 0 networks, τ_e,A ≈ 0.07 s, which is markedly close to our measured crossover time t₂ ≈ 0.06 s. This finding, along with the fact that α₁ scales roughly linearly with the fraction of actin in composites, suggests that the relaxation occurring between ∼0.02 and 0.06 s is due to actin bending modes. These nonaffine bending deformations (16) have been shown to result in stress softening rather than stiffening behavior. The clear transition to stiffening behavior as ϕ_T increases is further evidence that this fast relaxation mode is due to actin bending fluctuations that microtubules increasingly suppress as ϕ_T increases. We note that it is possible that ϕ_T-dependent reduction in α₁ is simply a result of fewer actin filaments in the network, so the bending fluctuations contribute less to the overall relaxation, rather than microtubules actively suppressing bending modes. In either case, as ϕ_T increases, the degree to which the composites can relax via bending is reduced. We also note that this fast relaxation mode does not appear to be present in our measurements of similar actin networks in standard actin network buffer conditions (Fig. S4). However, previous measurements on comparable actin networks in standard buffer conditions have reported evidence of fast relaxation modes arising from bending (14, 15).

We interpret our final relaxation phase, which begins at t₂ ≈ τ_e,A, as arising from reptation and tube disengagement. As described above, for t > τ_e, fast relaxation modes become negligible and filaments relax primarily via reptation out of deformed entanglement tubes (i.e. disengagement). Previous studies have shown that entangled biopolymer networks subject to nonlinear strains can exhibit power-law force relaxation arising from tube disengagement (47, 71). In previous microrheology experiments on entangled actin, force relaxation transitioned from exponential to power law, with a scaling exponent of ∼0.5, when the bead speed exceeded ∼3 μm/s (71). Our final phase scaling exponents (α₂ ≈ 0.34–0.53) are very close to this previously reported value, as well as to predictions based on a non-classical disengagement mechanism for entangled polymers subject to nonlinear strains (67, 71, 72). Within this framework, nonlinear strains dilate entanglement tubes such that, after strain, tubes shrink back to their original size over the same timescale that filaments reptate out of the deformed tubes. The result is that as each filament attempts to reptate out of its tube, the characteristic disengagement time grows longer, thereby producing power-law decay. Our measurements carried out at slower speeds show that composites transition from power-law to exponential relaxation at speeds of 2.5–5 μm/s (Fig. S8), similar to the previously reported crossover speed (71). This result is further evidence that the power-law relaxation is due to the nonlinear nature of the perturbation and the corresponding non-classical time-dependent tube confinement.

Although we cannot rule out contributions from the heterogeneous nature of the composites to the power-law behavior, the agreement with previously reported scaling exponents, the ϕ_T-independent crossover time (t₂ ≈τ_e,A), and the transition to exponential scaling at slow speeds all indicate that the power law arises from the non-classical time-dependent tube confinement. Further, our analysis on individual force curves (Fig. S6) shows that the power-law scaling is preserved for individual trials and that similar exponents are calculated from a small subset of trials compared to the full ensemble average.

The surprising nonmonotonic dependence of α₂ on ϕ_T, which had not been previously reported or predicted, suggests that reptation proceeds most quickly in equimolar composites (ϕ_T ≈ 0.5) compared to networks of actin or microtubules alone. This result could arise from the competition between the increase in ξ_C and the increase in filament rigidity as ϕ_T increases, as we describe above. Namely, although semiflexible actin filaments, which can reptate more quickly, are being replaced by slower rigid microtubules, the decrease in the density of entanglements offsets the increase in filament rigidity such that the force decay is steepest for intermediate ϕ_T values. This competition also likely contributes to the nonlinear dependence of the average force on ϕ_T during perturbation (Fig. 3 B). Specifically, as the fraction of microtubules increases, the measured force remains roughly constant until ϕ_T > 0.7, despite the increasing rigidity of the system as ϕ_T increases. Although network rigidity increases, which would increase resistive force, the mesh size is also increasing, allowing filaments to more easily move to alleviate stress, offsetting this resistance.

To shed more light on this surprising nonmonotonicity and to correlate the measured nonlinear stress characteristics with the corresponding steady-state dynamics, we quantify the mobility of actin and microtubules in steady-state composites by analyzing time series acquired using two-color fluorescence confocal microscopy (Figs. 5, S9, and S10). As described in Methods, we use the coefficient of variation of pixel intensities over time, σ_Ι /<I>, as a measure of mobility. We also examine temporal color maps of acquired movies to discern variations in mobility. As shown in Fig. 5, the mobility of both actin and microtubules within composites display a nonmonotonic dependence on tubulin fraction. Namely, mobility increases as ϕ_T increases to 0.5 after which it decreases. This effect can also be seen in the temporal color maps which show more color for ϕ_T = 0.5 composites compared to ϕ_T = 0 or ϕ_T = 1 networks. This nonmonotonicity is quite similar to that of α₂, demonstrating that the magnitudes of α₂ correlate with filament mobility. The drop in mobility for ϕ_T > 0.5 occurs at the same tubulin fraction at which composites transition from strain softening to stiffening (ϕ_T ≈ 0.7), supporting the evidence that stiffening arises from suppressed filament fluctuations. The increase in mobility as ϕ_T increases to 0.5 is less intuitive, as semiflexible actin filaments are being replaced with more rigid microtubules. However, as described above, although the composite is becoming more rigid as ϕ_T increases, the effective mesh size ξ_C is increasing, allowing both actin and microtubules to more easily move. The competition between increasing rigidity and increasing ξ_C leads to a peak in mobility at ϕ_T = 0.5.

It is important to note that the mobility trend is the same for actin and microtubules, indicating that the two filaments are sterically interacting and coupled to one another. For most composites, the microtubule mobility is less than that of actin, which is expected given the ∼100-fold increase in its persistence length and bending rigidity (5, 73). However, the difference in σ_I/<I> values for actin versus microtubules is less than a factor of two in all cases. Given the ∼100-fold difference in bending compliance of the two filaments (5), which has been shown to be proportional to the rotational diffusion coefficient (73), this result is rather surprising and further demonstrates that the two filament networks are co-entangled and strongly coupled.

To determine if filament mobility is different on timescales above and below τ_e, we performed mobility analysis for movies with 0.033 s (∼0.5τ_e) frames to compare to the 1 s (∼14τ_e) frame movies used in Fig. 5 (Fig. S10). The mobility for both filaments is higher for t <τ_e, which indicates that some of the fast relaxation modes, such as bending, become frozen out for t > τ_e. Although microtubules cannot easily undergo bending fluctuations because of their extreme rigidity, they can undergo rotational diffusion on timescales below τ_e, which becomes restricted once the microtubules are subject to tube confinement (73). The rotational diffusion of actin filaments, which is faster than that of microtubules, could also be contributing to their mobility and explain their faster mobility compared to microtubules. Strictly speaking, τ_e ≈ 0.07 s is only valid for actin in ϕ_T = 0 networks. However, computing the equivalent timescale for microtubules in ϕ_T = 1 networks gives τ_e,M ≈ 0.2 s, which is still well below the 1 s frames used in our analysis. So, we expect to see a drop in the mobility of both actin and microtubules for 1 s frames versus 0.033 s frames as fast relaxation modes are being frozen out and filaments are only undergoing reptation. Finally, the fact that the nonmonotonic dependence on ϕ_T is preserved for times below τ_e is further evidence that increased concentrations of microtubules suppress actin bending modes, as at these short timescales, contributions from reptation are not yet present.

Conclusions

We use optical tweezers microrheology and two-color fluorescence microscopy to characterize the mesoscale force response and mobility of co-entangled composites of actin and microtubules, which we create by in situ co-polymerization of actin monomers and tubulin dimers using custom-designed hybrid conditions. By systematically varying the relative concentrations of actin and microtubules (quantified by the molar fraction of tubulin ϕ_T), we show that composites exhibit a wide range of dynamical properties that can be tuned by ϕ_T. Our collective results demonstrate that microtubules suppress actin bending fluctuations, enabling composites to stiffen in response to strain and relax stress more slowly, whereas actin supports microtubules against buckling by providing a soft semiflexible mesh that permeates the larger microtubule mesh and partially absorbs stress. We also show that the interplay between varying mesh sizes and filament rigidity leads to emergent fast mobility in equimolar composites compared to networks of mostly actin or microtubules. Our quantitative analysis of the dependence of mechanical properties and mobility on composite composition provides important insights into how composite materials can be tuned to display user-defined mechanics.

Our results also demonstrate the synergistic ways in which thin, semiflexible actin filaments and thick, rigid microtubules can sterically interact to enable the myriad of mechanical processes and properties the cytoskeleton exhibits. In particular, structural interactions between actin and microtubules have been shown to be essential to cell migration, mitosis, apoptosis, and wound healing, as well as neuronal growth cone guidance and cortical flow in a wide range of cell types (1). Further, the role that Taxol plays in actin-microtubule mechanics during mitosis and apoptosis is of importance to the biomedical community, which uses Taxol to treat cancers (74, 75). The concentrations of microtubules and actin, as well as the structural and mechanical properties of actin-microtubule composites, vary widely between cell types and in varying regions within each cell, yet their interactions appear highly conserved (1, 76). Our in vitro platform offers an avenue for systematically probing these highly varied motifs, and our results provide the groundwork for future investigations on in vitro cytoskeletal composites that include cross-linking proteins, intermediate filaments, and motor proteins. These future studies will expand the phase space of mechanical properties that these bioinspired composite materials can exhibit and shed light onto the role that each additional component plays in the mechanics of the cytoskeleton.

Author Contributions

S.N.R. designed experiments, conducted experiments, analyzed data, and wrote the manuscript. J.L.R. advised experimental design, analyzed and interpreted data, and helped write the manuscript. R.M.R.-A. designed, advised, and oversaw experiments; analyzed and interpreted data; and wrote the manuscript.

Editor: Margaret Gardel.