A Zero-Inflated Box-Cox Normal Unipolar Item Response Model for Measuring Constructs of Psychopathology

Abstract

This research introduces a latent class item response theory (IRT) approach for modeling item response data from zero-inflated, positively skewed, and arguably unipolar constructs of psychopathology. As motivating data, the authors use 4,925 responses to the Patient Health Questionnaire (PHQ-9), a nine Likert-type item depression screener that inquires about a variety of depressive symptoms. First, Lucke’s log-logistic unipolar item response model is extended to accommodate polytomous responses. Then, a nontrivial proportion of individuals who do not endorse any of the symptoms are accounted for by including a nonpathological class that represents those who may be absent on or at some floor level of the latent variable that is being measured by the PHQ-9. To enhance flexibility, a Box-Cox normal distribution is used to empirically determine a transformation parameter that can help characterize the degree of skewness in the latent variable density. A model comparison approach is used to test the necessity of the features of the proposed model. Results suggest that (a) the Box-Cox normal transformation provides empirical support for using a log-normal population density, and (b) model fit substantially improves when a nonpathological latent class is included. The parameter estimates from the latent class IRT model are used to interpret the psychometric properties of the PHQ-9, and a method of computing IRT scale scores that reflect unipolar constructs is described, focusing on how these scores may be used in clinical contexts.

Background and Motivation

Over the last decade, item response theory (IRT) has played an increasing role in psychopathology research, commonly used in the assessment of constructs such as depression (e.g., Cole et al., 2013; Lee, Krishnan, & Park, 2012), anxiety (e.g., Roberson-Nay, Strong, Nay, Beidel, & Turner, 2007), and addiction (e.g., Liu, Hedeker, & Marmelstein, 2013; Muthén & Asparouhov, 2006). Although gaining more widespread use in psychology, the application of IRT to clinical assessment poses some unique challenges that are often overlooked in the clinical literature (Reise & Revicki, 2015; Reise & Rodriguez, 2016). Perhaps most fundamentally, IRT models assume that instruments measure bipolar constructs (Reise & Waller, 2009), likely stemming from IRT having its origins in educational measurement. Although it is reasonable to assume that many educational constructs are bipolar (e.g., math ability falls along a continuum from far below average to far above average), the bipolar assumption may be less justified in clinical assessment, where psychopathology constructs tend to be positively skewed (Lucke, 2015; Reise & Rodriguez, 2016; Reise & Waller, 2009; Wall, Park, & Moustaki, 2015).

To appreciate why the assumption of a bipolar latent variable may be unrealistic in clinical contexts, depression is considered as measured by the Patient Health Questionnaire (PHQ-9; Kroenke, Spitzer, & Williams, 2001). The PHQ-9 is used extensively in clinical practice and has undergone several psychometric evaluations in clinical and nonclinical samples that are beyond the scope of this research (Kocalevent, Hinz, & Brahler, 2013; Lowe, Kroenke, Herzog, & Grafe, 2004; Martin, Rief, Klaiberg, & Braehler, 2006). The measure comprises nine items that inquire about depressive symptoms over the last 14 days, to which respondents endorse not at all (0), several days (1), more than half the days (2), or nearly every day (3). Figure 1 shows the summed score frequencies for 4,925 individuals who completed the PHQ-9 as a depression screener on the 2012 National Health and Nutrition Examination Survey (NHANES; Centers for Disease Control and Prevention & National Center for Health Statistics, 2012). Approximately 35% of the respondents in this sample endorsed “not at all” for all nine items and received a summed score of 0, a value that corresponds to the lowest possible level of the latent variable.

Figure 1.

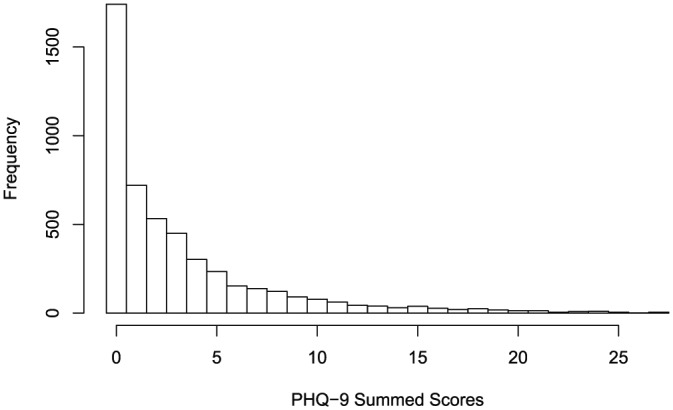
Summed score frequencies for 4,925 respondents on the PHQ-9.

Note. PHQ-9 = Patient Health Questionnaire.

For simplicity, Figure 1 presents summed scores for these 4,925 individuals, but one could also compute IRT scale scores. In this case, a summed score of 0 would map onto an IRT scale score that suggests a below average level of depression (i.e., a negative score); however, should individuals who endorse none of the items really be described as having “below average” levels of depression? Perhaps the lowest end of the latent variable continuum is not below average depression but the absence of depression (Reise & Revicki, 2015; Reise & Waller, 2009), and if so, scores not at the floor level may be more meaningfully interpreted as someone’s level of depression relative to someone who has no depression (Lucke, 2015). Thus, IRT models that assume a unipolar rather than bipolar latent variable may be better suited for assessing constructs of psychopathology (Reise & Rodriguez, 2016). The summed scores in Figure 1 reveal that depression, at least as measured by the PHQ-9 in a nonclinical sample, may be a unipolar construct (sometimes referred to as a quasi-trait, Reise & Waller, 2009). Some of the existing methodologies for the analysis of arguably unipolar constructs are reviewed first. Then, features of these existing methodologies are combined to develop a more flexible modeling approach for the analysis of the PHQ-9 data, with the possibility of application to other assessments of psychopathology. The computation of IRT scale scores that reflect unipolar constructs is also addressed.

A Log-Logistic IRT Model for Unipolar Constructs

Lucke proposed a class of IRT of models that he refers to as unipolar item response models (UIRMs), in which a nonnegative latent variable underlies someone’s responses to items on a clinical assessment (Lucke, 2014, 2015). Based on Stevens’ (1957) psychophysical power model (Thomas, 1983), Lucke’s model treats item responses as manifestations of a nonnegative latent variable $\theta$, where $\theta =0$ if the respondent possesses no level of the latent variable, and $\theta >0$ if the respondent falls at some level of the latent variable. Lucke describes a general class of UIRMs in which a variety of link functions can be used to link the latent variable to the probability of endorsing an item; here, attention is focused on the log-logistic model which is the UIRM analog of the common logistic IRT model (Lucke, 2015). The log-logistic trace line for a binary response to item $j$ is expressed as

$$T_j(U_j=u_j|\theta )=\frac{b_j{\theta }^{a_j}}{1+b_j{\theta }^{a_j}},$$

in which $a_j$ is an item discrimination parameter that relates the latent variable to the probability of endorsing the item, and $b_j$ is an easiness or multiplicative parameter with higher values shifting the trace line toward higher levels of the latent variable. In place of a standard normal population density, a log-normal(0,1) density can be used to describe the latent variable distribution.

The UIRM for dichotomous responses can be viewed as a transformation of the traditional 2 parameter logistic (2PL) IRT model that assumes a bipolar latent variable, and as pointed out in Reise and Rodriguez (2016), crude approximations of the UIRM item parameter estimates can be obtained through simple transformations of the 2PL item parameters: $a_j={\alpha }_j$ and $b_j=\exp (-{\alpha }_j{\beta }_j)$, where ${\alpha }_j$ and ${\beta }_j$ are the discrimination and threshold parameters, respectively, from the traditional 2PL IRT model. Although these models have identical log-likelihoods, there may be conceptual reasons to prefer the unipolar parameterization in the context of psychopathology assessment. First, unipolar models offer the advantage of having an absolute zero point on the latent variable scale, which may be more appealing in the measurement of constructs such as depression; traditional IRT models assume a hypothetical minimum value of $\theta =-\infty$. Second, an advantage of using the unipolar log-logistic model over the bipolar logistic model is that scores at higher levels of the latent variable, which correspond to individuals with severe levels of psychopathology, become more diffuse, resulting in clearer separation of individuals at higher levels of the latent variable (Reise & Rodriguez, 2016). This may be particularly useful in clinical settings where researchers are more likely to be interested in understanding individual differences among those with most extreme levels of psychopathology. Recent applications of Lucke’s log-logistic model include the assessment of gambling pathology (Lucke, 2015) and impulsivity (Reise & Rodriguez, 2016).

Box-Cox Normal Transformation for the Latent Variable Distribution

Lucke’s log-logistic model assumes that the latent variable follows a log-normal(0,1) distribution in the population. Although the log-normal distribution is commonly used to model nonnegative, positively skewed data, other latent variable densities may also be appropriate. One approach involves empirically estimating the latent variable density to account for nonnormality (Woods, 2006, 2007; Woods & Thissen, 2006). Another option is to approximate the latent variable density with a skew-normal distribution (Molenaar, 2015; Molenaar, Dolan, & de Boeck, 2012). Others have adopted a mixture modeling approach, using a mixture of normal and degenerate distributions to accommodate heterogeneous populations (Muthén & Asparouhov, 2006; Wall et al., 2015). For consistency with Lucke’s log-logistic model, the log-normal(0,1) population density is retained but additional flexibility is introduced by allowing the transformation parameter to be determined empirically. The Box-Cox transformation is a power transformation in which an additional parameter $\nu$ is estimated to characterize the degree of skewness in the data. The Box-Cox density function for latent variable $\theta$ can be written as

$$f\left(\theta \right)={\theta }^{\nu -1}\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp [-\frac{1}{2}{\left(\frac{{\theta }^{*}-\mu }{\sigma }\right)}^2],$$

where

$${\theta }^{*}=\{\begin{array}{c}\frac{{\theta }^{\nu }-1}{\nu }(\nu \ne 0)\hfill \\ \multicolumn{1}{c}{\log \theta (\nu =0)}\end{array}.$$

The log-normal distribution is a special case of the Box-Cox normal distribution in which $\nu =0$. Thus, estimates of $\nu$ near 0 provide empirical support for the use of a log-normal latent variable density. Within the IRT literature, the Box-Cox transformation has been used to find the optimal transformation for response time distributions that are conditional on a latent speed factor (Klein Entink, van der Linden, & Fox, 2009); however, to the authors’ knowledge, it has not been used to find the optimal transformation for a nonnegative, positively skewed latent variable density.

Latent Class Item Response Models for Zero-Inflated Data

A common artifact of measuring constructs of psychopathology is zero inflation—that is, a floor effect of summed or scale scores that is the result of a subset of individuals in the sample who do not exhibit any degree of the psychopathology that is being measured. One approach to modeling constructs of psychopathology that exhibit such zero inflation is mixture or latent class IRT, in which the latent variable density is specified as a mixture of normal and degenerate distributions to accommodate population heterogeneity (Finkelman, Green, Gruber, & Zaslavsky, 2011; Magnus & Thissen, 2017; Wall et al., 2015). According to the latent class IRT model, the trace line describing the conditional probability of endorsing a particular response category is expressed as a function of both a latent variable and a group membership,

$$T_j(U_j=u_j|\theta ,{\pi }_1,\dots ,{\pi }_G)=\sum _{g=1}^G{\pi }_g{P}_{\mathrm{gj}}(U_j=u_j|\theta ),$$

in which $g$ denotes latent class membership, ${\pi }_g$ specifies the probability of belonging to latent class $g$, and $P_{\mathrm{gj}}(U_j=u_j|\theta )$ is the conditional probability of observing response $u_j$ from someone in latent class $g$, where $\sum _{g=1}^G{\pi }_g=1$ (Hagenaars & McCutcheon, 2002). Wall et al. (2015) used a latent class IRT model to analyze data from a questionnaire about alcohol use disorder, in which a nontrivial subpopulation of respondents does not possess any level of the latent variable being measured (e.g., alcohol abstainers responding to items about alcohol dependence). Although their model can include any number of latent classes, the version most relevant to the data described here includes a latent class that comprises a subset of the individuals who do not endorse any of the items on a symptom checklist—what can be considered a nonpathological group. The IRT model for this class is degenerate, which Wall et al. represent with a point mass at an arbitrarily large negative value of the latent variable mean (e.g., ${\mu }_k=-100$). The other latent class in their model, which they refer to as a pathological group, describes individuals who do possess some level of the latent variable that is being measured; that is, they fall along the severity continuum that is implied by a bipolar IRT model that assumes a normal population distribution.

Finkelman et al. (2011) analyzed psychopathology data using a similar model, also including a latent class to account for a subset of the individuals who endorse all of the items on a symptoms checklist. More recently, Magnus and Thissen (2017) used latent class IRT to model zero-inflated and maximum-inflated symptom frequency data on a measure of emotional health. Applications of latent class IRT modeling demonstrate its usefulness in describing zero-inflated data that often arise in the assessment of nonclinical samples; however, existing applications of this method have assumed a normal density for those who fall along the latent variable continuum, implying a bipolar latent variable for members of the pathological class. If depression truly is a unipolar construct, a model that takes into consideration the unipolar nature of the construct within the pathological class while simultaneously accounting for the zero inflation that manifests from within the nonpathological class may be more appropriate. Individuals belonging to the nonpathological class can receive a score that is substantively meaningful within the framework of a unipolar latent variable: zero.

The Proposed Model

A latent class item response model that extends Lucke’s UIRM is proposed to (a) accommodate polytomous item responses that are frequently found on measures of psychopathology, and (b) account for zero inflation that can often occur on such measures. To enhance flexibility, the assumption of a log-normal population density is also relaxed by specifying a Box-Cox normal distribution for the latent variable. The skewness of the latent variable can then be characterized by a transformation parameter that is estimated directly from the item response data, with values near zero providing support for a log-normal population density. As shown here, maximum likelihood estimation can be used as an alternative to the Bayesian methods described by Lucke (2014, 2015).

Lucke’s UIRM model can be generalized to polytomous responses by introducing a category-specific easiness parameter, $b_{\mathrm{jk}}$. The probability of endorsing category $k$ on item $j$ can be parameterized as a model of differences between cumulative probabilities for adjacent categories that is analogous to the graded response model (GRM; Samejima, 1968). Thus, a log-logistic trace line for polytomous item responses with categories $k=1,\dots ,K$ can be expressed as

$$T_j(U_j=u_j|\theta )=\frac{b_{\mathrm{jk}}{\theta }^{a_j}}{1+b_{\mathrm{jk}}{\theta }^{a_j}}-\frac{b_{\mathrm{jk}+1}{\theta }^{a_j}}{1+b_{\mathrm{jk}+1}{\theta }^{a_j}},$$

where $a_j$ is a discrimination parameter for item $j$ that is assumed to be equal across all response categories, and $b_{\mathrm{jk}}$ is an easiness parameter for category $k$ such that larger values suggest that one must be at higher levels of the latent variable $\theta$ to endorse more severe response categories. As described in Lucke’s (2014) original paper, the discrimination and easiness parameters can be used to compute the severity of an item. In extending the concept of a severity parameter to the polytomous case, $K-1$ severity parameters for each item are estimated:

$$d_{\mathrm{jk}}={\left(\frac{1}{b_{\mathrm{jk}}}\right)}^{\frac{1}{a_j}}.$$

The severity parameter $d_{\mathrm{jk}}$ for item $j$ can then be interpreted as the point on the latent variable $\theta$ where one has a 50% probability of endorsing category $k$ or higher.

To allow for the possibility of a nonpathological group, a latent class IRT approach similar to that of Wall et al. (2015) is adopted. The nonpathological class represents some, perhaps many, of the people in the sample who do not endorse any of the symptoms and do not have any degree of depression. They can be thought of as being absent on or at some floor level of depression. The pathological class represents everyone else. Importantly, the pathological class is expected to include some individuals who do not endorse any of the symptoms but still have some degree of depression (i.e., their symptoms are not addressed by the measure). Anyone who endorses at least one of the symptoms is automatically a member of the pathological class. Importantly, everyone in the population is considered “at risk” of depression—there is no one to whom the construct does not apply. It is instead a question of whether all who are at risk are believed to have depression.

Let $I_p$ be in indicator variable denoting membership in the pathological class, with probability ${\pi }_p$. Assuming that the pathological and nonpathological latent classes are mutually exclusive, the general latent class model shown in Equation 4 can be written as

$$\begin{array}{c}\multicolumn{1}{c}{T_j(U_j=u_j|\theta ,{\pi }_p)=(1-{\pi }_p)[P_j(U_j=0)=1|\theta ,I_p=0]}\\ \multicolumn{1}{c}{+{\pi }_p\left[T_j(U_j=u_j|\theta ,I_p=1)\right]}\end{array},$$

where $u_j=\{0,1,2,3\}$ for items with four Likert-type response categories. The first line of Equation 7 shows that the IRT model for the nonpathological class is degenerate; that is, an IRT model does not underlie the responses of individuals belonging to this class. If someone is a member of the nonpathological class, they respond “not at all” to each symptom with a probability of 1. In contrast, item responses from the pathological class are described by an IRT model, as shown with the trace line that is expressed in the second line of Equation 7. It is important to recognize that according to this IRT model, some individuals belonging to the pathological class are expected to have all-0 response patterns.

Let $N_0$ be the number of people with response pattern $\mathit{U}=0$, an all-0 response pattern, and let $N_{\mathit{u}}$ be the number of people with response pattern $\mathit{U}=\mathit{u}$. Given response patterns $\mathit{U}=\mathit{u}$, the log likelihood of item parameters $\alpha =\{{\mathit{a}}_{\mathit{j}},{\mathit{b}}_{\mathit{jk}}\}$ for items $j=1,\dots ,J$ with response categories $k=1,\dots ,K-1$, the latent class proportion ${\pi }_p$, and the Box-Cox transformation parameter $\nu$, can be expressed as

$$\begin{array}{c}\log L(\alpha ,{\pi }_p,\nu ;\{\mathit{u}{\}}_1^J)=N_0\log [(1-{\pi }_p)+{\pi }_{p}T(\mathit{U}=0|\alpha ,\theta ,I_p=1)]\hfill \\ \multicolumn{1}{c}{+\sum _{\mathit{u}\ne 0}{N}_{\mathit{u}}\log \left[{\pi }_{p}T(\mathit{U}=\mathit{u}|\alpha ,\theta ,I_p=1)\right].}\end{array}$$

In Equation 8, $T(\mathit{U}=\mathit{u}|\alpha ,\theta ,I_p=1)$ traces the conditional probability of observing response pattern $\mathit{U}=\mathit{u}$ for someone in the pathological class, and $T(\mathit{U}=0|\alpha ,\theta ,I_p=1)$ traces the conditional probability of observing response pattern $\mathit{U}=0$ for someone in the pathological class.

Goals of the Current Research

The primary goal of this research was to combine existing psychometric approaches to model data where (a) the construct of interest is arguably unipolar, and (b) there is a large degree of zero inflation. Responses to the PHQ-9 serve as motivating data. First, Lucke’s log-logistic UIRM is extended to accommodate polytomous item responses. Then, flexibility is incorporated by using a Box-Cox normal transformation for the latent variable distribution. Finally, the issue of zero inflation that is not accounted for by the IRT model is addressed by including a latent class that describes a proportion of individuals who do not endorse any of the items and may be absent on the latent variable (i.e., they do not have depression). To test the usefulness of this approach over more parsimonious modeling techniques, four models are compared in sequence: a log-logistic UIRM with a log-normal prior, a log-logistic UIRM with a Box-Cox normal prior, a zero-inflated log-logistic UIRM with a log-normal prior, and a zero-inflated log-logistic UIRM with a Box-Cox normal prior. All model parameters were estimated with maximum likelihood using nlm, R’s general optimizer, by minimizing the negative of the log likelihood function specified in Equation 8 (R Core Team, 2016). As a secondary goal, a method of computing IRT scale scores “As a secondary goal, a method of computing IRT scale scores for unipolar latent variables in the presence of a nonpathological class is described.” for unipolar latent variables is described in the presence of a nonpathological class.

Empirical Analysis of the PHQ-9

Model Comparison

Table 1 contains model fit statistics and parameter estimates for the four models of interest. To compare the performance of the log-normal and Box-Cox normal priors, the two models in the upper panel of the table that do not include a nonpathological class are first considered. In this scenario, all individuals are assumed to belong to the pathological class. Of these two models, both the Akaike information criterion (AIC) and Bayesian information criterion (BIC) support the model with a log-normal prior. Furthermore, the Box-Cox transformation parameter is very close to 0 ($\nu =0.03$), providing empirical evidence that the log-normal prior sufficiently describes the latent variable distribution.

Table 1.

Fit Statistics and IRT Parameter Estimates for the Four Log-Logistic IRT Models.

Item	Log-logistic with log-normal prior							Log-logistic with Box-Cox normal prior
	$a$	$b_1\times 10$	$b_2\times 10$	$b_3\times 10$	$d_1$	$d_2$	$d_3$	$a$	$b_1\times 10$	$b_2\times 10$	$b_3\times 10$	$d_1$	$d_2$	$d_3$
1	2.39 (0.09)	1.30 (0.28)	0.17 (0.10)	0.06 (0.06)	2.35	5.48	8.71	2.44 (0.10)	1.29 (0.28)	0.17 (0.10)	0.06 (0.06)	2.31	5.30	8.35
2	3.09 (0.12)	0.80 (0.22)	0.06 (0.06)	0.02 (0.03)	2.26	5.26	8.04	3.16 (0.14)	0.79 (0.22)	0.06 (0.06)	0.02 (0.03)	2.23	5.09	7.71
3	1.79 (0.06)	4.37 (0.51)	0.78 (0.22)	0.33 (0.14)	1.59	4.15	6.74	1.82 (0.07)	4.41 (0.51)	0.79 (0.22)	0.33 (0.14)	1.57	4.05	6.53
4	2.02 (0.07)	7.98 (0.69)	0.67 (0.20)	0.23 (0.12)	1.12	3.82	6.42	2.04 (0.07)	8.07 (0.70)	0.68 (0.20)	0.24 (0.12)	1.11	3.73	6.23
5	1.93 (0.07)	1.65 (0.31)	0.32 (0.14)	0.13 (0.09)	2.55	5.92	9.63	1.96 (0.08)	1.65 (0.31)	0.33 (0.14)	0.13 (0.09)	2.50	5.73	9.23
6	2.70 (0.10)	0.51 (0.17)	0.07 (0.07)	0.02 (0.04)	3.01	6.16	9.32	2.76 (0.13)	0.51 (0.17)	0.07 (0.07)	0.02 (0.04)	2.95	5.94	8.89
7	2.42 (0.10)	0.55 (0.18)	0.10 (0.08)	0.04 (0.05)	3.31	6.60	10.01	2.47 (0.11)	0.55 (0.18)	0.10 (0.08)	0.04 (0.05)	3.24	6.36	9.54
8	2.30 (0.10)	0.30 (0.13)	0.07 (0.06)	0.03 (0.04)	4.60	8.59	12.16	2.36 (0.12)	0.30 (0.13)	0.07 (0.06)	0.03 (0.04)	4.46	8.21	11.53
9	2.31 (0.14)	0.06 (0.06)	0.02 (0.03)	0.01 (0.02)	9.22	16.30	22.81	2.37 (0.16)	0.06 (0.06)	0.02 (0.03)	0.01 (0.02)	8.78	15.29	21.22
								$\nu =0.03$
AIC = 51,359.28								AIC = 51,360.46
BIC = 51,593.35								BIC = 51,601.04
Item	ZI log-logistic with log-normal prior							ZI log-logistic with Box-Cox normal prior
	$a$	$b_1\times 10$	$b_2\times 10$	$b_3\times 10$	$d_1$	$d_2$	$d_3$	$a$	$b_1\times 10$	$b_2\times 10$	$b_3\times 10$	$d_1$	$d_2$	$d_3$
1	2.21 (0.09)	1.82 (0.39)	0.24 (0.14)	0.08 (0.08)	2.16	5.37	8.83	2.21 (0.09)	1.82 (0.39)	0.24 (0.14)	0.08 (0.08)	2.16	5.37	8.84
2	2.91 (0.12)	1.20 (0.32)	0.09 (0.09)	0.02 (0.04)	2.07	5.10	8.01	2.91 (0.12)	1.19 (0.32)	0.09 (0.09)	0.02 (0.04)	2.07	5.10	8.01
3	1.60 (0.08)	5.87 (0.70)	1.06 (0.30)	0.45 (0.19)	1.39	4.06	6.95	1.60 (0.08)	5.87 (0.70)	1.06 (0.30)	0.45 (0.19)	1.39	4.06	6.95
4	1.80 (0.09)	11.13 (0.96)	0.95 (0.28)	0.34 (0.17)	0.94	3.71	6.60	1.80 (0.09)	11.13 (0.96)	0.95 (0.28)	0.34 (0.17)	0.94	3.71	6.60
5	1.76 (0.08)	2.21 (0.43)	0.44 (0.19)	0.18 (0.12)	2.36	5.90	10.02	1.76 (0.08)	2.22 (0.43)	0.44 (0.19)	0.17 (0.12)	2.36	5.90	10.02
6	2.53 (0.11)	0.73 (0.25)	0.11 (0.09)	0.03 (0.05)	2.81	6.04	9.38	2.53 (0.11)	0.73 (0.25)	0.11 (0.09)	0.03 (0.05)	2.81	6.04	9.38
7	2.26 (0.10)	0.77 (0.25)	0.15 (0.11)	0.05 (0.07)	3.12	6.53	10.18	2.26 (0.10)	0.77 (0.25)	0.15 (0.11)	0.05 (0.07)	3.12	6.53	10.18
8	2.15 (0.10)	0.41 (0.18)	0.10 (0.09)	0.04 (0.06)	4.42	8.62	12.50	2.15 (0.10)	0.41 (0.18)	0.10 (0.09)	0.04 (0.06)	4.42	8.62	12.50
9	2.17 (0.14)	0.08 (0.08)	0.02 (0.04)	0.01 (0.03)	9.22	16.85	24.04	2.18 (0.14)	0.08 (0.08)	0.02 (0.04)	0.01 (0.03)	9.22	16.84	24.05
								$\nu \approx 0.00$
${\pi }_n=0.095$					${\pi }_p=0.905$			${\pi }_n=0.095$				${\pi }_p=0.905$
AIC = 51,350.24								AIC = 51,352.24
BIC = 51,590.82								BIC = 51,599.32

Note. Upper panel: Models without ZI component. Lower panel: Models with ZI component. The best-fitting model has AIC and BIC values in boldface. IRT = item response theory; AIC = Akaike information criterion; BIC = Bayesian information criterion; ZI = zero-inflated.

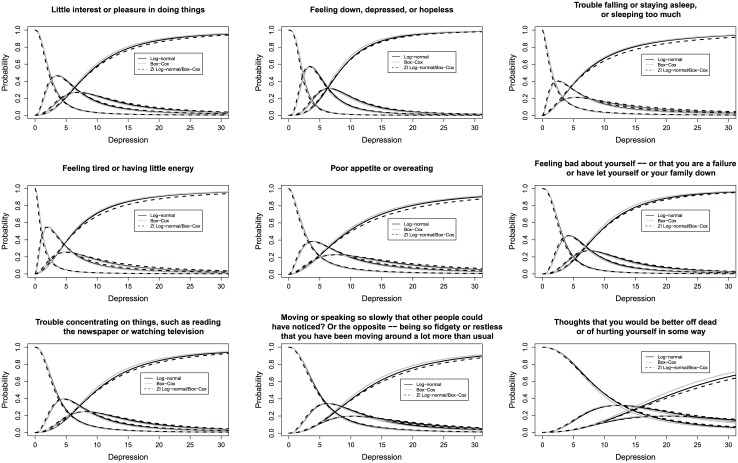
Item parameter estimates can also be found in Table 1. Note that easiness parameters $(b_{\mathrm{jk}})$ have been multiplied by 10 to avoid reporting excessive decimal places in the table; severity parameters $(d_{\mathrm{jk}})$ were computed from the original estimates of $b_{\mathrm{jk}}$. Item parameter estimates are similar between these two models, with slightly higher discrimination parameters and lower severity parameters associated with the Box-Cox normal prior. The accompanying trace lines for these two models are shown with the solid black and gray lines in Figure 2. There is a substantial degree of overlap between the two sets of trace lines, particularly for low levels of depression where the response category “not at all” has the greatest probability of endorsement. The two sets of trace lines diverge only at higher levels of depression, and this separation is only noticeable for the items that tend to be associated with more severe forms of depression (e.g., the item about thoughts of self-harm or suicide).

Figure 2.

Trace lines for the PHQ-9 items.

Note. Solid black lines: Log-logistic UIRM with a log-normal prior. Solid gray lines: Log-logistic UIRM with a Box-Cox normal prior. Dashed black lines: Zero-inflated log-logistic UIRM with a log-normal prior or Box-Cox normal prior. PHQ-9 = Patient Health Questionnaire; UIRM = unipolar item response model.

The two models that include a nonpathological class are considered next. Although the IRT model alone is expected to capture some of the all-0 response patterns, specifying a nonpathological class may be necessary to more completely account for the floor effect that is driven by those who do not endorse any of the symptoms. The fit statistics and parameter estimates from the zero-inflated UIRMs can be found in the lower panel of Table 1. Four findings are particularly noteworthy. First, both the AIC and BIC favor the zero-inflated UIRM with a log-normal prior over its Box-Cox normal counterpart. Second, the Box-Cox transformation parameter estimate is approximately 0, which indicates that after accounting for zero inflation in these data, the log-normal density adequately describes the latent variable distribution. Third, and related to the adequacy of the log-normal prior, the item parameter estimates of the two models are nearly identical. After incorporating a nonpathological class, there is essentially no difference between these two models when fit to the PHQ-9 data: The Box-Cox normal density becomes equivalent to the log-normal density. The trace lines for both models are shown with the dashed black lines in Figure 2. Because both models yield identical parameter estimates, the trace lines completely overlap; thus, only one set of dashed lines is shown. Fourth, it is the inclusion of the zero-inflated component, rather than allowing additional skewness in the latent variable density, that is able to capture the excess zeros in the data: Both versions of the zero-inflated model fit better than their counterparts without the nonpathological class.

In comparing across the four models, both the AIC and BIC support the zero-inflated log-logistic UIRM with a log-normal prior. The parameter estimates in Table 1 reveal that explicitly modeling the nonpathological class reduces the magnitudes of the item discrimination parameters by as much as 11%: Omitting the nonpathological class from the model suggests that the items have greater discriminatory power than they likely do, a finding consistent with prior research (Wall et al., 2015). This finding is not unexpected: As true of bipolar IRT models, unipolar models are susceptible to inflated discrimination parameters in the presence of excess zeros. Although it is the estimates of the discrimination parameters that are most affected, the magnitudes of the severity parameters also change depending on whether the nonpathological class is included. Differences can be seen more clearly in the trace lines in Figure 2. Incorporation of a nonpathological class has little effect at low levels of depression. For individuals with low depression levels ($\theta \le 7$), the probabilities of endorsing each response category are not conditional on whether a nonpathological class is included; however, as $\theta$ increases, the effects of incorporating the nonpathological class become more salient, particularly for items that are associated with more severe levels of depression. After accounting for the nonpathological class, members of the pathological class must have a higher level of depression before being expected to endorse “nearly every day”; that is, for the majority of items, respondents must be higher on depression to endorse the most extreme response category.

Interpretation of the Zero-Inflated Log-Logistic UIRM

Because model fit statistics and parameter estimates suggest that the zero-inflated log-logistic UIRM with a log-normal prior best describes the data, this is the model of interpretational focus for the remainder of the paper. Relevant parameter estimates can be found in the lower left corner of Table 1. Approximately 9.5% of the sample is estimated to belong to the nonpathological class. According to the model, these are individuals who, while at risk of depression, exhibit a complete absence on the latent variable. Of the 1,741 all-0 response patterns observed in the data, around 27% of them are expected to have come from members of the nonpathological class. The remaining 73% all-0 response patterns belong to individuals who possess some level of depression even though they did not endorse any of the symptoms.

Similar to conventional IRT models, items with higher discrimination parameters $(a_j)$ are more closely related to the latent variable. As might be expected based on content, the item about feeling down, depressed, or hopeless (i2) is most strongly related to the construct of depression, with the item related to feeling bad about oneself (i6) also being highly discriminating. Items that are less related to depression include those about energy levels (i4), sleeping habits (i3), and eating habits (i5). It is unsurprising that item discrimination parameters are lower for these items—it is likely that people may experience these symptoms without necessarily being depressed.

Interpretation of the severity parameter for category $k$ is analogous to the location parameter of the GRM: It is the level of the latent variable one must possess to have a 50% probability of endorsing category $k$ or higher. Because there are four response categories, each item has three severity parameter estimates. The items relating to sleep and energy have the smallest severity parameters across all three response categories. One can fall at a relatively low level of depression ($\theta =1.39$ for sleep and $\theta =0.94$ for energy) and still have 50% probability of endorsing the symptom. This is in contrast with more severe items where one must fall at a much higher level of depression to have a 50% probability of endorsing the symptom. For example, the item about thoughts of self-harm or suicide has comparatively large severity parameters: An individual must be located at $\theta =9.22$, $\theta =16.85$, or $\theta =24.04$ before having a 50% probability of endorsing “several days,”“more than half the days,” or “nearly every day,” respectively.

Based on the severity parameter estimates for the zero-inflated log-logistic UIRM in Table 1, there appear to be three “bundles” of items, a term introduced by Lucke (2015) to describe how sets of items relate to the severity of the psychopathology. The item bundle that best measures people who are low on depression includes those items asking about sleep and energy levels: Even individuals with low levels of depression are moderately likely to endorse these symptoms. In contrast, the item with the highest severity parameters, and thus the item that is most appropriate for measuring people with high levels of depression, asks about thoughts of self-harm or suicide. The remaining six items fall somewhere in the middle.

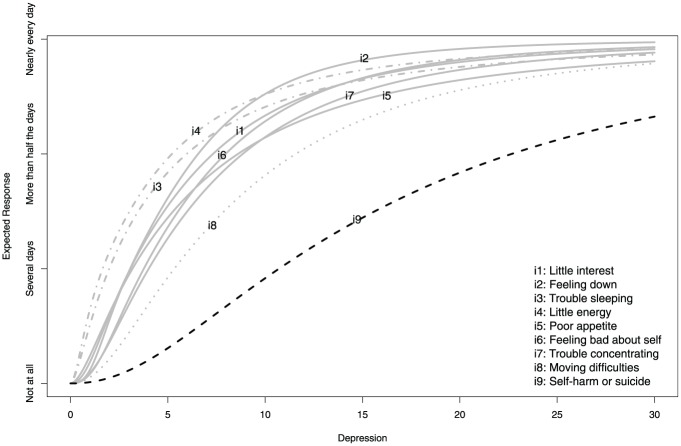
The item bundling is more easily described graphically in Figure 3, which depicts the relationship between someone’s underlying level of depression and the expected response category of endorsement. Most noticeably, one must be much higher on depression before being expected to endorse “several days” or higher for the item about thoughts of self-harm or suicide (i9), shown with the dashed black line. The item about difficulties with moving and speaking (i8), shown with the dotted gray line, also stands out for its higher severity, such that compared with the other items, one must be relatively high on depression before being expected to endorse one of the more extreme response categories. On the contrary, the items about sleep (i3) and energy (i4), shown with the pair of dashed gray lines, are rather easily endorsed, even at low levels of depression. As depression increases, however, most of the item bundling disappears, except for the item about thoughts of self-harm or suicide (i9).

Figure 3.

Expected response category endorsement as a function of depression.

Note. Item bundles are shown with lines of the same color and style.

Finally, the large degree of redundancy of the middle two response categories is noted: “several days” and “more than half the days.” This is most clearly seen in Figure 2. At low levels of depression (e.g., $\theta <5$), there is more noticeable separation between these two response categories, where “several days” has a higher probability of endorsement than “more than half the days.” Due to the ordinal nature of the response categories, one would expect “more than half the days” to have the greatest probability of endorsement at moderately high levels of depression; however, this is rarely the case. In fact, at no point on the latent variable continuum is “more than half the days” the most likely response, suggesting that including this category adds little value in measuring depression. Considering that the items inquire about thoughts and behaviors over a 14-day period, it is unsurprising that there is little distinction between “several days” and “more than half the days”: Many respondents may view these response options as equivalent.

Conditional Scoring

One of the advantages of zero-inflated UIRMs is that unlike IRT models that assume a bipolar latent variable, there is an absolute zero point that has a natural interpretation for members of the nonpathological class; a score of 0 implies an absence of depression. All other scores can be interpreted as the severity of depression relative to zero. Approximately 9.5% of the sample was estimated to belong to the nonpathological class. Based on this estimate, 468 of the all-0 response patterns belong to people who are absent on depression, and the remaining 1,273 all-0 response patterns belong to members of the pathological class. According to the model, these 1,273 individuals have some degree of depression, even though they did not endorse any of the symptoms. Unlike members of the nonpathological class, they receive scale scores that are slightly greater than 0 to indicate that they have some (mild) degree of depression that was not captured by the measure.

To compute scores, all response patterns that included the endorsement of at least one symptom ($n=3,184$) were assigned to the pathological class and scored according to the parameter estimates from the zero-inflated log-logistic UIRM with a log-normal prior in Table 1. Because these individuals endorsed at least one symptom, they must belong to the pathological class; thus, their class membership is known. These response patterns were scored according to the log-logistic UIRM, and scale score estimates (${\hat{\theta }}_{\mathrm{EAP}}$) were computed as the mean of the posterior distribution of $\theta$, where the posterior distribution is the product of the log-logistic trace lines for each response $u$ to item $j$ and the prior density. In this case, the prior is a log-normal(0,1) density. The mean of the posterior distribution was approximated using rectangular quadrature,

$$E\left(\theta \right)\approx \frac{\sum _1^Q\underset{j=1}{\overset{9}{\Pi }}{T}_{\mathrm{jq}}\left(u_j\right){\theta }_{q}d\theta }{\sum _1^Q\underset{j=1}{\overset{9}{\Pi }}{T}_{\mathrm{jq}}\left(u_j\right)d\theta },$$

where $T_j(u_j)$ is the trace line for item $j$. Standard errors of scale scores were computed as the standard deviation of the posterior distribution of $\theta$,

$$\mathrm{SD}\left(\theta \right)\approx \sqrt{\frac{\sum _1^Q\underset{i=1}{\overset{9}{\Pi }}{T}_j\left(u_j\right){({\theta }_q-{\hat{\theta }}_{\mathrm{EAP}})}^{2}d\theta }{\sum _1^Q\underset{i=1}{\overset{9}{\Pi }}{T}_j\left(u_j\right)d\theta }}.$$

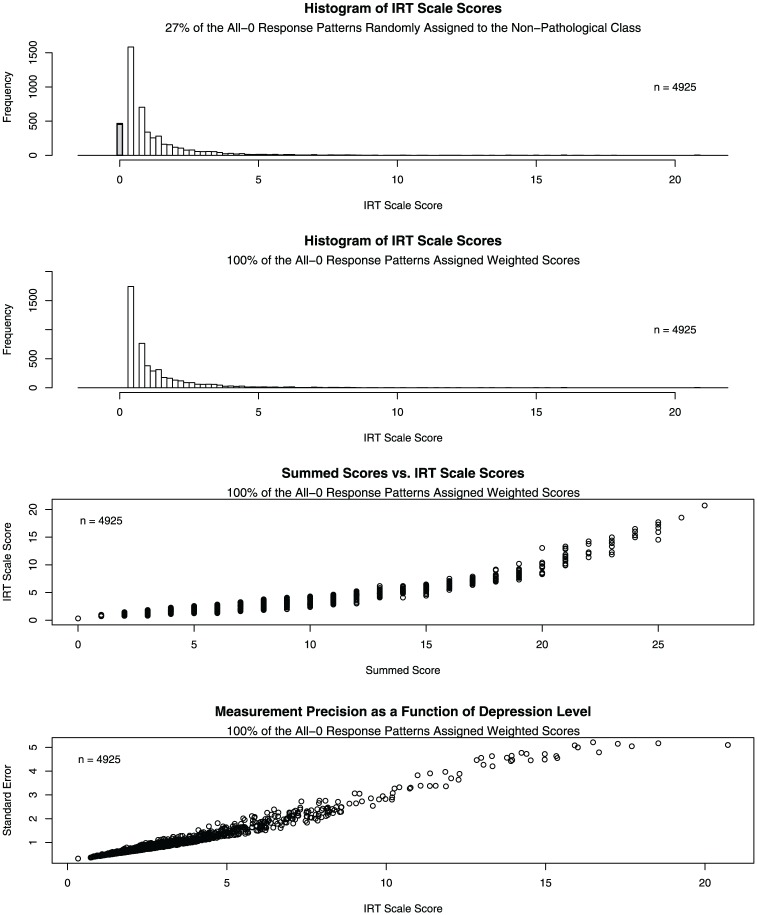
Assigning scores to individuals with all-0 response patterns is less straightforward. Unlike response patterns that include the endorsement of at least one symptom, which must belong to the pathological class, without additional data or covariates, all-0 response patterns cannot be directly classified at the individual level. If the goal is to simply identify the distribution of scores at the population level and not to assign scores to individual respondents, one option is to assign a score of 0 to 27% ($n=468$) of the all-0 response patterns and score the remaining 73% ($n=1,273$) of all-0 response patterns according to the zero-inflated log-logistic UIRM as shown in Equations 9 and 10. The results of this scoring approach are shown in the upper panel of Figure 4, where the gray histobar at ${\hat{\theta }}_{\mathrm{EAP}}=0$ represents 27% of the randomly selected all-0 response patterns classified as nonpathological, and thus, are thought to be at risk but absent on depression. The histobar to its immediate right represents the remaining 73% of all-0 response patterns that belong to people from the pathological class; these individuals have a nonzero scale score of ${\hat{\theta }}_{\mathrm{EAP}}=0.45$. Importantly, these are individuals who are believed to have some degree of depression to which the measure is not sensitive, perhaps because of the response options or the items themselves. For example, someone might select “not at all” not because they never experience the symptom, but because the next response category (“several days”) seems too extreme. Although randomly assigning some proportion of the all-0 response patterns to each class can provide information about the shape of the population-level distribution of scores (i.e., 9.5% of respondents belong to the nonpathological class), this scoring approach is unlikely to be satisfactory for clinicians who are concerned with assigning scores to individuals.

Figure 4.

IRT scale scores and summed scores for the PHQ-9

Note. Upper panel: Histogram of IRT scale scores computed from the zero-inflated UIRM with a log-normal prior, where 27% of the all-0 response patterns are randomly assigned to the nonpathological class; gray histobar shows scores for members of the nonpathological class. Second panel: Histogram of IRT scale scores computed from the zero-inflated UIRM with a log-normal prior, where all of the all-0 response patterns are assigned a weighted score based on the probability of class membership. Third panel: IRT scale scores as a function of summed scores. Lower panel: Posterior standard deviations (standard errors) as a function of IRT scale scores. IRT = item response theory; UIRM = unipolar item response models.

A second scoring approach is to use a posterior modal classifier to assign each of the all-0 response patterns to the latent class with the highest posterior probability. In the present case, the only information available to determine the posterior probability is the response pattern; thus, the posterior probability of belonging to the nonpathological class is 27% for everybody with an all-0 response pattern. Accordingly, 100% of the all-0 response patterns would be classified as pathological and receive scores based on the log-logistic UIRM. Unlike the previous scoring method, this approach does not require the random assignment of 73% of the all-0 response patterns to the pathological class; however, posterior modal classification is likely better suited for cases in which covariates are available to further differentiate the posterior probabilities among people with all-0 response patterns. For this reason, a third scoring method that does not require the assignment of all-0 response patterns to a latent class is proposed. The remainder of score interpretation is based on this alternative scoring method.

In the absence of additional data that may be able to differentiate all-0 response patterns belonging to members of the nonpathological class from those belonging to members of the pathological class, an alternative approach to scoring is to compute a weighted score for the all-0 response patterns that is based on the conditional probability of belonging to each class. Given that one has an all-0 response pattern, the probability of belonging to the pathological class is approximately 0.731. Thus, the expected scale score for an all-0 response pattern can be obtained by weighting the ${\hat{\theta }}_{\mathrm{EAP}}$ from each class by the probability of being in that class, conditional on having an all-0 response pattern:

$$\begin{array}{c}E(\theta |\mathit{U}=0)=E[E(\theta |\mathit{U}=0,I_p)|\mathit{U}=0]\hfill \\ =E(\theta |\mathit{U}=0,I_p=1)P(I_p=1|\mathit{U}=0)+E(\theta |\mathit{U}=0,I_p=0)P(I_p=0|\mathit{U}=0)\hfill \\ =(0.452)(0.731)+\left(0\right)(0.269)=0.329.\hfill \end{array}$$

A similar method can be used to derive the weighted posterior standard deviation for an all-0 response pattern:

$$\begin{array}{c}\mathrm{Var}(\theta |\mathit{U}=0)=E\left[\mathrm{Var}(\theta |\mathit{U}=0,I_p)\right]+\mathrm{Var}\left[E(\theta |\mathit{U}=0,I_p)\right]\hfill \\ \multicolumn{1}{c}{=\mathrm{Var}(\theta |\mathit{U}=0,I_p=1)P(I_p=1|\mathit{U}=0)}\\ \multicolumn{1}{c}{+\mathrm{Var}(\theta |\mathit{U}=0,I_p=0)P(I_p=0|\mathit{U}=0)}\\ \multicolumn{1}{c}{+{[E(\theta |\mathit{U}=0,I_p=1)-E(\theta |\mathit{U}=0)]}^{2}P(I_p=1|\mathit{U}=0)}\\ \multicolumn{1}{c}{+{[E(\theta |\mathit{U}=0,I_p=0)-E(\theta |\mathit{U}=0)]}^{2}P(I_p=0|\mathit{U}=0)}\\ \multicolumn{1}{c}{=(0.082)(0.731)+\left(0\right)(0.269)+{(0.452-0.329)}^2(0.731)+{(0-0.329)}^2(0.269)}\\ \multicolumn{1}{c}{=0.100.}\end{array}$$

According to the combined scoring approach, all-0 response patterns receive a scale score of ${\hat{\theta }}_{\mathrm{EAP}}=0.33$ with a posterior standard deviation of $\sqrt{0.10}=0.32$. These scale scores are shown in the second panel of Figure 4, with scores ranging from 0.33 to 20.72. The most common scale score is ${\hat{\theta }}_{\mathrm{EAP}}=0.33$; this is the depression level of people who endorse “not at all” for all nine items, regardless of whether they belong to the pathological or nonpathological class. This value can be viewed as a reasonable estimate of the depression scale score for someone with an all-0 response pattern when there is no additional information available. Even those who do not endorse any of the symptoms are viewed as at risk of depression; thus, everyone receives a scale score. In other data applications, this value may shift closer to or further from zero, depending on the item parameters and the proportion of people estimated to belong to the nonpathological class: If the proportion of individuals belonging to the nonpathological class is higher, the expected scale score for all-0 response patterns will move closer to zero. Of the people in the pathological class who endorse at least one symptom, the most common scale score is ${\hat{\theta }}_{\mathrm{EAP}}=0.76$. This score comprises those who endorsed “not at all” for all of the items except the one about fatigue (i4), for which they endorsed “several days.” Due to the multiplicative and absolute zero characteristics of the log-logistic model, scale scores can be interpreted with ratio properties. For example, someone who endorsed “several days” for little interest (i1), fatigue (i4), and feeling bad (i6) (${\hat{\theta }}_{\mathrm{EAP}}=1.60$) can be said to have nearly twice the level of depression as someone who endorsed “several days” only for fatigue (i4) (${\hat{\theta }}_{\mathrm{EAP}}=0.85$).

The third panel of Figure 4 shows the relationship between summed scores and IRT scale scores for all respondents, regardless of latent class membership. With the exception of people who respond to every item with “nearly every day,” there is substantial variability in the scale scores that correspond to each possible summed score. This is an advantage of using scale scores over summed scores: Even individuals with the same summed score may have different levels of depression. As summed scores increase, IRT scale scores tend to spread out, suggesting that scores from the UIRM are better able to differentiate among individuals who are high on the psychopathology.

The lower panel of Figure 4 shows standard errors as a function of scale scores for all respondents, where the standard error corresponding to the minimal scale score was computed as shown in Equation 12. In general, scores lose precision as depression levels increase. This feature is in contrast to what is typically found in fitting conventional IRT models, where scale scores near item location parameters tend to be estimated with the greatest degree of precision. Although the UIRM allows for better separation of individuals who are high on the latent variable, there is also greater uncertainty associated with these individuals’ scores.

Discussion and Conclusion

This research introduces a novel approach for modeling zero-inflated data that arise from potentially unipolar clinical constructs by combining two different methodologies: Lucke’s log-logistic UIRM for measuring unipolar constructs and a latent class IRT model that can account for population heterogeneity—that is, a nonpathological class. In addition to generalizing Lucke’s log-logistic UIRM to polytomous item responses, the model is further extended by using a Box-Cox normal prior to empirically determine a transformation parameter to describe the latent variable distribution in the population. The estimate of the Box-Cox parameter can provide support for use of the log-normal distribution, as shown in the present study, or it can suggest an alternative transformation. In either case, it is helpful in choosing an appropriate prior for the UIRM. Finally, as shown here, model parameters can be estimated within a maximum likelihood framework in addition to a Bayesian framework (Lucke, 2014, 2015).

Unipolar models may be inherently appropriate for measuring latent variables that are believed to have a natural zero point, which often coincides with zero inflation, but the results of this study suggest that a zero-inflated component is also needed to account for all of the people who do not endorse any of the psychopathology symptoms. Including a nonpathological class not only improves model fit, but it is substantively justified. When administering a psychopathology questionnaire to a nonclinical sample, it is likely that some respondents are absent on the construct that is being measured (Reise & Rodriguez, 2016; Wall et al., 2015). Thus, it is reasonable to treat these individuals as belonging to a qualitatively different class from those who do have some level of depression but do not endorse any of the symptoms. Rather than assigning individuals from the nonpathological class an arbitrarily large negative value of $\theta$ (e.g., ${\theta }_{\mathrm{EAP}}=-100$), or not assigning them a score at all, they are assigned a score of 0. A score of 0 is particularly meaningful in the UIRM framework because unlike the bipolar traits that are assumed in conventional IRT models, unipolar traits have a true zero point on the latent variable scale; nonzero scores can then be interpreted as some amount of depression relative to no depression.

One of the advantages of the proposed model is that the proportion of people who belong to the nonpathological class is estimated from the model; however, one of the disadvantages of the model is that without additional data, it is not possible to identify which all-0 response patterns belong to members of the nonpathological class. If a researcher is interested in scores only at the population level, this is not necessarily a problem. If a clinician wishes to score and diagnose individuals as being pathological or nonpathological, however, it is impossible to determine which score to assign to individuals with all-0 response patterns. A partial solution is offered by assigning these individuals a scale score that is a weighted average of the ${\hat{\theta }}_{\mathrm{EAP}}$ scores associated with (a) an all-0 response pattern from the nonpathological class, and (b) an all-0 response pattern from the pathological class. In the absence of any other person-level information, the resulting scale score may serve as a “best guess” of the individual’s true location on depression, because it also takes into account the proportion of the population that is expected to belong to the nonpathological class. A drawback of this scoring approach is that it treats those who really belong to the nonpathological class the same as those who belong to the pathological class; however, it is important to note that this scoring approach still accounts for the existence of a nonpathological class, both through the item parameter estimates and the weighting of scores by latent class probabilities. Ideally, future research could incorporate person-level covariates into an explanatory item response model to determine the posterior probability of being in the nonpathological class for each individual with an all-0 response pattern (de Boeck & Wilson, 2004). Scores could then be assigned based on most likely class membership. This is similar to the posterior modal classification that was previously described, only instead of 100% of the all-0 response patterns having the same posterior probability, posterior probabilities would vary based on the level of the covariate.

Although the primary goal of this study was to demonstrate the feasibility of applying a novel method to the analysis of general unipolar constructs, this research also reveals several features of the PHQ-9 that may be of interest to applied researchers. First, application of the zero-inflated log-logistic UIRM suggests a small number of item bundles. Items can be grouped into bundles according to the location of the latent variable where they are best able to measure individual differences. For example, the items pertaining to sleep and energy levels are better at separating individuals who are low on depression, whereas the item about thoughts of self-harm or suicide is most relevant at high levels of depression. Results also suggest that when respondents are asked to report symptom frequencies over a 14-day period, the “several days” and “more than half the days” response categories are largely indistinguishable. Thus, researchers may wish to consider combining these response categories before administering instruments with a similar recall period.

In this case, it is noted that the decision to use a unipolar model is based on a theoretical justification rather than an empirical one. Because the zero-inflated log-logistic UIRM proposed here is simply a transformation of a zero-inflated GRM that assumes a bipolar latent variable, statistical evidence is unable to support one model over the other: The model log-likelihoods are identical. However, the unipolar framework may be more conceptually appealing in measuring constructs such as depression because of its absolute zero point on the latent variable scale. Depression can arguably be viewed as a unipolar trait because, unlike other constructs, it is possible to possess no level of the psychopathology. Others have similarly argued that because the opposite of depression may be the absence of depression rather than happiness, it is reasonable to consider depression as a unipolar trait (Reise & Rodriguez, 2016; Reise & Waller, 2009). Lucke (2014, 2015) advocates for the use of substantive theory in guiding one’s decision about whether a trait is unipolar, suggesting that treating a trait as unipolar is justified in cases where there is likely to be a multiplicative effect of the latent variable on symptom manifestation. Finally, it should be noted that depression may be qualitatively different from other potentially unipolar constructs of psychopathology where some people are not at risk because they do not partake in the associated behaviors (e.g., gambling addiction). Further substantive research on the theory of depression may provide more compelling evidence that the treatment of depression as a unipolar construct for which everyone is at risk is warranted.