Significance
Soft materials have been made tough by introducing nanofiller particles, which significantly stiffen and toughen the material. Stiffening is understood, but the reason for the toughening is not. We have developed a model system of molecular composites where the filler is a continuous network embedded into a stretchy matrix. By combining design of networks, mechanical testing in the nonlinear regime, and incorporation of mechanophore molecules as cross-linkers, we demonstrate how the composites can stiffen at a desired level of extension; soften by breaking bonds in the stiff filler network; and, for certain compositions, resist crack propagation by transferring stress to the stretchy matrix network. Macroscopic and molecular insight provides a detailed picture of how failure occurs in complex soft materials.
Keywords: elastomer, mechanical properties, composite, network, polymer
Abstract
A classic paradigm of soft and extensible polymer materials is the difficulty of combining reversible elasticity with high fracture toughness, in particular for moduli above 1 MPa. Our recent discovery of multiple network acrylic elastomers opened a pathway to obtain precisely such a combination. We show here that they can be seen as true molecular composites with a well–cross-linked network acting as a percolating filler embedded in an extensible matrix, so that the stress–strain curves of a family of molecular composite materials made with different volume fractions of the same cross-linked network can be renormalized into a master curve. For low volume fractions (<3%) of cross-linked network, we demonstrate with mechanoluminescence experiments that the elastomer undergoes a strong localized softening due to scission of covalent bonds followed by a stable necking process, a phenomenon never observed before in elastomers. The quantification of the emitted luminescence shows that the damage in the material occurs in two steps, with a first step where random bond breakage occurs in the material accompanied by a moderate level of dissipated energy and a second step where a moderate level of more localized bond scission leads to a much larger level of dissipated energy. This combined use of mechanical macroscopic testing and molecular bond scission data provides unprecedented insight on how tough soft materials can damage and fail.
Soft materials are irreplaceable whenever large reversible deformations are needed and find widespread classical applications in engineering (1) and new ones in emerging fields such as soft robotics (2) and wearable electronics (3) and in the biomedical field where flexible and tough hydrogels appear very promising (4–6). However, an important limitation is the difficulty to combine fully reversible elasticity with high fracture toughness particularly for high-modulus unfilled elastomers (7, 8). Strategies have been used in the past to address this problem such as elastomers with short and long chains (9) or double-network elastomers made by imparting a second cross-linking to a lightly cross-linked elastomer in its stretched state (10, 11). However, for a noncrystallizable rubber this strategy does not really improve toughness significantly.
We demonstrated recently that such combination of properties can be obtained with multiple network elastomers where a well–cross-linked network is first swollen in monomer and subsequently polymerized to create a so-called double network (DN) (12–14). If the swelling and polymerization operation is repeated on the DN, one obtains a triple network (TN) displaying considerable toughness, attributed to a mechanism of internal damage dissipating energy and delaying crack propagation (14). Such a mechanism of strain-dependent damage has been also incorporated in recent phenomenological models (15–17). However, many questions remain on the structural requirements to obtain this remarkable combination of properties, and the purpose of this paper is to generalize the approach and demonstrate that this new class of elastomeric materials, inspired by hydrogels (18, 19), can be seen as a molecular version of the classical laminated or fabric composites made by imbibing stiff carbon or aramid fiber fabrics with a polymerizable epoxy resin (20). In the macroscopic composite, elastic properties are mainly controlled by the fibers, whereas in the multiple network elastomer they are mainly controlled by the first network.
The network synthesized first [referred to as SN in our first work (14)] can be seen as a continuous filler (like the fabric of the classical composite), and we will refer to it as “filler network.” The networks polymerized in steps 2, 3 (DN and TN in ref. 14), or more will be called matrix networks. Exploring a variety of intermediate degrees of swelling and one to three swelling steps, we show that the elastic properties of the composite network can be mainly described by two parameters: the maximum extensibility of the strands of the filler network and the fraction of that extensibility that is used in the swelling steps. We further demonstrate with mechanoluminescent molecules that localized (as opposed to random) bond breaking in the first network results in a stable necking process in an elastomer where both necked and unnecked regions coexist and display reversible rubber elasticity with different elastic constants.
Nonlinear Elasticity
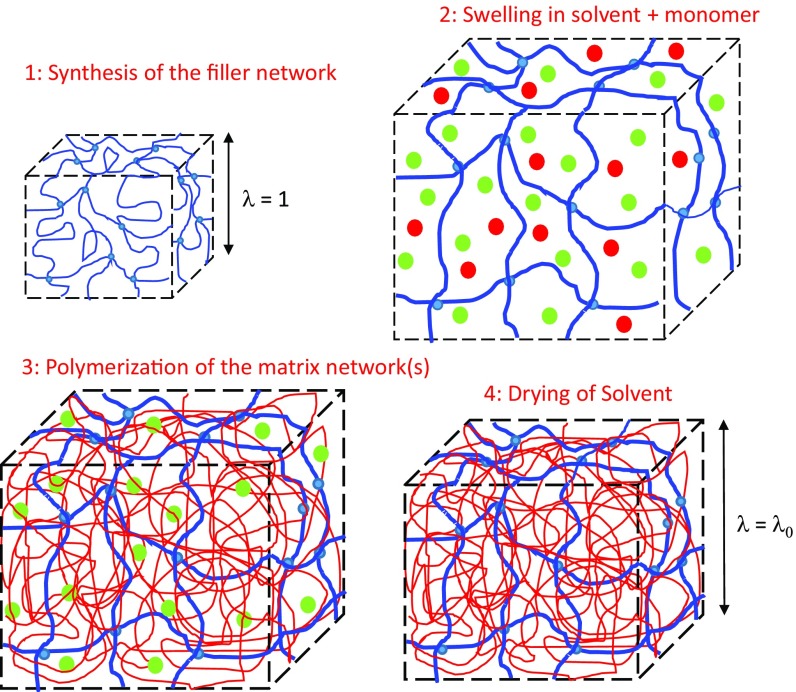
Fig. 1 describes schematically the synthesis of the molecular composite network by successive swelling and polymerization steps to create samples with increasing prestretching states and decreasing volume fractions of the filler network. The details of the synthesis and the exact composition of each material used here are reported in Materials and Methods and in SI Appendix, section S1 and Table S1. Because the filler network is much more cross-linked than the matrix networks that are synthesized during the subsequent swelling and polymerization steps, the composite network can be more accurately described by the degree of isotropic prestretching λ0 of the filler network strands than by the number of polymerization steps. An example of the tensile properties of two composite networks obtained from the same filler network stretched to the same degree λ0 but with a different number of steps is given in SI Appendix, Fig. S1, and the difference is within experimental error. The list of samples made from the same filler network but with different values of λ0 varying from 1 to 3.42 is shown in Table 1. For simplicity, samples will then be referred to as EA(λ0), where the first EA refers to the monomer used for the filler network. Although other monomers can be used (12), EA was the only monomer used for the matrix network(s) in this work. When the prestretching of the filler network λ0 changes, so does its volume fraction . Those two parameters are related by the relationship shown in Eq. 1.
| [1] |
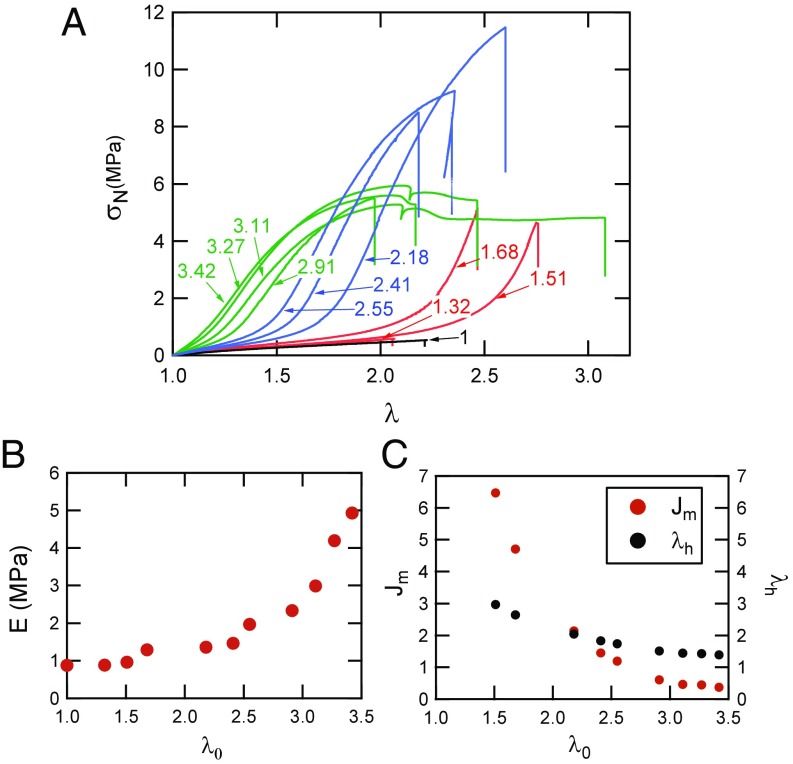
Every sample was cut in a dumbbell shape, and a uniaxial tensile test was performed. The results of the uniaxial tests to fracture at a constant stretch rate = 0.02 s−1 are displayed in Fig. 2A, where σN is the nominal stress and λ is the stretch. The degree of isotropic prestretching of the filler network indicated in the figure varies from a starting value of λ0 = 1 for the brittle standalone unstretched filler network to λ0 = 3.42 for a composite network containing less than 3 wt % of the highly stretched filler network. It is clear from the data that the qualitative behavior of the molecular composites changes significantly as the filler network is being progressively diluted and prestretched.
Fig. 1.
Synthesis of multiple networks with intermediate value of the prestretching λ0. Red dots, EA monomer; green dots, ethyl acetate; blue network, filler network; red network, matrix network.
Table 1.
List of samples synthesized with varying values of λ0 and volume fraction of filler network in the molecular composite
| Sample name | λ0 | Filler, wt % | No. of swelling/polymerization steps |
| EA(1) | 1 | 100 | 1 |
| EA(1.32) | 1.32 | 42.0 | 2 |
| EA(1.51) | 1.51 | 29.2 | 2 |
| EA(1.68) | 1.68 | 20.5 | 2 |
| EA(2.18) | 2.18 | 9.52 | 3 |
| EA(2.41) | 2.41 | 7.39 | 3 |
| EA(2.55) | 2.55 | 6.06 | 3 |
| EA(2.91) | 2.91 | 4.19 | 4 |
| EA(3.11) | 3.11 | 3.53 | 4 |
| EA(3.27) | 3.27 | 3.28 | 4 |
| EA(3.42) | 3.42 | 2.88 | 4 |
The last column shows the number of polymerization steps.
Fig. 2.
(A) Stress–strain curves of different composites EA (λ0) made from the same filler network. The value of λ0 is shown in the labels attached to each curve. The color corresponds to the number of polymerization steps: black, one; red, two; blue, three; and green, four. = 0.021 s−1 for all tests. (B) Young’s modulus as a function of the degree of prestretching λ0 of the filler network. (C) Evolution of Jm and λh obtained from the best fit to the Gent model as a function of λ0.
The Young’s modulus E of the material increases nonlinearly with λ0, as shown in Fig. 2B with a clear change of slope when λ0 reaches the value of 2.5–3. Fig. 2A also shows that λ0 has a very strong influence on the onset of strain hardening, and the initial portion of each curve shown in Fig. 2A can be fitted with an empirical constitutive model proposed by Gent (21) that specifically includes strain hardening. In uniaxial tension the nominal stress is given by
| [2] |
where in uniaxial tension and is the maximum admissible value of . This model was used to fit each stress–strain curve in Fig. 2A, and an example of the quality of the fit is shown in SI Appendix, Fig. S2. E, Jm, and hence λh, defined as the value of λ corresponding to J1 = Jm in uniaxial extension, were obtained for each curve. As shown in Fig. 2C, both Jm and λh decrease with increasing λ0; that is, the material becomes less extensible as the filler network is more prestretched.
For this set of samples, the filler network has been kept strictly identical so that the intrinsic average maximum elongation of its strands should be the same for every composite network. The theoretical value of this maximum elongation λlimit can be estimated from the cross-linking and trapped entanglement contribution to the elastic modulus, as obtained from the minimum in Mooney stress (22) as shown in SI Appendix, Fig. S3. For the filler network the cross-linking contribution to the tensile modulus is 0.76 MPa. The average molar mass between cross-links can then be obtained by using the affine network model of rubber elasticity (23), leading to (see SI Appendix for details), which can be compared with the experimental value of the maximum stretchability of the composite networks obtained by fitting the uniaxial extension data with Eq. 2. For multiple networks, where chains of the filler network are isotropically prestretched at λ0, we define the product λ0λh as the maximum experimental extensibility of the filler network due to the combined effect of swelling and uniaxial extension. The product λ0λh is relatively constant and around 4.5, only slightly higher than the theoretical limiting chain stretch λlimit (SI Appendix, Fig. S4). Because λ0 corresponds to triaxial deformation and λh corresponds to uniaxial deformation, this result implies that the strain hardening is controlled only by the few chains of the filler network oriented in the direction of the uniaxial deformation. Coming now back to Fig. 2B, the sharp upturn of the small strain modulus at high values of λ0 can be explained by the onset of the finite extensibility of the filler network chains. A value of λ0 ∼ 2.5 corresponds to about 55% of the experimental limiting chain stretch λ0λh, a regime where Gaussian elasticity breaks down and finite chain extensibility described by the Langevin relation becomes dominant (24).
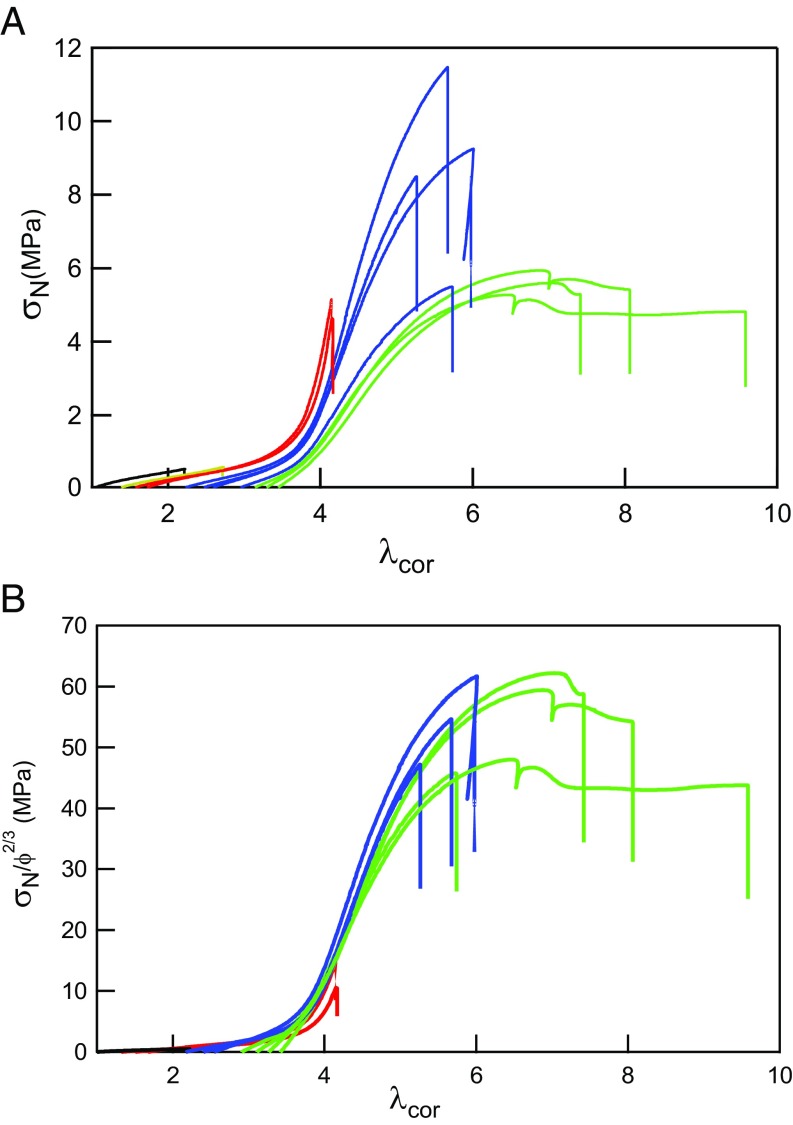
If the strain hardening is mainly controlled by the extension level of the filler network, it should be possible to create a master curve of the elastic behavior by rescaling and . For the renormalized stretch we can define corresponding to the actual stretch seen by the filler network strands (14), and the nominal stress can be renormalized by the areal density of filler strands ΣFN crossing the plane normal to the tensile direction. As the volume density of strands of the filler network is diluted by during the swelling and polymerization steps, ΣFN = for each multiple network. Fig. 3A shows the nominal stress as a function of the elongation of the filler network , whereas Fig. 3B shows the normalized stress as a function of . This renormalized representation of the stress and strain shows that the strain hardening kicks in at a common value for the whole set of materials made from the same filler network and that the correction of the nominal stress by the areal density of filler network strands gives a good master curve for the large strain part of the curves. The successful rescaling of Fig. 2A into Fig. 3B is consistent with a recently developed mechanical model of double and multinetwork elastomers (17). Nevertheless, it should be noted that the existence (or not) of a softening stage before fracture is not described by the dilution factor alone and requires further analysis. In particular, the simplified description of the multiple networks as a composite ignores the connectivity between the networks. Because the synthesis is carried out by free radical polymerization in the bulk, there will be some chain transfer to the polymer by hydrogen abstraction (25), and there will be some sparse covalent bonds connecting the networks together.
Fig. 3.
(A) Nominal stress σN as a function of λcor for the stress–strain curves of Fig. 2A. (B) Nominal stress renormalized by ϕ2/3 as a function of λcor for the stress–strain curves of Fig. 2A. In both figures the color corresponds to the number of polymerization steps: black, one; red, two; blue, three; and green, four. = 0.021 s−1 for all tests. = 0.021 s−1.
Softening and Damage Process
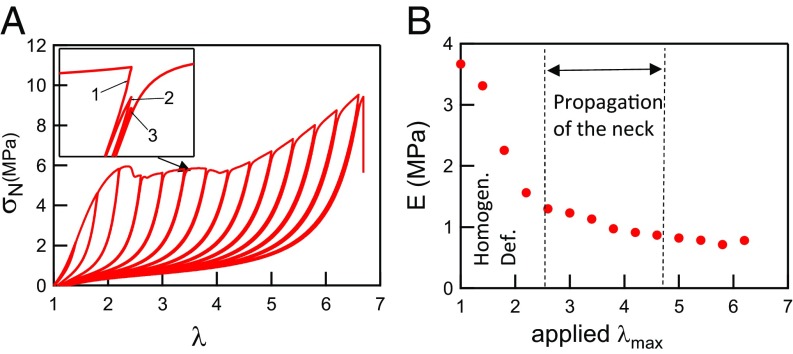
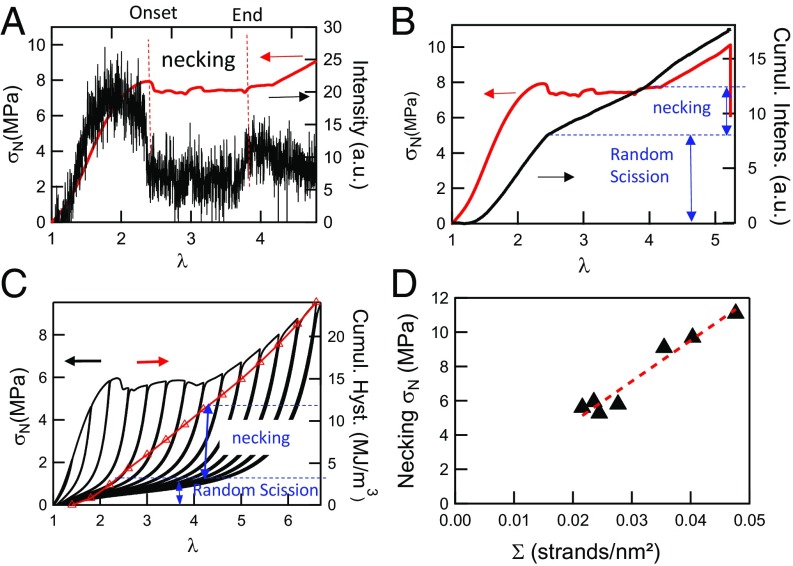
One of the most interesting results shown in Fig. 2A is the occurrence for certain sample compositions (very high λ0) of a plateau in nominal stress. This specific behavior, observed in double network hydrogels (26) and due to a necking phenomenon, has never been observed in elastomers. To better grasp the mechanism, it is first important to look at its reversibility. Fig. 4A shows a step-cycle experiment with increasing strain amplitude (three cycles have been carried out for each incremental value of λ) carried out on a highly prestretched material (λ0 = 3.42). A hysteresis starts to appear at λ ∼ 1.3. Then the nominal stress shows a plateau, and the hysteresis continues to increase after the beginning of the plateau (λ = 2.2). Finally, the nominal stress increases again and the sample fails. Two important points should be noted: first, after a cycle to a higher extension that causes some damage, the material always remains nearly fully elastic in the subsequent loading unloading cycles to the same extension (Fig. 4A, Inset), and second, the initial modulus E starts to decrease sharply before the point where the nominal stress becomes constant as shown in Fig. 4B. In the region where the nominal stress is constant (2.5 < λ < 4), the sample is split into two rubber elastic domains with different nonlinear elastic properties, an unnecked domain where the elongation is λ ∼ 2.5 and a highly damaged domain, where the elongation is λ ∼ 4. Both regions coexist at the same level of nominal stress, i.e., the same force. Images of the necked regions are shown in SI Appendix, Fig. S5.
Fig. 4.
(A) Step-cycle tensile experiment at = 0.020 s−1 carried out on EA(3.42) showing a large hysteresis and a second hardening for λ > 4. Three cycles are carried out at each incremental value of λ. (B) Evolution of the normalized Young’s modulus with the maximum deformation.
To visualize directly whether bond scission occurs during the necking process, we synthesized a sample containing mechanoluminescent molecules as cross-linker of the filler network. These molecules, based on bis-adamantane dioxetane, need to be specifically synthesized (27), and the procedure is detailed in SI Appendix. They emit light when the dioxetane cycle is broken and hence report chain scission (14, 28). This labeled sample was tested in uniaxial tension, and the results of this experiment are shown in Figs. 5 and 6.
Fig. 5.
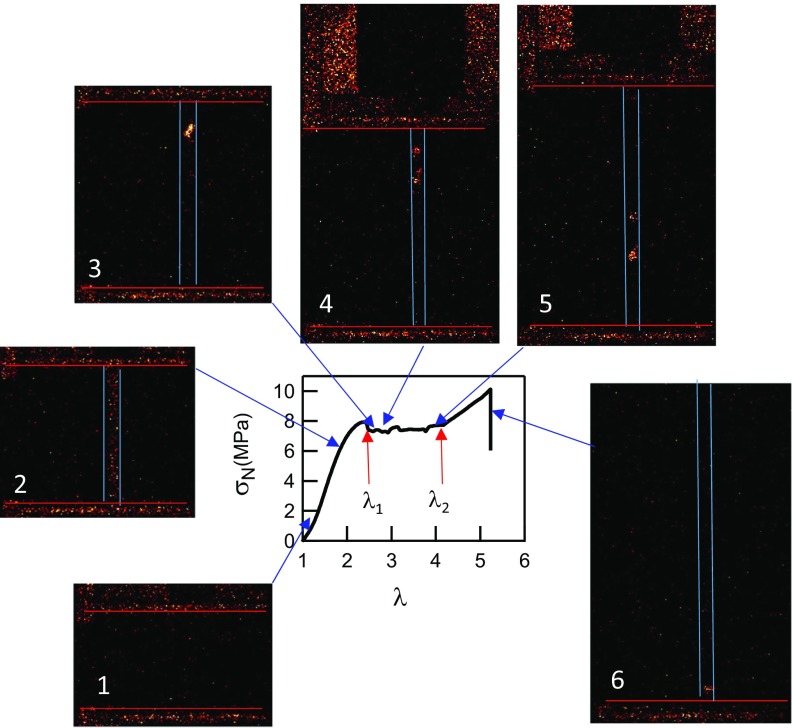
Stress–strain curve of the sample EA(d20)0.73(2.94)EA. The signal was obtained while images were recorded. Images showing the mechanoluminescent signal of the sample EA(d20)0.73(2.94)EA. Red horizontal lines correspond to the position of the clamps and the two blue vertical lines in panels 2–6 represent the position of the sample. The numbers are referring to the state of stress and strain of the sample when the signal is recorded. The color scale represents the count that can be compared between each picture, but its unit is arbitrary.
Fig. 6.
(A) Stress–strain curve (red line) and intensity of the mechanoluminescent signal (black line) as a function stretch for the sample EA(d20)0.73(2.94). (B) Cumulated intensity (black line) of the mechanoluminescent signal and nominal stress (red line) as a function of λ. (C) Cumulated mechanical hysteresis (red symbols) and nominal stress (black line) in a cyclic test carried out on the EA1.45(3.42) as a function of λ, along with the nominal stress. (D) Evolution of the necking stress as a function of the filler network’s areal density of strands.
The sample starts necking at a maximum in nominal stress, then the nominal stress remains constant while the necked region propagates, and finally, σN increases again. Although this labeled sample is slightly different from the one presented in Fig. 4, the qualitative behavior is exactly the same. The analysis of the different images can be summarized as follows:
At low elongation, no mechanoluminescent signal is detected, and the bond scission, if it occurs, is below the detection limit.
After the inflection point but before the maximum in stress, a homogeneous light signal is observed over the entire sample as also observed by Ducrot et al. (14), and the macroscopic modulus decreases sharply.
At the maximum in nominal stress the signal becomes less intense and is no longer homogeneous over the entire sample. A very localized damage region grows, corresponding to the volume where the necking initiates.
The two necking fronts move in opposite directions, and bond scission is concentrated in the region where the materials transition from λ = λ1 to λ = λ2. No light is detected over the rest of the sample.
The upper necking front has been stopped by the wider zone of the dumbbell, and the front moving down has probably been stopped by a heterogeneity (corresponding to the slight increase of stress shown at λ = 3). Following this, a new necked area is nucleated in the lower part of the sample, and the two new fronts are visible on the lower part of the sample.
When λ > 4.2, the necking has expanded over all of the central zone of the sample. Bond scission can be only seen in the bottom part (note that the top grip and the top part of the sample are now out of the field of view of the camera).
To complete the analysis of the phenomenon, the spatially averaged intensity of the signal was quantified as a function of stretch. Details of the image analysis method can be found in SI Appendix. As shown in Fig. 6A, the intensity emitted by the sample increased sharply at the onset of strain hardening (λ = 1.4), until it reached a plateau value. Following this plateau the intensity dropped when the actual necking started reflecting the localization of the bond scission in an active zone [a similar localization to that which occurs during the formation of crazes in glassy polymers (29)]. During the propagation of the necking fronts observed in the images of Fig. 5, the total signal appears to be relatively constant. The intensity of the light signal shown in Fig. 6A can be integrated for each image (for the same sample volume) to obtain the cumulated signal in Fig. 6B. In our previous work (14) we found a power-law relation between the cumulated intensity of the light emission and the cumulated mechanical hysteresis. Although we do not have the hysteresis and light emission data for exactly the same sample, we can still compare qualitatively both phenomena by examining the hysteresis measured as a function of λ for a very similar sample to that tested in Fig. 4A as a function of λ. Comparing Fig. 6 B and C, it is obvious that the damage in the material occurs in two stages: in a first stage, there is significant random bond scission in the material with a relatively modest energy loss by mechanical hysteresis, whereas in a second stage the necking triggers localized bond scission, which in turn causes significant mechanical hysteresis.
Molecular Fracture Criterion for the Necking
Because we demonstrated that the necking process was related to bond scission in the filler network, the value of the maximum nominal stress at the onset of necking should be linked to the nominal areal density of filler network strands crossing the fracture plane. The areal chain density inside a simple network can be calculated with some assumptions (30, 31). If the cross-linking is random and has a functionality of four, the areal chain density of the filler network ΣFN0 can be estimated using Eq. 3 with ν the number of cross-linking points per unit volume and the average distance between cross-links. From Gaussian statistics, we can then obtain Eq. 4, where all parameters are independently known: is the length of a C–C bond (1.54 Å), EFN0 is the tensile modulus of the filler network, C∞ is the polymer characteristic ratio, and Nx is the number of carbon bonds between cross-link points estimated previously. When the filler network is swollen with monomer during the multiple steps of polymerization, the initial surface chain density is diluted as described in Eq. 5, so that the filler network areal chain density can be estimated for our entire set of samples.
| [3] |
| [4] |
| [5] |
Fig. 6D plots the measured values of the nominal necking stress as a function of ΣFN, the filler network’s areal strand density calculated based on Eqs. 4 and 5, and the results are consistent with the prediction. Details of the determination of the necking stress are in SI Appendix, and an example is shown in SI Appendix, Fig. S6. The best fit of the experimental points shows that the intercept is very close to the origin. However, the slope of the curve is 0.24 nN per strand, which is roughly a tenth of the breakage strength of a C–C bond (32), a very similar value to that found by Matsuda et al. (33) for double-network gels. This is consistent with the results of Figs. 5 and 6 and suggests that the necking process is due to the presence of stress concentrations in the material leading to a localized failure of filler network bonds such as the microcracks proposed by Brown (34).
The results reported here paint a specific picture of the structure of these multiple-network elastomers. For the whole family of materials made from the same filler network the mechanical properties are highly nonlinear and transition from a behavior dominated by the total density of elastic strands per unit volume (in the Gaussian regime where matrix and filler are not highly stretched) to the areal density of the strands of the filler network alone and their Langevin elasticity in the chain stretching regime. At high strain, the topology of the network (i.e., how the strands are connected together) becomes increasingly important. In that sense they can be seen as molecular composites with a behavior dominated by the extensible matrix in small strain and by the stiff continuous filler network in large strain.
A key property of this set of materials is their fracture toughness, which becomes progressively much higher than that of the single network [compare the stress and strain at break of material EA(2.55) with that of EA(1)]. This improvement depends not only on the elastic properties but also, and mainly, on the way the damaged structure resists crack propagation as just discussed.
Role of the Matrix in the Toughening
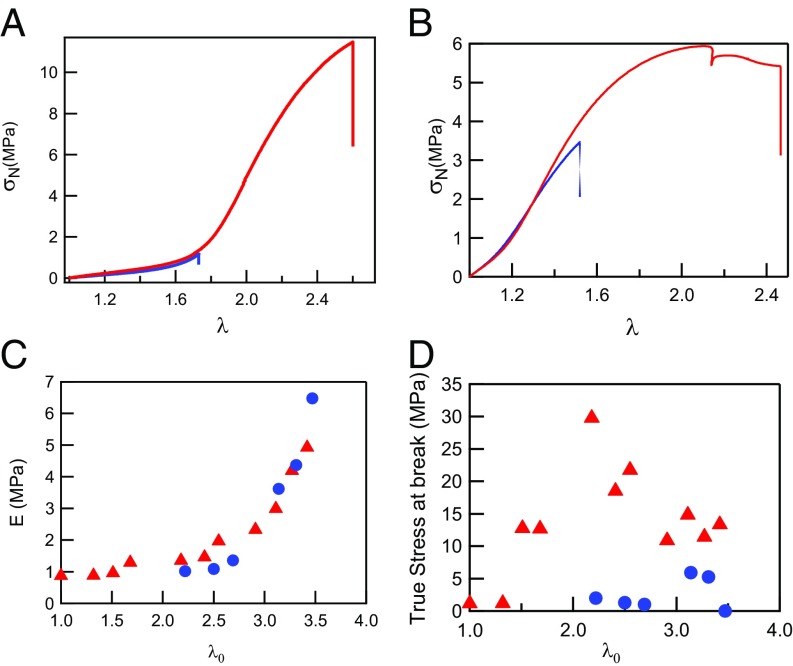
It is therefore interesting to investigate the role played by the matrix network in the increase in toughness and in the necking process. To probe that effect we have prepared two sets of samples (detailed composition of the samples is described in SI Appendix, Table S3) with nearly identical values of λ0 but where the last polymerization step was replaced by a simple swelling with a solvent. Fig. 7A shows the comparison between EA(1.68) swollen by dimethylsulfoxyde (DMSO) to λ0 ∼ 2.2 and the same network swollen by a monomer solution and polymerized to the same value of λ0. Fig. 7B shows the same comparison but for EA(2.53) swollen by 1-methyl-2-pyrrolidone (MPD) to λ0 ∼ 3.3 and its polymerized counterpart. More examples are shown in SI Appendix, Figs. S7 and S8.
Fig. 7.
(A) Stress–strain curves of EA(1.68) swollen by DMSO to λ0 = 2.22 (blue line) in comparison with EA(2.18), a fully polymerized sample with a similar prestretching (red line). = 0.021 s−1. (B) Stress–strain curves of EA(2.53) swollen by MPD to λ0 = 3.31 (blue line) in comparison with EA(3.27), a fully polymerized sample with a similar prestretching (red line). = 0.021 s−1. (C) Evolution of the modulus as a function of λ0 for standard samples (red triangles) and for samples partially swollen in solvent (blue circles). (D) True stress at break as a function of λ0 for standard samples (red triangles) and for samples partially swollen in solvent (blue circles).
If one compares a set of materials prepared with different values of λ0 but where the last step has been either solvent swelling or monomer swelling and polymerization, the moduli of both sets of materials is nearly identical (Fig. 7C), and the Gent fit to the strain hardening gives nearly the same best fit value for the fully polymerized sample and for the solvent swollen one (SI Appendix, Fig. S9). However, if one compares the true stress at break (Fig. 7D), the difference is obvious and particularly significant for the samples with 2 < λ0 < 3. At high values of λ0, the influence of the solvent on Young’s modulus and onset of strain hardening appears to be negligible, suggesting that in this regime the elastic properties are controlled by the highly diluted chains of the filler network alone. However, the strength and fracture resistance of the molecular composite is clearly due to the synergy between the unbroken filler network providing stiffness at low strain and the softened filler network and matrix network, which provides entanglements and a strain hardening mechanism at high strain that may stabilize a necking process and prevent crack propagation once the filler network is strongly softened.
Concluding Remarks
We have shown that multiple network elastomers can be seen in a simplified way as molecular composites with a stiff and continuous internal phase (the filler network), which is synthesized first, and a second phase (the matrix network) that acts as a highly extensible but incompressible matrix. The two important parameters controlling the elastic properties of the composite are the maximum extensibility of the filler network and its volume fraction. The elastic part of the uniaxial stress–strain curve can be represented as a master curve if one assumes that the stress is carried by the chains of the filler network alone. However, as observed for DN gels (33, 35, 36), the stress and strain at break of the material are highly dependent on the presence of the entangled matrix, and ductile behavior is only obtained when the load can be efficiently transferred from the filler network to the matrix network. We have conclusively shown with mechanoluminescent molecules that this process occurs in two steps: first, a random scission of highly loaded bonds in the filler network and then a second step where a more localized failure of bonds (macroscopically and at the molecular level) causes a sharp drop in stiffness. In conventional nanocomposites such as carbon-black filled rubbers (37) the nanofillers form also a percolating network (38). However, this particle-based network is fractal in nature, and damage starts from very low strain involving breakup of connecting bridges between particles and particle reorganization. Therefore, both the strain hardening and the damage is much more progressive than for the continuous filler composites reported here and as a result never leads to necking. Despite this difference, the breakup of the filler network and load transfer to the matrix network may occur at the crack tip in many tough elastomeric materials, and investigating in detail how the load is transferred from the filler network strands to the matrix network maybe highly relevant also for other types of elastomeric composites where an embedded stiff network (continuous or made of filler particles) increases fracture toughness by introducing an internal damage process into an extensible matrix.
Materials and Methods
The filler network was prepared from ethyl acrylate, butanediol bis(acrylate), and a UV initiator. All reagents were dissolved in an approximately equal mass of ethyl acetate, and the UV polymerization was carried out in a glove box inside a closed mold (14). Ethyl acetate was used instead of the previously used toluene (14) to limit chain transfer to the solvent during polymerization. After extracting the unreacted species and solvent and drying the sample, the filler network was swollen to equilibrium in a bath composed of ethyl acrylate monomer, a small amount of cross-linker (0.01 mol % relative to monomer), UV initiator, and 0–75 wt % of solvent (the solvent was not present in our previous work). The swollen piece of network is then taken out of the bath, and a new UV polymerization is carried out in between glass plates. Finally, the sample is fully dried of excess solvent and ready for testing or further swelling. Each polymerization step increases the volume of the sample isotropically and stretches the polymer strands of the filler network.
For the mechanoluminescence experiments we synthesized a filler network containing 0.73 mol % cross-linker, 20% of which was dioxetane. During three subsequent swelling and polymerization steps the matrix was then synthesized to give the material EA(d20)(2.94). Note that no dioxetane cross-linker was used for the matrix synthesis. The initial modulus and λ0 value of that labeled sample was very similar to the materials of Table 1 and Fig. 2A with λ0 ∼ 3. A sample was fixed in the clamps, and the tensile test was carried out while recording some images with a sensitive Andor iXon Ultra 897 EMCCD (electron multiplying charged coupled device) camera at the frame rate of two images taken per second and acquisition settings detailed in SI Appendix.
Supplementary Material
Acknowledgments
We thank the scientific staff at the Materials Science Center of the company Royal DSM for stimulating discussions on multiple networks. We gratefully acknowledge the support of the company Royal DSM for the funding of the PhD work of P.M.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1807750115/-/DCSupplemental.
References
- 1.Gent AN, editor. Engineering with Rubber. Vol 1 Hanser; Munich: 2001. [Google Scholar]
- 2.Martinez RV, Glavan AC, Keplinger C, Oyetibo AI, Whitesides GM. Soft actuators and robots that are resistant to mechanical damage. Adv Funct Mater. 2014;24:3003–3010. [Google Scholar]
- 3.Rogers JA, Someya T, Huang Y. Materials and mechanics for stretchable electronics. Science. 2010;327:1603–1607. doi: 10.1126/science.1182383. [DOI] [PubMed] [Google Scholar]
- 4.Lee KY, Mooney DJ. Hydrogels for tissue engineering. Chem Rev. 2001;101:1869–1879. doi: 10.1021/cr000108x. [DOI] [PubMed] [Google Scholar]
- 5.Minev IR, et al. Biomaterials. Electronic dura mater for long-term multimodal neural interfaces. Science. 2015;347:159–163. doi: 10.1126/science.1260318. [DOI] [PubMed] [Google Scholar]
- 6.Federico C, et al. Standards for dielectric elastomer transducers. Smart Mater Struct. 2015;24:105025. [Google Scholar]
- 7.Creton C. 50th anniversary perspective: Networks and gels: Soft but dynamic and tough. Macromolecules. 2017;50:8297–8316. [Google Scholar]
- 8.Roland CM. Unconventional rubber networks: Circumventing the compromise between stiffness and strength. Rubber Chem Technol. 2013;86:351–366. [Google Scholar]
- 9.Mark JE. Elastomeric networks with bimodal chain-length distributions. Acc Chem Res. 1994;27:271–278. [Google Scholar]
- 10.Mott PH, Roland CM. Mechanical and optical behavior of double network rubbers. Macromolecules. 2000;33:4132–4137. [Google Scholar]
- 11.Shinyoung K, Donghwa G, Changwoon N. Some physical characteristics of double-networked natural rubber. J Appl Polym Sci. 1997;65:917–924. [Google Scholar]
- 12.Ducrot E, Creton C. Characterizing large strain elasticity of brittle elastomeric networks by embedding them in a soft extensible matrix. Adv Funct Mater. 2016;26:2482–2492. [Google Scholar]
- 13.Ducrot E, Montes H, Creton C. Structure of tough multiple network elastomers by small angle neutron scattering. Macromolecules. 2015;48:7945–7952. [Google Scholar]
- 14.Ducrot E, Chen Y, Bulters M, Sijbesma RP, Creton C. Toughening elastomers with sacrificial bonds and watching them break. Science. 2014;344:186–189. doi: 10.1126/science.1248494. [DOI] [PubMed] [Google Scholar]
- 15.Zhao X. A theory for large deformation and damage of interpenetrating polymer networks. J Mech Phys Solids. 2012;60:319–332. [Google Scholar]
- 16.Wang X, Hong W. Pseudo-elasticity of a double network gel. Soft Matter. 2011;7:8576–8581. [Google Scholar]
- 17.Bacca M, Creton C, McMeeking RM. A model for the Mullins effect in multinetwork elastomers. J Appl Mech. 2017;84:121009. [Google Scholar]
- 18.Gong JP, Katsuyama Y, Kurokawa T, Osada Y. Double-network hydrogels with extremely high mechanical strength. Adv Mater. 2003;15:1155–1158. [Google Scholar]
- 19.Gong JP. Why are double network hydrogels so tough? Soft Matter. 2010;6:2583–2590. [Google Scholar]
- 20.Chawla KK. Composite Materials Science and Engineering. Springer; New York: 2012. [Google Scholar]
- 21.Gent AN. A new constitutive relation for rubber. Rubber Chem Technol. 1996;69:59–61. [Google Scholar]
- 22.Creton C, Ciccotti M. Fracture and adhesion of soft materials: A review. Rep Prog Phys. 2016;79:046601. doi: 10.1088/0034-4885/79/4/046601. [DOI] [PubMed] [Google Scholar]
- 23.Treloar LRG. The elasticity and related properties of rubbers. Rep Prog Phys. 1973;36:755–826. [Google Scholar]
- 24.Treloar LRG. The Physics of Rubber Elasticity. 2nd Ed Oxford Univ Press; London: 1958. [Google Scholar]
- 25.Ballard N, Hamzehlou S, Asua JM. Intermolecular transfer to polymer in the radical polymerization of n-butyl acrylate. Macromolecules. 2016;49:5418–5426. [Google Scholar]
- 26.Na YH, et al. Necking phenomenon of double-network gels. Macromolecules. 2006;39:4641–4645. [Google Scholar]
- 27.Chen Y, et al. Mechanically induced chemiluminescence from polymers incorporating a 1,2-dioxetane unit in the main chain. Nat Chem. 2012;4:559–562. doi: 10.1038/nchem.1358. [DOI] [PubMed] [Google Scholar]
- 28.Clough JM, Creton C, Craig SL, Sijbesma RP. Covalent bond scission in the Mullins effect of a filled elastomer: Real-time visualization with mechanoluminescence. Adv Funct Mater. 2016;26:9063–9074. [Google Scholar]
- 29.Miller P, Kramer EJ. Measurements of the craze-bulk interfacial active zone. J Mater Sci. 1991;26:1459–1466. [Google Scholar]
- 30.Miquelard-Garnier G, Hourdet D, Creton C. Large strain behaviour of new hydrophobically modified hydrogels. Polymer (Guildf) 2009;50:481–490. [Google Scholar]
- 31.Miquelard-Garnier G, Creton C, Hourdet D. Strain induced clustering in polyelectrolyte hydrogels. Soft Matter. 2008;4:1011–1023. doi: 10.1039/b717460h. [DOI] [PubMed] [Google Scholar]
- 32.Creton C, Kramer EJ, Brown HR, Hui CY. Adhesion and fracture of interfaces between immiscible polymers: From the molecular to the continuum scale. Adv Polym Sci. 2002;156:53–136. [Google Scholar]
- 33.Matsuda T, et al. Yielding criteria of double network hydrogels. Macromolecules. 2016;49:1865–1872. [Google Scholar]
- 34.Brown HR. A model of the fracture of double network gels. Macromolecules. 2007;40:3815–3818. [Google Scholar]
- 35.Nakajima T, Kurokawa T, Ahmed S, Wu W-l, Gong JP. Characterization of internal fracture process of double network hydrogels under uniaxial elongation. Soft Matter. 2013;9:1955–1966. [Google Scholar]
- 36.Ahmed S, Nakajima T, Kurokawa T, Anamul Haque M, Gong JP. Brittle–ductile transition of double network hydrogels: Mechanical balance of two networks as the key factor. Polymer (Guildf) 2014;55:914–923. [Google Scholar]
- 37.Mzabi S, Berghezan D, Roux S, Hild F, Creton C. A critical local energy release rate criterion for fatigue fracture of elastomers. J Polym Sci Part B Polym Phys. 2011;49:1518–1524. [Google Scholar]
- 38.Heinrich G, Kluppel M. 2002. Recent advances in the theory of filler networking in elastomers. Filled Elastomers Drug Delivery Systems, Advances in Polymer Science (Springer, Berlin), Vol 160, pp 1–44.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.