Abstract
We explored the changes in multi-digit synergies in patients with multiple sclerosis (MS) within the framework of the uncontrolled manifold hypothesis. Our specific hypotheses were that both synergy indices and anticipatory synergy adjustments prior to the initiation of a self-paced quick action would be diminished in the patients compared to age-matched controls. The MS patients and age-matched controls (n = 13 in both groups) performed one-finger and multi-finger force production tasks involving both accurate steady-state force production and quick force pulses. The patients showed significantly lower maximal finger forces and a tendency toward slower force pulses. Enslaving was increased in MS, but only in the “lateral” fingers (index and little). Indices of multi-finger synergies during steady-state force production were lower in MS, mainly due to the lower amount of inter-trial variance that did not affect total force. Anticipatory synergy adjustments were significantly delayed in MS. Our results show that MS leads to significant changes in multi-digit synergies and feed-forward adjustments of the synergies prior to a quick action. We discuss possible contributions of subcortical structures to the impaired synergic control.
Keywords: multiple sclerosis, hand, synergy, anticipatory synergy adjustment
1. Introduction
Many activities of daily living, such as eating, drinking, and brushing teeth rely on hand function. Poor hand performance, in particular in tasks requiring finger coordination, is commonly seen in multiple sclerosis (MS) (Steultjens et al. 2003; Ziemssen 2011). Earlier studies have documented a range of MS effects on finger coordination in a variety of tasks. For example, MS patients show unusually high grip force magnitudes when manipulating a hand-held object (Iyengar et al. 2009) associated with an increase in grip force variability (Marwaha et al. 2006). Such tasks are also associated with poor coordination of the grip and manipulation forces seen in both unimanual (Krishnan and Jaric 2008; Krishnan et al. 2008) and bimanual tasks (Gorniak et al. 2014).
Most of the earlier studies of the hand function in MS focused on the combined action of fingers on the hand-held object (for an exception see Bonzano et al. 2013). In this study, we focus on finger synergies defined as flexible patterns of finger involvement that ensure controlled stability of performance in multi-finger tasks (reviewed in Latash and Huang 2015). A method to quantify synergies has been developed within the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2007). According to the UCM hypothesis, the central nervous system is able to organize abundant (we prefer this term rather than the more common “redundant”, see Latash 2012) sets of elemental variables to stabilize task-specific salient variables. This means that deviations in directions that do not lead to changes in the salient variables are allowed to be relatively large compared to directions in the orthogonal to the UCM sub-space (ORT) where these salient variable change. Such task-specific stability is reflected in a number of indices. One of them is the structure of inter-trial variance in the space of elemental variables. Indeed, if a person performs several trials at a task using an abundant set of effectors, trajectories in the space of elemental variables are expected to diverge in less stable directions and converge in more stable directions. As a result, if a person stabilizes a particular salient performance variable, variance across trials quantified at a certain phase of the action is expected to be relatively high within the UCM for that variable as compared to variance in ORT. Variance along the UCM (VUCM) has no effects on the performance variable; it reflects flexible use of varying solutions to ensure the same level of performance. Variance along the ORT (VORT) reflects accuracy of performance. The difference between the two variance indices, VUCM and VORT, has been used as a synergy index (ΔV; reviewed in Latash et al. 2002b, 2007).
Several recent studies have shown that the synergy index in multi-finger accurate force production tasks is sensitive to a variety of states characterized by impaired hand function, from the healthy elderly (Shinohara et al. 2004), to persons with Down syndrome (Latash et al. 2002a; Scholz et al. 2003), Parkinson’s disease (Park et al. 2012; Jo et al. 2015) and multiple system atrophy (Park et al. 2013). The main goal of this study was to explore whether multi-finger synergies are affected in MS. Based on the earlier hypothesis that multi-finger synergies are highly sensitive to functioning of subcortical structures (Latash and Huang 2015), our first hypothesis was that the synergy index would be significantly reduced in MS patients. MS involves widespread lesions in both the brain and spinal cord, and many of them can affect the hand function. Note that involvement of subcortical pathways leading to changes in the cerebellar function has been documented in MS (Tornes et al. 2014) as well as more widespread motor connectivity in deep subcortical nuclei (Dogonowski et al. 2013).
Ensuring stability of steady-state performance is only one of the components of controlled stability of performance. The other component is the ability to reduce stability of performance in anticipation of an action that requires a quick change in the salient variable. Such anticipatory synergy adjustments (ASAs, Olafsdottir et al. 2005) are seen in healthy young persons about 300 ms prior to the action initiation, but are reduced in both magnitude and duration in patients with subcortical disorders (Park et al. 2012, 2013; Jo et al. 2015). Since deficits in feed-forward control have been documented in MS (Jacobs and Kasser 2012; Aruin et al. 2015), although in whole-body postural studies, our second hypothesis was that ASAs would be reduced in MS.
2. Methods
2.1. Subjects
Thirteen patients with MS (aged 47.1 ± 3.8; 3 males) and 13 healthy control subjects (CS; aged 46.5 ± 3.7; 4 males) were tested. None of the CS had any known neurological disorder or arthritis in their upper extremities. All the patients had undergone a full neurological examination. Descriptive data for the MS patients are presented in Tables 1 and 2. In this study, we purposefully selected patients with a relatively broad range of age (29 – 75), time since diagnosis (1.5 – 37.2 years), and the number and location of brain (from 3 to 50) and spinal (from 0 to 5) lesions to explore most general changes in multi-finger synergies with MS. Table 1 also presents the results of the neurological examination of the hand function; about half of the patients showed no identifiable abnormalities; in other patients, most common abnormalities included mild tremor and dysmetria. The locations of the main lesions are described in more detail in Table 2.
Table 1.
Descriptive data of MS patients
| Subject | Sex, M/F | Age, yr | Handedness, R/L |
Time since diagnosis, yr |
Number of brain lesions | Number of spinal lesions | Hand function on exam | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | F | 44 | R | 1.5 | 15 | 3–4 | No clear abnormalities | ||||||||
| 2 | F | 34 | R | 7.1 | > 50 | Unknown | No clear abnormalities | ||||||||
| 3 | M | 49 | L | 8.2 | > 30 | Unknown | No clear abnormalities | ||||||||
| 4 | F | 29 | R | 4.1 | 4 | 1 | No clear abnormalities | ||||||||
| 5 | F | 62 | R | 37.2 | 20–30 | 4 | No clear abnormalities | ||||||||
| 6 | F | 36 | R | 4.2 | 3 | 0 | No clear abnormalities | ||||||||
| 7 | F | 58 | R | 3.1 | 14 | 1 | No clear abnormalities | ||||||||
| 8 | F | 49 | R | 9.1 | 4 | 0 | Decreased sensation on the right side | ||||||||
| 9 | F | 33 | R | 13.1 | 8 | Unknown | Dysmetria on the right side | ||||||||
| 10 | M | 52 | R | 3.0 | 6 | 3 | Bilateral dysmetria | ||||||||
| 11 | M | 34 | R | 5.3 | 30 | 0 | Mild bilateral tremor and numbness in fingertips | ||||||||
| 12 | F | 57 | R | 3.4 | > 30 | 4–5 | Mild bilateral dysmetria and decreased light touch | ||||||||
| 13 | F | 75 | R | 24.2 | Unknown | Unknown | Mild bilateral dysmetria and tremor | ||||||||
Abbreviations: M/F, male/female; R/L, right/left. The number of brain and spinal lesions is presented only for patients who had an MRI within the last year. We acknowledge the lack of scan data for some patients as a limitation of our study.
Table 2.
Location of brain lesions in MS patients
| Subject | Lesion location |
|---|---|
| 1 | Periventricular region; Lt peritrigonal area |
| 2 | Supratentorial WM; corpus callosum; Rt frontal lobe |
| 3 | Periventricular, pericallosal, infratentorial and periatrial regions; cerebellum |
| 4 | Periventricular and pericallosal regions |
| 5 | Periventricular, supratentorial and infratentorial regions |
| 6 | Lt anterior periventricular WM; Lt frontal subcortical WM; Rt peritrigonal WM; Rt internal capsule |
| 7 | Periventricular region; occipital and temporal lobes; callosal septal interface; Lt frontal juxtacortical WM |
| 8 | Lt centrum semiovale |
| 9 | Periventricular and pericallosal regions |
| 10 | Rt frontal periventricular WM; occipital periventricular WM; subcortical WM; callososeptal interface; Lt thalamus; Lt caudate nucleus; Lt midbrain; pons; medulla |
| 11 | Periventricular regions; internal capsule; Lt temporal lobe; Lt thalamus; brainstem; brachium pontis |
| 12 | Periventricular, pericallosal and supratentorial regions; posterior parts of frontal lobes; Lt middle corona radiata |
| 13 | Unknown |
Abbreviations: Rt/Lt, right/left; WM, white matter.
We did not perform disability testing with the Expanded Disability Status Scale (EDSS) as it is heavily biased by performance in locomotor tasks, (Amato and Portaccio 2007) and our study focuses on the hand function. We had in our pool patients with comparably preserved hand function but broadly varying involvement of the lower extremities, from those with very mild involvement to wheelchair bound. The study protocol followed the Helsinki Declaration and was reviewed and approved by the Pennsylvania State University-Hershey Medical Center Institutional Review Board. Written informed consent was obtained from all subjects.
2.2. Apparatus
Four piezoelectric force sensors (model 208A03; PCB Piezotronics, Depew, NY) were used to measure vertical forces produced by the fingers. The sensors were placed into slots in a panel that allowed adjusting the sensor position in the anterior-posterior direction to fit the individual subject’s hand anatomy. The subjects determined the most comfortable location for each sensor. The distance between the centers of the sensors in the medio-lateral direction was 3 cm. Each sensor was covered with sandpaper (300-grit) to increase the friction between the fingertips and the top surface of the sensor to ensure that slippage was very unlikely. A custom-made wooden piece was placed underneath the subject’s palm to help maintain a constant hand and finger configuration during the tests. The metacarpophalangeal joints were at about 120°, and all the inter-phalangeal joints were slightly flexed so that the hand formed a dome. The four force signals were amplified and digitized at 200 Hz with a 16-bit resolution with a customized LabView program using National Instruments data acquisition boards.
2.3. Experimental Procedures
During the experiment, the subjects sat in a chair facing a 19-in computer monitor, with the shoulder at ~30° of abduction and ~45° of flexion. The elbow was flexed at ~135°. The monitor was at subject’s eye level and showed real-time finger force feedback. Prior to each trial, all sensor signals were set to zero when subjects placed their fingertips on the sensor centers and relaxed their hand. As a result, the sensors measured only active downward forces. The other hand rested on the lap of the subject.
The experiment involved three tasks: 1) Maximal voluntary contraction (MVC) task; 2) single-finger ramp tasks; and 3) quick force pulse production task. The subjects performed all three tasks with the left and right hands separately in a balanced across subjects order. Subjects were given an instruction before each task and a few practice trials until they acquired a reasonable level of accuracy and consistency. Typically, 1–2 trials were given prior to the ramp task and 5–8 trials prior to the force pulse production task; only one practice trial was performed prior to the MVC task. There were 5-min breaks after testing one hand. Subjects were offered rest at any time if they felt tired. Testing each hand took about 20–25 min, such that the entire experiment lasted under 1 h.
2.3.1. MVC task
In the MVC task, subjects were instructed to press on the sensors with the four fingers together as hard as possible in a self-paced manner and achieve maximal total force level within 8 s. The subjects were instructed to relax immediately after reaching a maximal force. The feedback showed the sum of the four finger forces (FTOT). The maximal total force (MVCTOT) and the forces of individual fingers (MVCi; i = I, index; M, middle; R, ring; and L, little) at the time of MVCTOT were measured and used to determine the target force levels for the next two tasks. The subjects performed two consecutive attempts and the trial with the higher MVCTOT was selected to set further tasks.
2.3.2. Single-finger ramp tasks
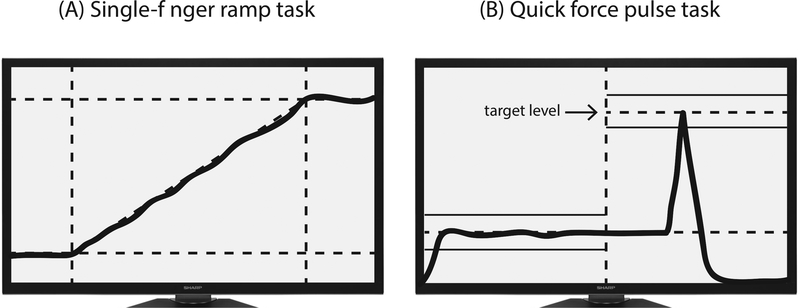
The purpose of this task was to quantify the interdependence among finger forces. In these trials, subjects were required to press with one of the fingers (the task finger) and match its force with the template shown on the screen (Figure 1A). The 20-s template consisted of a horizontal segment at zero force for the first 4 s, followed by a slanted line from 0% to 40% of MVCi of the task finger measured in the MVC test over the next 12 s, and a horizontal segment at 40% of MVCi for the last 4 s. Subjects were asked to pay no attention to possible force production by other fingers (non-task fingers) and to keep all the fingers on the sensors at all times.
Figure 1.
The feedback screen during single-finger ramp tasks (A) and quick force pulse production tasks (B).
2.3.3. Accurate force pulse production task
In this task, subjects were asked to produce a quick force pulse from a steady-state level of force into the target shown on the screen (Figure 1B) by pressing with all four fingers. During each trial, the feedback on FTOT was provided on the computer screen. Two horizontal lines showed an initial steady-state force level (set at 8% of MVCTOT) and a target force level (set at 25% of MVCTOT; with ±5% error margins). The instruction was to press on the sensors with all four fingers and match FTOT during the steady state with the 8%MVC target line as accurately as possible. A vertical line was shown corresponding to 5 s after the trial initiation. Once the cursor crossed the vertical line, the subjects were required to produce a very quick force pulse into the target at a self-selected time within the next 5 s. Each subject performed at least 25 trials and additional trials (over the minimum 25) were given if the subject made a major mistake (for example, pressing before the cursor reached the vertical line, pressing several times within 1 trial, or changing the baseline force slowly in preparation to pressing).
2.4. Data Analysis
The force data were digitally low-pass filtered at 10 Hz with a zero-lag, fourth-order Butterworth filter. The data processing was done using a customized Matlab code.
2.4.1. Single-finger ramp tasks
During these tasks, non-task fingers always produced force that increased in parallel with the force of the task finger (enslaving, Li et al. 1998). The enslaving matrix (E) was computed reflecting the involuntary force productions by non-task fingers when an instructed finger produces force (Zatsiorsky et al. 2000). For each single-finger trial, linear regressions of the force produced by individual fingers against FTOT over a 10-s time interval were computed. The first and last 1-s intervals were excluded to avoid edge effects. The regression coefficients in Fi,j = fi0 + ki,j × FTOT,j were used to construct:
Where i, j = {I, M, R, L}; j represents a task finger; Fi,j and FTOT,j indicate the individual i-finger force and FTOT, respectively, when j -finger was the task-finger. An overall index of enslaving, ENj, was computed for each finger as the average ki,j across the non-task fingers when j-finger was the task-finger: ENj = ∑ki,j/3 (i ≠ j). The enslaving matrix links finger force changes to changes in hypothetical variables, finger modes, that can be changed by subjects one at a time, at least hypothetically: ƒ = EmT, where ƒ is a four-dimensional force vector and m is a four-dimensional mode vector.
2.4.2. Accurate force pulse production tasks
The trials with the following errors were excluded from further analysis: The peak force was outside the ±5% error margins of the target force; the time to peak force was over 1 s; the baseline force was not stabilized prior to pressing; and/or the force pulse showed multiple peaks. The total number of accepted trials was 19.1 ± 0.5 for all subjects. It was about the same for the MS and CS groups, 19.3 ± 0.7 for the MS group and 18.8 ± 0.5 for the CS group. The following variables were computed only for the accepted trials.
The time (t0) of initiation of FTOT change was defined as the time when the first derivative of force (dF/dt) reached 5% of its peak value in that particular trial. All the accepted trials for each hand and each subject were aligned with respect to t0. The time to peak force (Tpeak) was defined as the time of peak force with respect to t0.
An index of multi-finger force stabilizing synergy was computed within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; for computational details see Latash et al. 2001). Finger forces were transformed into finger modes (m; Latash et al. 2001; Danion et al. 2003) with the help of the E matrix. Mode is a hypothetical neural variable reflecting the force production by all the fingers of the hand due to enslaving when only one finger is intended to produce force. The variance in the mode space across all the accepted trials for a subject was quantified separately in two sub-spaces for each time sample. The first sub-space (UCM) corresponded to no changes in FTOT. The second sub-space was the orthogonal complement (ORT) to the UCM; variance within ORT changed FTOT.
Note that enslaving is expected to lead to co-variation among finger forces independently of the control strategy: if one finger, by chance, shows higher force, other fingers are also expected to show larger forces compared to their average magnitudes. Hence, quantitative analysis of inter-trial variance may lead to different values in different directions in the space of finger forces. This may by itself result in unequal VUCM and VORT. To minimize these effects, we performed analysis of synergies in the space of finger modes that, by definition, can be modified by the controller one at a time.
The two variance components (VUCM and VORT) were further combined into a single metric, a synergy index, ΔV, which was computed for each time sample: ΔV = (VUCM – VORT)/VTOT, where VTOT stands for total variance and each variance index is normalized by the number of degrees-of-freedom in the corresponding spaces. The number of dimensions for TOT is 4 corresponding to the four fingers, ORT is one-dimensional since total force is one-dimensional, while dimensionality of UCM is (4 – 1) = 3.
We interpret ΔV > 0 as sign of a FTOT–stabilizing synergy; a higher ΔV implies a stronger synergy. For further statistical analysis, ΔV was log-transformed (ΔVZ) using the Fischer transformation applied for the computational boundaries, from −4 to +1.33.
The average value (ΔVSS) and its standard deviation (SDSS) of ΔVZ were computed for the steady-state interval (between −600 and −400 ms prior to t0). Anticipatory synergy adjustment (ASA, a change in ΔVZ prior to t0) was quantified using two indices, the difference in the ΔVZ between steady state and t0 (ΔVSS–t0) and the time of initiation of the ΔVZ drop (tASA). The time of initiation of ΔVZ change was defined as the time when ΔVZ dropped below ΔVSS by 2 SDSS. Negative values of tASA mean that ΔVZ started to drop before the initiation of FTOT changes.
2.5. Statistics
Standard descriptive statistics were used, and the data are presented as means and standard errors (SE). Mixed-design ANOVAs with repeated measures were used to explore how outcome variables (MVC, EN, Tpeak, VUCM, VORT, ΔVSS, ΔVSS–t0, and tASA) were affected by factors Group (MS and CS), Hand (right and left) and Finger (I, M, R, and L). The data were checked for violations of sphericity and Greenhouse-Geisser criterion was used to adjust the degrees-of-freedom when necessary. Pair-wise comparisons with Bonferroni corrections were used to explore significant ANOVA effects. VUCM and VORT were log-transformed for all comparisons to achieve a normal distribution (Shapiro-Wilk test, p < 0.05 level). Pearson correlation coefficients were used to determine significant relationships between variables. All statistical tests were performed with SPSS 19.0 (SPSS Inc, Chicago, IL, USA).
3. Results
3.1. Maximal force and enslaving
MS patients produced significantly lower peak forces in the MVC trials compared with CS. This was true for both hands. The average MVC of the MS group was only 62% of that of CS. The MVC values for the MS patients were 40.9 ± 5.5 and 41.5 ± 5.2 N for the right and left hand, respectively, whereas for the CS group these values were 69.5 ± 8.6 and 63.5 ± 7.7 N. A two-way ANOVA on Group and Hand showed a main effect of Group [F[1,24] = 7.05; p < 0.05] without other effects.
During the single-finger ramp tasks, unintended force production by non-task fingers (enslaving, EN) was seen in both MS and CS groups (Table 3). Whereas different fingers showed different amount of EN, for both groups, EN was largest in the ring finger task and smallest in the index finger task. Overall, the summed EN index over all trials (ENall) was larger for MS than the CS group (for the right and left hand, 0.24 ± 0.03 and 0.29 ± 0.03 in CS; 0.34 ± 0.06 and 0.33 ± 0.04 in MS). A three-way ANOVA with factors Hand, Finger and Group showed significant main effect of Finger [F[3,22] = 40.1; p < 0.001] without other effects. Pairwise comparisons confirmed that the ENI < ENM , ENL < ENR (p < 0.05). The group difference in ENall between groups was mainly in the lateral (index and little) finger tasks, with less of a difference in the medial (middle and ring) finger tasks. To test this effect, EN of the medial fingers (ENmed) and lateral fingers (ENlat) was analyzed separately using a two-way ANOVAs Group × Hand (see Table 3 for the ENmed and ENlat values). The ANOVA on ENlat showed a main effect of Group [F[1,24] = 4.66; p < 0.05] without other effects whereas the ANOVA for ENmed did not show any significant effects.
Table 3.
Indices of enslaving
| Group | Fingers | |||||||
|---|---|---|---|---|---|---|---|---|
| I | M | R | L | med | lat | all | ||
| MS | Rt | 0.062 | 0.074 | 0.123 | 0.083 | 0.20 ± 0.03 | 0.15 ± 0.03 | 0.34 ± 0.06 |
| Lt | 0.054 | 0.082 | 0.108 | 0.081 | 0.19 ± 0.02 | 0.14 ± 0.02 | 0.33 ± 0.04 | |
| CS | Rt | 0.025 | 0.054 | 0.111 | 0.049 | 0.17 ± 0.02 | 0.07 ± 0.01 | 0.24 ± 0.03 |
| Lt | 0.035 | 0.086 | 0.111 | 0.054 | 0.20 ± 0.02 | 0.09 ± 0.01 | 0.29 ± 0.03 | |
Means ± standard errors of enslaving indices (EN) are presented for each finger and combinations of fingers. Standard errors for individual fingers were omitted for simplicity. Abbreviations: MS, multiple sclerosis; CS, control subjects; Rt, right hand; Lt, left hand; I, index; M, middle; R, ring; L, little; med, medial (M and R) fingers; lat, lateral (I and L) fingers; all, all fingers.
3.2. Performance in the force pulse task
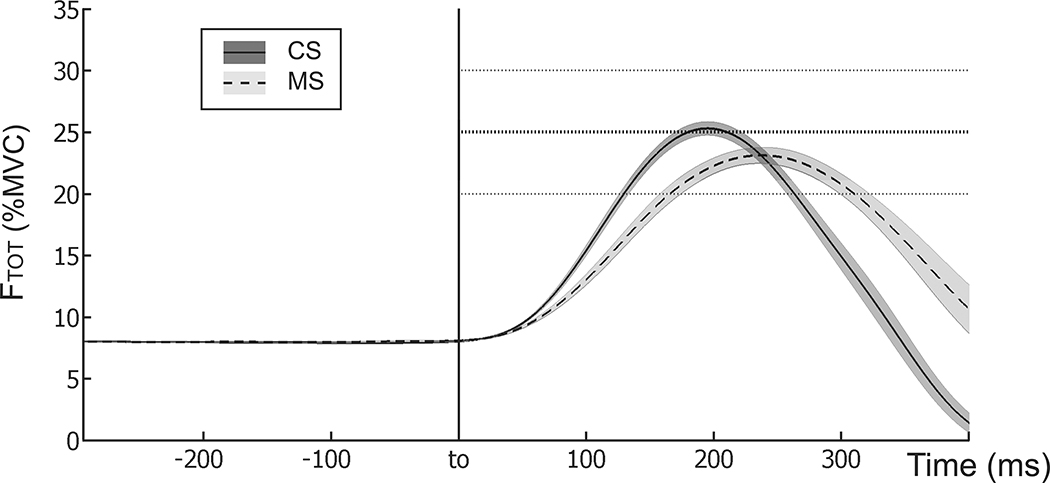
During the steady-state phase of the quick force pulse task, both MS and CS groups demonstrated accurate task performance, with FTOT close to the target level (8% of MVCTOT) before the pulse initiation. Figure 2 shows the averaged across trials performance of representative subjects from each group for the quick force production. Note the slower force pulse in the MS subject. On average, MS patients were slower than CS in reaching the peak force. Tpeak for the MS was 0.25 ± 0.03 and 0.22 ± 0.02 s, while Tpeak for the CS was 0.19 ± 0.01 and 0.18 ± 0.01 s for the right and left hand, respectively. This difference approached significance (p = 0.09) according to a two-way ANOVA Group × Hand.
Figure 2.
Time profiles of the averaged total force with SE shades computed across trials for typical subjects of each group during the quick force pulse task. The trials were aligned by the initiation of the force pulse (t0). The dashed line shows the data for the right hand of a MS subject (Tpeak = 0.255 s) and the solid line shows the data for the right hand of a CS (Tpeak = 0.197 s).
3.3. Indices of multi-finger synergies
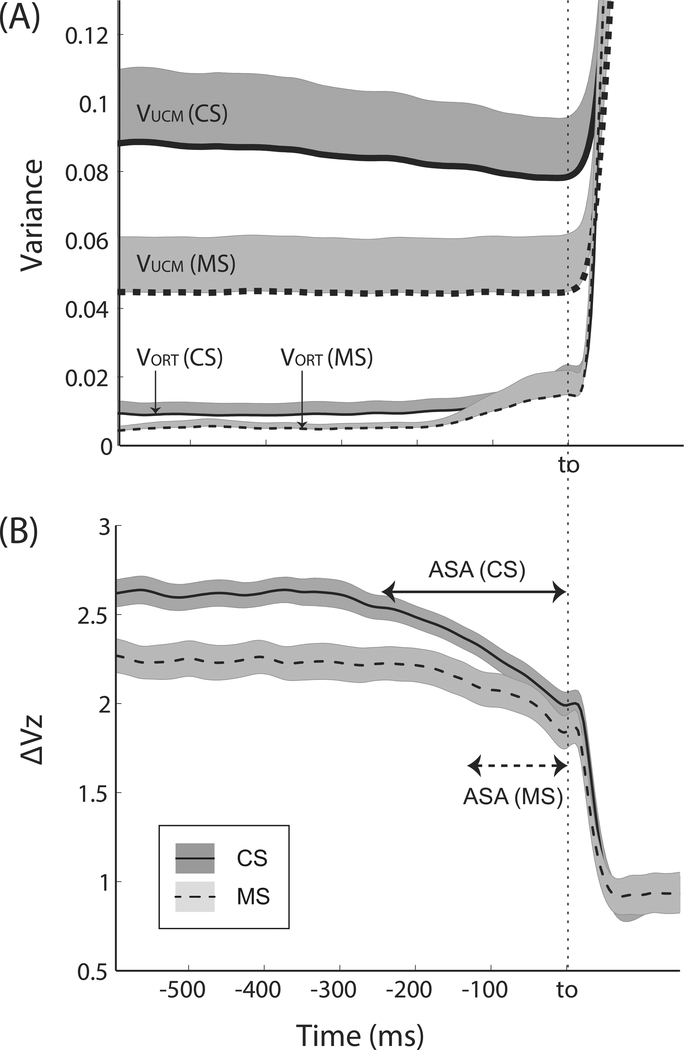
Both groups showed consistently positive synergy indices (ΔVSS) during the steady state prior to the force pulse initiation (Table 4). The large positive values of ΔVSS reflected the large amounts of variance (VUCM) in the space of commands to fingers that kept FTOT unchanged. In Figure 3A, the time profiles of the two variance components, VUCM and VORT, are presented for both groups. Note the twice as large VUCM values in CS compared to MS, while VORT was relatively similar in the two groups leading to higher synergy index (ΔVZ, Figure 3B) in CS. These results were supported by Group × Hand ANOVAs on VUCM, VORT, and ΔVSS, which showed significant main effects of Group for VUCM [F[1,24] = 5.21, p < 0.05] and ΔVSS [F[1,24] = 7.75, p < 0.05] without other effects. Note that while ΔV could change only within the range from –4 to +1.33 (see Methods), ΔVZ had no computational limits.
Table 4.
Synergy indices for the quick force production task
| VUCM | VORT | ΔVSS | ΔVSS–t0 | tASA (s) | ||
|---|---|---|---|---|---|---|
| MS | R | 0.044 ± 0.015 | 0.005 ± 0.002 | 2.23 ± 0.14 | 0.43 ± 0.07 | −0.13 ± 0.03 |
| L | 0.046 ± 0.018 | 0.005 ± 0.002 | 2.25 ± 0.13 | 0.37 ± 0.06 | −0.13 ± 0.03 | |
| CS | R | 0.083 ± 0.020 | 0.007 ± 0.003 | 2.55 ± 0.10 | 0.64 ± 0.07 | −0.22 ± 0.02 |
| L | 0.095 ± 0.027 | 0.011 ± 0.005 | 2.68 ± 0.10 | 0.62 ± 0.09 | −0.25 ± 0.02 |
Means ± SE of variance indices at steady-state (VUCM, VORT, and ΔVSS), magnitude (ΔVSS–t0) and time of anticipatory synergy adjustments (tASA) are presented for MS patients and CS. Abbreviations: R/L, right/left hand.
Figure 3.
(A) Two variance components (VUCM and VORT) and (B) the synergy index (ΔVZ) during the quick force pulse production tasks for the MS patients and CS. Averages across subjects within each group are presented with standard errors shades. Average data across both hands were used for each subject. Note the difference in ASA between MS and CS groups before the initiation of the force pulse (t0).
3.4. Anticipatory synergy adjustments
Before the initiation of the force pulse, there was a drop (ΔVSS–t0) in the synergy index in both groups (Figure 3B). The initiation of the ΔVZ drop was delayed in MS, on average by 43%, and the magnitude of the drop was smaller in MS by 37% (Table 4). These results were supported by two-way ANOVAs Group × Hand on ΔVSS–t0 and tASA [main effect of Group: F[1,24] = 7.38, p < 0.05 for ΔVSS–t0; F[1,24] = 13.44, p < 0.05 for tASA ]. There were no other effects. Figure 3 suggests that the longer and larger ASAs were primarily due to the drop in VUCM in CS without any visible changes in VUCM in MS.
4. Discussion
Both hypotheses formulated in the Introduction have been confirmed in the experiment. Indeed, as predicted by Hypothesis 1, we observed lower synergy indices (ΔVSS) in MS during steady-state force production. Hypothesis 2 predicted decreased anticipatory synergy adjustments (ASAs) in MS. The experiment showed significantly reduced duration and magnitude of ASAs (tASA and ΔVSS–t0) in the MS group. There were also effects of MS on general indices of performance and on indices of finger individuation (enslaving, Zatsiorsky et al. 2000).
Finger enslaving and its changes in MS
Enslaving (lack of individuation) has been discussed as reflecting both peripheral and central factors including passive links among fingers, multi-tendon, multi-finger extrinsic hand muscles, and overlapping cortical representations (reviewed in Schieber and Santello 2004). Changes in enslaving indices are typical across various groups with mildly impaired coordination including the healthy elderly (Shinohara et al. 2003, 2004; Park et al. 2012). Sometimes, these changes are counter-intuitive. In particular, healthy older adults show decreased indices of enslaving (better finger individuation) while their overall performance in hand tasks and indices of multi-digit synergies are impaired (Shim et al. 2004; Olafsdottir et al. 2007, 2008). Several earlier studies reported positive correlation between MVC and EN indices, i.e., lower enslaving in weaker persons (elderly vs. young and females vs. males, Shinohara et al. 2003, 2004). Our study showed a different result: MS patients were weaker than controls, and their EN indices were larger for the lateral fingers (index and little) without significant differences for the medial (middle and ring) fingers. These results suggest a change in enslaving specific to MS, which is not linked to the reduced ability to produce high forces.
The larger effect of MS on the lateral fingers, which typically show lower EN indices (Zatsiorsky et al. 2000), is an intriguing result. It suggests that MS leads to less differentiation across fingers compared to controls. Also noted was the trend towards higher EN and lower MVC in the left hands of controls (similar to earlier reports, Shinohara et al. 2003), while both indices were nearly identical for the two hands in MS. Whether one of the consequences of MS is indeed loss of differentiation across digits and hands deserves further investigation.
An earlier study of fast finger-to-thumb opposition movements (Bonzano et al. 213) documented significantly worse performance (lower rate) in MS compared to healthy controls. It is possible that these results are causally related to the worse individuation of the lateral fingers in our study (given that the index finger is one of the lateral fingers).
MS effects of synergic control
Neurophysiological mechanisms of synergies stabilizing salient performance variables are unknown. There are several models that account for the typical structure of inter-trial variance (VUCM > VORT) including optimal feedback control schemes (Todorov and Jordan 2002), schemes based on central back-coupling loops (Latash et al. 2005), and also a scheme that unites the idea of control with referent coordinates for salient variables and feedback loops (Martin et al. 2009). Within each of the mentioned models, however, the hypothesized schemes can potentially function at any level of the central nervous system. For example, the well-known system of Renshaw cells may be seen as a synergy stabilizing the output of the corresponding motorneuronal pool, while the tonic stretch reflex may be seen as a synergy stabilizing equilibrium between the muscle and external load (reviewed in Latash 2008). Studies of patients with various neurological disorders provide a rare opportunity to explore the contribution of different structures and loops within the central nervous system to motor synergies.
MS is characterized by a variety of clinical presentations depending on specific pathways within the CNS affected by the demyelinating process. As a result, motor deficits in MS can involve symptoms typical of damage to the corticospinal pathway, such as paresis and spasticity, as well as symptoms more typical of problems with subcortical loops, such as cerebellar symptoms (Tranchant et al. 1995). Recent studies have suggested that synergic mechanisms responsible for stable behavior in steady-state tasks show significant changes in subcortical disorders (such as Parkinson’s disease and multiple system atrophy), but not necessarily following cortical stroke (Reisman and Scholz 2003; Park et al. 2012; reviewed in Latash and Huang 2015).
In the current study, most of our subjects had subcortical lesions involving the periventricular region, internal capsule region, cerebellar, and pontine lesions. Given that MS commonly affects subcortical pathways, we expected, on average, a drop in the synergy index. This was indeed observed. It is important to emphasize that the drop in ΔV was associated not with higher VORT but lower VUCM. According to the definition of the variance components (see Introduction and Scholz and Schöner 1999), higher VORT means higher variance in the finger mode space that affects total force, i.e. less accurate performance. In contrast, lower VUCM means a lower range of solutions used by the subjects to reach the task force level, i.e. more stereotypical performance. An increase in VUCM has been reported in recent studies of the effects of specialized practice on multi-finger synergies (Wu et al. 2012, 2013). These observations bring an optimistic message that such practice schedules may have a beneficial effect for the synergic control of the hand in MS.
As emphasized in a recent review (Latash and Huang 2015), neurological disorders involving the basal ganglia and cerebellum lead to impaired control of movement stability, which has two components. The first, lower stability of steady-state actions, is reflected in the lower ΔV index. The second may be addressed as loss of agility reflected in impaired destabilization of performance variables in preparation to actions that require a quick change in such variables. The documented decrease in the ability to attenuate a synergy stabilizing a salient performance variable in persons with MS may lead to problems with the ability to initiate movement quickly. Note that MS leads to an increase in preparation time across a range of motor tasks (Remelius et al. 2008; Stoquart-Elsankari et al. 2010), which may be particularly pronounced under fatigue (Morgante et al. 2011; Barr et al. 2014).
Clinical relevance of our finding
This is the first study of multi-finger synergies in MS. It can be viewed as a proof of concept that requires a follow-up with a much larger group exploring changes in synergy indices as a function of location of demyelinating lesions and correlating them with changes in functional hand tests. The relatively small and varied sample of the patients may be viewed as a limitation; however, the fact that significant changes in the synergy index and ASAs were observed in the study suggests that these effects are strong. Given that our MS group involved patients with a variety of clinical signs, including those typical of subcortical lesions, we expected, on average, a drop in the synergy index and in ASAs. These were indeed observed. It is important to emphasize that the drop in ΔV was associated not with higher VORT (less accurate performance) but with lower VUCM (more stereotypical performance).
The procedure used in our study was not expected to induce fatigue: It used only a few trials with short-lasting high force production (MVC) while all other trials used low force levels. However, the documented increased fatigue in persons with MS (Krupp et al. 1988; Latash et al. 1996) is a concern even in such tests. We would like to emphasize that none of our patients complained of fatigue at the time of study. Moreover, studies of synergies under fatigue in healthy persons typically showed an increase in the synergy index (Singh et al. 2010), which is opposite to our findings in the MS group. Hence, we believe that fatigue was not a defining factor in our study.
Currently, the most commonly used disability scale in MS is the Expanded Disability Status Scale (EDSS). Though there is a motor functional system component, the scale is heavily weighted toward ambulation and a criticism of the scale is that it does not reflect well upon motor function in the upper extremities (Thompson and Hobart 1998; Amato and Portaccio 2007; Kragt et al. 2008 Cohen et al. 2012). Due to the limitations of the EDSS, the Multiple Sclerosis Functional Composite (MSFC) was conceived. This includes the Nine Hole Peg Test (9-HPT), which is a brief, standardized, quantitative test of upper extremity function. Though this test has good inter-rater and test-retest reliability and can be sensitive to detect minor impairments in hand function, the test is sensitive to practice effects and may not reflect changes when the level of impairment is severe (see the above references). In our study, we did not perform the MSFC test, partly to keep the testing time relatively short and avoid possible effects of fatigue; this is a study limitation. We hope that the synergic changes may provide a more objective and sensitive description of MS-related changes in the upper extremities, which may be useful for clinical trials. Of course, this would require modifying the testing procedure to reduce its time (currently about 20–25 min per hand). Our current study should be seen as the first step toward developing a clinical test of controlled stability of multi-finger actions, not the ultimate testing procedure useful in clinical patient evaluation. Future studies will have to 1) explore in-depth possible links between changes in the synergic control and performance of functional tasks; 2) investigate the potential of using synergic measurements as objective measures for functional disability. These studies may guide the future development of rehabilitation strategies in MS.
Acknowledgments
The present work was partially supported by National Institutes of Health (NIH) grants HD059783, NS035032, NS082151, and AR048563.
References
- Amato MP, Portaccio E (2007) Clinical outcome measures in multiple sclerosis. Journal of the Neurological Sciences 259: 118–122. [DOI] [PubMed] [Google Scholar]
- Aruin AS, Kanekar N, Lee Y-J (2015) Anticipatory and compensatory postural adjustments in individuals with multiple sclerosis in response to external perturbations. Neuroscience Letters 591: 182–186. [DOI] [PubMed] [Google Scholar]
- Barr C, McLoughlin J, Lord SR, Crotty M, Sturnieks DL (2014) Walking for six minutes increases both simple reaction time and stepping reaction time in moderately disabled people with Multiple Sclerosis. Multiple Sclerosis and Related Disorders 3: 457–462. [DOI] [PubMed] [Google Scholar]
- Bonzano L, Sormani MP, Tacchino A, Abate L, Lapucci C, Mancardi GL, Uccelli A, Bove M (2013) Quantitative assessment of finger motor impairment in multiple sclerosis. PLoS One 8(5): e65225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JA, Reingold SC, Polman CH, Wolinsky JS (2012) Disability outcome measures in multiple sclerosis clinical trials: current status and future prospects. Lancet Neurology 11: 467–476. [DOI] [PubMed] [Google Scholar]
- Danion F, Schöner G, Latash ML, Li S, Scholz JP, Zatsiorsky VM (2003b) A force mode hypothesis for finger interaction during multi-finger force production tasks. Biological Cybernetics 88: 91–98. [DOI] [PubMed] [Google Scholar]
- Dogonowski AM, Siebner HR, Sørensen PS, Wu X, Biswal B, Paulson OB, Dyrby TB, Skimminge A, Blinkenberg M, Madsen KH (2013) Expanded functional coupling of subcortical nuclei with the motor resting-state network in multiple sclerosis. Multiple Sclerosis 19: 559–566. [DOI] [PubMed] [Google Scholar]
- Gorniak SL, Plow M, McDaniel C, Alberts JL (2014) Impaired object handling during bimanual task performance in multiple sclerosis. Multiple Sclerosis International 2014: 450420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyengar V, Santos MJ, Ko M, Aruin AS (2009) Grip force control in individuals with multiple sclerosis. Neurorehabilitation and Neural Repair 23: 855–861. [DOI] [PubMed] [Google Scholar]
- Jacobs JV, Kasser SL (2012) Balance impairment in people with multiple sclerosis: preliminary evidence for the Balance Evaluation Systems Test. Gait and Posture 36: 414–418. [DOI] [PubMed] [Google Scholar]
- Jo HJ, Park J, Lewis MM, Huang X, Latash ML (2015) Prehension synergies and hand function in early-stage Parkinson’s disease. Experimental Brain Research 233: 425–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kragt JJ, Thompson AJ, Montalban X, Tintoré M, Río J, Polman CH, Uitdehaag BM. (2008) Responsiveness and predictive value of EDSS and MSFC in primary progressive MS. Neurology 70: 1084–1091. [DOI] [PubMed] [Google Scholar]
- Krishnan V, Jaric S (2008) Hand function in multiple sclerosis: force coordination in manipulation tasks. Clinical Neurophysiology 119: 2274–2281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan V, de Freitas PB, Jaric S (2008) Impaired object manipulation in mildly involved individuals with multiple sclerosis. Motor Control 12: 3–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krupp LB, Alvarez LA, Larocca NG, Scheinberg LC (1988) Fatigue in multiple sclerosis. Archives of Neurology 45: 435–437. [DOI] [PubMed] [Google Scholar]
- Latash ML (2008) Synergy. Oxford University Press: New York. [Google Scholar]
- Latash ML (2012) The bliss (not the problem) of motor abundance (not redundancy). Experimental Brain Research 217: 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Huang X (2015) Neural control of movement stability: Lessons from studies of neurological patients. Neuroscience 301: 39–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Kalugina E, Nicholas JJ, Orpett C, Stefoski D, Davis F (1996) Myogenic and central neurogenic factors in fatigue in multiple sclerosis. Multiple Sclerosis 1: 236–241. [PubMed] [Google Scholar]
- Latash ML, Kang N, Patterson D (2002a) Finger coordination in persons with Down syndrome: Atypical patterns of coordination and the effects of practice. Experimental Brain Research 146: 345–355. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G (2001) Structure of motor variability in marginally redundant multi-finger force production tasks. Experimental Brain Research 141: 153–165. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G (2002b) Motor control strategies revealed in the structure of motor variability. Exercise and Sport Science Reviews 30: 26–31. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G (2007) Toward a new theory of motor synergies. Motor Control 11: 276–308. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky V (2005) A central back-coupling hypothesis on the organization of motor synergies: a physical metaphor and a neural model. Biological Cybernetics 92: 186–191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM (1998) Force sharing among fingers as a model of the redundancy problem. Experimental Brain Research 119: 276–286 [DOI] [PubMed] [Google Scholar]
- Martin V, Scholz JP, Schöner G (2009) Redundancy, self-motion, and motor control. Neural Computation 21, 1371–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marwaha R, Hall SJ, Knight CA, Jaric S (2006) Load and grip force coordination in static bimanual manipulation tasks in multiple sclerosis. Motor Control 10: 160–177. [DOI] [PubMed] [Google Scholar]
- Morgante F, Dattola V, Crupi D, Russo M, Rizzo V, Ghilardi MF, Terranova C, Girlanda P, Quartarone A (2011) Is central fatigue in multiple sclerosis a disorder of movement preparation? J Neurol. 2011. February;258(2):263–72. [DOI] [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML (2005) Anticipatory covariation of finger forces during self-paced and reaction time force production. Neuroscience Letters 381: 92–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir H, Zhang W, Zatsiorsky VM, Latash ML (2007) Age related changes in multi-finger synergies in accurate moment of force production tasks. Journal of Applied Physiology 102: 1490–1501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir HB, Zatsiorsky VM, Latash ML (2008) The effects of strength training on finger strength and hand dexterity in healthy elderly individuals. Journal of Applied Physiology 105: 1166–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Wu Y-H, Lewis MM, Huang X, Latash ML (2012) Changes in multi-finger interaction and coordination in Parkinson’s disease. Journal of Neurophysiology 108: 915–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J, Lewis MM, Huang X, Latash ML (2013) Effects of olivo-ponto-cerebellar atrophy (OPCA) on finger interaction and coordination. Clinical Neurophysiology 124: 991–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisman D, Scholz JP (2003). Aspects of joint coordination are preserved during pointing in persons with post-stroke hemiparesis. Brain 126:2510–2527. [DOI] [PubMed] [Google Scholar]
- Remelius JG, Hamill J, Kent-Braun J, Van Emmerik RE (2008) Gait initiation in multiple sclerosis. Motor Control. 2008. April;12(2):93–108. [DOI] [PubMed] [Google Scholar]
- Schieber MH, Santello M (2004) Hand function: peripheral and central constraints on performance. Journal of Applied Physiology 96:2293–2300. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Kang N, Patterson D, Latash ML (2003) Uncontrolled manifold analysis of single trials during multi-finger force production by persons with and without Down syndrome. Experimental Brain Research 153: 45–58. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G (1999). The uncontrolled manifold concept: Identifying control variables for a functional task. Experimental Brain Research 126, 289–306. [DOI] [PubMed] [Google Scholar]
- Shim JK, Lay B, Zatsiorsky VM, Latash ML (2004) Age-related changes in finger coordination in static prehension tasks. Joural of Applied Physiology 97: 213–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinohara M, Li S, Kang N, Zatsiorsky VM, Latash ML (2003) Effects of age and gender on finger coordination in maximal contractions and submaximal force matching tasks. Journal of Applied Physiology 94: 259–270. [DOI] [PubMed] [Google Scholar]
- Shinohara M, Scholz JP, Zatsiorsky VM, Latash ML (2004) Finger interaction during accurate multi-finger force production tasks in young and elderly persons. Experimental Brain Research 156: 282–292. [DOI] [PubMed] [Google Scholar]
- Singh T SKMV, Zatsiorsky VM, Latash ML (2010) Fatigue and motor redundancy: Adaptive increase in force variance in multi-finger tasks. Journal of Neurophysiology 103: 2990–3000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steultjens EM, Dekker J, Bouter LM, Cardol M, Van de Nes JC, Van den Ende CH (2003) Occupational therapy for multiple sclerosis. Cochrane Database Systems Reviews (3): CD003608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoquart-Elsankari S, Bottin C, Roussel-Pieronne M, Godefroy O (2010) Motor and cognitive slowing in multiple sclerosis: an attentional deficit? Clinical Neurology and Neurosurgery 112: 226–232. [DOI] [PubMed] [Google Scholar]
- Thompson AJ, Hobart JC (1998) Multiple sclerosis: assessment of disability and disability scales. Journal of Neurology 245:189–196. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI (2002) Optimal feedback control as a theory of motor coordination. Nature Neuroscience 5: 1226–1235. [DOI] [PubMed] [Google Scholar]
- Tornes L, Conway B, Sheremata W (2014) Multiple sclerosis and the cerebellum. Neurologic Clinics 32: 957–977. [DOI] [PubMed] [Google Scholar]
- Tranchant C, Bhatia KP, Marsden CD (1995) Movement disorders in multiple sclerosis. Movement Disorders 10: 418–423. [DOI] [PubMed] [Google Scholar]
- Wu Y-H, Pazin N, Zatsiorsky VM, Latash ML (2012) Practicing elements vs. practicing coordination: Changes in the structure of variance. Journal of Motor Behavior 44: 471–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y-H, Zatsiorsky VM, Latash ML (2013) Control of finger force vectors with changes in fingertip referent coordinates. Journal of Motor Behavior 45: 15–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Li ZM, Latash ML (2000) Enslaving effects in multi-finger force production. Experimental Brain Research 131: 187–195. [DOI] [PubMed] [Google Scholar]
- Ziemssen T (2011) Symptom management in patients with multiple sclerosis. Journal of Neurological Sciences 311 Suppl. 1: S48–52. [DOI] [PubMed] [Google Scholar]