Reaction norm for yearling weight in beef cattle using single-step genomic evaluation

Abstract

When the environment on which the animals are raised is very diverse, selecting the best sires for different environments may require the use of models that account for genotype by environment interaction (G × E). The main objective of this study was to evaluate the existence of G × E for yearling weight (YW) in Nellore cattle using reaction norm models with only pedigree and pedigree combined with genomic relationships. Additionally, genomic regions associated with each environment gradient were identified. A total of 67,996 YW records were used in reaction norm models to calculate EBV and genomic EBV. The method of choice for genomic evaluations was single-step genomic BLUP (ssGBLUP). Traditional and genomic models were tested on the ability to predict future animal performance. Genetic parameters for YW were obtained with the average information restricted maximum likelihood method, with and without adding genomic information for 5,091 animals. Additive genetic variances explained by windows of 200 adjacent SNP were used to identify genomic regions associated with the environmental gradient. Estimated variance components for the intercept and the slope in traditional and genomic models were similar. In both models, the observed changes in heritabilities and genetic correlations for YW across environments indicate the occurrence of genotype by environment interactions. Both traditional and genomic models were capable of identifying the genotype by environment interaction; however, the inclusion of genomic information in reaction norm models improved the ability to predict animals’ future performance by 7.9% on average. The proportion of genetic variance explained by the top SNP window was 0.77% for the regression intercept (BTA5) and 0.82% for the slope (BTA14). Single-step GBLUP seems to be a suitable model to predict genetic values for YW in different production environments.

INTRODUCTION

Genetic models applied to beef cattle evaluation usually do not assume genotype by environment interaction (G × E). However, some authors have reported the existence of G × E in herds evaluated within the same country and among countries (Cardoso et al., 2011; Ambrosini et al., 2014). A more robust way to study G × E is through random regression models with reaction norm (Cardoso and Tempelman, 2012; Chiaia et al., 2015). Reaction norm models relate, linearly, the genetic merit of animals to changes in the environment gradient (EG) (Silva et al., 2014). Therefore, they enable the estimation of a specific breeding value for a given EG.

Studies that consider reaction norm models for beef cattle yearling weight (YW) evaluations have been conducted using pedigree and phenotypic information (Cardoso et al., 2011; Chiaia et al., 2015). The inclusion of molecular marker information can be beneficial for reaction norm models because the effect of each marker can be calculated in different environments, instead of assuming an average environment. Lillehammer et al. (2009) and Silva et al. (2014) proposed methodologies to investigate molecular markers associated with the intercept and the slope of reaction norm models and to select genes expressed differently in the EG using only genotyped animals. However, the joint use of genotyped and ungenotyped animals in the evaluation is now possible through the single-step genomic BLUP (ssGBLUP) proposed by Legarra et al. (2009) and Aguilar et al. (2010). This method allows the use of complicated models such as random regression and maternal models.

The objective of this study was to compare reaction norm models using the pedigree-based relationship matrix and the joint realized relationship matrix (pedigree and genomic relationships). The second objective was to identify genomic regions associated with YW in Nellore cattle for different production environments in Brazil.

MATERIALS AND METHODS

The dataset used in this study was provided by DeltaGen Genetic Improvement Program and included 67,996 YW records of Nellore cattle born between 1994 and 2012. The total number of animals in the pedigree was 116,264. The evaluated animals were raised on pastures of seven farms in the states of Bahia, Goias, Mato Grosso, Mato Grosso do Sul, and Sao Paulo. Heifers are generally bred at 24 mo of age in Brazil, but the heifers in those farms were bred at 14–18 mo. Both artificial insemination and natural mating were used, and the cows that were still open by the end of the breeding season were culled. The calves remained with their dams until they were 7 mo old on average (Neves et al., 2012).

The contemporary groups (CG) for YW were defined by a combination of year and farm of birth, sex, and management group at birth, at weaning, and at yearling. A total of 1,237 CGs with more than 16 animals and sires with at least 10 calves per CG were kept in the analyses. Records with ±3.5 standard deviations away from the CG mean were considered outliers and were excluded from the analyses. Means (SD) of YW and age of animals were 271.6 (41.23) kg and 507 (34) d, respectively. Numbers of sires, multiple sires, and dams were 1,059, 15,728 and 42,061, respectively. Phenotypes for YW were recorded on 37,565 males and 30,431 females. The percentage of artificial insemination was 76.9% and the natural mating was 23.1%.

A total of 5,091 animals were genotyped using a high-density panel containing 777,962 SNPs (High-Density I Illumina Bovine BeadChip). The genotype quality control was performed considering the following exclusion criteria: SNPs of non-autosomal regions; mapped in unknown or in the same position; frequency of observed and expected allele frequencies >0.15 (Hardy–Weinberg equilibrium test); minor allele frequency less than 2%; call frequency for SNP <95%; samples with call rates <90% and/or duplicates. After quality control, 412,993 SNPs and 5,091 genotyped animals remained for analyses. Among the genotyped animals, 1,505 had phenotypes recorded.

The EG consisted of the average weight gain (AWG) of CG. The CG for AWG were defined by a combination of year and farm of birth, sex, and management group at birth, at weaning, and at yearling. The CG for YW and AWG had the same set. Initially, EG solutions were estimated by an animal model as follows:

$$y=X\beta +Z\alpha +e$$

where y is the vector of AWG records,

$$\beta$$

is the vector of fixed effects (CG and age as covariable),

$$\alpha$$

is the vector of additive direct genetic coefficients, X and Z are the design matrices of the effects contained in

$$\beta$$

and

$$\alpha$$

, respectively, and e is the random residual vector.

All the EG solutions were submitted to the iterative procedure proposed by Calus et al. (2004) to correct the bias caused by either the preferential use of bulls or small numbers of animals in the same herd. After reaching the correlation value (≥0.99) between AWG expressed in different environments, the solutions for EG were corrected for the mean solution of each sex and were standardized from 0 to 1 as follows: standardized mean = environmental group mean − (lowest mean of environment group)/(highest mean of the environment group − lowest environment group). After the standardization, a total of 68 EGs were formed, where the smallest value (EG = 0) represented the lowest effect of CG on AWG, meaning a poor development in that environment.

In matrix notation, the linear mixed model for reaction norm was

$$y=X\beta +Z\alpha +e$$

where y is the vector of YW records,

$$\beta$$

is the vector of fixed effects (CG, age of the cow at birth, and EG as covariable),

$$\alpha$$

is the vector of additive direct genetic coefficients, X and Z are the design matrices of the effects contained in

$$\beta$$

and

$$\alpha$$

, respectively, and e is the random residual vector.

According to the model, the following assumptions were made.

$$E \left[\begin{array}{c}y\\ \alpha \\ e\end{array}\right]= \left[\begin{array}{c}X\beta \\ 0\\ 0\end{array}\right]; V\left[\begin{array}{c}\alpha \\ e\end{array}\right]= \left[\begin{array}{c}{\mathit{K}}_{\alpha }\otimes \mathit{A}\\ 0\end{array}\begin{array}{c}0\\ I\otimes \mathit{R}\end{array}\right]$$

where

$${\mathit{K}}_{\mathit{\alpha }}$$

is a 2 × 2 matrix of regression coefficients that define the covariance function for additive genetic direct effects, R is 2 × 2 matrix of regression coefficients that define the covariance function for the random residual variance, I is the identity matrix, A is the pedigree relationship matrix, and

$$\otimes$$

is the Kroneker product.

For traditional evaluations, the inverse of A (A⁻¹) was used in the mixed model equations, whereas the inverse of the realized relationship matrix (H⁻¹) was used in the ssGBLUP (Aguilar et al., 2010; Christensen and Lund, 2010). The H⁻¹ can be written as

$$H^{-1}=A^{-1}+\left[\begin{array}{c}0\\ 0\end{array}\begin{array}{c}0\\ G^{-1}-A_{22}^{-1}\end{array}\right]$$

where

$$A_{22}$$

is the pedigree relationship matrix for the genotyped animals and G is the blended genomic relationship matrix. To avoid singularity problems, G is constructed as 0.95 *

$$G_{\text{raw}}$$

+ 0.05 *

$$A_{22}$$

, where

$$G_{\text{raw}}$$

contains the proportion of identical by state alleles shared between individuals and is created following the first method presented as in VanRaden (2008). Both genomic and traditional evaluations were performed using the BLUPf90 family of programs (Misztal et al., 2016).

The additive direct genetic variances were obtained as follows:

$$(\text{Var}(\text{a})|\text{ EG})=\text{Var}\left({\text{a}}_{\text{i}}+{\text{b}}_{\text{i}}\text{*EG}\right)={\text{ σ}}_{\text{a}}^2+{\text{ σ}}_{\text{b}}^2{\text{EG}}^2+2{\text{EG* σ}}_{\text{a},\text{b}}$$

where

$$a_i$$

and

$$b_i$$

are the intercept and the slope of the reaction norm, respectively;

$${\sigma }_a^2$$

is the genetic variance for the intercept;

$${\sigma }_b^2$$

is the variance component of the slope, and

$${\sigma }_{a,b}$$

is the covariance component between the intercept and the slope; EG was defined as before.

The heterogeneous residual variance coefficients were modeled using a log-residual function (Foulley and Quaas, 1995), as implemented in AIREMLF90 (Misztal et al., 2016). Because the residual coefficients were obtained using a logarithmic function, the exponential function should be used to transform the values back to the observed scale.

$$(Var(e)| EG)=exp (w_0+w_1*EG$$

where

$$(Var(e)| EG)$$

are the residual variances given the EG,

$$w_0$$

is the intercept of the residual function for YW, and

$$w_1$$

is the slope of the residual function for YW in the reaction norm model, considering heterogeneous residual variance. The variance components were obtained by restricted maximum likelihood using the AIREMLF90 software (Misztal et al., 2016).

Heritability estimates (

$$h^2$$

) were given by the genetic and phenotypic variance ratio as follows:

$$({\text{h}}^2|\text{EG})=\frac{(\text{Var}(\text{a})|\text{ EG})}{(\text{Var}(\text{a})|\text{ EG})+(\text{Var}(\text{e})|\text{ EG})}$$

For investigating the ability to predict future performances, traditional EBV and genomic EBV (GEBV) were predicted for EG ranging from 0 to 1, with 0.20 interval. The GEBV predicted for each EG was given by

$$\left(G\right)EB{V}_{i|EG}=a_i+b_i*EG$$

, where

$$(G)EB{V}_{i|EG}$$

is the traditional or genomic EBV of animal i calculated in a certain EG,

$$a_i$$

is the intercept, and

$$b_i$$

is the slope of the reaction norm for animal i.

Genotyped animals in the validation group (n = 293, 19.43%) were born between 2009 and 2011. We used the traditional model with all phenotypic information up to 2011 (BLUP complete) as a benchmark for comparisons. After removing phenotypes for the validation animals and their contemporaries, we ran traditional BLUP and ssGBLUP. The accuracy of predicting future performance when using BLUP and ssGBLUP models was calculated as

$$\text{Accuracy}=(COR(\hat{Y}), \left(G\right)EBV)/h$$

where COR is the Pearson correlation,

$$\hat{Y}$$

is the phenotype adjusted for all fixed effects in the model when a complete BLUP model with phenotypes for all animals was used, and (G)EBV is the genomic or traditional EBV of the animals in the validation population. Accuracy was calculated as predictive ability divided by the square root of heritability (h) for each model.

The standard deviations for the functions of the variance components were obtained using the repeated sampling approach as suggested by Meyer and Houle (2013). Thus, 5,000 samples of variances and covariance components were obtained from an asymptotic multivariate normal distribution. Subsequently, the functions of the variance components were calculated for each sample. The standard deviation for each function was computed using values from all samples (Elzo et al., 2015).

The POSTGSf90 software (Misztal et al., 2016) was used to estimate SNP effects and their variances in windows of 200 adjacent SNPs according to the methodology described by Wang et al. (2012). The results were presented based on the variance ratio for each SNP window explained. Those windows that captured the largest variance explained by the markers in the intercept and the slope of the reaction norm were identified.

RESULTS AND DISCUSSION

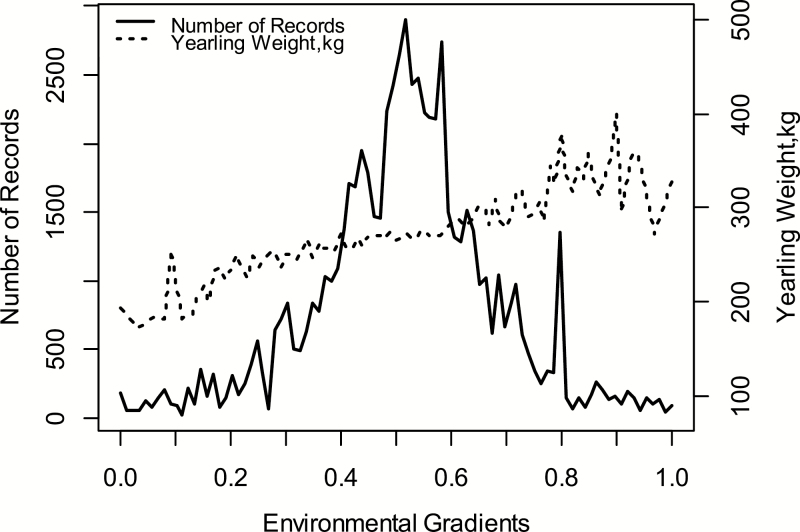
Environmental gradients were grouped by the standard deviation of the mean, rounded to 2 decimal digits. This rounding allowed to combine the environmental groups with fewer individuals and similar means (Figure 1). The mean YW increased gradually as the environmental conditions composed of environment groups improved. The phenotypic variation in YW was influenced by the environmental conditions of the production farm, the year of birth, and the management groups, in which the animals were grouped during the productive period on the farm.

Figure 1.

Average YW (kg), right side, and the number of records, left side, over the EGs.

If the EG equal to 0.0, formed by the less favorable environmental condition, the animals had lower YW, indicating that environmental conditions adversely affected animal productive performance. A large number of animals were grouped in the intermediate environmental groups (EG = 0.5), which can be observed by the distribution of the YW records on the continuous line in Figure 1. In more favorable environmental groups (EG from 0.6 to 1.0), there were fewer animals but YW was higher, indicating that better production environments tend to affect the productive performance positively, and the animals are more likely to express their genetic potential.

Variance components for the intercept and the slope of the reaction norm model and of the residual function are shown in Table 1. The values were similar between BLUP and ssGBLUP models, with largest differences observed for the intercept and the slope when the H⁻¹ matrix was used; however, the differences were within 2 standard deviations.

Table 1.

Variance components (standard errors) of the reaction norm model using inverses of pedigree (A⁻¹) and pedigree–genomic (H⁻¹) relationship matrices

Parameters	A −1	H −1
Additive genetic direct reaction norm
Intercept	180.88 (22.51)	206.39 (24.93)
Slope	294.59 (59.04)	363.05 (67.45)
Correlation (intercept, slope)	-0.32 (0.26)	-0.31 (0.25)
Residual function
Intercept	5.54	5.51
Slope	0.40 (0.06)	0.39 (0.06)

The coefficients of the residual function decreased by 0.5 and 1.6%, respectively, for the intercept and the slope when using H⁻¹ instead of A⁻¹. Likewise, models considering A and G matrices were compared by Forni et al. (2011) using a single-trait model and Silva et al. (2014) using reaction norm models reported similar magnitude of the estimated genetic parameters, including molecular marker information.

Correlations between intercept and the slope of the additive genetic direct reaction norm were negative and of moderate magnitude (−0.32 for BLUP and −0.31 for ssGBLUP). According to Pegolo et al. (2011), low magnitude correlations between the intercept and the slope indicate that the equation coefficients are almost independent, increasing the possibility of re-ranking of bulls according to the EG. The values obtained in our study indicated that the intercept and the slope were not totally independent, but re-ranking for some animals could be observed in a given EG. Genetic and residual variances increased with increasing G × E, indicating genetic differences among different EG.

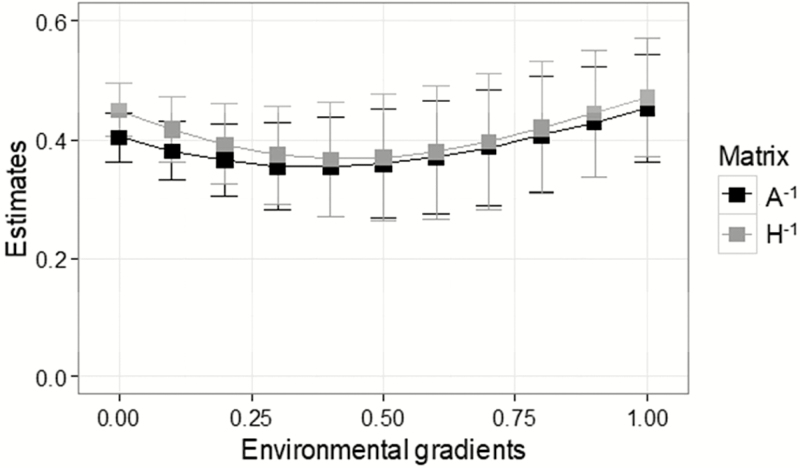
Heritability estimates varied from moderate to high environments, ranging from 0.35 to 0.46 with A⁻¹, and from 0.38 to 0.49 with H⁻¹ (Figure 2). The model with H⁻¹ presented higher estimates than with A⁻¹: 8.6% in EG 0; 6.0% in EG 0.5; and 6.7% in EG 1.0. Although differences among mean estimates were observed, the standard errors overlapped, meaning that the differences are most likely non-significant. It is expected that variance components are similar between pedigree and pedigree-genomic models, especially when the genotyped population is a good representation of the actual population.

Figure 2.

Means and standard deviations of heritabilites estimated using inverses of pedigree (A⁻¹) and pedigree-genomic (H⁻¹) relationship matrices for YW over the EGs.

Heritability estimates in our study were generally higher than those reported in the literature. Cardoso et al. (2011) investigated G × E in a Bayesian hierarchical reaction standard model using a single-step approach, and in two-steps for weight at 345 d in Hereford cattle. In the two steps, the authors reported heritability estimates between 0.08 and 0.23 evidencing G × E. Pegolo et al. (2011) studied G × E for weight at 450 d in Nellore cattle and observed moderate heritability estimates of 0.20–0.39 in the intermediate and the most favorable environment groups, respectively. However, Lemos et al. (2015) investigated YW in Nellore cattle using a three-trait reaction norm model and reported higher heritability estimates varying from 0.13 to 0.72 in EG. The difference observed between the results found in this study and those reported in the literature is possibly because of the methodology, the way EG were defined, and the number of observations in each EG. It is noteworthy that, differently from the studies mentioned above, the heritabilities reported by Araujo et al. (2014) and Knights et al. (1984)were not discrepant among the different environmental groups and were close to those observed in the analysis without EG.

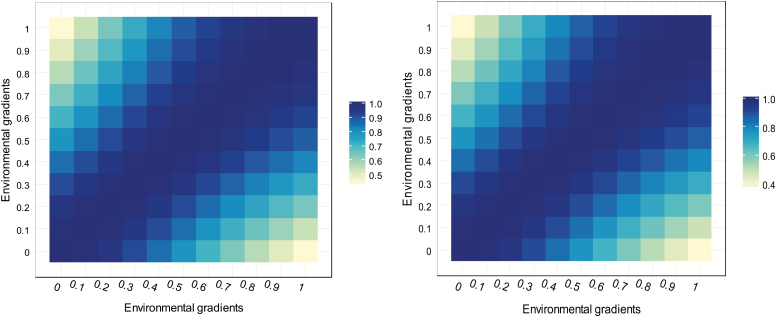
Genetic correlations were similar when using A⁻¹ or H⁻¹ (Figure 3). Using these two matrices resulted in moderate genetic correlations between the extreme EG, indicating the presence of G × E. Silva et al. (2014) investigated the number of piglets born using the genomic reaction norm models and observed similar genetic correlations when considering G⁻¹ or A⁻¹. In our study, genetic correlations were moderate to high for YW in the environmental gradients. Some authors have reported similar estimates for this trait in beef cattle (Lemos et al., 2015; Cardoso et al., 2011). Genetic correlations below 0.80 indicate the evidence of G × E (Robertson, 1959) and are shown in gradually lighter colors in Figure 3.

Figure 3.

Genetic correlations between EGs when using inverses of pedigree (A⁻¹) and pedigree-genomic (H⁻¹), respectively, relationship matrices for YW in the reaction norm models.

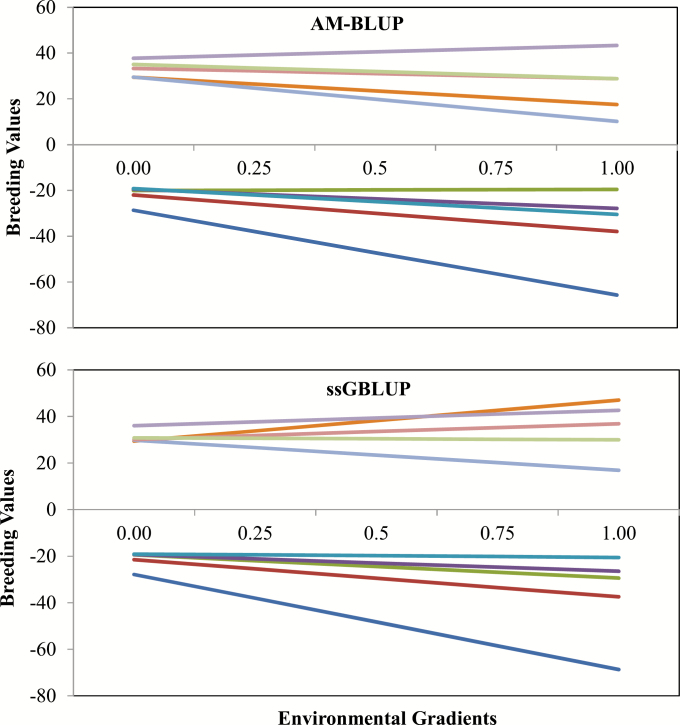
The genetic values of five best and five worst sires were calculated along the EG (Figure 4). The change in the trend for BLUP (pedigree) and ssGBLUP (pedigree-genomic) for the five worst bulls was less noticeable; however, the ranking of the best animals changed between those two models. The ssGBLUP model had two sires among the best five, even though they did not have evaluated progeny (young bulls) in the data used for evaluation. The genetic values of bulls common to both models had the same behavior. One of the advantages of using genomic information for evaluation purposes is the ability to predict the genetic merit of young sires before they have progeny information (VanRaden, 2008). The best and the worst animals were sensitive to the environment, because their genetic values varied from the less optimal to the high-quality environment. This indicates that variations in the EG influenced the phenotypic expression of YW. Lemos et al. (2015) observed more pronounced changes in EBV ranking for Nellore using YW in a three-trait reaction norm model.

Figure 4.

Estimated breeding values of five best and five worst bulls for YW in Nellore cattle, using inverses of pedigree (A⁻¹) and pedigree–genomic (H⁻¹) relationship matrices over the EGs.

The top 5% and top 10% of the coefficient of coincidence (CC) and the rank correlation (RC) of the 100% sires (bulls with progeny) for YW are shown, based on their EBV and GEBV, in Table 2. Positive values observed for CC top 5%, CC top 10%, and RC 100% indicate agreement between the models to select the best animals. These results may be due to the advantage of using H⁻¹ matrix intead of A⁻¹ when, for example, the farms adopt the multiple-sire mating system, which is common in Brazil (Teixeira et al., 2017). In such a situation, the relationship matrix based on pedigree is much less informative than the genomic relationship matrix due to the occurrence of many offspring with unknown paternity. When parents or ancestors are unknown, a common practice in dairy cattle is to use unknown parent groups, which helps to increase accuracy and reduce bias in the evaluations; however, this is not usual in beef cattle.

Table 2.

Coefficients of coincidence of top 5% (CC 5%), coefficients of coincidence of top 10% (CC 10%), and rank correlations of 100% (RC 100%) sires for YW using inverses of pedigree (A⁻¹) and pedigree–genomic (H⁻¹) relationship matrices

Environment gradient	CC 5%	CC 10%	RC 100%
0.0	0.91	0.86	0.91
0.5	0.82	0.91	0.82
1.0	0.82	0.91	0.82

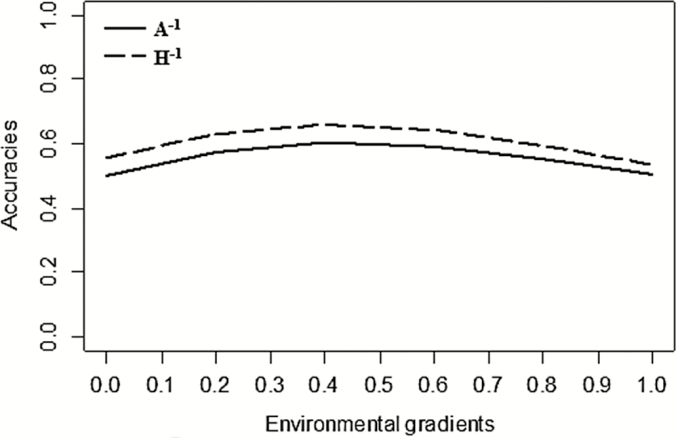
The accuracy in the ssGBLUP model was higher than in the traditional BLUP model (Figure 5). The mean value ​​of accuracy was 0.55 for A⁻¹, with maximum and minimum of 0.6 and 0.5, respectively. For H⁻¹, the average was 0.60, with maximum of 0.65 and minimum of 0.53. The inclusion of genomic information increased the ability to predict future performances compared with the traditional BLUP model.

Figure 5.

Accuracies of YW in Nellore cattle for reaction norm models using the inverses of pedigree (A⁻¹) and pedigree-genomic (H⁻¹) relationship matrices for YW over the EGs.

The genetic values of the animals in the validation population were estimated more accurately with H⁻¹. The GEBV predicted using H⁻¹ was, on average, 7.9% higher than the reaction norm model without genomic information, considering that the validation population consisted of the youngest animals of the herd. The shape of the accuracy curves can be explained by the number of animals present in the intermediate environment groups (Figure 1). The highest number of animals in the intermediate environment helped to better predict (G)EBV for relatives in the same environment.

The percentage of variance explained by the top 10 windows for the intercept and the slope of the reaction norm model are shown in Table 3. First, it is noticed that there is an overlap between the top 10 windows for the two parameters of the reaction norm curve. In fact, 5 of 10 top windows are in the same chromosome, but explain different proportions of variance. This indicates genes that respond differently according to the environment (presence of G × E) are associated with different regression parameters. The window 57754977–60836088 bp in chromosome 5 ranked first and second regions to explain intercept and slope variances, respectively. The window 109170245–110138379 bp in chromosome 7 is ranked second and the eighth region to explain intercept and slope variances, respectively. The window 53132988–54481098 bp in chromosome 14 ranked seventh and first regions to explain intercept and slope variances, respectively, whereas the window 79999917–81479704 bp in chromosome 6 ranked ninth region to explain the intercept variance and fourth region to explain the slope. Although we could identify some differences in variance explained for the intercept and the slope in different regions of the genome, the variance explained by those regions was very small, being responsible for a maximum of 0.77 and 0.82% of the total genetic variance.

Table 3.

Chromosomes (Chr), initial positions, final positions, and percentages (%) of the genetic variance explained by molecular markers, of curve parameters of reaction norms for YW in Nellore cattle

Intercept				Slope
Chr	Start	End	%	Chr	Start	End	%
5	57754977	60836088	0.77	14	53550213	54922181	0.82
7	109170245	110138379	0.65	5	57875453	60949768	0.62
14	29066464	30140126	0.47	24	60905721	61907273	0.50
3	101105270	102471446	0.43	6	79999917	81479704	0.45
13	82837235	84185047	0.43	2	133532431	13427863	0.36
29	34461880	35212258	0.39	16	76507199	77281589	0.35
14	53132988	54481098	0.38	18	16102077	17244081	0.34
8	36031677	36981710	0.37	7	109054576	109733472	0.33
6	79999917	81479704	0.35	23	49949142	51280200	0.33
10	87149990	88439651	0.35	9	55007839	56371776	0.32

CONCLUSION

Variance components and genetic parameters obtained via reaction norm models indicate the presence of genotype by environment interaction for YW in Nellore cattle. When genomic information is added to the model, accuracy of predicting breeding values increases, consequently helping beef cattle producers to better identify the animals that fit their production systems and that can cope with adverse environments.