Weighting genomic and genealogical information for genetic parameter estimation and breeding value prediction in tropical beef cattle

Abstract

A combined matrix that exploits genealogy together with marker-based information could improve the selection of elite individuals in breeding programs. We present genetic parameters for adaptive and growth traits in beef cattle by exploring linear combinations of pedigree-based (A) and marker-based (G) relationship matrices. We use a data set with 2,111 Brahman (BB) and 2,550 Tropical Composite (TC) cattle with genotypes for 729,068 SNP, and phenotypes for five traits. A weighted relationship matrix (WRM) combining G and A was constructed as WRM = λG + (1 − λ)A. The weight (λ) was explored at values from 0.0 to 1.0, at 0.1 intervals. Additionally, four alternative G matrices, in the WRM, were evaluated according to the selection of SNP used to generate them: 1) G_w: all autosomal SNP with minor allele frequency (MAF) > 1%; 2) G_g: autosomal SNP with MAF > 1% and mapped inside to gene coding regions; 3) G_p: autosomal SNP with MAF > 1% and previously reported to have significant pleiotropic effect in these two populations; and 4) G_c: autosomal SNP with MAF > 1% and with significant correlated effects previously reported in both BB and TC populations. In addition, two A matrices were evaluated: 1) A: all relationships between animals were considered after tracing back known ancestors; and 2) A_d: a distorted A matrix where a random 1% of the off-diagonal nonzero values were set to zero to simulate relationship errors. Five independent A_d matrices were explored each with a different random 1% of relationships masked. Criteria for comparing the resulting WRM included estimates of heritability (h²) and cross-validation accuracy (ACC) of genomic estimated breeding values. The choice of WRM had a greater impact on h² than on ACC estimates. The 1% errors introduced in pedigree relationships generated large distortion in genetic parameters and ACC estimates. However, employing a λ > 0.7 was an efficient mechanism to compensate for the errors in A. Additionally, although significant (P-value < 0.0001), we found no consistent relationship between the type of SNP used to compute G and h² or ACC estimates. We devised the optimal value of λ for maximum h² and ACC at λ = 0.7 suggesting a 70% and 30% weighting to genomic and genealogical information, respectively, as an optimal strategy to compensate for pedigree errors, to improve genetic parameters estimates and lead to more accurate selection decisions.

INTRODUCTION

The notion that realized relationships among individuals inferred from high-density SNP genotypes are more accurate than the expected from identity-by-descent theory and based on pedigree information helps to justify the investment in genomic technologies in livestock and plant breeding programs (Hickey et al., 2017). However, the choice of numerical measures of relatedness can be driven by optimizing criteria that are relevant to parameters, such as model likelihood and predictive accuracy (Speed et al., 2014). A linear combination of the pedigree- (A) with a genomic-based (G) relationship matrix is a common approach for single-step genomic BLUP (Misztal et al., 2013). A combined matrix that simultaneously exploits genealogy and marker information could provide more reliable estimates of genetic parameters and potentially capture parts of the genetic covariances among traits that are not accounted by either A or G alone (Momen et al., 2017). The optimal weighting factor (λ) to be assigned to G and A will depend on a number of attributes. These include genotype density, amount of incorrect or missing pedigree available, genetic architecture and heritability (h²) of the trait, and number of animals and phenotypes used in the genetic evaluation. For instance, high λ values attributed to the genomic information instead pedigree-based information have been successfully used in two situations where there were populations with smaller reference data set sizes and traits with low h² (Rodríguez-Ramilo et al., 2014). Instead of employing an ad hoc value for λ, a systematic statistical assessment of possible λ values will assist animal breeding programs.

Thus, the aim of this study was to comprehensively explore linear combinations of A and G and their impact on estimates of genetic parameters and accuracy of genomic predictions using a range of growth and adaptive phenotypes and two populations of tropical beef cattle.

MATERIALS AND METHODS

Animal Care and Use Committee approval was not obtained for this study because historical data were used and no animals were handled as part of the study. Analyses were performed on phenotypic data and DNA samples that had been collected previously as part of the Australian Cooperative Research Centre for Beef Genetic Technologies (Beef CRC; http://www.beefcrc.com/).

Animals, Phenotypes, and Genotypes

Animals, phenotypes, and genotypes used in this study were a subset of those used in Porto-Neto et al. (2014). In brief, we used data of 2,111 Brahman (BB) and 2,550 Tropical Composite (TC) cows and bulls genotyped using either the BovineSNP50 (Matukumalli et al., 2009) or the BovineHD (Illumina Inc., San Diego, CA) that includes more than 770,000 SNP. Animals that were genotyped with the lower density array had their genotypes imputed to higher density as described previously by Bolormaa et al. (2014).

The following five phenotypes were explored (Porto-Neto et al., 2015): 1) SHEATH: penile sheath score expressed as the correlated trait navel score in females and scored from 1 (very pendulous) to 9 (extremely tight against the ventral surface of the animal); 2) COLOR: coat color scored on a light (1) to dark (6) scale; 3) COAT: recorded during post weaning cool months at <12 mo of age. Subjectively scored at 1/3 score increments between 1 (extremely short and sleek coat) and 7 (very woolly coat). Coat scores were converted to a continuous 21-point scale; 4) COND: body condition visually assessed at an average of 30 mo of age at the end of a growing (wet) season. Subjectively scored at 1/3 score increments from 1 to 5, and subsequently converted to a continuous 15-point scale; and 5) YWT: yearling weight (kg); average, minimum, and maximum of age at yearling weight was 360, 302, and 416 d for BB, and 361, 319, and 403 d for TC, respectively.

Pedigree-Based, Genome-Based, and Weighted Relationship Matrices

The A matrix consisted of the pedigree data of 2,111 BB and 2,550 TC animals with phenotypic records and their known ancestors, resulting in 3,030 and 3,882 animals for BB and TC cattle, respectively. Also one alternative distorted A matrix (A_d) was computed by setting to zero a random 1% of nonzero off-diagonal values. In this case, the random sampling procedures was performed five times and the averaged heritability and accuracy estimates of distorted A matrix were showed in this paper.

Four alternative G matrices were evaluated according to the selection of SNP used to generate them:

• (1) G_w: all autosomal SNP with minor allele frequency (MAF) > 1%. This criterion resulted in 651,253 SNP for BB and 689,818 SNP for TC;

• (2) G_g: autosomal SNP with MAF > 1% and mapped inside gene coding regions according to the Bovine genome annotation and mining tools of Elsik et al. (2016). This criterion resulted in 250,829 SNP for BB and 266,235 SNP for TC;

• (3) G_p: autosomal SNP with MAF > 1% and with significant (P < 0.01) pleiotropic effect according to the test by Bolormaa et al. (2014) and resulting in 58,121 SNP for BB and 60,148 SNP for TC; and

• (4) G_c: autosomal SNP with MAF > 1% and with significantly correlated effects in the two populations, i.e., either always positive or always negative, according to the genomic correlation study of Porto-Neto et al. (2015) and resulting in 31,419 SNP for BB and 31,441 SNP for TC.

The number of SNP in common between G_g and G_p, G_g and G_c, and G_p and G_c in the BB (TC) population was 22,982 (23,775), 11,166 (11,178), and 3,256 (3,259), respectively. Also, there were 1,234 (BB) and 1,235 (TC) SNP in common across G_g, G_p, and G_c (Supplementary Figure S2). In all cases, the G matrices were computed separately for each breed (BB or TC) and each SNP group (G_w, G_g, G_p, or G_c) following Method 1 of VanRaden (2008).

To compute the weighted relationship matrix (WRM), we followed previously described approaches in Aguilar et al. (2009), more recently implemented in Momen et al. (2017). Accordingly, the WRM was computed as follows: WRM = λG + (1 − λ)A, where λ is a real parameter bounded between 0 and 1, inclusively. To assess the best weight, we applied the grid weight between 0 and 1, with pace of 0.1. Using these WRM, we evaluated the resulting estimates of h² and predictive ability (ACC). The ACC was measured by the correlation between predicted and adjusted phenotypes in the five data sets each one with 20% of randomly assigned missing data. The h² and ACC estimates were then averaged across the five cross-validation sets.

Statistical Analyses

The following general mixed model was employed for the estimation of variance and covariance components for each trait:

$$y_{ij}=X\beta +Zu+e_{ij}$$

where y_ij represents the phenotypic observations from the i-th individuals (I = 1 to 2,111 for BB or I = 1 to 2,550 for TC) at the j-th phenotype (j = 1 to 5), X is the incidence matrix relating fixed effects in β with observations in y_ij, Z is the incidence matrix that allocates records to breeding values in u for every individual in the relationship matrix, and e_ij is the random residual effect. Fixed effects included in the model were contemporary group (i.e., cohort, year of birth, and sex) and age as a linear covariate.

Finally, we used the procedure GLM of SAS 9.4 (SAS Inst. Inc., Cary, NC) to identify the optimal λ value for maximum h² and ACC in a linear model that contained both linear and quadratic regression terms of λ, plus the main effects of breed, type of SNP used in G (four levels), phenotype nested within breed, and the interaction between breed and type of SNP used to compute each G.

RESULTS

Estimates of kinship coefficients varied between A and G. For instance, based on G_w, the relationship coefficient among individual pairs with a relationship coefficient of 0.5 in A (i.e., either full-sibs or parent-offspring) in BB cattle (TC in brackets) averaged 0.418 (0.332) and ranged from 0.002 (0.000) to 0.694 (0.610). On the other hand, in both breeds, the correlation among diagonal and off-diagonal elements across the four alternative G matrices was high and greater than 0.7, except between diagonal elements of G_w and G_c (r = 0.53) and between diagonal elements of G_g and G_c (r = 0.55) in TC cattle (Supplementary Figure S1). Thus, the type of SNP used to compute G resulted in a small difference in the realized additive genetic covariance among individuals. The number of SNP in common to each G_g, G_p, and G_c (subsets of G_w) is showed in Supplementary Figure S2.

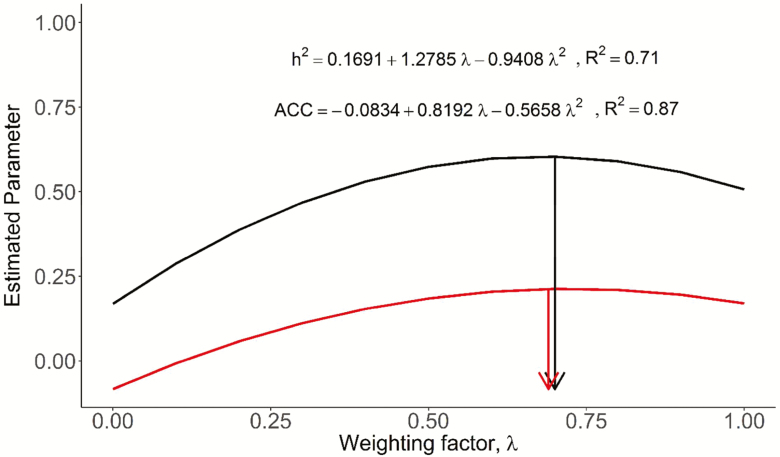
For all five traits and in the two populations, the WRM yielded higher estimates of h² and ACC with λ = 1 (marker-based information only) than with λ = 0 (pedigree-based information only) (Supplementary Figure S3). However, the highest estimates were not always observed at the upper bound of λ. For instance, in BB cattle, the highest h² (ACC) estimates were obtained with λ of 0.6 (0.6), 0.2 (0.9), 0.6 (1.0), 0.6 (1.0), and 0.6 (0.8) for COAT, COLOR, COND, SHEATH, and YWT, respectively (Supplementary Figure S3). The same values in TC cattle were 0.7 (1.0), 0.8 (1.0), 0.7 (0.6), 0.9 (1.0), and 0.6 (0.7). When all the results were examined by ANOVA and least-squares analyses, we derived a general prediction model for h² or ACC (Figure 1). With that, we predicted an optimum λ for the highest h² and ACC being λ = 0.7 (Figure 1).

Figure 1.

Overall predicted trend of weighting factor (λ) on heritability (black line) and accuracy (red line). The predicted maximum heritability (0.60) and accuracy (0.21) occurred at λ = 0.7 (black and red arrow) based on quadratic regression analysis.

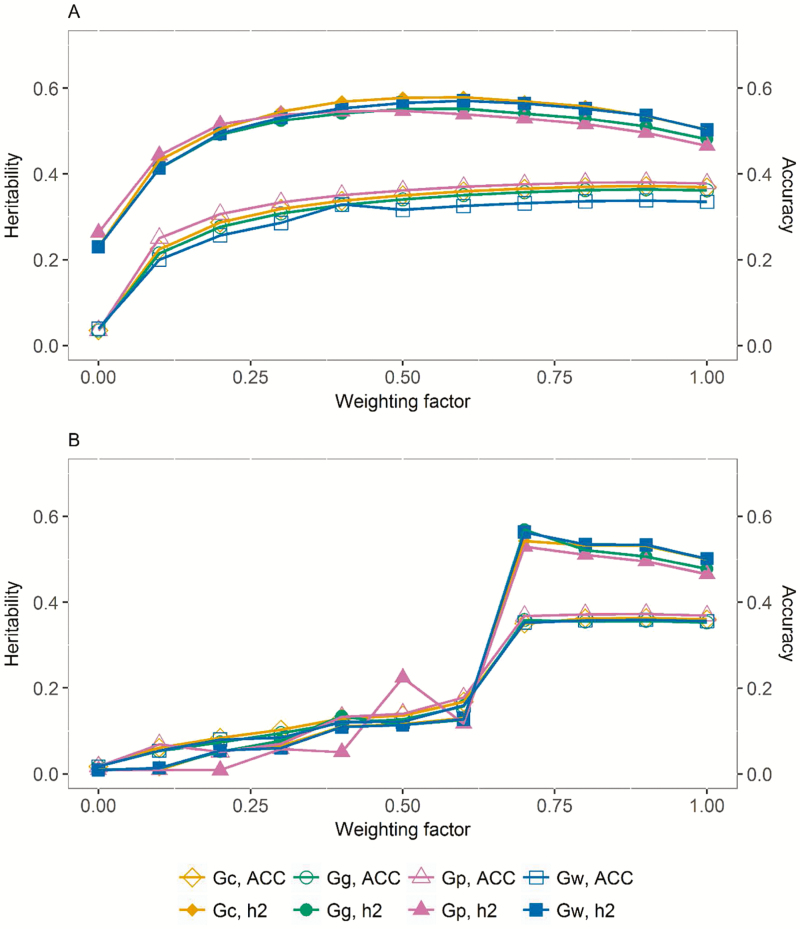
The value of genomic information was highlighted when pedigree errors were simulated as distorting A by setting to zero a random 1% of nonzero off-diagonal elements. In this situation, a value of λ = 0.7 allowing contribution from genomic information was need to compensate for the pedigree errors (Figure 2).

Figure 2.

Impact of weighting factor (λ) on average heritability (h², solid filled symbols) and accuracy estimates (ACC, empty filled symbols) across the five traits and two breeds for the original A (panel A) and the distorted A matrix (panel B, G_w = all SNP, G_g = coding region SNP, G_p = pleotropic SNP, and G_c = correlated SNP).

The ANOVA revealed the main effects of breed, trait within breed, and type of SNP used to compute G to be significant sources of variation (ANOVA P-value < 0.0001) for both h² and ACC. In addition, the interaction between breed and type of SNP was a significant source of variation (P-value < 0.0001) for ACC. Although significant, the observed differences were not consistent. Across all traits, λ values, and two breeds, the highest and lowest ACC estimate was observed for G_p and G_g, respectively, and ACC difference of 7.15% between them was observed. However, the highest and lowest h² estimates were observed for G_c and G_p, respectively, and with a difference of 5.12% between them (Figure 2).

DISCUSSION

Pedigree-based expected additive genetic covariance assumes constant and categorical covariance between relatives, while the realized genomic relationships capture the specific Mendelian sampling relationship between each pair of individuals, estimated by marker tracking of the alleles they share that are identical by descent or state. Thus, relationships estimated from marker data can in principle provide more precise estimates of genetic covariance between relatives. However, genetic parameter estimates from the combination of both sources of information could be more reliable (Momen et al., 2017).

Our results show that an optimal WRM is more efficient at capturing genetic variance than either A or G alone. The weight for maximum h² and ACC was trait-dependent, which agrees with a previous report (Rodríguez-Ramilo et al., 2014), but also breed-dependent. Higher h² estimates are preferred as they capture more genetic variation resulting in more genetic progress. However, averaged across all scenarios, 0.7 was established as the optimum value for λ. Rodríguez-Ramilo et al. (2014) observed that in dairy cattle, emphasis placed on genomic information was larger in production traits than in conformation traits, suggesting that most of the additive genetic variability in production traits was captured by G. Momen et al. (2017) evaluated the λ from 0 to 1, at 0.2 intervals on h² and ACC of BW, ultrasound area of breast meat (BM), and hen-house egg production in chickens (HHP). The highest h² estimates were obtained with λ of 0.4, 1, and 0 for BW, BM, and HHP, respectively. Thus, the result obtained in this paper and those published by Rodríguez-Ramilo et al. (2014) and Momen et al. (2017) suggest that trait specific λ could be used to recover higher amount of additive genetic variance; alternatively, the optimal λ for different traits could be tested in multiple-trait analysis (Gao et al., 2012).

In all cases explored in the present study, the smallest estimates of h² and ACC were obtained with λ = 0 (pedigree information only). Also, at λ > 0.4 only slight differences in accuracy estimates were observed. In agreement with our results, Gao et al. (2012) showed that the λ value used in single-step blending methods had a small effect on reliability. These authors showed that at λ = 0.8 the average reliability of genomic predictions for 16 traits in a Nordic Holstein population was slightly higher (0.3%) than the average reliability from the simple GBLUP (λ = 1).

In our study alternative G, using either coding region or pleotropic SNPs impacted on parameter estimates. Ni et al. (2017) reported similar findings when evaluating a trait-specific genomic relationship matrix for eggshell strength and feed intake in laying chickens, where the highest ACC was obtained with λ = 0.1 and G using coding region SNPs. It is also worth mentioning that multiple-trait GBLUP analyses are expected to increase the accuracy of predictions via “borrowing” information such as pleiotropy, marker-QTL and linkage disequilibrium relationships among markers (Gao et al., 2012). Thus, the increase in ACC obtained from using WRM in multi-trait models could be greater than those obtained in single-trait models.

To conclude, while the optimal λ value was trait-dependent, a value of λ = 0.7 may be a useful recommendation for identification and selection of sires and dams in breeding programs, to overcome pedigree errors and to estimate genetic parameters without loss in accuracy.

SUPPLEMENTARY DATA

Supplementary data are available at Animal Frontiers online.

Conflict of interest statement. None declared.