Abstract
Precision animal agriculture is poised to rise to prominence in the livestock enterprise in the domains of management, production, welfare, sustainability, health surveillance, and environmental footprint. Considerable progress has been made in the use of tools to routinely monitor and collect information from animals and farms in a less laborious manner than before. These efforts have enabled the animal sciences to embark on information technology-driven discoveries to improve animal agriculture. However, the growing amount and complexity of data generated by fully automated, high-throughput data recording or phenotyping platforms, including digital images, sensor and sound data, unmanned systems, and information obtained from real-time noninvasive computer vision, pose challenges to the successful implementation of precision animal agriculture. The emerging fields of machine learning and data mining are expected to be instrumental in helping meet the daunting challenges facing global agriculture. Yet, their impact and potential in “big data” analysis have not been adequately appreciated in the animal science community, where this recognition has remained only fragmentary. To address such knowledge gaps, this article outlines a framework for machine learning and data mining and offers a glimpse into how they can be applied to solve pressing problems in animal sciences.
Keywords: big data, data mining, machine learning, precision agriculture, prediction
INTRODUCTION
Recent developments in technologies have enabled them to make inroads into the livestock enterprise. Using these technologies, farmers, breeders’ associations, and other industry stakeholders can now continuously monitor and collect animal- and farm-level information using less labor-intensive approaches. In particular, the use of fully automated data recording or phenotyping platforms based on digital images, sensors, sounds, unmanned systems, and real-time noninvasive computer vision are gaining momentum and have great potential to enhance product quality, management practice, well-being, sustainable development, and animal health, ultimately contributing to better human health. Combined with rich molecular information such as genomics, transcriptomics, and microbiota from animals, the implementation of what is known as precision animal agriculture is within reach, where an individual animal is monitored or managed with information tailored to it. A recent issue of Animal Frontiers featured this trend in detail by referring to it as “precision livestock farming” to develop a real-time monitoring and management system that help farmers make quick and evidence-based decisions (Berckmans and Guarino, 2017). However, a new challenge to the successful implementation of precision animal agriculture stems from an unprecedented abundance of data streams. Accompanied with the enhanced capacity for data storage, high-throughput and fully automated technologies have been rapidly generating large-scale data in agricultural settings. The urgency of addressing this challenge requires a multifaceted approach to efficiently extract and summarize key information from “big data.” Furthermore, the growing global demand for animal products, expected to increase by 70% by 2050, calls for expanded and efficient production (FAO, 2009). Although scaling up to big data adds another layer of complexity, this challenge can be tackled by using techniques from machine learning and data mining. The objective of this article is to shed light on machine learning and data mining in the context of analyzing big data with particular emphasis on prediction. Specific examples of current forays of machine learning in animal science-related areas for predictive precision animal agriculture are also presented.
WHAT IS BIG DATA?
The advent of modern technologies permits us to collect ever more data at decreasing cost of acquisition. The term “big data” has received significant media attention in recent years; whereas, its definition tends to vary across disciplines. The number of rows (n) or columns (p), or both, in data is often large such that it limits visual inspection. Although classical statistical theories assume more data points than predictors, p frequently increases with n rather than staying constant. This results in a scenario where p is much larger than n (n << p), and requires appropriate statistical treatment to address the curse of dimensionality (Friedman et al., 2001). Moreover, big data are often not clean data: they may contain missing observations, confounding data, or outliers characterized as messy and noisy data. Thus, a considerable amount of data editing prior to model fitting may be required. Because the definition of “big” depends on the available computational resources, big data can be defined as data that consume more than one-third of the random-access memory of computing resources upon analysis owing to their large size. Thus, the definition of “big” is ever changing and there is the growing gap between the increasing size of big data and scientists’ data management skills (Barone et al., 2017). Moreover, although data visualization plays a crucial role in summarizing and identifying the characteristics of data, big data prevent the plotting of the entire picture. In such a case, interactive visualization, with capabilities to zoom in and out, helps investigate both global and local structures of graphs. The recent availability of the Shiny R package and Plotly to construct interactive Web applications is one example (Plotly Technologies Inc., 2015; Chang et al., 2017). Furthermore, reproducible research tools, such as Git/GitHub, R Markdown/Notebooks, and Jupyter Notebooks, need to be used so that big data analysis is reproducible. Big data offer exciting opportunities for data science (Donoho, 2017). One approach to gain insight from big data or transforming big data into knowledge is to use data mining and machine learning methods, which is the focus of this article.
MACHINE LEARNING FRAMEWORK
Machine learning, also known as statistical learning, is a subfield of artificial intelligence dedicated to the study of algorithms for prediction and inference. Learning from data is at the core of machine learning. Data mining shares a similar spirit with machine learning and is often discussed in the same context. If we are more stringent in definition, data mining encompasses the study of database systems, which becomes crucial in dealing with extremely large datasets. In most practical cases, machine learning ultimately aims to learn, or choose from, a pool of candidate probability models that can best predict unobserved data. Technically, the selection is called the “training process.” However, how can we measure the prediction ability of the selected function? Suppose, for example, that our task is to predict a phenotype of an animal from a set of genotypes and that we have a dataset consisting of pairs of phenotypes and corresponding genotypes. In machine learning, this type of task is called supervised learning, with the target of prediction (phenotype) referred to as the supervisory signal. If the phenotypes are discrete, such as disease status, the task here is more specifically called a classification task. If the phenotypes are quantitative, it is known as a regression task. In contrast, when the dataset is incomplete and only genotypes are available for the selected individuals (no phenotypes), the task is called unsupervised learning.
To choose a probability model with good prediction ability in supervised learning, we begin by splitting the dataset into two sets, a training and a testing dataset, where the latter of which playing the role of the dataset that are not available to us at the moment. When we select a probability model, we use the information from the training dataset exclusively. In particular, we construct an objective function based exclusively on the training dataset to represent the user’s choice of desirable properties for the function. We then choose from the pool of probability models the one that maximizes the objective function. One naive property used in this specific example is the likelihood of the probability model observing phenotypes in the training dataset given the corresponding genotypes in the training dataset. The deviation in the model’s prediction of the testing dataset based on the content of a real testing dataset is called testing error and serves as the measure of prediction ability. This process is called cross-validation.
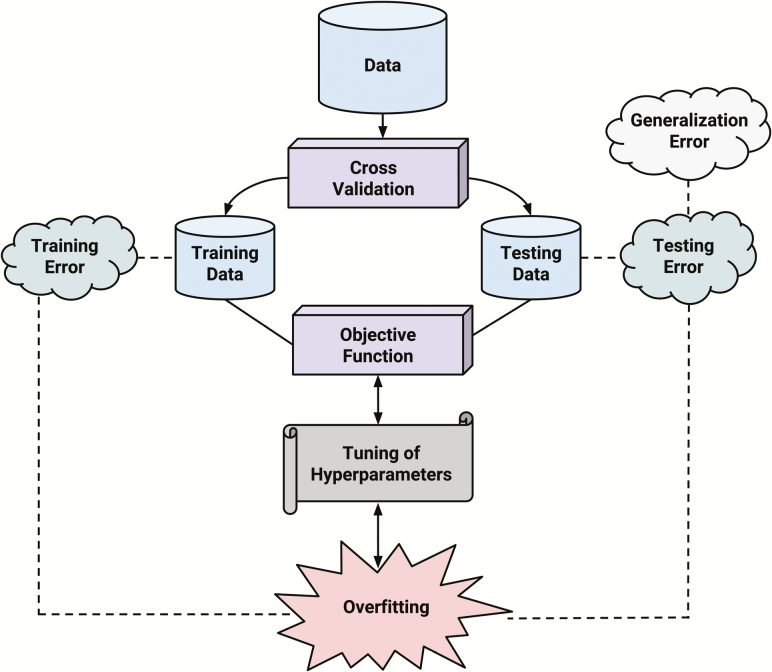
By construction, the selected probability model is good at reproducing phenotypes from genotypes on the training dataset, at least better than on the testing dataset. This is to say that the training error, or the error in the predictions of the probability model on the training dataset, is bound to be smaller than that on the testing dataset. Thus, we see that the training error is not a good measure of the prediction ability of the probability model because there is no point in predicting what we have already observed. Ideally, we look at an error as a random variable that measures the deviation of the prediction from the random sample from the true underlying distribution. The expectation of this random error is called generalization error. The testing error, or the error on the testing dataset, serves as an empirical approximation of the generalization error. In some of the literature, generalization error refers to the difference between testing error and training error. The generalization ability of a probability model is considered high if it yields low generalization error. By definition, generalization ability is the ability of the probability model to generalize our given knowledge to as-yet-unseen observations and is used as a measure of the extent of overfitting. Figure 1 shows a flowchart of the cross-validation framework.
Figure 1.
Overview of the cross-validation framework.
However, the definition of prediction ability might differ according to task. Not all experiments correlate each input with each output. For example, if our task is to predict the spatial swarm distribution of microorganisms, the task falls into the category of unsupervised learning. For this family of tasks, the target of our search is a probability distribution that closely resembles the observed empirical distribution. K-means (MacQueen, 1967) and principal component analysis (Pearson, 1901) were both developed for such tasks. Prediction ability here is measured by the extent to which samples from our selected probability distribution, as a set, resemble the observed set of samples. The deviation of the generated set of samples from the observed set is often quantified by a statistic called the Kullback–Leibler divergence (Kullback and Leibler, 1951).
Choice of Objective Function
In using machine learning techniques, it is critical to know the nature of the probability model that is selected by the method, which is completely determined by the objective function, or the standard by which the selection is made. The most basic objective function is likelihood, which consists of the model’s evaluation of the likeliness of observing what has been observed. That is, we transform the problem into that of finding a good parametric function about parameter θ that maximizes the probability p(x, θ) of observation x. If the model’s evaluation of the likelihood of the observation is small, it has little ability to reproduce the observation.
The choice of the parameter of the model using this principle is called maximum likelihood estimation. While the maximum likelihood principle is theoretically straightforward, it often suffers from overfitting. That is, the training process prioritizes training error over testing error and, therefore, over the generalization error. A function with low generalization ability is useless in prediction. For instance, any observed dataset of size n can be perfectly reproduced by a polynomial of degree n − 1. Polynomial fitting to the dataset, however, diverges outside a bounded domain, and such a function can result in extremely unnatural predictions. If observations are densely populated over regions of all possible observable values, overfitting is not a serious problem. However, naturally occurring datasets are often sparse. In general, functions with high complexity tend to overfit without some countermeasure. The core of the problem is ill-posedness (i.e., there are multiple [possibly infinite] probability models with different generalization ability that can approximate the observed values equally well). The problem of ill-posedness is especially clear when the number of parameters is greater than the number of samples, at the extreme one can even convert the parameters into observed values themselves. This is the essence of the n << p problem mentioned in the previous section.
Regularization and Generalization Ability
If we have dense observation over regions of all possible observable values, overfitting is not a serious problem. Therefore, the ultimate countermeasure against overfitting is to simply increase the size of the dataset, particularly over the space on which the current dataset is sparse. However, this can be unrealistic and costly at times. One alternative countermeasure is to introduce a heuristic penalty against the unnatural behavior of the probability model, where the definition of “naturality” is determined by the user. By augmenting the penalty function to the objective function, one can manipulate the training process into favoring the natural probability model. A popular measure of naturality is smoothness. This measure is built on the assumption that most naturally occurring phenomena are free of discontinuity. For example, the well-known L2 (Tikhonov) regularization penalizes the L2 norm (Hoerl and Kennard, 1970) of the parameter (i.e., the regression coefficient) and prevents the derivative of the function with respect to the input from becoming too large. This renders the function to smooth everywhere and known as a ridge regression. LASSO (Tibshirani, 1996) penalizes the L1 norm of the parameter. Group LASSO (Jacob et al., 2009) groups the parameters into several subsets and penalizes their L2 vector norm with varying strength. For other variations, elastic net (Zou and Hastie, 2005) uses a mixture of L1 and L2, and adaptive LASSO (Zou, 2006) chooses the strength of the penalty for each parameter in a controlled manner. All these methods have user-controllable hyperparameters that determine the strength of the penalty, and setting these parameters too high renders the function flat, leading to over-shrinkage. Mathematically, one can often appeal to the theory of Bayesian statistics to assign a probabilistic interpretation to the penalty function such that the maximization of penalized likelihood can be considered equivalent to finding an appropriate probabilistic model (Gelman et al., 2014). We can also prevent unnatural behavior of the function by simply restricting the pool of candidate functions. That is, we can declare at the outset that we will only select from the set of functions exhibiting natural behavior. Mathematically, this idea is closely related to that of the penalty presented above. For instance, one can consider a set of probability models for which the strength of correlation between output samples is determined solely by the Euclidean distance between the corresponding inputs after some transformation. This family of models is often defined using kernel functions. The representer theorem (Kimeldorf and Wahba, 1970) claims that there exists a penalty function to be added to the likelihood such that the maximization of the augmented likelihood is equivalent to searching a probability model from such a set of models. This is the essence of kernel methods.
The Choice of Pool of Candidate Functions
The measure of naturality cannot be explained by smoothness alone in many applications. Yet another countermeasure against overfitting and unnatural behavior involves using a physically sound probabilistic model. One can assume parameters from a specific known distribution based on the laws of nature. The pool of candidate functions built on specific prior knowledge is called the white-box model. In such models, every parameter has a specific biological meaning. By searching from a set of white-box models, one can not only rule out models that defy scientific laws but can also gain from the biological interpretation of the components of the selected model. However, if one imposes too strong an assumption on the model, it suffers from underfitting.
The other extreme is black-box models, a pool of models whose parameters do not contain much biological meaning. Free from the bound of physical rules, many black-box models boast the ability to reproduce highly complex nonlinear phenomena, including those for which theories have not been proposed yet. The most popular family of black-box models is neural networks (NN) or deep neural networks (DNN), a composition of many generalized regressions (Schmidhuber, 2015). One of the most popular generalized regressions is the logistic regression. When outputs are binary responses, the logistic regression model uses an assumption , or that the probability of witnessing response y when the input is x is a composition of a linear function and an activation function, called the logistic function. The DNN is a simple but large-scale extension of this framework that assumes that is a composition of hundreds of linear and activation functions. Technically, an NN with more than three compositional layers (hidden layers) is called a DNN. This family of models is used in supervised and unsupervised learning. A basic NN used for classification is the multilayer perceptron. Recent NN-based unsupervised learning techniques include the autoencoder (Vincent, 2008) and a family of generative adversarial networks (Goodfellow et al., 2014a). In a model like the NN, it is extremely difficult to attach a specific biological meaning to the parameters, which can count up to thousands in number.
However, one can attempt to restrict the pool of candidate models for NN by imposing some architectural restrictions. For example, convolutional neural networks (Krizhevsky et al., 2012) are a family of architectures fitted to extract shift-invariant features from images and time series. Recurrent neural networks (Graves et al., 2009) form an architecture specialized to process a sequence of inputs and are often used for voice and speech recognition.
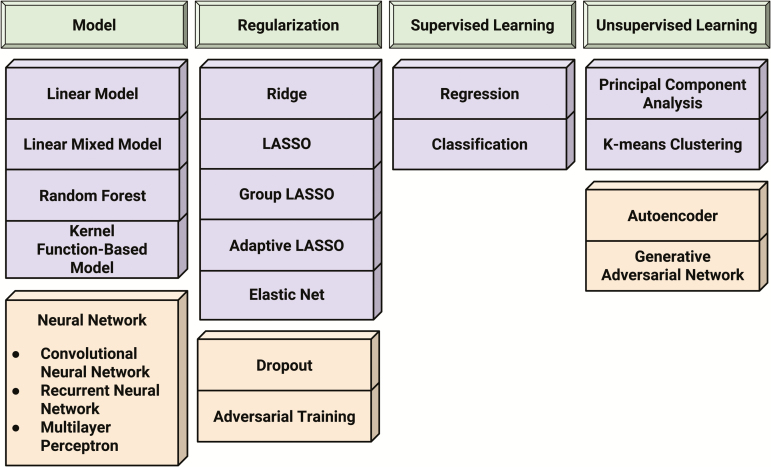
The number of parameters in a DNN can be tens of thousands. As such, it can overfit easily with a small sample set and often requires appropriate regularization for successful performance. Regularization methods for a DNN include dropout (Srivastava et al., 2014) and adversarial training (Goodfellow et al., 2014b; Miyato et al., 2015). We can also apply many of the aforementioned regularization methods to the DNN. The recent development of user-friendly open-source software libraries for machine learning, such as Chainer (Tokui et al., 2015), Keras (Chollet, 2015), and TensorFlow (Abadi et al., 2016), have allowed noncomputational scientists to set up NNs in a relatively straightforward manner. We can also mix the white-box and black-box models to balance complexity and generalization ability (Bohlin, 2006). For example, many linear mixed models in quantitative genetics fall into the intermediate category of grey-box models (Hauth, 2008) and are yielding impressive performance in empirical prediction problems. A comprehensive review of these models can be found in Morota and Gianola (2014). One can also ensemble multiple predictor functions so that prediction is not conducted by one overfitted function but a group. This approach is known as bagging. Random forest (Breiman, 2001a) is an application of the bagging philosophy. Finally, when choosing from a set of these models, we can further seek to improve our choice by adopting an information criterion (Watanabe, 2009) relating to the likelihood-based objective function. This criterion considers the approximated generalization error. Figure 2 summarizes the terminologies mentioned in this section.
Figure 2.
Summary of terminologies, including models, regularization, supervised learning, and unsupervised learning.
Summary and Perspective
Because of their success with big data, NNs and other machine learning models have gained a considerable amount of interest as a promising framework for biology. However, as mentioned above, models of high complexity tend to suffer from overfitting unless massive datasets are available. Naive applications of complex models can easily fail owing to overfitting. When faced with sparse datasets, interpolation-type techniques like kernel methods can be much more powerful than NNs with thousands of parameters. The key to applying machine learning techniques to animal science is therefore to 1) make continued efforts to construct appropriate prior knowledge for regularization and 2) continue accumulating datasets and unifying one with different modalities (i.e., data integration) to increase the sheer size of samples that can be used for training. One must also keep in mind the computational load required to analyze large integrated datasets. Whenever possible, one should always consider ways to make the model compatible with parallel computing. For instance, GPU cloud computing services provided by Cyber infrastructures such as Microsoft Azure (https://azure.microsoft.com/en-us/) and Amazon AWS (https://aws.amazon.com/) might prove useful. They also provide infrastructures to host, secure, and share big data. The next phase of growth in big data will be guided in part by efficient application of machine learning and data mining methods to inform all aspects of management decisions in the animal sciences.
EXAMPLES FROM ANIMAL SCIENCES
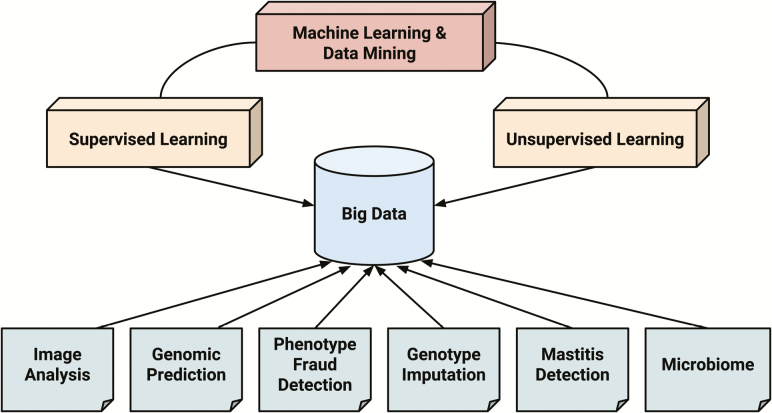
We now introduce examples of predictive big data analysis using machine learning in animal science. An overview of how these examples are related to big data analysis is provided in Figure 3.
Figure 3.
Overview of big data analysis in animal science using machine learning and data mining tools.
Genomic Prediction
Genetics has arguably made the earliest use of machine learning and data mining among the myriad of animal science fields, in the context of genome-enabled prediction of phenotypes using big data dating back to work by Long et al. (2007). Big data were referred to here as routine genetic evaluation at national- or company-level involving millions of animals with massive amounts of molecular information, such as SNPs. This continues to be a popular topic in genetics and has been extensively reviewed elsewhere (González-Recio et al., 2014; Pérez-Enciso, 2017).
Phenotype Fraud Detection
Outlier detection aims to identify profiles that may differ from all other members of a particular group. Genetic evaluation models used to compare animals and identify genetically superior ones can be affected by animals that are outliers in the dataset. Madsen et al. (2012) tested the use of the Mahalanobis distance on a dataset consisting of observations of the Jersey dairy cow using routine Nordic genetic evaluation. They reported increased accuracy of predicted breeding values for animals with one or more edited records, in addition to bias reduction for animals from the same contemporary group. Similarly, data electronically submitted by producers to genetic evaluation programs around the world may contain errors incurred during data-capture events. Outliers usually violate the mechanism that generates typical data and cannot be classified as noise. Machine learning models such as kernel-based algorithms were previously investigated successfully for outlier detection (Escalante, 2005) and can be applied to data filtering prior to genetic evaluation routines. The determination of supervised or unsupervised methods must be balanced according to the problem dimensions.
Genotype Imputation
Another demand for machine learning methods is related to the statistical inference of unobserved genotypes, a technique defined as imputation. Imputation accuracy, measured by the ratio of correct calls compared with the overall call rate, can only be determined by validation strategies that use masked genotypes from a high-density genotype panel, and not necessarily on commercially targeted animals. The prediction of imputation accuracy, based uniquely on the relatedness of low-density genotypes to those in a reference dataset using a high-density panel, was investigated by Ventura et al. (2016). These results introduced a method for determining the imputed animals to be used for further genomic studies using imputed genotypes with sufficient accuracy without causing bias in the future analysis. This method was based on a single parameter and can be improved upon by machine learning models that contain other information (e.g., the number of animals genotyped in both marker densities [low and high numbers of SNP markers], density of each panel, and breed composition of each animal from the reference and imputed set).
Mastitis Detection
According to De Vliegher et al. (2012), mastitis is a major disease in dairy cattle that affects production and udder health in the first and subsequent lactations. This significant disease in dairy herds is associated with a complex set of events triggered by various biological causes and followed by bacterial infection that promotes certain physiological and behavioral effects (Wang and Samarasinghe, 2005). Milking data such as electrical conductivity, milk yield, lactate dehydrogenase, and somatic cell scores are usually obtained over time by automatic milking machines and periodic lab tests as well as veterinarian diagnostic tests to determine the incidence of mastitis. A type of NN trained using unsupervised learning can be used to detect mastitis and provide farmers with diagnostic tools for managing mastitis. For instance, Sun et al. (2010) applied an NN to detect mastitis, with high accuracy, and to monitor the health status of a herd, especially for early intervention.
Image Analysis
Although animal behavior has been at the center of digital image analysis in animal sciences (e.g., Nasirahmadi et al., 2017; Valletta et al., 2017), BW determination in livestock is an emerging area for image analysis. Livestock body weight is critical for nutritional and breeding management because it is a direct indicator of animal growth, health status, and readiness for market. Therefore, accurate BW estimation is essential to livestock research. This domain separates itself from the traditional method to record BW using ground scales, which is a more laborious and less accurate practice. The application of image analysis for BW determination is a suitable technique to minimize these limitations, given that it is possible to automatically measure the dimensions of an animal’s images and use prediction equations to establish the relationship between them and live BW.
Recently, machine vision systems have been successfully used under the above framework (Kongsro, 2014; Gomes et al., 2016). In general, studies have reported the feasibility of biometric index analysis based on digital images. Infrared light-based depth sensors, such as a Microsoft Kinect (MK) device (Microsoft Corporation, Redmond, WA), are an appropriate vision system for this purpose. The system minimizes the steps of interferences in the captured images owing to ambient light and the animal’s hide color using depth mapping image technology (Kongsro, 2014). Images generated from an MK camera are analyzed through specific computational tools, such as the Image Acquisition Toolbox in MATLAB. In this tool, a depth map channel must be specified to ensure that good images can be acquired during the measurement process. For example, Kongsro (2014) and Gomes et al. (2016) assumed depth maps of 50 and 20 frames per acquisition, respectively, in BW studies on pigs and beef cattle. The images composed by these frames were stored and used to close the measurement session for a particular animal.
Depending on the aims of research, different sections of images can be utilized. For instance, Gomes et al. (2016) used section images of the top view of animals provided by the chest width, thorax width, abdomen width, body length, and dorsal height. They found that the chest width section correlated well (0.85) with BW. Kongsro (2014) used selected image sections to estimate pig volume, which was posteriorly correlated with BW. They reported a small average error in BW prediction using pigs of different sizes and breeds. Although the aforementioned studies indicate that digital images taken through the MK system have potential for use in BW estimation in livestock research, some challenges still exist. These include the automation of image data storage and statistical analysis. Along these lines, NN might be a feasible solution due to its flexibility and efficiency in terms of image recognition and prediction performance.
Microbiome
With advancements in next-generation sequencing methods, many opportunities have emerged for developments in animal agriculture. These include investigating complex traits, such as microbiome (Navas-Molina et al., 2017). Metagenomic investigations on species of livestock (Hobson, 1988; Fernando et al., 2007, 2010; Brulc et al., 2009; Pitta et al., 2010; Hess et al., 2011; Berg Miller et al., 2012; Anderson et al., 2016) have shed light on the importance of the microbiome to feed efficiency, animal health, performance, and productivity. However, although such metagenomic investigations have led to a better understanding of the microbiome in livestock health and productivity, a majority of the microbial genetic information generated is uncharacterized and underutilized. As such, the increasing number of metagenomic studies published has thus far failed to uncover the critical role of the microbiome and harness its metabolic capacity to increase animal productivity. This is mainly due to limitations in current bioinformatics-based approaches to identifying patterns of gene covariation to predict microbiome function (Blaser et al., 2016). Novel data mining and machine learning approaches are critical for future investigations on the microbiome to improve animal production and phenotype prediction in animal agriculture.
At present, a number of statistical approaches have been described to understand mechanistic relationships between the host microbiome and the environment (Xia and Sun 2017). Such approaches have enabled the investigation of the association between the host and environmental factors in the context of microbiome composition. However, few studies to date have attempted to predict animal phenotypes using the microbiome. Shabat et al. (2016) investigated a dairy cattle population of 78 animals representing the extremes of feed efficiency and showed that both the species and the gene composition of the rumen microbiome can be used to predict the feed efficiency phenotype with an accuracy of up to 91%. The species composition recorded an accuracy of 80%, whereas the gene composition was 91% accurate. These results underscore the importance of investigation beyond species’ composition and exploration of the functional features of the microbiome, as such features are better predictors of host phenotypes. Moreover, this study reported that features of the microbiome were highly predictive of physiological features, such as milk lactate and milk yield (Shabat et al., 2016). Similarly, Ross et al. (2013) reported the ability to predict the methane phenotype in dairy cattle populations. They reported an accuracy ranging from 0.163 to 0.553. The authors showed that training dataset size and training dataset variation have a significant effect on prediction accuracy (Ross et al., 2013). Furthermore, this study compared predictive models and reported that linear mixed models outperform random forests on metagenomic datasets. Such studies demonstrate the value of investigating large datasets for patterns in covariation to predict phenotypes. Developing such metagenomic prediction tools can yield global applications for disease prediction and diagnosis, trace-back, functional phenotyping, and selective breeding.
Due to advancements in DNA sequencing technology, DNA sequence information can be generated at high rate, but tools to harness such rich datasets are lacking. For example, the ability to annotate the functional relevance of microbiota in the gut is in its infancy. Furthermore, most studies identify correlations between shifts in the microbiota and host phenotypes but fail to identify causality. With the narrow ability of predicting how the microbiome reacts to changes and manipulations of the gut ecosystem in livestock species, the opportunities for microbiome manipulations are limited and require a multidisciplinary approach as well as novel data mining and machine learning approaches.
SUMMARY AND CONCLUSION
A fully automated data collection or phenotyping platform that enables precision animal agriculture is characterized not only by increasing amounts of data but also by the complex and dynamic nature of its collection in real time. With the support of data-intensive technologies, we can monitor animals continuously during production, and this information can be used to improve health, welfare, performance, and environmental load. The animal science community today often lacks the infrastructure and tools to make full use of these new types of data. When combined with molecular information, such as genomics, transcriptomics, and microbiota on individual animal basis, novel machine learning and data mining techniques can advance the implementation of precision animal agriculture to extract critical information and predict future observations from big data. To address such knowledge gaps, we have pointed to the availability of data mining and machine learning tools for analyzing big data, outlined their statistical framework, and illustrated examples from animal sciences. The cyberinfrastructure to host, secure, and share data can also be utilized to exploit big data. It is expected that predictive big data analysis will become increasingly common across all animal science disciplines. We contend that the first steps along this path involve grasping the advantages and pitfalls of these tools when applied to animal science-specific domains. Furthermore, close collaboration among transdisciplinary fields with complementary backgrounds, such as computer science, economics, engineering, mathematics, and statistics, along with industry, is indispensable to efficiently develop cutting-edge approaches to analyze high-throughput and heterogeneous data. As Breiman (2001b) once argued, predictive modeling is oftentimes more relevant than making inferences about the data-generating mechanism in practical scenarios. Precision animal agriculture allows farmers to formulate prompt management practices, and a predictive machine learning approach for big data-driven agriculture can prove invaluable for addressing challenges lying ahead in animal sciences.
Footnotes
S.C.F. acknowledges a support from USDA – Agriculture and Food Research Initiative (AFRI) grant (2012-68002-19823).
S.C.F., coauthor of this publication, has disclosed a significant financial interest in NuGUT LLC. In accordance with its Conflict of Interest policy, the University of Nebraska-Lincoln’s Conflict of Interest in Research Committee has determined that this must be disclosed.
Based on a presentation at The Big Data Analytics and Precision Animal Agriculture Symposium entitled “Applications of data mining and prediction methods to animal sciences” held at the 2017 ASAS-CSAS Annual Meeting, July 12, 2017, Baltimore, MD.
LITERATURE CITED
- Abadi M., Agarwal A., Barham P., Brevdo E., Chen Z., Citro C., Corrado G. S., Davis A., Dean J., Devin M.,. et al. 2016. Tensorflow: large-scale machine learning on heterogeneous distributed systems. arXiv:1603.04467.
- Anderson C. L., Schneider C. J., Erickson G. E., MacDonald J. C., and Fernando S. C.. 2016. Rumen bacterial communities can be acclimated faster to high concentrate diets than currently implemented feedlot programs. J. Appl. Microbiol. 120:588–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barone L., Williams J., and Micklos D.. 2017. Unmet needs for analyzing biological big data: a survey of 704 NSF principal investigators. PLoS Comput. Biol. 13:e1005755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berckmans D., and Guarino M.. 2017. Precision livestock farming for the global livestock sector. Anim. Front. 7:4–5. [Google Scholar]
- Berg Miller M. E., Yeoman C. J., Chia N., Tringe S. G., Angly F. E., Edwards R. A., Flint H. H., Lamed R., Bayer E. A., and White B. A.. 2012. Phage-bacteria relationships and CRISPR elements revealed by a metagenomic survey of the rumen microbiome. Environ. Microbiol. 14:207–227. [DOI] [PubMed] [Google Scholar]
- Blaser M. J., Cardon Z. G., Cho M. K., Dangl J. L., Donohue T. J., Green J. L., Knight R., Maxon M. E., Northen T. R., Pollard K. S.,. et al. 2016. Toward a predictive understanding of earth’s microbiomes to address 21st century challenges. mBio 7:e00714–e00716. doi:10.1128/mBio.00714-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohlin T. P. 2006. Practical grey-box process identification: theory and applications. Springer Science & Business Media. [Google Scholar]
- Breiman L. 2001a. Random forests. Mach. Learn. 45:5–32. [Google Scholar]
- Breiman L. 2001b. Statistical modeling: the two cultures. Stat. Sci. 16:199–231. [Google Scholar]
- Brulc J. M., Antonopoulos D. A., Miller M. E. B., Wilson M. K., Yannarell A. C., Dinsdale E. A., Edwards R. E., Frank E. D., Emerson J. B., Wacklin P.,. et al. 2009. Gene-centric metagenomics of the fiber-adherent bovine rumen microbiome reveals forage specific glycoside hydrolases. Proc. Natl. Acad. Sci. U.S.A. 106:1948–1953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang W., Cheng J., Allaire J., Xie Y., and McPherson J.. 2017. Shiny: web application framework for R. R package version 1.0.5. https://cran.r-project.org/web/packages/shiny/index.html.
- Chollet F. 2015. Keras https://github.com/fchollet/keras.
- De Vliegher S., Fox L. K., Piepers S., McDougall S., and Barkema H. W.. 2012. Invited review: mastitis in dairy heifers: nature of the disease, potential impact, prevention, and control. J. Dairy Sci. 95:1025–1040. [DOI] [PubMed] [Google Scholar]
- Donoho D. 2017. 50 years of data science. Princeton (NJ): Tukey Centennial Workshop. ; http://www.tandfonline.com/doi/abs/10.1080/10618600.2017.1384734. [Google Scholar]
- Escalante H. J. 2005. A comparison of outlier detection algorithms for machine learning. In: Proceedings of the International Conference on Communications in Computing; p. 228–237. [Google Scholar]
- FAO 2009. How to feed the world in 2050 http://www.fao.org/fileadmin/templates/wsfs/docs/expert_paper/How_to_Feed_the_World_in_2050.pdf. Food and Agriculture Organization of the United Nations (Accessed 14 September 2017).
- Fernando S. C., Purvis H. T., Najar F. Z., Sukharnikov L. O., Krehbiel C. R., Nagaraja T. G., Roe B. A., and DeSilva U.. 2010. Rumen microbial population dynamics during adaptation to a high-grain diet. Appl. Environ. Microbiol. 76:7482–7490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernando S. C., Purvis H. T., Najar F. Z., Wiley G., Macmil S., Sukharnikov L. O., Nagaraja T. G., Krehbiel C. R., Roe B. A., and DeSilva U.. 2007. Meta-functional genomics of the rumen biome. J. Anim. Sci. 85:569–569. [Google Scholar]
- Friedman J., Hastie T., and Tibshirani R.. 2001. The elements of statistical learning. Vol. 1 New York (NY): Springer Series in Statistics; p. 241–249. [Google Scholar]
- Gelman A., Carlin J. B., Stern H. S., Dunson D. B., Vehtari A., and Rubin D. B.. 2014. Bayesian data analysis. Boca Raton (FL): CRC Press. [Google Scholar]
- Gomes R. A., Monteiro G. R., Assis G. J. F., Busato K. C., Ladeira M. M., and Chizzotti M. L.. 2016. Estimating body weight and body composition of beef cattle through digital image analysis. J. Anim. Sci. 94:5414–5422. [DOI] [PubMed] [Google Scholar]
- González-Recio O., Rosa G. J. M., and Gianola D.. 2014. Machine learning methods and predictive ability metrics for genome-wide prediction of complex traits. Livest. Sci. 166:217–231. [Google Scholar]
- Goodfellow I. J., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., and Bengio Y.. 2014a. Generative adversarial nets. Adv. Neural Inf. Process Syst. 2672–2680. [Google Scholar]
- Goodfellow I. J., Shlens J., and Szegedy C.. 2014b. Explaining and harnessing adversarial examples. arXiv 1412.6572.
- Graves A., M Liwicki, S Fernández, R Bertolami, H Bunke, and J Schmidhuber. 2009. A novel connectionist system for unconstrained handwriting recognition. IEEE Trans. Pattern Anal. Mach. Intell. 31:855–868. [DOI] [PubMed] [Google Scholar]
- Hauth J. 2008. Grey-box modelling for nonlinear system [dissertation]. Fachbereich Mathematik der Technischen Universität Kaiserslautern. [Google Scholar]
- Hess M., Sczyrba A., Egan R., Kim T. W., Chokhawala H., Schroth G., Luo S. J., Clark D. S., Chen F., Zhang T.,. et al. 2011. Metagenomic discovery of biomass-degrading genes and genomes from cow rumen. Science 331:463–467. [DOI] [PubMed] [Google Scholar]
- Hobson P. N, editor. 1988. The rumen microbial ecosystem. London (UK): Elsevier Applied Science. [Google Scholar]
- Hoerl A. E., and Kennard R. W.. 1970. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12:55–67. [Google Scholar]
- Jacob L., Obozinski G., and Vert J. P.. 2009. Group lasso with overlap and graph lasso. In: Proceedings of the 26th annual international conference on machine learning Montreal, Quebec, Canada: ACM; p. 433–440. [Google Scholar]
- Kimeldorf G. S., and Wahba G.. 1970. A correspondence between Bayesian estimation on stochastic processes and smoothing by splines. Ann. Math. Stat. 41:495–502. [Google Scholar]
- Kongsro J. 2014. Estimation of pig weight using a Microsoft Kinect prototype imaging system. Comput. Electron. Agric. 109:32–35. [Google Scholar]
- Krizhevsky A., Sutskever I., and Hinton G. E.. 2012. Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems; Lake Tahoe, NV; p. 1097–1105. [Google Scholar]
- Kullback S., and Leibler R. A.. 1951. On information and sufficiency. Ann. Math. Stat. 22:79–86. [Google Scholar]
- Long N., Gianola D., Rosa G. J. M., Weigel K. A., and Avendano S.. 2007. Machine learning classification procedure for selecting SNPs in genomic selection: application to early mortality in broilers. J. Anim. Breed. Genet. 124:377–389. [DOI] [PubMed] [Google Scholar]
- MacQueen J. 1967. Some methods for classification and analysis of multivariate observations. In: Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability Vol. 1; p. 281–297. [Google Scholar]
- Madsen P., Pösö J., Pedersen J., Lidauer M., and Jensen J.. 2012. Screening for outliers in multiple trait genetic evaluation. Interbull Bull. 46. [Google Scholar]
- Miyato T., Maeda S. I., Koyama M., Nakae K., and Ishii S.. 2015. Distributional smoothing with virtual adversarial training. arXiv 1507.00677.
- Morota G., and Gianola D.. 2014. Kernel-based whole-genome prediction of complex traits: a review. Front. Genet. 5:363. doi:10.3389/fgene.2014.00363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasirahmadi A., Edwards S. A., and Sturm B.. 2017. Implementation of machine vision for detecting behaviour of cattle and pigs. Livest. Sci. 202:25–38. https://www.sciencedirect.com/science/article/pii/S1871141317301543. [Google Scholar]
- Navas-Molina J. A., Hyde E. R., Sanders J., and Knight R.. 2017. The microbiome and big data. Curr. Opin. Syst. Biol. 4:92–96. doi:10.1016/j.coisb.2017.07.003. https://www.sciencedirect.com/science/article/pii/S2452310017301270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson K. 1901. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dubl. Phil. Mag. 2:559–572. [Google Scholar]
- Pérez-Enciso M. 2017. Animal breeding learning from machine learning. J. Anim. Breed. Genet. 134:85–86. [DOI] [PubMed] [Google Scholar]
- Pitta D. W., Pinchak W. E., Dowd S. E., Osterstock J., Gontcharova V., Youn E., Dorton K., Yoon I., Min B. R., Fulford J. D.,. et al. 2010. Rumen bacterial diversity dynamics associated with changing from bermudagrass hay to grazed winter wheat diets. Microb. Ecol. 59:511–522. [DOI] [PubMed] [Google Scholar]
- Plotly Technologies Inc.. 2015. Collaborative data science Montréal (QC): Plotly; https://plot.ly. [Google Scholar]
- Ross E. M., Moate P. J., Marett L. C., Cocks B. G., and Hayes B. J.. 2013. Metagenomic predictions: from microbiome to complex health and environmental phenotypes in humans and cattle. PLoS One 8:e73056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidhuber J. 2015. Deep learning in neural networks: an overview. Neural Netw. 61:85–117. [DOI] [PubMed] [Google Scholar]
- Shabat S. K., Sasson G., Doron-Faigenboim A., Durman T., Yaacoby S., Berg Miller M. E., White B. A., Shterzer N., and Mizrahi I.. 2016. Specific microbiome-dependent mechanisms underlie the energy harvest efficiency of ruminants. ISEM J. 10:2958–2972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava N., Hinton G. E., Krizhevsky A., Sutskever I., and Salakhutdinov R.. 2014. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15:1929–1958. [Google Scholar]
- Sun Z., Samarasinghe S., and Jago J.. 2010. Detection of mastitis and its stage of progression by automatic milking systems using artificial neural networks. J. Dairy. Res. 77:168–175. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. 1996. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B (Methodol.) 58:267–288. [Google Scholar]
- Tokui S., Oono K., Hido S., and Clayton J.. 2015. Chainer: a next-generation open source framework for deep learning. In: Proceedings of Workshop on Machine Learning Systems (LearningSys) in the Twenty-Ninth Annual Conference on Neural Information Processing Systems (NIPS). [Google Scholar]
- Valletta J. J., Torney C., Kings M., Thornton A., and Madden J.. 2017. Applications of machine learning in animal behaviour studies. Anim. Behav. 124:203–220. [Google Scholar]
- Ventura R. V., Miller S. P., Dodds K. G., Auvray B., Lee M., Bixley M., Clarke S. M., and McEwan J. C.. 2016. Assessing accuracy of imputation using different SNP panel densities in a multi-breed sheep population. Genet. Sel. Evol. 48:71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent P., Larochelle H., Bengio Y., and Manzagol P. A.. 2008. Extracting and composing robust features with denoising autoencoders. In: Proceedings of the 25th International Conference on Machine Learning Helsinki, Finland: ACM; p. 1096–1103. [Google Scholar]
- Wang E., and Samarasinghe S.. 2005. On-line detection of mastitis in dairy herds using artificial neural networks. In: Proceedings of the Modeling and Simulation Congress, MODSIM 2005, Australia. [Google Scholar]
- Watanabe S. 2009. Algebraic geometry and statistical learning theory. Vol. 25 Cambridge, UK: Cambridge University Press. [Google Scholar]
- Xia Y., and Sun J.. 2017. Hypothesis testing and statistical analysis of microbiome. Genes Dis. 4:138–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H. 2006. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 101:1418–1429. [Google Scholar]
- Zou H., and Hastie T.. 2005. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 67:301–320. [Google Scholar]