Searching for Alcoholism Susceptibility Genes Using Markov Chain Monte Carlo Methods

Abstract

Markov chain Monte Carlo (MCMC) methods offer a rapid parametric approach that can test for linkage throughout the entire genome. It has an advantage similar to nonparametric methods in that the model does not have to be completely specified a priori. However, unlike nonparametric methods, there are no limitations on pedigree size and MCMC methods can also handle relatively complex pedigree structures. In addition MCMC methods can be used to carry segregation analysis in order to answer questions on the genetic components of a disease phenotype. Segregation analysis gave evidence for between two and eight alcoholism susceptibility loci, each having a modest effect on the phenotype. MCMC methods were used to map alcoholism loci using the phenotypes ALDX1 (DSM-III-R and Feighner criteria) and ALDX2 (World Health Organization diagnosis ICD-10 criteria). There was mild evidence for quantitative trait loci on chromosomes 2,10, and 11.

INTRODUCTION

Alcoholism is a complex trait which is likely to be affected by a variety of poorly known factors, both genetic and environmental. This complexity creates many problems for conventional likelihood analyses which require the genetic model to be fully specified prior to analysis. Incorrect specification of the model can lead to a loss of power to map trait loci [Clerget-Darpoux et al., 1986]. Even if the model were completely known, the complexity of the model coupled with the extended family pedigrees makes calculating multipoint likelihoods computationally difficult, if not impossible. Markov chain Monte Carlo (MCMC) methods offer sampling based solutions to these problems, allowing the use of complex, partially specified models on large pedigrees with many linked markers.

The analyses described here were performed using the program LOKI [Heath, 1997] which can be used for segregation and/or linkage analysis, and handles complications such as genetic heterogeneity and oligogenic traits. The results of the analyses are estimates of the number of trait loci involved, their effects on the trait, and an indication of where they are most likely to be located on the genome.

METHODS

The LOKI program was first used to carry out a segregation analysis to determine if there is evidence for major genes, and which covariates have an effect on the age of onset of the alcoholism phenotype. Two sets of analyses were carried out using ALDX1 (DSM-III-R and Feighner criteria) and ALDX2 (World Health Organization diagnosis ICD-10 criteria). Individuals who met the diagnosis criteria were considered affected; family members who were diagnosed either as being unaffected or having some alcoholism symptoms were classified as unaffected. Individuals who never drank were considered unknown. The preliminary analysis fit the age-of-onset model described in Daw et al. [1999] (analyzing age of onset for affected individuals and current age for unaffected study subjects). The preliminary analysis fit the age-of-onset model. The average age of onset for ALDX1 is 23.7 years (std 8) and for ALDX2 25.4 years (std 9), while for unaffected study subjects, the mean age is 40.6 years (15 std). The model assumes that everyone eventually becomes affected, and the effect of the trait loci is to shift the age of onset. A “disease” allele, therefore, will act to reduce the age of onset of alcoholism. Although this model is unrealistic, it has performed well with other diseases [Daw et al., 1999], and is simple to implement.

The following covariates were included in the analysis: sex, ethnicity, smoking (yes/no), number of packets per day for one year, MAOTRYP, harm avoidance subscale, novelty seeking subscale, and reward dependence subscale. Because in the segregation analysis ethnicity, MAOTRYP, harm avoidance subscale, and reward dependence subscale had no effect on the age of onset of alcoholism, they were removed from the model.

The LOKI program was then used to carry out the linkage analysis for the 22 autosomes first for ALDX1 and then for ALDX2. It should be noted that the results of the previous segregation analysis were not used in the linkage analysis; the genetic model was re-estimated for each run based upon the pedigree and marker data. The posterior probability of linkage for at least one quantitative trait locus (QTL) mapping to each chromosome was estimated. The prior probability of linkage to a chromosome region was set proportional to the map length ofthat region. The prior for a chromosome, therefore, was set proportional to the distance between the outermost markers. The total map length of the genome (required to calculate the prior) was set as 30 Morgans; this is a little lower than the true map length, resulting in the priors for all chromosomes (Table I) adding up to> 1.

TABLE I.

Cumulative Probability of the Number of QTLs Responsible for ALDX1 and ALDX2

Phenotype	OQTL	1 QTL	2 QTL	3 QTL	4 QTL	5 QTL	6 QTL	7 QTL	8 QTL
ALDXl	0	0	0.016	0.266	0.950	1.0	1.0	1.0	1.0
ALDX2	0	0	0	0.102	0.148	0.222	0.524	0.947	1.0

For each chromosome and each trait 100,000 sampling iterations were performed, with the first 10,000 iterations being discarded to allow the sampler time to equilibrate (burn-in). The analyses were then repeated for the chromosomes with the highest estimated posterior probability of linkage from the initial scan using an MCMC run of 250,000 iterations and a burn-in of 50,000 iterations. An arbitrary cutoff of 0.20 for the posterior probability was used to select chromosomes for the second analysis.

For a more detailed description of the methods used see Heath [1997] and Daw et al. [1999].

RESULTS

Segregation Analysis

Segregation analyses gave evidence for at least two QTLs affecting the age of onset of alcoholism. The most likely number of QTLs is five for ALDX1 and six for ALDX2. The cumulative probability of the number of QTLs controlling ALDX1 and ALDX2 is shown in Table I. The results indicate that although there is strong evidence of genetic effects on the traits, the data do not fit a single gene model of inheritance.

The effect of the QTL was measured by the square root of the variance of the age of onset of the alcoholism phenotype attributable to that particular QTL. The estimated effects of the QTLs vary, with most QTLs having an effect of lowering the age of onset by 2 to 4 years.

Linkage Analysis

An estimate of the posterior probability of linkage was obtained for all chromosomes (Table II). There was mild evidence for at least one QTL for ALDX1 on chromosome 11 (posterior probability of linkage 0.23). Stronger evidence was found when analyzing ALDX2 for QTL(s) on chromosome 2 (0.42) with weaker evidence for QTLs on chromosomes 8 (0.23) and chromosome 10 (0.35). These chromosomes were reanalyzed; this time the sampler was run for 250,000 iterations. For the second run the estimates of the posterior probability for linkage remained approximately the same for chromosome 11 (0.28), chromosome 2 (0.42), and chromosome 10 (0.27), while for chromosome 8 the estimate for the posterior probability of linkage reduced to 0.1. The prior probability of linkage for each of the autosomes is also shown in Table II.

TABLE II.

Prior Probabilities of Linkage and Estimates of the Posterior Probabilities of Linkage for the Autosomes after 100,000 (250,000) Sampling Iterations

Chromosome and (prior probability)	ALDX1	ALDX2	Chromosome and (prior probability)	ALDX1	ALDX2
1 (0.102)	0.09	0.19	12(0.061)	0.01	0.12
2 (0.097)	0.15	0.42 (0.42)	13 (0.036)	0.0	0.05
3 (0.075)	0.13	0.13	14 (0.037)	0.03	0.04
4 (0.068)	0.17	0.06	15 (0.045)	0.03	0.14
5 (0.072)	0.05	0.13	16(0.039)	0.01	0.07
6 (0.074)	0.03	0.09	17(0.037)	0.0	0.03
7 (0.068)	0.11	0.11	18 (0.036)	0.05	0.03
8 (0.056)	0.03	0.24 (0.10)	19 (0.035)	0.0	0.08
9 (0.058)	0.06	0.09	20 (0.027)	0.04	0.07
10(0.056)	0.03	0.35 (0.27)	21 (0.033)	0.01	0.04
11 (0.054)	0.23 (0.28)	0.06	22(0.017)	0.03	0.02

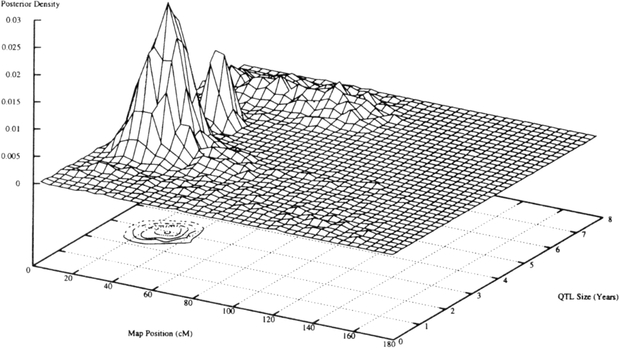
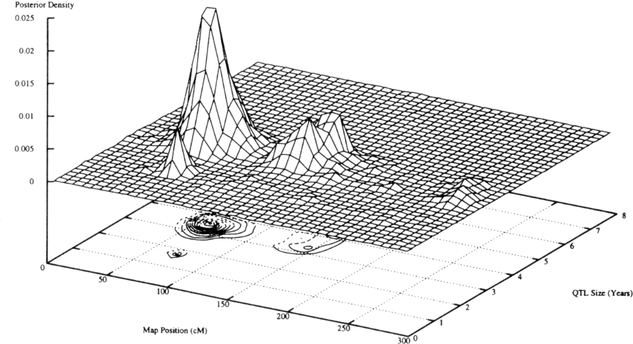
For chromosomes 11 and 2, 3-D diagrams are displayed in Figures 1 and 2, respectively. Each figure displays a 3-D diagram of the density of the QTL size (square root of the variance contributed by the QTL) against the chromosomal position estimated in the second run. Beneath the 3-D diagram a contour plot is shown that more clearly displays the region that the QTLs map to on the chromosome.

Fig. 1.

QTL density for chromosome 11.

Fig 2.

QTL density for chromosome 2.

For chromosome 11 the QTL(s) mapped to a 20 cM region between D11S1999 and D11S1977 from approximately 20 cM to 40 cM. The QTL(s) on chromosome 2 mapped to a 50 cM region, from 40 to 90 cM, between markers D2S320 and D2S379. On chromosome 10, the QTL(s) mapped to a 20 cM region from 90 cM to 110 cM between markers D10S215 and D10S670.

It should be noted that for both sets of runs the QTLs mapped to approximately the same regions; however, for chromosome 10 there was an additional 40 cM region from 30–70 cM which was identified in the initial analysis.

For the loci on chromosomes 11,2, and 10 the effect of the QTL was to reduce the age of onset by approximately 3 years.

DISCUSSION

The analyses indicate that there are multiple genes segregating that influence the age of onset of alcoholism. There is suggestive evidence of linkage to chromosome 11 when criteria ALDXl is used, and to chromosomes 2 and 10 when ALDX2 is used, but none of the signals are strong enough to confirm linkage.

Repeated analyses show similar results, but there are some differences in the estimates of the posterior probability of linkage and, sometimes, in the regions identified on a chromosome. These differences between sampling runs indicate mixing problems with the sampler, i.e., the sampler was not run long enough to obtain good estimates. Several approaches to improving the mixing characteristics of the sampler are being investigated, and it is hoped that this aspect of the method’s performance can be improved.

A useful quantity for assessing evidence for linkage is the posterior probability that a given chromosome region contains at least one QTL. If the prior probabilities take into account the total genome length (as they do for the analyses presented here), the posterior probabilities can be interpreted as genome wide probabilities, that is a probability of > 0.95 or > 0.99 is sufficient to indicate linkage at the 5% or 1% levels respectively. In this case, none of the chromosomes achieve significance, though several have an estimated posteriorrprior ratio of >1, indicating positive support for linkage. Note that for the chromosomes with relatively high estimated posterior probabilities, the posterior density on each chromosome is concentrated in a relatively small region, making the posterior:prior ratio higher. For example, for chromosome 11 with ALDXl the prior for the chromosome is 0.054 and the estimated posterior is 0.28, giving a posterionprior ratio of 5.2. However most of the posterior density on chromosome 11 is concentrated in a 20 cM region with a prior of 0.0067, giving a ratio of ~42. This ratio is not near the 1000:1 odds ratio normally required to declare linkage, but it is suggestive.

Daw and colleagues also used LOKI to carry out a genome scan on the COGA data set [Daw et al., this issue]. Their results were very different from those which this study found. This would be expected since both the models and the alcoholism phenotypes that they used in their analysis differ from the ones used here. It should also be noted that even within the analysis done here the results found for ALDXl and ALDX2 do not correspond to each other.

The power of this study could be increased by changing the age-of-onset model used for the analysis. The model used is somewhat unrealistic for this disease, and a model which, for example, allows for people never to become affected might be more appropriate. Additional improvements in power might be obtained by changing the phenotype definition; the differences in the results between ALDXl and ALDX2 show the effect of the phenotype definition on the linkage results. The MCMC method itself could also be improved, particularly with respect to its mixing characteristics. This should improve the reliability of the results, but would be unlikely to result in much increase in power. In conclusion, it is likely that obtaining significant evidence of linkage for alcoholism would require a substantially larger data set than was used. The analysis does, however, give hope for the future in that there is clear evidence for segregating genes, and the identified chromosome regions provide a focus for further study of this disease.