Private provision of social insurance: drug-specific price elasticities and cost sharing in Medicare Part D

Abstract

We explore how private drug plans set cost-sharing in the context of Medicare Part D. While publicly-provided drug coverage typically involves uniform cost-sharing across drugs, we document substantial heterogeneity in the cost-sharing for different drugs within privately-provided plans. We also document that private plans systematically set higher consumer cost sharing for drugs or classes associated with more elastic demand; to do so we estimate price elasticities of demand across more than 150 drugs and across more than 100 therapeutic classes. We conclude by discussing the various channels that likely affect private plans’ cost-sharing decisions.

Social insurance is a key function of modern governments. Historically, the public sector directly provided social insurance products, most importantly pensions and health insurance. Increasingly, however, social insurance is privately provided. Public pension systems in many countries now involve publicly-regulated but privately-run investment funds and annuities, and public health insurance is increasingly provided by private companies that are subsidized and regulated by the government.

What are the implications of this move toward privately-provided social insurance? Recently, a sizable academic literature has empirically examined the efficiency trade-offs inherent in the increased reliance on consumer choice in privately-provided insurance.¹ Other aspects that vary between public provision and private provision of social insurance have received less empirical attention. In this paper, we attempt to start closing this gap.

We focus on one design aspect of health insurance: the setting of consumer cost-sharing (also called consumer co-insurance). The consumer co-insurance rate refers to the share of the drug’s cost that must be paid out of pocket; a higher co-insurance rate corresponds to less risk protection for the consumer. Curiously, there tends to be limited variation in consumer cost-sharing provisions when health insurance is directly administered by the public sector. In a review of consumer cost-sharing provisions in public prescription drug plans of 34 OECD countries, Barnieh et al. (2014) suggests a limited scope of variation in cost-sharing across drugs.² In contrast, private insurance plans commonly set complex multi-tiered cost-sharing menus across different health care services.³

Our empirical context is Medicare Part D, the large federal insurance program that subsidizes and regulates the private provision of prescription drug insurance to the elderly in the United States. This setting is no exception to the general pattern of uniform public cost-sharing. The government-designed standard contract in Part D has a uniform, 25 percent, consumer co-insurance for any drug in the cost-sharing arm above the deductible and below the famous “donut hole.” Part D plans, however, are offered by private insurers, who have substantial discretion in designing their insurance contracts relative to this benchmark “standard contract,” including the ability to vary cost sharing across drugs. In Section I we provide more institutional detail on Medicare Part D, and describe the data sources we use to examine how private insurers vary consumer co-insurance across drugs with different price elasticities of demand.

The paper has two main parts. In the first part of the paper (Section II) we estimate the elasticity of demand with respect to the co-insurance rate for more than 150 common drugs and 100 common therapeutic classes. We use detailed micro data on prescription drug claims from more than 6 million beneficiary-years from 2007–2011. To estimate the demand response to price we exploit the variation in the out-of-pocket price for a drug created by the famous donut hole or “gap” in Part D coverage. This coverage gap makes insurance discontinuously much less generous at the margin, thus allowing us to observe the utilization response to a sharp increase in the out-of-pocket price. We previously used this research design to study the average behavioral response of drug utilization to cost-sharing and its heterogeneity across consumers (Einav et al. 2015, 2016, 2017). Here, we use a similar approach to estimate individual demand elasticities for specific drugs and therapeutic classes with respect to the out-of-pocket price. We find considerable heterogeneity in the price elasticity of demand across products. Across the approximately 150 common drugs, we estimate an average elasticity of −0.24 with a standard deviation of 0.49. Across the approximately 100 common therapeutic classes, we estimate an average elasticity of −0.15, with a standard deviation of 0.15. Since these product-specific elasticities may also be of interest and use to researchers for other reasons, we provide a complete listing of the product-specific estimates in the Appendix.

In the second part of the paper (Section III), we analyze consumer-cost sharing across drugs and classes in thousands of private Part D plans – with hundreds of unique plan designs (known as formularies) – from 2007–2011. We document substantial variation in consumer cost sharing across drugs within private plans. On average, the co-insurance rate for our common drugs was just over 40 percent, with a within-plan standard deviation of co-insurance across these drugs of 26 percent.⁴ Our key finding is that within a plan, private insurers set higher co-insurance for drugs with more elastic demand. This empirical pattern is a robust feature of the data.

We conclude the paper in Section IV with a more general discussion as to what one can (or should) make of the descriptive pattern we have documented. It seems natural to conjecture that uniform cost sharing across very different drugs – as is commonly observed in publicly-provided insurance – is unlikely to be socially optimal; it would be interesting to understand better why publicly-provided insurance programs tend to have this feature. Perhaps even more interesting is to take this uniform pattern of pricing of publicly-provided insurance as a (real or perceived) constraint, and ask whether the systematic pattern by which cost sharing varies across drugs in private plans is better or worse. In the classic theory (Feldstein 1973; Besley 1988) with risk averse and fully informed consumers, the documented variation raises social welfare by using cost sharing to efficiently trade off more moral hazard against risk protection. In the Appendix we lay out a stylized model in which private insurers’ profit maximization incentives produce the same qualitative gradient between co-insurance and the price elasticity of demand as the social planner would set. However, we also discuss several other important factors – such as behavioral biases by consumers (Baicker, Mullainathan, and Schwartzstein 2015; Handel and Kolstad 2015), bargaining with drug manufacturers (Hong 2015; Dafny et al. 2016), and externalities to non-drug medical plan choice and utilization (Starc and Town 2015; Lavetti and Simon 2016) that are not captured by our stylized framework; these likely impact private insurers’ decisions in setting co-insurance, while also making it more difficult to draw clear normative conclusions about the observed variation in co-insurance across drugs.

Our paper relates to several distinct topics in social insurance. Our empirical analysis of how private insurers vary cost sharing across drugs complements the theoretical literature on optimal health insurance design that trades off moral hazard and risk protection (Crew 1969; Feldstein 1973; Besley 1988; Ellis and Manning 2007; Goldman and Philipson 2007; Ellis, Jiang, and Manning 2015). Our comparison of private and public benefit design contributes to a small but growing literature analyzing the relative efficiency of private and public health insurance, such as Medicare Advantage compared to Traditional Medicare (Brown et al. 2014; Cabral, Geruso, and Mahoney 2014; Curto et al. 2015, 2017; Duggan, Gruber, and Vabson 2015), or service prices charged to providers by private insurance relative to public Medicare (Clemens, Gottlieb, and Molnar 2017). Our analysis of drug-specific consumer cost sharing intersects with the growing discussion of value-based health insurance design (VBID) (e.g. Chernew, Rosen, and Fendrick 2007). Naturally, our work also relates to the voluminous empirical literature examining moral hazard in health insurance (e.g. Cutler and Zeckhauser 2000; Einav et al. 2013; Aron-Dine et al. 2015), and the empirical literature on Medicare Part D (e.g. Abaluck and Gruber 2011, 2016; Ketcham and Simon 2008; Ketcham et al. 2012, 2015; Kling et al. 2012; Abaluck, Gruber, and Swanson 2015; Dalton, Gowrisankaran, and Town 2015; Decarolis 2015; Decarolis, Polyakova, and Ryan 2015; Polyakova 2016). Finally, our estimation of drug-specific elasticities contributes to the empirical literature that has estimated the price responsiveness of demand for specific drugs (e.g. Fisher Ellison et al. 1997; Goldman et al. 2004; Crawford and Shum 2005; Chandra, Gruber, and McKnight 2010; Joyce, Zissimopoulos, and Goldman 2013).

I. Setting and Data

A. Setting

Medicare Part D is a large federal insurance program that provides prescription drug coverage for seniors. Unlike traditional Medicare coverage for physician and hospital services, Medicare Part D, which was launched in 2006, is administered exclusively by private insurers. In 2015 the program covered about 42 million individuals and generated approximately $77 billion in budgetary outlays (Congressional Budget Office 2015). Part D coverage can be bundled with more comprehensive insurance provided by private plans (via Medicare Advantage), or can be purchased as a “stand-alone” coverage by Medicare beneficiaries who enroll in traditional, fee-for-service Medicare. In this paper we focus exclusively on this “stand-alone” segment of the market.

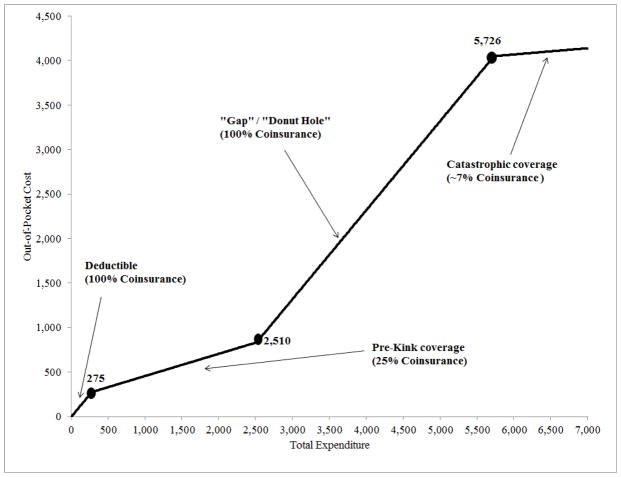
Enrollment in Part D is voluntary, but premiums are heavily subsidized. Those who choose to enroll can choose from among dozens of plans (about 30 on average) available in their (geographic) market. Part D plan design has two primary components: the overall coverage level and the detailed coverage and cost-sharing rules for specific drugs. Private insurers are required to offer coverage that is actuarially equivalent to or more generous than the standard benefit design, depicted (for 2008) in Figure 1. However, subject to this overall requirement regarding plan generosity, private insurers are given considerable flexibility as to which drugs to cover and how to assign the out-of-pocket cost to the consumers associated with each purchased drug. This latter aspect of the plan design is our primary focus.

Figure 1. Standard defined benefit (in 2008).

Figure shows the Part D Standard Defined Benefit (SDB) in 2008. The exact thresholds of the deductible, donut hole, and the catastrophic level increased over time. For example, the deductible increased from $250 in 2006 to $310 in 2011, and the donut hole level increased from $2,250 in 2006 to $2,840 in 2011.

B. Data

We use two administrative data sets. The first is a 20 percent random sample of Medicare Part D beneficiaries from 2007–2011, their plan enrollment, and their drug claims. We use these data to compute cost-sharing by plan for different drugs and therapeutic classes, and to estimate drug-specific and class-specific elasticities.

For each beneficiary, we observe the plan they enrolled in and its coverage details, as well as some basic demographics. Crucially, we also observe detailed, claim-level data on each prescription drug claim, including the date of the claim, the drug identifier (NDC code), the quantity purchased, the total amount spent on the claim, the amount paid by the plan, and the amount paid by the consumer out of pocket. We use the NDC code, together with additional data sources, to group claims by drug and by therapeutic class, to classify drugs as branded or generic, and to classify drugs as chronic or acute, and as maintenance or non-maintenance; the online appendix provides more detail on these additional data sources and how we use them. The classification of NDC codes into therapeutic classes allows us to group drugs that have similar chemical structures or mechanism of action and are frequently used to treat the same or related diseases. Thus, drugs within a therapeutic class are more likely to be substitutes than drugs across therapeutic classes.

The second data set consists of publicly-released, monthly files from the Centers for Medicare and Medicaid Services with detailed information about the formularies of all stand-alone Part D plans offered in 2007–2011.⁵ As we describe in more detail below, formularies are complete lists of covered drugs, partitioned into distinct sets of cost-sharing “tiers.” We use these data to identify on which tier each drug was placed in each formulary. Because there is plan and formulary entry, exit, and re-design year to year, we treat each plan-year as a distinct plan and each formulary-year as a distinct formulary; for convenience we refer to each simply as a “plan” or a “formulary” rather than a plan-year or a formulary-year.

II. Drug- and Class-Specific Elasticities

A. Sample construction

Baseline sample

The 20 percent random sample of Medicare Part D beneficiaries from 2007–2011 consists of about 50 million beneficiary-years. We make a number of key sample restrictions to create our baseline analysis sample in this section. First, we limit to individuals who are enrolled in stand-alone Part D plans (whose design is the focus of the second half of the paper). Second, we exclude individuals who are younger than 65 and those older than 65 that were eligible for Medicare for reasons other than the old age (e.g. due to disability). Third, we exclude individuals who receive third-party assistance with their out-of-pocket spending, such as dual Medicare/Medicaid eligibles or individuals receiving low-income subsidies; such individuals do not face the sharp change in cost-sharing at the donut hole that is key to our empirical strategy. Finally, and more trivially quantitatively, we exclude beneficiary-years who switch plans or die within the year. The final sample covers 6.5 million beneficiary-years, which are based on just over 2 million unique beneficiaries

Table 1 shows some descriptive statistics for our resulting, baseline sample. The unit of observation is a beneficiary-year. The average age is around 76, about two-thirds of the sample are females, and the vast majority (95 percent) are white. Beneficiaries in our baseline sample buy on average $1,910 worth of prescription drugs per year. About 5 percent do not fill any prescription drug claim during the year. The spending level at which beneficiaries enter the donut hole – $2,250 to $2,840 of total annual drug spending (depending on the year) – is around the 75th percentile of the expenditure distribution. The average annual out-of-pocket spending in our sample is $757. Beneficiaries fill, on average, around 31 claims a year, almost evenly split between branded and generic drugs. Our empirical strategy described below is focused on claiming propensity late in the calendar year, and about 75 percent of individuals fill at least one claim in December. Conditional on having at least one December claim, individuals have approximately 3.6 claims in December.

Table 1.

Baseline beneficiary sample

	Mean	Std. Dev.	10th pctile	90th pctile
Age	75.6	7.7	67	87
Female indicator	0.65
White indicator	0.95
Annual total spending ($US)	1,910	2,977	76	3,977
Annual out-of-pocket spending ($US)	757	937	27	1,872
Annual claim propensity
Number of claims	31.2	26.6	3	67
Number of branded claims	13.7	14.9	0	33
Number of generic claims	17.5	17.2	1	40
Share with at least one claim	0.95
Share with at least one branded claim	0.86
Share with at least one generic claim	0.90
December claim propensity
Number of claims	2.71	2.80	0	6
Number of branded claims	1.10	1.51	0	3
Number of generic claims	1.61	1.93	0	4
Share with at least one claim	0.75
Share with at least one branded claim	0.53
Share with at least one generic claim	0.63

Table based on our baseline sample described in Section II. The unit of observation is a beneficiary-year. The sample covers 6,520,716 beneficiary-years that represent 2,022,535 unique beneficiaries.

“Common” drugs and “common” therapeutic classes

In order to have sufficient power to estimate class-specific and drug-specific elasticities, we limit our analysis to frequently-claimed therapeutic classes and frequently-claimed drugs; we refer to these throughout as “common” therapeutic classes and “common” drugs, respectively. Appendix B provides more detail on our drug and therapeutic class classifications.

We define therapeutic classes using the American Hospital Formulary Service^® (AHFS) 8-level classification of 256 therapeutic classes. This classification groups drugs that have similar chemical structures or mechanism of action and are frequently used to treat the same or related diseases. We define “common” classes as ones that have at least 100,000 claims in the 2007–2011 data. This results in 108 therapeutic classes, constituting 86 percent of claims and 85 percent of expenditures. The first column of Appendix Table A14 provides a complete list.

The most frequently-claimed therapeutic class, representing 8 percent of total claims and 10 percent of total expenditures (around $1.2 billion in total) in our baseline sample, is MGH-CoA Reductase Inhibitors; this class includes anti-cholesterol drugs (e.g. Lipitor). The next most common therapeutic class is beta-Adrenergic Blocking agents, which represents 7 percent of claims and 3 percent of expenditures; this class includes Beta-blockers, which are used to treat heart attacks, arrhythmias, and high blood pressure.

We define a “drug” by its chemical compound (what the FDA refers to as “non-proprietary names”) and whether it is branded or generic. We define a drug as “common” if the sum of its branded and generic versions have at least 100,000 claims in the 2007–2011 data. Specifically, to identify “common drugs,” we begin with CMS’ 2011 list of the most frequently claimed drugs in stand-alone Prescription Drug Plans.⁶ CMS reports the most frequently claimed drugs at a chemical compound level, treating branded drugs and their generic equivalent as separate products; we amend their list to include both the generic and the branded version of each chemical if a generic is available. We apply the 100,000 claims frequency threshold to the number of claims at the chemical level, thus retaining, for example, small branded drugs that would not otherwise meet the frequency threshold.⁷

The result is 160 “common drugs,” where a “drug” is a chemical compound sold either as a brand or a generic. For example, “Atorvastatin Calcium” and its branded version (Lipitor) are counted as two different drugs. However, different packaging, dosages and strengths are not counted as separate drugs. There are 85 branded drugs and 75 generic drugs. The first column of Appendix Table A15 provides a complete list.

The 160 common drugs in our analysis account for around 65 percent of total claims and 54 percent of total expenditures in our baseline sample. The top 10 drugs in our sample of common drugs constitute 21 percent of all claims. A generic statin Simvastatin (generic version of Zocor) has the highest market share, accounting for 3 percent of total claims (6.9 million claims) and 1 percent of expenditures. The drug with the highest spending share in our sample is Lipitor, with almost 5.5 percent expenditure share. The least-frequently-claimed of our “common” drugs represents less than a 0.001 percent of claims (around 500 claims in total) in our baseline sample; in our empirical analysis in Section III.B, we explore the sensitivity of our results to the exclusion of infrequently-claimed “common” drugs.

In some of our analyses we focus on 29 of our 160 “common drugs.” These 29 drugs are less likely to have close substitutes. We identified this subset of “lower substitution” common drugs using one of two criteria. First, we selected those common drugs that account for more than 90 percent of all claims in their therapeutic class; seven drugs met this criterion. Second, we selected those pairs of branded and generic drugs for which the differences in out-of-pocket cost between the brand and generic was less than $5 in absolute value both before and after the kink. In other words, in the latter restriction we selected brand-generic pairs that did not really differ in price for consumers before or after the kink, and hence the substitution effect after the kink should be limited. 22 drugs satisfied this criterion. They account for 12 percent of all claims and 10 percent of spending in our common drugs sample.

B. Empirical strategy

Basic idea

Our goal is to measure the elasticity of demand for the product (a specific drug or therapeutic class) with respect to its out-of-pocket price. Our empirical strategy takes advantage of the sharp increase in the out-of-pocket price individuals face when they hit the “donut hole” associated with essentially every Part D insurance contract. All the plans are based around a government-defined standard benefit design, which includes four separate coverage arms for the calendar year.

Figure 1 illustrates this standard design in 2008; the kink points for the coverage arms change year-to-year but the basic structure has remained constant. In the initial deductible arm, the individual pays for all expenses out of pocket. Once she has spent $275, she enters a cost-sharing arm in which she pays only 25 percent of subsequent drug expenditures until her total drug spending reaches the kink in the budget set at $2,510. At this point the individual enters the famed “donut hole” (or “gap”), within which she must once again pay for all expenses out of pocket until total drug expenditures reach $5,726, the amount at which catastrophic coverage sets in and the marginal out-of-pocket price of additional spending drops substantially, to about 7 percent.

Insurers may offer plans that are actuarially equivalent to, or offer more coverage than the standard plan, so that the exact contract design varies across plans and hence across their enrollees. Nonetheless, a common feature of these plans is the existence of a sharp increase in the out-of-pocket price at the kink location. On average, in our baseline sample, out-of-pocket payments per drug more than triple when an individual enters the donut hole, from $17 in average out-of–pocket payments between the deductible and donut hole for a drug, to $58 in the donut hole. The co-insurance rate approximately doubles going from an average of 48 percent for pre-gap (but post-deductible) claims to 83 percent average co-insurance in the gap.

Our empirical strategy is to compare the propensity to purchase a specific drug (or therapeutic class) between individuals whose total annual spending is “just below” and individuals whose total spending is “just above” the kink location. Standard price theory suggests that individuals’ annual spending will “bunch” around the convex kink in the budget set at the donut hole. In previous work we documented this behavioral response to the price at the kink, showing the presence of an “excess mass” of individuals with annual drug spending right around the kink (Einav et al. 2015, 2016, 2017). Here, we use the same basic empirical design – with several additional years of data – to examine the behavioral response separately for different drugs and therapeutic classes and to translate this behavioral response into product-specific elasticities.

Our baseline measure of demand is the probability of purchasing that product in the last month of the year (December). We focus on December, which we used in our earlier work (Einav, Finkelstein, and Schrimpf 2015), because at that point forward looking behavior can reasonably be considered less important, as individuals have less uncertainty about their end-of-year price, and the relevant price associated with purchasing the drug is straightforward to measure (Abaluck, Gruber, and Swanson 2015; Dalton, Gowrisankaran, and Town 2015; Einav, Finkelstein, and Schrimpf 2015). The strategy would be even cleaner if we focused on purchasing decisions on December 31 of each year, but in order to gain statistical power a month seems a natural unit of time. In the sensitivity analysis we explore using shorter (last two weeks of December) and longer (November and December) time frames for our “end of year” window. We do not find that our results are sensitive to the exact definition of the time window. We also report results using a measure of the amount of the drug purchased rather than simply the probability of purchase as our demand measure.

Empirical elasticities

For each drug (or therapeutic class) d, we define its drug-specific (or class-specific) elasticity of demand by

$${\sigma }_d=\frac{\%\mathrm{\Delta }{Pr}_d(\mathit{Dec})}{\%\mathrm{\Delta }{\mathit{OOP}}_d}=\frac{\left({Pr}_d^{\mathit{obs}}(\mathit{Dec})-{Pr}_d^{\mathit{pred}}(\mathit{Dec})\right)/{Pr}_d^{\mathit{pred}}(\mathit{Dec})}{\left({\mathit{OOP}}_d^{\mathit{gap}}-{\mathit{OOP}}_d^{\mathit{pregap}}\right)/{\mathit{OOP}}_d^{\mathit{pregap}}}.$$ (1)

The changes are associated with the event of entering the donut hole. The denominator of the elasticity is the percentage change in the average (per claim) out-of-pocket cost of a given drug (or class) that occurs at the kink. ${\mathit{OOP}}_d^{\mathit{gap}}$ measures the average out-of-pocket payment (in absolute $) for a given drug (or class) in the donut hole (which comes quite close to the total cost of the drug in the vast majority of plans), and ${\mathit{OOP}}_d^{\mathit{pregap}}$ measures the average out-of-pocket payment for that drug between the deductible and the donut hole.⁸

The numerator of the elasticity is the corresponding percentage change in the probability of a December purchase for a given drug (or class). We define this as the difference between the actual probability of a December purchase, ${Pr}_d^{\mathit{obs}}(\mathit{Dec})$, and the predicted probability of a December purchase, ${Pr}_d^{\mathit{pred}}(\mathit{Dec})$ in the (counterfactual) absence of the donut hole. Both actual and predicted probabilities are measured for individuals whose annual spending is just above the kink; specifically, we focus on individuals who entered the donut hole, but whose annual spending is no more than $400 higher than the kink location. We then define the actual probability of a December purchase as the share of these individuals who have a purchase of drug (or class) d in December.

To construct the counterfactual (in the absence of the kink) December purchase probability ${Pr}_d^{\mathit{pred}}(\mathit{Dec})$ for individuals whose annual spending is between $0 and $400 above the kink, we estimate the statistical relationship between claim propensity and annual spending for individuals whose annual spending is below the kink. Specifically, we fit the following statistical relationship, separately for each drug or therapeutic class:

$$log(s_{db})={\alpha }_d-{\gamma }_d{e}_b+{\epsilon }_{db},$$ (2)

where the unit of observation is a total annual spending bin b, s_db is the share of individuals within the spending bin b without a claim for drug (or class) d in December, and e_b is the lower bound of the spending bin b (we use spending bins of $20 each). This specification is designed to make the probability of a December purchase monotone in the spending bin (as would be expected given that higher total spending is associated with sicker individuals and would mechanically correspond to greater claim propensities) and asymptote to one as the bin amount approaches infinity. Importantly, we fit this regression using only observations from individuals with total expenditures that are sufficiently below the kink location (we use all spending bins that are between $2,000 and $500 below the kink), assuming that late in the year individuals who are $500 or more below the kink are sufficiently certain to not hit the kink by the end of the year. We use the estimates from equation (2) to project it (out of sample) for spending bins that are above the kink, which gives us the predicted share of individuals without a claim. This projection assumes that absent the kink, individuals with spending slightly above the kink would have remained on the same spending trajectory as (in sample) individuals with spending below the kink. Computing the complement of the share of individuals without a claim, we get the predicted December claim propensity ${Pr}_d^{\mathit{pred}}(\mathit{Dec})$ for individuals with total spending of zero to $400 above the kink.

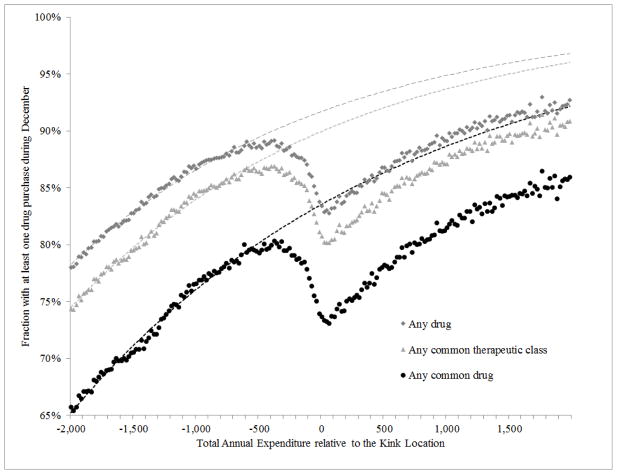
Figures 2 and 3 present our core approach to estimating the change in demand at the kink graphically. For illustrative purposes, Figure 2 shows results for any drug, any common drug, and any common therapeutic class. Since our core estimates are product specific, Figure 3 shows results for the top three common drugs and the top three therapeutic classes. In all figures, the horizontal axis reflects the annual total drug spending (across all drugs) of each individual, relative to the year-specific kink location. The vertical axis shows the share of beneficiaries in each $20-bin of annual spending who purchased that drug or therapeutic class in December. As would be expected, this purchase probability is increasing in total annual expenditures, reflecting the fact that individuals who spend more on drugs annually are more likely to purchase any given drug. However, for some of the products we see a sharp slowdown in the probability of a December purchase as individuals get close to the donut hole. Once they enter the coverage gap, the pattern reverts to the original monotone pattern (in which the probability of purchasing is rising with total annual spending), albeit at a lower probability of December purchases, presumably reflecting the higher cost-sharing in the gap.

Figure 2. Claim propensity in December as a function of annual spending –pooled estimates.

These three graphs plot the share of individuals within a $20 dollar spending bin that filled a claim in December for (i) any drug - marked with dark gray squares; (ii) any common therapeutic class - marked with light gray triangles; or (iii) any common drug - marked with black dots. The top scatter plot for “any drug” is an updated version (that is, additional years of data are included) of Figure V in Einav, Finkelstein, and Schrimpf (2015). The spending bins are recorded on the x-axis; the spending is calculated as relative to the kink location in the corresponding year. Each of the three dotted lines plots predictions from a regression described in Section II.B, which is fitted using observations that are to the left of $500.

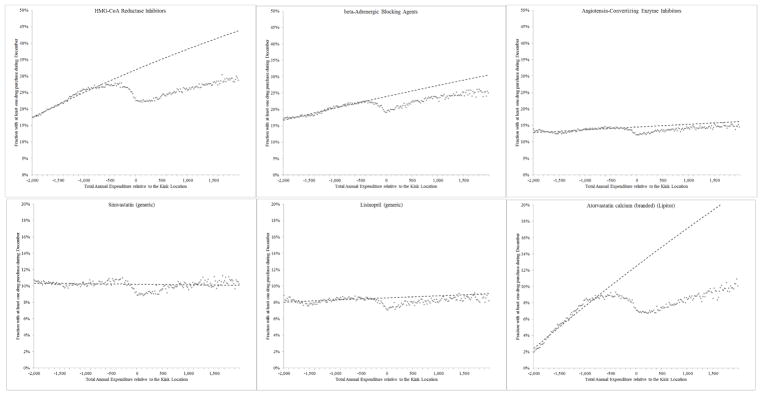
Figure 3. Claim propensity in December as a function of annual spending.

Figure shows the probability of filling a claim in December, for the top three “common” therapeutic classes (top panel) and the top three “common” drugs (bottom panel). The horizontal axis is the individuals’ total annual drug spending relative to the (year-specific) kink location; we bin spending in $20 bins. The vertical axis is the fraction of individuals within each bin with at least one claim in December associated with the drug (or class). The dashed lines are generated from the estimates of equation (2), as described in Section II, where we fit the line on all individuals whose spending is $500 below the kink location and lower.

The dotted lines in Figures 2 and 3 record our in- and out-of sample predictions of the probability of filling at least one claim in December for each product. These predictions are based on the predicted values from the estimation of equation (2). The fit appears quite good in sample (i.e. below −$500). The comparison of predicted and observed probabilities of purchase right around the donut hole allows us to quantify the demand response for each drug (or class) on our list. For example, for those products presented in Figure 3, we see a fairly large demand response for two products (top left and bottom right) and a much smaller one for the rest. To assess the statistical precision of our elasticity estimates, we use 100 bootstrap samples to repeat the same procedure and generate confidence intervals for quantity response. We then combine these estimates of the quantity response with the empirically observed change in out-of-pocket price at the donut hole to obtain elasticity estimates in each case.

Discussion and concerns

The key advantage associated with our empirical strategy for estimating product-specific elasticities is that it is scalable. That is, it is relatively easy to implement, and can be applied uniformly across a large range of drugs or therapeutic classes, and thus can result in elasticity estimates that are comparable across very different drugs and treatments. Naturally, however, any attempt to use the same strategy to estimate so many elasticities must involve some critical trade-offs and concerns. We discuss these below. Throughout the discussion, we point out that our primary use of the estimated elasticities later in the paper is in correlating them with cost-sharing decisions by insurers, making the ordinal ranking of these elasticities more important than the cardinal values. This may not be true in other contexts for which researchers might be interested in using our estimated product-specific elasticities.

The biggest (in our view) concern associated with our empirical strategy is that the key price change being used – the increase in co-insurance when the consumer enters the donut hole – is associated with price changes that affect all drugs, not only the drug for which the elasticity is being estimated.⁹ This implies that cross-drug substitution can affect our elasticity estimates. Any cross-drug substitution in response to the overall increase in co-insurance is likely to bias elasticity estimates (in absolute value) upwards for cheaper drugs and downward for expensive drugs. To see this, consider for example a branded drug and a generic alternative. If the percentage (out-of-pocket) price increase is similar for both drugs upon entering the coverage gap, the absolute price difference increases, and beneficiaries will likely substitute from the branded to the generic drug, making the generic demand response appear lower and the branded demand response higher relative to what they would have been if substitution were not important.

One way to directly address this concern is to estimate a more complete demand system for drugs, but we would still confront the fact that the main price changes in our data are correlated across drugs, making it less obvious how to separately identify own-price and cross-price substitution parameters without additional variation in drug-specific prices. Instead, other than acknowledging this limitation, two analyses that we report below make us less worried about this concern (in the context of our analysis). First, we also run our entire analysis at the therapeutic class level. To the extent that – by the nature of the definition of a therapeutic class – substitution across classes is much less common than substitution across drugs within a class, it is reassuring that the qualitative results later in the paper also hold at the class level. Second, we constructed a subset of our common drugs for which substitution is less likely, and for which therefore our drug-specific elasticity estimates may more closely approximate own-price elasticities; we described above the empirical construction of this “lower substitution” subset of drugs. As we will show, the qualitative results are quite similar for this subset of drugs, which is reassuring that our full set of common drug-specific elasticities may not be greatly affected by substitution.

More generally, the price elasticities of demand that we estimate should be interpreted in their specific context. We briefly highlight here four additional concerns about our empirical strategy for estimating elasticities. In the robustness analysis below we explore alternative specifications designed to address each one. Our main qualitative findings of heterogeneity in elasticities across products and higher co-insurance for products with more elastic demand are robust to all of these alternative specifications.

First, as emphasized by Aron-Dine et al. (2013, 2015), “the” price elasticity of demand is not a clearly defined object when individuals face a non-linear price schedule. Here, the elasticity we measure is the “short-run” elasticity of demand with respect to an end-of-year increase in the spot price of a drug. It does not measure the entire response to the non-linear budget set the individual faces, which may include “anticipatory” behavioral changes, and inter-temporal substitution of purchases across years; this may include stockpiling drugs for next year if one ends up below the donut hole, or delaying purchase of drugs to the next year if one ends up in the donut hole. In previous work (Einav, Finkelstein, and Schrimpf 2015), we explored such dynamic considerations and cross-year substitution and found that the drugs associated with elastic demand are (naturally) also associated with greater inter-temporal substitution. Below we show how we can adjust our elasticity estimates to account for such cross-year substitution, and also show results restricting attention to plans where it should be less of a concern.

Second, our elasticity estimates are local to the variation used. In particular, we are examining behavioral responses to price changes by individuals whose annual spending is around the donut hole (about the 75th percentile in the annual spending distribution). Behavioral responses are likely heterogeneous across individuals and therefore may well differ for consumers with different levels of annual drug spending. Again, as we have discussed, in our specific exercise the key is the ordinal ranking of elasticities across products rather than the magnitudes of the product-specific elasticities; the assumption that the ranking of elasticities is similar across populations seems a more reasonable one. However, we explore sensitivity to one specific, and more subtle version of this general concern about the local nature of our estimates: individuals may choose their plans in anticipation of their probability of reaching the gap and of their behavioral response to price changes in the gap (similar to the discussion of selection on moral hazard in Einav et al. 2013). In such a case, our elasticity estimates would be capturing the response of this selected sample of beneficiaries, who may have more elastic demand or experience lower price changes. We show that our results are robust to estimating the elasticities on a sub-sample of individuals who are enrolled in plans without coverage in the gap, and for whom the selection on moral hazard concern is therefore less pronounced.

Finally, as mentioned earlier, we show the robustness of our results to using alternative windows for measuring the “end of the year” and a measure of quantity based on the amount of the drug purchased rather than simply the probability of purchase.

C. Results

Elasticity estimates

We start by estimating an elasticity of purchasing any drug (common or not) in December to the change in out-of-pocket cost at the kink. Figure 2 showed the change in the probability of December purchases overall at the kink, relative to the predicted probability; we estimate a 9 percent decrease in the probability of claiming any drug in December once individuals enter the gap. As described earlier, we separately calculate that the average out-of-pocket price increases by 240 percent (from $17 to $58). These two estimates together imply that drugs are in general quite inelastic, with an elasticity of −0.038 (s.e. 0.0003); a one percent increase in out-of-pocket cost leads to a 0.038 percent decrease in the probability of filling a claim.

To see how representative our common drugs and common therapeutic classes are to the overall universe of drugs claimed within the Part D program, we calculated a pooled elasticity measures for all 160 common drugs and for all 108 therapeutic classes. The pooled elasticity measures the response of the probability of purchasing any common drug (or, respectively therapeutic class) to a one percent increase in the average out-of-pocket cost of all common drugs (or therapeutic classes). We found the pooled elasticity estimates to be very similar for our common drugs, common therapeutic classes, and all drugs samples; the percentage changes in the probability of purchase and in the average out-of-pocket price were also quite similar across these three groups. Specifically, we estimate an elasticity of −0.047 (s.e. 0.0004) for common drugs, and of −0.044 (s.e. 0.0003) for common therapeutic classes.¹⁰

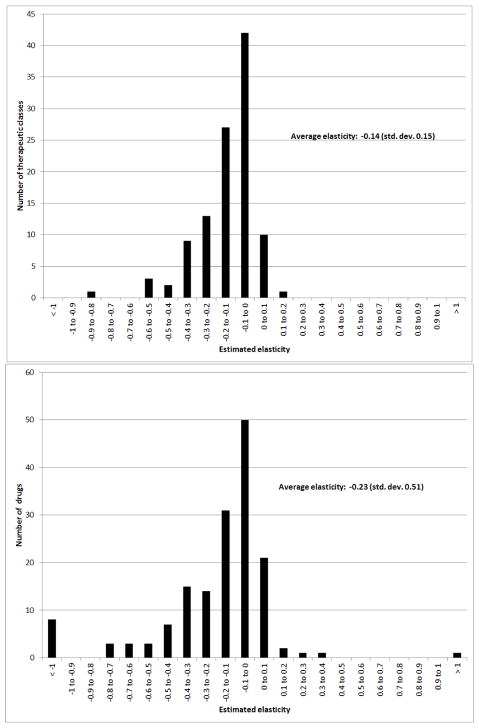
Figure 4 documents the distribution of the estimated elasticities across the common drugs and common therapeutic classes. The top panel reports the estimated distribution of elasticities across the 108 common therapeutic classes. The average (unweighted) elasticity across therapeutic classes is −0.15. They are all less than 1 in absolute value; we estimate 11 elasticities that are slightly greater than 0, which presumably reflects sampling error. There is substantial heterogeneity in the elasticities, with a standard deviation across therapeutic classes of 0.15. Panel A of Table 2 lists the elasticity estimates – as well as the denominator and numerator separately – for the top 10 most frequently claimed therapeutic classes. The elasticities are estimated quite precisely: Panel A in Appendix Figure A1 plots bootstrapped confidence intervals for the elasticity estimates for the top 10 common therapeutic classes, suggesting that the heterogeneity in the sensitivity of demand to changes in out-of-pocket is not driven by sampling variation. Appendix Table A14 provides a complete list of elasticity estimates for all common therapeutic classes. This “look-up” table also documents that the variation in elasticity estimates comes both from variation in the numerator and the denominator. The average change in the probability of purchase at the kink is −16 percent, with a standard deviation of 13 percent. The average increase in out-of-pocket cost is 155 percent, with a standard deviation of 81 percent.

Figure 4. Distribution of elasticity estimates.

Figures show the distribution of the estimated elasticities across the 108 “common” therapeutic classes (top panel) and 160 “common” drugs (bottom pane). Appendix Tables A14 and A15 report the complete list.

Table 2.

Elasticity estimates for ten largest common drugs and therapeutic classes

Therapeutic Class (1)	Drug example (2)	Claim share (3)	%3Q (4)	%3OOP (5)	Estimated elasticity (6)
HMG-CoA Reductase Inhibitors	Lipitor	0.077	−31.9	136.1	−0.23 (0.002)
beta-Adrenergic Blocking Agents	Propranolol	0.067	−17.5	125.5	−0.14 (0.003)
Angiotensin-Converting Enzyme Inhibitors	Lisinopril	0.047	−14.1	87.7	−0.16 (0.007)
Thiazide Diuretics	Diuril	0.045	−27.0	84.2	−0.32 (0.006)
Thyroid Agents	Levothyroxine	0.038	−18.1	21.4	−0.85 (0.029)
Dihydropyridines	Amlodipine	0.031	−19.5	138.0	−0.14 (0.004)
Proton-pump Inhibitors	Omeprazole	0.030	−26.6	243.0	−0.11 (0.002)
Selective Serotonin-reuptake Inhibitors	Prozac	0.023	−16.4	111.5	−0.15 (0.005)
Angiotensin II Receptor Antagonists	Losartan	0.022	−29.3	74.8	−0.39 (0.008)
Opiate Agonists	Morphine	0.022	−5.5	131.9	−0.04 (0.007)

Drug name (1)	Brand/Generic (2)	Claim share (3)	%3Q (4)	%3OOP (5)	Estimated elasticity (6)
Simvastatin	Generic	0.034	−10.8	110.8	−0.10 (0.006)
Lisinopril	Generic	0.028	−12.6	57.3	−0.22 (0.014)
Atorvastatincalcium	Brand	0.022	−48.3	143.3	−0.34 (0.003)
Levothyroxinesodium	Brand	0.021	−21.6	13.9	−1.56 (0.056)
Levothyroxinesodium	Generic	0.018	−13.9	38.8	−0.36 (0.027)
Amlodipinebesylate	Generic	0.018	−17.5	123.5	−0.14 (0.007)
Omeprazole	Generic	0.017	−24.3	242.9	−0.10 (0.003)
Warfarinsodium	Generic	0.017	−19.2	82.8	−0.23 (0.011)
Hydrocodonebitartrateandac	Generic	0.017	−3.7	98.5	−0.04 (0.011)
Hydrochlorothiazide	Generic	0.016	−20.4	38.1	−0.54 (0.025)

Table reports the estimated elasticities for the ten most frequently claimed therapeutic classes (top panel) and drugs (bottom panel). Column (3) reports the share of each class’ claims in the baseline sample. Column (4) reports the estimated percentage change in the observed (relative to the predicted) claim propensity in December for individuals who enter the donut hole. Column (5) reports the associated percentage change in the out-of-pocket price. Elasticities -- reported in clumn (6) -- are then estimated based on equation (1), with standard errors in parenthesis (based on 100 bootstrap samples from which we estimate the change in claim propensity). See Section II for more details.

The bottom panel of Figure 4 reports the drug-specific estimates across our 160 “common” drugs. The bottom panel of Table 2 lists the elasticity estimates for the top 10 most frequently claimed drugs; Appendix Table A15 provides a complete list. Panel B of Appendix Figure A1 plots the confidence intervals for the 10 largest common drugs, again suggesting that the variation in elasticities does not simply reflect sampling variation. The average (unweighted) price elasticity of demand for a given drug is about −0.24; the standard deviation of estimated elasticities across drugs is 0.49. The higher (in absolute value) average elasticity for drugs than for therapeutic classes is consistent with the idea that some of the drug-level elasticity estimates may be capturing substitution, while therapeutic class-level elasticities are more likely to only reflect the own-price response. Once again we estimate heterogeneity in elasticities, stemming both from variation in the probability of purchase response as well as variation in the change in out-of-pocket price. For the full set of common drugs the average change in the probability of purchase around the kink is −14 percent with a standard deviation of 18 percent. The average increase in out-of-pocket price is 148 percent, with a standard deviation of 108 percent.

Elasticity patterns across drug and class types

The above results documented that there is considerable heterogeneity in the price elasticity of demand across drugs and therapeutic classes. We examined some potential systematic sources of this heterogeneity. Table 3 reveals intuitive patterns. Drugs that treat chronic conditions are associated with elasticities that are 0.27 greater (in absolute value) on average relative to drugs that treat acute conditions; the latter presumably treat more symptomatic conditions for which the impact of interrupting treatment is likely more immediate and salient. Maintenance drugs – another way to define drugs associated with ongoing, chronic conditions which may have less measurement error (see Appendix B for details) – are likewise associated with greater elasticity than non-maintenance drugs, as are therapeutic classes which are predominantly composed of maintenance drugs.

Table 3.

Elasticity differences by drug categories

	Mean elasticity	Std. Dev.
Acute drugs	−0.14	0.25
Chronic drugs	−0.41	0.71
Non-maintenance drugs	−0.04	0.27
Maintenance drugs	−0.28	0.51
Branded drugs	−0.32	0.64
Generic drugs	−0.14	0.15
Predominantly non-maintenance classa	−0.10	0.09
Predominantly maintenance classa	−0.17	0.17

Table reports (unweighted) average (and std. dev.) estimated elasticities for different subsets of drugs (and therapeutic classes). See on-line appendix for details of how these classifications are constructed.

^aWe consider a class as “predominantly maintenance” if the majorty of the associated drugs are classified as to maintenance drugs; in most therapeutic classes all drugs are either maintenance or not.

We also find that generic drugs are associated with elasticities that are about 0.18 lower (in absolute value) than branded drugs. This might reflect lower own-price elasticities for generic than branded drugs, but it might also be driven by the substitution effect described earlier. As mentioned, as a way to assess the importance of substitution for our main results, we report results for a “lower substitution” subset of 29 drugs (of our 160 common drugs). The distribution of elasticities for the lower substitution sub-sample of common drugs is similar to the full sample of common drugs. The unweighted average elasticity is −0.28, with a standard deviation of 0.43. This makes the set of lower substitution drugs only somewhat more elastic on average than the entire set of common drugs. Overall, this is reassuring that our full set of common drug-specific elasticities may not be greatly affected by substitution.

III. Private Plan Design: Drug-Specific Cost-Sharing

In Section II we estimated product-specific elasticities, and provided evidence of substantial heterogeneity in the price elasticity of demand across therapeutic classes and across drugs. We now use this as an input for examining how private plans set cost-sharing across drugs with different elasticities. We begin by documenting the heterogeneity in cost-sharing across drugs within private part D plans, and then examine the empirical correlation between a product’s cost-sharing and its price elasticity of demand.

A. Heterogeneity in cost-sharing across drugs

The private insurer makes two distinct decisions in setting coverage rules in a specific plan. First, it creates a formulary.¹¹ This is a list of covered drugs, partitioned into a distinct set of cost-sharing “tiers.” In any plan, all drugs in a given tier within a formulary are assigned the same co-pay or co-insurance rate.¹² While there are no explicit regulatory requirements of cost-sharing levels across tiers (as long as plans satisfy the minimum actuarial requirement described earlier), CMS emphasizes that tier numbers should reflect an increasing level of cost-sharing, with the drugs in Tier 1 having the lowest cost-sharing (CMS 2011). CMS also requires that private Part D plans include a sufficient number of drugs on their formularies to cover all disease states; moreover, for all therapeutic classes, at least two chemically distinct drugs per class should be included on the formulary, while for six “protected” therapeutic classes all drugs have to be included (CMS 2011). It is common for a given formulary to be used in multiple plans by the same insurer; overall, we observe 7,958 plans and 426 distinct formularies.

When plans use the same formulary, they have the same set of drugs in each tier but the mapping between tiers and the level of cost-sharing may vary across plans. This creates the second decision the insurer must make: the level of consumer cost-sharing rates associated with the tiers of a plan’s chosen formulary. As noted, insurers face little regulatory constraints on how to vary cost-sharing across tiers, provided that their plan meets the minimum actuarial coverage required by the standard benefit design described in Figure 1. Consumer cost-sharing can be either in the form of co-pay (a fixed out-of-pocket dollar amount per prescription) or a co-insurance rate (a fixed percentage of the drug-specific pharmacy price that is paid out of pocket). For example, in 4-tier plans (which enrolled over 80 percent of beneficiary-years in our sample), tiers 1 through 3 are often associated with co-pays, while drugs in tier 4 often have co-insurance.

To operationalize the comparison across plans, drugs, and tiers, we convert all pricing decisions to co-insurance rates at the drug-plan level. Specifically, we calculate claim-level co-insurance as the ratio of out-of-pocket spending to total spending on that claim, using only claims between the deductible and the donut hole. We then average across claims to produce co-insurance estimates for each drug-plan pair.

In contrast to publicly provided drug insurance, we find a high degree of variation in consumer cost sharing across drugs within private plans. The average (pre-gap) co-insurance for common drugs is 43 percent, while the average standard deviation of (pre-gap) co-insurance within plans across common drugs is 26 percent.

Table 4 provides some summary statistics on plan design and drug pricing. It shows results for 3-tier, 4-tier and 5-tier plans which enroll, respectively, 8, 81, and 9 percent of our baseline sample. A few other plans (not reported) have 1, 2, or 6 tiers. We focus our discussion on 4-tier plans, but the patterns are similar for other types of plans.

Table 4.

Plan design and drug pricing

	No. of all drugs (1)	No. of “Common” drugs (2)	Share generics (3)	OOP ($US)a (4)	Total cost ($US)a (5)	Co-insurancea (6)	Claim share (all drugs) (7)	Claim share (“common” drugs) (8)
3-Tier plans (8% of enrollees; 12% of plans)
Tier 1	1,727.3	70.4	0.652	4.1	21.9	0.18	0.060	0.062
Tier 2	840.3	37.0	0.120	36.4	130.5	0.28	0.019	0.018
Tier 3	498.8	10.6	0.048	77.6	218.3	0.44	0.003	0.002
4-Tier plans (81% of enrollees; 61% of plans)
Tier 1	1,827.3	70.1	0.643	6.4	21.5	0.30	0.581	0.616
Tier 2	848.5	36.9	0.114	40.5	141.0	0.29	0.189	0.170
Tier 3	855.5	25.7	0.091	68.0	131.5	0.53	0.043	0.025
Tier 4	275.7	1.8	0.054	199.6	682.7	0.29	0.001	0.000
5-Tier plans (9% of enrollees; 21% of plans)
Tier 1	1,498.4	59.7	0.629	6.7	20.3	0.34	0.059	0.064
Tier 2	875.8	38.5	0.391	34.2	114.0	0.31	0.022	0.021
Tier 3	768.3	27.4	0.076	62.8	133.3	0.50	0.009	0.007
Tier 4	659.4	20.5	0.168	66.3	193.8	0.37	0.001	0.001
Tier 5	275.6	2.2	0.105	199.4	651.2	0.31	0.000	0.000

Table uses our baseline sample described in Section II. Each cell in the table reports average across plans that have the associated number of tiers. Column (1) reports the average number of drugs (defined here by the number of NDC11 codes on the formulary), column (2) reports the number of “common” drugs, and column (3) reports the share of all drugs that are generic. Columns (4) and (5) report, respectively, the average out-of-pocket and total cost per claim (for “pre-gap” claims) for all drugs. Column (6) converts the out-of-pocket costs to a co-insurance rates for all drugs. For each plan and tier we calculate the aggregate co-insurance as the ratio of OOP spending in that plan-tier to total spending on drugs in that plan-tier. We then average across plans. Columns (4), (5), and (6) reported weighted average (by plan enrollment), while the other columns are not weighted. Columns (7) and (8) record the share of each tier’s claims out of, respectively, all claims and “common drugs” claims in the sample.

^aOOP cost, total cost, and co-insurance rate are based only on claims that are above the deductible and under the donut hole.

About half of drugs are placed in tier 1, with another 20 percent in tier 2, and another 20 percent in tier 3 (column 1). This distribution of drugs across tiers is roughly similar for our subsample of common drugs (column 2). Almost two thirds of drugs in tier 1 are generic; generics are fairly uncommon in higher tiers (column 3).

The insurer chooses the out-of-pocket prices associated with different tiers on the formulary for each plan. There is a clear pattern of increasing average out-of-pocket costs paid by consumers in higher tiers. This is shown in column 4, which reports the average out-of-pocket payments per claim in each tier for claims made between the deductible and the donut hole (“pre-gap” claims). The average out-of-pocket cost goes up from $6 per claim for tier 1 drugs to $41 per claim for tier 2 drugs, and $68 per claim for tier 3 drugs. Tier 4, which is sometimes designated as a “specialty” tier, has expensive, rarely claimed drugs for which consumers pay on average $200 per claim out of pocket (but it accounts for less than 0.1 percent of claims, so we focus our analysis on tiers 1 through 3).

Some other patterns across tiers are worth noting. Total drug costs per claim are much higher in tier 2 or tier 3 than in tier 1 (column 5); this presumably reflects the disproportionate positioning of the often cheaper generic drugs on tier 1. Not surprisingly, given the differences in out-of-pocket costs for drugs across tiers (column 4), utilization is similarly concentrated in the lower tiers as drug counts; around 60 percent of claims are for tier 1 drugs, and another roughly 20 percent are for tier 2 drugs (see columns 7 and 8).

Our main object of interest is variation in consumer cost-sharing. As noted, consumer-cost sharing can either be in the form of a fixed out-of-pocket dollar amount (co-pay) per claim or a co-insurance rate. Differences in out-of-pocket payments may therefore reflect both cost-sharing rules and (in the case of co-insurance) total drug costs. To make it comparable, column 6 reports the average co-insurance for each tier (pre-gap) that we computed empirically from the observations of out-of-pocket payments and total cost of each claim. The result is a somewhat more nuanced pattern. Tiers 1 and 2 have quite similar co-insurance of about 30 percent, while tier 3 drugs have markedly higher consumer cost-sharing (of 53 percent).

The key empirical pattern in column 6 is that “higher cost-sharing” corresponds to tier 3 drug placement. We investigate this more systematically by analyzing cost-sharing by tier within plans. Table A2 in the Appendix shows that this pattern is even more pronounced when we include plan fixed effects. Co-insurance between tier 1 and tier 2 is substantively and statistically indistinguishable, but is 20 percentage points higher for tier 3 drugs. As a result, in our empirical analysis of the correlation of tier-placement and drug elasticity below, we will focus on the distinction between drugs in tier 3 relative to tier 1 and tier 2.

B. Correlations between drug elasticities and cost sharing

Drug Elasticities and Tier Placement

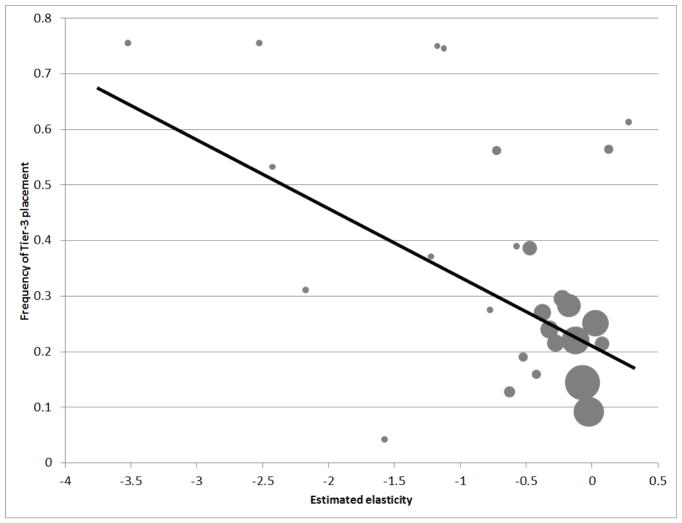
We begin by analyzing the relationship between a drug’s elasticity and whether it is placed on tier 3 (versus any other tier), which, as just shown, has systematically higher co-insurance than other tiers. Figure 5 shows an initial look at this pattern. Specifically, for our common drugs, it reports the frequency of tier-3 placement as a function of the elasticity for each drug (we bin drugs into 0.05 elasticity bins in the figure), which was estimated in Section II. The figure shows a clear pattern: drugs with more elastic demand are more likely to be placed in tier 3, where consumer cost-sharing is the higher.

Figure 5. Correlation between Tier 3 placement and drug elasticity.

Figure shows the correlation between the probability of a drug being placed in Tier 3 (which corresponds to the highest consumer cost-sharing) on the vertical axis and the estimated drug elasticity (on the horizontal axis). Each circle represent a set of drugs whose estimated elasticity falls in the same elasticity bin of size 0.05. The size of the circle represents the number of drugs in each bin. The vertical axis is the frequency (across formularies) with which drugs in the set are placed in Tier 3. The regression line is the fitted line across all the circles, weighting each data point by the number of drugs in that bin.

To analyze more systematically the relationship between a drug’s elasticity and its tier in a formulary, we run the following linear regression at the drug-by-formulary-by-tier level

$${\sigma }_d={\alpha }_f+{\sum }_{k=1}^K{\beta }_{k}1\{{\mathit{Tier}}_{df}=k\}+{\epsilon }_{df},$$ (3)

where σ_d is the estimated elasticity of demand for drug d from equation (1), and α_f denotes fixed effects for each of the 426 formularies. We include a series of indicator variables 1 {Tier_df = k} for whether drug d is located on tier k in formulary f. We include separate indicators for tiers 3, 4, 5, and 6. The omitted tier category is tiers 1 and 2. The key coefficient of interest is β₃, which measure the within-formulary difference in average elasticity of drugs in tier 3 relative to the reference tiers 1 and 2. By including formulary fixed effects, we are examining the relationship between drug elasticity and (ordinal) tier placement within a formulary.

Table 5 reports the results. Column (1) reports results without formulary fixed effects; it is therefore similar in spirit to the variation presented in Figure 5 although the exact estimates will differ because of differences in the implicit weighting and functional form. Column (2) shows the results with formulary fixed effects, which are quite similar. We estimate that, on average, drugs on tier 3 have 0.11 higher elasticity (in absolute value) relative to drugs on lower tiers.

Table 5.

Relationship between elasticity of common drug and its tier-positioning

Sample	Dependent Variable: Estimated demand elasticity
	All drugs & plans (1)	All drugs & plans (2)	4-tier plans (3)	High frequency drugs (4)	All drugs & plans (5)	“Lower subst.” drugs (6)
High co-insurance (Tier 3)	−0.108 (0.006)	−0.105 (0.005)	−0.115 (0.007)	−0.055 (0.004)	−0.179 (0.006)	−0.111 (0.013)
Formulary Fixed Effects	No	Yes	Yes	Yes	Yes	Yes
Drug price included	No	No	No	No	Yes	No
R-squared	0.012	0.020	0.020	0.011	0.057	0.025
No. of Obs.	49,392	49,392	29,538	34,371	49,392	10,058
Mean of Dep. Var.	−0.209	−0.209	−0.211	−0.203	−0.209	−0.250
Std. Dev. Of Dep. Var.	0.391	0.391	0.396	0.258	0.391	0.406

Table shows the relationship between the estimated demand elasticity of each drug and its tier placement, as in equation (3). We report the coefficient on being in Tier 3, relative to tiers 1 or 2; indicator variables for higher tiers are included in the regression (but not reported). The unit of observation is a drug-by-formulary-by-tier. Standard errors in parentheses are clustered at the formulary-tier level. Column (4) restricts the analysis to the 96 of our 160 “common drugs” that have at least 300,000 claims over our sample period. Column (5) adds a control for the total cost of the drug by year. Column (6) restricts the analysis to the 29 drugs for which substitution to other drugs is less likely.

The remainder of the columns investigate the sensitivity of this main result. As we saw in Table 4, the vast majority of enrollees and claims are in plans that use 4-tier formularies. Therefore, in column 3 we repeat the regression analysis separately for 4-tier formularies only. The results are quite similar. In column 4 we re-estimate the baseline specification from column 2, restricting to a higher frequency sub-sample of our common drugs. Specifically, we limited the sample to the 96 (out of 160) common drugs that have more than 300,000 claims, and hence presumably more precisely estimated elasticities. The magnitude of the estimated \beta_{3} is lower but remains statistically significant.

In column 5, we address a potential confounding variable by repeating the analysis in column 2 with the addition of a control for the average (total) price of the drug.¹³ There are two reasons to control for price levels. First, it makes the estimates between drugs with co-pay and co-insurance more compatible, as controlling for price in principle translates co-pays to co-insurance. Second, if price itself is a strong predictor of where insurers place their drugs, then controlling for prices allows us to explore whether conditional on the price of a drug, the insurer is more likely to place higher elasticity drugs on higher tiers. We find that controlling for price levels makes the relationship between drug elasticity and tier placement more pronounced.

Finally, as discussed, a limitation to our drug-specific elasticities is that they reflect a combination of own- and cross-price elasticities. Therefore, in column 6, we repeat the analysis in column 2 limited to the sub-sample of 29 “lower substitution” drugs; as described in Section II, these are drugs for which substitution concerns are less likely, and therefore the estimated elasticities may more closely approximate own-price elasticities. Comparing columns 2 and 6, we find that the point estimate for the magnitude of the relationship between a drug’s elasticity and placement on tier 3 is in fact larger for this sub-sample of drugs (although this difference is not statistically significance).

Drug elasticities and co-insurance

The preceding analysis allows for a relatively straight-forward examination of the drug’s elasticity and its tier placement. This has the attraction of corresponding closely to the decision the insurer makes (which tier to place a drug on). However, it stops short of the economic object of interest which is the relationship between a product’s elasticity and its co-insurance rate; this co-insurance rate depends both on the formulary chosen (which determines the drug’s tier) and the insurer’s decision regarding the level of consumer cost sharing in each tier of the chosen formulary. Here, therefore, we analyze the relationship between a drug’s average co-insurance rate and its elasticity.

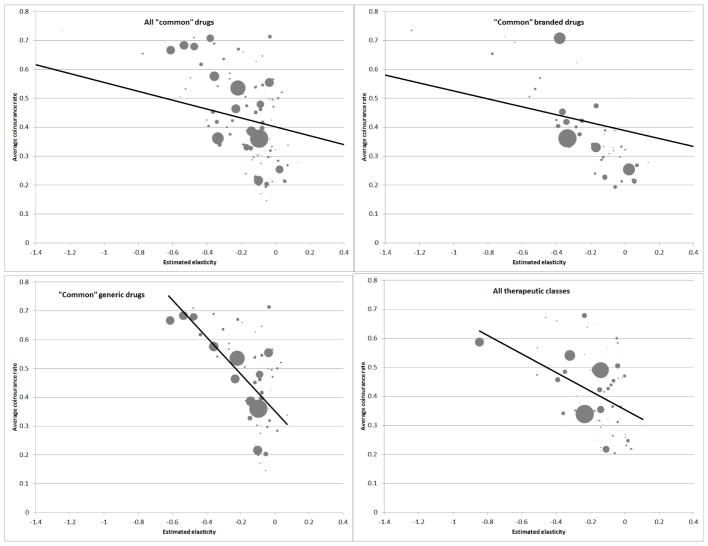
Once again, we begin with graphical evidence. Panel A in Figure 6 shows the correlation between the elasticity of a drug and the average co-insurance for that drug (for “pre-gap” claims, as described earlier).

Figure 6. Correlation between co-insurance and elasticity.

Figures shows the correlation between the average co-insurance for a drug (or class) on the vertical axis and the estimated elasticity for the drug (or class) on the horizontal axis. Average co-insurance is defined as the pre-gap co-insurance rate. Each circle corresponds to a specific drug (or class); circle sizes are proportional to the number of claims for each drug (or class) in the data. For ease of graphical presentation, the figures are limited to estimated elasticities between 0.4 and −1.4. This omits fewer than 2 percent of claims from all panels. Fitted regression lines are in all panels; these are fitted using equal weights for all drugs, and include the data points that are outside of the elasticity range shown.

The figure shows a clear negative relationship: drugs with higher (in absolute value) elasticities have higher average co-insurance rates.¹⁴ One concern with this analysis is that we have already seen that generic drugs are disproportionately on tier 1 (i.e. lower consumer co-insurance) and, as discussed, our estimated elasticities are likely biased downward (in absolute value) for generic drugs relative to branded drugs due to likely substitution within a therapeutic class from branded to generic drugs at the donut hole. Therefore, in the second and third panel of Figure 6 we plot the same relationship separately for generic or branded drugs. As can be seen, the qualitative relationship remains stable in each case, although it is quantitatively stronger for generics. To more directly tackle this concern about substitution, the final panel of Figure 6 illustrates similar patterns for therapeutic classes which, as discussed, likely have little cross-class substitution. We observe that therapeutic classes for which we estimate higher elasticities (in absolute value) have higher co-insurance.

Since cost-sharing is set separately by plan, we also analyze the within-plan relationship between cost-sharing and drug elasticity. To do so, we run the following linear regression at the drug (d) by plan (j) level:

$$p_{dj}^{\mathit{pregap}}={\alpha }_j+\beta {\sigma }_d+{\epsilon }_{dj},$$ (4)

where $p_{dj}^{\mathit{pregap}}$ denotes the pre-gap co-insurance rate for a drug (or class) in plan j, α_j denotes the plan fixed effects, and σ_d denotes the elasticity of product d estimated in Section II. The coefficient of interest, β, measures the correlation between pre-gap co-insurance and elasticity. One potential concern with this specification is a version of a “division bias” – prices for product d in plan j that enter the denominator of the co-insurance measure $p_{dj}^{\mathit{pregap}}$ are also part of the elasticity calculation for product d. Given the high frequency of data and hence a relatively small impact of each plan j on the calculation of average prices in the elasticity term, we would not expect a large division bias in the point estimates of β. To assess this concern quantitatively, we report several specification checks that calculate “leave one out” (at different levels of aggregation) elasticities for each product d and plan j pair in Appendix C.6. The results are broadly the same as the baseline results discussed below.

Table 6 reports the estimates of \beta. Panel A reports drug-level analysis, and Panel B reports therapeutic-class level analysis. We start in column (1) with a specification that uses all common drugs or therapeutic classes, thus effectively reproducing Figure 6 Panel A or D (albeit with differences in implicit weighting and functional form). Column (2) repeats this specification, adding plan fixed effects; the results are quite similar. We estimate that, on average, a drug with a 0.1 higher (in absolute value) elasticity has a 0.028 higher co-insurance rate, and a therapeutic class with a 0.1 higher (in absolute value) elasticity has a 0.03 higher co-insurance rate.

Table 6.

Relationship between co-insurance and elasticity

Sample	Dependent Variable: Co-insurance rate
	All drugs & plans (1)	All drugs & plans (2)	High frequency drugs (3)	All drugs & plans (4)	“Lower subst.” drugs (5)	Branded drugs (6)	Generic drugs (7)
Panel A. Drug-level analysis
Estimated demand elasticity	−0.283 (0.044)	−0.284 (0.044)	−0.336 (0.081)	−0.236 (0.037)	−0.315 (0.098)	−0.264 (0.032)	−0.619 (0.075)
Plan fixed effects	No	Yes	Yes	Yes	Yes	Yes	Yes
Drug price included	No	No	No	Yes	No	No	No
R-squared	0.083	0.342	0.37	0.426	0.493	0.303	0.518
No. of Obs. (plan years)	654,270	654,270	521,358	654,270	139,965	277,684	376,586
Mean of Dep. Var.	0.435	0.435	0.441	0.435	0.485	0.400	0.462
Std. Dev. Of Dep. Var.	0.306	0.306	0.304	0.306	0.339	0.266	0.33
Panel B. Class-level analysis
Estimated demand elasticity	−0.308 (0.064)	−0.310 (0.065)	−0.316 (0.074)	−0.256 (0.053)
Plan fixed effects	No	Yes	Yes	Yes
Drug price included	No	No	No	Yes
R-squared	0.030	0.305	0.34	0.387
No. of Obs. (plan years)	587,050	587,050	463,507	587,050
Mean od Dep. Var.	0.408	0.408	0.416	0.408
Std. Dev. Of Dep. Var.	0.267	0.267	0.267	0.267

Table shows the relationship between a drug’s (Panel A) or class’ (Panel B) pre-gap co-insurance rate and its estimated elasticity. The unit of observation is a drug (or class) by plan. Standard errors in parentheses are clustered at the drug (or class) levels.

The remainder of the columns investigate the sensitivity of this main result. In column (3) we re-run the baseline specification on the sub-sample of 96 out of 160 “common” drugs with high frequency of claims in our sample, which restricts the sample of common drugs or common therapeutic classes to the set with more than 300,000 claims in the sample that arguably have more precisely estimated elasticities. The coefficient of interest increases in magnitude with this restriction, both for the drugs and for the therapeutic classes, as would be expected with classical measurement error in our estimates of σ_d.

An important limitation to our result is that it is inherently cross-sectional. Therefore any omitted variable correlated with elasticity and co-insurance may be driving the estimated relationship. One natural possibility is the total price of the drug – perhaps lower priced drugs both have lower consumer cost-sharing (to encourage their use) and are less elastic. This is particularly a concern at the drug level where we are concerned that our elasticity estimates are biased toward zero for cheaper drugs that are substitutes for more expensive drugs; it is arguably less of a concern at the therapeutic class level since substitution should primarily occur within, not across classes. In either case, controlling for the total drug price in column (4) slightly attenuates the magnitude of the relationship between elasticity and cost sharing but does not change the sign.

Finally, the last three columns investigate an issue specific to the analysis at the drug level in Panel A, and discussed in the context of the previous analysis as well: the drug-specific elasticity estimates may reflect cross-drug substitution in response to the overall price increase, as well as the own-price effect. As noted, this issue is less likely to arise at the therapeutic class level in Panel B. As one way of addressing this issue for the drug-level analysis in Panel A, column (5) shows the results of limiting to the “lower substitution” sub-sample of drugs; the estimated relationship changes very little. A further way of addressing this concern is reported in columns (6) and (7). Here, we separate the results by branded and generic drugs, so that we can test our theoretical prediction on branded drugs only, which we believe are less likely to include a significant degree of cross-price elasticities in their elasticity estimates. The estimated coefficient is much lower for branded relative to generic drugs, and in both cases the estimated magnitudes of the correlation are far from zero, statistically significant, and continue to show more elastic drugs facing higher consumer cost sharing. The results from these alternative drug-level specifications – as well as the results by therapeutic class – leave us relatively sanguine that substitution effects are not driving our primary findings.

Additional sensitivity analysis

In Section II.B we described some concerns with our empirical strategy for estimating drug elasticities. A key concern was that the increase in co-insurance at the donut hole that we use to estimate elasticities is a price change that affects all drugs, so that cross-drug substitution may affect our elasticity estimate. To try to address this, we showed that our results above are robust if we limited to a subsample of drugs that were unlikely to have substitutes, and we re-did our analyses at the therapeutic class level, since substitution is likely to occur within, not across, therapeutic classes.

In the Appendices we undertake additional analyses designed to address four other potential concerns with our elasticity estimates that we discussed above. We briefly summarize them here. In each case, we re-estimate our elasticities for “common” drugs and therapeutic classes and re-examine the relationship between co-insurance and product elasticity (i.e. Table 6). We find that the alternative elasticity estimates are highly correlated with our baseline estimates (although in some cases of different magnitudes), and that our finding of higher co-insurance for more elastic products persists when we use these adjusted elasticities.

First, our baseline estimates focus on the end-of-year response to the price increase at the donut hole, thus ignoring potential cross-year substitution. Individuals who end up in the gap may delay purchases to the following year (“delays”), and individuals who are confident that they will not reach the gap this year may increase their purchases at the end of the year before the contract restarts and they face a deductible in January (“stockpiling”). Either type of response would increase the size of our estimated elasticities, although it is not obvious whether or how it would change their ranking across products. In Appendix C.1, to account for potential delays in purchase we follow an approach similar in spirit to that implemented by Einav, Finkelstein, and Schrimpf (2015) and re-estimate elasticities that are adjust for “excess purchases” early in the next year for individuals who ended up in the donut hole this year. In Appendix C.2 we restrict attention to the approximately 70 percent of individuals enrolled in no-deductible plans, and re-estimate our elasticities on this “low stockpiling incentives” sub-sample.

Second, our use of December as the “end of the year” is somewhat arbitrary. In Appendix C.3, we therefore recalculate elasticities using two alternative definitions of the “end of the year”: a larger window that includes November and December, and a narrower window that is limited to December 16–31.

Third, our baseline elasticity estimates analyze a particular measure of quantity: the extensive margin of whether the individual has a claim for a given product in December, rather than the amount of the drug purchased. Recall that we use this measure to compute the percentage decline in claim propensity in December, %ΔPr_d(Dec), so as long as the relationship between December claim propensity and December claimed quantity (the number of claims, or total number of days supply) is invariant to the price changes, the results should not be affected. However, in order to accommodate the possibility that some beneficiaries may not completely forgo filling a prescription upon entering the coverage gap, but may reduce the quantity of their purchase, in Appendix C.4 we recompute elasticities using an alternative quantity measure – “days supply” – which captures a potential intensive margin response as well; we analyze both the total response of “days supply” and the response conditional on making any purchase.

Finally, individuals may choose their plans in anticipation of their probability of reaching the gap and their behavioral response to it. To quantify the scope for such selection concerns, in Appendix C.5 we estimated elasticities restricting attention to the approximately 85 percent of individuals that were enrolled in plans without gap coverage.

IV. Discussion

Public insurance plans tend not to vary co-insurance across drugs, while private plans do. In this paper we used the context of Medicare Part D to examine how co-insurance varies across drugs in privately-provided insurance plans. We exploited the sharp change in out-of-pocket prices faced by consumers as they enter the famed donut hole in order to estimate the price elasticity of demand for specific drugs and therapeutic classes. We documented substantial variation in the price elasticity of demand across drugs. This heterogeneity exists within and across broad therapeutic classes and exhibits intuitive patterns. We then showed that private insurers participating in the Part D program systematically set higher consumer co-insurance (i.e. less risk protection) for drugs that exhibit a higher price elasticity of demand.

In debates over whether to have private provision of public insurance, two arguments are often advanced in favor of private provision. First, private provisions may result in more and better choices for consumers. Second, competition among private insurers may lead to more efficient provision of the goods or services in question. While a substantial empirical literature has analyzed the first of these arguments, there is relatively little work on the second, and the empirical findings described above may begin to shed some light on this aspect.

Is it socially beneficial for private insurers to charge consumers more when demand is more elastic? The classic theory (Feldstein 1973; Besley 1988) emphasizes that the socially optimal consumer cost-sharing mimics standard Ramsey-style optimal commodity taxation results: health events that are more prone to moral hazard (i.e. have a higher price elasticity of demand) should be associated with less risk protection (i.e. higher co-insurance). As we show in more detail in Appendix A, in a context of a stylized conceptual framework where demand elasticity is driven by moral hazard, market forces may indeed lead to efficient benefit design: profit-maximization incentives lead to the same gradient in the trade-off between risk protection and moral hazard as in the socially optimal insurance contract. Viewed through this lens of neoclassical theory with risk averse, utility-maximizing consumers, our empirical results suggest that the private sector may have a comparative advantage over the public sector in the design (or “production”) of insurance given that, as with many other publicly provided prescription drug plans, the government-defined standard benefit plan for Part D features uniform consumer cost-sharing across drugs.

Of course, reality is more complex than the stylized model we write down in the appendix. On the demand side, heterogeneity in the price elasticity of demand across drugs may not only reflect heterogeneity in moral hazard, but also in behavioral biases, information frictions, or adherence, thus making it more difficult reaching normative recommendation from observed choices (Baicker, Mullainathan, and Schwartzstein 2015; Handel and Kolstad 2015; Spinnewijn 2017). In our specific context of pharmaceutical drugs, normative analysis is further complicated by the fact that much of the social cost is in the research and development stage, and the marginal cost of an extra pill is much lower than the per-unit price charged by the manufacturer for the drug; as a result, unlike in the classic theory, co-insurance may be socially inefficient in the presence of moral hazard (Lakdawalla and Sood 2009). On the supply side, private insurers have other reasons for cost-sharing setting and tier placement, beyond their attempt to trade off moral hazard and adverse selection. For example, they may use tier placement as a bargaining tool vis-a-vis upstream drug manufacturers (Hong 2015; Dafny et al. 2016), or they can use formulary design as a way to select particular types of more profitable beneficiaries (Starc and Town 2015; Lavetti and Simon 2016).

Another interesting question that our analysis does not address is why public insurance plans do not also vary co-insurance of drugs. One possible explanation is the “costs of complexity” of determining drug-specific demand elasticities and setting cost-sharing accordingly, interacted with the lack of profit-seeking incentives in the public sector that might otherwise induce designers to incur those costs. Alternatively, there may be political economy concerns about who and how the co-insurance decisions would be made, thus pushing toward uniformity in cost sharing. Finally, there may be equity concerns across individuals; for example, if the social planner assigns different social welfare weights to individuals with different diseases (treated by different drugs), that could affect the socially optimal cost-sharing across drugs relative to the benchmark model.