Conceptual relations compete during auditory and visual compound word recognition

Abstract

Previous research has shown that compound word recognition involves selecting a relational meaning (e.g., ‘box for letters’ for letterbox) out of a set of competing relational meanings for the same compound. We conducted five experiments to investigate the role of competition between relational meanings across visual and auditory compound word processing. In Experiment 1 conceptual relations judgments were collected for 604 English compound words. From this database we computed an information-theoretic measure of competition between conceptual relations – entropy of conceptual relations. Experiments 2 and 3 report that greater entropy (i.e., increased competition) among a set of conceptual relations leads to longer latencies for compounds in auditory lexical decision. Experiments 4 and 5 demonstrate the same result in two visual lexical decision studies. These findings provide evidence that relational meanings are constructed and evaluated during compound recognition, regardless of whether compounds are recognized via auditory or visual input.

Introduction

It is well-established that a stage of visual compound word recognition involves access to a relational meaning which is constructed out of the meanings of its constituents (for a review see Gagné & Spalding, 2014). For example, understanding the compound word fireball requires computing the implied relational meaning ‘ball made of fire’. The notion that compound word meaning is underpinned by a relational structure which is not explicitly specified in the surface form was identified in early theoretical accounts (Downing, 1977; Gleitman & Gleitman, 1970; Kay & Zimmer, 1976; Lees, 1962; Levi, 1978; Li, 1971). Moreover, empirical support for this notion has been obtained in behavioural experiments in which effects of visual word processing were observed by manipulating the availability of underlying conceptual relations of compounds (Gagné & Spalding, 2004; 2009; Spalding & Gagné, 2011) and modifier-noun phrases (e.g., space station; Gagné, Spalding, Figueredo & Mullaly, 2009; Spalding, Gagné, Mullaly & Ji, 2010).

Recently, a number of experiments have drawn attention to competition between conceptual relations as a central mechanism for the processing of relational information (Gagné & Shoben, 1997; Pham & Baayen, 2013; Spalding & Gagné, 2014; Schmidtke, Kuperman, Gagné & Spalding, 2016). In particular, Schmidtke et al. (2016) found evidence that conceptual integration of compound word meaning involves the construction of multiple relation-based conceptual representations in concert, and that these meanings subsequently compete to be selected as the most likely relational candidate. This study reported that there is a cost to the lexical processing of compound words when there is greater competition among their relational meanings. For example, arriving at the relational meaning of a compound such as seaweed depends on the strength of the dominant relational meaning, such as ‘weed located in sea’, relative to all other possible relational meaning candidates that are generated by the language system for that word. When that relational meaning is not a strong competitor, i.e., when there are other strongly available candidate meanings such as ‘weed from sea’, then recognizing the word requires greater cognitive effort.

The focus of the present paper is to further address the role of relational competition during compound word processing. The purpose of the report is two-fold. The primary objective is to extend the empirical and theoretical base of the relational competition effect. This effect is formalized within the relational-interpretation-competitive-evaluation (rice) theory of modifier-noun compound processing (Spalding et al., 2010), yet specific components of this theory require further investigation. We address the primary objective by providing two empirical contributions to this line of research. The first contribution is a study in which we investigate the effect of relational competition during visual lexical decision with a much larger and diverse set of compound words. The second is an investigation of auditory compound word processing, about which little is known in general or in relation to the role of relational information specifically (see discussion below). The secondary objective of the present paper is to provide a publicly available lexical database of conceptual relations information for compound words. This objective aims to facilitate future research on relational structures and their function during compound word processing and to estimate reliability of human judgments of possible relations. In what follows we provide an empirical and theoretical review, before outlining our motivation for the experimental component of the study.

A large body of evidence for competition between conceptual relations has come from a series of experiments which demonstrate that established and novel compounds are interpreted with less cognitive effort when they follow a compound with the same modifier and relational structure than when they follow a compound with a different relational structure (e.g., Gagné & Shoben, 1997; Gagné & Spalding, 2004, 2009; Gagné et al., 2009; Spalding et al., 2010; Spalding & Gagné, 2011). For example, Gagné & Spalding (2009) found that spacesuit (suit for space) is recognized faster following spaceship (ship for space) than following spaceman (man located in space). In a different experimental design, Spalding and Gagné (2011) reported slower response times in a condition in which the conceptual relation across the prime and target was different (e.g., watercolour as a prime for waterfall) relative to a condition in which the prime for the compound was its stand-alone modifier (e.g., water as a prime for waterfall). However, compared to the same baseline, neither facilitation nor inhibition was observed in a condition in which the prime and target were the same relation (e.g., waterdrop as a prime for waterfall). This finding demonstrated that the processing of compounds is affected by competition between relational interpretations in that the priming of a different relation increases the difficulty in selecting the established relation for the target compound.

Further evidence for relational competition has come from experiments which have used information theoretic measures as a method of operationalizing the magnitude of competition between potential relational candidates for a given compound word. In one such experiment, Spalding and Gagné (2014), quantified competition between semantic relations using data obtained from the “possible relations task”. In this task, participants were presented with a series of compounds, and for each compound were asked to select the most appropriate conceptual relation, out of 16 potential relations (defined by Levi, 1978; see also Shoben, 1991; Gagné & Shoben, 1997). This data was then used to generate a frequency distribution of responses to possible relations for a compound word. Spalding and Gagné (2014) computed two measures from this data set and found that they independently predicted response times in lexical decision. Lexical processing of transparent English compound words (e.g., carwash) was faster for compounds with a relatively large number of potential relations (high Relational Diversity Ratio) and a small number of strong potential candidates (a low Relational Relative Entropy score). For opaque compounds (e.g., hogwash), processing speed was slower for compounds with a small number of potential relations (low Relational Diversity Ratio) and a large number of potential relational candidates (high Relational Relative Entropy). Thus, when the constituents of a compound provide a lot of relational information, this results in a processing benefit for transparent compounds. However, for opaque compounds, the computed meanings are inconsistent with the established meaning, which slows processing. In sum, this research provides evidence that the conceptual and semantic information of the constituent words are actively used to construct meaning, and that this process may be competitive.

The Relational Relative Entropy score is a metric of how the distribution of possible interpretations for all compound words differs from the distribution of possible relations for the specific compound under recognition. An effect of this measure indicates that during processing, the overall expectation of a conceptual relation for a compound word is adjusted for the set of possible relations that are produced for the compound that is being currently recognized. In addition, the Relational Diversity Ratio measure provides an index of the range of potential relations that are generated upon recognition of a compound word. An effect of this measure is a reflection of the number of relational candidates that are generated during compound word recognition. Importantly, neither Relational Relative Entropy nor Relational Diversity Ratio suitably quantifies the amount of competition that might exist between conceptual relations for the specific compound word under recognition. Though competitive in essence, Relational Relative Entropy does not identify competition that might stem from conceptual relations irrespective of the aggregated population-wide frequency distribution of conceptual relations. Moreover, the Relational Diversity Ratio metric simply provides an estimate of the number of potential relational candidates, but is not informative about the degree of competition that exists between them.

To address this issue, a more parsimonious measure of relational competition for established compounds was introduced by Schmidtke et al. (2016). This research used the same possible relations data from Spalding and Gagné (2014) and Gagné and Spalding (2014), yet this time calculated Shannon entropy (Shannon, 1948) over the probability distribution of possible relations associated with each particular compound. The resulting measure, henceforth referred to as ‘entropy of conceptual relations’, was a significant predictor of reaction times across two independent lexical decision mega-studies. Schmidtke et al. (2016) found that increased entropy of conceptual relations was associated with slower reaction times to sets of compound words attested in the British Lexicon Project database (BLP; Keuleers, Lacey, Rastle & Brysbaert, 2012) and the English Lexicon Project (ELP; Balota, Yap, Hutchison, Cortese, Kessler, Loftis, Neely, Nelson, Simpson & Treiman, 2007). In other words, the results indicated that multiple conceptual relations are concurrently activated during compound word processing and greater uncertainty about the dominant meaning in a compound’s distribution of possible relations lead to longer lexical decision response times.

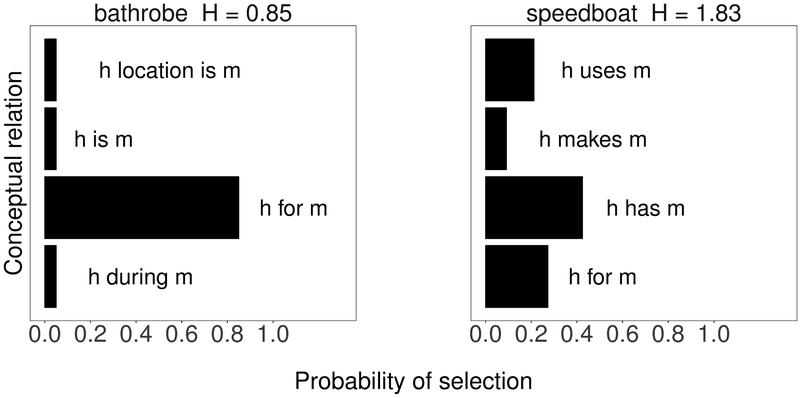
The theoretical motivation for examining entropy of conceptual relations as an operationalization of competition is illustrated in Figure 1. The plot visualizes the results of the possible relations task for two compounds. The right panel displays the results of the possible relations task for the compound speedboat, which yielded a probability distribution of responses that are more or less equally apportioned across four possible conceptual relations (‘boat uses speed’, 0.21; ‘boat makes speed’, 0.1; ‘boat has speed’, 0.42; ‘boat for speed’, 0.27). This uncertainty in the frequency distribution is indicated by a large entropy value (H = 1.83). Thus, as it was difficult for participants in the possible relations task to converge on any one relational meaning, speedboat represents a compound for which there was greater competition among possible relations and slower lexical processing.

Figure 1.

An example of the distribution of possible relations judgements of two compounds in Experiment 1. H = entropy of conceptual relations; h = head; m = modifier.

On the other hand, the left panel demonstrates bathrobe as an example of a compound for which there is a strong competitor relation. Like speedboat, this compound is also associated with four possible conceptual relations, but instead has a single dominant meaning relative to all other relational candidates in the distribution: ‘robe for bath’ yielded a selection probability of 0.85. For this compound, the low average uncertainty in selection choices across the distribution of possible relations is expressed with a relatively small entropy value (H = 0.85). Therefore, relative to speedboat, the compound bathrobe elicited less relational competition and facilitated word recognition.

The results of Schmidtke et al.’s study (2016) are predicted within the rice theory of modifier-noun compound processing (Spalding, et al., 2010; Gagné & Spalding, 2014). Within this theory, competition between relational interpretations is expected to emerge at an ‘evaluation stage’. This is a stage at which semantic information associated with the head and the modifier is accessed, along with concurrent access of multiple relational links which combine the semantic information of the modifier and head. Once multiple relational meaning candidates are generated, the most likely relational interpretation is selected. Thus, this stage of processing can be summarized as a point at which many potential combined concepts are generated, and then subsequently evaluated via a process of elimination.

While Schmidtke et al.’s (2016) study adds to a wealth of research on the rice theory of conceptual combination, this body of research lacks an important and necessary piece of evidence. So far, experimental work on the role of conceptual combination during compound word recognition has been investigated using paradigms which have exclusively examined orthographic word processing. Therefore, up to this point, our knowledge about the processing of conceptual relations is based on the specific domain of visual word processing. Given the results obtained in visual word processing studies, it is conceivable that conceptual relations are equally important for recognizing compound words from speech input. To elaborate, based on the rice theory, we reason that if effects of conceptual relations are truly caused by the automatic processing of implicit semantic information about compounds, i.e., conceptual information that is absent in the surface form of a compound, then one should expect to find such effects irrespective of the modality in which the compound word is presented. Thus, because effects of relational information are assumed to be driven by semantic information that is independent of the surface form of the compound word, we predict that both visual and auditory word processing of compound words will be sensitive to effects of relational structure.

Indeed, there is a reason to suspect that conceptual structure of compound words may not play a role during auditory word recognition. Auditory word recognition differs from visual word recognition in that the acoustic signal unfolds over time, which has ramifications for the way in which lexical information is accessed. The Cohort model accounts for this phenomenon by proposing that the unfolding phonological sequence progressively narrows down the set of possible phonological candidates, i.e., the number of words that are potential matches with the word to be recognized (Marslen-Wilson & Tyler, 1980; Tyler, 1984; Marslen-Wilson, 1987). The point at which the word under recognition has become uniquely distinguishable from its cohort of competitors is the uniqueness point, and this has been established as an important predictor of compound word recognition (Balling & Baayen, 2008; 2012). It may be possible that reaching the uniqueness point of the compound word, via the bottom-up accrual of perceptual phonemic information, will override the reliance of relational information.

In what follows we provide a direct test of the hypothesis that the precise role of conceptual relations for compound word recognition is indifferent to the modality of the linguistic input. To our knowledge, the role of conceptual combination has so far not been tested during auditory compound word recognition. We remedy this by determining whether the effect of competition between conceptual relations initially observed in visual lexical decision (Schmidtke et al., 2016) extends to auditory lexical decision. We predict that processing either the orthographic or phonetic form of a compound word (e.g., dishwater or [dɪ∫wɑɾɹ̩]) will elicit a qualitatively equivalent effect of entropy of conceptual relations. Specifically, we expect that a greater uncertainty about the conceptual relation for a compound word will generate a processing cost during word recognition.

Overview of experiments

We report a series of experiments to provide evidence for activation of competing relational structures during auditory and visual compound word recognition. In Experiment 1 we conduct a large-scale online version of the possible relations task, in which we generated a large list of concatenated English compound words and asked participants to select the best relational meaning for each compound. With this larger database of selection distributions for relational interpretations of compound words, we were able to compute the measure of Entropy of conceptual relations (Schmidtke et al., 2016).

Next, in Experiments 2 and 3, we address the main question of relational competition during auditory comprehension of compounds by reporting the results of two auditory lexical decision studies of compound word recognition. Experiment 2 reports the results of an auditory lexical decision mega-study, an auditory variant of the ELP and BLP lexical decision mega-studies. Experiment 3 reports the results of an auditory lexical decision experiment which was designed specifically to determine the use of a ‘uniqueness point’ as a processing cue in English compounds.

In Experiments 4 and 5, we performed two analyses of the virtual mega-study originally conducted by Schmidtke et al. (2016), in which we verify whether visual compound word processing also involves the computation and competition among conceptual relations. Using lexical decision latencies taken from the ELP and BLP, we provide a critical test of the generalizability of the claim that competition between conceptual relations occurs irrespective of the linguistic modality in which a word is presented. Using the Entropy measure derived from the new norms collected in Experiment 1, we are also able to provide an essential test of the effect generalizes to a larger and more comprehensive sample of existing English compound words than that reported in Schmidtke et al. (2016). Moreover, by using the same databases containing the visual lexical decision responses collected from the same participants as a benchmark, we can examine whether the new set of conceptual relations judgements produce the same effect as the possible relations data which was originally collected by Spalding and Gagné (2014) and Gagné and Spalding (2014). Thus, these studies will also enable us to examine the reliability of the entropy measure as an index of competition between activated conceptual relations.

Experiment 1

The goal of Experiment 1 was to generate a database of conceptual relations for English compound words based on the results of the possible relations task. An online version of the possible relations task was administered on the Amazon Mechanical Turk (MTurk) data collection platform. Aside from the web-based interface of the experiment, the task procedure, presentation and set of possible relations was identical to the experiment reported in Spalding and Gagné (2014), which is the same possible relations dataset that was subsequently used in Schmidtke et al. (2016).

Methods

Materials.

A total of 604 concatenated English compound words were randomly sampled from a larger corpus of compounds which was compiled by the first author. Approximately 220 compounds in this corpus were sampled from materials used in prior compound word processing studies (Kuperman & Bertram, 2013; Falkauskas & Kuperman, 2015; Schmidtke, Van Dyke & Kuperman, 2017). These compounds were either extracted from the CELEX database (Baayen, Piepenbrock & Gulikers, 1995), or were compiled from written text materials by students at the University of Alberta. The remainder of the compounds were sampled directly from the ELP database directly (Balota, Cortese, Hutchison, Neely, Nelson, Simpson & Treiman, 2002). The complete list of 604 compounds were assigned to 6 separate 100-word sublists (two lists contained 102 items). Compounds were selected to represent an equal spread of high and low frequencies across each list. Each list had 4 practice trials.

Participants.

All MTurk responders were constrained to those currently residing in the USA, but no requirement of English being the participant’s first language or only language was applied. In addition to the possible relations task, other demographic information was collected. Participants were asked to report their age, gender, first language or languages, which country/state they had lived in the longest between birth and the age of seven, and the educational level that describes them best (some high school; high school graduate; some college, no degree; associate degree; bachelors degree; or masters degree or doctorate). Each experimental list was administered to 50 participants and each list was made available on Amazon Turk at the same time. Participants were paid USD $1.20 for a validly completed list.

Procedure.

For each trial of the possible relations task a compound word was presented in a spaced format, such that both constituents were presented in the order that they appear in the compound itself (e.g., sea weed). At the beginning of the experiment, participants were instructed to pretend that they are learning English and are familiar with each of the constituents, but have never seen them used together. Their task was to choose the most likely literal meaning for the pair of constituents. Participants were asked to make their choice out of the set of 16 possible relational interpretations which were presented beneath the spaced compound (e.g, ‘weed causes sea’, ‘weed caused by sea’, ‘weed has sea’, ‘weed by sea’, ‘weed makes sea’, ‘weed from sea’, ‘weed made of sea’, ‘weed is sea’, ‘weed used by sea’, ‘weed uses sea’, ‘weed located sea’, ‘sea located weed’, ‘weed for sea’, ‘weed about sea’, ‘weed during sea’, and ‘weed by sea’). The set of possible relations were adapted from Levi’s (1978) original range of conceptual relations. Prior to the experiment, participants were provided with an exemplar of each relation. An exemplar of each relation is provided in Table 1. The experiment took about 30-40 minutes to complete.

Table 1.

Semantic relations coding. h: head; m: modifier.

Conceptual relation	Compound example
h about m	newsflash
h by m	handclap
h causes m	joyride
h caused by m	sunbeam
h derived from m	seafood
h during m	nightlife
h for m	mealtime
h has m	bookshop
m has h	doorframe
h location is m	farmyard
M location is h	neckline
h made of m	snowman
h makes m	honeybee
h is m	girlfriend
h uses m	steamboat
h used by m	witchcraft

Results and discussion

A total of 285 MTurk workers collectively contributed a total of 28,882 judgements to critical trials. The cleaning process included the removal of all trials for which a response was not given, the elimination of responses from all non-native or bilingual speakers of English, the removal of any data that was collected from a participant’s second or third experimental session¹, and the elimination of any participants who selected the same conceptual relation more than 50% of the time. This process involved removing 2,482 (8.6%) trials, including the complete removal of all trials pertaining to 22 participants. The final data source contained a total of 26,400 possible relations judgements collected from 263 (163 female; 99 male; 1 undisclosed) MTurk workers with an age range of 18 - 76 (mean = 37, SD = 13). The number of judgements per compound ranged from 35 to 49 with a median of 44 judgements provided per compound word.

This study relies on collections of multiple human ratings per item, and thus the reliability of the judgements (from which further measures are derived) depends on the degree of variability, or agreement, among participants. To measure the extent of error introduced into the study from inconsistency among individual participants, we performed tests of interrater reliability. Interrater reliability was examined using the split-half reliability procedure. For each experimental list, participants and their responses were randomly selected and split into two groups such that there was an even number of participants in each group. For each group we then calculated the total number of selections of each conceptual relation per compound word. For each compound, we then assessed the strength of the relationship between each group’s distribution of chosen relations using the Spearman correlation method. This step produced a Spearman’s rank coefficient for each compound word in the experimental list. We then calculated the mean Spearman correlation coefficient across all words. We repeated this process 10,000 times which resulted in 10,000 mean correlation coefficients per experimental list. Finally, we took a grand mean of these 10,000 correlation coefficients as an estimate of the split-half reliability for each experimental list. The outcome indicated that split-half reliability was high, ranging from ρ = 0.706 to ρ = 0.792 across lists (List 1, ρ = 0.746, 95% CI [0.7455, 0.7462]; List 2, ρ = 0.772, 95% CI [0.771, 0.772]; List 3, ρ = 0.754, 95% CI [0.754, 0.7546]; List 4, ρ = 0.792, 95% CI [0.791, 0.792]; List 5, ρ = 0.706, 95% CI [0.7056, 0.7063]; List 6, ρ = 0.753, 95% CI [0.7523, 0.7534]). Based on these results, we conclude that there is a high degree of consensus among MTurk raters’ possible relations judgements, indicating that the possible relations task produces an internally reliable measure.

The original possible relations judgement norms (Spalding & Gagné, 2014; Gagné & Spalding, 2014) were collected in an experiment which was conducted offline (i.e., in an isolated room supervised by an experimenter) and used university students as the sample population. The current study conditions were different: the experiment was conducted online and used a more heterogeneous sample population. The demographic statistics for the current study reflect the methodological differences between the current study and the previous one reported by Spalding and Gagné (2014) and Gagné and Spalding (2014). In the current Amazon Turk implementation, the age range is much broader (see above), the educational background of participants is more diverse (51% of participants had at least a bachelor’s degree), and the provenance of the participants is different (all MTurk participants are American, whereas the original possible relations experiment was conducted exclusively with students attending a Canadian university).

Crucially, we found that these methodological differences did not influence the reliability of the ratings. We determined this by comparing judgements for compounds from the current data collection with judgements of the same compounds from the initial offline study (Spalding & Gagné, 2014; Gagné and Spalding, (2014). A total of 81 (13.41%) compounds overlapped across these data sets. For each compound, we correlated the distribution of possible relations judgements from the original study with those collected in the current study. The mean correlation coefficient was moderate, ρ = 0.587, 95% CI [0.52, 0.65]. For each dataset presented in this paper, we then tested whether the critical effect of entropy differed across compounds with high correlation coefficients vs. low correlation coefficients. The diagnostic for the potential influence of the strength of the correlation between the two data collection procedures was the presence of an interaction between entropy and the resulting correlations on lexical decision times for each experimental dataset. We did not find any significant interactions across each dataset. This result suggests that the measure of entropy of conceptual relations, and its effect on lexical decision response times, is reliable and consistent despite differences in the presentation (offline versus online format) and population sample used during the collection procedure.

The supplementary materials consist of the database of possible relations judgements for 604 compounds that were collected in this experiment. Contained within the database are the compound words and the selection frequency for each relational interpretation per compound word. Each cell of the results matrix indicates how many participants chose that particular relation as the best interpretation for that particular compound. This matrix allows us to calculate Shannon entropy over the set of relations per compound (as defined below). This measure is included in the database. Correlations between entropy calculated over the set of conceptual relations, and other lexical variables, are reported in Experiments 2-5.

Experiment 2

Schmidtke et al. (2016) reported that entropy calculated over the probability distribution of a compound’s set of possible relational interpretations reliably affected visual word recognition processing speed. As argued in the introduction, if relational information is represented in semantic memory, then one would expect to find effects of relational competition irrespective of the modality of the linguistic input. Thus, we propose that further experimental verification for the rice theory would be granted by the demonstration of qualitatively equivalent effects of relational competition across linguistic modalities.

The goal of Experiments 2 and 3 is to test this proposal by testing the predictions of the rice theory during auditory comprehension of compound words. We do so by examining the effect of entropy of conceptual relations on the results of two separate auditory lexical decision experiments. We hypothesize that the cognitive bottleneck generated by uncertainty in the process of selecting a compound’s relational interpretation will slow down lexical processing. In other words, the effect of entropy of conceptual relations is expected to follow the same pattern as observed by Schmidtke et al. (2016): greater entropy of conceptual relations leads to longer lexical decision latencies.

Methods

Dependent variables.

Trial-level auditory lexical decision latencies were obtained from the Massive Auditory Lexical Decision [MALD] database (Tucker et al., submitted). MALD contains 228,016 trial-level auditory lexical decision latencies for 28,511 words and 11,400 non-words, collected from 283 monolingual English speaking participants at the University of Alberta, Canada. All items were produced by a male Western Canadian English speaker (age 32) and were recorded in a sound attenuated booth. Participants responded to stimuli using their dominant hand for word responses and their non-dominant hand for non-word responses. We removed all non-word trials, which reduced the dataset to 114,016 trials. The clean-up procedure included eliminating all trials for which there was an incorrect response or an outlier response time. Outlier removal included eliminating the top and bottom 1% of each participant’s distribution of RTs. Altogether, these clean-up procedures led to a loss of 4,894 (4.3%) data points. The remaining data set contained 109,122 auditory lexical decision latencies for 230 Canadian monolingual speakers (182 Female; 48 Male) within an age range of 17 and 29 (M = 20; SD = 2.3).

Materials.

We extracted from MALD trial-level auditory lexical decision responses for a total of 416 compounds which were matched with the compound list used in Study 1, and are also attested with both semantic similarity scores (see Independent variables below).

Independent variables.

Entropy of conceptual relations.

The critical variable of interest is Shannon entropy calculated over the probability distribution of interpretations of conceptual relations for a given compound. This measure was estimated for the dataset reported in Experiment 1. Entropy of conceptual relations is defined as H = –Σp_i log₂ p_i, where p_i is the probability of a relation within the respective distribution of chosen possible relations for a given compound. Moreover, in order to eliminate noise, and to reduce the potential influence of accidental responses, the probability distribution was estimated only for relations that were selected more than once. For example, the compound headband has the following distribution of possible relations judgements; ‘band for head’ (selected 19 times), ‘head has band’ (9), ‘band used by head’ (7), ‘band located head’ (3), ‘band uses head’ (2) and ‘band from head’ (2). The respective probability distribution for these relations is 0.45, 0.21, 0.17, 0.07, 0.05 and 0.05, which yields an Entropy value of 2.115 bits. To see an illustration of how Entropy of conceptual relations is an operationalization of competition, please refer to the Introduction.

Control variables.

Semantic similarity.

In keeping with Schmidtke et al.’s (2016) previous study on Entropy of conceptual relations, we controlled for effects of the semantic association between constituents and compound words by estimating the semantic similarity between (i) the compound word meaning and the left constituent (Left-Whole similarity; e.g., dog and doghouse), and (ii) the compound word meaning and the right constituent (Right-Whole similarity; e.g., house and doghouse). Effects of semantic similarity during compound word recognition are expected to influence behavioural response times in such a way that greater semantic similarity leads to shorter lexical decision latencies or fixation durations during reading (for a review see Schmidtke et al., 2017).

We gauged semantic similarity using Latent Semantic Analysis (Landauer & Dumais, 1997). The term-to-term LSA scores for Left-Whole and Right-Whole similarity for the target compounds were collected from http://zipf.ugent.be/snautenglish, with a default setting of 300 factors and a window of 6 words (Mandera, Keuleers & Brysbaert, 2017). These LSA scores were calculated over word occurrences in the 201 million-token SUBTLEX-UK corpus of film subtitles (Van Heuven, Mandera, Keuleers & Brysbaert, 2014). The degree of semantic similarity between the words that those vectors represent is estimated by the cosine of the angle between the vectors, ranging from 0 to 1. We inverted the raw scores (by multiplying by negative one) that were collected from the web interface for comparability with other LSA scores. After the inversion, values closer to 1 imply a greater semantic similarity between the pair of words under comparison. Crucially, these measures of semantic similarity are only weakly correlated with the critical measure of Entropy of conceptual relations (and other lexical controls, see Tables A1-4 in Appendix A for correlation matrices for Experiments 2-5 respectively). This allows us to statistically estimate the critical effect of Entropy of conceptual relations without any of the interpretational problems imposed by issues of multicollinearity.

Frequency and family size.

Finally, we included a set of lexical control variables that were the same as those used in Schmidtke et al. (2016): compound frequency and frequencies of the compound’s left and right constituents. Moreover, words with larger families tend to be recognized faster (Moscoso del Prado Martin, Deutsch, Frost, Schreuder & De Jong, 2005). To account for this, we also considered the positional family size of the left and right constituents (defined as the number and summed frequency of compounds that share a constituent with the fixed position of either the left or right constituent of the target compound). Word frequencies were obtained from the 51 million-token SUBTLEX-US corpus (Brysbaert & New, 2009), based on subtitles from US film and media, for all ELP compounds and their respective constituents. Frequency-based characteristics all pertain to compounds in their concatenated format. Family size estimates were calculated with the morphological parsing of the 18 million-token English component of the CELEX lexical database (Baayen et al., 1995).

For frequency-based statistics, we compared models fitted with SUBTLEX-US written word frequencies to the same frequencies (for the left constituent, right constituent and the whole word) estimated from spoken word usage. Spoken word frequencies were taken from the 109 million token spoken word sub-section of the Corpus of Contemporary American English (COCA; Davies, 2008). These frequencies were estimated from transcripts of unscripted conversations from more than 150 different TV and radio programs. Comparison of AIC values across models fitted with written and spoken word frequencies was conducted using the Chi-square test for homogeneity of variance. The results demonstrated that SUBTLEX-US word frequencies produced a better model fit for the current auditory lexical decision experiment and also for the auditory lexical decision experiment reported in Experiment 3.

Uniqueness points.

In addition, we also controlled for each item’s spoken word duration (in milliseconds) and the uniqueness point of the acoustic signal, i.e., the point in the acoustic signal of the compound at which all other potential word candidates are eliminated and the signal matches only the compound that is under recognition. Balling and Baayen (2008) and Balling and Baayen (2012), demonstrated that, for complex words, there are two points at which the compatibility of the target word and the acoustic input influences auditory recognition. The first is the initial uniqueness point (UP1), which is reached when morphologically unrelated competitors are no longer compatible with the acoustic input. The second point is the complex uniqueness point (CUP), at which morphologically related competitors become incompatible with the input.

We computed UP1 and CUP as is documented in Balling and Baayen (2008;2012). The two measures were determined in the following way. For a given compound, we queried its phonemic transcription of MALD. UP1 was defined as the position at which the query returned only words that were morphologically related to the continuation forms of the first constituent. For example the UP1 for the compound snowflake - /snoʊfleɪk/ - is at the phoneme /oʊ/, which is the phoneme at which snowflake deviates from snug, snip, sniper etc.

The CUP, by contrast, occurs when the second constituent of a compound deviates from other second constituents (and suffixes) attested as continuations of the first constituent. CUP was thus defined as the position at which the query returned only continuation forms of the whole word. For example, the CUP for snowflake is at the phoneme /f/. This is when snowflake deviates from all continuations in its morphological paradigm, e.g., snowman, snowball, snowplough and snowy. Both uniqueness points were measured as the number of phonemes up to and including the uniqueness point.

To anticipate the results, only CUP influenced auditory response latencies in Experiment 2. Since both variables are correlated at r = 0.51 (Experiment 2) and r = 0.5 (Experiment 3), there could be an underlying issue of collinearity. For completeness, we fitted linear models with both UP1 and CUP added as predictors separately, but found that these results did not change when either measure was included on their own. Moreover, we interacted Entropy of conceptual relations separately with both uniqueness point measures but we did not find a significant effect. This indicates that accessing the relational structure of a compound word is not determined by the point at which the compound word becomes uniquely identifiable from all other word candidates. We do not discuss these measures further as neither are correlated with Entropy of conceptual relations and are also not the central theoretical focus of this paper.

Distributional characteristics of all original and transformed lexical variables and RTs for Experiment 2 are reported in Part A of Table 2. Table A1 in Appendix A provides a correlation matrix of independent variables used in Experiment 2.

Table 2.

Descriptive statistics for the dependent and independent variables used in Experiment 2 and Experiment 3: Reported are the range, mean and standard deviations of the original and transformed variables after selection and trimming procedures.

Variable	Original			Transformed
A. Experiment 2	range	mean	sd	range	mean	sd
Reaction time, ms	478:2678	941	267	−2.1:−0.37	−1.1	0.25
Entropy of conceptual relations	0.57:3.3	2.1	0.57	−2.6:2	0.03	0.96
Left-Whole similarity (LSA)	0:0.65	0.31	0.13	−2.3:2.6	−0.01	1
Right-Whole similarity (LSA)	−0.01:0.63	0.3	0.13	−2.2:2.4	0	0.99
Compound Frequency (US frequency)	1:1940	99	221	−1.5:2.9	0	0.99
Left constituent Frequency (US frequency)	18:102467	6127	11045	−0.61:7.9	−0.01	0.98
Right constituent Frequency (US frequency)	8:204428	11308	22303	−0.53:8.6	−0.01	1
Left constituent Family Size	1:54	12	12	−1:3.7	0.02	1
Right constituent Family Size	1:155	18	27	−0.64:5.3	0.02	1
Uniqueness point	2:6	3.8	0.74	−2.3:3.1	0.02	1
Complex uniqueness point	1:7	4.3	0.87	−2.7:3.1	0.02	1
Compound duration, ms	−0.95:−0.36	−0.6	0.09	−3.8:2.5	−0.01	1
B. Experiment 3	Original			Transformed
Reaction time, ms	531:2583	995	253	−1.9:−0.37	−1.1	0.22
Entropy of conceptual relations	0.66:3.3	2.1	0.56	−2.5:2	0.04	0.96
Left-Whole similarity (LSA)	0.01:0.65	0.31	0.13	−2.3:2.6	−0.02	0.99
Right-Whole similarity (LSA)	−0.01:0.63	0.3	0.13	−2.3:2.5	−0.01	0.98
Compound Frequency (US frequency)	1:1940	97	217	−1.8:2.8	−0.03	0.98
Left constituent Frequency (US frequency)	18:102467	6379	12106	−0.59:7.7	−0.01	0.98
Right constituent Frequency (US frequency)	19:204428	11936	24712	−0.49:8.4	0	1
Left constituent Family Size	1:54	12	12	−0.92:3.6	0	1
Right constituent Family Size	1:155	17	25	−0.67:5.8	0.02	1.1
Uniqueness point	2:6	3.7	0.78	−2.2:2.9	0	1
Complex uniqueness point	1:7	4.3	0.88	−2.6:3	0	1
Compound duration, ms	0.41:2.1	0.7	0.11	−2.5:11	−0.01	0.95

Statistical considerations.

We fitted linear mixed-effects models to transformed auditory reaction time latencies. (Baayen, 2008; Baayen, Davidson, & Bates, 2008; Pinheiro & Bates, 2000). The distributions of lexical decision responses were positively skewed and thus required transforming to conform with a normal Gaussian distribution. The Box-Cox power transformation (Box & Cox, 1982) indicated that the most appropriate correction for lexical decision responses is the inverse-transform method (computed as −1000/RT). We used the lme4 (Bates, Maechler, Bolker & Walker, 2013) package in the R statistical computing software program (R Core Team, 2014) to compute statistical models. For all models described in this study, we used restricted maximum likelihood (REML) estimations. This procedure ensures that nuisance parameters are restrained by producing unbiased estimates of variance and covariance parameters. We used logarithmically transformed values of frequency-based predictor variables to account for their distributional skewness and all continuous independent variables were scaled (z-transformed) to allow the predictors to be compared on the same scale. Models also included trial number as a fixed effect and also included by-item and by-participant random intercepts. We also included by-participant random slopes for trial and Entropy: according to model comparisons using likelihood ratio tests, these random slopes did not significantly improve model fit and were therefore excluded from all models. The experimental list number (1-6) used in the possible relations experiment reported in Experiment 1 was also included as a covariate in all models. It did not show either a main effect or an interaction with any of the variables of interest, nor improve model fit, suggesting that all lists are equivalent for the purposes of the present study: we did not consider experimental list in further analyses. Furthermore, we refitted the final model after removing outliers from both data sets by excluding standardized residuals exceeding −2.5 or +2.5 standard deviations (Crawley, 2002; Baayen & Milin, 2010). Collinearity between compound and constituent frequency-based measures was high (multicollinearity condition number, κ > 30): importantly, it had no bearing on model estimates for our critical variable of Entropy. This is because Entropy and frequency-based measures correlated very weakly (all absolute values of r < .15).

Results and discussion

The data pool for Experiment 2 contained 1,708 trials. We removed four compounds with log frequencies greater than three standard deviations from the mean log frequency. The final data source for Experiment 2 contained 1,693 trials to 412 English compound words. Below we report the results of the linear mixed-effect regression model fitted to auditory lexical decision latencies for the partial fixed effect of Entropy of conceptual relations. Effect sizes are defined as the amount of change in reaction time latency (back transformed into milliseconds) estimated for the contrast between the minimum and maximum values of Entropy of conceptual relations.

Entropy of conceptual relations.

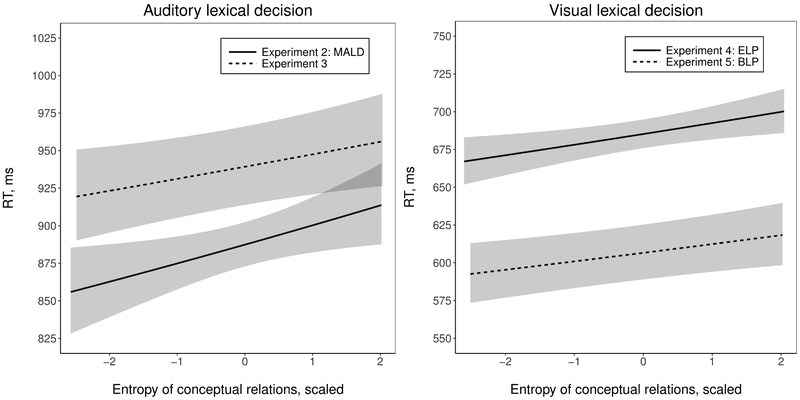
There was a significant main effect of Entropy of conceptual relations on auditory lexical decision reaction times [$\widehat{\beta }=0.016$; SE = 0.007; t = 2.4; p = 0.017, effect size = 58 ms]. The effect was such that greater Entropy led to slower response times, and was qualitatively identical to the result for visual lexical decision as reported by Schmidtke et al. (2016). Figure 2 (right panel) illustrates the partial fixed effect of entropy of conceptual relations on auditory lexical decision response times. Table B1 in Appendix B reports the final linear mixed-effects model fitted to response times for this auditory lexical decision dataset.

Figure 2.

The partial effect of Entropy of relational competition (scaled) on visual lexical decision RTs in Experiment 4 (ELP: left panel) and Experiment 5 (BLP: right panel), and on auditory lexical decision RTs in Experiment 2 (MALD: left panel) and Experiment 3 (right panel) samples. Slopes represent predicted values of the linear mixed-effects models fitted separately to Experiment 2, 3, 4 and 5 samples. Grey bands represent lower and upper limit of 95% confidence intervals for each model.

Semantic similarity, frequency, and family size.

We observed significant effects of semantic similarity on auditory lexical decision response latencies. The model showed that Right-Whole semantic similarity exerted a significant effect on auditory lexical decision times [$\widehat{\beta }=-0.015$; SE = 0.007; t = −2.3; p = 0.02, effect size = 56 ms]. The effect demonstrates that greater similarity between the right constituent meaning and the compound word meaning (e.g., stick and drumstick) leads to shorter response latencies. This finding is in line with prior evidence from EEG studies of auditory compound word recognition, in which opaque compounds that were presented aurally elicited greater negative deflections in the ERP waveform relative to transparent compounds (Koester, Holle, & Gunter, 2009; MacGregor & Shtyrov, 2013).

The Right-Whole semantic similarity facilitation effect is expected under processing accounts (e.g., El-Bialy, Gagné, & Spalding, 2013; Libben, Gibson, Yoon, Bom, & Sandra, 2003) which posit that compound word recognition is aided by the conjunctive activation of strongly associated connections within a semantic network (i.e., for the case of compounds in which the meanings of the compound and the constituents are similar). Moreover, as was shown by Schmidtke et al. (2017), such facilitatory effects are also expected for the population sample tested in the current population. Student participants are expected to have greater reading experience, and, as a result, are less likely to be impeded by the processing cost of discriminating between strongly associated semantic concepts.

Lastly, we found significant facilitatory effects of compound frequency, but did not find reliable effects for the left or right constituent frequency, or family size (for the right and left constituent). The null effect of family size is in line with Balling and Baayen (2012) and accords with the Shortlist B model of spoken word recognition (Norris & McQueen, 2008). Under this account, decomposing a complex word’s internal morphological structure, as indexed by family size, is not integral to the word recognition process. Instead, bottom-up evidence from the unique phoneme sequence in the unfolding acoustic signal (or from the word’s a priori likelihood in connected speech) narrows down the most likely lexical candidate without the need to resort to morphological structure (for further discussion see Balling & Baayen, 2008; 2012).

Experiment 3

The previous experiment reported the novel finding that competition between conceptual relations influences the auditory recognition of a compound word. In the current experiment, we test this effect further by reporting an additional auditory lexical decision study in which a different set of participants provided lexical decision responses to an overlapping set of compound words. We obtained unpublished and unreported raw data from an auditory lexical decision experiment of English compound words (Tucker and Baayen, 2011). This experiment followed the format of a simple auditory lexical decision task, in which participants judged the lexicality of existing English concatenated compounds, and concatenated nonword-word combinations of the form AX (word-nonword) and XB (nonword-word).

Methods

Dependent variables.

Stimuli.

All real words in the stimuli list consisted of 1,200 compound words, which were generated using the CELEX database (Baayen et al., 1995). All 1,200 nonwords were generated using the Wuggy nonword generator (Keuleers & Brysbaert, 2010). Half of the nonword stimuli were AX nonwords and the remaining half were XB items. None of the real words embedded within nonword compounds occurred as constituents or whole word compounds in the real word stimuli list.

Apparatus and procedure.

All items in the stimuli set were produced by a female Western Canadian English speaker (an undergraduate student at the University of Alberta) and were recorded in a sound attenuated booth. Recordings were made with a Countryman E6 headmounted microphone (with phantom power supplied by a Multimix 8) and an Alesis CD recorder. All recordings were completed in the same booth, with the same equipment, and at the same time of day (two separate days in one week). All stimuli were normalized and parsed using Praat.

The entire stimuli list was split into four sub-experiments of 600 words (300 compound words and 300 nonwords (150 AX and 150 XB). Each experiment was presented using the ePrime software. Participants were seated in a sound attenuated booth and the items were presented aurally via headphones. They were instructed to press the “yes” button on a keyboard when they heard a word and the “no” button when they heard a non-word as quickly and accurately as they could. Participants responded to stimuli using their dominant hand for word responses and their non-dominant hand for non-word responses.

Participants.

A total of 55 monolingual Canadian English speaking participants (42 Female; 13 Male) within an age range of 17 - 31 (M = 21, SD = 3) took part in the experiment for course credit. Participants were recruited from the undergraduate participant pool at the University of Alberta and received course credit for their participation. All participants reported having normal hearing.

The data set contained 24,911 auditory lexical decision latencies to compound words. We eliminated all trials for which there was an incorrect response or an outlier response time. We removed all reaction times from the top and bottom 1% of each participant’s distribution of RTs. These data cleaning steps resulted in a loss of 3,675 (15%) data points. The final data set contained 21,236 trial-level observations.

Materials.

We extracted from the experimental dataset trial-level auditory lexical decision responses for a total of 426 compounds. These were all the compounds that were present in the experiment which were also attested with a full set of entropy scores (were present in the Amazon Turk database described in Experiment 1) and a full set of LSA semantic similarity ratings (see Independent variables in Experiment 4 for information on the collection of LSA scores).

Independent variables.

Distributional characteristics of all original and transformed lexical variables and RTs for Experiment 3 are reported in Part B of Table 2. Table A2 in Appendix A provides a correlation matrix of independent variables used in Experiment 3.

Statistical considerations.

The same modelling software, procedure and model template, as described in Statistical considerations for Experiment 2, was applied to the current data set. The Box-Cox transform method (Box & Cox, 1984) indicated that the most appropriate transformation method MALD auditory lexical decision latencies was the inverse transform.

Results and discussion

The data pool for Experiment 3 contained 8,157 trials. We removed four compounds with log frequencies greater than three standard deviations from the mean log frequency and two compounds with entropy scores greater than three standard deviations from the mean entropy score. The final data source for Experiment 3 contained 8,002 trials to 418 English compound words. Below we report the results of the linear mixed-effect regression model fitted to auditory lexical decision latencies for the partial fixed effect of Entropy of conceptual relations. The reported effect sizes are the same as is defined in Experiment 2.

Entropy of conceptual relations.

There was a significant main effect of Entropy of conceptual relations on auditory lexical decision reaction times $\widehat{\beta }=0.009$; SE = 0.004; t = 2.3; p = 0.022, effect size = 37 ms]. The effect replicates Experiment 2: for auditory compound word recognition greater Entropy of conceptual relations was associated with longer lexical decision reaction times. Figure 2 (right panel) illustrates the partial fixed effect of entropy of conceptual relations on auditory lexical decision response times.

Semantic similarity, frequency, and family size.

Moreover, the model indicated a significant effect of Left-Whole semantic similarity [$\widehat{\beta }=-0.013$; = −0.013; SE = 0.004; t = −3.3; p < 0.0001, effect size = 56 ms]. This result indicates that lexical decision responses were faster when there was greater the semantic similarity between the left constituent meaning and the compound word meaning (e.g., drum and drumstick). The null results for family size in Experiment 2 was replicated here. Lastly, we found a significant effect of right frequency of the compound word. Table B2 in Appendix B reports the final linear mixed-effects model fitted to response times for this auditory lexical decision dataset.

Interestingly, the effects of Left-Whole and Right-Whole semantic similarity across both auditory lexical decision studies are in complementary distribution. In Experiment 2, only Right-Whole semantic similarity, and not Left-Whole semantic similarity, elicited a significant facilitation effect on response times. In Experiment 3 however, the opposite was found. We speculate that this differentiation may be due to dissimilarities in the experimental designs of Experiment 2 and Experiment 3, which may have impacted individual strategies of morphological processing. In Experiment 3, only compounds were used as real-word stimuli, which may have increased participants’ expectation that the upcoming word is multimorphemic. If participants were expecting a compound word, they may have shifted semantic processing resources to the earlier portion of the unfolding acoustic signal in order to get a ‘head-start’ in narrowing down the meaning of the compound word. Thus, processing attention is directed to the earlier point of the acoustic signal, i.e., when the left constituent of the compound is revealed, and processing resources become more heavily devoted to ascertaining how strongly the meaning of the left constituent is to the compound word (as indexed by the effect Left-Whole similarity). However, in Experiment 2, compound words (and other complex and simplex words) were intermixed with monomorphemic real words. This mixed stimuli design may have fostered an unconscious processing strategy in which participants were less expectant of the upcoming word being multimorphemic. This in turn may have allocated semantic processing resources from a reliance on accessing the semantic field of the early part of the word, to the latter part of the compound word (as indexed by the effect Right-Whole similarity).

Taken together, Experiments 2 and 3 demonstrate that competition between conceptual relations influences the auditory recognition of a compound word. This finding suggests that the competitive process of selecting an interpretation of a compound word is indifferent to whether the compound is presented orthographically or acoustically.

Experiment 4

Using the expanded set of norms that are reported in Experiment 1, the goal of this experiment was to test whether conceptual combination during visual compound word recognition is competitive in nature. Schmidtke et al. (2016) reported that entropy calculated over the probability distribution of a compound’s relational interpretations reliably affected visual word recognition processing speed. They found that greater entropy inhibited lexical decision response times to a set of 184 compound words in the British Lexicon Project (Balota et al., 2007) and 141 compounds in the English Lexicon Project (Keuleers et al., 2012).

In what follows, we report two experiments in which we take the results of the data reported in Experiment 1, compute the measure of entropy of conceptual relations, and examine its predictive role on RTs obtained from much larger sets of visually presented compound words taken from the ELP database (Experiment 4) and from the BLP (Experiment 5).

Methods

Dependent variables.

We obtained trial-level visual lexical decision latencies from the English Lexicon Project [ELP; Balota et al., 2007]. The ELP provides visual lexical decision latencies for 40,481 words and an equal number of non-words, collected from 816 participants. All participants were drawn from undergraduate participant pools across six US universities. Participants responded to stimuli using their dominant hand for word responses and the non-dominant hand for non-word responses. All non-words were not pseudocomplex in that they did not contain strings that are existing English compound constituents. We removed trials for which there was an incorrect response or an outlier response time. Outlier removal involved eliminating the top and bottom 1% of the RT distributions of each participant. Altogether, the clean-up procedure led to a loss of 2.15% of the total data points.

Materials.

We extracted 505 compounds from the ELP dataset. These were all compounds from the ELP dataset that matched the list of compounds used in the possible relations collection study in Experiment 1.

Independent variables.

The critical variable of interest is Entropy of conceptual relations. We also included estimates of family size for left and right constituents, and LSA scores (Left-Whole and Right-Whole) as estimates of semantic similarity (see Experiment 2 for details). We also included word length (in characters) as a control variable. We verified our inclusion of word length as measured in characters and not syllables. A comparison of Akaike Information Criteria (AIC) estimates (as a diagnostic of model deviance) for models fitted with word length in characters versus word length measured in syllables confirmed this. The statistical procedure was also identical to the visual lexical decision study reported by Schmidtke et al. (2016).

Distributional characteristics of all original and transformed lexical variables and RTs for the ELP dataset are reported in Part A of Table 3. Table A3 provides a correlation matrix of all independent variables used in this experiment.

Table 3.

Descriptive statistics for the dependent and independent variables used in Experiment 4 and Experiment 5: Reported are the range, mean and standard deviations of the original and transformed variables after selection and trimming procedures.

Variable	Original			Transformed
A. Experiment 4 (ELP)	range	mean	sd	range	mean	sd
Reaction time, ms	207:2929	749	274	−4.8:−0.34	−1.5	0.42
Entropy of conceptual relations	0.57:3.3	2.1	0.58	−2.6:2	0.02	0.98
Left-Whole similarity (LSA)	0:0.65	0.31	0.13	−2.4:2.6	−0.03	0.99
Right-Whole similarity (LSA)	−0.01:0.63	0.3	0.13	−2.3:2.5	−0.01	0.98
Compound Frequency (US frequency)	1:1940	88	203	−2.5:2.8	−0.07	0.96
Left constituent Frequency (US frequency)	18:102467	6338	12171	−3.5:2.6	−0.03	1
Right constituent Frequency (US frequency)	8:204428	12117	24923	−3.1:2.3	−0.04	1
Left constituent Family Size	1:54	11	11	−0.99:3.8	−0.01	0.99
Right constituent Family Size	1:155	17	25	−0.69:5.4	−0.01	0.99
Compound Length	6:13	8.5	1.2	−2.1:3.7	−0.01	1
B. Experiment 5 (BLP)	Original			Transformed
Reaction time, ms	311:2062	643	187	−3.2:−0.48	−1.7	0.4
Entropy of conceptual relations	0.57:3.3	2.1	0.59	−2.5:2	0.03	0.98
Left-Whole similarity (LSA)	0.01:0.65	0.31	0.13	−2.3:2.6	−0.05	0.99
Right-Whole similarity (LSA)	−0.01:0.64	0.3	0.13	−2.3:2.6	−0.02	1
Compound Frequency (UK frequency)	2:13098	438	1260	−2.5:2.8	−0.16	0.99
Left constituent Frequency (UK frequency)	327:358568	24246	33769	−2.8:2.6	−0.04	1
Right constituent Frequency (UK frequency)	47:540985	43279	78198	−3.3:2.1	−0.04	1
Left constituent Family Size	1:45	11	10	−1.1:3.2	−0.02	0.98
Right constituent Family Size	1:155	17	25	−0.71:5.5	0	1
Compound Length	6:11	8.2	1	−2.2:2.7	−0.01	1

Statistical considerations.

We fitted linear mixed-effects models to transformed ELP reaction time latencies. A Box-Cox power transformation (Box & Cox, 1982) indicated that the inverse-transform method was the most appropriate method of transforming response times for latencies. Moreover, the same modelling procedure as used for visual lexical decision was applied to both experiments (see Experiment 2 for model specifications, variable transformations and scaling). All models included trial number as a fixed effect and included by-item and by-participant random intercepts. We also included by-participant random slopes for trial and Entropy: according to the model comparison likelihood ratio tests, these random slopes did not significantly improve model fit and were therefore excluded from all models. Furthermore, we refitted models after removing outliers from both data sets by excluding standardized residuals exceeding −2.5 or +2.5 standard deviations from the mean standardized residual.

Results and discussion

The ELP data pool contained 15,355 trials. We removed seven compounds with log frequencies that were greater than three standard deviations from the mean log frequency and two compounds with entropy scores greater than three standard deviations from the mean entropy score. The final data source contained 15,145 trials to 497 English compound words. Below we report the results of the linear mixed-effect regression model fitted to lexical decision latencies for the fixed effect of Entropy of conceptual relations. The reported effect size measurement is the same as is defined in Experiment 2.

Entropy of conceptual relations.

Entropy of conceptual relations produced a reliable inhibitory effect on lexical decision reaction times to compound words in the ELP dataset $\widehat{\beta }=0.015$; SE = 0.006; t = 2.8; p = 0.006, effect size (defined in preceding paragraph) = 33 ms]. The pattern of the effect indicates that a greater amount of entropy is associated with longer response times, i.e., the more uncertainty regarding the relational interpretation for a given compound, the more processing effort is required to recognize the word. The partial effects of Entropy are visualized in the left panel of Figure 2 (to aid interpretability, plots depict back-transformed values of response times, in milliseconds). Table B3 in Appendix B reports the fixed effect coefficients for final linear mixed-effects model fitted to ELP response latencies.

Semantic similarity, frequency, and family size.

The results showed that Right-Whole semantic similarity did not produce a reliable effect on visual lexical decision scores [t = 1.63; p = .103]. Furthermore, Left-Whole semantic similarity exerted a borderline significant effect on ELP lexical decision times [$\widehat{\beta }=-0.01$; SE = 0.006; t = −1.8; p = 0.07]. These effects did not arise as statistically significant in Experiment 5 either. In sum, we conclude that both Right-Whole and Left-Whole semantic similarity did not show any reliable effects on lexical decision latencies.

As can be viewed in correlation Tables B3 (and B4 for Experiment 5) in Appendix B, the relationships between Entropy and semantic similarity measures are weak to moderate (r < .2), thus it is not likely that the null effects of semantic similarity are due to the influence of entropy. However, it is possible that an interaction exists between one of both of the measure and Entropy of conceptual relations. We examined this possibility by performing two-way interactions of Entropy with each LSA measure (with both interactions included in the same model). We did not find any support for these interactions in the ELP dataset (nor in any of the other datasets reported in this study). We therefore conclude that the effect of entropy of conceptual relations is independent of any effect of the semantic similarity between a compound word’s meaning and the meanings of its constituents.

Finally, for completeness, the results indicated that lexical decision times in the ELP dataset were also predicted by the following lexical control variables: Compound frequency, Left constituent frequency and Right constituent frequency. The effect of frequency was facilitatory, such that compounds that are more frequent or have more frequent constituents were recognized faster. Furthermore lexical decision times in the ELP were predicted by the Left constituent family size. These findings reconfirm earlier results which show that compounds with larger morphological families, more frequent constituents and more frequent surface forms are processed faster (cf. De Jong, Schreuder, & Baayen, 2000 ; Juhasz & Berkowitz, 2011; Andrews, Miller, & Rayner, 2004; Zwitserlood, 1994). However, we express caution in the interpretation of these control variables: as Table A3 (and also Table A4 for Experiment 5) of Appendix A indicates, there is high collinearity (r > .6) among family size and the frequency measure of the respective constituent. Multicollinearity among these predictors could have been reduced, but the outcome of these variables was not the focus of this study (we do not report the results of these predictors for visual lexical decision in Experiment 5).

In summary, the results of Experiment 4 replicate the results of Schmidtke et al. (2016): with a separate and larger set of compound word ratings, we found that increased entropy of conceptual relations, i.e., greater competition among possible relational meanings for a compound, slows down compound word recognition. In the next experiment, we test whether the same pattern of results are found in a separate visual lexical decision mega-study.

Experiment 5

The goal of Experiment 5 was to test whether the effect of Entropy of conceptual relations on visual lexical decision latencies also extends to a different sampling population (BrE speakers). This experiment also provides an additional test of the original results reported by Schmidtke et al. (2016) but this time with a larger and more representative set of compound words.

Methods

Dependent variables.

For this experiment, we obtained trial-level visual lexical decision latencies from the British Lexicon Project [BLP; Keuleers et al., 2012]. The BLP is a database of lexical decision latencies to over 14,000 words and an equal number of non-words in English collected from 78 students and employees of Royal Holloway University of London. Participants responded to stimuli using their dominant hand for word responses and the non-dominant hand for non-word responses. We removed trials for which there was an incorrect response or an outlier response time. Outlier removal involved eliminating the top and bottom 1% of the RT distributions of each participant in the BLP dataset. Altogether, this clean-up procedure led to a loss of 2.15% of the total data points.

Materials.

We extracted all available compounds that were attested in the BLP and were also present in the Amazon Turk database described in Experiment 1. Of the total number of compounds available in the database, 422 were present in the BLP data source².

Independent variables.

The critical independent variable and lexical control measures were identical to those used in Experiment 4. The only difference was that, due to the provenance of the population sample, word frequencies from the 201 million-token SUBTLEX-UK corpus (van Heuven, Mandera, Keuleers & Brysbaert, 2014), based on UK television (BBC) subtitles, were used for all BLP compounds and their constituents.

Distributional characteristics of all original and transformed lexical variables and RTs for the BLP dataset are reported in Part B of Table 3. Table A4 provides a correlation matrix of all independent variables used in this experiment.

Statistical considerations.

The same modelling software, procedure and model template, as described in Statistical considerations for Experiment 2, was applied to the current data set. The Box-Cox transform method (Box & Cox, 1984) indicated that the most appropriate transformation method for BLP lexical decision latencies was the inverse transform.

Results and discussion

The BLP data source contained 13,516 trials. As in Experiment 4, we removed three compounds that were greater than 3 standard deviations from the mean log frequency, and two compounds with entropy scores greater than three standard deviations from the mean entropy score. Thus, the final BLP data source contained 13,354 trials to 417 English compound words. Below we report the results of the linear mixed-effect regression model fitted to lexical decision latencies for the fixed effect of Entropy of conceptual relations. The reported effect size is as defined in Experiment 4.

Entropy of conceptual relations elicited a reliable inhibitory effect on lexical decision reaction times in the BLP dataset $\widehat{\beta }=0.016$; SE = 0.005; t = 2.8; p = 0.005, effect size = 26 ms]. The effect replicates the findings observed in Experiment 4 and the effect originally reported in BLP by Schmidtke et al. (2016). The result indicates that there is a processing cost during compound word recognition when there is more uncertainty regarding the relational interpretation of the compound word under visual inspection. The partial effects of Entropy are visualized in the left panel of Figure 2 (to aid interpretability, plots depict back-transformed values of response times, in milliseconds). Table B4 in Appendix B reports the fixed effect coefficients for the final linear mixed-effects model fitted to BLP response latencies.

General discussion

This study tested the claim of the rice theory that conceptual relations compete for selection during compound word recognition. Using Shannon Entropy as an index of competition, Schmidtke et al. (2016) demonstrated that there is a processing cost to compound word recognition when no single conceptual relation has a clear dominance over other possible relational meanings, i.e., when entropy calculated over the distribution of a compound’s possible conceptual relations is relatively high. We tested this hypothesis in a series of five experiments.

In Experiment 1 we conducted a large scale possible relations study, which enabled us to estimate the reliability of possible-relations judgments, and compute the measure of entropy of conceptual relations for 604 English compound words. We then used this data to test whether Schmidtke et al.’s (2016) finding extends to the auditory domain of compound word processing, and also to determine whether the initial finding for visual lexical decision generalizes to a much larger data set. In doing so, this study provides the following two empirical contributions. First, in Experiments 2 and 3 we extend the finding to the auditory domain and find that the inhibitory effect of entropy of conceptual relations extends to lexical decision response times to spoken words. Second, in Experiments 4 and 5 we found, for a much larger set of compounds, Schmidtke et al.’s (2016) finding that entropy conceptual relations has an inhibitory effect on visual lexical decision response times.

The results of the present work adds to the evidence base that both visual and auditory compound word recognition is sensitive to competition among conceptual relations. The novel finding that spoken word comprehension of compounds is affected by entropy of conceptual relations broadens the empirical base of the rice model of conceptual combination to the domain of auditory comprehension. That is, we show that the process of accessing relational meanings is integral to word recognition in general, and is not just limited to the visual domain. The evidence that relational selection is not tied to either visual or auditory processing further reinforces a claim of the rice theory (Spalding et al., 2010), which is that the locus of the competition effect resides at a conceptual, rather than formal level, of lexical processing. This is despite the possibility that the unfolding of the acoustic signal over time and the strong influence of a word’s cohort could make identification of a word possible without a retreat to its semantics.

The evidence presented across the four lexical decision studies further suggests that the mechanism by which relational meanings are generated is combinatorial in nature. That is, we argue that the effects of the measure of entropy of conceptual relations reflects a process during which relational meanings of established compounds are concurrently generated ‘on the fly’. We base this interpretation on two observations. First, if the entropy effect instead reflects, say, just the retrieval of entrenched and consolidated relational meanings, then one would also expect this same process for novel compounds or modifier-noun phrases. Novel compounds, by definition, are highly likely to be encountered by a language user for the first time, which entails that in order to comprehend a novel compound, the language system would need to make an attempt at computing a compositional meaning from the individual constituents of the phrase. Indeed, studies suggest that the comprehension of novel compounds and modifier-noun phrases does involve the online construction of a compositional meaning (e.g., Gagné, 2002; Gagné & Spalding; 2007, see also Štekauer, 2005, for studies which assess competition and meaning dominance among potential meanings for novel noun-noun combinations). This leads us to believe that the process of online conceptual combination outlined in the rice theory is common to novel compounds and established compound words.

Second, if the effect of entropy of conceptual relations is an index the access of a stored bank of relational meanings, then it is unclear how exactly such meanings would be stored and accessed each time the same compound word is encountered. Consider that the current measure of entropy differs from prior implementations of entropy as measures of competition within morphological paradigms (e.g., Moscoso del Prado Martín, Kostić, & Baayen, 2004; Milin, Kuperman, Kostić, & Baayen, 2009; Milin, Đurđević, & Moscoso del Prado Martín, 2009). These measures of entropy are based on distributional information that is available in the orthographic signal, and as a result are able to be memorized and stored via exposure to the surface form of the word. On the other hand, the measure of entropy reported in the current study is computed over ‘invisible’ entities that are not present in the acoustic or orthographic signal. Moreover, most of the meanings that entropy is computed over are not attested at all in the language – they are only possible meanings that may be suggested by generating a new way of combining the constituents of the compound. In sum, this suggests that unlike these prior implementations of entropy, entropy of conceptual relations reflects the instantaneous activation of an array of potential interpretations about the meaning of the compound word that is being recognized.

Notably, entropy of conceptual relations was not the only semantic predictor to reliably influence lexical decision response times. In Experiment 2, we found that auditory lexical decision latencies were also significantly predicted by the semantic similarity between the meanings of the right constituent and the compound word (i.e., Right-Whole similarity; the LSA distance between bar and crowbar), and, in Experiment 3, the similarity between the meanings of the left constituent and the compound word (i.e., Left-Whole similarity; the LSA distance between crow and crowbar). For visual lexical decision (Experiment 4), we found that Left-Whole similarity demonstrated a borderline significant effect. The processing boost associated with high semantic similarity between a compound and either of its constituents (e.g., the compound rainstorm) is argued to be an outcome of “conjunctive activation” between dense and strongly interconnected conceptual representations in semantic memory (El-Bialy et al., 2013; Libben, 1998). For auditory complex word recognition, the results of Experiment 2 and 3 accord with this view and complement the findings of a small number of prior auditory comprehension studies which show that a greater semantic association between meanings of morphemes and whole compound words facilitates lexical processing (Koester, Holle, & Gunter, 2009; MacGregor & Shtyrov, 2013). For the case of visual lexical decision, the observed non-existent effects of semantic similarity of constituents is not unexpected, since this predictor is not consistently observed across behavioural studies of visual compound word recognition or reading (for an overview see, Juhasz, Lai & Woodcock, 2015; Schmidtke et al., 2017).

Taken together, the present results indicate that the semantic processing of compound words in the auditory domain is not only boosted by reduced uncertainty about the relational interpretation of the word, but also by the conjunctive activation of similar modifier, head and compound word meanings. Thus, the co-activation of the semantics of constituent meanings and whole-words on its own is not sufficient for the mental process of recognizing a compound word. The consistency of the effect of competition between relational meanings across all experiments indicates that structural information about how constituents combine with one another is also necessary for the recognition of the compound word. Moreover, given the reliability and nature of the effect of relational competition, which gives prominence to the notion that the language system concurrently activates numerous semantic representations, our results are consistent with models of compound word processing which argue for simultaneous access to multiple sources of information (Kuperman, Schreuder, Bertram, & Baayen, 2009; Kuperman, Bertram, & Baayen, 2010; Libben 2005; 2006). These models suggest that in order to maximize the opportunity of obtaining the meaning of a complex word, readers will attempt to utilize all available processing cues. In sum, we argue that the theoretical implications of the present results, that the language system generates multiple relational meanings, can be incorporated within these aforementioned multiple-route processing frameworks.

Finally, as well as demonstrating the critical finding regarding entropy of conceptual relations, our results shed light on the further aspects of morphological processing. In auditory lexical decision, unlike visual lexical decision, stand-alone frequencies of either the left or right constituent (e.g., corn or dog for the compound corndog) did not produce across the board significant effects. Only the right constituent frequency produced a significant facilitatory effect in Experiment 3. In addition, unlike the visual lexical decision studies, the Left-constituent family size measure did not reach significance in either auditory study (nor did Right-constituent family size across all experiments). Frequency effects of constituents have been used in experimental word recognition research as diagnostic measures for access to decomposed morpheme representations (Bertram, Schreuder, & Baayen, 2000; Kuperman, Bertram, & Baayen, 2008; Pham & Baayen, 2015; Taft & Forster, 1976), while morphological family size measures are interpreted as access to morphological structure (Baayen, Dijkstra, & Schreuder, 1997; Meunier & Segui, 1999; Moscoso del Prado Martín, 2005). Following from this view, it is interesting that we observe that indices of access to decomposed morphemes are absent in the company of significant effects of semantic similarity. This may indicate that access to the individual morphemes or morphemic structure is not a requisite for access to morpheme meanings. That is, the conjunctive activation of meanings of the constituents and whole word meanings, as indexed by effects of semantic similarity, is distinct from and does not necessitate access to morphological representations. We suggest that processes of conjunctive semantic activation and relational composition are two processes that operate over information that is conceptual and not strictly morphemic.

To conclude, the study reported here shows that the process of constructing and evaluating relational meanings is critical to both auditory and visual recognition of compound words. A coherent pattern emerged from the experiments reported here, which is that uncertainty about the conceptual relation of a compound word is a key predictor of visual and auditory compound word recognition. Collectively these results provide evidence for the view that compound word processing involves constructing multiple relational meanings and that these meanings compete with one another (Spalding et al., 2010; Gagné & Spalding, 2014). In addition, the database of possible conceptual relations for English compound words will provide word recognition researchers with new relational-semantic measures for inclusion in future studies exploring questions related to English compound word recognition.

Appendix A

Correlation matrices

Table A1.

Correlation matrix of lexical variables used in Experiment 2.

	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.
1. Entropy
2. Left-Whole LSA	−0.15**
3. Right-Whole LSA	−0.21***	0.18***
4. Compound freq.	0.19***	0.10*	−0.09
5. Left freq.	0.14**	−0.08	−0.08	0.24***
6. Right freq.	0.26***	0.06	−0.31***	0.26***	0.16**
7. Left fam. size	−0.01	−0.02	−0.05	0.09	0.56***	0.04
8. Right fam. size	0.12*	0.03	−0.18***	0.06	0.01	0.60***	−0.17***
9. UP	0.03	−0.05	−0.01	0.02	−0.14**	0.03	−0.15**	−0.01
10. CUP	0.04	0.02	0.02	0.00	−0.07	0.04	−0.18***	0.08	0.51***
11. Compound duration	0.08	0.03	0.06	0.11*	0.06	0.03	0.08	0.08	0.00	−0.20***

Lower triangle provides Spearman correlation coefficients.

^***Correlation is significant at the .001 level.

^**Correlation is significant at the .01 level.

^*Correlation is significant at the .05 level.

Table A2.

Correlation matrix of lexical variables used in Experiment 3.

	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.
1. Entropy
2. Left-Whole LSA	−0.13**
3. Right-Whole LSA	−0.22 ***	0.16 ***
4. Compound freq.	0.06	0.16 ***	0.11*
5. Left freq.	0.09	−0.04	−0.04	0.18***
6. Right freq.	0.17 ***	0.06	−0.25 ***	0.18***	0.13**
7. Left fam. size	0.03	−0.02	−0.04	0.07	0.63***	0.06
8. Right fam. size	0.10*	0.05	−0.19 ***	0.09	−0.05	0.63***	−0.14**
9. UP	−0.02	−0.02	0.02	−0.03	−0.11*	0.06	−0.14**	0.01
10. CUP	−0.01	0.05	0.02	−0.03	−0.10	0.07	−0.16***	0.10*	0.50***
11. Compound duration	−0.04	−0.09	−0.05	−0.21***	−0.11*	−0.07	−0.07	0.02	0.09	0.30***

Lower triangle provides Spearman correlation coefficients.

^***Correlation is significant at the .001 level.

^**Correlation is significant at the .01 level.

^*Correlation is significant at the .05 level.

Table A3.

Correlation matrix of lexical variables used in Experiment 4.

	1.	2.	3.	4.	5.	6.	7.	8.
1. Entropy
2. Left-Whole LSA	−0.18***
3. Right-Whole LSA	−0.19***	0.19***
4. Compound freq.	0.08	0.15***	0.11*
5. Left freq.	0.04	−0.02	−0.02	0.15***
6. Right freq.	0.14**	0.06	−0.21***	0.21***	0.11*
7. Left fam. size	0.00	−0.02	−0.06	0.08	0.59***	0.01
8. Right fam. size	0.08	0.04	−0.17***	0.12**	−0.05	0.65***	−0.15***
9. Compound length	−0.01	0.10*	0.03	−0.03	−0.07	−0.10*	−0.22***	−0.04

Lower triangle provides Spearman correlation coefficients.

^***Correlation is significant at the .001 level.

^**Correlation is significant at the .01 level.

^*Correlation is significant at the .05 level.

Table A4.

Correlation matrix of lexical variables used in Experiment 5.

	1.	2.	3.	4.	5.	6.	7.	8.
1. Entropy
2. Left-Whole LSA	−0.17***
3. Right-Whole LSA	−0.19***	0.17***
4. Compound freq.	0.07	0.16**	0.02
5. Left freq.	0.07	−0.01	−0.02	0.17***
6. Right freq.	0.11*	0.11*	−0.25***	0.21***	0.14**
7. Left fam. size	0.01	−0.01	−0.07	0.05	0.64***	0.02
8. Right fam. size	0.06	0.04	−0.19***	0.11*	−0.04	0.70***	−0.16***
9. Compound length	−0.07	0.12*	0.06	0.03	−0.10	−0.06	−0.23***	−0.04

Lower triangle provides Spearman correlation coefficients.

^***Correlation is significant at the .001 level.

^**Correlation is significant at the .01 level.

^*Correlation is significant at the .05 level.

Appendix B

Model summaries

The following tables provide the fixed effects coefficients of the final models in which significant effects of Entropy of conceptual relations were found.

Table B1.

Fixed effects of the linear mixed-effects model fitted to auditory lexical decision RTs in Experiment 2. Conditional R² = 0.5. SD of the residual = 0.15. SD for the random effect of Compound = 0.08. SD for the random effect of Participant = 0.11. N = 1,693. N after trimming = 1,659.

	Estimate	Std. Error	t	p
Intercept	−1.128	0.010	−118.219	0.000
Entropy of conceptual relations	0.016	0.007	2.399	0.017
Left-Whole similarity	−0.006	0.006	−0.894	0.372
Right-Whole similarity	−0.015	0.007	−2.342	0.020
Compound frequency	−0.055	0.007	−8.114	0.000
Left constituent frequency	−0.000	0.008	−0.064	0.949
Right constituent frequency	0.010	0.008	1.265	0.207
Left constituent family size	0.005	0.007	0.708	0.479
Right constituent family size	0.002	0.007	0.220	0.826
Uniqueness point	0.011	0.007	1.578	0.115
Complex uniqueness point	−0.016	0.007	−2.176	0.030
Compound duration	−0.065	0.006	−10.176	0.000
Trial number	−0.028	0.005	−5.901	0.000

Table B2.

Fixed effects of the linear mixed-effects model fitted to auditory lexical decision RTs in Experiment 3. Conditional R² = 0.41. SD of the residual = 0.15. SD for the random effect of Compound = 0.07. SD for the random effect of Participant is 0.1. N = 8,002. N after trimming = 7,809.

	Estimate	Std. Error	t	p
Intercept	−1.066	0.015	−70.560	0.000
Entropy of conceptual relations	0.009	0.004	2.294	0.022
Left-Whole similarity	−0.013	0.004	−3.317	0.001
Right-Whole similarity	−0.001	0.004	−0.148	0.883
Compound frequency	−0.040	0.004	−9.696	0.000
Left constituent frequency	0.001	0.005	0.297	0.767
Right constituent frequency	0.012	0.005	2.570	0.011
Left constituent family size	0.005	0.004	1.117	0.265
Right constituent family size	−0.006	0.004	−1.417	0.157
Uniqueness point	−0.000	0.004	−0.033	0.974
Complex uniqueness point	0.006	0.005	1.242	0.215
Compound duration	0.029	0.004	6.952	0.000
Trial number	−0.015	0.002	−8.245	0.000

Table B3.

Fixed effects of the linear mixed-effects model fitted to ELP lexical decision RTs in Experiment 4. Conditional R² = 0.53. SD of the residual = 0.26. SD for the random effect of Compound = 0.09. SD for the random effect of Participant = 0.26. N = 15,145. N after trimming = 14,938.

	Estimate	Std. Error	t	p
Intercept	−1.462	0.010	−141.294	0.000
Entropy of conceptual relations	0.015	0.006	2.751	0.006
Left-Whole similarity	−0.010	0.006	−1.817	0.070
Right-Whole similarity	0.009	0.006	1.634	0.103
Compound frequency	−0.086	0.006	−14.733	0.000
Left constituent frequency	−0.016	0.006	−2.633	0.009
Right constituent frequency	−0.034	0.006	−5.290	0.000
Left constituent family size	−0.013	0.006	−2.084	0.038
Right constituent family size	0.010	0.006	1.591	0.112
Compound length	0.018	0.005	3.410	0.001
Trial number	−0.016	0.002	−6.639	0.000

Table B4.

Fixed effects of the linear mixed-effects model fitted to BLP lexical decision RTs in Experiment 5 Conditional R² = 0.41. SD of the residual = 0.3. SD for the random effect of Compound = 0.08. SD for the random effect of Participant = 0.22. N = 13,208. N after trimming = 14,977.

	Estimate	Std. Error	t	p
Intercept	−1.652	0.025	−65.706	0.000
Entropy of conceptual relations	0.016	0.005	2.837	0.005
Left-Whole similarity	−0.004	0.006	−0.736	0.462
Right-Whole similarity	−0.006	0.006	−0.997	0.320
Compound frequency	−0.098	0.006	−17.774	0.000
Left constituent frequency	−0.010	0.006	−1.650	0.100
Right constituent frequency	−0.013	0.006	−2.127	0.034
Left constituent family size	−0.015	0.007	−2.318	0.021
Right constituent family size	−0.007	0.006	−1.218	0.224
Compound length	−0.004	0.005	−0.661	0.509
Trial number	−0.001	0.010	−0.120	0.905