Investigating the effects of subconcussion on functional connectivity using mass-univariate and multivariate approaches

Abstract

There are concerns about the effects of subconcussive head impacts in sport, but the effects of subconcussion on brain connectivity are not well understood. We hypothesized that college football players experience changes in brain functional connectivity not found in athletes competing in lower impact sports or healthy controls. These changes may be spatially heterogeneous across participants, requiring analysis methods that go beyond mass-univariate approaches commonly used in functional MRI (fMRI). To test this hypothesis, we analyzed resting-state fMRI data from college football (n = 15), soccer (n = 12), and lacrosse players (n = 16), and controls (n = 29) collected at preseason and postseason time points. Regional homogeneity (ReHo) and degree centrality (DC) were calculated as measures of local and long-range functional connectivity, respectively. Standard voxel-wise analysis and paired support vector machine (SVM) classification studied subconcussion’s effects on local and global functional connectivity. Voxel-wise analyses yielded minimal findings, but SVM classification had high accuracy for college football’s ReHo (87%, p = 0.009) and no other group. The findings suggest subconcussion results in spatially heterogeneous changes in local functional connectivity that may only be detectible with multivariate analyses. To determine if voxel-wise and SVM analyses had similar spatial patterns, region-average t-statistic and SVM weight values were compared using a measure of ranking distance. T-statistic and SVM weight rankings exhibited significantly low ranking distance values for all groups and metrics, demonstrating that the analyses converged on a similar underlying effect. Overall, this research suggests that subconcussion in football may produce local functional connectivity changes similar to concussion.

Introduction

Multiple concussions over the course of a long career in American football can affect a player’s brain long after participation in the sport has ended, possibly increasing the player’s susceptibility for multiple neurodegenerative disorders, including chronic traumatic encephalopathy (Iverson et al. 2015; Lehman et al. 2012; McKee et al. 2013; Omalu et al. 2006; Stein et al. 2014). However, the majority of sports-related head impacts do not cause concussion, but there is mounting evidence that even subconcussive head impacts can affect brain structure (Davenport et al. 2014; Koerte et al. 2012; Zhang et al. 2013), function (Abbas et al. 2015; Breedlove et al. 2012, 2014; Johnson 2014; Militana et al. 2015; Robinson et al. 2015; Shenk et al. 2015; Svaldi et al. 2016; Talavage et al. 2010), and performance (Hwang et al. 2016; Kawata et al. 2016; Tsushima et al. 2016). While there is no official definition of subconcussion, Bailes et al. (2013) defined it as “a cranial impact that does not result in a known or diagnosed concussion on clinical grounds.” Aggregately, these studies suggest that subconcussive head impacts might produce spatially heterogeneous effects on the brain, that are similar to, but less severe than, the effects from concussion (Bailes et al. 2013).

Functional magnetic resonance imaging (fMRI) is a noninvasive method for measuring functional activity in the brain that has proven capable of detecting functional changes in the brain related to subconcussion. The first studies to indicate that subconcussive head impacts cause functional changes in the brain used fMRI with a working memory task (Breedlove et al. 2012, 2014; Robinson et al. 2015; Shenk et al. 2015; Talavage et al. 2010). These studies identified a group of athletes who were not diagnosed with a concussion but exhibited functional impairment in multiple regions and experienced a higher subconcussive head impact load compared to athletes without functional impairment. Using task-independent resting state fMRI (rs-fMRI), Johnson et al. (2014) found changes in functional connections between multiple regions in the default mode network (DMN) (Johnson 2014), and Abbas et al. (2015) found changes in the number of regions connected to the DMN (Abbas et al. 2015) after exposure to repetitive subconcussive head impacts. Task-based fMRI has found changes in working memory and rs-fMRI has found changes in the functional connectivity of the DMN, but there is no reason to assume that these tasks and networks are the only, or even the primary, areas affected by subconcussion (Breedlove et al. 2012, 2014; Robinson et al. 2015; Shenk et al. 2015; Talavage et al. 2010). If the physiological effects of subconcussion have heterogeneity similar to concussion, then it may be more appropriate to use whole-brain fMRI analyses that are independent of specific brain functions and networks.

Resting-state fMRI data can be used to calculate many aspects of functional connectivity for each grey matter voxel (Telesford et al. 2011), including metrics reflecting local and global functional connectivity of a voxel. Regional homogeneity (ReHo) is a commonly used measure of local connectivity that calculates connectivity between a grey matter voxel and its immediate spatially contiguous neighboring voxels. Degree centrality (DC) is a commonly used measure of global connectivity that calculates connectivity between one grey matter voxel and all other grey matter voxels in the brain. Meier et al. (2016) recently investigated whether ReHo and DC changed after athletes sustain a concussion and made several compelling findings. Their analyses revealed several brain regions that contained areas with statistically significant changes in ReHo one-month after a concussion, including the left paracentral lobule and postcentral gyrus, and the right postcentral gyrus, lingual gyrus, fusiform gyrus, middle temporal gyrus and superior temporal gyrus, among others (Meier et al. 2016). However in the same study, no areas experienced a significant change in DC (Meier et al. 2016). If repetitive subconcussive head impacts affect changes similar to concussion, then ReHo and DC may be useful metrics to detect those changes.

In fMRI data analysis, mass-univariate application of the general linear model (GLM) accounts for the vast majority of publications over the last 20 years, including the majority of fMRI studies of mTBI to date. Mass-univariate analysis of fMRI data is most useful for identifying situations where the same region shows the same type of change across a majority of the population under investigation. However, if the underlying change of interest exhibits spatial heterogeneity across participants, mass-univariate application of the GLM becomes poorly matched to the problem under investigation. Studies of mTBI from different domains - clinical, biomechanical, and fMRI - support the idea that spatial heterogeneity of injury is likely a dominant feature of mTBI. It is well-described that concussion presents with a variable set of signs and symptoms (Belanger and Vander-ploeg 2005), to the point that physicians who see concussion patients are fond of the statement, “If you have seen one concussion, you have seen one concussion”. Data from both biomechanical simulations and live action sports competition suggest the clinical variability may exist because each unique head impact likely imparts different forces on different brain regions (Beckwith et al. 2013; Broglio et al. 2010; Crisco et al. 2010; Rowson et al. 2012; Wilcox et al. 2015). The existing fMRI studies of concussion support this idea, with many reporting different areas of change in brain activity (Yuh et al. 2014), suggesting spatial differences between populations with similar mechanisms of injury. If we hypothesize that subconcussion affects similar brain regions as concussion but in a less severe manner, then mass-univariate application of the GLM may be insufficient to detect changes related to subconcussion.

To address some of the weaknesses of mass-univariate analysis, some fMRI researchers have started using multivariate analyses as a complement to standard mass-univariate analyses (Mahmoudi et al. 2012; Vergara et al. 2016). For example, multivoxel pattern analyses (MVPA) can probe the information in distributed neural patterns without assuming a specific spatial model. MVPA is often performed within the framework of supervised learning classification, using a training set of data to create classification algorithms that discriminate between two known groups, before testing classifier performance on novel data (Mahmoudi et al. 2012). The resulting algorithms differentially weight voxels across the brain that might collectively discriminate between two (or more) groups of interest. This general approach has the benefit of being more robust in detecting changes that are spatially heterogeneous or spatially distributed across a group. Linear support vector machine (SVM) classification is an increasingly common technique in fMRI that tries to create a hyperplane decision boundary that separates the two groups’ feature sets with the maximum possible margin (Cortes and Vapnik 1995; Vapnik 2000). For fMRI data, the strength of linear SVM lies in its ability to deal with high dimensionality data and resistance to overtraining (Formisano et al. 2008; Meier et al. 2012); but a significant weakness is the open question of whether resulting classifier weight maps contain useful information about spatial distribution of effects in the brain (Haufe et al. 2014).

We hypothesized that the hundreds of subconcussive head impacts sustained in college football produce spatially heterogeneous changes in brain functional connectivity that should be measurable with rs-fMRI. To test this hypothesis, the present study collected preseason and postseason rs-fMRI data from college football, soccer, and lacrosse players and a matched control group. At each time point, ReHo and DC were respectively used as voxel-based measures of local and global functional connectivity throughout the brain. Changes in ReHo and DC between the two time points were tested with both: (1) mass-univariate application of the GLM and (2) paired implementation a linear SVM classification. In addition, a ranking distance measure was used to test if the spatial information resulting from the mass-univariate analysis shared any information with the weight maps resulting from the SVM classification, despite the disparate ways these maps are generated.

Methods

Participants

From 2013 to 2015, preseason and postseason resting-state fMRI data was collected from 31 college football players (CF), 18 college men’s lacrosse players (CL), 14 college men’s soccer players (CS), and 30 male controls (MC) (mean (SD) age: 20.3 (1.5) years, 20.2 (1.2) years, 20.4 (1.2) years, 21.7 (3.3) years, respectively). For all college athletes, preseason data was collected no later than one week after the first practice of the sports season, and before any competitive games; postseason data was collected no later than two weeks after the final game or practice of the season or postseason (mean (SD) days between scans: CF = 133.5(9.2), CL = 63.6(13.2), CS = 86.6(4.5)). Football player data was collected during their fall competitive season, while lacrosse and soccer player data was collected during their respective fall and spring practice seasons. For male controls, the two scanning sessions were separated by 3–4 months to approximate the length of an athletic season (mean (SD) days between scans: 108.7 (6.4)). College athletes were volunteers from NCAA Division I teams without a history of developmental or neurological disorder, or moderate to severe traumatic brain injury. Nineteen CF, seven CL, and six CS players had a self-reported history of diagnosed concussion prior to the start of the season, but were not excluded from the study. Male controls were drawn from a mixed-gender university population screened for history of neurologic disease, including concussion. Four football players sustained an injury or illness that resulted in substantial lost playing time, and three additional players were diagnosed with a concussion during the season; these athletes were excluded from further analyses. For the rs-fMRI analyses, the participants were divided into three groups: college football players (CF), other sports (OS) including both college lacrosse and soccer players, and male controls (MC). The three groups represented high, medium, and low subconcussive exposure, respectively (Reynolds et al. 2017). Six football players had a position and playing status that resulted in no game time and little to no expected head impact exposure during practice (ex. redshirt quarterback or back-up kicker), and were therefore excluded from further analysis. The OS athletes also serve as a college athlete control group to account for possible aerobic training confounds, or other factors that may differentiate college athletes from their nonathlete peers.

Data acquisition

Data for this study was collected at the University of Virginia Health System on a Siemens MAGNETOM Trio MRI. A whole brain multiband BOLD sequence (University of Minnesota, CMMR sequence, https://github.com/CMRR-C2P/MB) (Feinberg et al. 2010; Moeller et al. 2010; Xu et al. 2013) (TR/TE = 1000 ms/32 ms, slice thickness = 3 mm, slice spacing 0.75 mm, in-plane dimensions 3 × 3 mm, flip angle = 90°, matrix = 64 × 64, multiband factor = 4, volumes = 480) was acquired during an eyes-open resting state: the participants were instructed to lie still and remain awake. A three-dimensional high resolution T1 magnetization-prepared rapid gradient-echo (MPRAGE) sequence (TR/TE = 1200/2.27, slice thickness = 1 mm, in-plane dimensions = 0.977 X 0.977 mm, flip angle = 9°, matrix=256 × 256) was acquired as an anatomical reference.

Data preprocessing

Each participant’s anatomical image was brain extracted using Advanced Normalization Tools (ANTs) (Avants et al. 2011) antsBrainExtraction.sh script. A college athlete and control (CAC) template was created from a random selection of 30 participants’ anatomical scans using antsMultivariate-TemplateConstruction2.sh. The Desikan-Killiany-Tourville (DKT) atlas (Klein and Tourville 2012) was applied to the CAC template using antsJointLabelFusion.sh and 20 hand-labeled brains from the OASIS-TRT dataset (2012). The following preprocessing steps were performed in ANTs with R (ANTsR) (Avants et al. 2015) unless otherwise specified. The first 10 time points of the rs-fMRI were removed to allow the MRI to reach signal equilibrium. White matter signal, CSF signal, component based grey matter noise (CompCor) (Behzadi et al. 2007), six-degrees of motion parameters and their squares, and derivatives of original and squared motion parameters were regressed from the rs-fMRI images. Time points that exceeded a framewise displacement of 0.5 mm were removed from subsequent analyses, along with the following time point, and were replaced with β-spline interpolation. If either a participant’s preseason or postseason scan had a mean translation across all time points greater than 0.25 mm compared to the participant’s average BOLD image, that participant was removed from further analyses; this excluded three football players, two lacrosse players, two soccer players, and one control. The remaining subjects’ mean head translation and mean head rotation during the fMRI scan were compared to identify any head movement differences across groups and time points, with unpaired and paired t-tests respectively. Rs-fMRI images were then diffeomorphically and affine transformed to the CAC template using antsRegistration and antsApplyTransforms commands. Supplemental Table S1 summarizes the participants’ demographics, including their sport, the position played in that sport, if they were included in the subsequent analyses, and if not, why they were excluded.

Calculating measures of functional connectivity (Fig. 1)

Fig. 1. Analysis framework.

At each time point (Preseason and Postseason), regional homogeneity (ReHo) and degree centrality (DC) metrics are calculated for each participant’s preprocessed rs-fMRI data, resulting in ReHo and DC values for each grey matter voxel. To control for variability between subjects, metric difference maps (Δ Metric) are created by subtracting the participants’ preseason metric map from their postseason metric map. Then the metric difference maps are analyzed using mass-univariate (general linear model) and multivariate (support vector machine) analyses, resulting in group t-statistic and SVM weight maps

Preprocessed BOLD images were used to calculate measures of functional connectivity using the Data Processing Assistant for Resting State fMRI (DPARSF) version 4.0 (Yan and Zang 2010). A cortical grey matter mask, segmented from the CAC template, was used to mask the data before metric calculation. BOLD images were then bandpass filtered (0.01–0.10 Hz) before calculation of the two metrics (Biswal et al. 1995). Regional homogeneity (ReHo) and degree centrality (DC) were calculated for each set of BOLD images. ReHo is the Kendall’s coefficient of concordance (KCC) for a 27 voxel cube surrounding the reference voxel, and is a measure of local functional connectivity within that small neighborhood (Zang et al. 2004). Weighted degree centrality (DC) is the sum of Pearson correlations between a voxel’s time series and that of all other grey matter voxels, and is a measure of global functional connectivity. To improve normality, the resulting correlation coefficient brain maps were then Z transformed by subtracting the mean metric value for grey matter from each voxel and dividing by the corresponding standard deviation, using DPARSF (Yan et al. 2013). Metric difference maps ΔReHo and ΔDC) were created, by subtracting a participant’s preseason metric map from their postseason metric map (ex. postReHo - preReHo = ΔReHo).

Mass-univariate analyses

Individual metric post-pre difference maps for subjects within a group were merged into 4D images using the Oxford Centre for Functional MRI of the Brain (FMRIB) Software Library’s (FSL) fslmerge command (Jenkinson et al. 2012). In order to identify voxel clusters of statistically significant metric change over the course of the season, a permutation-based one-sample two-tailed t-test was performed with FSL’s randomise (v5.0, 5000 permutations) (Winkler et al. 2014) using threshold-free cluster enhancement (TFCE) (Smith et al. 2009).

Multivariate analyses

Linear support vector machine (SVM) classification was chosen as the multivariate analysis method (Mourao-Miranda et al. 2005; Orru et al. 2012). Classifier training and testing was implemented using Pattern Recognition for Neuroimaging Toolbox (PRoNTo v2.0) (Schrouff et al. 2013b). A linear kernel was used to avoid overtraining due to the high dimensionality of the data set (thousands of voxels) with relatively few examples (participants) (Braun et al. 2008; Muller et al. 2001; Vapnik 2000). A paired version of the SVM was implemented for each group and metric to distinguish between the participants’ metric difference maps and its opposite (Sripada et al. 2013). This involved training a classifier to differentiate between a group’s metric difference map (ex. CF postseason ReHo minus CF preseason ReHo = CF ΔReHo) and its opposite (ex. CF preseason ReHo minus CF postseason ReHo = CF ΔReHo), for a total of six separate classifiers (CF ReHo, CF DC, OS ReHo, OS DC, MC ReHo, and MC DC). A paired SVM is analogous to a paired t-test, in which the mean of a subject’s two observations is subtracted from their values, except in this case the postseason minus preseason (and vice versa) difference maps account for the longitudinal nature of the data rather than subtracting the mean of the two time points. The paired nature of the SVM ensures that each subject’s two metric maps (ex. ΔReHo and -ΔReHo) end up on opposite sides of the classification decision line. This feature of the paired SVM results in equivalent class accuracy and total accuracy for each particular group and metric. Sripada et al. (2013) demonstrates application of paired SVM to BOLD fMRI data with detailed description of the underlying method and theory. As a supplemental analysis, an unpaired SVM was implemented to compare the preseason and postseason metric maps between each group. The SVM classifier is trained through leave-one-out cross-validation (LOOCV) on all but one subject’s difference maps and then the classifier is tested on the left-out subject. LOOCV is a method to train with the maximum number of examples without testing the classifier on a subject on which the classifier was trained. Each LOOCV iteration results in a weight map, this weight map is multiplied by the difference map being classified and then summed to get a single classifier value that indicates the predicted class. Further weight map analyses used the average weight map among all LOOCV iterations. For permutation testing, the classification labels were permuted 5000 times to determine the statistical strength of the classifier’s accuracy, with a significance level of p < 0.05 (Golland and Fischl 2003; Pereira et al. 2009; Schrouff et al. 2013b).

Ranking distance comparison of brain regions

Ranking distance is a measure of correspondence between any two rankings that consist of the same items (Lempel and Moran 2005), in this case brain regions. Schrouff et al. (2013a) used a very similar measure to compare the correspondence between SVM weight maps (Schrouff et al. 2013a). Unthresholded t-statistic and SVM weight maps were divided into 66 regions using the DKT atlas. The regions were ranked according to each region’s average t-statistic or SVM weight values, resulting in a t-statistic region (T_ROI) ranking and SVM weight region (W_ROI) ranking for each group and metric. The correspondence between the T_ROI and W_ROI rankings for a particular group and functional connectivity metric was calculated using a measure of distance:

$$RD\left(T_{ROI},W_{ROI}\right)=\frac{2}{n\ast (n-1)}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{I}_{(T_{ROI},W_{ROI})}}}(i,j)$$

Where

if $T_{ROI}(i)<T_{ROI}(j)and{W}_{ROI}(i)>W_{ROI}(j),$ then $I_{(T_{ROI},W_{ROI})}(i,j)=1$else $I_{(T_{ROI},W_{ROI})}(i,j)=0$

with RD(T_ROI, W_ROI) as the distance between the T_ROI and W_ROI rankings, and n as the number of ROI (66). The ranking distance values range from 0 (identical rankings) to 1 (exactly opposite rankings) (Schrouff et al. 2013a). If the rankings have low ranking distance values, it indicates the mass-univariate and multivariate analyses are converging on similar underlying trends in the data. Statistical significance of the ranking was determined by randomly shuffling the rankings for 5000 permutations and identifying how many random permutations had a lower ranking distance than the actual rankings. The ranking distance was also calculated for W_ROI rankings from ReHo and DC analyses in the college football cohort, to determine if the two functional connectivity metrics are experiencing similar spatial trends.

College football metric difference maps

To visualize and compare college football’s longitudinal trends related to subconcussion with Meier, Bellgowan, and Mayer’s (2016) findings in concussion, we created a region average brain map where group mean ΔReHo and ΔDC values were averaged over each region in the DKT atlas.

Results

Head movement analyses

MC had more movement at postseason compared to preseason for both translation (p = 0.002) and rotation (p = 0.018). MC also had lower translation (p = 0.003) and rotation (p = 0.011) than OS at preseason, and MC had lower translation (p = 0.027) but not rotation (p = 0.569) than CF at preseason. There were no significant differences for CF or OS between time points for either translation or rotation (p > 0.05). There were no differences in either translation or rotation between CF and OS at preseason, or between any groups at postseason (p > 0.05). Means and standard deviations for each group and time point are presented in Supplemental Table S2.

Mass-univariate analyses

For the TFCE voxel-wise analyses testing for spatially homogeneous preseason to postseason differences in ReHo and DC, a nine-voxel cluster of increased ReHo was found in the posterior superior temporal sulcus for college football players (TFCE corrected p = 0.033) (Supplemental Figure S1). Additionally, a two-voxel cluster of increased ReHo was found in the left superior parietal lobule for the male control group (TFCE corrected p = 0.040). No other group or metric had significant findings.

Multivariate analyses

For the paired SVM classifier trained with a linear kernel using LOOCV, only one metric and group produced a statistically significant accuracy. CF had a significant class accuracy for ReHo (87%, p = 0.009) (Fig. 2a, c), but OS and MC did not (50%, p = 0.617, 62%, p = 0.102). CF did not have significant class accuracy for DC (73%, p = 0.084) (Fig. 2b, d), OS and MC were also not significantly accurate (OS: 57%, p = 0.317; MC: 55%, p = 0.311) (Table 1). Due to the paired t-test design, class accuracy and total accuracy are equivalent for each comparison. Results from multivariate analyses directly comparing metric maps between groups at preseason and postseason time points are presented in Supplemental Tables S3 and S4, for ReHo and DC respectively. All reported p-values in this section are the result of 5000 permutation tests for that comparison.

Fig. 2. SVM classification for college football.

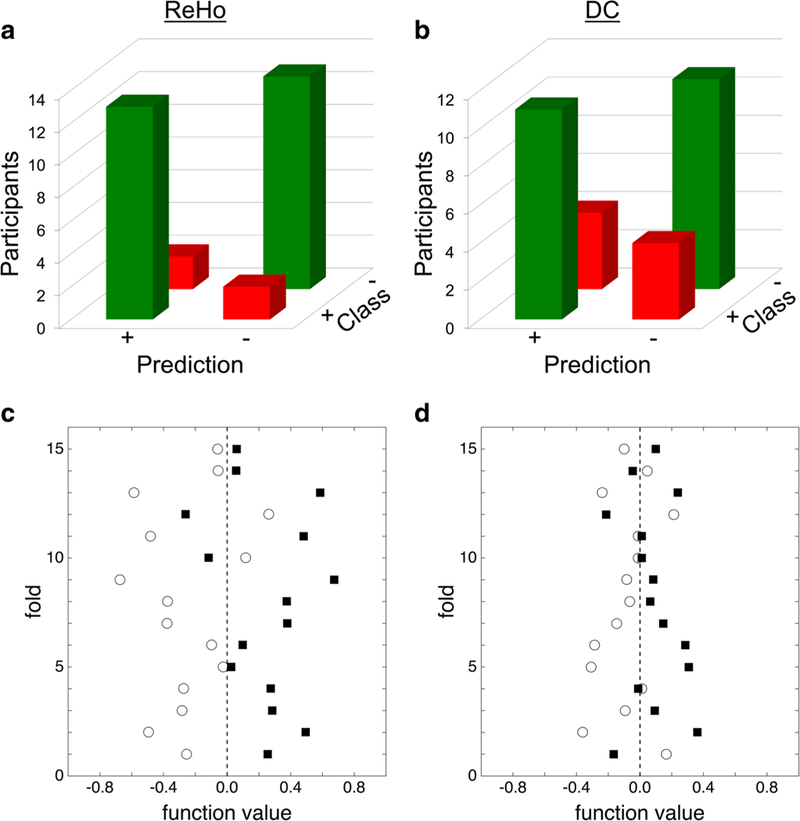
College football’s SVM classification confusion matrix for ReHo (a) and DC (b) depict the number of correct and incorrect predictions for each class (ex. ΔReHo vs -ΔReHo). The SVM prediction plot for ReHo (c) and DC (d) shows result of the SVM decision function for each participant. Dotted line at zero represents the decision threshold which is zero-centered by the paired nature of the SVM. Closed black squares represent metric difference maps (ex. ΔReHo) and open circles represent their opposite (ex. -ΔReHo). ReHo regional homogeneity, DC degree centrality

Table 1.

Support vector machine classification accuracy for ReHo and DC difference maps

Metric	Group	Class accuracy	Total accuracy	P-value
ReHo	CF	86.67%	86.67%	0.009
	OS	50.00%	50.00%	0.617
	MC	62.07%	62.07%	0.102
DC	CF	73.33%	73.33%	0.084
	OS	57.14%	57.14%	0.317
	MC	55.17%	55.17%	0.311

CF college football, OS other sports (soccer and lacrosse), MC male controls, ReHo regional homogeneity, DC degree centrality

Ranking distance between weight maps and t-statistic maps

While SVM weight maps are not considered to be spatially interpretable, spatial information is a key component of t-statistic maps output from mass-univariate analyses. Ranking distance is a way to test if the spatial information of an SVM weight map is similar to the spatial information of the corresponding t-statistic map, and low ranking distances would indicate that these mass-univariate and multivariate approaches are converging upon similar underlying effects in the data. In comparing the region rankings for SVM weight map and t-statistic values for ReHo, all groups had statistically significant low ranking distances (CF: RD = 0.120, p < 0.001; OS: RD = 0.145, p < 0.001; MC: RD = 0.122, p < 0.001). All groups also had statistically significant low ranking distances for DC (CF: RD = 0.073, p < 0.001; OS: RD = 0.142, p < 0.001; MC: RD = 0.089, p < 0.001) (Table 2). These ranking distance values were substantially lower than all values calculated during permutation testing, indicating a very high level of correspondence between the t-statistic and SVM weight maps (Fig. 3). All reported p-values in this section are the result of 5000 permutation tests for that comparison.

Table 2.

Ranking distance for each group’s comparison of TROI and WROI rankings

Metric	Group	Ranking distance	P-value
ReHo	CF	0.120	< 0.001
	OS	0.145	< 0.001
	MC	0.122	< 0.001
DC	CF	0.073	< 0.001
	OS	0.142	< 0.001
	MC	0.089	< 0.001

Ranking distance of 0 indicates identical rankings and 1 indicates opposite rankings

GLM general linear model, SVM support vector machine, CF, college football, OS other sports (soccer and lacrosse), MC male controls, ReHo regional homogeneity, DC degree centrality

Fig. 3. Ranking distance results and permutation testing.

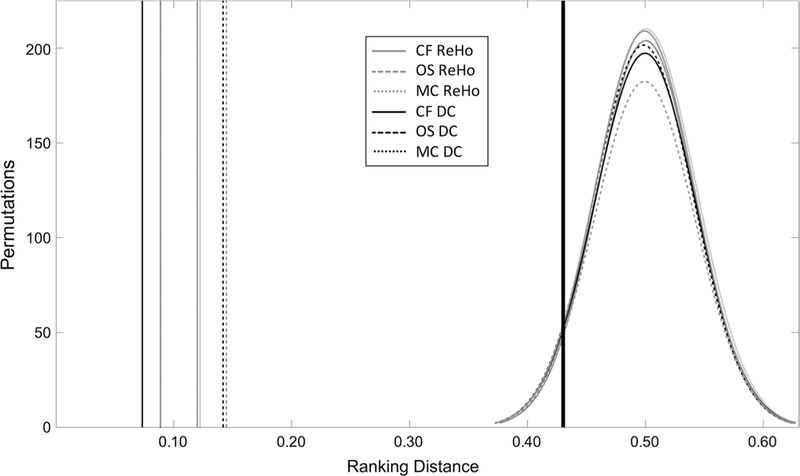
Six tests are shown for two metrics (ReHo and DC) in three groups (CF, OS, and MC). Vertical lines on the left of the figure depict the calculated ranking distance for each of six comparisons of T_roi and W_ROI rankings. Curves on the right depict the distributions for each of the sixpermutation tests (5000 iterations) of ranking distance. Thick black vertical line (actually six superimposed vertical lines) represents the p < 0.05 decision lines for the six permutation tests. CF college football, OS other sports(soccer and lacrosse), MC male controls, ReHo regional homogeneity, DC degree centrality

Ranking distance between ReHo and DC weight maps

While the SVM did not produce a significantly high classification accuracy for DC in college football, there appeared to be a trend towards significance. To determine if this trend in DC exhibited a similar spatial pattern as CF’s effects in ReHo, SVM weight maps were compared using ranking distance with 5000 iterations of permutation testing to determine significance. Ranking distance comparison between college football’s ReHo and DC W_ROI rankings resulted in a significantly low ranking distance of 0.398 (p = 0.007).

College football metric difference maps

In college football among the 66 regions in the DKT atlas, the five most increased regions for ReHo are (in order) the left pericalcarine cortex, right lingual gyrus, left lingual gyrus, right pericalcarine cortex, and left postcentral gyrus. The five most decreased regions for ReHo are the right rostral anterior cingulate, left caudal anterior cingulate, right pars triangularis, left rostral anterior cingulate, and left pars orbitalis (Supplemental Table S5). The five most increased regions for DC are the right parahippocampal gyrus, right entorhinal cortex, left temporal pole, right fusiform gyrus, and left parahippocampal gyrus. The five most decreased regions for DC are the right pars triangularis, right rostral middle frontal gyrus, right supramarginal gyrus, right inferior parietal gyrus, and left caudal anterior cingulate (Supplemental Table S6).

Discussion

This study used a combination of mass-univariate and multivariate analyses applied to rs-fMRI data to investigate effects of subconcussion on metrics thought to represent local (ReHo) and global (DC) functional connectivity. Mass-univariate analyses found minimal changes (9 voxels of increased ReHo for CF and 2 voxels of increased ReHo for MC), and the paired SVM found significantly high class accuracy for preseason-to-postseason ReHo changes in only the college football players (87%, p = 0.009). At a superficial level, this finding agrees with prior studies of ReHo in concussion (Meier et al. 2016; Zhan et al. 2015), although direct comparison to these prior results is limited by the nature of the spatial information resulting from SVM analyses. However, our ranking distance finding of significant correspondence between the t-statistic maps and SVM weight maps for all six statistical tests supports the ideas that: (1) these disparate mass-univariate and multivariate analyses are converging upon similar underlying effects and (2) meaningful spatial information may exist in the SVM weight maps. An exploratory comparison of the raw ΔReHo maps against published ReHo results in concussion further supports the idea that changes in functional brain connectivity related to subconcussion may reflect a milder version of what occurs after a clinical concussion.

Comparing mass-univariate and multivariate analyses

While mass-univariate analyses were only able to detect small changes in ReHo for CF and MC, paired SVM classification demonstrated highly significant classification accuracy for CF’s ReHo difference maps (p = 0.009). High accuracy of the SVM indicates that college football players’ local functional connectivity changed over the course of a single season. The fact that the multivariate analysis, which can use information from across the brain, was able to detect a change that was only minimally detectable for mass-univariate analyses agrees with the hypothesis that changes affected by subconcussion are spatially heterogeneous across subjects and/or spatially distributed within subjects. Mass-univariate analyses in this study only identified a very small region of effect, whereas SVM detected changes were more robust in response to concussion, suggesting that subconcussion may produce similarly distributed but subtler effects than concussion.

Comparing SVM weight maps and mass-univariate t-statistic maps

Results from a paired SVM alone cannot identify the directionality of changes (i.e. increased or decreased ReHo), nor can they identify which regions are responsible for driving any changes (Sripada et al. 2013). However, results from the ranking distance analyses showed that the mass-univariate analyses and paired SVM classification have a remarkable level of spatial correspondence. Every comparison between t-statistic and SVM weight region rankings resulted in a ranking distance that was substantially lower than the lowest value calculated in permutation testing (Fig. 3). It is surprising that these maps have such a high level of agreement, as they use mathematically dissimilar processes to produce their results. While voxel-wise analyses ostensibly treat the effects in each voxel independently, the SVM classifier is trained to weight a number of spatially distributed voxels to discriminate between the two groups. The resulting SVM weight maps are not generally considered to be spatially interpretable (Haufe et al. 2014), but the high spatial correspondence with the t-statistic maps suggests that meaningful spatial information may be contained in the weight maps.

Similarity to findings in concussion

Zhan et al. (2015) measured ReHo in patients diagnosed with a mild traumatic brain injury (mTBI) a few days after injury and compared them to matched controls. Patients with mTBI, compared to the control group, had lower ReHo values in the left insula, left precentral (PrG) and postcentral gyri (PoG), and the supramarginal gyrus (SMG) (Zhan et al. 2015). Meier et al. (2016) measured DC and ReHo at multiple time points after athletes had sustained a sports-related concussion (SRC) (mean days after injury: T1 = 1.7, T2 = 8.4, T3 = 32.4) and compared those measures to those found in a healthy athlete (HA) control group. Similar to our data, they found no changes in DC at any time point relative to the athlete control group. At one-month post injury (T3) concussed athletes, compared to the HA control group, had increased ReHo at the bilateral postcentral gyri (PoG), left paracentral lobule (PCL), right lingual gyrus (LgG), right fusiform gyrus (FuG), right superior temporal gyrus (STG), right middle temporal gyrus (MTG), and the right supplementary motor area (SMA), and decreased ReHo in the right middle frontal gyrus (MFG), right superior frontal gyrus (SFG), and superior medial frontal gyrus (SMFG) (Meier et al. 2016).

Similar to the published results from Zhan et al. (2015) and Meier et al. (2016) the region average brain map (Fig. 4) indicated increased ReHo in bilateral PoG, right LgG, right FuG, right STG, and decreased ReHo in left insula and SMG, and right superior and medial frontal gyri (Supplemental Table S5). In the DKT atlas, the SMA and SMFG are included in the superior frontal gyrus, preventing direct comparison to those regions in which Meier et al. showed increases and decreases, respectively. The only direct contradictions are with Meier et al.’s increases in the right MTG and left PCL, and Zhan et al.’s decreases in the left PrG and PoG. Furthermore, while CF’s significant 9 voxel cluster of increased ReHo was in the left superior temporal sulcus, a region not indicated in the previous studies, increased ReHo was found in the right STG and MTG in Meier et al. (2016).

Fig. 4. Absolute changes in ReHo and DC for college football players.

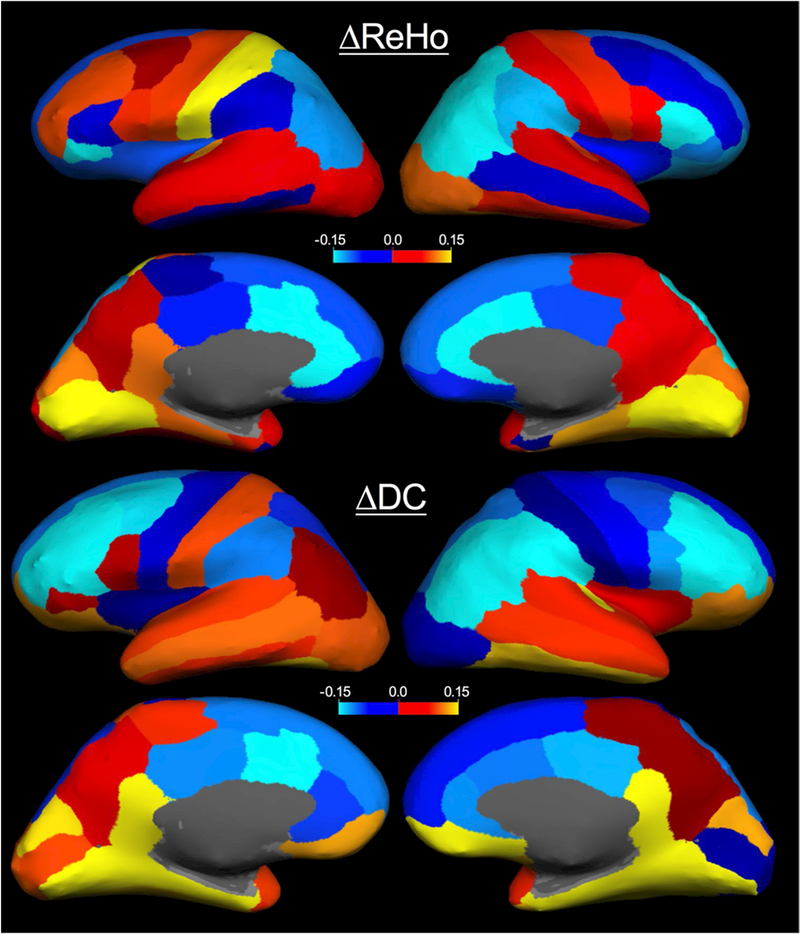
Longitudinal changes for college football’s ReHo and DC metrics were averaged over each region in the DKT atlas. Trends are depicted with warm colors depicting increases and cool colors depicting decreases. In preprocessing functional connectivity metric were Z transformed, therefore values indicate preseason-topostseason changes in the Z value. ReHo regional homogeneity, DC degree centrality

Across the published findings for ReHo in concussion, our trends matched 9 of 13 previously published region findings, with agreement in two additional regions unable to be determined. If the effects of concussion are spatially heterogeneous as indicated by heterogeneity in concussion’s clinical presentation (Rosenbaum and Lipton 2012), then Zhan et al. and Meier et al.’s voxel-wise analyses may only be detecting a subset of the changes occurring in their participants. The areas of change found in their studies may be more susceptible to head impacts than other regions, but different populations may result in different findings. In this study of subconcussion, the spatial heterogeneity combined with subtler effects result in only small significant clusters from voxel-wise analysis, but the underlying spatial trends in football seem to agree remarkably well with the published findings in concussion. The lack of significant findings in college soccer and lacrosse athletes does not necessarily confirm that there are no functional connectivity changes in these athletes, but only that if there are similar changes they are more subtle than those occurring in college football.

ReHo and DC comparison

Low ranking distance in comparing CF’s ReHo and DC rankings suggest that the effects for ReHo and DC may be similar, although the SVM classifier does not reach a significance for CF’s DC difference maps (p = 0.084). Increased local connectivity could result in a modest increase in global connectivity, or some other physiological change in these regions could independently cause changes in these two metrics. Resting-state measures of functional connectivity are sensitive to a large number of underlying physiological changes in the brain. Previous research in mTBI, concussion, and subconcussion suggests several possible injury mechanisms that could be responsible for changes in ReHo and DC metrics, including glial activation and chronic inflammation (Shultz et al. 2012), and cytoskeletal disruption in neural axons and somas (Hemphill et al. 2011; Longhi et al. 2005).

In concussed athletes, a disruption in the functional connectivity of the default mode network has been associated with increased cerebrovascular reactivity (CVR) - a measure of how cerebral blood flow increases in response to a stimulus (Militana et al. 2015). Svaldi et al. (2016) found that CVR was decreased in high school girls’ soccer, and those players who experienced greater subconcussive impact load were more affected (Svaldi et al. 2016). While any of the proposed mechanisms could play a role in subconcussion’s effect on ReHo, CVR has the most direct pathway to affect fMRI-measured functional connectivity, and has already been shown affected by subconcussive head impacts. Furthermore, the lack of a strong effect in global functional connectivity suggests that damage to long-range white matter tracts may not be the primary mechanism of subconcussive injury, as global functional connectivity should be theoretically more sensitive to white matter damage than local connectivity.

Limitations

Several factors related to our participant groups may affect the generalizability of our findings. First, the athlete populations in this study are small and are all from the same Division I university. The college football sample was especially small due to our removal of athletes with limited head impact, diagnosed concussion during the season, and excess head movement during scanning; making the CF group (n = 15) roughly half the sample size of the OS and MC groups (n = 28 and n = 29, respectively). Second, previous research in football has shown that head impact can be affected by player position (Baugh et al. 2014), offensive style (Martini et al. 2013), or practice types (Reynolds et al. 2016), all of which could be different at other universities or teams. Differences may also exist at lower levels of collegiate competition or for other levels of play (youth, adult amateur, and professional). Youth athletes tend to experience less severe subconcussive head impacts but may be more susceptible to their effects (Daniel et al. 2012). While our subset of athletes represents a wide variety of player positions, it may not offer an accurate cross-section of the entire team. Third, head motion during MRI scanning did differ between the two time points for MC, and also between MC and the other two groups at the preseason scan. While head motion can create false positives in functional connectivity comparisons, the most robust findings in our study involve the comparisons where no differences in head motion are present.

No longitudinal clinical measures were collected from the participants during this study, which limits the ability to link these functional connectivity changes to behavioral changes. Recent research has suggested that subconcussive head impacts can cause vestibular dysfunction (Kawata et al. 2016), disruption of the ocular-motor system (Hwang et al. 2016), and impaired processing speed and reaction time (Tsushima et al. 2016). If the local connectivity changes correlated with a specific behavioral change in our football players, then we might conclude that the connectivity changes are the neural cause of the behavioral changes. Whereas, if there was no correlation between the local connectivity changes and behavioral measures, then we may identify the connectivity changes as having a subclinical effect. While correlating the local connectivity changes to clinical metrics would be valuable, the importance of these changes in local functional connectivity is not negated by the absence of such a correlation.

To control for differences between a collegiate athlete population and a non-athlete population, such as higher cardiorespiratory fitness (Voss et al. 2016), we collected data from athletes in lower impact sports like soccer and lacrosse (Reynolds et al. 2017). However, it is possible that the athlete groups still differed in their cardiovascular training during their respective seasons, affecting group comparisons of functional connectivity. Other differences could also exist between CF and OS/MC groups that may be responsible for the differential longitudinal changes in the groups. Some factors that could be different and were not collected or controlled for between our two group samples, and which could affect functional connectivity, include: caffeine use (Rack-Gomer et al. 2009; Wong et al. 2014), alcohol use (Chanraud et al. 2011), cannabis use (Cheng et al. 2014), wakefulness during the rs-fMRI scan (Stoffers et al. 2015), and prescription medications (Sripada et al. 2013). Given the longitudinal nature of the study, these uncontrolled confounds would need to have changed between preseason and postseason time points to produce the demonstrated effects.

While these alternative factors cannot be entirely excluded as explanations for these effects, the authors believe that correspondence with ReHo changes in concussion support subconcussive head impacts as the most likely cause of these effects.

Conclusions

This study demonstrates how mass-univariate analyses and paired SVM classification of rs-fMRI data can be combined to provide insight on the effect of subconcussion on functional brain connectivity. The results of combining these techniques suggest the effects of subconcussion may be on the same spectrum as sports-related concussion but with a smaller magnitude of change. While American football was the high-impact sport under study, it is unlikely to be the only sport in which these subconcussive effects occur; other high-impact sports like ice hockey, rugby, and combat sports may also result in similar effects. Further research will be needed to determine the quantity and severity of subconcussive exposure needed to produce these functional connectivity disruptions by biomechanically measuring head impact and acquiring longitudinal rs-fMRI in the same cohort. Furthermore, the neurophysiological underpinnings of these changes should be studied by acquiring multiple MRI modalities in the same cohort, and comparing their effects across modalities.