Linking V1 Activity to Behavior

Abstract

A long-term goal of visual neuroscience is to develop and test quantitative models that account for the moment-by-moment relationship between neural responses in early visual cortex and human performance in natural visual tasks. This review focuses on efforts to address this goal by measuring and perturbing the activity of primary visual cortex (V1) neurons while non- human primates perform demanding, well-controlled visual tasks. We start by describing a conceptual approach—the decoder linking model (DLM) framework—in which candidate decoding models take neural responses as input and generate predicted behavior as output. The ultimate goal in this framework is to find the actual decoder—the model that best predicts behavior from neural responses. We discuss key relevant properties of primate V1 and review current literature from the DLM perspective. We conclude by discussing major technological and theoretical advances that are likely to accelerate our understanding of the link between V1 activity and behavior.

1. INTRODUCTION

An organism’s visual system evolved to support the tasks the organism performs in order to survive and reproduce. Thus, we expect the structure of the visual system and its neural computations to be matched (at least to some extent) to the natural tasks and natural signals that are relevant for performing those tasks. In primates, which are the main focus of this review, these natural tasks include, for example, identifying objects and materials, identifying image features due to the effects of lighting (e.g., shadows), representing the three-dimensional (3D) structure of the scene, determining object and self-motion, and planning and controlling movements of the eyes, limbs, and body. These tasks are difficult because of the complex statistical structure of natural scenes and because the visual system must recover the 3D structure of the scene from the two-dimensional retinal images. Yet despite this complexity, the visual system is able to support rapid and accurate performance in a wide range of natural tasks, including those listed above. A long-term goal of visual neuroscience is to characterize and predict neural responses along the visual pathway in such natural tasks and to characterize and predict behavioral performance from these neural responses.

In primates, visual information is carried by the limited number of ganglion cells (∼1.2 million per eye in humans) that form the optic nerve ( Jonas et al. 1992). The ganglion cell responses are then relayed, via the lateral geniculate nucleus (LGN) of the thalamus, to the primary visual cortex (V1), which is the first stage of a cortical hierarchy. In V1, there is a massive expansion of the neural representation of visual information—the number of output neurons from V1 is at least two orders of magnitude larger than the number of inputs from the LGN (Barlow 1981). Several of the most fundamental local image properties (e.g., orientation, motion direction, binocular disparity) are first explicitly encoded in V1. The outputs from V1 project to multiple extrastriate areas that are involved in combining local image properties to obtain high-level representations. For these reasons, and because of the high degree of similarity between the visual systems of humans and macaque monkeys, a great deal of effort has been directed at measuring and modeling single-neuron and neural-population responses in V1 of macaque monkeys.

The primary aim of this review is to describe what is known about the relationship between neural activity in macaque V1 and behavior. First, we discuss some general conceptual, methodological, and theoretical issues relevant for characterizing and modeling how neural activity is decoded into behavior. Second, we briefly mention some of the anatomical and physiological properties of V1 that are relevant for understanding and modeling the decoding performed in the subsequent cortical areas. Third, we describe specific studies that have compared neural activity in V1 with behavior, with a focus on detection and discrimination tasks. We describe studies that compare neural sensitivity with behavioral sensitivity as well as studies that compare neural responses and behavior on a trial-by-trial basis. A central theme of this review is that in order to better understand the link between neural activity and behavior, these two lines of research should be combined.

2. CONCEPTUAL FRAMEWORK FOR STUDYING THE LINK BETWEEN V1 RESPONSES AND BEHAVIOR

2.1. Feedforward and Feedback Processing in V1

The visual system uses a multistage hierarchical representation. Local image properties are first measured, then those properties are combined in novel ways in parallel pathways, each composed of successive stages, to obtain multiple high-level scene representations that are each useful for a particular task or a family of tasks.

An important property of the connections between the successive stages in the processing hierarchy is that each neuron at a given stage receives converging local input from the earlier stage such that the receptive fields of neurons in the recipient area cover a greater fraction of the retinal image than the neurons in the source area cover (e.g., Maunsell & Newsome 1987). These extrastriate areas send a large number of projections back to V1 (e.g., Callaway 1998). Relatively little is known about the functional role of these feedback projections.

To usefully combine local image properties, the visual system must exploit knowledge of the statistical structure of the environment. This knowledge is built into the visual system through evolution and is often refined through experience. For example, one of the major computational steps in identifying objects and in representing the 3D structure of the scene is to group together local image features that are likely to arise from the same physical contour, surface, or object. Features that arise from the same physical source tend to be statistically correlated in specific ways (Simoncelli & Olshausen 2001, Geisler 2008). Local orientation features that arise from the same physical contour tend to be colinear or more generally coparabolic. Local features that arise from the same surface or object tend to have similar statistical distributions of color, orientation, disparity, texture, etc. Surfaces or objects that are in the foreground tend to create a pattern of orientation discontinuities (T junctions) at the surface of occluded objects’ boundaries (Figure 1).

Figure 1.

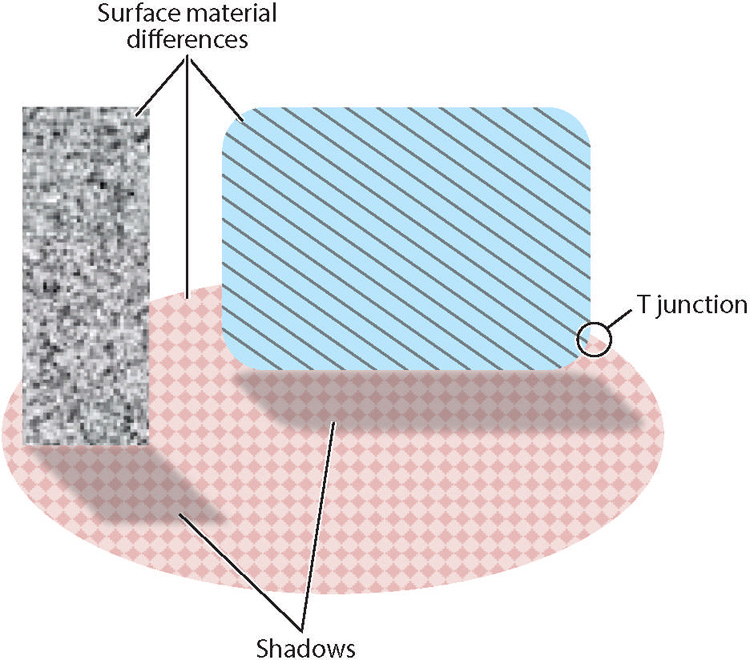
Properties of natural scenes include material properties, such as surface reflectance and surface roughness, lighting properties such as shadows and shading, and occlusion-related features such as T junctions. Feedback to the primary visual cortex (V1) from subsequent stages that estimate surface material properties needs to be subtle enough that it does not disrupt the input to subsequent stages that estimate lighting properties, and vice versa. The same logic holds for all properties of natural scenes that are estimated by subsequent stages in the visual system. Thus, it is expected that under most circumstances, V1 responses will be dominated by feedforward signals and modestly influenced by feedback signals.

One of the major open questions in visual science is how all this statistical knowledge is rep-resented and exploited in V1 and in the subsequent stages of neural computation. The simplest hypothesis is that each successive stage of parallel processing takes the inputs from the previous stage and applies, in a feedforward fashion, rules of combination that exploit the prior knowledge. Recent computer-vision studies of object recognition in natural scenes show that such feedforward architectures (i.e., deep convolutional neural networks) can reach or exceed human performance in specific domains (see Kriegeskorte 2015).

A more complex hypothesis is that V1 is part of a feedback loop with higher visual cortical areas, where V1 initially represents the local features in the retinal image, but these representations, which can be noisy and ambiguous, are then dynamically refined by feedback from higher visual areas that perform computations such as grouping and segmentation (Hochstein & Ahissar 2002, Roelfsema 2006, Gilbert & Li 2013, Roelfsema & de Lange 2016). In this framework, this cycle of refined encoding and subsequent interpretation continues until the visual system converges on a solution (i.e., a high-level interpretation of the scene).

While a feedback system could provide increased computational flexibility and efficiency, it would need to be more complex and subtle, because the same image features initially encoded in V1 must simultaneously support many different higher-level representations and perceptual tasks. For example, the visual system must simultaneously represent the material properties of surfaces (e.g., reflectance and roughness) and scene properties due to the effects of lighting, such as shadows (Figure 1). In representing the material properties, shadows must be ignored or discounted, whereas in representing shadows, the material properties must be ignored or discounted. If the circuits extracting/representing surface material properties were to strongly suppress, via feedback, the V1 features encoding the shadows, then the circuits extracting/representing the shadows would lose their driving input, and vice versa if the circuits extracting/representing shadows were to suppress V1 features encoding material properties. Thus, the feedback would need to be sufficiently subtle to bias the higher-level computations in the right direction for all subsequent computations. If such feedback for image interpretation exists, it is likely to be fast and automatic and to operate in parallel across the visual field.

Another potential role for feedback is to support selective, task-specific processing. For exam-ple, if a task involves preferential processing of information at a specific spatial location and/or of specific features, then top-down attention mechanisms could selectively modulate the rele- vant V1 responses (e.g., Motter 1993, Desimone & Duncan 1995, Chen & Seidemann 2012, Maunsell 2015). However, even task-specific modulations in V1 are likely to be subtle in order to not interfere with other critical parallel computations.

These considerations of the potential role of feedback suggest that the responses of neural populations in V1 (at least during the interval leading to the formation of a perceptual decision) should be primarily determined by feedforward processing of the retinal image and should be relatively weakly modulated by feedback from higher cortical areas. This view is largely consistent with measurements of neural responses in V1 of behaving primates and with the observation that the magnitude of top-down attentional modulation tends to increase along the visual cortical hierarchy (e.g., Maunsell 2015). In this review, we consider the existing literature using this feedforward-centric conceptual framework. We later revisit the question of the balance between feedforward and feedback processing in primate V1.

2.2. Decoder Linking Models Framework—a General Paradigm for Linking V1 Activity and Behavior

A powerful paradigm for studying the link between neural responses and behavior is to measure and/or manipulate neural responses in subjects while they perform well-controlled perceptual tasks. Combined psychophysics and physiology in behaving macaque monkeys has been a particularly useful paradigm for studying the neural basis of human visual perception. This approach has been successful for two main reasons. First, the macaque visual system is similar to the human visual system in terms of its anatomy, physiology, and perceptual capabilities (De Valois & De Valois 1980). Second, macaques can be trained to perform complex perceptual tasks and then perform these tasks several hours per day over extended periods of time, thus providing high-quality psychophysical measurements that can be directly compared with human psychophysical measurements using identical tasks and stimuli.

In reviewing what is known about the link between V1 activity and behavior, we adopt the conceptual decoder-linking-model (DLM) framework illustrated in Figure 2 (see Seidemann et al. 2009 for a related framework). In this framework, we assume that most perceptually relevant visual information in primates passes through V1 (i.e., V1 is the dominant, mostly feedforward, pathway) and that we have simultaneous measurements of V1 neural responses and of the animal’s behavior.

Figure 2.

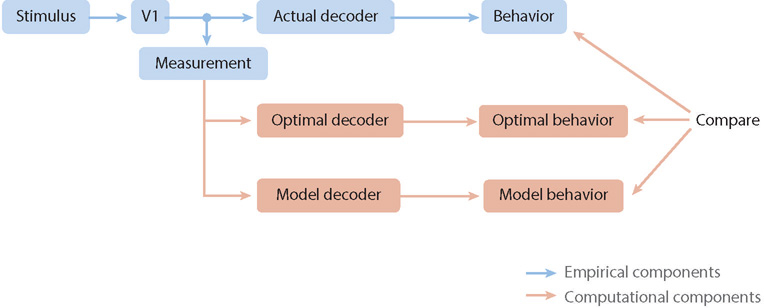
Measuring and analyzing the relationship between visual stimuli, neural activity in the primary visual cortex (V1), and behavior. Stimuli give rise to neural activity in V1, which is processed (decoded) by subsequent areas of the brain to produce a behavioral response. In neurophysiology experiments, responses are measured in V1, generally with some loss of information. Optimal and suboptimal model decoders are applied to the measured responses and compared to the animal’s behavior.

Consider first a simple thought experiment where the subject is discriminating between two similar stimuli, a and b. Imagine that while the subject performs this task, we have access to the precise spiking activity of all the projection neurons in V1 that carry task-relevant information during the specific temporal interval over which the subject forms the perceptual decision and that we can collect enough repeats with identical stimuli to reliably characterize both the neuronal and behavioral responses. How should we go about studying the link between these neural responses and behavior? A principled first step would be to consider how well the task could potentially be performed based solely on neural signals from V1, given the goals of the task (e.g., maximizing response accuracy). This step involves determining the computations on the neural responses that would provide optimal performance in the task—the optimal V1 decoder. Here we refer to any set of computations carried out to perform a specific task as a decoder. Thus, a decoder at any stage of processing refers to computations that take the response of that stage as input and produce behavioral responses in the task as output. Thus, a stimulus decoder would take the retinal image as input and a V1 decoder would take V1 responses as input (Figure 3a). Determining the optimal V1 decoder would provide principled initial hypotheses for the neural circuits and responses in areas subsequent to V1. Comparison of the predicted behavior of the optimal V1 decoder with the actual behavior of the subject could reveal what aspects of the subject’s behavior can be predicted from first principles. Typically, the optimal decoder is a Bayesian observer that incorporates the appropriate cost function, likelihood distributions, and prior probability distributions (Kersten et al. 2004, Geisler 2011).

Figure 3.

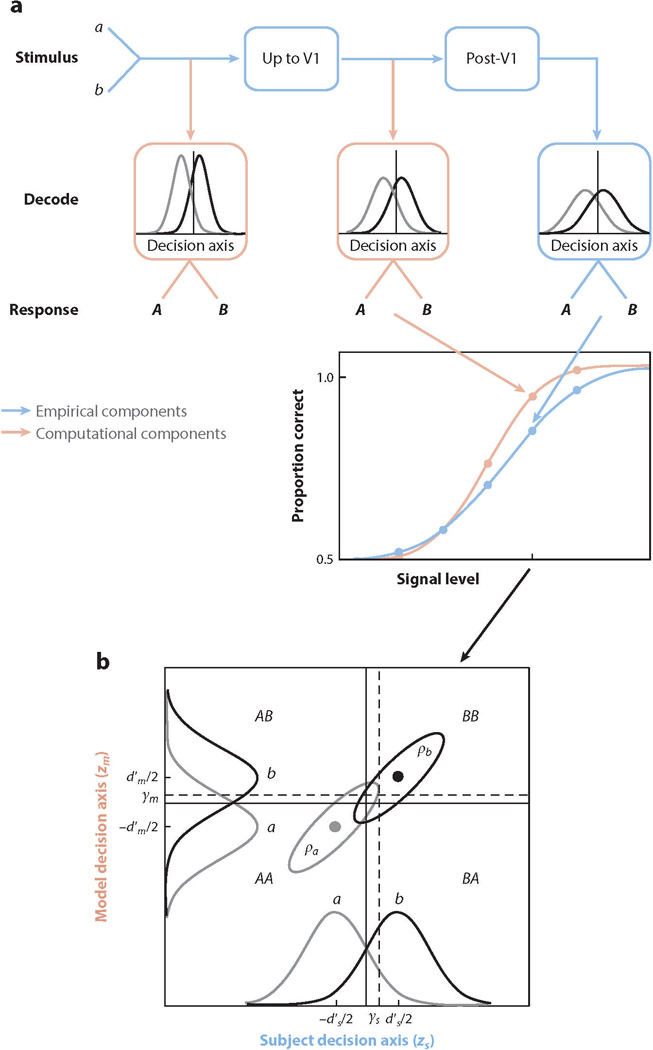
Decoders in a two-alternative identification task. (a) In the signal detection theory (SDT) framework, a decoder takes the input signal on each trial and computes the value of a scalar decision variable—nominally, the log of the ratio of the probability of stimulus b to the probability of stimulus a, given the specific input signal received on that trial. If the value of the decision variable exceeds a decision criterion γ (represented by the vertical lines in the boxes), then the observer reports that the stimulus is B; otherwise, that it is A. A model stimulus decoder (first pink box) takes a noisy stimulus as input and generates behavioral responses in the task. A model V1 decoder (second pink box) takes the V1 output as the input and generates behavioral responses in the task. The actual stimulus decoder encompasses all the processing in the stimulus-to- behavior pathway (all blue boxes). The actual V1 decoder encompasses all processing subsequent to V1 (last two blue boxes). In a typical experiment, performance is measured as function signal level (difference between stimulus categories a and b). Proportion correct as function of signal level for an arbitrary model decoder is a neurometric function (pink data points) and, for the subject, is a psychometric function (blue data points). (b) SDT also provides a framework for analyzing trial-by-trial performance at any given signal level (e.g., the level indicated by the tick mark in panel a). The horizontal axis represents the value of the subject’s decision variable, and the vertical axis represents the value of a model’s decision variable (see Sebastian & Geisler 2018 for more details; see also Michelson et al. 2017). The Gaussians on each axis represent the distributions of the decision variable (normalized to a standard deviation of 1.0) for the two stimulus categories (a and b). The ellipses represent the joint (bivariate) distribution of the decision variables for the two stimulus categories. The bivariate distributions are completely described by four parameters: the subject’s level of discriminability (referred to as $d^{\prime }$) (${d^{\prime }}_s$ ), the model decoder’s level of discriminability (${d^{\prime }}_m$ ), and the decision-variable correlations ${\rho }_a$ and ${\rho }_b$ . The four quadrants defined by the decision criteria (dashed lines) represent the different possible pairs of responses (the first letter is the response of the subject, and the second is the response of the model). The eight proportions of these response pairs, corresponding to the four quadrants for each of the two stimulus categories (a and b), uniquely determine the discriminabilities of the subject and model (${d^{\prime }}_s,{d^{\prime }}_m$), the decision criteria of the subject and model (${\gamma }_s,{\gamma }_m$), and the decision-variable correlations (${\rho }_a,{\rho }_b$).

A second step would be to evaluate various suboptimal V1 decoders obtained by removing or degrading various components of the optimal decoder (e.g., by spatial blurring of signals across neighboring neurons). These model decoders can be thought of as specific hypotheses for what we refer to as the actual decoder—the computations that the rest of the visual system uses in order to perform the task given the V1 signals. These model decoders can then be tested by comparing model and subject behaviors, by perturbing V1 responses and assessing the behavioral consequence, and by measuring neural responses in subsequent brain areas.

In this review, we focus on task-specific decoders that take measured neural activity and generate predicted behavioral responses. We refer to this approach as the DLM framework. A closely related but more abstract approach considers known (or potential) properties of neurons and asks how well neural populations having those properties could be decoded to perform perceptual tasks (Dayan & Abbott 2001). For example, a common strategy is to compute the Fisher information of the theoretical neural population for given perceptual estimation or discrimination tasks (Dayan& Abbott 2001, Averbeck et al. 2006, Ganguli & Simoncelli 2014, Wei & Stocker 2017). This approach plays an important role in understanding the link between neural activity and behavior by identifying general neural computational principles that can be tested in neurophysiological studies and could form the basis for models, like those considered here, that are used to directly decode measured neural activity or to generate trial-by-trial predictions of behavior.

Unlike the simple thought experiment, current technology (and technology in the foreseeable future) does not give us access to the spiking activity of all the potentially relevant projection neurons in V1. Even the simplest, most spatially localized stimulus elicits changes in spiking activity in millions of projection neurons in V1 that are spread out over multiple square millimeters (see Section 3 below) (Hubel & Wiesel 1974, Palmer et al. 2012). Current studies generally either measure precise spiking activity from a tiny fraction of the potentially relevant neurons (up to several hundred) or measure locally pooled spiking and/or membrane potential activity with a limited spatial resolution. Therefore, in applying the logic of the framework in Figure 2, one must take into account the limitations of the physiological measurements. Given the limitations of current technologies, an important future direction is to combine techniques with different coverage and resolution and to develop better quantitative understanding of the relationship between measurements of neural activity obtained at different spatial scales and with different techniques.

2.3. Comparing V1 Activity and Behavior in the Two-Alternative Identification Task

Most of the studies that have quantitatively compared neural activity with behavior in the macaque monkey have used two-alternative discrimination or detection tasks, which can be regarded as special cases of the two-alternative identification task. In each trial, the subject is presented with a stimulus from one of two possible categories, a and b, and then indicates the judged category, typically with an eye movement or lever press. The two possible responses can be represented by A and B.

In reviewing the relationship between neural activity and behavior, we discuss two related kinds of studies. The first measures neural activity and behavior in detection or discrimination experiments and asks how well the sensitivity of optimal or model decoders compares with the behavioral sensitivity. The second asks how well the choices of the subject on individual trials with identical visual stimuli (which are randomly interleaved with other trials) can be predicted from the choices of the optimal or model decoder on the same trials. This property is commonly quantified as choice probability—the probability that the model decoder makes the same choice as the subject, based solely on the neural responses to identical stimuli. In this latter case (e.g., frozen noise, in the case of a stochastic stimulus), one examines how measured internal variability is correlated with fluctuations in behavior. We believe that the distinction between these two lines of research is somewhat arbitrary. We therefore argue that the more general question is how well the choices of the subject can be predicted from the choices of a model neural decoder when the stimulus is allowed to vary arbitrarily (in signal strength and in signal variability, as in external variability). Ultimately, the goal of both lines of research is to reveal the actual decoder.

In comparing model-decoder predictions and subject performance in two-alternative identification tasks, it is often appropriate to use the framework of signal detection theory (Green & Swets 1966). Each decoder takes the neural signals during the relevant temporal interval as an input, combines these signals over neurons, and over time computes a decision variable (a scalar) that is then compared to a decision criterion (Figure 3a). For example, in a two-alternative discrimination task, the decoder would respond A if the decision variable is below the criterion and B if the decision variable is above the criterion [versions of decoders in which the decision variable is computed dynamically and which also make a decision about when to respond are also possible in this framework (e.g., Chen et al. 2008)]. For each possible decoder, one can construct a neurometric function (Tolhurst et al. 1983, Parker & Newsome 1998), which describes the average accuracy of the decoder as a function of signal strength. This neurometric function can then be directly and quantitatively compared with the psychometric function, which describes the subject’s accuracy in the task. As shown in Figure 3a, the framework also applies to model decoders that operate directly on the stimuli. We do not review such models here but include this panel to emphasize that if there is substantial variability in the stimuli (external variability), then a large fraction of the variability in the V1 activity may be inherited from the stimulus.

If V1 is the major pathway of task-relevant visual information, and if we have access to all the task-relevant neural signals projecting from V1, then performance of the optimal decoder must equal or exceed the performance of the subject. Conversely, if the subject outperforms the optimal decoder, then V1 is not the exclusive pathway—other pathways that bypass V1 must carry substantial information used to perform the task. Also, each possible decoder generates a behavioral response (a decision) on each trial of an experiment that can be used to compute choice probabilities or decision-variable correlations (see later and Figure 3b).

If the performance of the optimal decoder equals the performance of the subject, this implies that the actual decoder for the task is equivalent computationally to the optimal decoder. Such a result would put strong constraints on the nature of the connectivity between the subsequent areas in the visual hierarchy and on their neural computations. Results reviewed below suggest that in most cases, the neural sensitivity of optimal decoders of neural responses in V1 (and other visual cortical areas) exceeds the behavioral sensitivity of the subject. Such a result implies that there are inefficiencies in the subsequent processing stages and that the actual decoder falls short of the optimal decoder.

What might be the sources of these inefficiencies? One possible source is independent components of the variability in subsequent processing stages that degrade performance relative to the performance achievable using the measured sensory signals. This noise could be broadly distributed throughout the decoding circuits or could be concentrated at certain stages. For example, a major source of variability may be in the decision criterion. In tasks with stable stimulus probabilities, such fluctuations in the criterion are a form of noise that will degrade performance relative to a decoder with a fixed, optimally placed, criterion. We refer to these sources of decoder inefficiency as noise inefficiency.

Another possibility is that subsequent processing stages may not perform optimal pooling of information. As information is transmitted and transformed through the hierarchy of visual cortical areas, some information could be lost because it is combined in a suboptimal way from the perspective of the current task. This is likely to happen because the visual system evolved to perform a large number of tasks simultaneously. As mentioned above, the goal of the visual system is to interpret natural scenes and guide behavior in natural tasks. Given that a main goal of the visual system is to represent surfaces, objects, and scenes (Figure 1), it is not surprising that some information about low-level features may be lost during this process. We refer to these deterministic sources of decoder inefficiency as pooling inefficiency.

For the actual decoder to be optimal, it must have no noise or pooling inefficiencies. To have no pooling inefficiencies, the decoding circuits may need to have precise knowledge regarding the tuning properties, noise characteristics, and noise covariations of all the relevant neurons in the population. This assumption is related to the concept of labeled lines—the notion that decoding circuits can “read out” the neural signals in an optimal way for any given task, because they have a complete knowledge (presumably learned and stored in their connectivity) of every neuron’s response properties. To account for subjects’ ability to perform a wide range of visual tasks, labeled-line decoders require either nearly infinite decoding resources or a complex control mechanism for routing information that allows higher areas to identify the informative neurons and combine their activity optimally without being affected by other noninformative neurons, and these decoders must achieve this without disrupting other concurrent computations. Below, we review behavioral and neurophysiological studies suggesting that inefficiencies in pooling are common in the visual system and are a major source of neural inefficiency. These results are generally inconsistent with labeled-line decoders of V1 responses.

In any given task, there may be a large number of model decoders that perform better than the subject, and therefore degraded versions of these decoders are viable candidates for the actual decoder. How can we determine which of these algorithms is most consistent with the actual decoder? One approach is to search for the algorithm that best predicts the subjects’ behavioral sensitivity from the measured neural responses (Figure 3a). A more powerful and general approach is to search for the algorithm that best predicts the subject’s trial-by-trial choices (Figure 3b). If most of the inefficiency in the actual decoder is pooling inefficiency, then the best algorithm [the one that most closely matches the pooling of the actual decoder and therefore maximizes the decision-variable correlation (Figure 3b)] should be able to predict the subject’s accuracy and trial-by-trial responses (choices). However, if most of the inefficiency is noise inefficiency, then even the best algorithm would not be able to predict perfectly the subject’s trial-by-trial responses from V1 activity.

A more direct experimental approach for distinguishing between candidate decoders is to directly manipulate the neural responses in ways that are expected to produce different behavioral effects under the different decoders. At the moment, our ability to manipulate neural responses in behaving primates is quite limited. Nevertheless, studies that use various techniques to coarsely manipulate neural responses in behaving primates still provide useful insight into the link between neural response and behavior.

In the framework discussed above, every V1 decoder can be viewed as a hypothesis regarding the computations in subsequent processing stages. For some tasks, such as detection and discrimination of localized stimuli, plausible model decoders might involve relatively simple computations (e.g., linear pooling followed by a simple nonlinear decision rule). For other tasks, such as identification of natural objects in natural scenes, plausible model decoders will generally consist of many linear and nonlinear operations (e.g., as in multilayer convolutional neural networks). For complex neural-network models, there will generally not be enough measured neural data to train the decoder. In this case, the best option is probably to develop a model of the neural population activity (in V1) and then train the neural networks on simulated population activity. Regardless of whether the model decoder is simple or complex, if it has few unknown parameters, then it can be tested by measuring V1 responses, generating decoding-model predictions from those responses and comparing those predictions to the animal’s behavioral responses. Obviously, additional tests of model decoders might be possible by looking for evidence of the key steps of the decoder in subsequent cortical areas. Finally, we note that the extent to which the framework described above is useful for studying V1 depends on the role and magnitude of top-down effects in V1. We revisit this issue later (see Section 4.4).

3. KEY PROPERTIES OF V1 REPRESENTATION

Here we discuss two properties of V1 that are directly relevant for the topics covered in this review. First, V1 representations are widely distributed. Because receptive fields of neighboring V1 neurons largely overlap, the cortical point image (CPI) (i.e., the V1 area that encompasses all the neurons whose receptive fields contain a given point in the visual filed) spreads over an area of multiple square millimeters in the superficial layers of V1. The average diameter of the spiking CPI (at 10% of its maximum) is ∼3–4 mm (Palmer et al. 2012), an area containing several million V1 neurons, while the average diameter of the subthreshold CPI, which more closely reflects the extent of the divergent feedforward connections from the retina to the superficial layers in V1, is about twice as large as the spiking activity CPI (Palmer et al. 2012). A second key property of primate V1 is its topographic organization.

3.1. V1 Topography—Theoretical Considerations

At a coarse (millimeter) scale, V1 contains a retinotopic map (Hubel and Wiesel 1974, Van Essen et al. 1984, Tootell et al. 1988, Adams & Horton 2003, Yang et al. 2007). At a finer (submillimeter) scale, V1 contains periodic topographic maps for stimulus orientation, eye of origin, spatial frequency, and perhaps other dimensions such as color and phase (Hubel & Wiesel 1968, Hubel & Wiesel 1977, Callaway 1998, Sincich & Horton 2005, Nauhaus et al., 2012). Because the CPI is much larger than the periodicity of these finer scale columnar maps (e.g., ∼1.3 cycles/mm for orientation) (Hubel et al. 1978, Chen et al. 2012), all stimulus properties are fully represented at each location in the visual field.

Topography can reduce the demand for the specificity of the connections between the pre- and postsynaptic neurons. In a topographic map, random connectivity between presynaptic neurons within a restricted region (that does not vastly exceed the periodicity of the map) and a single postsynaptic neuron will lead to a cell that can still be selective to the relevant stimulus dimension. Some degree of randomness in the connectivity is in fact essential to explain why neurons across the visual pathway do not become increasingly more selective to properties such as orientation. For example, if V2 neurons were to receive converging inputs from V1 neurons with identical preferred orientation, the orientation tuning width of V2 neurons would have been significantly narrower than that of their inputs. This is due to the threshold nonlinearity, which sharpens the selectivity of the output relative to the selectivity of the input (Priebe & Ferster 2008). However, V2 neurons have similar orientation tuning width as V1 neurons (Levitt et al. 1994), consistent with significant randomness in connections between V1 and V2.

In addition to simplifying and reducing the required precision of connectivity for feedforward connections, topography could be useful for simplifying feedback modulations. While feedback projections retain their topographic nature at the retinotopic scale, the extent to which feedback connections retain their specificity at the finer columnar scale is still an active area of research (e.g., Angelucci & Bressloff 2006).

Topography is likely to have important implications for how neural responses in V1 are decoded by subsequent stages. The reason is that the degree of precision of the connectivity between successive stages of processing in the visual system is likely to limit the range of actual decoders that could be implemented in the visual system. Specifically, a labeled-line decoder requires highly precise connectivity. However, the presence of topography raises the possibility that in some visual tasks, the actual decoder could combine V1 signals at the relevant topographic scale—for example, at the scale of the orientation columns. If this were the case, then the fundamental unit of information would be individual columns rather than single neurons, and to account for the subject’s behavior, it would be necessary and sufficient to consider the summed activity of the thousands of neurons within each column.

Such a hypothetical columnar-scale decoder is an example of a topographic code, where information is represented by the summed activity at each location in the topographic map. A decoder could use linear or nonlinear rules to extract information from this topographic representation. Irrespective of the evolutionary, developmental, or functional causes of a given topographic representation, it seems likely that this representation would be exploited by downstream circuits.

How can a hypothetical topographic code be tested? One way to reject a topographic code is by finding two or more stimuli that are perceptually discriminable yet are indistinguishable by neural responses at the scale of the topographic map. Evidence in favor of a topographic code can be obtained by demonstrating that perceptual capabilities are aligned with the capabilities of a topographic decoder but not with the (finer) capabilities of a labeled-line decoder. As an example of the latter approach, in a recent study, which combines optical imaging in macaque V1 and human psychophysics, we showed that the spread of activity in V1’s retinotopic map could influence coarse shape perception (Michel et al. 2013). These results, while indirect, suggest that topography at the retinotopic scale contributes to the perception of shape and size.

Finally, a number of studies using electrical microstimulation in behaving macaques demonstrate perceptual consequences of stimulation that are well predicted by the position of the tip of the stimulating electrode relative to the topographic map (Salzman et al. 1992, DeAngelis et al. 1998). Microstimulation activates a large and widespread population of neurons in a way that is unlikely to mimic the precise pattern of activity produced by the visual stimulus (Seidemann et al. 2002, Histed et al. 2009); the specificity of the perceptual effects of stimulation is therefore consistent with the hypothesis that stimulation-evoked signals are being decoded using a topographic code that operates at a coarse scale.

3.2. V1 Topography—Practical Considerations

In addition to its possible role in decoding, topography has important practical implications for research and for future clinical interventions such as sensory neuroprosthetics.

An important challenge of sensory neuroscience is that existing techniques for measuring and manipulating neural responses suffer from a fundamental trade-off between their coverage and resolution (or sampling density). Techniques that have cellular resolution are limited to either high-density sampling over a small region (e.g., multi-photon imaging and stimulation) or sparse sampling over a larger region (e.g., multi-electrode arrays). In contrast, techniques with large coverage, such as widefield (single photon) optical imaging of fluorescent indicators [e.g., voltage-sensitive dyes (Grinvald & Hildesheim 2004) and widefield imaging of genetically encoded indicators (Seidemann et al. 2016)], provide access to a large area with high (and flexible) sampling density but have low resolution because the signals from each pixel represent the summed activity of a local population of neurons. Indirect estimates of the extent of this blurring in macaque V1 suggest that the signals measured in a standard widefield system have a combined point-spreadfunction (PSF) with a radius (at half height) of about 250 µm (Chen et al. 2012). Importantly, because this PSF is smaller than the periodicity of the columnar maps in macaque V1, widefield techniques can measure and activate neurons at the scale of orientation columns in the behaving macaque (Chen et al. 2012, Seidemann et al. 2016).

Because the CPI in macaque V1 is large, techniques with cellular resolution can access only a negligible fraction of the neurons that could carry task-relevant information even in tasks involving a localized stimulus. However, if in a certain task the code operates at the scale of the topographic map, there is no need to measure the activity of every individual neuron to account for the subject’s behavior. In this case, techniques that provide access to the pooled neural responses at the relevant spatial scale in the topographic map would be sufficient to address questions about the nature of the encoded and decoded information. Furthermore, if one were to develop a sensory prosthetic device to assist patients with damage to peripheral sensory representations by directly activating neurons in the cortex, artificially generating the pattern of neural activity that is normally elicited by a visual stimulus at the topographic scale might be sufficient to recreate perception similar to that generated by that stimulus. In other words, even though the artificially generated neural response and the response elicited by the visual stimulus would be quite different at the single- neuron level, their equivalence at the topographic scale would render them neural metamers (i.e., distinguishable patterns of neural responses that lead to indistinguishable percepts). Thus, understanding how much of visual perception can be accounted for by “reading” and “writing” neural responses at the scale of topographic maps is an important goal of visual neuroscience. It is likely that the principles that will be learned from such studies will be relevant for other sensory and nonsensory cortical representations.

4. DECODING NEURAL RESPONSES

This section reviews four major topics relevant for understanding how neural responses are related to behavioral performance. The first two topics concern quantitative measurements of the relationship between neural activity and behavior. The third topic concerns the different sources of decoding inefficiencies subsequent to V1. The fourth topic concerns the potential limitations of the present feedforward-centric decoding framework.

4.1. Comparing Neural and Behavioral Sensitivities

4.1.1. Single cortical neurons.

There is a long history of studies comparing the sensitivity of single cortical neurons with behavioral sensitivity of humans and nonhuman primates (NHPs) in detection and discrimination tasks (reviewed by Parker & Newsome 1998). An initial driving force behind this line of research was the lower envelope hypothesis, which was originally developed to explain the relation between the sensitivity of single peripheral sensory fibers and the behavioral sensitivity of the organism. According to this hypothesis, sensory thresholds are determined by the most sensitive neurons, and at the extreme, by a single most sensitive neuron. Barlow (1995) extended this hypothesis to the central nervous system and suggested that perception is limited by the most sensitive cortical neuron(s). This influential hypothesis provided the motivation for many of the studies discussed below that quantified the sensitivity of single cortical neurons and compared it to behavioral sensitivities.

From the perspective of the DLM framework outlined above, the lower envelope hypothesis can be viewed as a specific form of a suboptimal decoder—one that ignores the responses of the vast majority of neurons that carry task-relevant information and bases its decision on a small number of highly sensitive neurons. Therefore, to fully test the lower envelope hypothesis, one may still need to record all the task-relevant neurons and show that decoders that use signals from less sensitive neurons are inconsistent with behavior. Irrespective of their value in testing the lower envelope hypothesis, these single-unit studies provided important information regarding the quality of neural signals carried by single cortical neurons, which is an important step toward understanding the principles of cortical coding.

Early studies were based on measurements of neural responses in anesthetized animals and behavioral measurements collected separately, using non-identical stimuli, and in many cases were based on measurements of behavioral responses in human subjects rather than in macaques. These studies focused on the sensitivity of single V1 neurons in pattern detection and discrimination in anesthetized (Tolhurst et al. 1983, Parker and Hawken 1985, Hawken & Parker 1990, Geisler & Albrecht 1997) and awake fixating macaques (Vogels & Orban 1990). The results of these studies were quite surprising. Despite the distributed nature of cortical representations, when the stimulus is optimized for the tuning properties of the recorded neuron (i.e., matches receptive field position and size, preferred spatial and temporal frequencies, etc.), single cortical neurons can be highly sensitive in detection and discrimination tasks, with the most sensitive neurons having comparable sensitivity to the subject. Furthermore, neurometric functions constructed from the most sensitive neurons have comparable shape (including slope) to the psychometric function [though the same can be true for neurometric functions constructed from large populations of neurons (Geisler & Albrecht 1997)].

The first attempts to collect combined behavioral and neurophysiological signals simulta- neously from the same NHP subject were performed by Newsome, Movshon, and colleagues in the late 1980s and early 1990s (Newsome et al. 1989, Britten et al. 1992). These studies focused on the role of the middle temporal area (MT) in a coarse direction discrimination task in which subjects discriminate the direction of motion in a dynamic random-dot stimulus. The outcome of these studies was even more striking. The average sensitivity of single MT neurons was comparable to the average sensitivity of the subject (i.e., nearly half of MT neurons were more sensitive than the animal). This result demonstrates clearly that, at least in this specific task, the decoder is highly suboptimal.

Since the pioneering work of Newsome, Movshon, and colleagues, multiple studies have re-visited this issue and compared behavioral sensitivities to the sensitivity of single cortical neurons in a variety of tasks and visual cortical area (e.g., Prince et al. 2000; Cook & Maunsell 2002a; Uka & DeAngelis 2003, 2006; Purushothaman & Bradley 2005; Nienborg & Cumming 2006, 2009, 2014; Palmer et al. 2007; Cohen & Newsome 2008).

An important issue examined in some of these studies is the temporal interval over which neural and behavioral sensitivities are compared. While in the early studies, stimulus duration was long (typically 1 or 2 s), some later studies showed that restricting stimulus duration (by using a shorter stimulus presentation period or by allowing the subject to control stimulus duration using a reaction-time design) has a larger detrimental effect on neural sensitivity than on behavioral sensitivity (Cook & Maunsell 2002b, Palmer et al. 2007, Cohen & Newsome 2009). These results suggest that subjects are not combining neural signals optimally over time, a specific form of suboptimal pooling (see Section 4.3). Additional behavioral studies tested directly how subjects weight sensory evidence over time and showed that macaques tend to weigh early evidence more than late evidence (Nienborg & Cumming 2009). Therefore, when restricting the analysis of neural sensitivity to the temporal interval over which subjects are forming their perceptual decisions, the sensitivity of single cortical neurons tends to fall short of behavioral sensitivity.

Nevertheless, while neural sensitivities of individual neurons may fall short of the behavioral sensitivity of the subject, under realistic stimulus presentation periods, single neurons still carry surprisingly high-quality information relative to the entire organism. Given the distributed na- ture of cortical representations, these results suggest that under most circumstances, behavioral sensitivity falls far short of the neural sensitivity of the optimal decoder that uses signals from all available V1 neurons.

4.1.2. Neural populations.

Studies comparing the sensitivity of single cortical neurons with behavioral sensitivity represented a major step toward understanding the link between neural activity and perception. However, they fall short of the (admittedly unrealizable) gold standard of our thought experiment (see Section 2.2). First, these experiments sampled (sequentially) a negligible fraction of the neurons that could carry task-relevant information in any given cortical area. Second, these studies typically optimized the stimulus for the recorded neuron. This means that we do not know how much information other neurons that are not optimally tuned for this stimulus could potentially contribute. Third, to understand how much gain can be attained by combining signals from multiple neurons, one has to characterize the covariations between neurons. Thus, an important step toward understanding the neural sensitivity of population decoders was characterizing pairwise correlations between simultaneously recoded neurons. Here we briefly describe some of the key results regarding these correlations.

A large number of studies have demonstrated that the variability in the activity of pairs of single cortical neurons in response to identical visual stimuli is weakly and positively correlated (noise correlations) (Zohary et al. 1994; reviewed in Cohen & Kohn 2011; see, for an exception, Ecker et al. 2010, 2014). A related concept—signal correlations—quantifies the degree of similarity between the tuning properties of a pair of neurons. Noise correlations are widespread, and while they depend on the tuning properties of the two neurons (similarly tuned neurons tend to have higher noise correlations), even neurons with nonoverlapping receptive fields and different preferred stimulus properties tend to be positively correlated (e.g., Zohary et al. 1994, Kohn & Smith 2005). The effect of noise correlations on optimal and suboptimal decoding in large populations is complex but is relatively easy to understand for two neurons. If the noise correlation of the two neurons has the same sign as their signal correlation, then the correlation will have a detrimental effect on sensitivity. If noise correlation has the opposite sign as signal correlation, then the correlation will be beneficial to sensitivity. Finally, if the two neurons have zero signal correlation, then any noise correlation will be beneficial (Abbott & Dayan 1999, Averbeck & Lee 2006, Averbeck et al. 2006, Chen et al. 2006, Kohn et al. 2016). The analysis of noise correlations and their impact on encoding and decoding is further complicated by the findings that these correlations can be (modestly) modulated by the stimulus (Kohn et al. 2016), by the task that the subject performs (Cohen & Newsome 2008, Bondy et al., 2018) and by cognitive factors such as attention (Cohen & Maunsell 2009, Mitchell et al. 2009). Better understanding of actual decoders and better demarcation of the temporal intervals over which a perceptual decision is formed are necessary for determining the impact of noise correlations (and their modulations) on perception.

Even if noise correlations are a major limiting factor on perception, given the single-unit results discussed in the previous section and the population decoding results discussed below, it is likely that in most visual tasks, an optimal decoder that bases its decisions on the activity of all V1 neurons will largely outperform the subject. Therefore, addressing questions about the nature and source of decoding inefficiency is of great importance (see Section 4.3).

Several recent studies have looked at the performance of various decoders based on multiple simultaneously recorded, well-isolated single neurons or multi-unit sites (nonisolated neural signals) in V1 of anesthetized or awake, fixating macaques (Graf et al. 2011, Berens et al. 2012, Shooner et al. 2015, Arandia-Romero et al. 2016). Two common findings emerge from these studies. First, even moderate size populations (several tens of neurons) are significantly more sensitive than the most sensitive single neuron in the population. Second, under most circumstances, decoders that ignore noise correlations perform worse than decoders that take these correlations into account. These findings are likely to generalize to larger populations.

In the only study that we are aware of in which neural sensitivity of decoded population responses was directly compared to the behavioral sensitivity of the subject, neural responses were collected from V1 using voltage-sensitive-dye imaging (VSDI) while monkeys performed a visual detection task (Chen et al. 2006, 2008). This study had two key findings. First, optimal decoding involved linearly pooling the population responses with positive weights at the region of the peak response to the target and negative weights in the surrounding region. These negative weights reduced the detrimental effect of the positive and widespread noise correlations. Second, the optimal decoder outperformed the monkeys in terms of accuracy (Chen et al. 2006) and speed (Chen et al. 2008), despite the coarse nature of the VSDI signals and the various sources of non- neural noise that could contaminate them. These results show that in some tasks, a suboptimal decoder that coarsely pools local neural signals in topographic maps could still outperform the subject, and therefore, such decoders cannot be rejected as a possible actual decoder.

4.2. Choice-Related Activity

4.2.1. Single cortical neurons.

Newsome, Movshon, and colleagues were the first to report small but significant covariations between the activity of single MT neurons and behavior (termed choice probabilities) in monkeys performing a coarse direction discrimination task (Celebrini & Newsome 1994, Britten et al. 1996). Since then, such single-unit choice probabilities have been observed in many cortical areas, including V1 (e.g., Dodd et al. 2001; Cook & Maunsell 2002a; Uka & DeAngelis 2004; de Lafuente & Romo 2005; Purushothaman & Bradley 2005; Nienborg & Cumming 2006, 2009, 2014; Palmer et al. 2007). Choice probabilities tend to be higher for neurons that are more sensitive in the task, but positive choice probabilities can also be observed for neurons with poor sensitivity.

The sources of the neural variability in sensory cortex that correlates with perceptual decisions are not known and could include feedforward (bottom-up) and feedback (top-down) contributions (Cumming & Nienborg 2016). While feedback contributions to some choice-related activity are well documented (e.g., Nienborg & Cumming 2009), their relative contribution to perceptual decisions is unknown. This important and active area of research is discussed below (see Section 4.4).

Single-unit choice probabilities are small, indicating that single neurons capture only a small fraction of the choice-related variability. Because noise correlations between neurons are low, the majority of the choice-related variability that is not accounted for by single sensory neurons may still be present in the sensory area and be distributed across a large population of sensory neurons. In other words, perceptual decisions may be formed by pooling large populations of weakly correlated neurons, in which case the activity of each single neuron is only weakly correlated to the pooled response and therefore to choice (e.g., Shadlen et al. 1996). Another possibility is that a significant portion of the choice-related neural variability is due to downstream noise inefficiency. Distinguishing between these possibilities requires measuring neural population responses in behaving subjects.

4.2.2. Neural populations.

As discussed above, a powerful tool for studying neural decoding is to examine trial-by-trial covariations between decoder and behavioral choices, yet unfortunately, such studies are extremely rare in macaque visual cortex. In a recent study, we used VSDI in V1 of monkeys performing a reaction-time visual detection task to examine the trial-by-trial covariations between decoded V1 population responses and the monkey’s choices (Michelson et al. 2010, 2017) (Figure 3a). The main goal of this study was to determine the relative contribution of variability that is present in V1 population responses (“up to V1”) versus independent variability downstream to V1 (“post-V1” variability) to the monkey’s choices. We found that V1 population responses in the period immediately prior to the decision correspond more closely to the monkey’s report than to the presence/absence of the visual target. Specifically, in false-alarm trials in which no target was presented, V1 activity was elevated at the location corresponding to the target and at the time that the target-evoked response would have occurred, and this false-alarm signal exceeded the visual responses in trials in which the target was present but missed. By combining these empirical results with several plausible pooling algorithms and the simple computational model outlined in Figure 3 (Michelson et al. 2017, Sebastian & Geisler 2018), we were able to show that the majority of choice-related variability in this task is likely to be present in V1. These results suggest that a major source of suboptimal performance in detection tasks is inefficiency in pooling V1 responses rather than noise inefficiency downstream to V1.

4.2.3. Choice-related activity and causal role.

The presence of choice-related activity in a given neuron or neural population does not necessarily imply a causal role in perception. In our thought experiment, there may be many candidate decoders that rely on different subsets of neurons to achieve similar decision-variable correlations. In this case, even neurons that do not contribute to the decision can still show significant choice-related activity simply because they are correlated with other neurons that do contribute to the decision (see Nienborg et al. 2012, Pitkow et al. 2015). Under this scenario, determining which of these is the actual decoder will require additional experiments (e.g., by perturbing neural responses to assess causal role).

4.3. Evidence for Pooling Inefficiencies

Inevitably, in a large hierarchical network with divergent and convergent connections between successive processing stages such as the primate visual system, some information is likely to become lost as it is transmitted through the hierarchy. Here we briefly describe several examples of such information loss, where information that is readily available at an early stage of cortical processing (such as V1) is unavailable to the entire organism. Within our DLM framework, this form of information loss amounts to an inefficient pooling of signals from an early processing stage. These examples suggest that information loss due to inefficient pooling is prevalent in perceptual systems.

An important form of pooling inefficiency is limitations in the ability to optimally integrate visual information over time (Watson 1986) and space (Wilson et al. 1990). Another important form of pooling inefficiency is intrinsic uncertainty. In the spatial domain, V1 neurons’ receptive fields are highly sensitive to the precise retinal position of a stimulus, and therefore, precise retinotopic location can be decoded from V1 population responses (e.g., Yang et al. 2007). However, human subjects are poor at judging the location of stimuli away from the fovea, demonstrating that information about precise location is lost along the visual processing stream. This intrinsic spatial uncertainty is substantial—it increases linearly with eccentricity and has a radius at half height of ∼15% of the eccentricity (Michel & Geisler 2011). Such an intrinsic uncertainty, which is likely to extend to stimulus dimensions other than spatial position, is an important form of pooling inefficiency that contributes to suboptimal performance in many tasks and could have contributed to the inefficient decoding reported by Chen et al. (2006, 2008) and Michelson & Seidemann (2012).

A related phenomenon to intrinsic spatial uncertainty is the inability of subjects to judge local phase. While many V1 neurons are sensitive to the precise phase of a local grating that falls within their receptive field, human subjects are remarkably poor at judging local phase away from the fovea (e.g., Bennett & Banks 1987).

Another conceptually related phenomenon is crowding. Human subjects are poor at isolating and discriminating individual elements from multi-element displays presented in the periphery even when the elements are sufficiently small and far apart to support independent representations in V1 (for a review, see Pelli 2008). While intrinsic spatial uncertainty and crowding are conceptually related, their specific properties suggest that they are caused by different forms of pooling inefficiencies (Michel & Geisler 2011).

Another example is pattern discrimination. Different samples of random textures from the same texture family (i.e., containing the same image statistics) are likely to be discriminable based on decoding of V1 population responses, yet human subjects are likely to do poorly at discriminating such patterns. This is because the visual system is designed to group similar textures together to a single category rather than to discriminate individual patterns within the same texture family (Landy & Graham 2004).

In general, these results point to significant pooling inefficiencies that are caused by the nature of the connections between successive stages in the visual system. Such results appear inconsistent with a labeled-line decoder in which the observer is assumed to have access to the tuning properties of each neuron (implying no information loss), which is still implicitly assumed in many modeling studies of optimal neural population decoding (e.g., Seung & Sompolinsky 1993, Ma et al. 2006, Graf et al. 2011).

4.4. Possible Contribution of Top-Down Modulations to Decoding

As discussed earlier, this review considers a framework in which V1 is viewed as primarily extracting and transmitting bottom-up sensory information originating in the retinae. However, V1 receives large numbers of extraretinal inputs from many cortical and subcortical structures.

A variety of top-down effects have been observed in V1 and in extrastriate cortical areas (for a recent review, see Maunsell 2015). Top-down signals have been shown to change the average stimulus-evoked response (either by an additive or a multiplicative term) and the variability (including the covariance) of neural responses. The purpose of these top-down effects and their impact on decoding are not clear. One possible role of top-down effects is to reduce the detrimental impact of task-irrelevant stimuli on behavior (as in attentional selection). Another possible role is to enhance neural sensitivity to behaviorally relevant stimuli (as attentional signal-to-noise enhancement). A recent study of population responses in V1 found evidence for the former but not for the latter (Chen & Seidemann 2012). Understanding the significance and role of top-down effects on neural sensitivity depends on the nature of the actual decoder. For example, top-down modulations of a specific aspect of the noise covariance may have no effect on neural sensitivity (and choice) if the actual decoder is insensitive to this aspect of the covariance.

If top-down effects are themselves variable, they introduce variability into V1 responses (Goris et al. 2014, Arandia-Romero et al. 2016). However, such variability may have no choice-related consequences either because the actual decoder is simply insensitive to such variability (i.e., the variability may fall in the decoder’s null space—for example, variability in baseline with a decoder that is insensitive to baseline) or because the decoder may have independent access to this variability and can compensate for it (for example, by getting an efferent copy of the variable top-down signal and subtracting it from the V1 signals). While the first case can be analyzed within the feedforward framework outlined above, this second possibility poses a potential problem to our feedforward framework. In this case, one could create a situation in which optimal decoding of V1 responses falls short of the subject’s performance because the actual decoder has access to (and can therefore remove) some variability that cannot be removed by an optimal decoder restricted to V1 signals.

When considering possible top-down signals in sensory cortical areas, it is essential to distinguish between signals that occur during the temporal interval over which the perceptual decision is formed and those that arise from post-decisional top-down signals that may be trivially correlated with choices. Studies that focus on the early part of the response and/or rely on a reaction-time task design are less prone to suffer from such post-decisional contamination.

There are many tasks where perceptual decisions appear to be made early in the time course of the V1 response to the stimulus. These tasks range from detection and discrimination of simple stimuli to identification of natural scene categories and objects under time-constrained conditions. For these tasks, it is likely that the feedforward framework emphasized here (Figures 2 and 3) is an appropriate and useful approximation. However, many real-world tasks are best regarded not as a sequence of brief independent perceptual decisions and responses but as a sequence of highly interrelated decisions and responses. In these cases, delayed feedback signals in V1 may play an important role in the computations controlling the perceptual decisions and behavior. For example, under natural conditions, delayed feedback may primarily exist to prepare V1 to process the next stimulus in a related sequence (e.g., prepare to select information from some new scene location). In these cases, the distinction between encoding and decoding of V1 responses becomes blurred, reducing the usefulness of the simple feedforward framework.

5. SUMMARY AND CONCLUSIONS

We started this review by describing a conceptual and computational framework for studying the link between neural responses in V1 and behavior in tasks that involve rapid perceptual decisions. This DLM framework assumes that V1 responses in such tasks are primarily determined by feedforward processing of the retinal image, and we argue that this is likely to be the case. At the heart of this framework is the model decoder of V1 neural activity, which is a set of computations that takes V1 responses in single trials as an input and produces a behavioral choice in the task as an output (Figure 2). Each decoder model is a quantitative hypothesis regarding the way in which neural responses from V1 are combined and transformed by downstream circuits to form perceptual decisions. The ultimate goal in this framework is to discover the actual decoder, which describes how the rest of the visual system uses V1 activity to perform the task.

Traditionally, studies that attempt to identify the actual decoder have relied on two strategies. One strategy has been to compare the subject’s behavioral sensitivity as a function of task difficulty (the psychometric function) with the inferred neural sensitivity of the decoder (the neurometric function). Another strategy has been to examine trial-by-trial covariations between behavioral and decoder choices on trials with identical stimuli. Such covariations examine how internally generated variability at the level of V1 could impact subject and decoder choices. An important theme in this review is that it would be beneficial to combine these two approaches and examine trial-by-trial covariations between subject and decoder choices [which we quantify using a decision-variable correlation parameter (Figure 3b)] over a broad range of stimulus strengths and multiple levels of external noise (in addition to internal noise). Searching the algorithm that maximizes decision-variable correlations in this broad regime is a powerful and general approach for discovering the actual decoder (Michelson et al. 2017, Sebastian & Geisler 2018).

One factor that could limit the ability of decoders that use V1 activity to predict behavior is the extent to which perception is limited by variability that is present in V1 versus independent variability that is added downstream to V1. We term this independent downstream variability noise inefficiency. We briefly describe a recent study that examined trial-by-trial covariations between V1 population responses and behavior and discovered that in a detection task, the majority of the variability that correlates with the subject’s choices is already present in V1 (Michelson et al. 2010, 2017). Understanding to what extent these results generalize to other visual tasks is an important goal for future studies.

A fundamental question is how the neural sensitivity of the actual decoder (which, per definition, equals the behavioral sensitivity of the subject) compares to the sensitivity of an optimal decoder of V1 responses. Two factors can reduce the sensitivity of the actual V1 decoder relative to the sensitivity of the optimal V1 decoder. First, as discussed above, noise inefficiency will degrade the performance of the actual decoder relative to the optimal V1 decoder that is not affected by independent downstream noise. Second, due to various limitations, the actual decoder may fall short of the optimal decoder in how it combines V1 signals. We reviewed multiple lines of evidence that suggest that such pooling inefficiencies are common in primate vision. Understanding the nature and mechanisms underlying these inefficiencies is another important direction for future research.

We discuss two key features of V1 representations that are likely to impact the nature of the neural code in V1. First, because the V1 cortical point image (CPI) spreads over more than 10 mm2 , V1 representations are widely distributed. Second, key visual parameters are topographically organized in V1, raising the possibility that some stimulus features may be represented by a topographic code in V1. In other words, the actual decoder in some tasks may rely on the overall level of population activity at the topographic scale (e.g., at the level of orientation columns) rather than the activity of individual neurons.

The distributed nature of V1 representations creates a technical challenge. Current and near- future technologies for monitoring and/or manipulating neurons with cellular resolution in behaving primates (e.g., multi-photon imaging/stimulation) can access only a negligible fraction of the many millions of V1 neurons that could carry task-relevant information even in the simplest visual tasks. In contrast, imaging techniques with larger coverage (e.g., single-photon imaging) that capture the entire task-relevant population of V1 neurons are limited to the resolution of cortical columns. However, if in some tasks the actual decoder operates at the scale of the topo- graphic map, there is no need to measure the activity of every individual neuron to account for the subject’s behavior. In this case, techniques that provide access to the pooled neural responses at the relevant spatial scale in the topographic map would be sufficient to address questions about the nature of the encoded and decoded information.

An obvious conclusion of this review is that our understanding of the link between V1 activity and behavior in primates is quite rudimentary. Progress will require advancements along multiple experimental and computational directions. First, we need better tools for measuring and manipulating neural population responses in subjects that are engaged in demanding visual tasks. A promising direction is using genetic tools for targeting cells on the basis of their role in the computation and using more powerful optical techniques for measuring and perturbing larger populations of neurons. Second, given the limitations of current technologies, an important future direction is to combine techniques with different coverage and resolution and to develop better quantitative understanding of the relationship between measurements of neural activity obtained at different spatial scales and with different techniques. In many tasks, understanding the link be- tween V1 activity and behavior will necessitate measuring neural responses in V1 and multiple key downstream areas (ideally simultaneously), as animals are engaged in performing more general and natural behavioral tasks. Finally, we need more refined encoding and decoding models and careful evaluation of their underlying assumptions. To end on a positive note, the major techno- logical and theoretical advances over the past several years suggest that progress in understanding the link between V1 activity and behavior will dramatically accelerate in the next decade.

Decoder:

the computations that map the neural activity in a sensory area into behavioral responses

Optimal decoder:

the computations that achieve the best possible behavioral performance in a given task from the neural activity in a sensory area

Decision-variable correlation:

the correlation between the decision variables of a decoder and the organism as defined in the standard signal-detection-theory framework

Actual decoder:

the computations that most accurately predict an observer’s behavioral performance in a given task from the neural activity in a sensory area

Internal variability:

trial-by-trial neural variability that occurs when the same exact stimulus is presented repeatedly

External variability:

trial-by-trial variability in the stimuli presented within a given experimental condition

Decision variable:

a one-dimensional variable that represents the output of a decoder at the processing step just prior to generation of a behavioral response

Neurometric function:

performance accuracy of a decoder applied to neural activity, as a function of a given stimulus variable

Psychometric function:

behavioral performance accuracy as a function of a given stimulus variable

Noise inefficiency:

suboptimal performance that results from intrinsic noise that arises subsequent to the measured neural activity

Pooling inefficiency:

suboptimal performance that results from suboptimal deterministic computations subsequent to the measured neural activity

Labeled-lines decoders:

the family of decoders where all stimulus-response tuning properties of each neuron in the input to the decoder is known and exploited

Cortical point image (CPI):

the spatial spread of neural activity in visual cortex produced by a spatially localized stimulus

Topographic code:

a neural code for a given stimulus property that is represented by a spatial activity map over an anatomically defined neural population

Neural metamers:

different patterns of neural activity indistinguishable in their effect on an observer’s behavior

Lower envelope:

the threshold boundary determined by the most sensitive neuron in a population at each point over a given stimulus space

Noise correlations:

correlation of neural activity in space and/or time across multiple presentations of the same stimulus

Signal correlations:

correlation of mean neural activity when the stimulus is varied over space and/or time