Supplementary data for the quantum chemical calculation of free radical substitution reaction mechanism of camptothecin

Abstract

This data article contains the truncated view of the transition states for methyl radical attacking camptothecin at the site of 9, 10, 11, 12 and 14 in acidic conditions obtained from quantum computation of Gaussian 09 with B3LYP/6–31+G(d,p) level, also the truncated view of transition states for H abstraction by singlet O₂ from sites of 9, 10, 11 and 12 of the intermediates of methyl combination with camptothecin and that by triplet O₂ from site 9 of the intermediate of methyl combination with camptothecin in acidic condition are included. The corresponding parameters of reaction rate constant calculation for the formation of methyl radical from acetaldehyde, the first and second step of radical substitution of camptothecin under acidic conditions are listed. The data of the basic parameters for the computation of the total energy of the spin-projection of singlet oxygen, and the S² values for the reactants, transition states and intermediates in the free radical substitution reaction of camptothecin are also included.

Specifications Table

Subject area	Chemistry
More specific subject area	Molecular graphics and modeling
Type of data	graph, figure, table
How data was acquired	By ChemBio3D Ultra 12.0
Data format	Raw
Experimental factors	Some transition state structures come from computation of Gaussian 09
Data source location	Tianjin, China.
Data accessibility	No

Value of the data

• •To facilitate the reader׳s understanding of this study.
• •Extend readers׳ knowledge about the free radical reaction of camptothecin.
• •To lay a foundation for further study on the mechanism of free radical substitution of natural medicines.

1. Data

Data provided in this article are based on computation performed applying Gaussian 09 [1] at B3LYP/6–31+G(d, p) level [2], [3] and the figures are treated using ChemBio3D Ultra 12.0 [4]. The corresponding parameters for the calculation of reaction rate constant, for the computation of the total energy of the spin-projection of singlet oxygen, and the S² values for the reactants, transition states and intermediates in the free radical substitution reaction of camptothecin are included.

2. Experimental design, materials and methods

The truncated 3D structures of the reactants, transition states (TSs) and intermediates in the reaction in Fig. 1, Fig. 2, Fig. 3 are all sketched using ChemBio3D Ultra 12.0 based on the TS optimization of the corresponding transition states with Gaussian 09 at B3LYP/6–31+G(d,p) level.

Fig. 1.

The truncated view of TS_ac (9), TS_ac (10), TS_ac (11), TS_ac (12), and TS_ac (14) corresponding for the transition states of methyl radical attacking camptothecin at the site of 9, 10, 11and 12 in acidic conditions respectively.

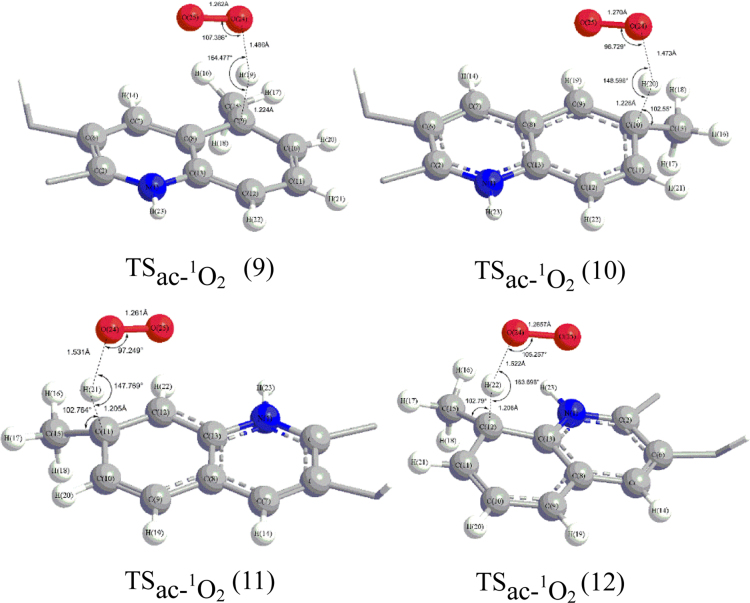
Fig. 2.

The truncated view of TS_ac-¹O2 (9), TS_ac-¹O2 (10), TS_ac-¹O2 (11), and TS_ac-¹O2 (12) corresponding for transition states of H abstraction by singlet ¹O₂ from sites of 9, 10, 11 and 12 of the intermediate of methyl combination with camptothecin in acidic condition respectively.

Fig. 3.

The truncated view of TS_ac-³O2 (9) corresponding for the transition state of H abstraction by triplet O₂ from site 9 of the intermediate of methyl combination with camptothecin in acidic condition.

In this paper, some abbreviations were used for the convenience of description, the reactants, transition states, intermediates and products are expressed by R, TS, M and P respectively, and the Arabic numerals indicate the order. The neutral reaction conditions are denoted by n, and the acidic reaction conditions are represented by ac. The singlet O₂ and the triplet O₂ are denoted by ¹O₂ and ³O₂, respectively.

F_TS stands for the absolute value of the frequency of the transition state. κ is the tunnel effect correction factor. It can be calculated by Wigner method based on the virtual frequency of the transition state. ΔE is the static potential threshold on the minimum energy response path (MEEP). Q_A and Q_B are the partition functions of the reactants A and B. And Q_TS is the partition function for the transition state.

The molecular structures and the tables are shown below:

Fig. 1 shows the truncated view of the transition states for methyl radical attacking camptothecin at the site of 9, 10, 11, 12 and 14 in acidic conditions. The truncated view of transition states for H abstraction by singlet O₂ from sites of 9, 10, 11 and 12 of the intermediates of methyl combination with camptothecin in acidic condition is shown in Fig. 2. The structure of transition states for H abstraction by triplet O₂ from site 9 in acidic condition is illustrated in Fig. 3.

The corresponding parameters for the calculation of reaction rate constant of the formation of methyl radical from acetaldehyde, the first and second step of radical substitution of camptothecin under acidic conditions are listed in Table 1, Table 2, Table 5 respectively. The data of the basic parameters for the computation of the total energy of the spin-projection of singlet oxygen, and the S² values for the reactants, transition states and intermediates in the free radical substitution reaction of camptothecin are also included in Table 3, Table 4 respectively.

Table 1.

The corresponding parameters of reaction rate constant calculation for the formation of methyl radical from acetaldehyde.

Step	FTS (cm−1)	κ	QAa	QTS	ΔE (kcal/mol)
1	−148.84	1.022	1.24 × 1014	4.52 × 1013	3.215
2	−247.14	1.059	2.51 × 1015	5.47 × 1012	19.70

^aRepresents that the reactant of acetaldehyde molecule.

Table 2.

The corresponding parameters of reaction rate constant calculation for the first step of radical substitution of camptothecin under acidic conditions.^c (298.15 K).

Site	FTS1 (cm−1)	κ	QA1a	QB1b	QTS1	ΔE1 (kcal/mol)
7	−280.81	1.027	1.27 × 1010	4.47 × 1022	2.50 × 1024	5.42
9	−396.00	1.054	–	–	2.68 × 1024	8.28
10	−412.99	1.059	–	–	2.25 × 1024	9.16
11	−368.16	1.047	–	–	2.19 × 1024	8.16
12	−444.43	1.068	–	–	2.46 × 1024	6.88
14	−362.43	1.045	–	–	2.43 × 1024	7.35

^aRepresents that the protonated camptothecin molecule.

^bRepresents that the methyl radical.

^c“-” represents that the value is same as above.

Table 5.

The corresponding parameters of reaction rate constant calculation for the second step of radical substitution of camptothecin under acidic conditions.* (298.15 K).

Site	FTS2 (cm−1)	κ	QA2	QB2	QTS2	ΔE2 (kcal/mol)
7	−1396.24	1.054	1.02 × 1029	8.75 × 108	1.63 × 1025	8.35
9	−1114.48	1.429	1.93 × 1029	–	1.22 × 106	5.76
10	−399.56	1.055	1.65 × 1027	–	1.94 × 1025	0.98
11	−300.07	1.031	2.64 × 1030	–	2.15 × 1025	3.26
12	−922.35	1.294	3.19 × 1028	–	9.57 × 1025	6.04

^a represents that the intermediate produced by the first step reaction.

^b represents that the singlet oxygen.

^* “-” represents that the value is same as above.

Table 3.

The basic parameters for the computation of the total energy of the spin-projection of singlet oxygen.

$E^{AP}$	$E^{BS}$	$E^{HS}$	${\langle S^2\rangle }^{BS}$	${\langle S^2\rangle }^{HS}$	α	$\beta$
−150.324	−150.311	−150.317	2.009	1.004	2	1

Table 4.

S² values for the reactants, transitions and intermediates in the reaction.

Site	Step 1						Step 2
	Neutral conditions			Acidic condition			Acidic condition
	Rna	TSnb	Mnc	Raca	TSacb	Macc	Rac-1O2a	TSac-1O2b	Pac-1O2c
7	–	0.7828	0.7843	–	0.7673	0.7678	0.76784	0.7662	0.7539
9	–	0.7883	0.7797	–	0.7813	0.7715	0.7715	0.7666	0.7539
10	–	0.7862	0.7867	–	0.7850	0.7844	0.7844	0.7775	0.7539
11	–	0.7835	0.7803	–	0.7738	0.7663	0.7663	0.8108	0.7539
12	–	0.7533	0.783	–	0.7883	0.7824	0.7824	0.7690	0.7539
14	–	0.7533	0.7667	–	0.7853	0.7561	–	–	–
CH3	0.7533	–	–	0.7533	–	–	–	–	–
1O2	–	–	–	–	–	–	1.004448	–	–

* “-” represents that the value does not exist.

Transparency document. Supplementary material

Supplementary material

.

Appendix A. Supplementary material

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.

Supplementary material

.