On the Collisionless Asymmetric Magnetic Reconnection Rate

Abstract

A prediction of the steady state reconnection electric field in asymmetric reconnection is obtained by maximizing the reconnection rate as a function of the opening angle made by the upstream magnetic field on the weak magnetic field (magnetosheath) side. The prediction is within a factor of 2 of the widely examined asymmetric reconnection model (Cassak & Shay, 2007, https://doi.org/10.1063/1.2795630) in the collisionless limit, and they scale the same over a wide parameter regime. The previous model had the effective aspect ratio of the diffusion region as a free parameter, which simulations and observations suggest is on the order of 0.1, but the present model has no free parameters. In conjunction with the symmetric case (Liu et al., 2017, https://doi.org/10.1103/PhysRevLett.118.085101), this work further suggests that this nearly universal number 0.1, essentially the normalized fast-reconnection rate, is a geometrical factor arising from maximizing the reconnection rate within magnetohydrodynamic-scale constraints.

Plain Language Summary

To understand the evolution of many space and astrophysical plasmas, it is imperative to know how fast magnetic reconnection processes the magnetic flux. Researchers found that reconnection in both symmetric and asymmetric geometries exhibits a normalized reconnection rate of order 0.1. In this work, we show that this nearly universal value in asymmetric geometry is also the maximal rate allowed in the magnetohydrodynamic scale. This result has applications to the transport process at plasma boundary layers like Earth’s magnetopause.

1. Introduction

Magnetic reconnection at Earth’s magnetopause not only allows the transport of solar wind plasmas into Earth’s magnetosphere but also enhances the convection of magnetic flux to Earth’s nightside (Dungey, 1961). The magnetic fields and plasma conditions on the two sides of the magnetopause current sheet are typically different (e.g., Phan & Paschmann, 1996), a feature that also applies to current sheets in planetary (Fuselier et al., 2014; Masters, 2015), solar (Murphy et al., 2012), laboratory (Yoo et al., 2014), fusion (Mirnov et al., 2006), and turbulent (Servidio et al., 2009; Zhdankin et al., 2013) plasmas. Reconnection with these different upstream conditions is commonly called asymmetric. To model the global circulation of magnetospheric plasmas around Earth and the magnetic energy release therein, it is crucial to understand how fast the magnetic flux is processed by asymmetric reconnection at Earth’s magnetopause (Borovsky, 2008; Borovsky & Birn, 2013).

One measure of the reconnection rate is the strength of the reconnection electric field inside the reconnection diffusion region that, according to Faraday’s law, is proportional to the magnetic flux change rate at the diffusion region. In the symmetric limit, simulations and theories suggest a normalized rate of an order 0.1 (Birn et al., 2001; Cassak et al., 2017; Comisso & Bhattacharjee, 2016; Hesse et al., 1999; Liu et al., 2017; Parker, 1973; Shay etal., 1999). At Earth’s magnetopause, directly measuring the reconnection electric field has been conducted although it remains challenging (e.g., Chen et al., 2017; Mozer & Retinό, 2007; Vaivads et al., 2004). A good proxy of the reconnection rate is the convective electric field upstream of the diffusion region induced by the inflowing plasma. Such an electric field was inferred from the ion velocity into the ion diffusion region (e.g., Fuselier et al., 2005; Mozer & Hull, 2010; Phan et al., 2001; Wang etal., 2015), or from the electron velocity into the electron diffusion region (Chen et al., 2017). The reconnection rate can also be estimated from the magnitude of reconnected magnetic fields downstream of the ion diffusion region (Phan et al., 2001) using Sweet-Parker scaling (Parker, 1957; Sweet, 1958) or from the energy conversion rate (Rosenqvist etal., 2008).

Observational evidence (Fuselier etal., 2016; Mozer&Hull, 2010; Wang etal., 2015) suggests that the strength of the reconnection electric field follows the scaling

$$E_{\text{CS}}=2\left(\frac{B_1{B}_2}{B_1+B_2}\right)\left(\frac{V_{\text{out}}}{c}\right){\left(\frac{\delta }{L}\right)}_{\text{eff}}$$ 1

that is derived using conservation laws in an asymmetric geometry (Cassak & Shay, 2007). B₁ and B₂ are the reconnecting component of magnetic fields at the magnetosheath and magnetosphere sides, respectively. The outflow speed $V_{\text{out}}={\left(B_1{B}_2/4\pi \overline{\rho }\right)}^{1/2}$ is the hybrid Alfvén speed based on a hybrid density $\overline{\rho }=\left(B_1{\rho }_2+B_2{\rho }_1\right)/\left(B_1+B_2\right)$ Here (𝛿/L)_eff is the effective aspect ratio of the diffusion region, which is a free parameter in this model for collisionless reconnection. Observations suggest that (𝛿/L)_eff is of order 0.1. Numerical simulations have also confirmed this scaling and demonstrated that (𝛿/L)_eff ~ 0.1; these include local magnetohydrodynamic (MHD) simulations with a localized resistivity (Birn et al., 2008), local two-fluid (Cassak & Shay, 2008) and local particle-in-cell (PIC) (Malakit et al., 2010; Pritchett, 2008) simulations, global magnetospheric MHD simulations (Borovsky, 2008; Borovsky & Birn, 2013; Komar & Cassak, 2016; Ouellette et al., 2013; Zhang et al., 2016), and global Vlasov simulations (Hoilijoki et al., 2017). This scaling along with (𝛿/L)_eff ~ 0.1 was then employed to develop a quantitative model of the coupling between the solar wind and Earth’s magnetosphere (Borovsky, 2008; Borovsky & Birn, 2013). Given these successes of equation (1), it remains not understood why the effective aspect ratio in this model should be of order 0.1. This obviously requires an explanation.

In this Letter, we provide a theoretical explanation for the collisionless asymmetric reconnection rate. We generalize the approach discussed in Liu et al. (2017) that was used to model the symmetric reconnection electric field. Through analyzing force balance at the inflow and outflow regions, we cast the reconnection electric field into the form of a function of the opening angle made by the upstream magnetic field on the weak field side. A prediction is then obtained by maximizing this rate as a function of this opening angle, which we find to agree with E_cs within a factor of 2, with agreement in the scaling sense over a wide range of upstream plasma parameters. This comparison demonstrates that this nearly universal effective aspect ratio of order 0.1 in the collisionless limit (Cassak & Shay, 2008) can also be explained by geometrical constraints on the MHD scale, independent of the dissipation mechanism.

2. Constraint on the Reconnecting Field

We consider the geometry and notation illustrated in Figure 1. The asymptotic field B_x2 on side 2 is larger than the asymptotic value B_x1 on side 1.Thus, sides 1 and 2 nominally correspond to typical conditions at the magnetosheath and magnetosphere, respectively. Unlike the model in Cassak and Shay (2007), the strength of the reconnecting field immediately upstream of the ion diffusion region can be different from the asymptotic field on each side. We use a subscript “m” in B_xmi to indicate the microscopic ion diffusion region scale, and i = 1,2 indicates the two inflow sides. V_out,m is the outflow speed immediately downstream of the diffusion region. During the nonlinear stage of reconnection, the angle θ_i,· (as sketched for side 1) made by the upstream magnetic field lines opens out on each side. This geometry unavoidably induces a tension force B ·$\nabla B_Z/4\pi$ directed away from the x line (as sketched for side 1), which is mostly balanced by the magnetic pressure gradient force $-{\left(\nabla B^2/8\pi \right)}_z$ directed toward the x line (as sketched for side 1). Such a finite magnetic pressure gradient requires the reduction of the reconnecting magnetic field immediately upstream of the diffusion region. This effect is modeled in Liu et al. (2017) that results in an expression

$$B_{xmi}\simeq B_{xi}\frac{1-S_i^2}{1+S_i^2}$$ 2

Figure 1.

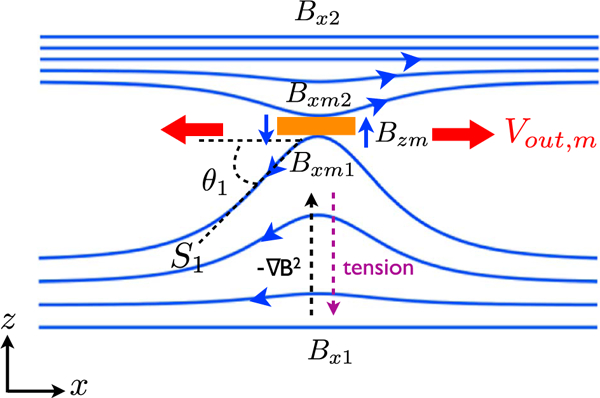
The geometry of magnetic fields upstream of the diffusion region for asymmetric reconnection. The orange box marks the diffusion region. <DI>S₁ = tan|𝜃₁|10, </DI> | marks the slope of the magnetic field line on side 1. The strength of the magnetic field is illustrated by the field line density.

Here S_i = tan|θ_i| is the slope of the upstream magnetic field line on each side, as sketched for side 1 in Figure 1. From equation (2), the reconnecting magnetic field B_xmi vanishes as the opening angle approaches 45° (i.e., S_i → 1). In the 2-D approximation, we can write $B=\nabla \times A_v\widehat{y}+B_v\widehat{y}$ The sample field lines in Figure 1 are evenly spaced contours of the flux function A_y; hence, the “line density” illustrates the strength of the in-plane magnetic field. The field lines approaching the diffusion region become less dense (i.e., weaker) compared with its asymptotic value on each side, illustrating the reduction of the reconnecting field due to the opening out of the upstream magnetic field lines.

The reconnected field immediately downstream of the diffusion region scales as

$$B_{\text{zm}}\simeq B_{xmi}{S}_i$$ 3

This assumes that the reconnected field calculated from sides 1 and 2 is identical, which naturally leads to a larger opening angle on side 1, as illustrated in Figure 1. This also means that the reduction of reconnecting magnetic field on the weaker field side has a stronger effect in limiting the reconnection rate.

Because the field strength of the reconnecting field on side 1 is weaker than that on side 2, all possible solutions of this model must be found in the range 0 < S₁ < 1. Therefore, we write B_zm as a function of S₁:

$$B_{zm}\left(S_1\right)\simeq \left(\frac{1-S_1^2}{1+S_1^2}\right)S_1{B}_{x1}$$ 4

3. Constraint on the Outflow Speed

To estimate the reconnection electric field, E_y ≃ B_zmV_out,m/c, we need to calculate the outflow speed V_out,m. We consider the notation and geometry in Figure 2. The dimension of the diffusion region is 2L x 2𝛿. Lines a - c and a - d represent the separatrices on side 2 and side 1, respectively, and “a” marks the x line. We first derive the outflow density ρ as a result of mixing of plasmas from two sides. The integral form of Gauss’ law fora 2-D system is ∮ B⋅dl = 0 where dl is along the perimeter of a closed 2-D area. By applying this rule to the triangle area a - b - c in Figure 2, we get ${\displaystyle {\int }_a^b{B}_z}\text{d}x+{\displaystyle {\int }_b^c{B}_x}\text{d}z+{\displaystyle {\int }_c^{a}B}\cdot \text{d}l=0$ The last integral vanishes identically because the magnetic separatrix passes the upper right corner at point “c.” Thus, $\left(B_{zm}/2\right)L\simeq \left(B_{xm2}/2\right){\delta }_2$ The factor of 2 in the denominator arises from the assumption that B_x and B_z vary linearly with distance along z and x, respectively. A similar exercise reveals $B_{zm}L\simeq B_{xm1}{\delta }_1$ Combined with the relation ${\delta }_1+{\delta }_2=2\delta$, we get

$$B_{\text{zm}}=2\left(\frac{B_{xm1}{B}_{xm2}}{B_{xm1}+B_{xm2}}\right)\left(\frac{\delta }{L}\right)$$ 5

Figure 2.

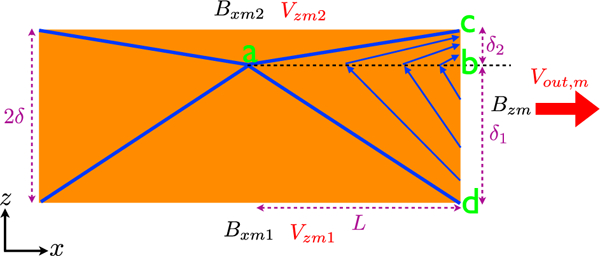
The geometry and dimension of the diffusion region. The strength of the magnetic field is illustrated by the field line density. Here<DI> &_λ + δ₂ = 25.</DI> The label “a” marks the reconnection x line.

We now estimate the mass density as in Cassak and Shay (2007), taking care to note that the conservation laws are evaluated at the microscopic “m” scale. Mass conservation gives $2\overline{\rho }{V}_{\text{out}}\delta \simeq {\rho }_1{V}_{zm1}L+{\rho }_2{V}_{zm2}L$ In a 2-D steady state, the out-of-plane electric field E_y is uniform around the diffusion region and hence $\text{V \_ { z m 1 } B \_ { X m 1 } =}{V}_{\text{zm}2}{B}_{xm2}=V_{\text{ out },m}{B}_{\text{zm}}$ Eliminating the velocities gives the hybrid mass density (Cassak & Shay, 2007),

$$\overline{\rho }\simeq \frac{B_{xm1}{\rho }_2+B_{xm2}{\rho }_1}{B_{xm1}+B_{xm2}}$$ 6

Now we have enough information to derive the outflow speed from the momentum equation in the outflow direction $\widehat{x}$, which is written as $(\rho /2){\partial }_x{V}_x^2\simeq B_z{\partial }_z{B}_x/4\pi -{\partial }_x{B}^2/8\pi$ Note that we have ignored the thermal pressure gradient by the same reasoning discussed in Birn et al. (2010). To get an averaged outflow speed, we follow a process similar to Swisdak and Drake (2007); we apply ${\displaystyle {\int }_0^{L}d}x{\displaystyle {\int }_{-\delta }^{\delta }d}z$ to the momentum equation, assuming ${\text{B}}_z={\text{B}}_z(x),{\text{B}}_x={\text{B}}_x(z),V_x=V_x(x)$, and a uniform density $\rho =\overline{\rho }$ inside the diffusion region. These lead to $(\overline{\rho }/2)V_{\text{out}}^{2}2\delta \simeq \left(B_{\text{zm}}/2\right)L\left(B_{\text{xm}2}+B_{\text{xm}1}\right)/4\pi -B_{\text{zm}}^{2}2\delta /8\pi$ Substituting equation (5) for B_zm, we get

$$V_{\text{ out },m}\simeq \sqrt{\frac{B_{xm1}{B}_{xm2}}{4\pi \overline{\rho }}\left[1-4\frac{B_{xm1}{B}_{xm2}}{{\left(B_{xm1}+B_{xm2}\right)}^2}{\left(\frac{\delta }{L}\right)}^2\right]}$$ 7

The first term inside the square brackets results from the averaged magnetic tension force and is the speed obtained in previous studies (Cassak & Shay, 2007; Swisdak & Drake, 2007). The reduction of the reconnecting field discussed in the previous section decreases the tension force that drives the outflow away from the diffusion region. The second term proportional to (𝛿/L)² is a new term that arises from the magnetic pressure gradient, and it further reduces the outflow speed. However, the prefactor dependent on B_xm1 and B_xm2 is 1 for the symmetric case (Cassak et al., 2017; Liu et al., 2017) and decreases for increasing field asymmetries, so the correction by the magnetic pressure gradient to the outflow speed is weakened even more for asymmetric reconnection than symmetric reconnection (Liu et al., 2017).

We cast the outflow speed into a function of S₁(≃ 𝛿₁/L) instead,

$$V_{\text{out},m}\left(S_1\right)\simeq \sqrt{\frac{B_{xm1}{B}_{xm2}-S_1^2{B}_{xm1}^2}{4\pi \overline{\rho }}}$$ 8

The associated reconnection electric field is

$$E_y\left(S_1\right)\simeq B_{zm}\left(S_1\right)V_{\text{ out },m}\left(S_1\right)/c$$ 9

which is a function of S₁ using equations (2), (4), (6), and (8). We hypothesize that the reconnection rate corresponds to the maximum allowable value. Our prediction of the reconnection electric field is E_R = max(E_y), which can be found in the range 0 ≤ S₁ ≤ 1.

Note that writing B_xm2 as an explicit function of S₁ can be done, but there is no simple expression for it. We need to use the relation B_xm2S₂ = B_xm1 S₁ and equation (2) to derive S₂(S₁) first, which involves finding the roots of a cubic function $E_y\left(S_1\right)\simeq B_{zm}\left(S_1\right)V_{\text{ out },m}\left(S_1\right)/c$ is then plugged into equation (2) to get B_xm2(S₁). These calculations can be performed numerically in a straightforward fashion.

4. Prediction

In the following, we find the maximum reconnection electric field E_R from equation (9) numerically. The result for a wide parameter range of magnetic field ratio B_x1/B_x2 and density ratio n₁/n₂ is shown in Figure 3. The predicted opening angles on the two sides of the current sheet are shown in Figures 3a and 3b. The opening angle θ₁ of the upstream magnetic field line on side 1 increases mildly from ≃18.2° in the symmetric limit to ≃21.5° in the strong field asymmetry limit. In the same limit, the field line opening angle θ₂ on side 2 becomes small (→0°) because the magnetic field is much stiffer on side 2 compared to that on side 1. This qualitatively agrees with all previous asymmetric reconnection simulations, which show θ₁ >θ₂. In Figure 3c, the reconnection electric field ${\widehat{E}}_R\equiv C{E}_R/V_{A\times 1}{B}_{\chi 1}$ is normalized to the Alfvén speed $V_{A\times 1}\equiv B_{\chi 1}/\sqrt{4\pi {\rho }_1}$ and the field strength B_x1 at the magnetosheath (side 1).The normalized rate Ê_R is ≃ 0.2 in the symmetric limit (i.e., log(Ê_R) ≃ −0.7 when n₁/n₂ = 1 and B_x1/B_x2 = 1), as expected from Liu et al. (2017). In Figure 3d, we compare our prediction to E_CS with (𝛿/L)_eff = 0.1. It is important to learn that this prediction agrees with E_CS within a factor of 2, and they scale together over a wide range of parameter space. In conjunction with the symmetric case discussed in Liu et al. (2017), this consistency in the asymmetric limit suggests that the geometrical factor, (𝛿/L)_eff ≃ 0.1, left unexplained in equation (1), also arises from the MHD-scale constraints imposed at the inflow and outflow regions.

Figure 3.

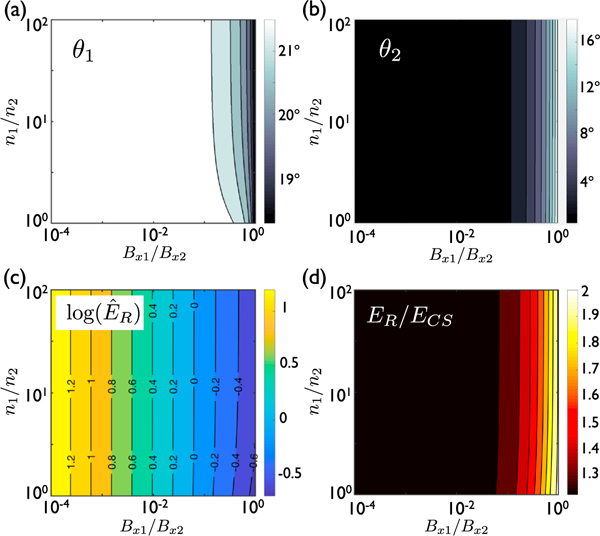
(a) The predicted opening angle made by the upstream magnetic field on side 1 is plotted as a function of B_x1 /B_x2 and n₁ /n₂. (b) The predicted opening angle made by the upstream magnetic field on side 2. (c) The contour of the predicted reconnection electric field normalized by the side 1 (magnetosheath) value. (d) The ratio of the predicted reconnection electric field to the prediction in equation (1) assuming 𝛿/L = 0.1.

To understand better the difference in different models, we plot the predictions as a function of B_x1 /B_x2 with a fixed n₁ /n₂ = 1 in Figure 4a and as a function of n₁/n₂ with a fixed B_x1/B_x2 = 1 in Figure 4b. Red curves show the value of E_CS normalized to V_Ax1 B_x1/c, solid black curves are Ê_R (our prediction), dashed black curves are the maximum of equation (9) using $V_{\text{ out }m}\left(S_1\right)\simeq {\left(B_{xm1}{B}_{xm2}/4\pi \overline{\rho }\right)}^{1/2}$ instead of equation (7); that is, the reduction of the outflow speed from the magnetic pressure gradient is not considered. The red and solid black curves exhibit a similar scaling, as suggested in Figure 3d. The dashed black curve is very close to the solid black curve in each panel, suggesting that the reduction of the reconnecting field, rather than the reduction in V_out,m due to the magnetic pressure gradient force, is the dominant mechanism that constrains the rate.

Figure 4.

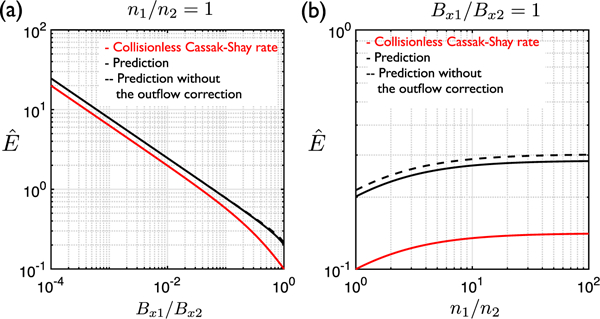
The predicted reconnection electric field normalized by the side 1 (magnetosheath) conditions is plotted as a function of B_x1 /B_x2 with a (a) symmetric density and as a function of n₁ /n₂ with a (b) symmetric reconnecting magnetic field. The prediction is shown in solid back, the prediction of equation (1) in red, and the prediction without the outflow correction in dashed black.

5. Summary and Discussion

In this Letter, we derive the collisionless asymmetric magnetic reconnection rate using a new approach. The prediction is obtained through maximizing a model rate that considers the MHD-scale constraints at both the inflow and outflow regions. The predicted value is found to be within factor of 2 of the collisionless asymmetric reconnection rate that was widely examined (Cassak & Shay, 2007, 2008). This comparison suggests that constraints at the MHD scale explain the geometrical factor (𝛿/L)_eff of order 0.1 inferred but not explained in the rate model of Cassak and Shay (2008), putting the scaling in equation (1) on solid footing. The analysis further shows that the dominant limiting effect that constrains the maximum reconnection rate is the field reduction at the weakfield (magnetosheath) side.

We have assumed that the system self-selects the maximum energy conversion rate, that is, that it assumes the maximum possible reconnection rate. We acknowledge that this is an assumption ultimately requiring a rigorous proof at some future time. In the meantime, we point out that Birn et al. (2008) showed, in the framework of MHD with a localized resistivity, that the maximum possible asymmetric reconnection rate is capped by the value of order 0.1, no matter how strong a localized dissipation is employed. By comparing 3-D and 2-D PIC simulations, Liu et al. (2015) showed that the x line orientation in a 3-D system can be determined by finding the oblique 2-D plane that maximizes the reconnection rate. While this is not a proof in the strict sense, these results indicate that our assumption is reasonable.

Additional caveats need to be kept in mind when applying this theory. An out-of-plane guide field does not affect the in-plane tension force but can contribute to the magnetic pressure gradient in the force balance. The same prediction applies to a general case with a guide field only if the reconnection process does not significantly alter the guide field strength near the x line. The normalized rate remains to be ~ 0.1 in the strong guide field limit, at least, for symmetric cases (Liu et al., 2014). This model does not include the effect of the diamagnetic drift driven by the combination of the pressure gradient across the sheet and a finite guide field. The diamagnetic drift can suppress magnetic reconnection (Beidler&Cassak, 2011; Liu & Hesse, 2016; Swisdak et al., 2003,2010). Flow shear commonly present at the flank of the magnetopause can also reduce the reconnection rate (Cassak & Otto, 2011; Doss et al., 2015). Potential 3-D and turbulence effects (Daughton et al., 2014; Ergun et al., 2016; Le et al., 2017; Liu et al., 2015; Price et al., 2016) are not included in this 2-D analysis. Finally, while this theory works in most models, including PIC, hybrid, two-fluid models, and MHD with a localized resistivity, it does not apply to MHD systems with a uniform resistivity; a uniform resistivity does not seem to support the maximum rate allowed by the constraints imposed at the upstream and downstream regions. Researchers found that a fast-growing plasmoid instability enhances the reconnection rate in high-Lundquist number MHD simulations (Biskamp, 1986; Cassak et al., 2009; Huang & Bhattacharjee, 2010; Loureiro et al., 2007; Murphy et al., 2013; Samtaney et al., 2009; Uzdensity et al., 2010). The relation of this instability to the present results remains to be explored.

Nevertheless, by comparing with the well-established scaling (Cassak & Shay, 2007, 2008) previously found in the asymmetric limit of collisionless plasmas, the consistency demonstrated in this Letter confirms the capability of this new approach (Cassak et al., 2017; Liu et al., 2017) in explaining the fast reconnection rate in a more general configuration. This result is timely to the study of collisionless magnetic reconnection in Earth’s magnetosphere. The high cadence electric field measurement on board of NASA’s Magnetospheric Multiscale spacecraft and their close deployment provide an invaluable opportunity to study the reconnection rate (Chen et al., 2017) and perhaps the effective aspect ratio of diffusion region in both the magnetopause and magnetotail.

Key Points:

• The asymmetric reconnection rate is modeled as a function of the opening angle made by the weaker upstream magnetic field

• The maximum rate exhibits the same scaling ofthe widely studied asymmetric reconnection rate over a wide parameter regime

• The normalized maximum rate of order 0.1 is limited by the constraints imposed at MHD scales