Three-dimensional virtual histology of human cerebellum by X-ray phase-contrast tomography

Significance

The complex cytoarchitecture of human brain tissue is traditionally studied by histology, providing structural information in 2D planes. This can be partly extended to 3D by inspecting many parallel slices, however, at nonisotropic resolution. This work shows that propagation-based X-ray phase-contrast tomography, both at the synchrotron and even at a compact laboratory source, can be used to perform noninvasive 3D virtual histology on unstained paraffin-embedded human cerebellum at isotropic subcellular resolution. The resulting data quality is high enough to visualize and automatically locate ∼10⁶ neurons within the different layers of the cerebellum, providing unprecedented data on its 3D cytoarchitecture and spatial organization.

Abstract

To quantitatively evaluate brain tissue and its corresponding function, knowledge of the 3D cellular distribution is essential. The gold standard to obtain this information is histology, a destructive and labor-intensive technique where the specimen is sliced and examined under a light microscope, providing 3D information at nonisotropic resolution. To overcome the limitations of conventional histology, we use phase-contrast X-ray tomography with optimized optics, reconstruction, and image analysis, both at a dedicated synchrotron radiation endstation, which we have equipped with X-ray waveguide optics for coherence and wavefront filtering, and at a compact laboratory source. As a proof-of-concept demonstration we probe the 3D cytoarchitecture in millimeter-sized punches of unstained human cerebellum embedded in paraffin and show that isotropic subcellular resolution can be reached at both setups throughout the specimen. To enable a quantitative analysis of the reconstructed data, we demonstrate automatic cell segmentation and localization of over 1 million neurons within the cerebellar cortex. This allows for the analysis of the spatial organization and correlation of cells in all dimensions by borrowing concepts from condensed-matter physics, indicating a strong short-range order and local clustering of the cells in the granular layer. By quantification of 3D neuronal “packing,” we can hence shed light on how the human cerebellum accommodates 80% of the total neurons in the brain in only 10% of its volume. In addition, we show that the distribution of neighboring neurons in the granular layer is anisotropic with respect to the Purkinje cell dendrites.

Digitalizing the 3D structure of human brain tissue at (sub)cellular resolution is an essential step toward deciphering how brain function is enabled by the underlying cytoarchitecture. It can also indicate which changes become relevant in neurodegenerative disorders such as multiple sclerosis or in brain tumor development. To this end, 3D data have to be acquired with sufficient resolution, contrast, and throughput. The gold standard in biomedical research is histology, a destructive imaging method in which the specimen is sliced into micrometer-thick slices, stained with specific staining agents, and examined under a light microscope. However, artifacts can be created not only by fixation and staining, but also by the slicing itself via shear forces or due to slicing-associated constraints, which narrow the choice of fixation or impose changes in temperature. Most importantly, histology provides excellent results in 2D, but resolution in 3D is always limited by the slice thickness. Hard X-ray computed tomography (CT), when augmented by phase contrast (1–7), can provide sufficient 3D image resolution and contrast for neuronal tissues (8–10). Compared with classical absorption radiography, related to the imaginary part of the X-ray index of refraction $n\left(\mathbf{r}\right)=1-\delta \left(\mathbf{r}\right)+i\beta \left(\mathbf{r}\right)$, X-ray phase shifts arise from variations in the real part $\delta \left(\mathbf{r}\right)$ which is orders of magnitude larger for soft biological tissue (11). By free propagation and self-interference of a coherent beam behind the object, the phase shifts are converted into measurable signals (1, 2). Nowadays, phase-contrast tomography can indeed be realized not only with synchrotron radiation (SR), but also with laboratory microfocus ($\mathrm{\mu }$-CT) instruments, which can be made more broadly available for clinical and biomedical research or even clinical diagnostics. This progress has been enabled in particular by new sources which provide just enough partial coherence to exploit phase-contrast (12–16) as well as submicrometer resolution (15, 17). However, sufficient contrast in unstained neuronal tissue has so far been achieved only for fairly sparse features such as very large neurons (18), but not for small and densely populated neurons or dendrites. Visualization of individual cells required invasive contrast enhancement by staining, for example in kidney (19) and in neuronal tissue (10), or by drying (16). Overall, persisting deficits in image quality have largely restricted 3D analysis of tissues to SR, and even in this case resolution and contrast for unstained tissue were mostly too modest for automated detection of cells.

In this work we now demonstrate noninvasive imaging of paraffin-embedded human brain tissue by phase contrast based on electron density variations without any additional staining and at an image quality which enables reliable and automated rendering of up to $1.8\cdot 10^6$ neurons in the reconstruction volume. This progress has been enabled by a careful optimization and choice of image recording parameters and reconstruction algorithms. To this end, we use two optimized tomography instruments designed and implemented by our group, a laboratory $\mathrm{\mu }$-CT setup equipped with a liquid jet anode source, as well as a high-resolution SR instrument with special X-ray waveguide optics for coherence and spatial filtering (20). While the $\mathrm{\mu }$-CT offers large volume, the SR setup provides a zoom-in into the laboratory dataset at higher resolution. In both cases, we have optimized optical and geometrical parameters for samples of low contrast and have identified suitable reconstruction algorithms. Importantly, we have implemented and validated algorithms for automated 3D image segmentation and extraction of neuron locations. For this proof-of-concept demonstration, we have chosen the example of the human cerebellum. Specifically, we quantify the positions of all neurons and from these data the distribution functions describing difference vectors between neighboring neurons in the densely packed granular layer. We also cover the interface to the Purkinje cell layer where we show that image quality and contrast are high enough to segment the characteristic dendritic trees of Purkinje cells, as well as the molecular layer with its much sparser population of neurons.

Several approaches have already been introduced to implement automated segmentation. For example, Dyer et al. (8) first used manual training of an object classifier to obtain probability maps for neurons or for specific sample features. This was shown to work well for osmium-stained mouse cortex recorded with synchrotron radiation. Hieber et al. (9) used a Frangi filtering step to extract tubular and spherical microstructures of Purkinje cells in unstained human cerebellum embedded in paraffin, also recorded with synchrotron data. To locate up to $10^6$ neurons in a 1-mm punch from a human cerebellum embedded in paraffin, we here make use of the spherical Hough transform which we tune to detect the cell nuclei of expected size in the entire 3D search space. The algorithm does not need any manual training and can accurately locate even unstained and small neurons. At the achieved level of data volume, image quality, and segmentation reliability, more statistical quantifications of anatomical structure become possible. We illustrate this by showing highly resolved histograms of structural parameters, such as cell–cell distance and gray values representing electron density. Borrowing concepts from condensed-matter physics, we also compute the associated pair correlation function and structure factor from the retrieved cellular position vectors. The resulting curves indicate a highly structured 3D assembly for the granular layer where the first and second correlation shells of nuclear positions can clearly be distinguished from the associated maxima.

Results

High-Resolution Synchrotron CT.

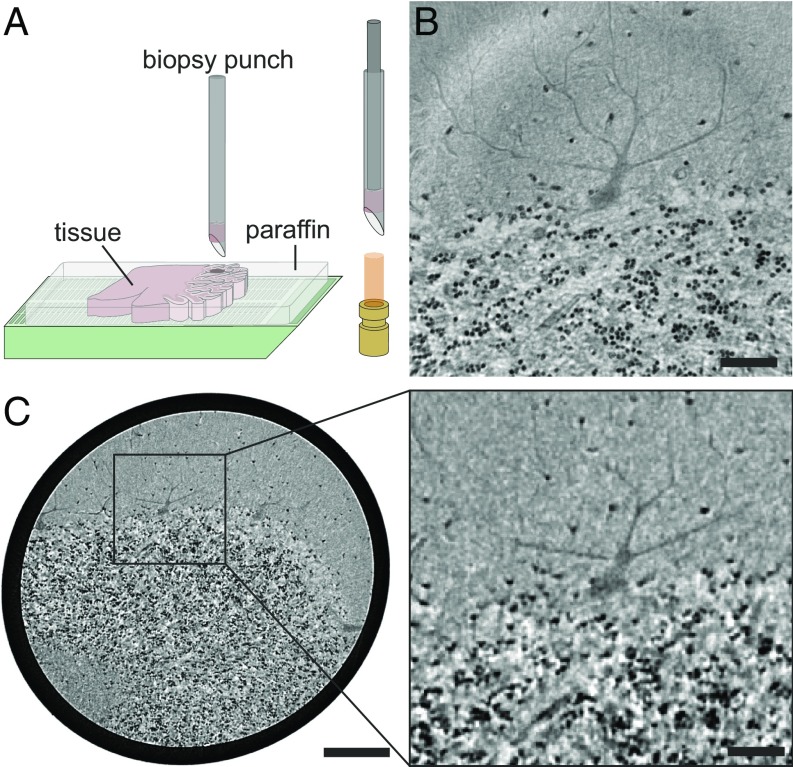
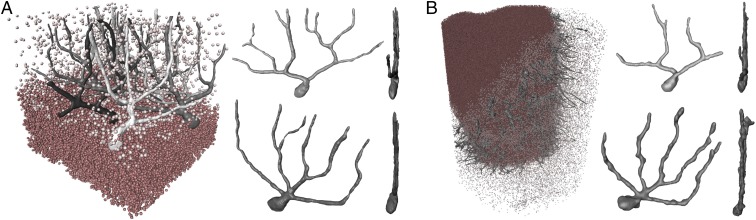
The synchrotron measurements were recorded in a highly coherent and divergent 8-keV radiation cone behind the X-ray waveguide optics of the Göttingen Instrument for Nano-Science with X-rays (GINIX) endstation (SI Appendix, Fig. S4A), installed at the P10/PETRAIII beamline (20). Fig. 1B shows a virtual slice through the tomographic reconstruction, clearly resolving the transition between the cell-rich granular layer in the bottom and the low-cell molecular layer at the top. At the interface, the monocellular Purkinje cell layer can be identified. One exemplary cell of this layer is depicted in the presented slice, including its large dendritic tree protruding into the molecular layer. To better visualize the 3D structure of the reconstructed volume, a cellular segmentation is shown in Fig. 2A and in SI Appendix, Movie S1. The automated segmentation of cells in the molecular and granular layer based on the spherical Hough transform (21, 22) is detailed in Material and Methods. For the Purkinje cell layer, a semiautomatic approach was used, as detailed in Materials and Methods. Different characteristics of the cerebellar layers become immediately evident. The cells of the granular and molecular layer are significantly smaller compared with the Purkinje cells which have a highly branched dendritic tree. The segmentation of the single Purkinje cells in Fig. 2A, Right (note that the cell in Fig. 2A, Lower Right is the same as shown in Fig. 1C) also shows the typical flat shape of the Purkinje cell which is almost 2D.

Fig. 1.

Virtual histology of human cerebellum. (A) Sample preparation for tomographic experiments. Biopsy punches were taken from paraffin-embedded human cerebellum and placed into a Kapton tube for mounting in the experimental setups. (B) Transverse slice through the reconstructed volume of the synchrotron dataset revealing the interface between the low-cell molecular and the cell-rich granular layer, including a cell of the monocellular Purkinje cell layer. (C, Left) Corresponding slice of the laboratory dataset (same plane, same specimen as in B), showing the larger volume accessible by the laboratory setup while maintaining the resolution required for single-cell identification. (C, Right) Magnified view of the region marked by the rectangle in C, Left corresponding to the field of view of the synchrotron dataset in B. [Scale bars: 50 $\mathrm{\mu }$m (B and C, Right) and 200 $\mathrm{\mu }$m (C, Left).]

Fig. 2.

Volume representation of the data. (A) Cellular segmentation of the cells in the granular layer (dark red), the molecular layer (light red), and the Purkinje cell layer (shades of gray) with two exemplary Purkinje cells shown separately (Right), from front and side views. (B) The same segmentation for the laboratory dataset. Note that the individual Purkinje cells are the same as for the synchrotron dataset and that the thick branches of the dendritic tree can already be resolved with the laboratory setup.

Cell Quantification in the Molecular and Granular Layer.

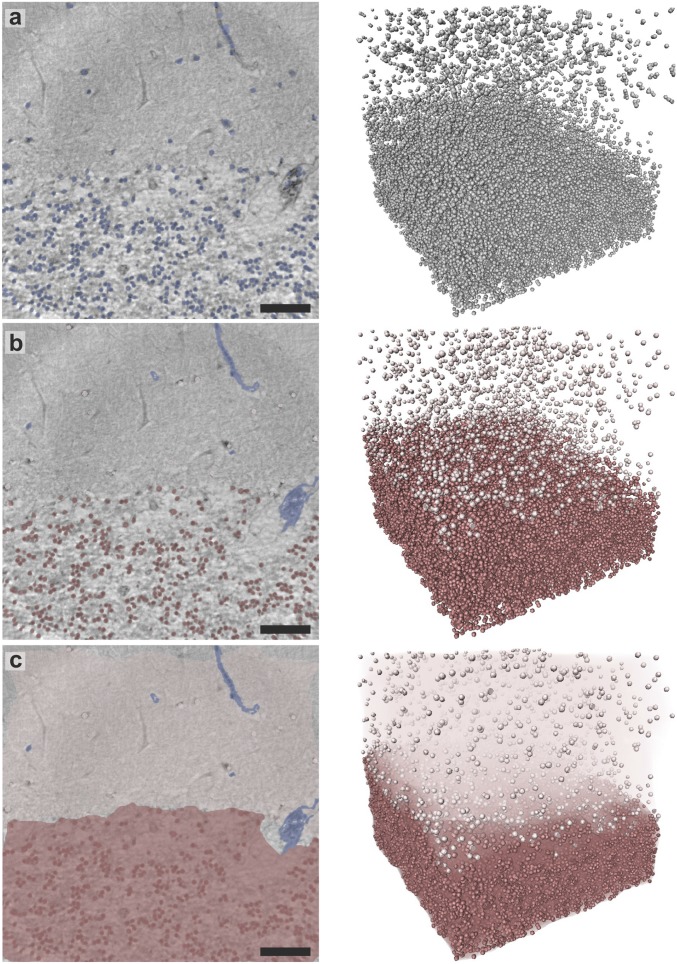
The output of the automatic cellular segmentation based on the spherical Hough transform is depicted in Fig. 3, both for an exemplary slice and for the entire volume. In total, the algorithm determined ∼40,000 cells in the granular and 1,700 cells in the molecular layer. To obtain a measure for cellular density, the volume of the two layers is estimated via an envelope around all cells contained in that layer (Fig. 3C). As a criterion for the separation between the low-cell molecular layer and the cell-rich granular layer the mean distance to the 35 nearest neighbors is used. The density is determined as $\rho =9.9\cdot 10^4$ mm⁻³ in the molecular layer and $\rho =2.7\cdot 10^6$ mm⁻³ in the granular layer. Note that this corresponds to the average density of the entire layer. In SI Appendix, Fig. S12, a local density estimation for the granular layer is depicted, showing large variations throughout the layer. The cell density is also found to decrease toward the molecular layer, resulting in a smooth transition between these two layers.

Fig. 3.

Results of the automated segmentation procedure, shown in an exemplary 2D slice through the reconstruction volume as well as in a 3D view. (A) Overlay of all cell nuclei detected by the algorithm (blue). (B) Result after manual removal of blood vessels (blue) and separation into ML (light red) and GL (dark red), based on the mean distance to the 35 nearest neighbors of each cell. (C) Volume estimation for each layer used for determination of the cell densities in the two regions. (Scale bars: 50 $\mathrm{\mu }$m.)

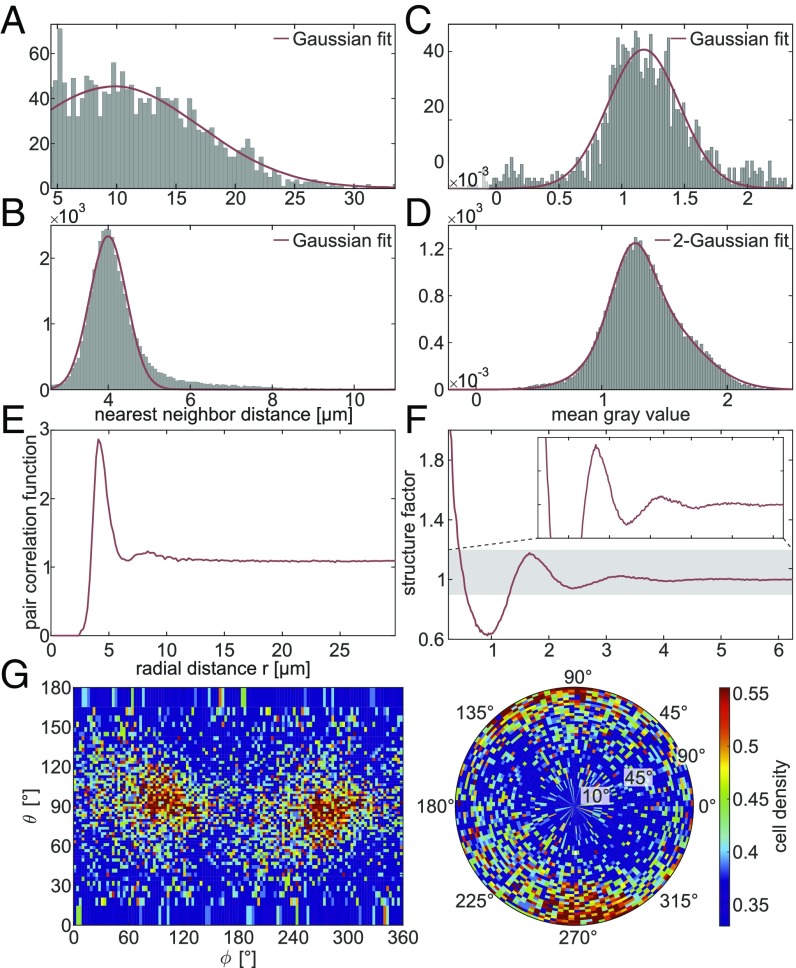
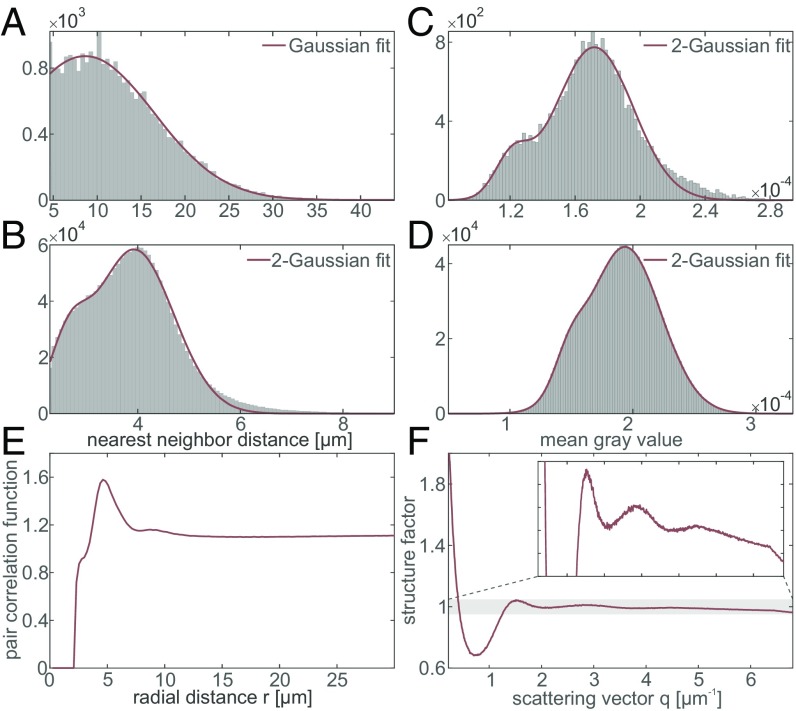
From the positions of the cell nuclei within the volume, several statistical measures can be determined (Fig. 4). The distribution of nearest-neighbor distances in the molecular layer (ML) and granular layer (GL) is shown in Fig. 4 A and B, revealing mean distances of $9.7\pm 0.8$ $\mathrm{\mu }$m (ML) and $4.00\pm 0.02$ $\mathrm{\mu }$m (GL). Considering the mean radius of cellular nuclei in the two layers (2.4 $\mathrm{\mu }$m in the ML and 2.1 $\mathrm{\mu }$m in the GL), this indicates that within the GL most of the cells have at least one neighboring cell in direct contact whereas in the ML the distance to the nearest cell is several cell radii larger. The mean gray value within the volume of a single-cell nucleus can be considered as a measure of electron density, as the reconstruction value is proportional to the sample’s real part of the refractive index. In Fig. 4C the corresponding histograms are shown, indicating that the cells of the GL are in general denser than the cells in the ML. The structural arrangement of the cells in the GL is further quantified by computing the pair correlation function and the angular averaged structure factor, as shown in Fig. 4 E and F. The correlation function shows two distinct peaks at $4.16\pm 0.04$ $\mathrm{\mu }$m and $8.5\pm 0.3$ $\mathrm{\mu }$m. Hence, the second correlation shell is about twice the distance of the first one, indicating a clustering, which can be confirmed by visual inspection. This is in line with the fact that the first nearest-neighbor distance $r_1=4.14$ $\mathrm{\mu }$m is significantly smaller than the mean internuclei distance computed from the density $r_m={\rho }^{-1/3}=7.2$ $\mathrm{\mu }$m. In contrast to a highly coordinated liquid or amorphous state, e.g., with coordination number 12 as for hard spheres, the coordination number of the present structure is ∼5, again indicating an arrangement in small clusters. Next, we investigate the angular distribution of interneuron distance vectors, going beyond the conventional assumption of isotropy in the computation of the pair correlation function (SI Appendix, SI Methods). Interestingly, we indeed observe a characteristic enhancement in the angular probability function along a director axis. This axis, indicating the predominant direction of neighboring neurons, lies within the plane of the dendritic tree of the Purkinje cells and parallel to the interface between the ML and GL (Fig. 4G). We have repeated the analysis chain for tissues of additional individuals, showing the same behavior (compare SI Appendix, Figs. S2 and S14).

Fig. 4.

Statistical measures obtained from the automatically determined cell positions. (A) Histogram showing the nearest-neighbor distances in the ML. The Gaussian fit reveals a mean nearest-neighbor distance of $9.7\pm 0.8$ $\mathrm{\mu }$m (95% confidence interval) with SD $\sigma =7.3\pm 0.8$ $\mathrm{\mu }$m. (B) Histogram of the nearest-neighbor distances in the GL, with a Gaussian fit indicating a mean of $4.00\pm 0.02$ $\mathrm{\mu }$m with SD $\sigma =0.45\pm 0.02$ $\mathrm{\mu }$m. (C) Histogram showing the mean gray value within the automatically detected cell volume in the ML. A Gaussian fit leads to $\left(1.17\pm 0.02\right)\cdot 10^{-3}$ with SD $\left(\sigma =2.9\pm 0.2\right)\cdot 10^{-4}$. (D) Histogram of the mean gray value in the GL. The shape is best fitted by a 2-Gaussian function with peak values of $\left(1.24\pm 0.01\right)\cdot 10^{-3}$ and $\left(1.6\pm 0.1\right)\cdot 10^{-3}$ and SDs ${\sigma }_1=\left(1.6\pm 0.1\right)\cdot 10^{-4}$ and ${\sigma }_2=\left(3.4\pm 0.1\right)\cdot 10^{-4}$ in an approximate ratio of 30:70. (E) Angular averaged pair correlation function of the cells in the GL revealing two distinct peaks at $4.16\pm 0.04$ $\mathrm{\mu }$m and $8.5\pm 0.3$ $\mathrm{\mu }$m. (F) Angular averaged structure factor of the cells in the GL. (G) Angular distribution of nearest neighbors in the GL, where $\theta \simeq 90^{○}$ corresponds to the plane in which the dendritic tree of the Purkinje cells is spreading and $\varphi =90^{○}$ is approximately parallel to the interface between the ML and GL (SI Appendix, SI Methods).

Next, we quantify the performance of the segmentation algorithm by comparison with a manual segmentation used as ground truth in several subvolumes of the whole dataset (SI Appendix, Figs. S6 and S7), yielding mean precision $p$ and recall $r$ values of $\left(p,r\right)=\left(0.89,0.98\right)$ for the ML and $\left(p,r\right)=\left(0.994,1\right)$ for the GL. This indicates an almost perfect performance of the automated segmentation algorithm. The small difference between the two regions can be explained by the higher diversity of shapes in the ML, making it more difficult to find a parameter set suitable for all cells (SI Appendix, Fig. S10).

Laboratory-Based CT with a Liquid-Metal Jet Source.

The laboratory measurements were carried out using a liquid-metal jet microfocus source with Galinstan as anode material (14, 16). A slice through the tomographic reconstruction of the dataset is shown in Fig. 1C. The results prove that even in the laboratory dataset single cells are resolved in all layers of the cerebellum. The magnified region in Fig. 1C, Right also reveals the large Purkinje cell where the thick branches of the dendritic tree can already be resolved. In Fig. 2B a cellular segmentation of the sample is shown, again via a semiautomatic approach for the Purkinje cell layer and the automatic approach based on the spherical Hough transform for the GL and ML (see SI Appendix, Fig. S5 and Movie S2, for more details and visualization).

To quantify the performance of the segmentation algorithm, the precision and recall are also determined for the laboratory dataset. As the manual segmentation proved to be challenging due to the lower resolution and signal-to-noise ratio, the automatic segmentation results from the synchrotron are considered as ground truth (SI Appendix, Figs. S8 and S9). The analysis yields a precision and recall of $\left(p,r\right)=\left(0.71,0.72\right)$ for the ML and $\left(p,r\right)=\left(0.85,0.93\right)$ for the GL. This shows that especially for the GL the performance of the algorithm is remarkably high and comparable to results obtained at synchrotron sources (8). In the ML around 26,000 cells were identified automatically whereas in the GL the algorithm found ∼1,760,000 cells, resulting in densities of 7.4$\cdot 10^4$ mm⁻³ and 3.4$\cdot 10^6$ mm⁻³, respectively. The deviation in the ML compared with the synchrotron results can be explained by the lower precision and recall for this layer. Contrarily, in the GL where precision and recall are high in both cases, the difference in the determined cell density must be attributed to the different probing volumes, as the synchrotron dataset probes a much smaller subvolume compared with the laboratory dataset. As can be recognized in SI Appendix, Fig. S13, the cellular density decreases when approaching the transition to the ML and the highest cell densities occur in the center of the GL. This indicates that the dataset recorded at the synchrotron comprises a less dense part of the GL, which explains the difference in overall cell density. To confirm this assumption, the cell density in the corresponding subvolume of the laboratory dataset is determined as well, resulting in 2.9$\cdot 10^6$ mm⁻³. This value deviates by about 11% from the synchrotron dataset, which is in agreement with the precision and recall values for this layer. The laboratory dataset also confirms that the grainy structure of the local density, resulting from a clustering of cells, persists throughout the entire GL. This is further visualized in SI Appendix, Fig. S13.

From the segmentation results the same statistical measures as for the synchrotron dataset are determined (Fig. 5). The mean cell radii for the ML and GL are 1.6 $\mathrm{\mu }$m and 1.5 $\mathrm{\mu }$m, respectively. The distribution of nearest-neighbor distances in the ML and the GL is shown in Fig. 5 A and B. An estimate for the relative electron density is given by the mean gray value within the volume of the single cells (Fig. 5 C and D). Note that in this case, this is an effective value due to the broad bremsspectrum of the laboratory source used for imaging and the contrast formation. Further, the reconstruction values correspond to a mixed contrast with a superposition of attenuation as well as phase effects. However, as this applies equally for the entire sample, a relative comparison between the two layers is still reasonable, indicating that the cells of the GL show a slightly higher electron density. The pair correlation function and structure factor of the entire GL are shown in Fig. 5 E and F. In the correlation function three maxima at $2.50\pm 0.05$ $\mathrm{\mu }$m, $4.74\pm 0.04$ $\mathrm{\mu }$m, and $8.7\pm 0.1$ $\mathrm{\mu }$m are visible, the first of which is only a very small modulation. This again indicates a characteristic local structure associated with the clustering of the cells in this layer, which is already visible in the local density shown in SI Appendix, Fig. S13. Note that the peak with the smallest radial distance has only a hardly recognizable counterpart in the synchrotron dataset, indicating that either these smaller cell distances are a property of the inner part of the GL, which is not inside the field of view of the synchrotron dataset, or this small feature is an artifact of falsely detected cells. Analogous to the synchrotron dataset, the angular distribution of nearest neighbors in the GL can be computed, which again shows that the majority of cells are distributed in parallel to the large dendritic tree of the Purkinje cells (SI Appendix, Fig. S3).

Fig. 5.

Statistical measures obtained from the laboratory dataset. (A) Histogram of the nearest-neighbor distances in the ML. The Gaussian fit reveals a mean nearest-neighbor distance of $8.6\pm 0.4$ $\mathrm{\mu }$m (95% confidence interval) with SD $\sigma =7.8\pm 0.4$ $\mathrm{\mu }$m. (B) The same histogram for the cells detected in the GL. A 2-Gaussian function with peaks at $3.93\pm 0.02$ $\mathrm{\mu }$m and $2.64\pm 0.02$ $\mathrm{\mu }$m with SDs ${\sigma }_1=0.77\pm 0.03$ $\mathrm{\mu }$m and ${\sigma }_2=0.35\pm 0.04$ $\mathrm{\mu }$m (approximate aspect ratio 86:14) fitted the data best. (C) Histogram of the mean gray value within the volume of a single cell. The 2-Gaussian fit leads to peaks at $\left(1.72\pm 0.01\right)\cdot 10^{-4}$ and $\left(1.21\pm 0.02\right)\cdot 10^{-4}$ with SDs ${\sigma }_1=\left(2.4\pm 0.1\right)\cdot 10^{-5}$ and ${\sigma }_2=\left(1.1\pm 0.2\right)\cdot 10^{-5}$ and an approximate weight ratio of 90:10. (D) Histogram of the mean gray values within the detected cells of the GL. The 2-Gaussian fit reveals peaks at $1.936\pm 0.001\cdot 10^{-4}$ and $1.483\pm 0.001\cdot 10^{-4}$ with SDs ${\sigma }_1=\left(2.92\pm 0.01\right)\cdot 10^{-5}$ and ${\sigma }_2=\left(1.23\pm 0.02\right)\cdot 10^{-5}$ (approximate aspect ratio 90:10). (E) Pair correlation function of the cells in the GL with the two principle peaks at $4.74\pm 0.04$ $\mathrm{\mu }$m and $8.7\pm 0.1$ $\mathrm{\mu }$m and also a minor modulation at $2.50\pm 0.05$ $\mathrm{\mu }$m. (F) Structure factor of the GL.

Discussion

The present work shows that propagation-based phase-contrast tomography can be used for virtual histology of paraffin-embedded unstained human brain tissue, digitalizing 3D volumes with isotropic resolution and subcellular detail. In contrast to classical histology the 3D density maps can be virtually sliced in every possible orientation, and much larger volumes can be sampled. The optimized compact laboratory tomography setup and image reconstruction pathway make this method also available for a broad range of studies which cannot easily be carried out at large-scale synchrotron facilities, for example because they require continuous availability. Ongoing technological progress both in source and in detection could substantially decrease scanning time at the laboratory and pave the way for biomedical studies requiring a large number of samples. Note that by carefully adjusting the geometrical parameters of the setup, comparable results can also be obtained at microfocus sources with a larger source diameter (SI Appendix, Fig. S15), enabling the implementation of 3D virtual histology at the laboratory scale even with quite standard commercial instrumentation.

The demonstrated data quality enables automatic cell segmentation of up to millions of neurons in millimeter-sized tissue. This allows for the analysis of 3D cell distributions and their spatial organization with high statistical significance and for a large number of specimens as required for biomedical studies. The distribution of cells in the GL exhibits average densities in good agreement with manual cell counting in 2D histological sections (23), but in addition shows a strong short-range order leading to a local clustering of cells accompanied by characteristic positional correlations as quantified by pair correlation functions. The large amount of different statistical measures which can be inferred from the location of neurons enables approaches to correlate tissue function with structure and possibly also the identification of structural biomarkers for diagnostic or research purposes, e.g., in the course of neurodegenerative diseases or tumor growth. The capability to study cellular distributions in 3D allows for a precise quantification of nearest-neighbor distances or pair correlation functions. This information is not accessible from thin histological sections without additional assumptions (24). In the present example this has enabled us to observe anisotropies governed by the principle directions of the Purkinje cell layer and interface which persist deep in the granular layer. This could possibly be explained by an optimized morphology for the projections of granule cells to the Purkinje cell dendrites.

Materials and Methods

Sample Preparation.

Formalin-fixed and paraffin-embedded cerebellar tissue obtained at routine autopsy in agreement with the ethics committee of the University Medical Center Göttingen was studied. For CT experiments, a 1-mm punch was taken from the embedded tissue and mounted in a Kapton tube which was glued to a sample holder (Fig. 1A).

Synchrotron Setup (P10@PETRAIII).

A sketch of the main components of the GINIX setup (20), installed at the P10 beamline of the PETRAIII storage ring at Deutsches Elektronen-Synchrotron (Hamburg), is shown in SI Appendix, Fig. S4A. The X-rays are generated by an undulator and monochromatized to an energy of 8 keV by a Si(111) channel-cut monochromator. Subsequently, the X-rays are prefocused by a pair of Kirkpatrick–Baez (KB) mirrors to an approximate size of 300 $\times$ 300 ${\mathrm{n}\mathrm{m}}^2$ and coupled into an X-ray waveguide placed in the focal plane (25). This leads to a smooth illumination with increased spatial coherence, as well as a secondary source size below 20 nm (bidirectional). Farther downstream, the sample is placed on a fully motorized sample stage which allows for a precise alignment of the sample’s region of interest into the field of view. Approximately 5 m behind the sample a scintillator-based fiber-coupled scientific CMOS detector with a pixel size $p=6.5$ $\mathrm{\mu }$m (2,048 $\times$ 2,048 pixels; Photonic Science) is placed. Due to the geometrical magnification of the setup, the effective pixel size can be tuned by varying the source-to-sample distance $z_1$. Together with the sample-to-detector distance $z_2$ this leads to a geometrical magnification of $M=\left(z_1+z_2\right)/z_1$ and therefore an effective pixel size $p_{\text{eff}}=\frac{p}{M}$. Detailed information about experimental parameters is listed in SI Appendix, Table S1.

Data Processing (P10).

Phase retrieval was performed with the contrast transfer function (CTF)-based algorithm proposed by Cloetens et al. (2, 26) on all empty-beam corrected projections. The different effective pixel sizes in the images due to the changing source-to-sample distances are accounted for by scaling all images to the one with the smallest effective pixel size, aligning them to each other, and cropping them to the same field of view. Before tomographic reconstruction, a simple ring removal algorithm was applied (27). The 3D information was reconstructed by using the Matlab (Mathworks) integrated function iradon with a standard Ram-Lak filter. The 3D visualization of the reconstructed data was carried out with Avizo Lite 9 (FEI Visualization Sciences Group). For the segmentation of the Purkinje cells, the Magic Wand tool, using a gray-value–based region growing algorithm, was applied. As smaller structures could not be segmented automatically with this tool due to a comparably low signal-to-noise ratio, the segmentation was manually refined.

Laboratory Setup.

A sketch of the laboratory setup is shown in SI Appendix, Fig. S4B (14–16). It consists of a liquid-metal jet microfocus X-ray source (Excillum) with Galinstan as anode material, yielding a characteristic photon energy of 9.25 keV (Ga-$K_{\alpha }$). It was operated at 40 kV acceleration voltage with an electron power of 57 W at a projected focus size of $10\times 10$ μm² (FWHM). As in the case of the synchrotron setup the sample is placed downstream on a fully motorized sample tower. Behind the sample a scintillator-based lens-coupled CCD detector with a pixel size of 0.54 $\mathrm{\mu }$m is located (2,504 $\times$ 3,326 pixels; Rigaku). Due to the high resolution of the detector, the sample is placed in close proximity so that source blurring effects can be minimized (14, 16). The experimental parameters are listed in SI Appendix, Table S1.

Data Processing (Laboratory Setup).

Phase retrieval was performed with the Bronnikov aided correction (BAC) algorithm (28) on all empty-beam corrected projections. The tomographic reconstruction was carried out via the cone-beam reconstruction implementation of the ASTRA toolbox (29, 30). For a better signal-to-noise ratio, all projections were resampled by a factor of 2 before tomographic reconstruction and the tomographic slices were filtered with a Gaussian filter with a SD of 1 pixel. The 3D visualization was performed the same as for the synchrotron data.

Automatic Cell Segmentation.

The automatic cell segmentation is based on the spherical Hough transform which is designed to find (imperfect) spheres of varying radius in a 3D dataset. Here, a slightly modified version of the Matlab implementation by Xie was used (31), based on the algorithm published in ref. (22). More information on the algorithm can be found in SI Appendix, SI Methods.

Erythrocytes, which are contained in the blood vessels, are of similar size to that of the granule cell nuclei (SI Appendix, Fig. S11) and are therefore segmented as well. To remove these false positives, they are manually excluded from the automatic segmentation. In the future, vessel segmentation based for example on the Frangi filter (9) could be used to automatize the identification of these regions. For the division into ML and GL, the mean distance to the 35 nearest neighbors was chosen as a measure and the threshold was again set based on visual inspection. The volume of each of the layers, used for the calculation of the cell density, was determined via the Matlab-implemented function boundary which determines a 3D hull enveloping all cells contained within the ML or GL. This function also enables the choice of a shrinking factor, where 0 gives a convex hull and 1 gives a compact boundary. Here, the standard shrinking factor of 0.5 was chosen.

The nearest neighbor was determined by calculating all cell-to-cell distances and finding the minimum for each individual cell. For the mean gray value, the values of the pixels contained in each single cell were summed up and divided by the corresponding cell volume. A pixel was included if its radial distance to the center pixel was smaller than the radius. The pair correlation function was calculated by counting the number of cells in a spherical shell of a given radius and 0.5-pixel width around a single cell in the GL and averaging this over all cells. For the structure factor the angular average over the 3D Fourier transform of the array containing the center positions of each sphere was computed. The procedure for determining the angular distribution of neighboring cells in the GL is described in SI Appendix, SI Methods.