Bayesian Communication

Abstract

Abstract Objective: To develop a model for Bayesian communication to enable readers to make reported data more relevant by including their prior knowledge and values.

Background: To change their practice, clinicians need good evidence, yet they also need to make new technology applicable to their local knowledge and circumstances. Availability of the Web has the potential for greatly affecting the scientific communication process between research and clinician. Going beyond format changes and hyperlinking, Bayesian communication enables readers to make reported data more relevant by including their prior knowledge and values. This paper addresses the needs and implications for Bayesian communication.

Formulation: Literature review and development of specifications from readers', authors', publishers', and computers' perspectives consistent with formal requirements for Bayesian reasoning.

Results: Seventeen specifications were developed, which included eight for readers (express prior knowledge, view effect size and variability, express threshold, make inferences, view explanation, evaluate study and statistical quality, synthesize multiple studies, and view prior beliefs of the community), three for authors (protect the author's investment, publish enough information, make authoring easy), three for publishers (limit liability, scale up, and establish a business model), and two for computers (incorporate into reading process, use familiar interface metaphors). A sample client-only prototype is available at http://omie.med.jhmi.edu/bayes .

Conclusion: Bayesian communication has formal justification consistent with the needs of readers and can best be implemented in an online environment. Much research must be done to establish whether the formalism and the reality of readers' needs can meet.

Over the past 30 years, the National Library of Medicine has promoted the use of the research literature by clinicians.¹ The movement of evidence-based medicine has gone even further in advocating that rational therapeutics be based on an intelligent reading and use of the literature.² Unfortunately, the language for statistical discourse that medicine has used for the past 80 years is derived from other domains—industrial statistical quality control and decision making for research and populations. Clinicians' needs to make decisions regarding individuals do not fall within those domains, so clinicians have labored under a handicap in being forced to speak a language that does not apply to them.

A reader of a report of a clinical trial wants to know, “How should I, as an individual clinician with a specific practice and a specific set of clinical experiences, respond to a study's published data?” Or, how do I apply the generalities of the paper to my specific situation? An answer might be, “Given what you've said about your local experience and concerns, it makes sense to wait for more results,” or “Given your uncertainties, stick with current practice,” or “Unless your experience is that the mortality is above the following threshold, you should use the new treatment.”

As a running example through this paper, consider the following. You are a pediatrician caring for premature infants in a Level III neonatal intensive care unit. You know that appropriate oxygenation is a key goal of care, and that hyaline membrane disease is a major cause of mortality and morbidity. Beyond current standard of care, you are interested in whether novel treatments are beneficial. You read an article by Konduri and colleagues,³ which says that adenosine is beneficial. Should you use the new treatment? Current evidence-based medicine frameworks⁴ would have you evaluate the internal validity and the general representativeness of the study as well as its applicability to your situation. As part of the evaluation of internal validity, you are given quantitative answers to these questions only through heuristics—e.g., P values and confidence levels. In fact, the P value in the adenosine study is “significant,” with P < 0.05. If you are like most readers, you are not sure what this really means. You know it means that less than 1 in 200 times, the conclusion is wrong, and you understand that that seems like a low risk across a population of studies and technologies. But this may be too population-oriented⁵ for your comfort. Is this one of those times? The study had only 18 patients. Does your own background knowledge about hyaline membrane disease in general, or adenosine in particular, affect your take-home message?

Our concern, from an informatics point of view, is to consider what formal methods there might be for providing the types of answers readers desire and to consider the role that information technology might play in that implementation.

Bayesian communication^{6,7,8,9,10,11,12} is the formal process best suited to provide a grounding for these answers. It is the process where a reader is encouraged to express prior beliefs regarding a research study of interest, and where the posterior beliefs and their implications are calculated as a function of the prior beliefs and the study data. The formally derived implications of those posterior beliefs are presented to the reader so as to provide the answers desired by the reader.

In this paper, we lay out the specifications for Bayesian communication. In so doing, we show how a Web-based implementation can satisfy the specifications. Although the general concept is old,^13,14 it is only with the nascent World Wide Web that the promise can be elaborated, tested, and fulfilled.

Background

The statistical measures currently presented to medical readers¹⁵ and at the heart of clinical epidemiology fall within the framework of frequentist statistics, where probability is defined as the frequency of numerator events divided by the frequency of denominator events. Communication focuses on sufficient statistics—the minimal summary of the data needed for inference (e.g., arithmetic mean summarizes the data for inferring the mean of a population)—and functions of the sufficient statistics, like t tests. A key statistical goal is to provide inference from the observed data to unobservable parameters of interest that describe a problem. The frequentist interpretation helps in the analysis of many datasets and in some population-oriented settings, but breaks down when attempting to provide at least three key epistemologic functions of statistical measures: a sense of how well the data support one hypothesis over another,^16,17 the likelihood of a hypothesis on the basis of the data, or a recommendation for action.

Most Bayesian statisticians^{11,18,19,20,21} view probability as a measure of belief. Linked to an action threshold, the probability can be used to define action.^22,23

The heart of Bayesian statistics is the Likelihood Principle,^24,25 which states that the only statistic—summary of data—needed for inference regarding hypothesized parameters is the likelihood function,

P (observed data | different values of the parameters of interest)

which is thus a function of the parameters and not of the data. The likelihood function has a number of important properties:

• It captures the statistical model that the statistician has determined is the best for the problem and the data under consideration.

• It is a function of the parameters.

• It is a function of data that were observed only, unlike the P value, which depends on data not observed.¹⁷

• It can be combined with prior knowledge of the parameters to result in posterior belief in different values of parameters: posterior P (parameter values | observed data) is proportional to the likelihood function × prior P (parameter values).

In Bayesian communication, the author provides the reader with the appropriate likelihood function, the reader provides prior belief and threshold values, and the machine calculates the implications.

Research in Bayesian methods has burgeoned in the past 15 years, including their application to clinical trials.²⁶ Some classical clinical trials have been re-examined in the Bayesian light. We shall refer several times to Brophy and Joseph's re-analysis²⁷ of the GUSTO thrombolytic trial comparing streptokinase to t-PA (tissue plasminogen activator).

Methods of communicating with the final consumer of the research have not received commensurate attention. In fact, a review of Bayesian textbooks, review articles, and primary research articles^* shows that these sources discuss statisticians, clients, and decision makers (in general terms), but almost never refer to the readers of the article finally produced. Even software that is widely distributed to teach statistics³⁸ or to make analysis more accessible³⁹ is aimed at statisticians and not at consumers of research results.

There are exceptions. Hildreth¹⁴ raised the issue explicitly 35 years ago and offered paper-based graphs that would work as nomograms: The reader finds his prior belief on the x-axis, and the curve shows the corresponding posterior belief. Dickey⁴⁰ provides a similar tactic. Hilden⁴¹ together with Habemma,⁴² laid out a decision-analytic framework for a reader's use of clinical research data. The framework has not, to our knowledge, been implemented or evaluated. Lehmann^43,44,45 designed and implemented a similar approach, focusing on the reader's desire to take into account threats to internal validity. Hughes⁴⁶ reviews the statistical methods for reporting Bayesian analyses.

There are a few current efforts in line with our agenda. Sim's trial banks⁴⁷ represent a model of storing methodologic information and the data themselves, using an ontology based on the work of inferring knowledge from clinical trials. McLellan⁴⁸ writes that she looks forward to seeing “results that are available on demand in both graphic and tabular form” and “statistical methods that are linked to a short description of the tests' mechanics and appropriate uses,” two helpful desiderata.

Formulation

We present our model as specifications in terms of the participants: readers, authors, publishers and computers. Authors include the investigators and the statistical analysts. Readers include professional literature synthesists,⁴⁹ opinion leaders,⁵⁰ academic clinicians, practicing clinicians, and patients. Publishers include the editors and publishers (professional societies and commercial organization).

The details of our specifications are derived from literature review and from our experience in the PIERRE^† project, trying to implement a Web-based environment for Bayesian communication. Soundness and completeness have been assessed through presentations to statistical colleagues and through ongoing user interaction.

Model Description

The specifications for readers (#1 to #8) and authors (#9 to #11) and a comparison of implementations in the Bayesian and evidence-based medicine paradigms, presented in ▶, serve as an index for this discussion. Specifications for publishers (#12 to #14) and for computers (#15 to #17) are provided in the text only.

Table 1.

Specifications for Readers and Authors, and Comparison of Bayesian and Evidence-based Medicine Implementations

Specification	Bayesian Communication*	Evidence-Based Medicine
1. Express prior knowledge	Assess prior beliefs; sensitivity analysis for uncertainty in prior (F)	—
2. View effect size and variability	Mean of posterior beliefs; contaminated models for surprise (F)	Point estimate (F); confidence interval (H)
3. Express thresholds	Minimally clinically important difference (F if based on utilities)	Number needed to treat (H)
4. View inferences	Tail probability, credible set, Bayes factor, equivalence (F)	Post-hoc adjustments (H)
5. Receive explanations	Dynamic algorithms based on influence diagrams (F)	Static textbook explanations (H)
6. Evaluate study and statistical quality	Likelihood debiasing (F)	Quality inventories (H)
7. Synthesize multiple studies	Confidence profile method, Bayesian meta-analysis (H)	Meta-analysis; Cochrane trial banks (F)
8. View beliefs of the community	Archived priors (F)	Postpublication peer review (H)
9. Protect authors' investment	Likelihood function (F)	Sufficient statistics (F)
10. Provide enough information	Information defined by decision problem (F)	Sufficient statistics, Outcomes research (F)
11. Make authoring easy	Applet libraries	Current program of education and tool-provision

^*F indicates formal solution; H, heuristic.

Readers' Specifications

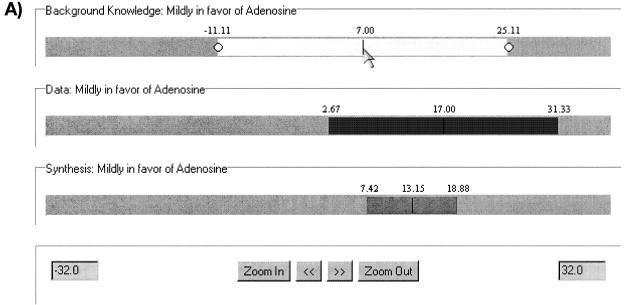
Specification 1: The reader shall express prior belief. Some clinicians have referred to this sort of knowledge as “external,” “background,” or “consistent with previous results.” Conventional approaches forbid the formal inclusion of this knowledge, while the Bayesian approach necessitates that it be put into the form of a prior probability. For instance, if the clinical question is whether to use adenosine in treating neonates with respiratory distress, as discussed earlier, then the key parameter is the true difference in arterial oxygen tension (P_O2) that results from adenosine compared with nontreatment or placebo (saline). The reader must think, based on prior knowledge, what that difference might be. If she feels skeptical, she can say that the difference is negative, meaning that placebo is better. Or she might want to be skeptical, but not much so. This translates into a probability distribution for the difference with a negative mean and a modestly wide standard deviation. Alternatively, she might want to plead ignorance, insisting that the data drive her belief. An example of a relatively ignorant but nonskeptical prior belief would have the prior difference be 7 mm Hg partial pressure of oxygen (i.e., adenosine is given the benefit of the doubt), but with a standard error of 9 mm Hg, which gives a prior confidence interval (see Specification 4 of -11 to +25 mm Hg, quite a large range.^‡ The art of computer-based prior assessment is in helping the user to translate these verbal notions into a quantitative assessment.

Can readers express their belief in terms of probabilities? There is a fair literature on calibration that suggests that physicians can be calibrated through training^51,52 or through experience. Our own data (unpublished) on 825 microbial culture predictions by pediatric residents suggest that, untrained, residents' predictions between 20 and 80 percent are calibrated, but, as others have shown, they are overconfident for high probabilities and underconfident for low.⁵³ (Note that Keren⁵⁴ shows that these errors at the extremes may be an artifact of calculation.) There is also a fair literature on assessment of prior beliefs.^{55,56,57,58,59,60} Few investigators have tested the abilities of general readers to express their prior beliefs.

A source of prior belief available only through information technology is the local computer-based patient record (CPR)—in particular, the data warehouse that preserves across-patient data. One can imagine an environment in which the clinician can use proportions from the data warehouse (e.g., What is my local experience with neonatal mortality for different arterial oxygen partial pressures?) as an anchor to form a prior belief and to estimate a certainty in that prior belief.

Orthodox Bayesian tenets would say that prior belief ought to be assessed before the data are viewed. This sequence is impractical because, first, the reader will become involved in a Bayesian interaction only after having seen at least an abstract of the target paper. Second, although it introduces anchoring bias,⁶¹ the user will probably want to see the data to understand the nature of the assessment involved.

Is a Bayesian approach necessary for representing prior knowledge? Classical statisticians have raised the importance of prior, external knowledge in assessing the implications of research but have no formal way of doing so. For instance, leading analysts of clinical trials, Peto et al.⁶² point out that the interpretation of the P value depends on whether, based on prior knowledge, a claim is “reasonable” or whether the reader is “skeptical.” However, they do not give formal guidelines for assessing that prior belief or integrating it with the calculated P value, so as to find the claim “convincing,” on the one hand; to remain “almost as skeptical as before,” on another; or to “change your mind,” although “you would still retain a secret little doubt,” on the third.

Specification 2: The reader shall view the effect size and its variability. The effect size is the magnitude of the difference between posterior estimates of parameters of interest and is derived directly from the posterior probability distributions of the parameters of interest. The variability, certainty, or precision in the estimate is also derived directly from the posterior probability. For instance, if the data show a difference of 17 mm Hg between adenosine and saline (i.e., adenosine is apparently better) and the prior belief is as suggested in Specification 1, then the posterior effect size is 13—not as effective as the data say, but more effective than the prior belief. Brophy and Joseph's paper²⁷ focus on effect size.

Statisticians have advocated for decades the use of confidence intervals (which get at variability) rather than P values, to ensure that readers would see estimates of the effect size.^63,64,65 Clinical epidemiologists are advocating the use of other measures,⁶⁶ including numbers needed to treat,^67,68,69 as a more interpretable measure of effect size. Still other authors have gone beyond purely probabilistic measures to consider the desired effect size as a quantity to assess separately from the data.^70,71,72,73 For instance, Braitman⁶⁵ suggests that the reader inspect the limits of the confidence interval before making his decision. However, few of these authors give explicit guidelines on how to evaluate the endpoints of the confidence interval or how to arrive at the desired effect size. Recent exceptions are attempts by Naylor and Llewellyn-Thomas⁷⁴ and Redelmeier et al.⁷³ to base the clinically important difference on a formal, patient-based method.

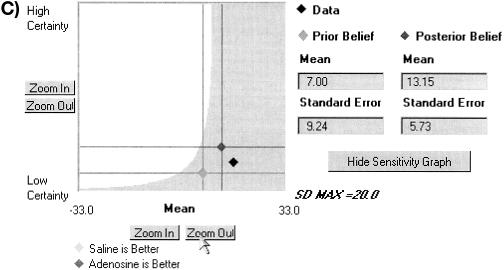
Specification 3: The reader shall express thresholds involved in making a clinical decision related to the target article. Tradeoffs are crucial in interpreting research results. Decision analysis is a formal approach for addressing tradeoffs and is inextricably linked to Bayesian statistics.²⁵ Hilden alone⁴¹ and with Habemma⁷⁵ provides a framework based on decision analysis for applying results of clinical trials to clinical care. Introducing formal utility assessment into the process of reading a paper goes beyond the scope of the present paper, but thresholds are well defined: they are points above which one action is preferred and below which another action is preferred, and they are functions of assessors values. A reader might say, for instance, that if adenosine did not raise the P_O2 10 mm Hg higher than did saline, then she would not consider using it, because the potential risks are not significantly outweighed. Brophy and Joseph²⁷ call this the threshold of “clinical superiority.”

Chinburapa and Larson⁷⁶ surveyed 527 physicians to document that, while physicians in different practice settings agreed about the incidence of drug side effects, they differed about whether they would prescribe the medications, indicating that different physicians trade off drug efficacy against drug side effects differently. Churchill et al.⁷⁷ explicitly assessed patients' values in terms of time tradeoffs but defined a difference in time of 10 percent maximal time to be “clinically significant,” without indicating why the 10 percent number was used. “Number needed to treat” has become a popular way of generating a measure that clinicians could use to judge whether to act on research results.⁶⁷ Riegelman and Schroth⁷⁸ provide a measure that ties together numbers needed to treat (NNT) and explicit assessments of tradeoffs. Moher et al.⁷⁹ and Lindgren et al.⁸⁰ stress that the desired effect size should be explicitly considered as part of study design, prior to data collection. Both these authors and those advocating NNT view their measures as a way of dealing with the tradeoffs involved in deciding to use novel therapies. Other researchers have begun focusing on the minimal clinically important difference (MCID),⁷³ another term for threshold and the reciprocal of NNT, when focusing on rates.

Specification 4: The reader shall make inferences based on the posteriors. The power of the Bayesian paradigm is the freedom in devising measures—functions of the likelihood function—that embody questions that users have, but with a formal justification. For instance, the P value is often interpreted as the probability that the true difference is greater than some threshold. This last probability actually describes the tail probability of a posterior probability: P (θ > δ) ≥ α, where θ is the parameter of interest, like the true difference between experimental and control treatments, δ is a threshold value, and α is a threshold probability value. If δ were zero, this measure would express how likely it is that experimental treatment is better than control, given the data and prior belief.

Thus, a result might be that the posterior probability that the difference between adenosine and saline is greater than zero (i.e., that adenosine is better than saline) is 0.989. If our threshold probability is 0.95, then we would conclude that adenosine is, in fact, better.

Clinicians want to know how likely it is that the true effect lies between two specific numbers, which is how they misinterpret confidence intervals. This desideratum exactly defines the Bayesian credible set—{a, b | P(θ ∈ [a,b]) ≥ α}—often called the Bayesian confidence interval. Thus, in our running example, the result would be that, in light of prior belief and the data, there is 95 percent probability that the true difference lies between an improvement of +7.42 and +18.08 mm Hg.

Readers want to know how likely one hypothesis is compared with another (usually a null hypothesis). The relative betting odds⁶ or Bayes factor^81,82,83 formally provides exactly this measure—P(H₀ | data)/P(H_A | data), where H₀ is the null hypothesis and H_A is the alternative. In our example, if we take as the traditional null hypothesis that the difference is zero, and as the alternative that adenosine is better (greater than zero), we get a small probability of about 0.001 around zero, and a probability of 0.999 for differences greater than zero, for a Bayes factor of 0.001—that is, 1000 to 1 against the null hypothesis. This is very different from a P value of 0.001, which can give a Bayes factor no higher than 50 to 1 against the null hypothesis with a sample size of 20 or so.¹¹

On the opposite side of demonstrating difference, readers want sometimes to be convinced that two treatments are equivalent. This is the hypothesis that θ ∈ [-δ, +δ]. If we use the threshold of 10 mm Hg, we find that the probability of equivalence is 0.28. With a probability threshold of 0.95, we would conclude that the treatments are not equivalent.

We are familiar with the ubiquitous phrase, “further research needs to be done,” yet we are also aware that research is often performed after the validity of an effect has been demonstrated.^84,85 Two formal measures can help in this assessment: prospective sample size⁸⁶ (the number of subjects that would be needed to change a conclusion) and expected value of information.²³ Explication of these measures is beyond the scope of this paper.

Although orthodox Bayesian analysis would insist that only one prior belief be assessed and used, this approach is not practical, if only because the novelty of the Bayesian approach may make some users skittish. Sensitivity analyses can be used to manage that uncertainty. By viewing what sets of prior beliefs result in the same decision, the reader can decide whether the extra effort to be more certain will provide any gain. Thus, if we felt uncertain about specifying one prior belief in adenosine but we were sure that adenosine would not raise the P_O2 5 mm Hg or more than would saline, then we would conclude that adenosine is not better, because all those prior beliefs result in a posterior value less than 10 mm Hg, our threshold of clinical significance.

All these measures or functions need a dynamic, computational environment.

Specification 5: The reader shall get an explanation of the results. The problem of explanation is as old as the first rule-based expert systems.⁸⁷ In Bayesian communication, there are two levels of explanation. First, the unfamiliar Bayesian paradigm must be explained, for instance, through a hyperlinked glossary or tutorial. The reader will want, more specifically, an explanation of why the posterior probability is as it is or why the inference turned out in a particular way. The explanation might be “the tail probability is less than your desired certainty level of 95 percent because your prior certainty was very low.” A higher-level explanation might also contain some suggestions like, “Because the posterior mean is so far away from your prior mean, you might be surprised by the results.” The model we are using assumes that data always make you more certain. If we want to find out how surprising results are, we must take alternative approaches⁸⁸ that are beyond the scope of this paper.

Specification 6: The reader shall be able to evaluate study and statistical quality. Advocates of evidence-based medicine have advocated assessment of study quality for decades, and some such assessment is included in every meta-analysis. In these venues, the quality assessment generally results in an ad hoc adjustment after the formal measures are calculated. The Bayesian strategy is to incorporate study quality issues into the statistical model of the analysis, and therefore into the likelihood function. David Spiegelhalter has called this likelihood debiasing (oral communication, 1988). Lehmann and Shachter⁴⁵ used this strategy in building THOMAS. Eddy⁸⁹ shows how to discount dubious data in a formal manner. Both these methods involve reviewing and modifying the statistical model of the study in the course of reading the paper.

Specification 7: The reader shall be able to synthesize the results of multiple studies. The “reader” is more likely to be a literature synthesist or opinion leader than a clinician. Like confidence intervals and other statistical techniques, however, meta-analysis⁹⁰ does not address tradeoffs. The Cochrane Collaboration⁴⁹ addresses tradeoffs implicitly by having the Metaview computer tool lay side by side evidence for different aspects of clinical problem, leaving to the reader the task of integrating benefits and burdens.

Bayesian meta-analysis is a growing field.^12,32,89,91 Because the technique is flexible, statistical models can be constructed that reflect concerns difficult to include in conventional models, such as interstudy correlation. However, because of this flexibility, design and implementation are more complex than for the single study.

Specification 8: The reader shall be able to view the prior beliefs of the community. Postpublication peer review^92,93 is increasingly important and is viewed by many authors as a unique aspect of Web-based publishing that has the potential to change the very nature of scientific communication.⁹⁴ The Bayesian form of this is to express those peer opinions in a formal way, as prior probabilities, thresholds, and likelihood debiasing submodels. A reader viewing those values can judge the extent to which her own opinion differs from others. Although this may bias the reader, this specification is an extension of Specification 1, in which community belief is used to inform the individual's assessment of her own prior belief. A value added by such communal priors is that researchers will have a better sense of how to aim their studies, since their sample size calculations implicitly incorporate prior belief.

Authors' Specifications

Recall that “author” refers to both the investigators and the analysts.

Specification 9: Authors' intellectual investment shall be protected. The power and ease of Internet-based publication will place pressure on authors to make their raw data available over the Web; we might call this “full-data publishing” to parallel full-text publishing. More than ten years ago, there was interest in making the data available for all federally funded clinical trials.⁹⁵ The pressure is mounting now. For instance, Bero⁹⁶ writes that “with a click of the mouse button, the real data behind the tables could appear and readers will be able to critically appraise a paper on the basis of more complete information.” Reflecting this pressure, a legislative bill has already been introduced in the Senate to induce investigators to make their data publicly available.⁹⁷

Full-data publishing is problematic in three ways. First, it puts the load of the interpretive work on the reader, who may not have the skills necessary for the analysis and who will probably, therefore, arrive at faulty conclusions. Second, full-data publishing ignores the value added to the data by the analyst's profound understanding of the dataset and by the implicit decisions made by the analyst in selecting the appropriate statistical model for the data. Third, it may violate rights of intellectual property ownership.

The Bayesian paradigm provides a middle way. By posting the likelihood function, a statistician communicates exactly the decisions made in analysis, and an author limits the secondary analyses that a reader can make. Of course, the authors can choose to post the data as well.

Specification 10: Authors shall publish enough information for the reader to draw a conclusion. At a low level, this specification means that the proper statistics must be reported. The sufficient statistic for data that are not normally distributed is not always the mean. For hospital length of stay, for example, the sufficient statistic for this skewed population is the geometric mean of a sample. At a higher level, this specification means that more than just a sufficient statistic—for drug efficacy, for instance—must be provided, such as information about side effects and other important components of tradeoffs. The Bayesian paradigm, by making trade-offs and decision making explicit, challenges authors to provide this information.

Specification 11: Authors shall have tools to make Bayesian publishing as easy as possible. Since the Bayesian paradigm has its own problems of diffusion and infusion within statistics, let alone content areas like medicine, it is reasonable to make it easy for Bayesian nonsophisticated publishers to use the paradigm. This means that tools must be easily available to help authors to translate their data analysis into the Bayesian paradigm. At the least, this specification suggests the need for an accessible library of models and applets. At the most, it suggests the creation of expert, intelligent aids.

Publishers' Specifications

Recall that, by “publisher,” we refer both to academic societies as well as to commercial enterprises.

Specification 12: Publishers shall not be held liable for actions taken by readers. Or, “Readers should not cheat.” A major impetus for the statistics we have now is the warrant they make for “objectivity.”^98,99 Subjectivist Bayesian communication seems to work against that objectivity. A criticism of Bayesian communication is that it appears to permit the reader to manipulate her prior belief in different applications of research results to lead to answers she desires, rather than to answers that are true. This specification is placed here because the professional society wants to maintain the scientific integrity of its reports and the publisher does not want to face legal liability if decisions are made on the basis of a reader's manipulation of the data.

One technical method of dealing with this critique is to have the applet create an audit trail of the reader's prior beliefs. But this method may violate the reader's autonomy and civil liberties.

Specification 13: The publication solution shall be general enough to scale up to entire libraries of research studies. Although it is unrealistic in the short term, we should design this eventuality into the original specifications.

Specification 14: The publisher shall be rewarded for providing the extra information and interactivity that goes along with Bayesian publishing. A business model that takes into account the community of priors and the extra tools used in Bayesian communication must be established.

Computer Specifications

Two lower-level specifications speak to how Bayesian communication should be implemented.

Specification 15: The Bayesian interaction shall be part of the reading process. The purpose of this specification is to ensure that we go beyond creating Bayesian calculators,³⁸ that simply perform the arithmetic. Work in expert systems over its first two decades showed that stand-alone systems will not be used.^100,101 Decision support systems (as Bayesian communication most assuredly is) must be sited in day-to-day activity.

Specification 16: Prior belief shall be assessed (and posterior belief shall be displayed) using interface metaphors that are familiar to the reader. Possible metaphors include graphs of distributions (like those of Brophy and Joseph²⁷), bars similar to confidence intervals, expressing certainty in terms of the number of patients previously treated.²⁶ The challenge here is to match interface elements to Bayesian concepts, and the need is for novel elements that are, paradoxically, familiar.

Validation Through Example

We have developed a prototype Web site (http://omie.med.jhmi.edu/bayes ) that implements a subset of the specifications and is discussed more thoroughly by Lehmann and Wachter¹⁰²; the screen shots shown here (Figure ▶,▶,▶,▶) represent the latest implementation. The prototype deals with the Bayesian equivalent of a t test, where the focus is on a difference between two treatments. There is a single applet, called NormalDifferenceSDKnown. The parameters of the applet are the names of the experimental and control arms, the sample sizes, the mean results, the standard deviations, the units of the outcome, and a flag indicating whether more of the outcome is better for a patient or worse. Although not all the specifications are satisfied, here are some comments about that those that are:

Figure 1A.

Example of Bayes applet. Slider panel. User has specified prior belief (upper bar) in the difference between adenosine and normal saline as normally distributed, with a mean of 7 mm Hg and a 95 percent Bayesian confidence interval from -11.11 to +25.11. The machine describes, or explains, this prior belief as “Mildly in favor of adenosine.” The data from the study provide an estimate of 17, with a sampling confidence interval of +2.67 to +31.33 (middle bar), also explained by the machine as “Mildly in favor of adenosine.” The machine then presents the calculated posterior 95 percent Bayesian confidence interval (lower bar), +7.42 to +18.88, which is still “Mildly in favor.”

Figure 1B.

Example of Bayes applet. Tail probability. The applet has calculated the probability of 0.989 that the true difference is greater than zero (i.e., that adenosine is better than normal saline placebo).

Figure 1C.

Example of Bayes applet. Minimal clinically important difference and sensitivity analysis. The user has specified (see below) that 10 mm Hg is the threshold below which she would not change her clinical behavior. The graph shows a number of things. The confidence intervals taken from the slider panel (A) are represented as single points in this plane, where the x-axis represents the mean difference between the arms, and the y-axis represents certainty (inversely related to standard deviation). The applet has also calculated two regions—the area where prior beliefs would lead to a posterior belief less than 10 (light grey), and the area where prior beliefs would lead to a posterior belief greater than 10. The current prior is in the latter region.

Figure 1D.

Example of Bayes applet. The probability that the difference is greater than the desired threshold is less than 95 percent. Data from Konduri et al.³

• Specification 1, Specification 2, and Specification 16: Prior belief, its assessment, and effect size. There are two interface methods, one based on confidence intervals and another, novel interface that plots the prior mean difference and its certainty as one point in a plane, making clear the effect size and its certainty.

• Specification 3: Thresholds. The prototype asks the user to specify the minimal clinically important difference (MCID).

• Specification 5: Explanation. It labels the beliefs verbally (e.g., “prior to skeptical against the experimental drug”).

• Specification 4: Inference. The prototype calculates tail probabilities, credible sets, equivalence, and sensitivity analysis for prior beliefs with respect to the MCID.

• Specification 9: Protect author's investment. Data for the prototype come directly from the published articles and do not need further information.

• Specification 10: Publish enough information. The MCID stands in for real data about side effects and other issues that compete with treatment efficacy in readers' decision making.

• Specification 13: Scale up. By taking an approach that places all the computing responsibility on the client, the prototype can scale up to an arbitrary set of articles. Around 15 are posted now on the prototype Web site.

Discussion

Clinical epidemiologists,^49,103 developers of clinical practice guidelines,^104,105,106 and others have decried the slow pace of innovation diffusion and the lag between establishment of treatment efficacy and implementation by a majority of clinicians. Two reasons for this lag are the mistrust that clinicians have for the reported research results¹⁰⁷ and the lack of adaptation by investigators of the reported conclusions to local needs.^108,109 Because the Bayesian paradigm explicitly invites such adaptation, Bayesian communication can play a unique role.

The efforts made by the Cochrane Collaboration to deliver computer-based syntheses that could be used by clinicians at the bedside speak to the interest of evidence synthesists in having research evidence inform day-to-day action and not just future research. Clinical epidemiologists and others have published guidelines for reading the literature.^110,111,112 Sackett et al.,⁴ for instance, identify study quality (randomization, all patients accounted for), outcomes, applicability (patients, physicians), statistical significance, and clinical significance as crucial factors for separating useful from useless or harmful interventions, similar to our empirical observation. Our approach wends a middle way between the cookbook version of evidence-based medicine that Tonelli⁵ warns of and the nonevidential approach that evidence-based medicine aims to displace. Bayesian communication permits clinical judgment and concerns about an individual patient to be represented formally and their implications made explicit. This work extends the work of evidence-based medicine researchers and outcome researchers. In an important paper on NNT, Lapaucis et al.¹¹³ ask “How Should the Results of Clinical Trials Be Presented to Clinicians?” The present paper shows that the answer to that question rests on more than alternative calculations of the data. Outcome researchers and those interested in what Geyman¹¹⁴ calls “patient-oriented evidence that matters” have prodded the research community to supply responses to Specification 10, the need to publish enough data to aid in decision making.

Through the years, there have been critics of the Bayesian approach. For instance, Efron⁹⁸ gave four reasons that “everyone isn't a Bayesian.” They are that the analysis is too complicated, that it requires too much information, that it is not objective, and that there is more to statistics than inference. Bayesian communication is a restricted domain. We deal with complexity by retaining the statistician's choice of model; with the need for information by limiting the information the user must provide; with the need for objectivity by focusing on an individual's decision (not all of science); and with the realm of statistics by pointing out that readers have been taught to focus on inference.

The approach we describe here opens up a wide research agenda for medical informatics and the electronic scholarship community. At a broad level, this work challenges the electronic publishing community to ask how the process of electronic publishing can or will change the language of discourse between investigator and reader, in particular, with regard to reporting the data themselves.

The challenge may be addressed along a number of dimensions. Different audiences will need different tools, as suggested in the specifications. Evidence synthesists will want to see multiple studies (Specification 7), with a focus on study quality (Specification 6) and the essential sufficient statistics (the data). Opinion leaders will also want to evaluate multiple studies, but with a focus on tradeoffs (Specification 2) and applicability. Clinicians will need the simplest tools, perhaps text interpretations derived from the mathematical manipulations.

The probability model presented in the prototype is very simple. The clinical research literature is more sophisticated now.¹¹⁵ We need models at least for proportions, time series, and multivariate regression. Making the Bayesian statistical models accessible to clinician readers is not a trivial task.

Much work needs to be done on the models for assessing priors. We discussed some assessment issues in Specification 1. More profoundly, how should ignorance be assessed? Which priors should be assessed? For instance, in the problem of differences, as in the adenosine example, should a prior be assessed on the difference alone, or on the control treatment (about which much may be known) and the difference (about which the reader may wish to plead ignorance)? Specific answers lead to different implementations.

Although, by the Likelihood Principle, we need to derive all our measures from the likelihood function, there are many possibilities. In all cases, research must document whether the extra cognitive cost provides benefit in terms of improved decision making.

Finally, the notion of a Bayesian community begs for definition and application. A formal definition goes back to Aumann's definition¹¹⁶ of common knowledge. There are many implications of this capability. Does viewing the prior beliefs of others violate the cardinal rule of Bayesian reasoning, of not double-counting data? Will it lead to coercive feedback (“Dr. Jones, we notice that your beliefs are always out of line with the community...”)? Can it be used to formalize the hypertextual process advocated by many, of having readers post their comments on active article servers?

Stakeholders whom we have not discussed would be affected by this paradigm. Agents of technology change would find Bayesian communication helpful as a tactic for getting global policies to change locally.¹⁰⁸ Librarians would have a new source of scholarly material (prior beliefs and tradeoffs) to manage. Regulators might be tempted to view the prior beliefs of the community—and the individual. Commercial interests might use those prior beliefs for marketing purposes.

We have defined a grand challenge for informatics—using information technology to provide clinicians with research data in a manner that will be the most useful to them to speed the technology-diffusion process,¹¹⁷ but based on formal, Bayesian statistics. This paper has outlined specifications that collectively could meet this challenge. We do not mean to imply that our model will be instantiated as formulated. We do contend that each specification provides grist for further research and development. The answers provided by that research, together with those from other lines of research, should come together to enable our objective, which is the effective translation of new knowledge into practice.