Multilevel Spatiotemporal Change-point Models for Evaluating the Effect of an Alcohol Outlet Control Policy on Changes in Neighborhood Assaultive Violence Rates

Abstract

Many previous studies have suggested a link between alcohol outlets and assaultive violence rates. In 1997 the City of New Orleans adopted a series of policies, e.g., increased license fee, additional enforcement staff, and expanded powers for the alcohol license board. The policies were specifically enacted to address the proliferation of problem alcohol outlets believed to be the source of a variety of social problems including assaultive violence. In this research, we evaluate the impact of a city level policy in New Orleans to address the problem alcohol outlets and their influence on assaultive violence. The spatial association between rates of assaultive violence at the census tract level (n=170) over a ten year period raises a challenge in statistical analysis. To meet this challenge we developed a hierarchical change-point model that controls for important covariates of assaultive violence and accounts for unexplained spatial and temporal variability. While our model is somewhat complex, its hierarchical Bayesian analysis is accessible via the WinBUGS software program. Keeping other effects fixed, the implementation of the new city level policy was associated with a decrease in the positive association between census tract level rates of assaultive violence and alcohol outlet density. Comparing several candidate change-point models using the DIC criterion, the positive association began decreasing the year of the policy implementation. The magnitude of the association continued to decrease for roughly two years and then stabilized. We also created maps of the fitted assaultive violence rates in New Orleans, as well as spatial residual maps which, together with Moran’s I’s, suggest that the spatial variation of the data is well accounted for by our model. We reach the conclusion that the implementation of the policy is associated with a significant decrease in the positive relationship between assaultive violence and the off-sale alcohol outlet density.

1. Introduction

Over the past two decades, many researches have studied the contextual role of alcohol outlets on a variety of social problems such as assaultive violence. These studies focused on the relationship between alcohol outlet density and social problems, and how the change of alcohol outlet density affects the rate of social problems. For example, the first studies looked at the association between the alcohol environment (the availability of alcohol) and assaultive violence at the city level (Scribner, MacKinnon et al. 1995; Watts and Rabow 1983). As geographical information systems (GIS) software became well-developed and widely available, more local units (e.g., census tracts) were used for analysis when modeling the presumable relation between alcohol outlets and assaultive violence in a neighborhood. (Scribner, Cohen et al. 1999; Speer, Gorman et al. 1998). The assaultive violence rates in contiguous neighborhoods are likely correlated due to the fact that alcohol availability can spread to neighboring areas, leading to spatial clustering. Such spatially autocorrelated outcomes could not only reveal interesting spatial relation, they also introduce bias if not being accounted for. Studies now tend to include spatial data analysis techniques to address spatial autocorrelation (Scribner, Johnson et al. 2008; Gorman, Speer et al. 2001; Gruenewald 2000; Zhu, Gorman et al. 2004). More recently, temporal dimensionality is being incorporated into these studies to analyze temporal trends (Zhu, Gorman et al. 2004; Scribner, Theall et al. 2007; Gruenewald and Remer 2006).

The advantage of being able to account for the spatial as well as the temporal dependence of the estimates has been making Bayesian methods more popular in subject fields including epidemiology, environmental science, and social science. The conditionally autoregressive (CAR) model (Besag 1974) was introduced to account for spatial autocorrelation in neighboring areas. It was later applied to extract spatial patterns in regional disease maps (Besag et al. 1991). Hierarchical Bayesian spatial models were applied to examine the relationship between alcohol outlet density and violence in some areas (Britt, Carlin et al. 2005; Zhu, Gorman et al. 2006). Yu et al. (2008) proposed a dual-change-point model within the Bayesian framework to investigate the association between assaultive violence and alcohol outlet availability based on the natural experiment provided by a 1992 California civil unrest which resulted in decreasing in the number of liquor outlets. In our study, we move one step forward to investigate how specific policies targeting alcohol outlets may have affected the association between alcohol environment and assaultive violence rates, where we focus our research on a set of policy changes for alcohol outlet administration in New Orleans in 1997. The findings are of potential importance in guiding policy making for law makers, regulators, and social workers.

The current study is designed around a policy change that could be considered a societal intervention. In 1997 the City of New Orleans adopted a series of policies (e.g., increased license fee, additional enforcement staff, and expanded powers for the alcohol license board) to address the proliferation of problem alcohol outlets believed to be the source of a variety of social problems including assaultive violence. Consequently, the loss of these more problematic alcohol outlets should attenuate the relationship between alcohol outlet density and the social problems they are assumed to generate. Therefore, the objective of this study is to determine how the global effect of the policy affected the association between assaultive violence rates and alcohol outlet density. We add a temporal change-point dimension to the modeling in order to analyze the indirect effect of policy change on assaultive violence rates in New Orleans at the census tract-level.

2. Background and data description

The target of the 1997 policy change in New Orleans was the proliferation of problem alcohol outlets across the city. Over the summer of 1997 the New Orleans City Council approved 20 changes to laws affecting alcohol outlets including higher license fees, stiffer fines for violations, expanded enforcement authority for the Alcohol Control Board, and bans on selling alcohol through windows (Donze 1997). In addition, a full time officer was assigned to the enforce liquor laws and investigate alcohol outlets for the Alcohol Control Board. The result was increasing rates of alcohol license suspensions and revocations. Finally, the city liquor license fee was increased by thirty five percent (Schleifstein 1997).

Sociodemographic data.

A number of sociodemographic variables were collected in this project. The investigators focus interest on three of them: percentage of less than high school education in a particular census tract, percentage living below the poverty line, and percentage of housing that is vacant. The values for these variables are averages from the 2000 census obtained from the US Census website. The intercensal data are obtained from the Claritas corporation. Claritas provides intercensal estimates of population stratified by age, race, and sex at the census tract level. The estimates take into account births, deaths, and immigration data to adjust the intercensal interpolation.

Alcohol Outlet Density.

Exposure to alcohol outlets are assessed in terms of alcohol outlet density. Three measures of alcohol outlet density are obtained: 1) total outlet density, 2) on sale outlet density, and 3) off sale outlet density. All outlet data originates from the Louisiana Alcohol and Tobacco Control (ATC) office, the licensing agency for the state of Louisiana. The ATC only maintains an active file of currently licensed outlets. The researchers have been maintaining a biannual archive of alcohol outlets since 1995.

To generate annual outlet density measures, biannual outlet data were accessed and the total numbers of alcohol outlets by outlet type were generated for each census tract. Outlet densities are generated from these outlet totals using two denominators 1) census tract square miles, and 2) total census tract roadway miles. Each method has its advantages and disadvantages. As recommended, outlet densities obtained with both methods were used in analyses to determine if the results were sensitive to type of method used to generate the measure (Scribner, Cohen et al. 1999).

Assaultive Violence Rates.

The assaultive violence data are obtained from the New Orleans Police Department (NOPD). NOPD provides Uniform Crime Reports (UCR) Part 1 offenses by address of offense for all police beats within the study area for all years from 1994 to 2004. From these data summary counts of assaultive violence offenses (i.e., homicide, rape, robbery, and aggravated assault) by census tracts were generated for all census tracts (n=170) in New Orleans based on the 1990 census tract designations. Annual rates of assaultive violence for each tract are then generated by dividing the total number of assaultive violences in a tract by the total intercensal population for the same year. The proportion is then multiplied by 1,000 to yield an annual assaultive violence rate per 1,000 population.

3. Spatiotemporal Change-point Modeling

In this section, we describe the development of a spatiotemporal change-point model to identify the relationship between assaultive violences and alcohol availability and how the 1997 policy change may have affected this relationship. In the model, we explore the changing relationship over time while controlling for important factors (percentage of less than high school education in a particular census tract, percentage living below the poverty line, and percentage of housing that is vacant) that might have an independent influence on the assaultive violence rate.

3.1. Change-point model

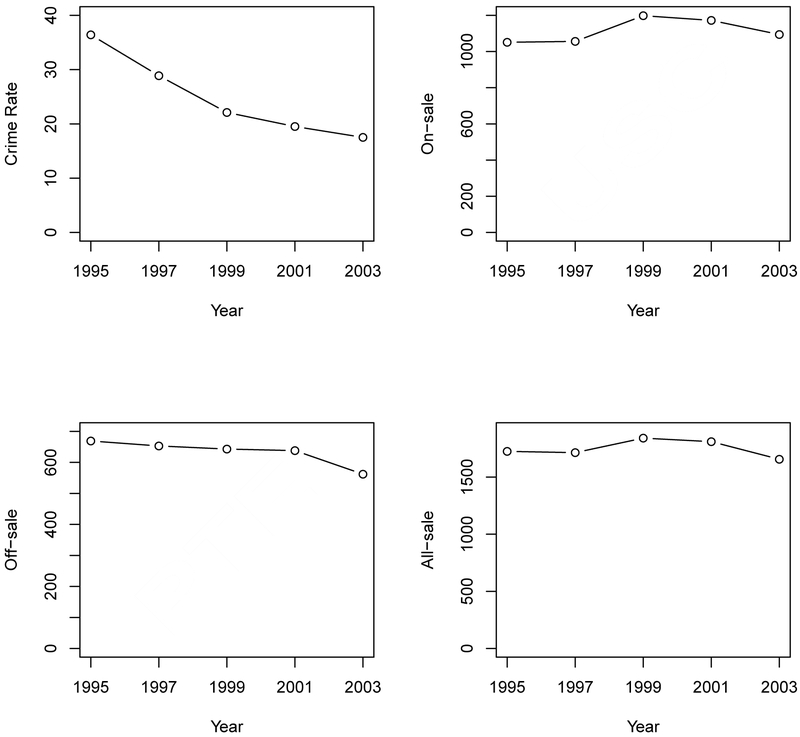
Figure 1 shows a rough picture of the relationship between alcohol availability and assaultive violence rates. On average, the assaultive violence rate decreased over the investigation period, but not for on-sale and off-sale alcohol outlet densities. If alcohol availability is positively associated with the assaultive violence rate and the city policy has an effect in diminishing this association by removing or disciplining problem alcohol outlets, there should be a significant drop in the positive association between assaultive violence rates and on-sale alcohol outlet density and/or off-sale alcohol outlet density in the affected census tracts following the enactment of the city policies.

Figure 1:

Mean plot of crime rate, on-sale, off-sale, and all-sale alcohol outlet densities over time.

We wanted to test the hypothesis that the 1997 policy had a preventive effect on the contribution of alcohol environment, measured as census tract alcohol outlet density, on census tract assaultive violence. We also wanted to find out when the policy effect, if any, started and when it became stabilized. Change-point models have been applied in the hierarchical modeling literature (Carlin, Gelfand et al. 1992; Green 1995, Yu, Scribner et al. 2008), with the benefit of enabling changes in parameters. Therefore, it can be adopted for our purpose of testing the aforementioned assumptions. We built the following spatiotemporal change-point models.

3.2. Model Details and Comparison

Let y_ij be the observed assaultive violence rates (number of assaultive violence cases per 1000 population) in census tract j and year i, where j ranges from 1 to 170 for 170 census tracts and i ranges from 1 to 5 for 10 years of data summarized biannually. μ_ij is the expected logarithmic crime rate for each census tract-year combination. Our model assumes a Log-normal distribution of the crime rates, with the following form:

$$\mathit{log}\left(y_{ij}\right)~N({\mu }_{ij},{\sigma }^2)$$

where

$$\begin{array}{cc}\hfill {\mu }_{ij}=& {\beta }_1+{\beta }_2\ast i+{\beta }_3\ast {\mathit{pctlthsgra}}_{ij}+{\beta }_4\ast {\mathit{pctbelowpo}}_{ij}\hfill \\ \hfill & +{\beta }_5\ast {\mathit{pctvacant}}_{ij}+{\beta }_6\ast {\mathit{onden}}_{ij}+{\beta }_7\ast {\mathrm{of}f\mathrm{den}}_{ij}\hfill \\ \hfill & +{\beta }_8\ast {\mathit{onden}}_{ij}\ast {\mathit{cp}}_i+{\beta }_9\ast {\mathrm{of}f\mathrm{den}}_{ij}\ast {\mathit{cp}}_i+u_{i,j}\hfill \end{array}$$

where u_i,j is the spatial error term used to control the spatial relationship for contingent census tracts within the same year. In the model, we assume there is a linear trend in the expected crime rate along year, controlling for all other variables. To control the potential multicollinearity problem, the year index i was centralized in our model, i.e., −2 for 1995, −1 for 1997, etc. PCTLTHSGRA, PCTBELOWPO, and PCTV ACANT are covariates (percentage with less than high school education, percentage with income below the poverty line, and percentage of vacant housing, respectively) with corresponding coefficients β₃, β₄, andβ₅. ONDEN and OFFDEN refer to on-sale alcohol outlet density and off-sale alcohol outlet density, and cp is the indicator variable specifying the change-point in the model. Therefore, β₆ and β₇ represent the effect of ONDEN and OFFDEN on crime rate; while β₈ and β₉, the coefficients of the interaction terms of alcohol outlet densities and the indicator cp, reveal the effectiveness of city policies in reducing the contribution of alcohol outlets to neighborhood crime. If the policies have effect, the coefficients for ONDEN and OFFDEN would change over time at the magnitude of β₈ and β₉. Indicator cp is designed to reflect when the policy effect started and when it reached its maximum, i.e., the effect of alcohol outlet densities became stabilized.

In this study, eight sets of possible cp values were tried, as listed in Table 1. The values of cp represent different scenarios of policy effects with respect to when to start and when to reach maximum. It is reasonable to assume that the policy effect started within two years after the implementation of the policies in early 1997. We are interested in seeing how long it will take the policies to reach maximum effect and how profound this effect is if it is statistically significant. We use model selection methods to check which scenario best fits the observed data.

Table 1:

Values of indicator “cp” for different models

model	cp
	1995	1997	1999	2001	2003
1	0	0	0	0	0
2	0	1	1	1	1
3	0	1	2	2	2
3	0	1	2	3	3
5	0	1	2	3	4
6	0	0	1	1	1
7	0	0	1	2	2
8	0	0	1	2	3

We use the conditionally autoregressive (CAR; (Besag 1974)) model for the spatial random effects to account for possible spatial autocorrelation between neighboring tracts. Given the other spatial effect terms, the prior mean of the spatial effect in tract k equals the average effect in the tracts that are adjacent to it. Let n_k be the number of tracts adjacent to tract k. The CAR prior distribution of u_ij has the form:

$$u_{i,j=k}\mid u_{i,j\ne k}=N(\sum _{j~k}\frac{1}{n_k}{u}_{i,k},\frac{1}{n_k{\tau }_i})$$

where j ~ k means all census tracts that is adjacent to tract k; τ_i is the precision parameter controlling the degree of spatial smoothing in year i. The τ_i are smoothed temporally via a moderately informative gamma hyperprior distribution having mean 1 and variance 10. Noninformative prior distributions (i.e., normal distributions centered at 0 with precision 0.000001) are assumed for all other coefficients β.

The posterior distributions for all parameters of interest were obtained via Markov Chain Monte Carlo (MCMC) algorithms implemented in WinBUGS (see Appendix 1 for the code). We used two MCMC chains to simulate from the posterior distributions for each model. For each chain, 3000 iterations were run after burning in the first 1000 iterations.

We use DIC (Deviance Information Criterion; Spiegelhalter, Best et al. 2002) as the criterion to select the best model. DIC accounts for both the goodness-of-fit and complexity of the models. It is defined as:

$$DIC=\stackrel{‒}{D}+p_D$$

where D̅ is the posterior mean of the deviance, and p_D is the effective number of model parameters, calculated as posterior mean of the deviance minus the deviance obtained by substituting in the posterior means (Spiegelhalter, Best et al. 2002). Since we prefer models that are simple (small p_D) and fit the data well (small D̅), we generally choose the model having the smallest DIC score, where a difference of 5 or higher is worth mentioning (http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/dicpage.shtml).

3.3. Spatial correlation

We use the test statistic Moran’s I (Banerjee, Carlin et al. 2004) to test whether there are spatial correlations in the observed and predicted crime rates, the spatial error, and the residuals. Moran’s I is calculated as:

$$I=\frac{n\sum _j\sum _k{w}_{ijk}(Y_{ij}-{\stackrel{‒}{Y}}_i)(Y_{ik}-{\stackrel{‒}{Y}}_i)}{\left(\sum _{j\ne k}{w}_{ijk}\right)\sum _j{(Y_{ij}-{\stackrel{‒}{Y}}_i)}^2}$$

where n is the number of areal units; Y_ij is the measurement for area j at year i and Y̅_i is the mean measurement of all the areas at year i; w_ijk equals 1 if areas j and k share some common boundary, and equals 0 otherwise.

4. Results and discussion

To describe possible policy effects, we fitted eight models, each of which corresponds to one pattern of change in coefficients for ONDEN and OFFDEN. Table 2 presents the DIC and p_D values for each of the 8 models. The DIC values suggest that Model 3 has the best balance between the model simplicity and goodness-of-fit. Therefore, it is most suitable in evaluating the impact of policy change on the association of crime rates and and alcohol outlet densities. According to this model, the effect of policy began in the year that the policy was implemented, and it became stabilized 2 years later.

Table 2:

Summary of model selection criterion (DIC) and effective number of parameters (p_D)

model	pD	DIC
1	525.253	902.209
2	541.732	869.822
3	610.427	697.348
4	544.239	863.032
5	523.106	910.326
6	597.199	728.756
7	527.648	899.611
8	529.564	896.171

Table 3 presents the posterior estimates of the coefficients in Model 3. As can be seen in the model description, the covariates were transformed to the log scale before modeling. To see the multiplicative effect of the corresponding covariateon on the relative risk of assaultive violence per unit change, we listed the “exp” column which converts the coefficients back to the original scale. The positive estimates of the coefficients for both on-sale (β₆) and off-sale (β₇) alcohol outlet densities suggest a positive association between alcohol availability and crime rate. For example, in the year 1995 if census tract A has one more on-sale alcohol outlet per square mile than tract B, keeping all other factors as constant, we expect the crime rate in tract A to be 1.048 times that of tract B. The negative estimate of the coefficient for “year” (β₂) indicates that the crime rates decreased by roughly 15% every two years from 1995 to 2003. Also, tracts that have a higher proportion of people with less than high school education, higher proportion of people living under poverty, or higher proportion of housing vacancy tended to have higher crime rates due to the positive effect of these three factors. Finally, the coefficient for the interaction term “cp * offden” is negative, meaning that the city policy change had an effect on reducing the positive correlation between off-sale alcohol outlet density and crime rates. The effect began in the year it was enacted, and became stabilized about 2 years later in 1999. On average, one unit increase of off-sale density is related with 4% less increase in crime rate every two years until it stabilized in 1999. The policy change also showed slight indications of effect on reducing the positive association between on-sale alcohol outlet density and crime rate, but that effect is not statistically significant.

Table 3:

Inferences for Model 3

parameter	mean	exp	sd	MC error	2.50%	median	97.50%
β1	1.997	7.367	0.049	0.00244	1.901	1.997	2.097
β2	−0.164	0.849	0.011	3.89E-04	−0.187	−0.164	−0.142
β3	0.0027	1.003	0.0024	8.97E-05	−0.0021	0.0026	0.0074
β4	0.013	1.013	0.0021	7.55E-05	0.0091	0.0133	0.0173
β5	0.013	1.013	0.0030	1.22E-04	0.0071	0.0130	0.0190
β6	0.047	1.048	0.0081	3.55E-04	0.0310	0.0473	0.0625
β7	0.182	1.199	0.020	5.72E-04	0.142	0.182	0.222
β8	−0.0068	0.993	0.0057	2.96E-04	−0.0178	−0.0068	0.0043
β9	−0.041	0.960	0.0118	4.01E-04	−0.0643	−0.0410	−0.0174

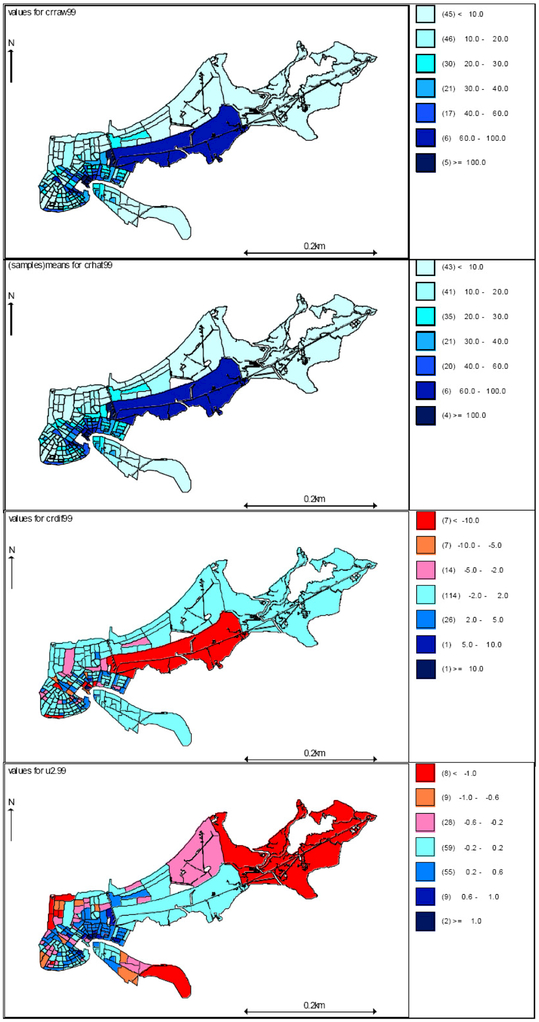
Figure 2 maps the distribution of the crime rates in 1999 in the New Orleans area. The upper two panels map the original and the fitted crime rates separately, in the units of the number of crimes per 1000 census tract residents. Comparing the two panels, the model had reasonably good fit to the original data. We can also see a concentration of crime in the downtown areas and their immediate neighbors. The lower two panels maps the residuals (i.e., the raw crime rate minus the fitted crime rate at each census tract in 1999) and the fitted spatial error, respectively.

Figure 2:

From top to bottom: the original crime rates in 1999, the fitted crime rates in 1999, the residuals, and the fitted spatial error.

Table 4 shows the Moran’s I for the original and the fitted data, along with the residual and the spatial error, over the years from 1995 to 2003. The residual resulting from our model showed much smaller spatial correlation compared to the original data, fitted data, and the spatial errors, suggesting that the major spatial variation of the data is largely explained by the chosen model. Table 5 lists the spatial precision parameter τ_i for different years. Since τ_i reflects the precision of the spatial term, larger values of τ_i reveal more spatial correlation among the spatial error terms. Its trend along year matches that revealed by Moran’s I in Table 4.

Table 4:

Moran’s I for original data, fitted data, the residual and the spatial effect in different years

Year	Moran’ I
	original	fitted	residual	spatial
1995	0.618	0.585	−0.049	0.497
1997	0.570	0.575	−0.057	0.531
1999	0.597	0.620	−0.037	0.455
2001	0.604	0.646	−0.130	0.415
2003	0.564	0.601	−0.117	0.252

Table 5:

Posterior means of τ_year by year; larger τ_year means higher similarity in the spatial residuals for that year.

Year	1995	1997	1999	2001	2003
τyear	1.87	2.01	1.17	1.01	0.51

5. Conclusions and future researches

The contextual effects of the neighborhood alcohol environment have attracted much research interest. Researchers are advocating policies to address alcohol related social problems like neighborhood assaultive violence. Consequently, the evaluation of policy changes affecting alcohol outlets in the New Orleans area is of particular importance for researchers and policy makers. However, the complexity of the available data in terms of its structure presents challenges for modeling the relationships. The change-point model used in this paper represents an approach that essentially compares the trend in assaultive violence rates over time across census tracts, which varied in terms of changes in outlet density resulting from the policy while simultaneously controlling for some important factors and accounting for spatial autocorrelation among the spatial error terms. By selecting the best change-point model with DIC criterion, we can identify the trends of change in associations of interest.

We adopted a CAR model to address spatial autocorrelation and control for other factors that might have an influence on the crime rate. We have demonstrated that the policy change in alcohol outlet administration in the New Orleans area in 1997 was related with a decrease in the positive association between crime rate and alcohol outlet density at the census tract level. This effect is reflected in a decrease in the slope when we use the alcohol outlet density (off-sale) to explain the crime rate. This indicates that the positive association between off-sale alcohol outlet density and crime rate was decreasing following implementation of the policy changes. We compared several candidate change-point models using the DIC criterion, and the accordingly selected model suggests that the drop in the positive association is best seen as having begun in the year of the policy implementation, and continued for roughly two years and then stabilized.

Due to the temporal nature of policy change, it is inevitable that the crime trend by year is confounded with the policy effect. In order to discriminate between the policy effect and the crime trend by year, our analysis assumed a linear trend for the latter. A control group from an area that did not undertake policy changes during the same time periods, such as Baton Rouge crime data, would be valuable in making more accurate inference regarding the policy effect. We are currently in the process of obtaining these data. Our future research will utilize the Baton Rouge crime data to control the crime trend by year, so that more accurate inference on the policy effect can be drawn. We will also categorize the crimes into groups, i.e., assault, robbery, rape, and homicide, and perform multivariate spatial analysis on our data.

Appendix 1: Model written in WinBUGS

model
{
for(i in 1:N) {
logcr[i])<-log(CRIMERT[i])
logcr[i] ~ dnorm(mu[i],tau)
mu[i]<- beta[1]
+ beta[2] * Time[i]
+ beta[3] * PCTLTHSGRA[i]
+ beta[4] * PCTBELOWPO[i]
+ beta[5] * PCTVACANT[i]
+ beta[6] * ONDEN[i]
+ beta[7] * OFFDEN[i]
+ beta[8] * ONDEN[i]* cp[i]
+ beta[9] * OFFDEN[i]* cp[i]
+ u2[(Time[i]+3),TRACTMASTE[i]]
}

for (k in 1:170)
{
u2.95[k]<-u2 [1,k]
u2.97[k]<-u2[2,k]
u2.99[k]<-u2 [3,k]
u2.01[k]<-u2 [4,k]
u2.03[k]<-u2[5,k]
crhat95[k]<-exp(mu[5*(k-1)+1])
crraw95[k]<-CRIMERT[5*(k-1)+1]
crdif95[k]<-crhat95[k]-crraw95[k]
crhat97[k]<-exp(mu[5*(k-1)+2])
crraw97[k]<-CRIMERT[5*(k-1)+2]
crdif97[k]<-crhat97[k]-crraw97[k]
crhat99[k]<-exp(mu[5*(k-1)+3])
crraw99[k]<-CRIMERT[5*(k-1)+3]
crdif99[k]<-crhat99[k]-crraw99[k]
crhat01[k]<-exp(mu[5*(k-1)+4])
crraw01[k]<-CRIMERT[5*(k-1)+4]
crdif01[k]<-crhat01[k]-crraw01[k]
crhat03[k]<-exp(mu[5*(k-1)+5])
crraw03[k]<-CRIMERT[5*(k-1)+5]
crdif03[k]<-crhat03[k]-crraw03[k]
}

for(j in 1:sumNumNeigh) {weights[j] <-1}

for(m in 1:5)
{
u2[m,1:n2] ~ car.normal(adj[], weights[], num[], tau2[m])
tau2[m] ~ dgamma(0.1,0.1)
}

for (n in 1:9) { beta[n] ~ dnorm(0,1.0E-6) }

tau ~ dgamma(0.1,0.1)
}