Transmission of cytokinesis forces via E-cadherin dilution and actomyosin flows

Abstract

During epithelial cytokinesis, the remodelling of adhesive cell–cell contacts between the dividing cell and its neighbours has profound implications for the integrity, arrangement and morphogenesis of proliferative tissues^1–7. In both vertebrates and invertebrates, this remodelling requires the activity of non-muscle myosin II (MyoII) in the interphasic cells neighbouring the dividing cell^1,3,5. However, the mechanisms that coordinate cytokinesis and MyoII activity in the neighbours are unknown. Here we show that in the Drosophila notum epithelium, each cell division is associated with a mechanosensing and transmission event that controls MyoII dynamics in neighbouring cells. We find that the ring pulling forces promote local junction elongation, which results in local E-cadherin dilution at the ingressing adherens junction. In turn, the reduction in E-cadherin concentration and the contractility of the neighbouring cells promote self-organized actomyosin flows, ultimately leading to accumulation of MyoII at the base of the ingressing junction. Although force transduction has been extensively studied in the context of adherens junction reinforcement to stabilize adhesive cell–cell contacts⁸, we propose an alternative mechanosensing mechanism that coordinates actomyosin dynamics between epithelial cells and sustains the remodelling of the adherens junction in response to mechanical forces.

During cytokinesis, contractile ring constriction deforms the dividing cell and the neighbouring cell membranes, which co-ingress at the rim of the ring and remain apposed^1,3–6 (Fig. 1a, Extended Data Fig. 1a, b and Supplementary Video 1). Concomitantly, in the cells neighbouring the dividing cell, MyoII accumulates near the base of the ingressing membrane, where it promotes the formation of a long adhesive contact between the future daughter cells^1,5,6 (Fig. 1a, b and Extended Data Fig. 1c, d). Accordingly, MyoII accumulation in the neighbours contributes to the remodelling of the daughter cell adherens junction (AJ) and the overall tissue dynamics^1,3,5,6. Here, we analysed, in the Drosophila notum epithelium, whether and how the dividing cell signals to its neighbours to regulate MyoII dynamics.

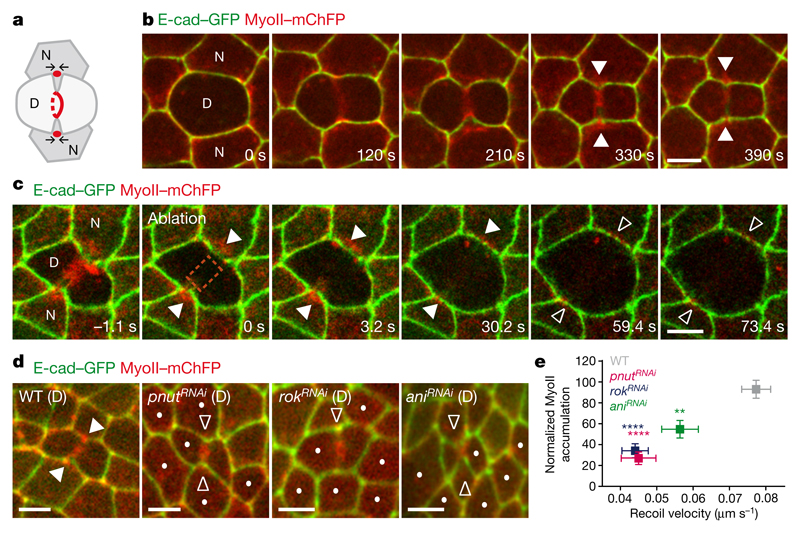
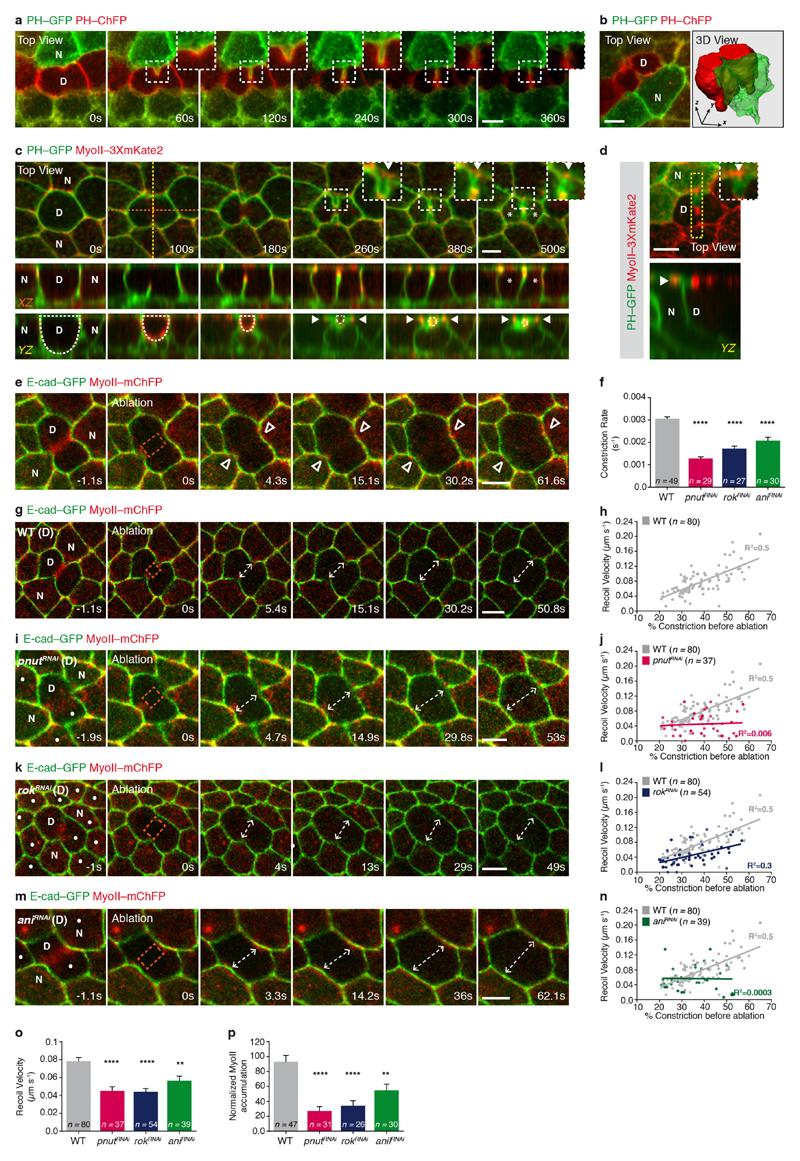
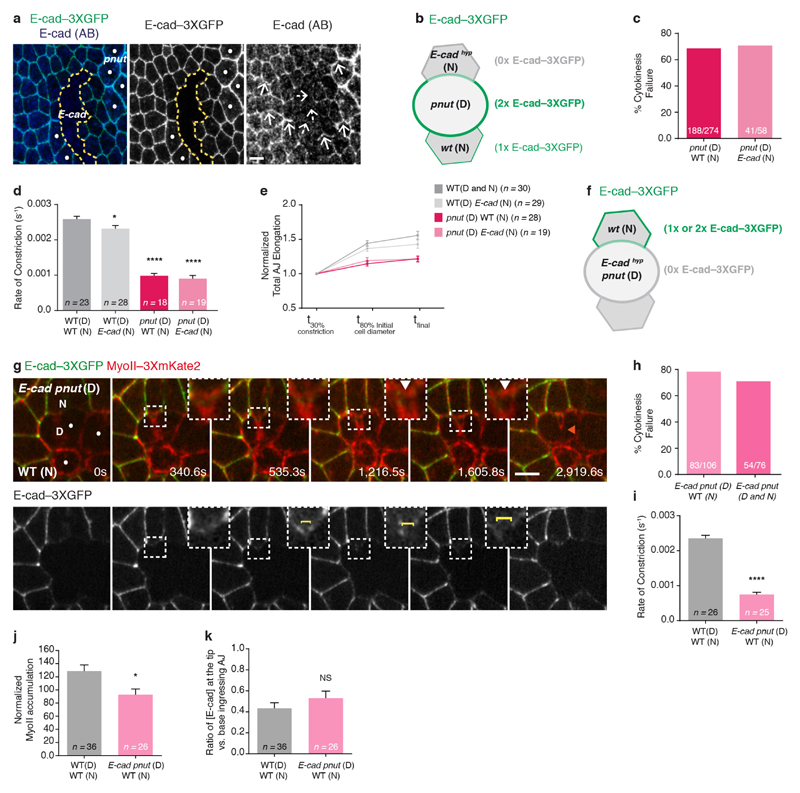
Figure 1. Contractile ring forces trigger MyoII accumulation in the neighbours.

a, Schematic of MyoII accumulation (red circles) upon ring constriction (red lines). Arrows denote MyoII-dependent forces promoting membrane juxtaposition in daughter cells. b, c, E-cad–GFP and MyoII–mChFP during cytokinesis (b, n = 23 cells, 4 pupae) and upon ring laser ablation (c, n = 32 ablations, 4 pupae). Laser ablation (t = 0 s; orange box denotes ablated region) performed after MyoII–mChFP accumulation in neighbours. d, E-cad–GFP and MyoII–mChFP in cells neighbouring wild-type (WT; n = 47 cells, 5 pupae), pnut^RNAi (n = 31 cells, 4 pupae), rok^RNAi (n = 26 cells, 11 pupae) and ani^RNAi (n = 30 cells, 4 pupae) dividing cells. Dots denote RNA interference (RNAi) cells marked by lack of cytosolic GFP. e, Normalized MyoII accumulation in the neighbours at 80% of initial cell diameter versus recoil velocity upon ring laser ablation for wild-type (n = 47 cells, 5 pupae; n = 80 cells, 4 pupae), pnut^RNAi (n = 31 cells, 4 pupae; n = 37 cells, 3 pupae), rok^RNAi (n = 26 cells, 11 pupae; n = 54 cells, 5 pupae) and ani^RNAi (n = 30 cells, 4 pupae; n = 39 cells, 3 pupae) dividing cells. **P < 0.01, ****P < 0.0001, Kruskal–Wallis test (both axes). Data are mean ± s.e.m. In b–d, white filled arrowheads denote MyoII–mChFP accumulation in neighbours; white open arrowheads indicate reduced MyoII–mChFP accumulation in neighbours. D, dividing cell; N, neighbouring cell. Scale bars, 5 μm.

As MyoII accumulation in the neighbours is observed at the level of the AJ from mid-constriction onwards (Fig. 1b and Extended Data Fig. 1c, d), we investigated whether the contractile ring pulling forces have a role in MyoII accumulation. To estimate the magnitude of these forces, we used laser ablation to sever the ring and measured the AJ initial recoil velocity. The recoil velocity increases with the amount of ring constriction, indicating that the pulling forces build up during cytokinesis (Extended Data Fig. 1g, h). Moreover, the ablation of the contractile ring before or after mid-constriction prevented or abolished MyoII accumulation in the neighbours, respectively (Extended Data Fig. 1e, Fig. 1c and Supplementary Video 2a). To probe the role of force in the neighbouring cells response further, we tested whether reducing the pulling forces exerted by the dividing cell affected MyoII accumulation. Although pnut (peanut, a Drosophila septin), Rok (Rho kinase) and ani (anillin, also known as scraps) have distinct roles during cytokinesis⁹, decreasing their function in the dividing cell reduced both the rate of contractile ring constriction and the AJ recoil velocities after ring laser ablation compared with wild-type cells (Fig. 1e and Extended Data Fig. 1f–o). Moreover, MyoII accumulation is reduced in cells neighbouring pnut, rok and ani dividing cells and it scales with the magnitude of the forces produced in the dividing cells (Fig. 1d, e, Supplementary Video 2b and Extended Data Fig. 1o, p). Cytokinesis therefore provides an endogenous and local force generator to study the mechanisms of force sensing and MyoII dynamics during remodelling of the AJ.

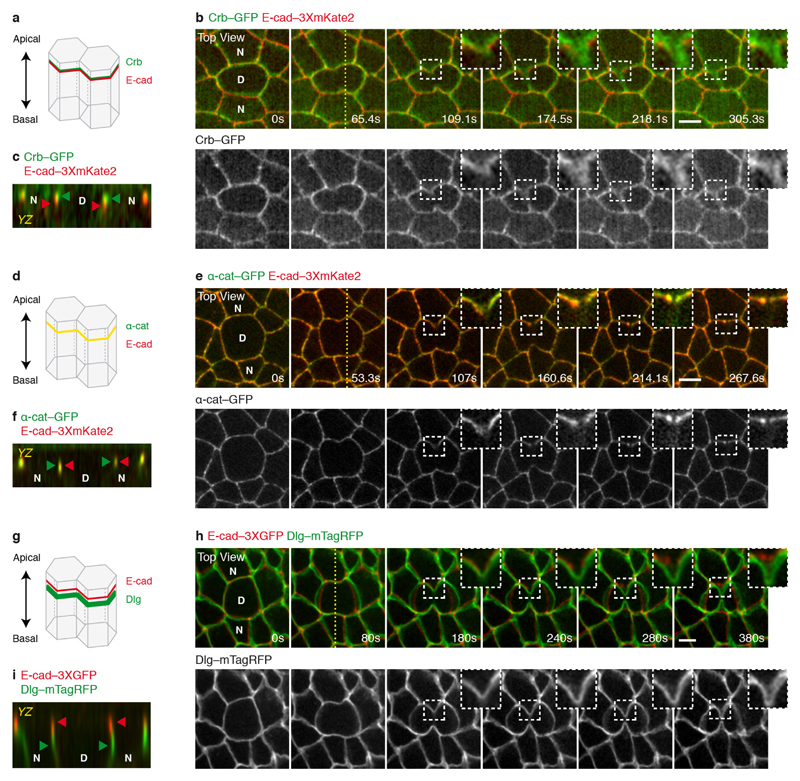
To decipher how pulling forces promote MyoII accumulation in the neighbours, we analysed the distributions of E-cadherin and cortical MyoII during cytokinesis. As constriction proceeds, the AJ at the edges of the furrow locally elongates, becomes increasingly curved, and the green fluorescent protein (GFP)-tagged E-cadherin (E-cad–GFP) signal locally decreases^1,3 (Fig. 2a, b and Supplementary Video 3). Concomitantly, the signals of E-cad–GFP and monomeric cherry fluorescent protein (mChFP)-tagged MyoII (MyoII–mChFP) in the neighbouring cells separate and no longer co-localize (Fig. 2a, b and Supplementary Video 3), indicative of local cortex detachment. This is further supported by the analysis of the distribution of the cortical marker β_H-spectrin, which remains co-localized with MyoII, while E-cad keeps ingressing with the cell membranes (Extended Data Fig. 3a and Fig. 2c). Soon after, and while the E-cad–GFP signal remains low in the ingressing AJ, MyoII–mChFP accumulates (Fig. 2a, b and Supplementary Video 3). While the apical maker Crumbs (Crb) and the septate junction marker Discs-large (Dlg) remain in the ingressing membrane, the α-catenin (α-cat) signal decreases concomitantly to E-cad, suggesting that the E-cad–Catenin complex concentration decreases along the ingressing membrane (Extended Data Fig. 2a–i). The accumulation of MyoII in the neighbouring cells is therefore preceded by local detachment of the cortex and a local decrease of the E-cad–Catenin concentration along the ingressing AJ.

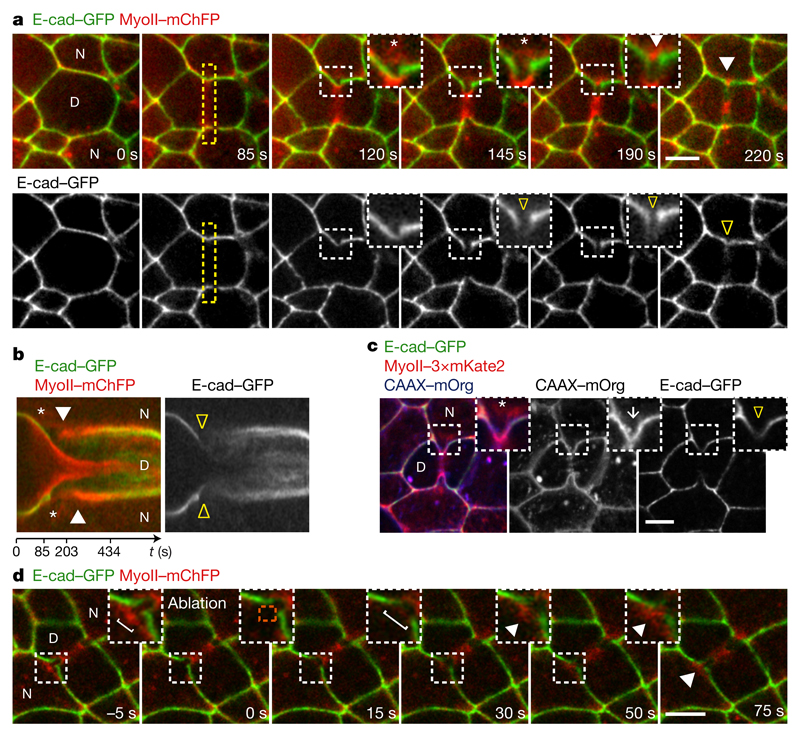
Figure 2. Cortex detachment and E-cad decrease precede MyoII accumulation.

a, b, E-cad–GFP and MyoII–mChFP during cytokinesis. Kymograph in b along the yellow box. Asterisks denote MyoII–mChFP and E-cad–GFP signal separation. Yellow open arrowheads indicate reduced E-cad–GFP at the ingressing AJ; white arrowheads denote MyoII–mChFP accumulation in neighbours. n = 23 cells (4 pupae). c, E-cad–GFP, MyoII–3 × mKate2 and CAAX–mOrg upon ring constriction. White arrow denotes AJ ingression; asterisk and arrowhead as in a, b. n = 42 cells (8 pupae). d, Laser ablation of detached cortical MyoII (t = 0 s, ablated region: orange box). Brackets denote ingressed AJ width, indicating neighbour relaxation upon ablation. White arrowheads indicate MyoII–mChFP re-accumulation upon ablation. n = 24 ablations (3 pupae). Scale bars, 5 μm.

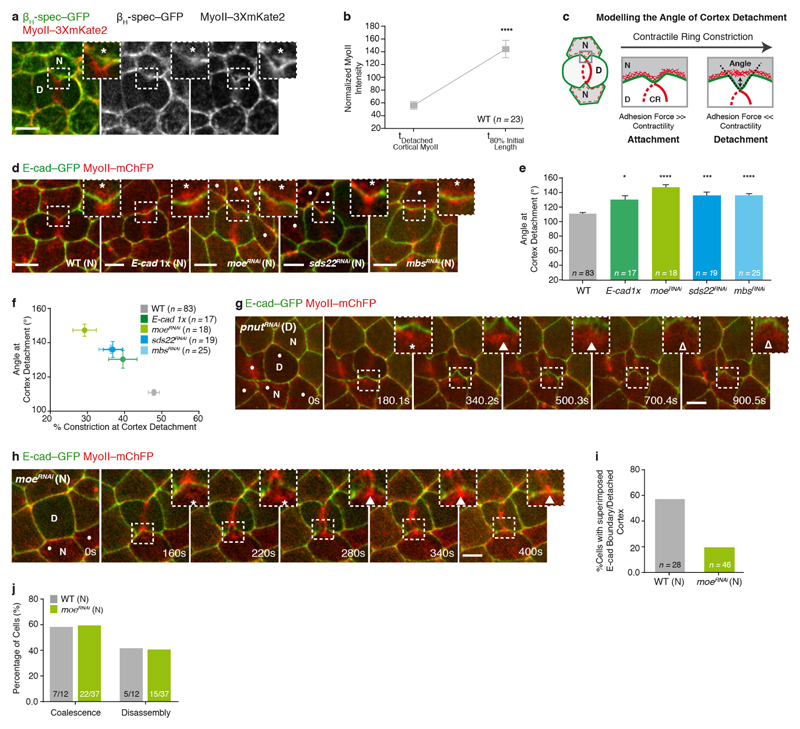
Having determined that cortex detachment, in response to the contractile ring forces, depends on a balance between membrane curvature, membrane-cortex adhesion and contractility (Extended Data Fig. 3c–f), we tested whether MyoII accumulation could arise from the contraction of the detached cortical MyoII. However, several data argue against this model. First, the MyoII total intensity at the detached cortex only represents one-third of the total MyoII accumulation (Extended Data Fig. 3b). Second, upon ablation of the detached cortex, MyoII re-accumulates in the neighbours (Fig. 2d and Supplementary Video 4a). Third, in cells neighbouring pnut dividing cells, cortex detachment occurs without a subsequent steady accumulation of MyoII (n = 10 out of 20 cells; Extended Data Fig. 3g and Supplementary Video 4b). Finally, we induced precocious cortex detachment by reducing Moesin (Moe) function, so that the detached cortical MyoII was localized further away from the ingressing membrane (Extended Data Fig. 3c–f, h and Supplementary Video 4c, d). While a transient MyoII accumulation is observed around the position of the detached cortex, MyoII becomes strongly enriched away from it, at the base of the ingressing AJ, near the boundary between low and high E-cad–GFP signals (Extended Data Fig. 3h–j and Supplementary Video 4c, d). Collectively, these data indicate that MyoII accumulation does not arise solely from the contraction of the detached cortex and that the position of accumulation is determined by the boundary between the low and high E-cad concentration domains.

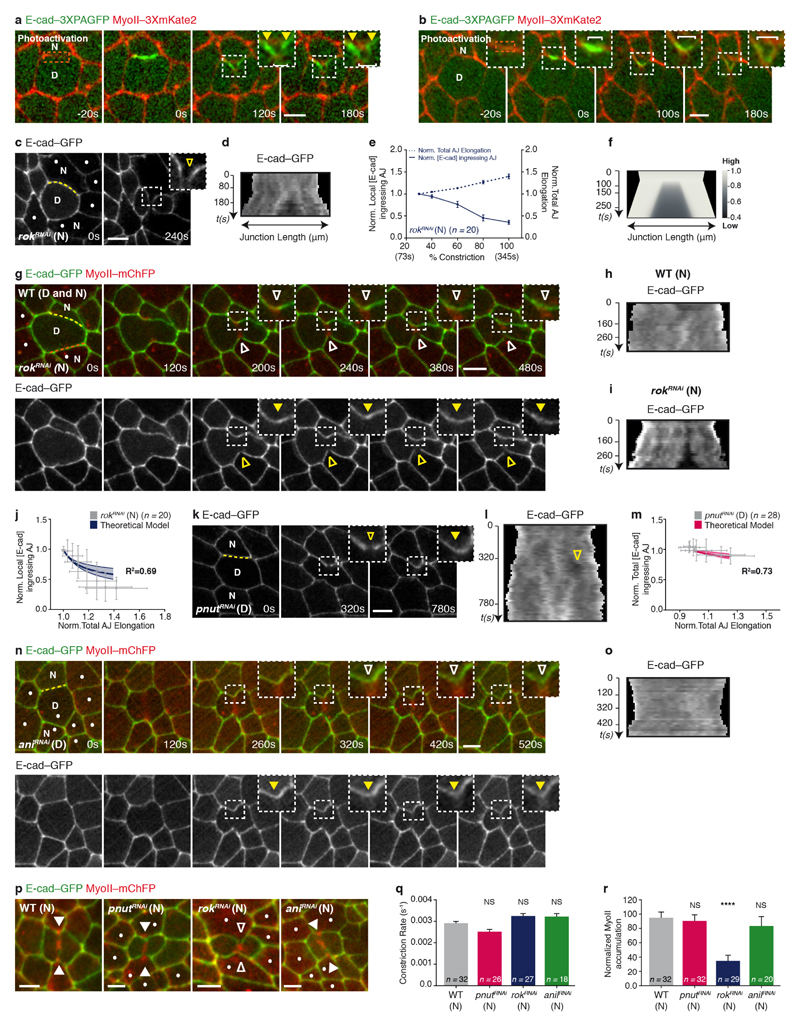
We therefore analysed the mechanisms underlying the decrease in E-cad concentration at the ingressing AJ, as well as its role in the response of the neighbours. Two mechanisms can account for a local reduction in E-cad concentration: a local decrease in the total amount of E-cad, or a local E-cad dilution. Since affecting E-cad trafficking does not prevent the reduction of E-cad concentration at the ingressing AJ (Extended Data Fig. 4a–d) and the total amount of E-cad–GFP does not decrease during AJ ingression (Extended Data Fig. 4e), we examined whether the reduction of E-cad concentration results from its dilution due to junction elongation (Extended Data Fig. 4h). Kymographs along the ingressing junction showed that the local E-cad decrease is concomitant to junction elongation (Fig. 3a–c). Notably, junction elongation is a local process, since the width of the ingressing AJ remains small during ring constriction whereas its height increases progressively (Extended Data Fig. 4i, j). To analyse whether this local increase in junction length is sufficient to reduce E-cad concentration at the ingressing AJ, we modelled E-cad dynamics on a locally elongating junction (Supplementary Note). As the experimentally measured E-cad diffusion is low and its immobile fraction is large on the time scale of cytokinesis (Supplementary Table 1), numerical simulations illustrate that local junction elongation is sufficient to reduce E-cad concentration locally, and to maintain this decrease in time, similarly to our experimental findings (Fig. 3d and Extended Data Fig. 4l). Accordingly, we also found that: (1) activation of photoactivatable GFP (PAGFP)-tagged E-cad (E-cad–3 × PAGFP) at the rim of the ring upon membrane ingression leads to local dilution of photoactivated E-cad–3 × PAGFP along the ingressing junction (Extended Data Fig. 5a, b and Supplementary Video 5); (2) in the absence of Rok activity in the neighbours, which abrogates MyoII accumulation¹, the E-cad signal still decreases, indicating that its decrease is not caused by MyoII accumulation (Extended Data Figs 4f, i–k, 5c–j and p–r); (3) pnut dividing cells, which do not show a marked E-cad decrease³, display significantly lower and less local junction elongation (Fig. 3e–g and Extended Data Fig. 4g, i–k); and (4) this lower and less local junction elongation is sufficient to reproduce the lower decrease of E-cad concentration in our numerical simulation (Fig. 3h and Extended Data Fig. 5k–m). Together, these findings indicate that the pulling forces exerted by ring constriction promote local AJ elongation, which can account for the local decrease in E-cad concentration at the ingressing AJ.

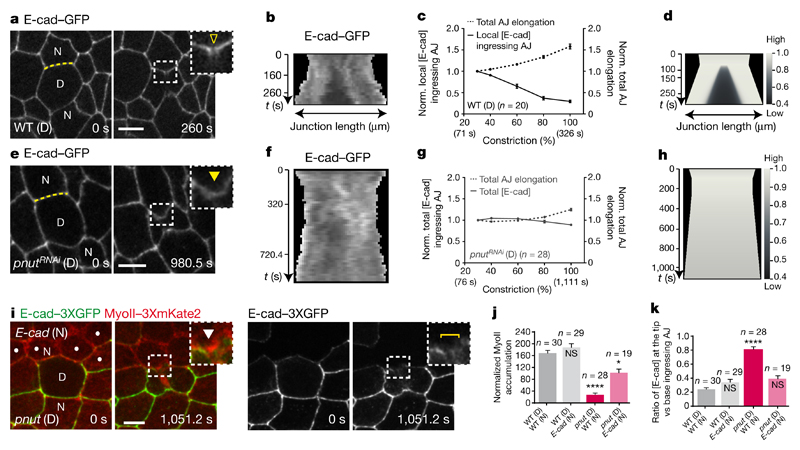
Figure 3. Lowering E-cad concentration at the ingressing AJ promotes MyoII accumulation.

a, b, e, f, E-cad–GFP in wild-type (a, b, n = 20 cells, 5 pupae) or pnut^RNAi (e, f, n = 28 cells, 6 pupae) cells. Kymographs in b and f along the yellow lines in a and e, respectively (see Methods). Yellow open arrowhead denotes reduced E-cad–GFP at the ingressing AJ; yellow filled arrowhead indicates absence of a notable E-cad–GFP decrease. All cells in e are pnut^RNAi, marked by lack of cytosolic GFP. c, g, Normalized local (c) or total (g) E-cad–GFP intensity at the ingressing AJ (solid line), and normalized total AJ elongation (dashed lines) versus ring constriction, respectively in wild-type (c) or pnut^RNAi (g) dividing cells (5 or 6 pupae, respectively). d, h, Numerical integration of E-cad levels on a locally or globally elongating AJ, as measured in wild-type (d) or pnut^RNAi (h) dividing cells. i, MyoII–3 × mKate2 in a pnut dividing cell (marked by two E-cad–3 × GFP copies) and its E-cad mutant neighbour (dots, marked by lack of E-cad–3 × GFP). Brackets denote E-cad–3 × GFP transient reduction at ingressing AJ. White arrowheads indicate MyoII–3 × mKate2 accumulation in neighbours. n = 19 cells (15 pupae). j, Normalized MyoII accumulation at 80% of the initial cell diameter in wild-type or E-cad mutant cells neighbouring wild-type or pnut dividing cells (6, 11, 15 and 15 pupae, respectively). k, E-cad–3 × GFP intensity ratio at the tip versus the base of ingressing AJ in wild-type or E-cad mutant cells neighbouring wild-type or pnut dividing cells (6, 11, 15 and 15 pupae, respectively). n indicates cell number throughout. NS, not significant. *P < 0.05, ****P < 0.0001, Kruskal–Wallis test. Data are mean ± s.e.m. Scale bars, 5 μm.

Next, we asked whether the decrease in E-cad levels is sufficient to drive MyoII accumulation. We hypothesized that, if lowering E-cad concentration is pivotal for MyoII accumulation, reducing E-cad levels using a hypomorphic e-cad allele would rescue MyoII accumulation in cells neighbouring a pnut dividing cell, which produces lower pulling forces and junction elongation. Although pnut dividing cells facing an E-cad (also known as shotgun) mutant neighbour still constrict at a lower rate and often fail cytokinesis, MyoII accumulation in the neighbours is rescued, at the position where a further decrease of the E-cad–3 × GFP signal is observed (Fig. 3i–k, Supplementary Video 6 and Extended Data Fig. 6a–k). Therefore, reducing E-cad levels is sufficient to rescue the neighbouring cell response upon reduced forces and membrane elongation, supporting that the decrease in E-cad concentration mediates the response of the neighbour to cytokinesis forces.

To analyse how a decrease in E-cad concentration triggers MyoII accumulation, we considered both the signalling and mechanical roles of the E-cad adhesion receptor. In agreement with the observed cortex detachment, Vinculin (Vinc) was dispensable for MyoII accumulation in the neighbours (Extended Data Fig. 7a–e). Moreover, affecting the function of Rho GTPase, Formins, Arp2/3 or Enabled at most delays MyoII accumulation in the neighbours, suggesting that neither Rho activity nor a specific F-actin nucleator can fully account for the response of the neighbours (Extended Data Figs 7f–r and 8a, b). We therefore investigated whether changes in the interaction of E-cad–Catenin complex with the underlying actomyosin cortex promote MyoII accumulation. We modelled the actomyosin cortex as a one-dimensional viscous and contractile active gel^10–12, adhered to a membrane (Supplementary Note). Theoretically, it was shown that when MyoII contractility exceeds a threshold, an otherwise uniform cortex destabilizes into a local accumulation^13,14. Since E-cad, via the Catenin proteins, is physically linked to the actomyosin cortex and can restrict its dynamics^8,15–17, we modelled its function as an effective friction and investigated whether it has a role in determining the cortex stability threshold. This minimal model suggests that locally lowering E-cad concentration, that is, lowering the effective friction locally, is sufficient to spontaneously generate actomyosin flows and drive a local actomyosin accumulation (Extended Data Fig. 8c–h), even for uniform MyoII contractility and F-actin polymerization (Extended Data Fig. 8c–e, g). Using a 2D model taking into account the geometry of the ingressed junction, we found that a decrease of friction along the AJ is sufficient to drive actomyosin flows towards the boundary between low and high E-cad concentrations (Fig. 4a–c and Extended Data Fig. 8i–o).

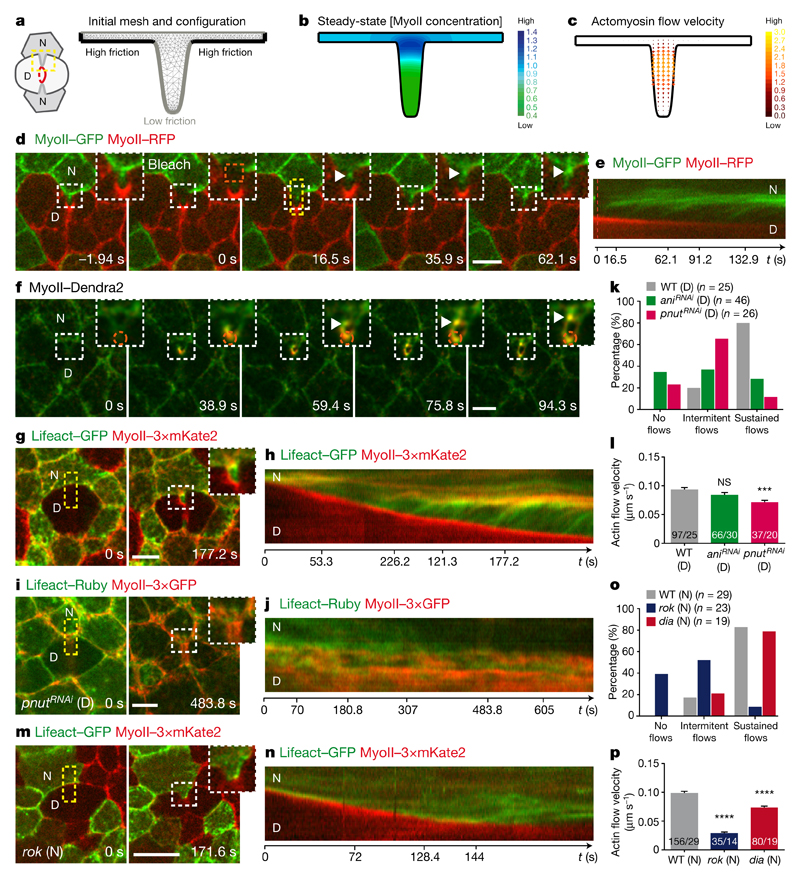
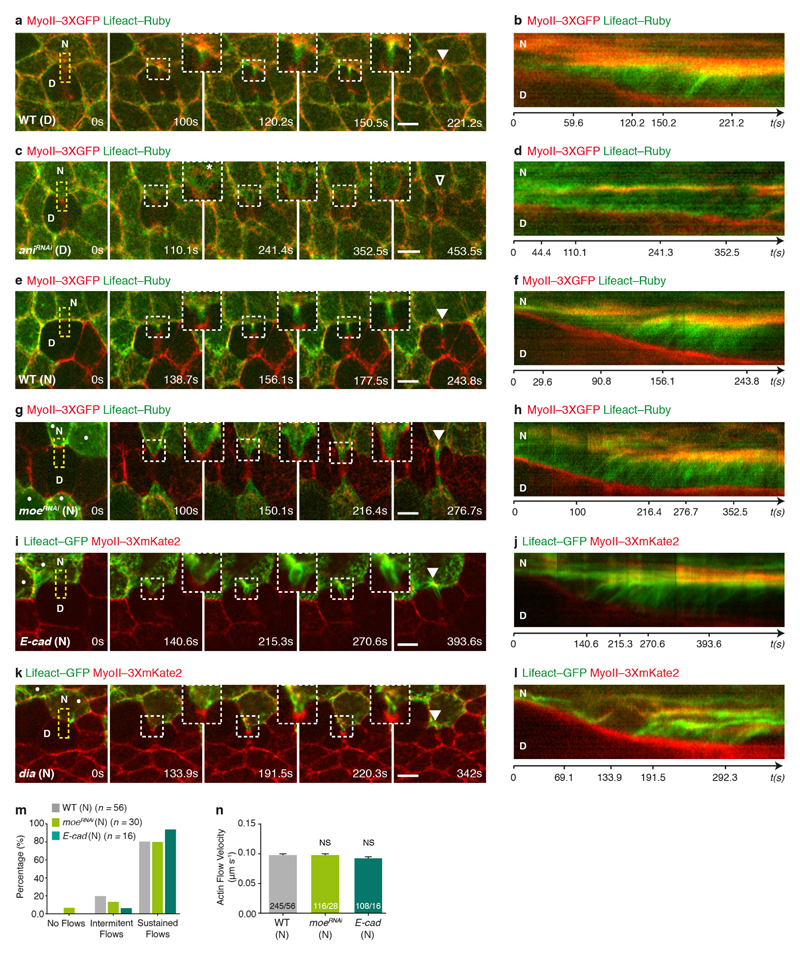
Figure 4. Actomyosin flows drive the response of the neighbours.

a–c, Finite element numerical integrations of active gel equations. a, Domain geometry and initial mesh (light grey lines). Thick grey and black lines indicate low and high friction, respectively. b, Steady-state MyoII concentration. c, Actomyosin gel steady-state velocity field. d, e, MyoII–GFP photobleaching in MyoII–GFP facing a MyoII–RFP patch (t = 0 s; orange boxes denote the photobleached region). Kymograph in e along the yellow box. Arrowheads denote MyoII–GFP speckles flowing from the tip to the base of ingressing AJ. n = 18 cells (8 pupae). f, MyoII–Dendra2 photoconversion at the tip of ingressing AJ (orange circle). Arrowheads as in d. n = 40 cells (23 pupae). g, h, Lifeact–GFP-expressing cells facing a dividing cell in MyoII–3 × mKate2 tissue. Kymograph in h along the yellow box. n = 29 cells (7 pupae). i, j, pnut^RNAi cells, marked by Lifeact–Ruby, in a MyoII–3 × GFP tissue. Kymograph in j along the yellow box. n = 29 cells (4 pupae). k, Percentage of cells exhibiting no flows, intermittent flows (< 3 speckles), or sustained flows (≥ 3 speckles) facing wild-type, ani^RNAi or pnut^RNAi dividing cells (4, 8 and 4 pupae, respectively). l, F-actin flow velocity in cells neighbouring wild-type, ani^RNAi or pnut^RNAi dividing cells (4, 8 and 4 pupae, respectively). m, n, rok neighbour, marked by Lifeact–GFP, facing a wild-type dividing cell in MyoII–3 × mKate2 tissue. Kymograph in n along the yellow box. n = 23 cells (8 pupae). o, Percentage of wild-type, rok or dia neighbours (7, 8 or 3 pupae, respectively;) exhibiting no flows, intermittent flows or sustained flows (see k). p, F-actin flow velocity for wild-type, rok or dia neighbours facing wild-type dividing cells (7, 8 or 3 pupae, respectively). n denotes cell number; n/n indicates speckle number/cell number. ***P < 0.001, ****P < 0.0001, ANOVA (l) and Kruskal–Wallis test (p). Data are mean ± s.e.m. Scale bars, 5μm.

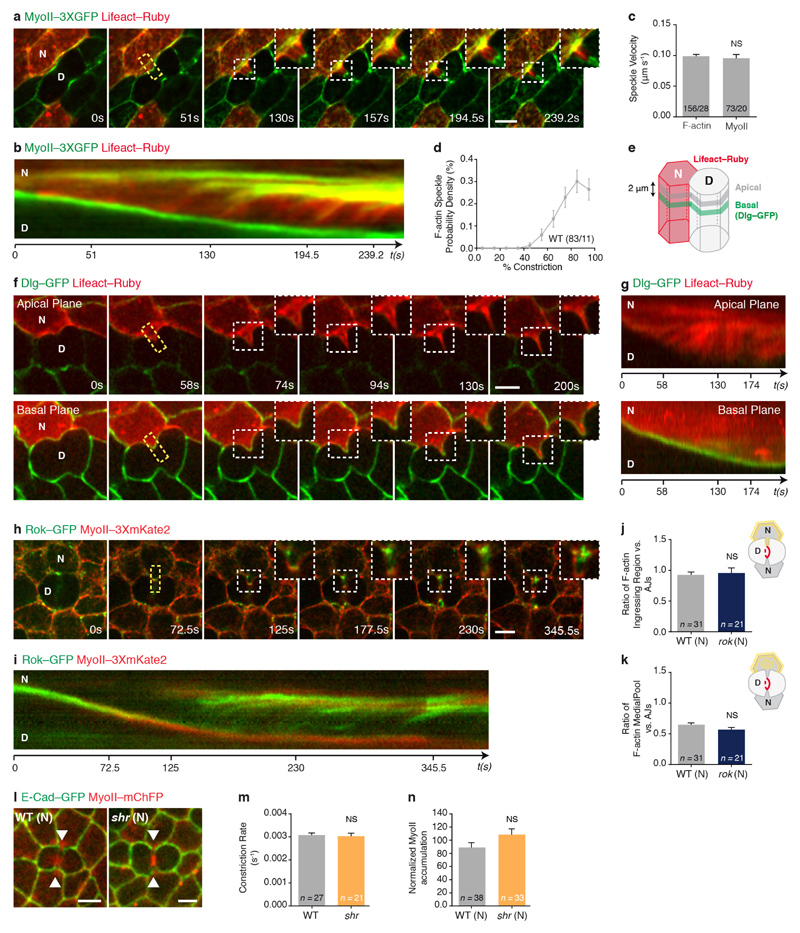
To test the predictions of the model, we analysed the existence and direction of the actomyosin flows, as well as their contribution for MyoII accumulation. We first performed complementary time-lapse, photobleaching and photoconversion experiments and showed that MyoII and the F-actin probe Lifeact form speckles that flow along the ingressing cell membranes, and accumulate at the base (Fig. 4d–h, Extended Data Fig. 9a, b and Supplementary Videos 7a–d). Moreover, in agreement with our 2D modelling: (1) the velocity of MyoII and Lifeact speckles is identical (Extended Data Fig. 9c); (2) the number of F-actin speckles within the ingressing region increases as constriction proceeds (Extended Data Fig. 9d); and (3) the flows take place in the AJ plane (Extended Data Fig. 9e–g and Supplementary Video 7e). Second, to test the role of the retrograde actomyosin flows in MyoII accumulation, we characterized the flow dynamics in several mutant conditions (Fig. 4i–p, Supplementary Video 8 and Extended Data Fig. 10a–n). In particular, cells neighbouring pnut or ani dividing cells, which generate lower forces and less E-cad decrease at the ingressing AJ (Figs 1e, 3e–g, Extended Data Figs 1i, j, m–o and 5k–o), exhibit lower MyoII accumulation and reduced the frequency of sustained Lifeact–Ruby flows or their velocities (Figs 1d, e, 4i–l, Extended Data Fig. 10a–d, Supplementary Videos 2b and 8a). Finally, loss of Rok-dependent contractility in the neighbours markedly reduced both MyoII accumulation and Lifeact–GFP speckle frequency and velocity (Fig. 4m–p, Supplementary Video 8b and Extended Data Fig. 5p–r), whereas loss of function of the formin Diaphanous (Dia) delays MyoII accumulation and induces only a weak decrease in speckle velocity (Fig. 4o, p, Extended Data Figs 7i, j and 10k, l). Together, our experimental data and theoretical analysis suggest that a decrease in E-cad concentration at the ingressing AJ, resulting from the pulling forces produced by contractile ring constriction, has a major role in driving the actomyosin flows in the neighbours.

Proposed mechanotransduction mechanisms function to stabilize cell–cell junctions under mechanical forces and involve increased binding of α-cat to E-cad and F-actin, reduced F-actin turnover and recruitment of Vinc, as well as MyoII to the AJ^7,16,18–22. Here, we provide evidence that under physiological forces, resulting from contractile ring constriction in the dividing cell, AJ mechanosensitivity arises from the local decrease in E-cad concentration and results in actomyosin flows in the neighbouring cells. Actomyosin flows produce forces to organize cell polarity, cell shape, cell movement, as well as junction remodelling^{11,13,17,23–25}. Our work now highlights an additional role of actomyosin flows in force sensing and transmission between epithelial cells. The integration of the roles of actomyosin flows in force production, sensing and transmission should provide a framework to understand the coordination of epithelial cell dynamics.

Methods

Fly stocks and genetics

Drosophila melanogaster stocks and associated references are listed in Supplementary Table 2. Flies were crossed and experiments were performed at 25 °C (except for form3^RNAi, frl^RNAi, rok^RNAi and shi^ts experiments and their respective control experiments, which were conducted at 29 °C). Loss-of-function, gain-of-function and dual-colour patch experiments were carried out using the FLP/FRT or the MARCM techniques^26–28. Somatic clones were induced in the second instar larval stage by heat-shock (from 10 min to 1 h 30 min) and analysed 2–4 days after clone induction in 15–18 h after puparium formation pupae.

Molecular biology

The vinc^Δ3, GFP–Vinc, E-cad–3 × GFP, E-cad–3 × mTagRFP and E-cad–3 × mKate2 alleles were generated by CRISPR/Cas9-mediated homologous recombination at their respective endogenous loci, using the vas-Cas9 line²⁹.

To generate the vinc^Δ3 and GFP–Vinc alleles, the single-guide RNAs (sgRNAs) were cloned into the pU6B-sgRNA-vector³⁰. For the vinc^Δ3 allele, which deletes the vinc coding sequence, the oligonucleotides used were respectively 5′-ATGGTTTTTGTGTGAAAGACGGG-3′ and 5′-CACTGACAATCGCCTAGTACTGG-3′; whereas for GFP–Vinc we used the following oligonucleotides: 5′-ATGGTTTTTGTGTGAAAGACGGG-3′ and 5′-GATGGTTTTTGTGTGAAAGACGG-3′. Homology sequences were cloned into a homologous recombination vector harbouring a hs-miniwhite cassette flanked by loxP sites³¹ and a GFP sequence for tagging (vector and respective map available upon request). The two homologous regions (HR1 and HR2) flanking the sites of CRISPR/Cas9 cuts were cloned using the following primers: (i) for vinc^Δ3: (HR1) 5′-CCGGGCTAATTATGGGGTGTCGCCCTTCGCTCTGTGCTCCCACTGGCTGGA-3′ and 5′-CTTCGTATAGCATACATTATACGAAGTTATCATTTTGGCTGCGCTTTTCGTCTG-3′; (HR2) 5′-TCGTATAATGTATGCTATACGAAGTTATTGTAGGCGATTGTCAGTGCCTACGG-3′ and 5′-AATTTTGTGTCGCCCTTGAACTCGATTGACCCCACTGAGGGCATTGCTCAAAC-3′; (ii) for GFP–Vinc: (HR1) 5′-CCCGGGCTAATTATGGGGTGTCGCCCTTCGTCTGTGCTCCCACTGGCTGGA-3′ and 5′-CCCGGTGAACAGCTCCTCGCCCTTGCTCACCATTTTGGCTGCGCTTTTCGTCTGATT-3′; (HR2) 5′-AGTTCGGGGTCCAGCGGTTCTTCAGGCAGTCCAGTCTTTCACACAAAAACCATCGAGAGC-3′ and 5′-GCCCTTGAACTCGATTGACGCTCTTCGACTCCTCTCGCTGACGCCGAATGT-3′.

The E-cad–3 × GFP, E-cad–3 × mTagRFP and E-cad–3 × mKate2 alleles were generated in two steps following the strategy used previously^31,32. First, an attP site was introduced along with a 4.8 kb deletion of the E-cad locus. The following CRISPR/Cas9 guides were used: 5′-AAGGTTTTCTGTATCGAACCGGG-3′ and 5′-TTTGTGTTTCCCTAAATGTGTGG-3′. The HR1 and HR2 homology sequences were cloned into a vector harbouring an attP site and a white shRNA flanked by loxP sites, using the following primers: (HR1) 5′-CGCCAAGCTTGCATGCCTGCAGGTCGACTCTAGAGGATCCGCGGCCGCAAAGTGAACGAAAATATCAGCCAGAGCAGC-3′ and 5′-AACTGAGAGAACTCAAAGGTTACCCCAGTTGGGGCACTACGCAATGAACCCAAAACCCGTCTCCAAGTGG-3′; (HR2) 5′-ATGCTATACGAAGTTATGCGGAGGATCCGGCGGCGGTGGGATTTAGGGAAACACAAATGGGGTAGAAATAAA-3′ and 5′-AACGACGGCCAGTGAATTCGAGCTCGGTACCCGGGGATCCGCGGCCGCAACAACCAGCTAGACATACATACCATTAATC-3′. According to ref. 31, ϕ31-mediated recombination was then used to complement the E-cad locus with transgenes harbouring the E-cad tagged-versions with either three mGFP, mTagRFP or mKate2 sequences in tandem. The E-cad–3 × mTagRFP, E-cad–3 × mKate2 and E-cad–3 × GFP alleles can be homozygous viable.

Dlg–mTagRFP was cloned by fusing the mTagRFP sequence with the Dlg cDNA sequence into the pUbi transformation vector. To generate the MyoII–3 × mKate2, the MyoII–3 × GFP and the MyoII–Drendra2 P-element transgenes, a C-terminal triple tandem repeat of the mKate2, GFP or a single Drendra2 sequence was respectively cloned into the sqh genomic rescue construct, which expressed the Myosin II regulatory light chain under the control of its endogenous promoter³³. The functionality of the MyoII–3 × mKate2 and MyoII–3 × GFP alleles were verified by rescue of the sqh^AX3 null allele. All injections were performed by Bestgene, except for ϕ31-mediated recombination.

Immunohistochemistry and fixed tissue imaging

Pupae were dissected and fixed as previously described³⁴. The primary and secondary antibodies used were rat anti-E-cad35 (1:300) and Cy5 donkey-anti-rat IgGs (1:300, Interchim), respectively. Images were collected with a LSM880 confocal microscope from Carl Zeiss and a 63× numerical aperture (NA) 1.4 OIL DICII PL APO objective (optical zoom 2×) in single-photon bidirectional scan mode. All images are sum projections at the level of the AJs (0.5 μm step size; 1.5–2 μm from a 7.5–10 μm stack).

Live imaging microscopy

Pupae were prepared for live imaging as described previously¹. Samples were imaged at 25 °C or 29 °C with an inverted confocal spinning disk microscope from Nikon or Zeiss, using either 60× NA 1.4 OIL DIC N2 PL APO VC, 63× NA 1.4 OIL DICII PL APO or 100× NA 1.4 OIL DIC N2 PL APO VC objectives and either a CoolSNAP HQ2 (Photometrics) or a CMOS (Hamamtsu) camera. Live imaging of E-cad–GFP, MyoII–3 × mKate2 and CAAX–mOrg was performed using a confocal microscope (LSM880, Carl Zeiss) with a 63× NA 1.4 OIL DICII PL APO objective (optical zoom 2×). To improve the signal-to-noise ratio, the CAAX–mOrg channel was denoised using the Feature J Derivatives, a Fiji plugin.

All experiments were performed during the first round of cell divisions in the anterior-central region of the notum tissue (15–18 h after puparium formation). In the analyses (unless mentioned otherwise), the time (t = 0) was set to zero at cytokinesis onset, identified by the initial cell constriction. All images correspond to sum projections at the level of the AJs (0.5 μm step size; 1.5–2 μm from a 7.5–10 μm stack), except the actomyosin flow experiments shown in Fig. 4 and Extended Data Figs 9 and 10, which correspond to single plane acquisition at the level of maximum MyoII–GFP, MyoII–Dendra2, MyoII–3 × mKate2 or MyoII–3 × GFP intensity. Note that in Extended Data Fig. 9f, g, we performed two-plane imaging as sketched in Extended Data Fig. 9e to visualize F-actin dynamics apically and at the level of the septate junctions.

The 3D reconstitution shown in Extended Data Fig. 1b and Supplementary Video 1 was generated from a high-resolution confocal z-stack of a dividing cell expressing the PH domain of PLCγ fused to ChFP (PH–ChFP) facing a PH–GFP-expressing neighbour. Such dual-colour analysis allowed us to discriminate the plasma membranes of the dividing cell and its neighbour during cytokinesis (0.5 μm step size; 18–20 μm stack), and perform a manual segmentation of each cell outline, using Imaris.

Photobleaching, photoactivation and photoconversion experiments

To determine E-cad–GFP dynamics, fluorescence recovery after photobleaching (FRAP) experiments were performed in wild-type and pnut^RNAi interphase cells in E-cad–GFP-expressing pupae. Regions, corresponding to approximately one-third of the total AJ length, were bleached (491 nm laser at 100% power, 40–50 iterations) using an inverted confocal spinning disk microscope from Nikon, a 100× NA 1.4 OIL DIC N2 PL APO VC objective and a CoolSNAP HQ2 (Photometrics) camera. Following photobleaching, confocal images were acquired at the level of the AJs every 5 s. To determine E-cad–GFP dynamics in wild-type dividing cells, similar FRAP experiments were conducted in the AJs of cells undergoing cytokinesis. In this case, images were acquired every second to correct for z-drift.

To analyse the relative contribution of the medial pool versus the ingressing region for MyoII accumulation in the neighbouring cells, adjacent cell patches of MyoII–GFP and MyoII–RFP-expressing cells were generated. MyoII–GFP accumulation was exclusively photobleached in the neighbouring cells at the clone boundary using the experimental setup described above (491 nm laser at 100% power, 40–50 iterations). Following photobleaching, confocal images were acquired every second at the plane of maximum MyoII–GFP intensity.

Photoactivation experiments were performed in E-cad–3 × PAGFP and MyoII–3 × mKate2 expressing pupae to analyse the dynamics of E-cadherin at the ingressing junction. The full AJ established between the dividing cell and its neighbour or a region of ±1 μm in diameter, corresponding to the tip of the ingressing AJ, were photoactivated using the setup described above and the 491 nm laser at 100% power (10–20 iterations). Following photoactivation, a confocal z-stack (0.5 μm step size; 1.5 μm stack) was acquired at the level of the AJs every 20 s and maximum projections are shown in Extended Data Fig. 5a, b and Supplementary Video 5 to maximize the signal-to-noise ratio.

MyoII photoconversion experiments were performed during cytokinesis in MyoII–Dendra2 expressing pupae. MyoII–Dendra2 was repeatedly photoconverted (every 1 s) in a region of ±1 μm in diameter, which corresponds to the tip of the ingressing junction, with the same experimental setup and the 491 nm laser, set at 100% power. Following photoconversation, confocal images were acquired every 2 s at the plane of maximum MyoII–Dendra2 intensity.

Laser ablations

Contractile ring laser ablations were performed in flies expressing E-cad–GFP and MyoII–mChFP. Images were acquired using a confocal laser-scanning microscope (LSM710 NLO, Carl Zeiss) equipped with a 63× NA 1.4 OIL DICII PL APO objective (optical zoom 2×) in single-photon bidirectional scan mode. The contractile ring was severed, at the level of the AJs, using the two-photon Ti:Sapphire laser (Mai Tai DeepSee, Spectra Physics) at 800 nm with < 100 fs pulses with a 80 MHz repetition rate, typically set at 25% power. Following laser ablation, a confocal image was acquired every second at the level of the AJs.

To test the contribution of the detached cortex for MyoII accumulation in the neighbouring cells, the initially detached cortex, labelled by MyoII–mChFP, was severed before MyoII accumulation was detectable, using the Ti:Sapphire laser at 800 nm with < 100 fs pulses with a 80 MHz repetition rate, typically set at 25% power. Confocal images were then acquired at the level of the E-cad–GFP labelled AJ every 5 s.

Recoil velocity upon contractile ring laser ablation

To measure the recoil velocity upon contractile ring laser ablation, time-lapse videos were generated as described above. For the quantification, we generated kymographs along the contractile ring, encompassing both the dividing cell and its neighbours. Using the kymograph, the dividing cell diameter over time was measured using a custom made MATLAB code. The recoil velocity was then measured between t₀ and t₂₀ (averaging the two time points closest to t₂₀)³⁶.

The amount of constriction before contractile ring laser ablation was determined as the difference in cell diameter before contractile ring laser ablation and upon full cell relaxation divided by the cell diameter upon full cell relaxation.

Rate of contractile ring constriction

To determine the rate of contractile ring constriction, time-lapse movies of E-cad–GFP or E-cad–3 × GFP and MyoII–mChFP or MyoII–3 × mKate2 were generated. The contractile ring length from the onset of cytokinesis t₀ (t = 0) to full constriction was manually measured using a Fiji macro. The rate of constriction was determined as the slope of the linear fit of the contractile ring length normalized to its length at the onset of cytokinesis (t₀) as a function of time³⁶. For pnut^RNAi (or pnut mutant cells), rok^RNAi and ani^RNAi dividing cells, which constrict very slowly, only the linear part of the curves was fitted to determine the constriction rate.

MyoII accumulation in the neighbouring cells

MyoII accumulation in the neighbours was determined in E-cad–GFP or E-cad–3 × GFP and MyoII–mChFP or MyoII–3 × mKate2 tissues. Since initial quantifications showed that the maximum of MyoII accumulation in wild-type cells is observed at 80% of the initial cell diameter, MyoII–mChFP or MyoII–3 × mKate2 accumulation in the neighbouring cells was quantified at this time point in all experimental conditions.

Upon determination of the time-point corresponding to 80% of the initial cell diameter, MyoII–mChFP or MyoII–3 × mKate2 accumulation was determined as the average of the 2 time points closest to 80% of the initial cell diameter. To quantify MyoII–mChFP or MyoII–3 × mKate2 accumulation in an unbiased manner using Fiji, the mean MyoII intensity of the neighbouring cells in each frame was used to threshold the image and select pixels above the mean intensity and thus obtain a ROI of the regions of MyoII–mChFP or MyoII–3 × mKate2 accumulation. The integrated density of the ROI at the base of the ingressing AJ was then determined. MyoII–mChFP or MyoII–3 × mKate2 accumulation in the neighbouring cells was normalized by the mean MyoII–mChFP/MyoII–3 × mKate2 cortical intensity in the neighbours.

Angle formed by the ingressing AJ

To determine the angle formed by the ingressing AJ, E-cad–GFP and MyoII–mChFP time-lapse movies were generated and the angles were measured manually using a Fiji Macro, as schematically represented in Extended Data Fig. 3c. Note that the angle of cortex detachment was only determined in neighbouring cells where cortical MyoII detachment was clearly detectable.

E-cad–GFP recovery upon photobleaching

To analyse E-cad–GFP dynamics, the FRAP time-lapse movies were first bleach-corrected (histogram matching option) using Fiji. To determine E-cad–GFP turnover, E-cad–GFP mean intensity in the bleached region was then measured manually in Fiji, using a 3-pixel-wide box centred at the position of the AJs (pixel size: 0.13 × 0.13 μm). To quantify the E-cad coefficient of diffusion, the E-cad–GFP mean intensity across the entire AJ was measured, using a plot profile of a 3-pixel-wide line drawn manually using Fiji (pixel size: 0.13 × 0.13 μm). The fitting strategies used to extract the turnover time, the mobile and the immobile fractions and the coefficient of diffusion are detailed in the Supplementary Note.

E-cad–GFP intensity along the ingressing AJ

Time-lapse movies of E-cad–GFP and MyoII–mChFP were acquired as a z-stack every 20 s (0.5 μm step size; 7.5–10 μm stack). The sum projection of the z-stack was corrected for photobleaching using Fiji (histogram matching option). Then, custom MATLAB codes were used to obtain the total AJ length, the E-cad–GFP mean intensity at the AJ and a stretched kymograph.

First, a MATLAB code was used to segment the E-cad–GFP cell contours³⁷. Upon manual correction of the segmented contours, in particular at the position of the ingressing AJ, where the E-cad–GFP signal is low (we used both the remaining E-cad–GFP signal, as well as the MyoII–mChFP signal, which labels the contractile ring in the dividing cell, as an additional landmark), a second MATLAB code was used to track the cell junctions³⁸. Third, the pixel contour of the AJ was extracted at each time point and a stretched kymograph along the ingressing AJ was generated, using a 3-pixel-wide averaging box sliding along the pixel contour at each time point (pixel size: 0.13 × 0.13 μm).

At the onset of contractile ring constriction, the total AJ length slightly decreases and elongation starts on average at 30% of constriction. Thus, we used this time point to normalize the total AJ length, the E-cad–GFP-integrated density at the AJ, the mean E-cad–GFP intensity at the tip of the ingressing AJ and the total E-cad–GFP intensity at the ingressing AJ.

To measure the E-cad–GFP-integrated density along the ingressing AJ, we multiplied the mean E-cad–GFP intensity at the ingressing AJ by the total AJ length before AJ elongation (t_{30% constriction}) and upon full contractile ring constriction (t_final).

The kymographs along the ingressing junction were also used to quantify the local E-cad–GFP concentration at the ingressing AJ, by defining a 10-pixel-wide box centred at the tip of the ingressing AJ and measuring the mean E-cad–GFP intensity as a function of time (pixel size: 0.13 × 0.13 μm). The mean GFP background intensity was determined at the centre of each quantified cell and subtracted to the average E-cad–GFP intensity.

Width and height of the ingressing AJ

Using E-cad–GFP and MyoII–mChFP time-lapse movies generated in different experimental conditions, we measured the width and height of the ingressing AJ, using Fiji. The width is defined as the distance between the inflection points at the base of the ingressing AJ, whereas the height corresponds to the distance between the tip and the base of the ingressing AJ, as represented in Extended Data Fig. 4i, j (pixel size: 0.13 × 0.13 μm).

Ratio of E-cad–3 × GFP intensity at the tip versus the base of the ingressing AJ

E-cad–3 × GFP intensity was determined at 60% of contractile ring constriction in wild-type or E-cad mutant cells neighbouring a wild-type or a pnut dividing cell. For that, we measured E-cad–3 × GFP intensity at the tip and at the base of the ingressing AJ, using a 4-pixel-wide circle in Fiji (pixel size: 0.13 × 0.13 μm). A similar strategy was used to quantify the intensity of E-cad–3 × GFP at the ingressing AJ in wild-type cells, marked by two copies of E-cad–3 × GFP, neighbouring either wild-type or pnut E-cad double-mutant dividing cells.

Velocity of the actin and myosin flows

To determine the velocity of the F-actin flows in the neighbouring cells, we performed time-lapse confocal imaging of Lifeact–GFP expressing neighbours in a MyoII–3 × mKate2 tissue at the rate of one image per second. Kymographs parallel to the ingressing membrane encompassing 10–20 pixels in width were then generated (pixel size: 0.065 × 0.065 μm or 0.13 × 0.13 μm, respectively; see, for example, Fig. 4g, h). The velocity of the F-actin speckles (defined as the boundary between the high and low Lifeact–GFP signals) was manually determined using Fiji, by fitting a line and determining its slope on each kymograph speckle trajectory. Similar analyses were performed for rok, dia and E-cad neighbouring cells marked by Lifeact–GFP expression, for wild-type and moe^RNAi neighbours marked by Lifeact–Ruby expression, and for cells neighbouring wild-type, pnut^RNAi and ani^RNAi dividing cells, also marked by Lifeact–Ruby expression. Importantly, to clearly visualize F-actin dynamics in the cells neighbouring pnut^RNAi and ani^RNAi dividing cells, as well as their respective wild-type control, we photobleached Lifeact–Ruby in the dividing cell before acquisition.

To determine the velocity of the MyoII flows in the neighbouring cells, we performed time-lapse confocal imaging of Lifeact–Ruby-expressing neighbours in a MyoII–3 × GFP tissue at the rate of one image per second. Kymographs parallel to the ingressing membrane were generated and the velocity of the MyoII speckles was manually determined as described above, using Fiji.

To determine the F-actin speckle probability density, we used time-lapse movies of wild-type dividing cells facing Lifeact–GFP labelled neighbours in a MyoII–3 × mKate2 tissue, acquired as described above. We then determined the amount of contractile ring constriction at the time of the appearance of each speckle.

F-actin intensity at the ingressing AJ, the medial pool or the remaining AJs

To determine whether rok regulates F-actin levels in the neighbours, we measured both the ratio of F-actin at the ingressing AJ and the remaining AJs, and the F-actin ratio at the medial pool and the remaining AJs. For that, we generated time-lapse movies of wild-type and rok neighbouring cells, expressing Lifeact–GFP facing wild-type dividing cells in a MyoII–3 × mKate2 tissue. Using Fiji, we manually measured Lifeact–GFP intensity at the ingressing AJ, at the medial pool and at the remaining AJs (using a 5-pixel-thick line for movies acquired with pixel size: 0.13 × 0.13 μm and a 10-pixel-wide line for movies acquired with pixel size: 0.065 × 0.065 μm) at 80% of the initial cell diameter. A schematic representation of the quantification strategy is included in Extended Data Fig. 9j, k.

Statistics

No statistical methods were used to determine sample size, which are all reported in the figure legends. The biological replicate is defined as the number of pupae used in each experiment. No inclusion/exclusion or randomization criteria were used and all analysed samples are included. In the figures, except noted otherwise, the graphs show mean ± s.e.m., while in Supplementary Table 1 we show the s.d., as it was used to determine the intervals of confidence of the numerical integrations shown in Extended Data Figs 4 and 5 (for additional details see the Supplementary Note). The s.e.m. and s.d. error bars are calculated and shown based on the number of cells. The statistical test used to access significance is stated in the figure legends and was chosen after the distribution normalities of each group were tested using the D’Agostino and Pearson omnibus normality test. To compare two groups, we used either a two-tailed Student’s t-test or a two-tailed Mann–Whitney U-test, depending on whether the dataset shows a normal distribution. When using the t-test, the variances were accessed using the F-test. If the variances were significantly different, a Welch correction was used. To compare more than two groups, we used either an ANOVA or a Kruskal–Wallis test, depending on the whether the dataset shows a normal distribution. In these cases, a correction was used to increase statistical power. The statistical analyses were performed with GraphPad Prism. No blind allocations were used during the experiments, nor when assessing their outcome.

Code and data availability

The MATLAB codes used to segment and track cells are described previously³⁷, whereas the remaining MATLAB code used to extract the kymographs along the neighbouring cell junction and the Fiji macros used to quantify the rate of contractile ring constriction, MyoII accumulation in the neighbouring cells and the angle formed by the ingressing AJ are available upon request³⁶. The codes used to perform simulations are provided as Supplementary Data files. The data supporting the findings of this study are either provided as Source Data or available from the corresponding author upon reasonable request.

Extended Data

Extended Data Figure 1. Estimation of the pulling forces produced during contractile ring constriction in wild-type, pnut^RNAi, rok^RNAi and ani^RNAi dividing cells.

a, Top view of a PH–GFP neighbour facing a PH–ChFP dividing cell during cytokinesis. Insets highlight the tight apposition of both cell membranes throughout cytokinesis. n = 12 cells (8 pupae). b, Top view and 3D reconstruction of a PH–GFP neighbour facing a PH–ChFP dividing cell (see Supplementary Video 1). n = 11 cells (7 pupae). c, PH–GFP and MyoII–3 × mKate2 distribution during cytokinesis. Insets highlight the progressive membrane deformation observed during cytokinesis, as well as MyoII accumulation in the neighbours (filled arrowheads). Orange and yellow dashed lines correspond to the orthogonal view of the dividing cell and its neighbours, respectively XZ and YZ planes. White dashed line in the YZ plane outlines the contractile ring throughout cytokinesis; asterisks indicate daughter cells. n = 18 cells (6 pupae). d, PH–GFP cell neighbouring a dividing cell in a MyoII–3 × mKate2 tissue. YZ view generated along the yellow box. Arrowheads as in c. n = 15 cells (5 pupae). e, E-cad–GFP and MyoII–mChFP localization upon contractile ring laser ablation (n = 48 ablations, 4 pupae). Laser ablation was performed before MyoII–mChFP accumulation in the neighbours (t = 0 s; orange box shows ablated region). Open arrowheads highlight absence of MyoII–mChFP accumulation in the neighbours. f, Rate of contractile ring constriction in wild-type, pnut^RNAi, rok^RNAi and ani^RNAi dividing cells (8, 6, 11 and pupae, respectively). g, i, k, m, Estimation of pulling forces produced by the contractile ring (labelled by MyoII–mChFP) on the AJ (marked by E-cad–GFP) by laser ablation in wild-type (g, n = 80 cells, 4 pupae), pnut^RNAi (i, n = 37 cells, 3 pupae), rok^RNAi (k, n = 54 cells, 5 pupae) and ani^RNAi (m, n = 39 cells, 3 pupae) dividing cells (t = 0 s; orange box shows ablated region). Dots indicate pnut^RNAi, rok^RNAi and ani^RNAi expressing cells, marked by the absence of cytosolic GFP. Dashed arrows indicate the dividing cells relaxation upon ring ablation. h, j, l, n, Recoil velocity upon contractile ring laser ablation versus the amount of ring constriction at the time of the ablation in wild-type (h, j, l, n), pnut^RNAi (j), rok^RNAi (l) and ani^RNAi (n) dividing cells. In pnut^RNAi, rok^RNAi and ani^RNAi dividing cells, the recoil velocity upon ring laser ablation is on average lower than in wild-type dividing cells (see o), and it scales less with the amount of contractile ring constriction at the time of the ablation (4, 3, 5 and 3 pupae, respectively). o, AJ recoil velocity upon contractile ring laser ablation in wild-type, pnut^RNAi, rok^RNAi and ani^RNAi dividing cells (4, 3, 5 and 3 pupae, respectively). p, Normalized MyoII accumulation at 80% of the initial cell diameter in cells neighbouring wild-type, pnut^RNAi, rok^RNAi and ani^RNAi dividing cells (5, 4, 11 and 4 pupae, respectively). Note that for pnut^RNAi and ani^RNAi dividing cells, we included wild-type and pnut^RNAi or ani^RNAi neighbours in our analysis, as when facing a wild-type dividing cell both pnut^RNAi or ani^RNAi neighbours accumulate MyoII to normal levels (Extended Data Fig. 5p–r). For rok^RNAi dividing cells, we analysed wild-type neighbours exclusively, as Rok function is also essential in the neighbours (Extended Data Fig. 5p–r). n denotes number of cells throughout. **P < 0.01, ****P < 0.0001, Kruskal–Wallis test. A re-plot of the dataset in o and p is provided in Fig. 1e. Data are mean ± s.e.m. Scale bars, 5 μm.

Extended Data Figure 2. Crb, α-cat and Dlg distribution during cytokinesis.

a, d, g, Schematic representation of the localization of E-cad and the supra-apical marker Crb (a), α-cat (d) or the septate junction marker Dlg (g) along the apical–basal axis of epithelial cells. b, e, h, Top view of E-cad–3 × mKate2 or E-cad–3 × GFP and Crb–GFP (b; n = 47 cells, 2 pupae), α-cat–GFP (e; n = 58 cells, 2 pupae) or Dlg–mTagRFP (h; 85 cells, 8 pupae) distribution in the dividing cell and its neighbours during cytokinesis. Insets highlight that although the E-cad–3 × mKate2 or E-cad–3 × GFP signals progressively decrease at the ingressing membrane, both Crb–GFP and Dlg–mTagRFP signals are still present in the supra-apical membrane and at the septate junctions, respectively. Conversely, E-cad–3 × mKate2 and α-cat–GFP signals decrease concomitantly at the ingressing AJ. Crb–GFP, Dlg–mTagRFP and E-cad–3 × mKate2 or E-cad–3 × GFP were projected from two different apical–basal confocal sections, which correspond to the planes of maximum intensity of Crb–GFP or Dlg–mTagRFP and the AJ, respectively. Yellow dashed lines used to generate the side views in c, f and i. c, f, i, Side view (YZ) of E-cad–3 × mKate2 or E-cad–3 × GFP and Crb–GFP (c; n = 47 cells, 2 pupae), α-cat–GFP (f; n = 58 cells, 2 pupae) or Dlg–mTagRFP (i; 85 cells, 8 pupae) distribution in the dividing cell and its neighbours at the onset of cytokinesis. Green arrowheads denote Crb–GFP (c), α-cat–GFP (f) or Dlg–mTagRFP (i), while red arrowheads indicate E-cad–3 × mKate2 (c, f) or E-cad–3 × GFP (i) localization along the apical–basal axis of epithelial cells. Scale bars, 5 μm.

Extended Data Figure 3. Contraction of the detached cortical MyoII is not sufficient to sustain MyoII accumulation in the neighbours.

a, β_H-spectrin–GFP (β_H-spec–GFP) and MyoII–3 × mKate2 distribution upon contractile ring constriction. Asterisk denotes co-localization of MyoII–3 × mKate2 and β_H-spec–GFP away from the ingressing AJ. n = 103 cells (4 pupae). b, Normalized MyoII intensity of the detached cortical MyoII and at 80% of the initial cell diameter in wild-type dividing cells (4 pupae). c, Schematic representation of the theoretical model describing cortex detachment in the neighbours. The AJs are highlighted in green, while the actomyosin cortex is shown in the red dashed line and in further detail in the insets. CR denotes the contractile ring. Double arrow indicates separation of the actomyosin cortex from the AJ—cortex detachment. Dashed black lines indicate the angle formed by the ingressing AJ. To probe the potential role of cortex detachment for MyoII accumulation in the neighbours, we analysed theoretically the detachment event. The cortex is a contractile layer lining the AJ, thus if it becomes curved, either because of an external deformation (that is, contractile ring constriction in the dividing cell) or a pressure difference between two cells (as observed during blebbing), this produces inward forces perpendicular to the membrane that need to be balanced by adhesion to prevent cortex detachment. The biophysical role of E-cad in this membrane–cortex interaction has been studied in vitro³⁹, but to a lesser extent in vivo. Following the classical active gel theory^10,40,41, we model the cortex as a thin viscous layer, of thickness h. γ is the local tension in the cortex, χ is the contractility due to MyoII motor power-stroke, and η is the cortical viscosity. Thus, along the direction x parallel to the membrane, the tension γ is the sum of active and viscous contributions γ = h(χ + η∂_xv), with v the local velocity in the layer, under the lubrication regime⁴⁰. If we consider a cortex connected to an AJ that can be curved with local curvature κ(x, t), in the quasi-static regime of the ingressing AJ during cytokinesis³⁹, the cortex will detach if the normal forces γκ are greater than the maximal adhesion force density f_c, which is proportional to the adhesion strength between the cortex and the membrane, as well as the local concentration c(x) of linker proteins. This is analogous to the de Gennes criteria for the unbinding of adhesive vesicles⁴². Therefore, for constant tension and adhesion strength, one expects the cortex to detach once a well-defined curvature κ_c, imposed by the contractile ring, is reached, such that κ_c = f_c/γ. Thus, the model predicts that the critical curvature of cortical detachment can be modulated in vivo: the maximal curvature at detachment should increase with either an increase in membrane–cortex attachment, or a decrease in cortical tension (and vice versa). We tested this model by manipulating experimentally either cortical tension or membrane–cortex attachment (d–f). As curvature cannot be robustly defined in the ingressing AJ given the length scales examined, we alternatively measured the angle θ between the two sides of the ingressing junction (c). With d₀ being the characteristic width of the ingressing region, this angle is related to curvature via κ ∝ (π − θ)/d₀. To manipulate the adhesion force, we analysed cortex detachment in moe^RNAi neighbours, as well as in E-cad heterozygous background (E-cad1x). Moesin is the only ERM protein in flies and it has an essential role in membrane–cortex attachment, since it directly binds both F-actin and the membrane⁴³. As predicted theoretically, upon moe^RNAi or in the E-cad1x mutant condition, cortex detachment occurs at higher angles than in wild-type neighbours; thus, the initially detached cortical MyoII is localized further away from the ingressing membrane during contractile ring constriction (d, e and h). Similarly, increasing the neighbours’ contractility by generating either sds22^RNAi neighbours, which increases phospho-MyoII and phospho-Moe at the AJs⁴⁴, or mbs^RNAi neighbours, which globally increases phospho-MyoII by blocking the activity of the MyoII phosphatase⁴⁵, results in cortex detachment at higher angles (d, e). Moreover, the angle of cortex detachment in these experimental conditions anti-correlates with the amount of constriction at detachment (f). Altogether, these data suggest that a balance between the adhesion force, cortex contractility and local membrane curvature regulates cortex detachment, in response to the pulling forces generated in the dividing cell. d, E-cad–GFP and MyoII–mChFP localization at cortex detachment in wild-type (n = 83 cells, 11 pupae), E-cad1x heterozygous mutant (n = 17 cells, 2 pupae), moe^RNAi (n = 18 cells, 6 pupae), sds22^RNAi (n = 19 cells, 5 pupae) and mbs^RNAi (n = 25 cells, 6 pupae) neighbours. Dots indicate moe^RNAi, sds22^RNAi or mbs^RNAi cells, marked by the absence of cytosolic GFP. Asterisks denote separation of MyoII–mChFP and E-cad–GFP signals at the ingressing region. e, Angle of cortex detachment in wild-type, E-cad1x, moe^RNAi, sds22^RNAi and mbs^RNAi neighbours (11, 2, 6, 5 and 6 pupae, respectively). For all conditions, except E-cad1x, the dividing cell is wild-type. Note that the rate of constriction is similar for wild-type and E-cad1x cells and no detectable defects were observed during cytokinesis. f, Anti-correlation between the angle of cortex detachment (in e) and the amount of contractile ring constriction at detachment in wild-type, E-cad1x, moe^RNAi, sds22^RNAi and mbs^RNAi neighbours (11, 2, 6, 5, pupae, respectively). Slope is −1.97 ± 0.15 (R² = 0.98). P < 0.001, F-test for a slope different from 0. g, E-cad–GFP and MyoII–mChFP localization in a pnut^RNAi dividing cell and its neighbours during cytokinesis. Filled arrowheads indicate transient MyoII–mChFP accumulation in the neighbours; open arrowheads denote reduced MyoII–mChFP accumulation in the neighbours. n = 10 out of 20 cells (5 pupae). h, E-cad–GFP and MyoII–mChFP localization in the dividing cell and its moe^RNAi neighbour. In g and h, dots denote pnut^RNAi (g) and moe^RNAi (h) cells, marked by the absence of cytosolic GFP, and asterisks denote separation of MyoII–mChFP and E-cad–GFP signals at the ingressing AJ. At t = 208 s, arrowhead indicates the transient accumulation of MyoII–mChFP at the detached cortex; at t = 340 s and 400 s, arrowheads indicate the re-localization of the MyoII–mChFP accumulation near the boundary between high and low E-cad–GFP (see Supplementary Video 4c). n = 18 cells (6 pupae). i, Percentage of wild-type and moe^RNAi neighbours (11 and 20 pupae, respectively), where the detached cortex and the E-cad boundary are superimposed. j, Percentage of wild-type and moe^RNAi neighbours (7 and 17 pupae, respectively), where the detached cortex either coalesces with the MyoII accumulation positioned at the E-cad boundary, or disassembles during cytokinesis (see Supplementary Video 4d). n denotes number of cells throughout. n/n indicates number of cells/total number of cells. *P < 0.05, ***P < 0.001, ****P < 0.0001. Student’s t-test (b) and Kruskal–Wallis test (e). Data are mean ± s.e.m. Scale bars, 5 μm.

Extended Data Figure 4. Decrease of E-cad concentration at the ingressing AJ is not impaired after Dynamin, Rab11 or Sec5 loss-of-function.

a, E-cad–GFP dividing cell facing an E-cad–3 × mTagRFP neighbour. Yellow open arrowheads denote concomitant decrease of E-cad–GFP and E-cad–3 × mTagRFP at the ingressing AJ. n = 17 cells (5 pupae). b, E-cad–GFP localization in the dividing cell and its neighbour expressing a dominant-negative temperature-sensitive dynamin allele, shi^ts (dots, marked by absence of cytosolic GFP) at 29 °C. n = 21 cells (3 pupae). c, d, E-cad–GFP localization in a YFP–Rab11^DN dominant-negative (c; n = 22 cells, 3 pupae) or sec5 (d; n = 9 cells, 4 pupae) dividing cell and its neighbours. Dots indicate YFP–Rab11^DN (c) or sec5 (d) cells, marked by YFP expression or by the absence of nls–GFP. Open arrowheads in b–d denote E-cad–GFP decrease at the ingressing AJ. e–g, Integrated density (IntDen) of E-cad–GFP at the ingressing AJ at the onset of AJ elongation (t_{30% constriction}) and upon full contractile ring constriction (t_final) for wild-type dividing cells facing either wild-type (e) or rok^RNAi neighbours (f), and pnut^RNAi dividing cells (g; 5, 7 and 6 pupae, respectively). h, Schematic representation of the E-cad dilution model. In this model, local membrane elongation, due to contractile ring (CR) constriction, progressively dilutes E-cad along the ingressing AJ (highlighted in the lighter green line used at the ingressing junction). i, j, Width of ingressing region normalized by total curvilinear AJ length (i) and height of the ingressing region (μm, j) as a function of the amount of constriction for wild-type dividing cells facing wild-type or rok^RNAi neighbours and pnut^RNAi dividing cells (5, 7 and 6 pupae, respectively). Insets represent the width and height of the ingressing region (E-cad–GFP, green; MyoII–mChFP, red, also shown in Fig. 2a). For wild-type dividing cells facing wild-type neighbours, the normalized width of the ingressing AJ is small (average 0.12) and decreases during constriction, whereas the height increases, thereby indicating that AJ elongation is a rather local process. Similarly, in wild-type dividing cells facing rok^RNAi neighbours, the normalized width remains small during constriction (average 0.26) and the height increases, indicating that the elongation of the AJ is also mainly local. Contrary to this, in cells neighbouring pnut^RNAi dividing cells, the normalized width of the pulled region is much wider (average 0.49) and the height is much smaller and remains constant during constriction. This argues for a more global elongation of the ingressing AJ. k, Normalized total AJ elongation upon full contractile ring constriction of wild-type dividing cells (t_final) facing wild-type or rok^RNAi neighbours and pnut^RNAi dividing cells (5, 7 and 6 pupae, respectively). l, Normalized local E-cad–GFP intensity at the ingressing AJ versus the normalized total AJ elongation in wild-type dividing cells (5 pupae), and the corresponding theoretical integration (line corresponds to best-fit parameters measured by E-cad–GFP FRAP, shaded regions correspond to 1 s.d. confidence interval). The coefficient of determination and the s.d. of the residuals is respectively R² = 0.82 and S = 0.12. n denotes number of cells throughout. NS, not significant, *P < 0.05, **P < 0.01, ****P < 0.0001. Paired Student’s t-test (e–g) and Kruskal–Wallis test (k). Data are mean ± s.e.m. (e–g, i–k) or ± s.d. (l). Scale bars, 5 μm.

Extended Data Figure 5. Local AJ elongation is sufficient to trigger a decrease of E-cad concentration at the ingressing AJ.

a, b, Photoactivation of E-cad–3 × PAGFP at the AJ shared between the dividing cell and its neighbour (a; n = 19 cells, 5 pupae) or at the tip of the ingressing AJ (b; n = 25 cells, 6 pupae) in a MyoII–3 × mKate2 tissue (t = 0 s, orange boxes denote photoactivated regions). White brackets indicate reduction of photoactivated E-cad–3 × PAGFP signal at the ingressing AJ. Yellow filled arrowheads indicate that at the base of the ingressing AJ, the photoactivated E-cad–3 × PAGFP signal remains high. c, d, E-cad–GFP distribution in the dividing cell and its rok^RNAi neighbours (dots, marked by the absence of cytosolic GFP). Kymograph in d along the yellow box. Yellow open arrowheads denote reduced E-cad–GFP signal at the ingressing AJ. n = 20 cells (7 pupae). e, Normalized local E-cad intensity at ingressing AJ (solid line), and normalized total AJ elongation (dashed line) versus the amount of constriction in wild-type dividing cells facing rok^RNAi neighbours (7 pupae). f, Numerical integration of E-cad levels on a locally elongating AJ, as measured in wild-type dividing cells facing rok^RNAi neighbours. g–i, E-cad–GFP and MyoII–mChFP distribution in a wild-type dividing cell facing a rok^RNAi and a wild-type neighbour. Kymographs in h and i generated along the yellow and orange lines, respectively. White open arrowheads denote reduced MyoII–mChFP accumulation in the neighbours; yellow filled arrowheads denote absence of E-cad–GFP decrease at the ingressing AJ; yellow open arrowheads denote decrease of E-cad–GFP at the ingressing AJ. In 15% of cases (n = 20, 7 pupae), the contractile ring is positioned off-centre. In these cases, junction elongation on the wild-type side is small and no decrease in E-cad is observed (h). Furthermore, MyoII does not accumulate in this wild-type neighbour. As shown above, in the rok^RNAi side, the junction elongates and E-cad decreases (c–f, i). This further argues that junction elongation is an important factor in the local decrease in E-cad signal. j, m, Normalized local (j) or total E-cad–GFP (m) intensity at the ingressing AJ versus the normalized total AJ elongation in wild-type dividing cells facing rok^RNAi neighbours (j; 7 pupae), or pnut^RNAi dividing cells (m; 6 pupae) and the corresponding theoretical integrations, respectively (line corresponds to the best-fit parameters measured by E-cad–GFP FRAP, shaded regions correspond to 1 s.d. confidence interval). The coefficient of determination and s.d. of the residuals are respectively R² = 0.69, S = 0.14 (j) and R² = 0.73, S = 0.03 (m). k, l, E-cad–GFP distribution in a pnut^RNAi dividing cell and its neighbours. Kymograph in l along the yellow line. Yellow arrowheads as in g. In 14 out of the 28 cells analysed (6 pupae), cells neighbouring pnut^RNAi dividing cells show a transient decrease in E-cad–GFP levels at the ingressing AJ. In all cases, these reductions in E-cad levels occur during earlier stages of contractile ring constriction. All cells shown express pnut^RNAi, marked by the absence of cytosolic GFP. n, o, E-cad–GFP and MyoII–mChFP distribution in an ani^RNAi dividing cell and its neighbours (dots, marked by absence of cytosolic GFP). Kymograph in o generated along the yellow line. Arrowheads as in g. ani^RNAi dividing cells exert lower pulling forces (see Fig. 1e and Extended Data Fig. 1m–o) on the neighbour membranes during constriction and induce a less pronounced decrease in E-cad signal along the ingressing AJ. Note that in comparison to the upper junction, the lower junction exhibits a partial reduction of E-cad levels. Accordingly, a small MyoII accumulation can be observed. n = 17 cells (3 pupae). p, E-cad–GFP and MyoII–mChFP localization in wild-type (n = 32 cells, 5 pupae), pnut^RNAi (n = 32 cells, 4 pupae), rok^RNAi (n = 29 cells, 11 pupae) and ani^RNAi (n = 20 cells, 4 pupae) neighbours facing a wild-type dividing cell. Dots denote pnut^RNAi, rok^RNAi and ani^RNAi cells, marked by the absence of cytosolic GFP. White filled and open arrowheads indicate MyoII–mChFP accumulation and reduced accumulation in the neighbours, respectively. Note that the phenotype of rok^RNAi neighbouring cells is specific, as pnut^RNAi and ani^RNAi neighbours facing a wild-type dividing cell still accumulate MyoII similarly to wild-type neighbours (see r). q, Rate of contractile ring constriction in wild-type dividing cells facing wild-type, pnut^RNAi, rok^RNAi and ani^RNAi neighbours (5, 4, 11 and 4, respectively). Although Rok abrogates MyoII accumulation in the neighbours, it doesn’t affect the rate of constriction in the dividing cell (see r). r, Normalized MyoII accumulation at 80% of the initial cell diameter in wild-type, pnut^RNAi, rok^RNAi and ani^RNAi neighbours (5, 4, 11 and 4 pupae, respectively) facing wild-type dividing cells. n denotes number of cells throughout. ****P < 0.0001, Kruskal–Wallis test. Data are mean ± s.e.m. (e, q, r) or ± s.d. (j, m). Scale bars, 5 μm.

Extended Data Figure 6. Lowering E-cad concentration in cells neighbouring a pnut dividing cell rescues MyoII accumulation.

a, E-cad (dashed outline), wild-type and pnut (dots) cells marked by 0, 1 and 2 copies of E-cad–3 × GFP, respectively. The residual E-cad levels inside the E-cad hypomorphic mutant cells (E-cad^hyp) were assessed by antibody staining. White full and dashed arrows denote E-cad staining and decreased staining at the AJ, respectively. n = 79 clones (11 fixed pupae). b, Representation of the experimental setup in Fig. 3i, in which a pnut dividing cell, marked by 2 copies of E-cad–3 × GFP, is facing a wild-type neighbour and an E-cad^hyp neighbour, marked by 1 and 0 copies of E-cad–3 × GFP, respectively. c, Percentage of cytokinesis failure of pnut dividing cells facing either wild-type or E-cad neighbours (53 or 35 pupae, respectively). In contrast to previous findings³, our data show that the cytokinesis failure of pnut dividing cells is not rescued by reducing E-cad levels in the neighbours. d, Rate of contractile ring constriction in wild-type and pnut dividing cells facing either wild-type or E-cad neighbours (6, 11, 15 and 15 pupae, respectively). In agreement with c, the rate of constriction is similar in pnut dividing cells facing either wild-type or E-cad neighbours. e, Normalized AJ elongation at the onset of AJ elongation (t_{30% constriction}), at 80% of the initial cell diameter (timing in which MyoII accumulation in the neighbours was measured) and upon full contractile ring constriction (t_final) of wild-type and pnut dividing cells neighboured by wild-type or E-cad neighbours (6, 11, 15 and 15 pupae, respectively). f, Representation of the experimental setup in g, in which an E-cad^hyp pnut double-mutant dividing cell, marked by 0 copies of E-cad–3 × GFP, is facing a wild-type neighbour, marked by E-cad–3 × GFP. g, MyoII–3 × mKate2 distribution in a wild-type neighbouring cell, marked by E-cad–3 × GFP expression, facing an E-cad pnut double-mutant dividing cell (dots), marked by the absence of E-cad–3 × GFP. White arrowheads denote MyoII–3 × mKate2 accumulation in the neighbour. Yellow brackets indicate reduced E-cad–3 × GFP signal at the ingressing AJ. Orange arrowhead indicates cytokinesis failure, evident by the detachment of the midbody from the dividing cell membranes. n = 26 cells (10 pupae). h, Percentage of cytokinesis failure of E-cad pnut double-mutant dividing cells facing wild-type or E-cad pnut neighbours (11 or 10 pupae, respectively). These findings further support that the cytokinesis defects observed in pnut mutant cells (c) are intrinsic to the dividing cell. i, Rate of contractile ring constriction in wild-type or E-cad pnut double-mutant dividing cells facing wild-type neighbours (6 or 10 pupae, respectively). j, Normalized MyoII accumulation at 80% of the initial cell diameter in wild-type cells neighbouring wild-type or E-cad pnut double-mutant dividing cells (6 or 10 pupae, respectively). k, Ratio of E-cad–3 × GFP intensity at the tip versus the base of the ingressing AJ in wild-type cells neighbouring wild-type or E-cad pnut double-mutant dividing cells (6 or 10 pupae, respectively). n denotes number of cells throughout. n/n indicates the number of cells that failed cytokinesis/total number of cells. *P < 0.05, ****P < 0.0001, ANOVA (d) or Mann–Whitney U-test (i–k). Data are mean ± s.e.m. Scale bars, 5 μm.

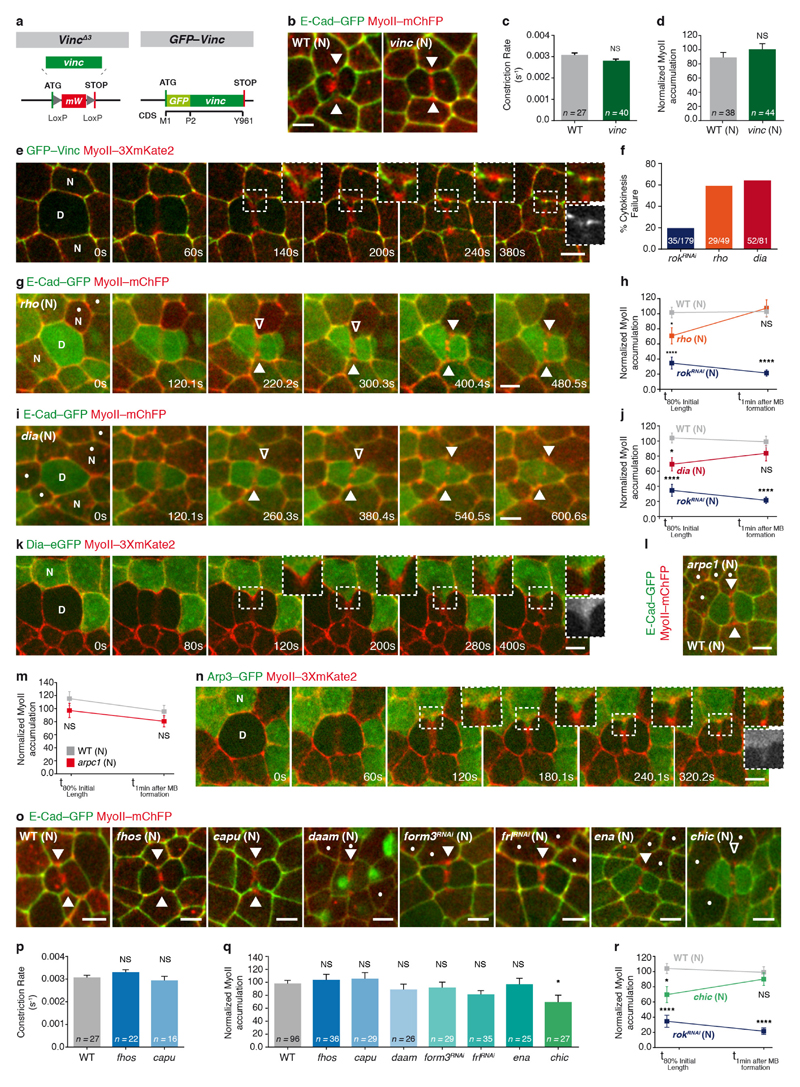
Extended Data Figure 7. Analysis of the role of Vinc, Rho and several F-actin nucleators in MyoII accumulation in the neighbours.

a, Structure of vinc^Δ3 and GFP–Vinc alleles generated by CRISPR/Cas9-mediated homologous recombination, showing position of GFP tag insert relative to vinc coding sequence. M1, methionine 1; P2, proline 2. b, E-cad–GFP and MyoII–mChFP localization in wild-type (n = 38 cells, 2 pupae) and vinc (n = 44 cells, 2 pupae) neighbours. Filled arrowheads denote MyoII–mChFP accumulation in the neighbours. c, Rate of contractile ring constriction in wild-type and vinc dividing cells (2 and 2 pupae, respectively). d, Normalized MyoII accumulation at 80% of the initial cell diameter for wild-type and vinc neighbours (2 and 2 pupae, respectively). e, GFP–Vinc and MyoII–3 × mKate2 localization during cytokinesis. During constriction, GFP–Vinc is reduced along the ingressing AJ and does not accumulate with MyoII–3 × mKate2 at the base of the ingressing membrane. Greyscale inset shows GFP–Vinc localization upon full contractile ring constriction. n = 46 cells (3 pupae). f, Cytokinesis failure in rok^RNAi, rho and dia dividing cells. n/n indicates the number of cells that failed cytokinesis/total number of cells (10, 10 and 7 pupae, respectively). The percentage of cytokinesis failure in rho and dia dividing cells is higher than that observed in rok^RNAi dividing cells. However, loss of Rho or Dia function in the neighbours only delays MyoII accumulation in the neighbours, whereas rok^RNAi in the neighbours strongly impairs it (g–j). g, i, E-cad–GFP and MyoII–mChFP localization in a rho (g; n = 30 cells, 10 pupae) or a dia (i; n = 26 cells, 7 pupae) mutant cell neighbouring a wild-type dividing cell (dots, marked by the absence of nls–GFP). Open arrowheads denote decreased MyoII–mChFP accumulation from mid-constriction until 80% of the initial cell diameter and MyoII–mChFP accumulation following midbody formation, respectively. h, j, Normalized MyoII accumulation at 80% of the initial cell diameter and 1 min after midbody formation in wild-type (n = 53 cells, 9 pupae), rok^RNAi (n = 29 cells, 11 pupae) and rho (h; n = 30 cells, 10 pupae) or dia (j; n = 26 cells, 7 pupae) neighbouring cells facing wild-type dividing cells. k, n, Dia–eGFP (k; n = 33 cells, 9 pupae) or Arp3–GFP neighbours (n; n = 30 cells, 2 pupae) facing a dividing cell in a MyoII–3 × mKate2 tissue. Greyscale insets denote Dia–eGFP (k) or Arp3–GFP (n) localization upon full contractile ring constriction. Both Dia–eGFP and Arp3–GFP are uniformly localized along the ingressing region throughout constriction in the dividing cell. l, E-cad–GFP and MyoII–mChFP localization in wild-type and arpc1 mutant neighbours (dots, marked by the absence of nls–GFP) facing a wild-type dividing cell (n = 27 cells, 7 pupae) at 80% of the initial cell diameter. Arrowheads as in b. m, Normalized MyoII accumulation at 80% of the initial cell diameter and 1 min after midbody formation for wild-type (n = 25 cells, 5 pupae) and arpc1 (n = 27 cells, 7 pupae) neighbours facing wild-type dividing cells. o, E-cad–GFP and MyoII–mChFP localization in wild-type (n = 96 cells, 12 pupae), fhos (n = 36 cells, 3 pupae), capu (n = 29 cells, 4 pupae), daam (n = 26 cells, 5 pupae), form3^RNAi (n = 29 cells, 7 pupae), frl^RNAi (n = 35 cells, 13 pupae), ena (n = 25 cells, 8 pupae) and chic (n = 27 cells, 6 pupae) neighbours. Since Capu and fhos loss-of-function mutants are viable, MyoII accumulation was analysed in capu or fhos tissues. Notably, the rate of contractile constriction in both fhos and capu dividing cells is similar to wild-type cells and no detectable defects were observed during cytokinesis (p). For all other conditions, the dividing cell is wild-type. Dots denote daam, form3^RNAi, frl^RNAi, ena and chic mutant cells, marked by the absence of His2a–GFP, cytosolic GFP or nls–GFP. Filled and open arrowheads denote MyoII–mChFP accumulation and reduced accumulation in the neighbours, respectively. p, Rate of contractile ring constriction in wild-type, fhos or capu dividing cells (2, 3 or 4 pupae, respectively). q, Normalized MyoII accumulation at 80% of the initial cell diameter for wild-type, fhos, capu, daam, form3^RNAi, frl^RNAi, ena and chic neighbours (12, 3, 4, 5, 7, 13, 8 or 6 pupae respectively). r, Normalized MyoII accumulation at 80% of the initial cell diameter and 1 min after midbody formation for wild-type (n = 57 cells, 10 pupae), chic (n = 27 cells, 6 pupae) or rok^RNAi (n = 29 cells, 11 pupae) neighbours facing wild-type dividing cells. n denotes number of cells. *P < 0.05, ****P < 0.0001, Mann–Whitney U-test (c), Student’s t-test (d), ANOVA (m, q), Kruskal–Wallis test (h, j, p, r). Data are mean ± s.e.m. Scale bars, 5 μm.

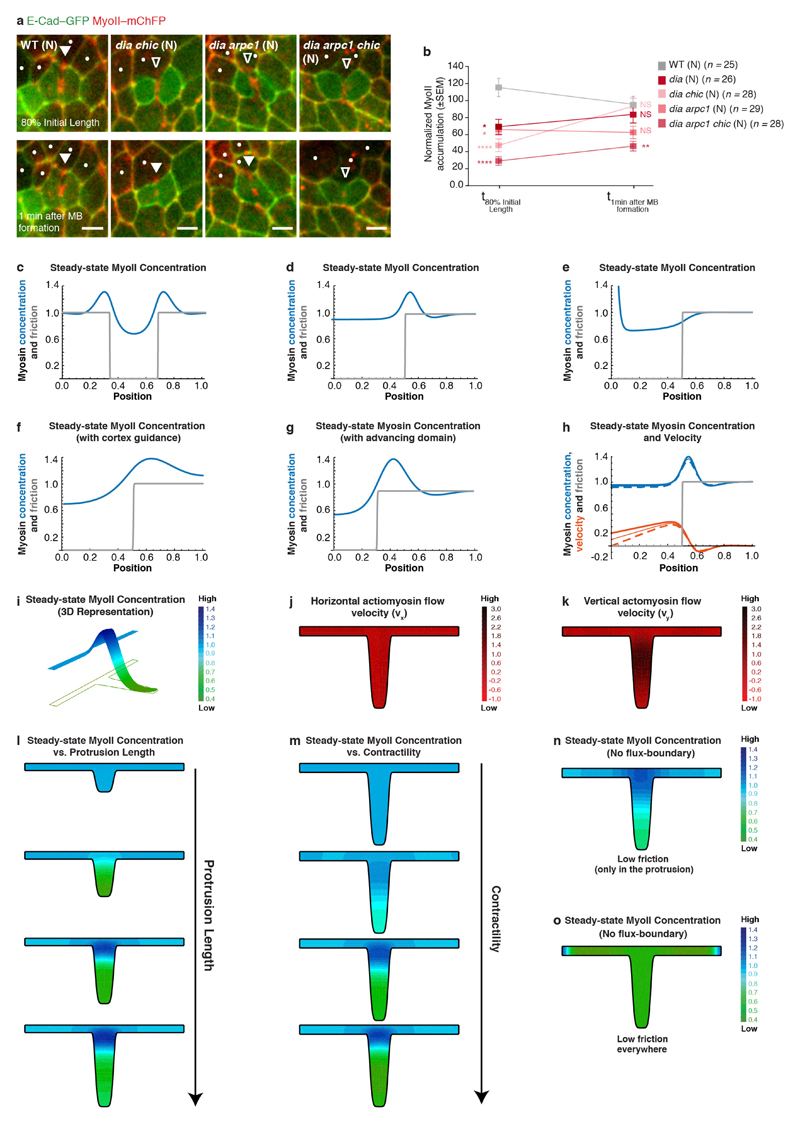
Extended Data Figure 8. Modelling the neighbouring cell’s response.

a, E-cad–GFP and MyoII–mChFP localization in wild-type (n = 25 cells, 5 pupae), dia chic (also known as profilin) double-mutant (n = 28 cells, 7 pupae), dia arpc1 double-mutant (n = 29 cells, 7 pupae) and dia arpc1 chic triple-mutant (n = 28 cells, 4 pupae) cells neighbouring wild-type dividing cells at 80% of the initial cell diameter and 1 min after midbody formation. Dots denote dia chic, dia arpc1 or dia arpc1 chic cells, marked by the absence of nls–GFP. Filled and open arrowheads indicate MyoII–mChFP accumulation and reduced accumulation in the neighbours, respectively. As single Formin, Arp2/3 or Enabled mutants show at most a delay in accumulation of MyoII (see Extended Data Fig. 7), we tested whether a drastic reduction of F-actin nucleation might impair the neighbours’ response. Loss of arpc1 function does not impair MyoII accumulation in the neighbours (see Extended Data Fig. 7l, m), but the dia aprc1 double mutant has a stronger phenotype than dia alone, especially upon midbody formation (see Extended Data Fig. 7i, j). However, loss of both dia and aprc1 function does not fully abrogate MyoII accumulation. We therefore repeated these experiments in a sensitized background by reducing the overall levels of F-actin using a chic mutant, which has a general role in actin polymerization in epithelial cells⁴⁶. While reducing chic function in a dia mutant background modestly enhances the phenotype of dia loss of function, we found that loss of Dia, Arp2/3 and Profilin function (dia arpc1 chic triple-mutant cells) strongly affects MyoII accumulation both at 80% of the initial cell diameter and after midbody formation (see b). These results argue that either Dia or the Arp2/3 complex can generate the necessary F-actin network to promote MyoII accumulation, and that only a marked reduction in F-actin polymerization using the triple-mutant combination can efficiently abrogate MyoII accumulation in the neighbours. Together, these analyses argue against the role of a single specific Actin nucleator or the involvement of a specific F-actin network in promoting MyoII accumulation in the neighbours. b, Normalized MyoII accumulation at 80% of the initial cell diameter and 1 min after midbody formation for wild-type, dia single-, dia chic double-, dia arpc1 double- and dia arpc1 chic triple-mutant cells neighbouring wild-type dividing cells (5, 7, 7, 7 and 4 pupae, respectively). *P < 0.05, **P < 0.01, ****P < 0.0001. Kruskal–Wallis test. c–h, One-dimensional numerical integration of the active gel equations. The friction coefficient is shown in grey and the steady-state MyoII concentration is in blue. c, For a decreased value of the friction coefficient at the centre of the integration box, MyoII shows two accumulations at both interfaces between high and low friction. d, e, For a decreased value of the friction coefficient at the edge of the simulation box, Myosin final intensity shows two possible solutions: accumulation at the boundary between the low and high friction domains (d), or accumulation at the low friction edge of the simulation box (e). f, g, Same one-dimensional numerical integration as in (d and e), but with either preferential polymerization in the high friction zone (f), or advancing low friction region to mirror AJ ingression during contractile ring constriction (g). In both cases, MyoII robustly accumulates at the interface between the high and low friction domains. h, Same one-dimensional numerical integration as in (d and e), but with a boundary condition of non-zero velocity at the tip (v(x = 0,t) = 0.1 thin lines, v(x = 0,t) = 0.2 thick lines). The dashed lines show v(x = 0,t) = 0 (d) for comparison. We show that the MyoII concentration profile (blue) is unaffected by this boundary condition, and the velocity profile (orange) becomes flatter for increasing boundary velocity (see Supplementary Note). i, Same numerical integration as in Fig. 4b with a three-dimensional representation of the steady-state MyoII concentration. j, k, Steady-state velocity of the actomyosin flows in the horizontal and vertical direction, respectively v_x (j) and v_y (k). l, Steady-state MyoII concentration for increasing protrusion lengths, at constant contractility (colour-code as in i). Actomyosin flows can only occur above a critical length threshold, and the amount of MyoII accumulation increases with the protrusion length. m, Steady-state MyoII concentration for increasing contractility, at constant protrusion length (colour-code as in i). Actomyosin flows can only occur above a critical contractility threshold, and the amount of the accumulation increases with contractility. n, Steady-state MyoII concentration for intermediate contractility, protrusion length and friction parameters as in (i), with a zero-flux boundary condition. Results are qualitatively similar to (i), with the peak of MyoII accumulation showing a slight shift downwards. o, Steady-state MyoII concentration with friction uniformly low everywhere (remaining parameters are similar to n). Under these conditions, MyoII accumulation can have multiple and random locations (right- and left-side vertices in this simulation), instead of a robust accumulation at the base of the protrusion. n denotes number of cells throughout. Data are mean ± s.e.m. Scale bars, 5 μm.

Extended Data Figure 9. Dynamics and apical-basal localization of the actomyosin flows in the neighbours.

a, b, Lifeact–Ruby expressing cells neighbouring a wild-type dividing cell in a MyoII–3 × GFP tissue. Insets highlight progressive accumulation of MyoII–3 × GFP and Lifeact–Ruby in the neighbours. Kymograph in b along the yellow box. n = 25 (18 pupae). c, Velocity of F-actin and MyoII flows in wild-type neighbours facing wild-type dividing cells (7 and 15 pupae, respectively). d, F-actin speckle probability density in wild-type neighbours facing wild-type dividing cells (4 pupae). Error bars denote s.e.m. of a multinomial distribution. e–g, Lifeact–Ruby expressing neighbour facing a dividing cell in a Dlg–GFP tissue. Top panel corresponds to apical plane; bottom panel corresponds to a more basal plane, at the level of the septate junctions (schematically represented in e). Kymograph in g along the yellow boxes. Insets and kymographs show that the Lifeact–Ruby flows observed in the ingressing junction during cytokinesis are restricted to the apical domain. Note that the bright dots visible in the basal kymograph correspond to Lifeact–Ruby aggregates, and not directional speckles (see Supplementary Video 7e). n = 8 cells (5 pupae). h, i, Rok–GFP and MyoII–3 × mKate2 distribution during cytokinesis. Kymograph in i generated along the yellow box. During cytokinesis, Rok–GFP is localized at the membrane/cortex and also flows with MyoII–3 × mKate2 during the ingression of the future daughter cell’s membranes (insets and kymograph). The localization of Rok is therefore in full agreement with previous findings reporting that this kinase can bind to the membrane in both vertebrates and Drosophila^47,48. Moreover, Rok flows were already reported in germband cells and shown to depend on MyoII activity⁴⁹. Overall, the constitutive nature of the ROCK kinase⁴⁷, its known binding to the membrane and MyoII fully support the notion that self-organized actomyosin flows are triggered by the local decrease in E-cad concentration. n = 25 (3 pupae). j, k, Ratio of F-actin intensity (labelled by Lifeact–GFP) at the ingressing region versus the remaining AJs (j) and the ratio of F-actin intensity at the medial pool versus the AJs (k) in wild-type or rok cells neighbouring a wild-type dividing cell (7 or 7 pupae, respectively). Note that F-actin intensity within the ingressing region is similar to its intensity at the remaining AJs for both wild-type and rok neighbours, indicating that loss of Rok activity does not reduce the amount of F-actin within the ingressing region. l, E-cad–GFP and MyoII–mChFP localization in wild-type (n = 38 cells, 2 pupae) and Shroom (shr; n = 33 cells, 4 pupae) dividing cells, as well as its neighbour. Arrowheads denote MyoII–mChFP accumulation in the neighbours. To test further the role of Rok in F-actin polymerization, we analysed whether Shroom and fhos, two Rok effectors known to regulate F-actin polymerization^48,50, would be required for MyoII accumulation in the neighbours. Neither the loss of fhos (Extended Data Fig. 7o–q) nor Shroom activity affects MyoII accumulation (see n), arguing against a role of Rok in F-actin polymerization. m, Rate of contractile ring constriction in wild-type and shr dividing cells (4 and 4 pupae, respectively). n, Normalized MyoII accumulation at 80% of the initial cell diameter for wild-type and shr neighbours (2 and 4 pupae, respectively). n denotes number of cells throughout. In c and d, n/n = number of speckles quantified/corresponding number of cells quantified. Mann–Whitney U-test (c, j, m) and Student’s t-test (k, n). Data are mean ± s.e.m. Scale bars, 5 μm.

Extended Data Figure 10. Actomyosin flows in wild-type and ani, moe, E-cad and dia mutant conditions.

a–d, Wild-type (a, b; n = 25 cells, 4 pupae) or ani^RNAi (c, d; n = 46 cells, 8 pupae) dividing and neighbouring cells expressing Lifeact–Ruby in a MyoII–3 × GFP tissue. Kymographs in b and d along the yellow boxes in a and c, respectively. Insets and respective kymograph in (a, b) highlight progressive accumulation of MyoII–3 × GFP and Lifeact–Ruby in the neighbours cells, via actomyosin flows, while in (c, d) it denotes a reduction in the actomyosin flows observed in cells neighbouring an ani^RNAi dividing cell, as well as the diminished accumulation of MyoII–3 × GFP and Lifeact–Ruby at the base of the ingressing AJ (see Fig. 1d, e, Supplementary Video 2b and Fig. 4k, l). Note that in c and d, all cells express ani^RNAi cells, marked by Lifeact–Ruby. To visualize F-actin dynamics exclusively in the neighbours in a–d, we photobleached the dividing cell before contractile ring constriction. e–h, Lifeact–Ruby-expressing wild-type (e, f; n = 27 cells, 5 pupae) or moe^RNAi (g, h; n = 30 cells, 10 pupae) cells neighbouring a wild-type dividing cell in a MyoII–3 × GFP tissue. Kymographs in f and h along the yellow boxes in e and g, respectively. Insets and kymographs highlight the progressive accumulation of MyoII–3 × GFP and Lifeact–Ruby in both the wild-type and moe^RNAi neighbours, via actomyosin flows. Dots denote moe^RNAi cells, marked by Lifeact–Ruby. In agreement with our observation that MyoII accumulation occurs in moe^RNAi neighbouring cells (Extended Data Fig. 3h and Supplementary Videos 4c, d), the F-actin flows are similar in velocity and amount to those observed in wild-type neighbouring cells (see m, n). i–l, E-cad (i, j, n = 16 cells, 5 pupae) or dia (k, l, n = 19 cells, 3 pupae) cells, marked by Lifeact–GFP, neighbouring a wild-type dividing cell in a MyoII–3 × mKate2 tissue. Dots denote E-cad (i) or dia (k) mutant cells. Kymographs in j and l generated along the yellow boxes in i and k, respectively. E-cad neighbours accumulate actomyosin at the base of the ingressing AJ (see Fig. 3j) and exhibit actomyosin flows similar to wild-type neighbours (see m and n). By contrast, dia neighbours exhibit delayed accumulation of MyoII (Extended Data Fig. 7i, j). Accordingly, in this context the F-actin flows are slower than in wild-type neighbours (see Fig. 4o, p). m, Percentage of wild-type, moe^RNAi and E-cad neighbouring cells (12, 10, 5 pupae, respectively) exhibiting no flows, intermittent flows (< 3 detectable speckles), or sustained flows (≥ 3 detectable speckles) when facing wild-type dividing cells. n, Actin flow velocity for wild-type, moe^RNAi and E-cad neighbours facing wild-type dividing cells. n/n indicates number of speckles/number of cells (12, 9 and 5 pupae, respectively). Kruskal–Wallis test. Scale bars, 5 μm.

Supplementary Material

Supplementary Information is available in the online version of the paper.