Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jun 14;122(27):15706–15712. doi: 10.1021/acs.jpcc.8b02699

Cuboidal Supraparticles Self-Assembled from Cubic CsPbBr3 Perovskite Nanocrystals

Julia S van der Burgt †, Jaco J Geuchies †, Berend van der Meer ‡, Hans Vanrompay §, Daniele Zanaga §, Yang Zhang §, Wiebke Albrecht ‡, Andrei V Petukhov ∥,⊥, Laura Filion ‡, Sara Bals §, Ingmar Swart †, Daniël Vanmaekelbergh †,*
PMCID: PMC6143281  PMID: 30245760

Abstract

graphic file with name jp-2018-02699m_0007.jpg

Colloidal CsPbBr3 nanocrystals (NCs) have emerged as promising candidates for various opto-electronic applications, such as light-emitting diodes, photodetectors, and solar cells. Here, we report on the self-assembly of cubic NCs from an organic suspension into ordered cuboidal supraparticles (SPs) and their structural and optical properties. Upon increasing the NC concentration or by addition of a nonsolvent, the formation of the SPs occurs homogeneously in the suspension, as monitored by in situ X-ray scattering measurements. The three-dimensional structure of the SPs was resolved through high-angle annular dark-field scanning transmission electron microscopy and electron tomography. The NCs are atomically aligned but not connected. We characterize NC vacancies on superlattice positions both in the bulk and on the surface of the SPs. The occurrence of localized atomic-type NC vacancies—instead of delocalized ones—indicates that NC–NC attractions are important in the assembly, as we verify with Monte Carlo simulations. Even when assembled in SPs, the NCs show bright emission, with a red shift of about 30 meV compared to NCs in suspension.

Over the past decade, a lot of research has been devoted to the properties and improvement of hybrid organic–inorganic perovskite materials (e.g., CH3NH3PbX3, X = Cl, Br, or I) for solar cell applications,1 which has led to an increase in efficiency from 3.8%2 to over 20%.3 This success has motivated researchers all over the world to study other types of perovskite materials and extend their optoelectronic applications to photodetectors,4,5 light-emitting diodes,6−8 and one-9 and two-photon10 pumped gain media for lasers. Recently, cesium lead halide (CsPbX3) perovskite nanocrystals (NCs) have been reported as a new and promising branch of perovskites. These colloidal NCs can be synthesized with a facile hot injection method and possess bright emission and readily tunable opto-electronic properties.11 In comparison to the hybrid CH3NH3PbX3 compounds, the all-inorganic CsPbX3 has a better temperature stability.5 Moreover these NCs show narrow emission peaks with a full width at half-maximum (fwhm) of 50–80 meV and exhibit quantum yields of up to 90% without any extra passivation of the NC surface.12 The emission can be tuned over the full visible spectrum by varying the composition of the X-anionic sublattice, either directly or by postsynthetic anion-exchange reactions.13−15

NCs with low polydispersity and high photoluminescence (PL) quantum yields are ideal building blocks for larger structures with predesigned opto-electronic functionalities. In these superlattices, new properties can arise from the electronic and/or magnetic coupling between constituent NCs. For example, the new functionality that arises from the ordered structures of NCs has been used already in magnetic devices16 and for electronic applications.17 Here, we report on the self-assembly of cubic-shaped CsPbBr3 NCs into cuboidal supraparticles (SPs), each SP consisting of several hundreds to thousands of NCs. Using in situ X-ray scattering measurements, we show that the SPs nucleate and grow in the solution upon increasing NC concentration or by addition of a nonsolvent. The structure of the superlattices has been studied with (scanning) transmission electron microscopy [(S)TEM], electron diffraction (ED), and high-angle annular dark-field (HAADF) STEM tomography. We show that the NCs form a simple cubic lattice and are atomically aligned but not connected. We observed empty superlattice positions, that is, vacancies similar to those in an atomic crystal, in the bulk as well as on surface lattice positions. Vacancies positioned at the lattice sites should be distinguished from delocalized vacancies predicted for the hard-cube model.18 Our results thus indicate that attractive interactions between the constituent NCs are important in the self-assembly process. We studied the PL of individual SPs with confocal microspectroscopy. Despite the fact that exciton energy transfer can occur, the SPs still show a bright PL, red-shifted by 30 meV compared to a diluted NC solution.

Results and Discussion

Formation of Cuboidal SPs

In general, two methods can be used to induce aggregation of NCs in solution: (1) solvent evaporation, also shown by Kovalenko and Bodnarchuk,19 which increases the NC concentration, and (2) addition of antisolvent, increasing the potential energy per NC. We used methyl acetate as an antisolvent because it is one of the few polar solvents that does not damage the NCs.20 The use of other polar media, such as methanol, ethanol, acetone, and acetonitrile, as an antisolvent leads to dissolution of the individual NCs. Both methods give identical SPs, however larger SP sizes are obtained by solvent evaporation (see the Supporting Information, Figure S4). The drawback of solvent evaporation is that the SP formation takes rather long (>1 month at room temperature). When we consider self-assembly in a reasonable lab-time period of hours, care has to be taken to operate the assembly under nearly reversible conditions, as fast kinetics can lead to disordered, nonequilibrium structures. Indeed, we observed large clusters with an irregular shape and disordered structure on the NC length scale, when a relatively high amount of antisolvent was added (see the Supporting Information, Figure S5) to speed up the SP formation. The structures that we will discuss were obtained under nearly reversible conditions. A more detailed description of the parameters, which were used during the self-assembly process, can be found in the Supporting Information.

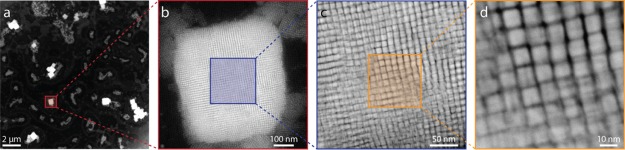
Figure 1 shows self-assembled NC SPs in a series of HAADF-STEM images with increasing magnification. A low magnification image is presented in Figure 1a. The SPs appear as large white cuboids on a dark background. At higher magnifications, it becomes clear that each SP consists of several hundreds of NCs (Figure 1b–d). Moreover, the columns of NCs are clearly distinguished at the highest magnification image (Figure 1d). The degree of ordering inside the SP is apparent through the observed contrast in the HAADF-STEM images, hinting toward a simple cubic stacking of the NCs inside the cuboidal SP. The NCs are clearly not atomically attached as has been observed for superlattices of PbSe NCs,21 but they are still separated from each other most likely by their oleate and oleylamine ligands. The alignment must hence be related to the dense cubic stacking of the NC building blocks. The contrast in between the particles seems to be blurred out slightly, which we tentatively ascribe to some positional and rotational disorder of the NCs inside the SP. More images of the formed SPs can be found in the Supporting Information, Figure S3. Although cubic particles can theoretically achieve high packing fractions up to 100%, they are not often encountered in nature. In the CsPbBr3 SPs discussed here, cubic symmetry emerges over three length scales: on the scale of the atomic lattice, the NC building blocks in the supra particle superlattice, and the cuboidal shape of the SP itself.

Figure 1.

Figure 1

Open in a new tab

Structure of CsPbBr3 NC SPs. (a) Low-magnification overview image, showing a relatively low coverage of large, cuboid-shaped SPs. (b) Zoom-in on the marked region in (a) showing a single SP with a nearly cubic shape. (c) Zoom-in on the marked area in (b) showing nearly aligned NCs in a dense cubic stacking. The individual NCs in the SP are clearly visible. (d) Further zoom-in on the marked area in (c). Clearly visible columns of NCs in the lattice of the SP, hinting toward a simple-cubic packing of the constituent NCs inside the SP.

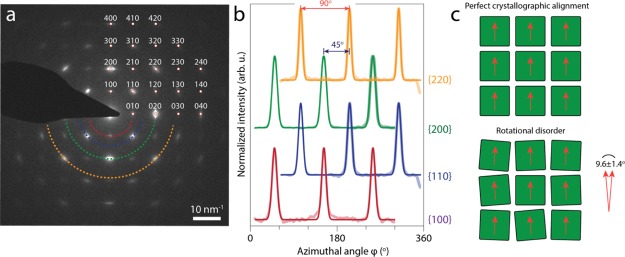
To properly quantify the rotational freedom of the CsPbBr3 NCs inside the SPs, we performed ED experiments on the SP presented in Figure 1. The selected area ED pattern is shown in Figure 2a. The presence of well-defined diffraction spots, instead of powder rings, already indicates that the particles are (nearly) atomically aligned, with the three [001] type zone-axes directed in the principal directions of the NC superlattice (i.e., one of the NC {100} facets pointing upward). The diffraction pattern can be indexed up to reflections from the {420} atomic planes. In Figure 2b, azimuthal traces at the constant scattering vector q are presented for reflections from the {100}, {110}, {200}, and {220} planes (depicted in red, blue, green, and yellow, respectively). The 12 peaks are fitted with Gaussian functions to obtain an average fwhm of 9.6° ± 1.4°, which reflects an upper limit of their in-plane rotational freedom. The high degree of atomic alignment of the NCs inside the SPs originates from the densest possible stacking of NC building blocks with a uniform cubic shape and size.

Figure 2.

Figure 2

Open in a new tab

ED analysis of a single SP consisting of CsPbBr3 NCs. (a) ED pattern acquired along the [001] NC zone axis of the SP shown in Figure 1. The appearance of well-defined diffraction spots indicate that the NCs are atomically aligned. The diffraction spots can be indexed clearly up to reflections from the {420} atomic planes. (b) Azimuthal traces at constant scattering vectors q for different atomic reflections, as indicated by the colored semicircles in (a). Fitting the 12 peaks with Gaussian functions (solid lines) gives an average fwhm of 9.6° ± 1.4°, which provides an upper limit of the in-plane rotational freedom of the NCs inside the SP. (c) Two-dimensional schemes of a planar section perpendicular to the [001] superlattice axis, demonstrating the effect of slight rotational disorder. The orange arrows represent the [100] atomic axis of each of the nanocubes.

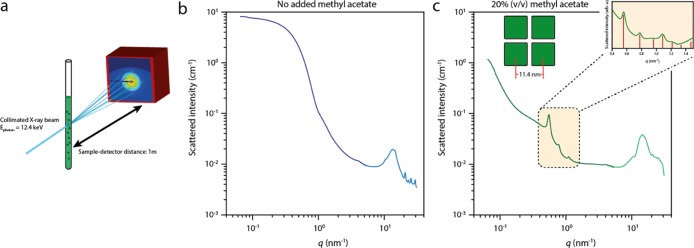
It is also relevant to characterize the structure of the NC assemblies formed in the suspension before they are scooped and dried on a transmission electron microscopy grid. Therefore, we performed in situ transmission small/wide-angle X-ray scattering (SAXS, WAXS) measurements on pure stable NC suspensions and on suspensions in which the NC assembly was initiated by adding methyl acetate as an antisolvent. A schematic of the experiment is shown in Figure 3a. A solution of NCs is added into a quartz capillary with an outer diameter of 1.5 mm and placed inside a LINKAM stage, positioned at a distance of 1 m from the SAXS detector. The WAXS detector, collecting the atomic diffraction of the NCs, was positioned at the inlet of the vacuum tube holding the SAXS detector. The SAXS and WAXS patterns of a stable suspension are shown in Figure 3b. The SAXS region (light blue) only shows form factor scattering from dispersed NCs. The WAXS signal (dark blue) shows sharp diffraction peaks originating from the atomic perovskite lattice of the NCs. A sample with a volume fraction of 0.2 methyl acetate was measured after 3 days of incubation and is presented in Figure 3c. The SAXS pattern shows clear Bragg peaks at positions of 0.55, 0.78, 1.1, and 1.23 nm–1. Their relative peak positions correspond to 1:√2:2:√5, which corresponds to scattering from the {100}, {110}, {200}, and {210} lattice planes of a simple cubic lattice of NCs. The measured NC–NC distance inside the SPs in suspension is determined to be 11.4 ± 0.1 nm, corresponding to NCs still separated by their oleate and oleylamine ligands. The fwhm of the {100} reflection is 0.378 nm–1, which corresponds to spatial extension of the periodic order of roughly 166.3 nm. The SP formation is reversible, as the constituent NCs readily redisperse upon diluting the solution of SPs (see the Supporting Information, Figure S6).

Figure 3.

Figure 3

Open in a new tab

Transmission X-ray scattering of NC solutions during the formation of SPs. (a) Scheme of the experimental setup. A quartz capillary is loaded with a solution of NCs and placed in a LINKAM stage, which is located 1 m from the detector to collect the SAXS signal. The formation of SPs can be initiated by addition of an antisolvent. (b) SAXS pattern of the NC dispersion without addition of the antisolvent, showing only form factor scattering of the individual NCs in solution. (c) SAXS pattern of the diluted NC solution after 3 days of incubation upon addition of 20% (v/v) of methyl acetate antisolvent; the Bragg reflections indicate the formation of crystalline SPs in the solution. The inset shows a zoom on the region with the Bragg peaks, which is scaled by the form factor scattering from (b). The red lines indicate the expected peak positions for a simple-cubic packing of the NCs inside the SPs.

Recent work by Bertolotti et al. also showed that the CsPbBr3 NCs have the tendency to stack in solution,22 similar to concentrated solutions of perovskite nanoplatelets.23 They argue that the stacking direction occurs most likely in the {100} NC direction, similar to the NCs in the SPs in this work. Others have also found that these perovskite NCs readily assemble into one-dimensional chains by addition of molecular clusters24,25 or through ligand–solvent interactions.26 Such stacks could hence be a precursor phase in the formation of the SPs presented in this work. However, this remains to be verified by performing in situ time-resolved SAXS and WAXS on the self-assembly process, which is beyond the scope of this article.

NC Vacancies inside a SP Studied with HAADF-STEM Tomography and Monte Carlo Simulations

To study the geometric structure of the NCs inside the SPs in more detail, a single SP was studied using HAADF-STEM tomography. A series of projection images was acquired with an angular range of −70° to 78° and a tilt increment of 2°. Orthogonal to that, a second tilt series was acquired from −76° to 76° to reduce the missing wedge of tilt angles to a missing pyramid.27 Using this dual tilt series as an input for several mathematical reconstruction algorithms, we found that the quality of the reconstruction was greatly improved compared to the reconstruction that was obtained from just using the one tilt series.

A visualization of the acquired tomogram is presented in Figure 4a. Unfortunately, we are not able to clearly resolve all individual NC positions inside the SP; the missing pyramid of tilt angles smears out the information in the z-direction of the cuboidal SP. Nonetheless, the orthoslices taken through the center of the structure in Figure 4b–d show interesting features. In all three orthogonal directions, we observe empty places on lattice positions. They appear to be localized single point vacancies and vacancy clusters. From the tomogram, we are able to estimate the volume fraction of vacancies in the bulk of the SP of 3.3%, assuming cubic symmetry of the NC lattice (see the Supporting Information for more details). Furthermore, we also performed secondary electron-STEM to acquire information on the surface of the SPs, which can be found in the Supporting Information (Figures S7 and S8). Also, on the surface of the SPs, we observe localized NC vacancies and groups of missing NCs. We estimate that the amount of missing surface NCs roughly equals 5.5 ± 1.5%.

Figure 4.

Figure 4

Open in a new tab

Looking inside SPs with HAADF-STEM tomography. (a) Visualization of the three-dimensional reconstruction of a single SP, acquired by rotating the sample over two orthogonal tilt series and reconstructed using a SIRT algorithm. Orthoslices through the xy (b), xz (c), and yz (d) directions of the tomogram reveal several localized NC vacancies and groups of missing NCs in the bulk of the SP. All vacancies are clearly defined on a lattice position.

Interestingly, the localized nature of the NC vacancies is in contrast to previous Monte Carlo and molecular dynamics simulations for hard cubes, that is, cubes that interact only through excluded volume interactions. Smallenburg et al. showed that for hard cubes, vacancies manifest themselves as a finite-length chain of particles along one of the principal axes in the crystal.18 The vacancy is thus spread over many lattice positions. More specifically, in this hard-cube system, the equilibrium concentration of vacancies is very high (up to 6%) because of the fact that creating a vacancy provides additional free volume for multiple nearby particles, which increases the entropy of the crystal. Note that in a system of attractive cubes, Rossi et al. observed localized NC vacancies, where colloidal cubes of roughly 1 micron are self-assembled into simple cubic lattices through addition of a depletant, which induces effective attractions between the cube facets.28 As such, we propose that the localization and grouping of NC vacancies in our experiments point toward attractive interactions between the NCs during the self-assembly. Specifically, for sufficiently large NC–NC attractions, the free energy will be minimized when the particles in the vicinity of the vacancy are sitting on regular lattice positions, as the cost of breaking cohesive bonds will dominate over the entropic gain associated with vacancy delocalization.

To understand the observed localization of the vacancies, we performed Monte Carlo simulations of cubes in the NVT ensemble, where N (the number of particles), V (the volume), and T (the temperature) are fixed, and the cube–cube attraction can be changed from zero to several times the thermal energy. As a minimal model that captures the repulsive core and attraction, we model the interactions between the cubes as a combination of a cubic hard-core repulsion and a spherically-symmetric square well attraction originating from the center of the cube. The range of the attractive square well was fixed to Δ = 1.14σ, with σ is the edge length of the cubes, and we varied the well depth βε, with β = 1/kbT. Thus, for βε = 0, our model reduces to the hard-cube model with delocalized vacancies, and we can study the effect of increasing the attraction strength βε on the vacancy structure. While the nucleation of these SPs is described in the Supporting Information (Figure S12), we will now focus on the (de)localization of defects in the bulk of the crystal. In these simulations, we start off from a perfect simple cubic crystal at a fixed packing fraction of φ = 0.80 and initialized a single vacancy by removing a single particle. In agreement with ref (22) we observe NC vacancies to be delocalized over many lattice positions for the hard-cube system, βε = 0 (Figure 5a). Yet, upon introducing a slight attraction between the cubes, βε = −0.5, the long delocalized NC vacancies are not observed anymore (Figure 5b). Instead, the NC vacancies spread only over a couple of lattice sites. Thus, already for a moderate attraction strength between the particles, we observe the defect structure to be dominated by the cohesive bonds between the particles. For slightly larger attractions, βε = −1, we observe the particles in the vicinity of the NC vacancies exclusively on lattice positions, and no delocalized NC vacancies are observed (Figure 5c), similar to the tomography experiments presented in Figure 4.

Figure 5.

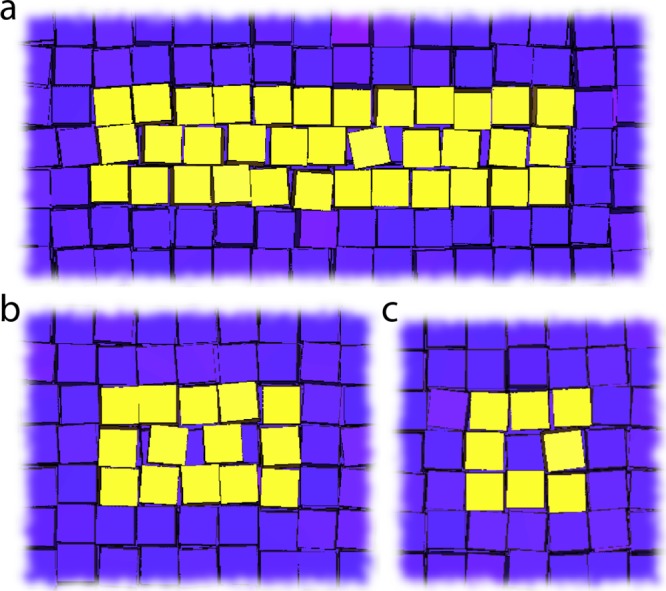
Figure 5

Open in a new tab

Monte Carlo simulations of (de)localized NC vacancies inside the SPs as a function of the attraction strength. (a) ε = 0 kbT, the NC vacancy is delocalized over many lattice positions. (b) ε = −0.5 kbT, long delocalized NC vacancies are not observed anymore, only weak delocalization of the NC vacancies over a maximum of a few lattice sites are observed. (c) ε = −1 kbT, NC vacancies are exclusively observed on lattice positions and do not delocalize. The latter is also observed in the tomography experiments presented in Figure 4.

Optical Properties of SPs Compared to NCs in Solution

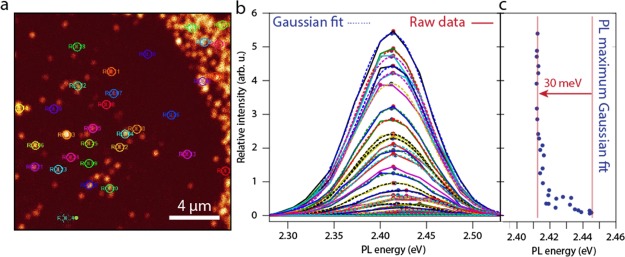
Often, quantum dot (QD) solids suffer from a reduced PL quantum yield, as exciton energy transfer between the NCs in the solid enhances the probability of nonradiative energy transfer. We found that CsPbBr3 SPs deposited on a glass slide remained strongly emissive, with a PL quantum yield of 26%, as determined with an integrating sphere. This is good news for several opto-electronic applications requiring a QD solid as the optically active material. To study the optical properties of individual SPs in more detail, we performed confocal microspectroscopy. A dispersion containing the SPs was drop-cast on a microscope slide, and the solvent of the dispersion was allowed to evaporate. A droplet of immersion oil was placed on the sample, and a second cover slide was placed on top of the sample. The results are presented in Figure 6 and in the Supporting Information, Figure S13.

Figure 6.

Figure 6

Open in a new tab

Confocal microspectroscopy on individual CsPbBr3 NC SPs. (a) Confocal micrograph of a glass slide covered with SPs, which appear as high intensity areas on a dark background. The circles indicate the areas in which the PL signal was integrated. (b) PL spectra of a large number of different regions in the confocal micrograph shown in (a). The solid lines indicate raw data, whereas the dashed lines are Gaussian fits to the data. (c) Comparing the peak intensity to the PL energy, a red shift of roughly 30 meV is observed for the SPs compared to the NC monolayer background.

Figure 6 shows the PL spectra of many spots observed on the glass slide. Figure 6a shows the confocal micrograph of a glass slide covered with SPs. The circled areas indicate the regions where the PL signal was integrated. In Figure 6b, we present the peak energies of 30 spots versus the intensity and observe a gradual red shift (shown in Figure 6c), which abruptly becomes constant at a sufficiently high spot intensity, the overall red shift being roughly 30 meV. A similar red shift is observed when the PL spectra of dispersed NCs and dispersed SPs are compared (Supporting Information, Figures S14 and S15). We hence conclude that the bright spots present regions of SPs and the weak spots present individual NCs or smaller clusters.

The red shift observed in the emission of the SPs with respect to individual NCs could have several causes: Kovalenko and Bodnarchuk reported in their recent work19 that the relative increase in the dielectric constant of the NC environment can cause a red shift if the electron and hole both become more delocalized. Furthermore, the excitons in the NCs are in the weak confinement regime; the electronic coupling between NCs inside a SP could thus also cause a weak red shift of the PL spectrum. Third, exciton energy transfer results in a spatial diffusion of the excitons over the superlattice, always with a trend toward lower exciton energy. Di Stasio et al. reported a similar shift of the PL in concentrated solutions of CsPbBr3 NCs and solid-state films.29 This effect is also shown in concentrated solutions of the cubic CsPbBr3 NCs and is reversible upon diluting the NC dispersion.30 In our time-resolved PL experiments (Figure S14), we observe that the shift in the PL peak position occurs faster than the time resolution of our setup (∼250 ps), which is probably faster than the exciton energy transfer. This indicates that energy transfer is not the cause for the observed red shift. We must conclude here that although the red shift occurring in CsPbBr3 NC SPs is well-established, its main cause remains an outstanding question.

In summary, we have shown that CsPbBr3 nanocubes self-assemble into SPs that have an overall cuboidal shape. In the superlattices, the NCs are atomically aligned but separated by the capping ligands. Vacancies form real point defects instead of being delocalized, indicating that attractive interactions play a role in the self-assembly process. The SPs show a bright PL, red-shifted by 30 meV with respect to that of individual NCs. The fact that the obtained SPs are still highly emissive makes them promising candidates for opto-electronic applications. For example, they possibly can be used as microcavities to study the confinement of the PL and lasing inside SPs.

Acknowledgments

The authors thank Dr. Rajeev Dattani and Jacques Gorini from the ID02 beamline of the ESRF for their excellent assistance during the X-ray scattering experiments. We also thank Carlo van Overbeek, P. Tim Prins, and Federico Montanarella for their support during the synchrotron experiments. The authors gratefully acknowledge Prof. Dr. Alfons van Blaaderen for fruitful discussions. D.V. acknowledges funding from NWO-CW TOPPUNT “Superficial superstructures.” J.J.G. acknowledges the joint Debye and ESRF graduate programs for the financial support. H.V. gratefully acknowledges the financial support by the Flemish Fund for Scientific Research (FWO grant 1S32617NN). S.B. acknowledges the financial support from the European Research Council (ERC Starting grant #335078-COLOURATOMS). Y.Z. acknowledges the financial support from the European Union’s Horizon 2020 research and innovation program, under the Marie Sklodowska-Curie grant agreement #665501 through a FWO [PEGASUS]2 Marie Sklodowska-Curie fellowship (12U4917N). W.A. acknowledges the financial support from the European Research Council under the European Unions Seventh Framework Program (FP-2007-2013)/ERC Advanced grant agreement 291667 HierarSACol.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.8b02699.

  • Synthesis of CsPbBr3 NCs, purification of the NCs, self-assembly of the NC solutions into SPs, transmission SAXS and WAXS experiments, and optical spectroscopy (PDF)

Author Contributions

# J.S.v.d.B. and J.J.G. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

jp8b02699_si_001.pdf (4.1MB, pdf)

References

  1. Kulbak M.; Cahen D.; Hodes G. How Important Is the Organic Part of Lead Halide Perovskite Photovoltaic Cells? Efficient CsPbBr3 Cells. J. Phys. Chem. Lett. 2015, 6, 2452–2456. 10.1021/acs.jpclett.5b00968. [DOI] [PubMed] [Google Scholar]
  2. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  3. Eperon G. E.; Leijtens T.; Bush K. A.; Prasanna R.; Green T.; Wang J. T.; McMeekin D. P.; Volonakis G.; Milot R. L.; May R.; et al. Perovskite-Perovskite Tandem Photovoltaics with Optimized Bandgaps. Science 2016, 354, 861. 10.1126/science.aaf9717. [DOI] [PubMed] [Google Scholar]
  4. Gao J.; Nguyen S. C.; Bronstein N. D.; Alivisatos A. P. Solution-Processed, High-Speed, and High-Quantum-Efficiency Quantum Dot Infrared Photodetectors. ACS Photonics 2016, 3, 1217–1222. 10.1021/acsphotonics.6b00211. [DOI] [Google Scholar]
  5. Ramasamy P.; Lim D.-H.; Kim B.; Lee S.-H.; Lee M.-S.; Lee J.-S. All-Inorganic Cesium Lead Halide Perovskite Nanocrystals for Photodetector Applications. Chem. Commun. 2016, 52, 2067–2070. 10.1039/c5cc08643d. [DOI] [PubMed] [Google Scholar]
  6. Wang N.; Cheng L.; Ge R.; Zhang S.; Miao Y.; Zou W.; Yi C.; Sun Y.; Cao Y.; Yang R.; et al. Perovskite light-emitting diodes based on solution-processed self-organized multiple quantum wells. Nat. Photonics 2016, 10, 699–704. 10.1038/nphoton.2016.185. [DOI] [Google Scholar]
  7. Wang P.; Bai X.; Sun C.; Zhang X.; Zhang T.; Zhang Y. Multicolor Fluorescent Light-Emitting Diodes Based on Cesium Lead Halide Perovskite Quantum Dots. Appl. Phys. Lett. 2016, 109, 063106. 10.1063/1.4960662. [DOI] [Google Scholar]
  8. Zhang X.; Lin H.; Huang H.; Reckmeier C.; Zhang Y.; Choy W. C. H.; Rogach A. L. Enhancing the Brightness of Cesium Lead Halide Perovskite Nanocrystal Based Green Light-Emitting Devices through the Interface Engineering with Perfluorinated Ionomer. Nano Lett. 2016, 16, 1415–1420. 10.1021/acs.nanolett.5b04959. [DOI] [PubMed] [Google Scholar]
  9. Yakunin S.; Protesescu L.; Krieg F.; Bodnarchuk M. I.; Nedelcu G.; Humer M.; De Luca G.; Fiebig M.; Heiss W.; Kovalenko M. V. Low-Threshold Amplified Spontaneous Emission and Lasing from Colloidal Nanocrystals of Caesium Lead Halide Perovskites. Nat. Commun. 2015, 6, 8056. 10.1038/ncomms9056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Xu Y.; Chen Q.; Zhang C.; Wang R.; Wu H.; Zhang X.; Xing G.; Yu W. W.; Wang X.; Zhang Y.; et al. Two-Photon-Pumped Perovskite Semiconductor Nanocrystal Lasers. J. Am. Chem. Soc. 2016, 138, 3761–3768. 10.1021/jacs.5b12662. [DOI] [PubMed] [Google Scholar]
  11. Lignos I.; Stavrakis S.; Nedelcu G.; Protesescu L.; deMello A. J.; Kovalenko M. V. Synthesis of Cesium Lead Halide Perovskite Nanocrystals in a Droplet-Based Microfluidic Platform: Fast Parametric Space Mapping. Nano Lett. 2016, 16, 1869–1877. 10.1021/acs.nanolett.5b04981. [DOI] [PubMed] [Google Scholar]
  12. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Nedelcu G.; Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Grotevent M. J.; Kovalenko M. V. Fast Anion-Exchange in Highly Luminescent Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, I). Nano Lett. 2015, 15, 5635–5640. 10.1021/acs.nanolett.5b02404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Akkerman Q. A.; D’Innocenzo V.; Accornero S.; Scarpellini A.; Petrozza A.; Prato M.; Manna L. Tuning the Optical Properties of Cesium Lead Halide Perovskite Nanocrystals by Anion Exchange Reactions. J. Am. Chem. Soc. 2015, 137, 10276–10281. 10.1021/jacs.5b05602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Koscher B. A.; Bronstein N. D.; Olshansky J. H.; Bekenstein Y.; Alivisatos A. P. Surface- vs Diffusion-Limited Mechanisms of Anion Exchange in CsPbBr 3 Nanocrystal Cubes Revealed through Kinetic Studies. J. Am. Chem. Soc. 2016, 138, 12065. 10.1021/jacs.6b08178. [DOI] [PubMed] [Google Scholar]
  16. Dong A.; Chen J.; Vora P. M.; Kikkawa J. M.; Murray C. B. Binary Nanocrystal Superlattice Membranes Self-Assembled at the Liquid-Air Interface. Nature 2010, 466, 474–477. 10.1038/nature09188. [DOI] [PubMed] [Google Scholar]
  17. Dong A.; Jiao Y.; Milliron D. J. Electronically Coupled Nanocrystal Superlattice Films by in Situ Ligand Exchange at the Liquid-Air Interface. ACS Nano 2013, 7, 10978–10984. 10.1021/nn404566b. [DOI] [PubMed] [Google Scholar]
  18. Smallenburg F.; Filion L.; Marechal M.; Dijkstra M. Vacancy-Stabilized Crystalline Order in Hard Cubes. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 17886–17890. 10.1073/pnas.1211784109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kovalenko M. V.; Bodnarchuk M. I. Lead Halide Perovskite Nanocrystals: From Discovery to Self-Assembly and Applications. Chim. Int. J. Chem. 2017, 71, 461–470. 10.2533/chimia.2017.461. [DOI] [PubMed] [Google Scholar]
  20. Swarnkar A.; Marshall A. R.; Sanehira E. M.; Chernomordik B. D.; Moore D. T.; Christians J. A.; Chakrabarti T.; Luther J. M. Quantum Dot–Induced Phase Stabilization of α-CsPbI3 Perovskite for High-Efficiency Photovoltaics. Science 2016, 354, 92. 10.1126/science.aag2700. [DOI] [PubMed] [Google Scholar]
  21. Evers W. H.; Goris B.; Bals S.; Casavola M.; de Graaf J.; van Roij R.; Dijkstra M.; Vanmaekelbergh D.; Vanmaekelbergh D. Low-Dimensional Semiconductor Superlattices Formed by Geometric Control over Nanocrystal Attachment. Nano Lett. 2013, 13, 2317–2323. 10.1021/nl303322k. [DOI] [PubMed] [Google Scholar]
  22. Bertolotti F.; Protesescu L.; Kovalenko M. V.; Yakunin S.; Cervellino A.; Billinge S. J. L.; Terban M. W.; Pedersen J. S.; Masciocchi N.; Guagliardi A. Coherent Nanotwins and Dynamic Disorder in Cesium Lead Halide Perovskite Nanocrystals. ACS Nano 2017, 11, 3819. 10.1021/acsnano.7b00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Bekenstein Y.; Koscher B. A.; Eaton S. W.; Yang P.; Alivisatos A. P. Highly Luminescent Colloidal Nanoplates of Perovskite Cesium Lead Halide and Their Oriented Assemblies. J. Am. Chem. Soc. 2015, 137, 16008–16011. 10.1021/jacs.5b11199. [DOI] [PubMed] [Google Scholar]
  24. Zhang X.; Lv L.; Ji L.; Guo G.; Liu L.; Han D.; Wang B.; Tu Y.; Hu J.; Yang D.; et al. Self-Assembly of One-Dimensional Nanocrystal Superlattice Chains Mediated by Molecular Clusters. 2016.138.3290. 10.1021/jacs.6b00055 [DOI] [PubMed] [Google Scholar]
  25. Zhang X.; Lv L.; Wu G.; Yang D.; Dong A. Cluster-Mediated Assembly Enables Step-Growth Copolymerization from Binary Nanoparticle Mixtures with Rationally Designed Architectures. Chem. Sci. 2018, 9, 3986–3991. 10.1039/c8sc00220g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Soetan N.; Erwin W. R.; Tonigan A. M.; Walker D. G.; Bardhan R. Solvent-Assisted Self-Assembly of CsPbBr3 Perovskite Nanocrystals into One-Dimensional Superlattice. J. Phys. Chem. C 2017, 121, 18186–18194. 10.1021/acs.jpcc.7b03939. [DOI] [Google Scholar]
  27. Arslan I.; Tong J. R.; Midgley P. A. Reducing the Missing Wedge: High-Resolution Dual Axis Tomography of Inorganic Materials. Ultramicroscopy 2006, 106, 994–1000. 10.1016/j.ultramic.2006.05.010. [DOI] [PubMed] [Google Scholar]
  28. Rossi L.; Sacanna S.; Irvine W. T. M.; Chaikin P. M.; Pine D. J.; Philipse A. P. Cubic Crystals from Cubic Colloids. Soft Matter 2011, 7, 4139–4142. 10.1039/c0sm01246g. [DOI] [Google Scholar]
  29. Di Stasio F.; Imran M.; Akkerman Q. A.; Prato M.; Manna L.; Krahne R. Reversible Concentration-Dependent Photoluminescence Quenching and Change of Emission Color in CsPbBr3 Nanowires and Nanoplatelets. J. Phys. Chem. Lett. 2017, 8, 2725–2729. 10.1021/acs.jpclett.7b01305. [DOI] [PubMed] [Google Scholar]
  30. de Weerd C.; Gomez L.; Zhang H.; Buma W. J.; Nedelcu G.; Kovalenko M. V.; Gregorkiewicz T. Energy Transfer between Inorganic Perovskite Nanocrystals. J. Phys. Chem. C 2016, 120, 13310–13315. 10.1021/acs.jpcc.6b04768. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp8b02699_si_001.pdf (4.1MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES