Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Aug 22;18(9):5981–5988. doi: 10.1021/acs.nanolett.8b02810

Large Conductance Variations in a Mechanosensitive Single-Molecule Junction

Davide Stefani †, Kevin J Weiland ‡, Maxim Skripnik §,∥, Chunwei Hsu †, Mickael L Perrin †,⊥, Marcel Mayor ‡,#,∇,*, Fabian Pauly §,∥,*, Herre S J van der Zant †,*
PMCID: PMC6143316  PMID: 30134105

Abstract

graphic file with name nl-2018-028106_0007.jpg

An appealing feature of molecular electronics is the possibility of inducing changes in the orbital structure through external stimuli. This can provide functionality on the single-molecule level that can be employed for sensing or switching purposes if the associated conductance changes are sizable upon application of the stimuli. Here, we show that the room-temperature conductance of a spring-like molecule can be mechanically controlled up to an order of magnitude by compressing or elongating it. Quantum-chemistry calculations indicate that the large conductance variations are the result of destructive quantum interference effects between the frontier orbitals that can be lifted by applying either compressive or tensile strain to the molecule. When periodically modulating the electrode separation, a conductance modulation at double the driving frequency is observed, providing a direct proof for the presence of quantum interference. Furthermore, oscillations in the conductance occur when the stress built up in the molecule is high enough to allow the anchoring groups to move along the surface in a stick–slip-like fashion. The mechanical control of quantum interference effects results in the largest-gauge factor reported for single-molecule devices up to now, which may open the door for applications in, e.g., a nanoscale mechanosensitive sensing device that is functional at room temperature.

Keywords: Quantum interference, mechanically controlled break-junctions, single-molecule, nanoscale transport, molecular electronics, density functional theory

In recent years, studies on single-molecule junctions have rapidly become a mature research field.1,2 The combination of the structural diversity accessible by synthetic chemistry with the continuously improving skills of experimental and theoretical physics enabled the exploration of individual molecules as the tiniest functional building blocks for electronic circuits and sensors.3,4 The steady refinement of the break-junction technique also allowed to study correlations between mechanical manipulations and transport features at the single-molecule level in a systematic way.5 Examples include binary switching through mechanical control of the metal–molecule contact geometry6 or through stereoelectronic effects,7 mechanical-stress-sensitive redox chromophores,8 and coordination compounds that show spin-state switching under mechanical stress.9 Furthermore, the sensitivity of the technique makes it possible to observe intermolecular behaviors such as π-stacking,10,11 and more recently, the interdependence of conductance and frontier orbitals involved in the π-stacking12,13 could be directly demonstrated.14

Particularly interesting are destructive quantum interference effects leading to a strong suppression of electron transmission at specific energies, which make them an ideal feature for applications in, e.g., thermo-15 or voltage-dependent switching.16 Their manipulation has been reported by external means including solid-state17 or electrochemical gating,18 humidity,19 and the sliding of π-stacked molecules relative to each other.14 Deliberate manipulation of the latter, however, remains elusive as it requires strict temperature conditions and is based on intermolecular interactions. In particular, the intermolecular character requires the coincidental presence of two molecules inside the junction. For this reason, approaches that intramolecularly imitate intermolecular π-stacking move into the focus of interest. Along these lines, the [2.2]paracyclophane (PC) compound is highly appealing.20 First described by Farthing et al. in 1949, it consists of two stacked benzene rings that are mechanically stabilized by two nonconjugated linkers.21 Integrated as central unit of an oligo-phenylene-ethynylene (OPE) rod with terminal binding groups to gold electrodes (Figure 1), we show here that using a mechanically controlled break junction (MCBJ) the π-stacking (and, therefore, the conductance) can be modulated by exerting a mechanical shear force to it. Simulations based on density functional theory (DFT) reveal a sensitive correlation between electrode displacement and molecular conductance, which is interpreted in terms of quantum interference effects between the frontier orbitals.

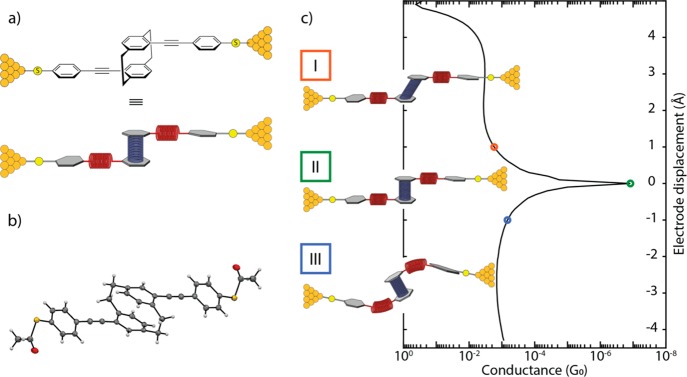
Figure 1.

Figure 1

Open in a new tab

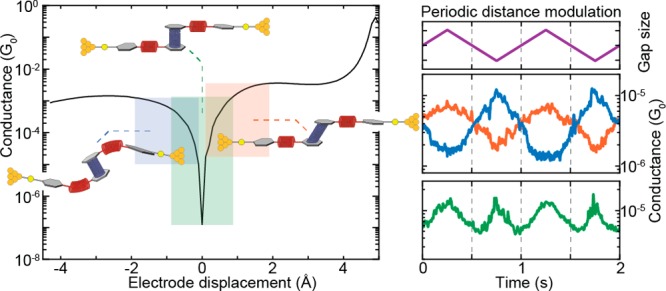
(a) Schematic illustration of the break-junction experiment of the OPE-linked PC molecule trapped between nanoelectrodes (top panel), together with a presentation displaying, as springs, the combinations of mechanosensitive structures in the molecular design (bottom drawing in this panel). (b) Solid-state molecular structure determined by single-crystal X-ray analysis. (c) Possible behavior of the molecule under applied force: (I) elongation of the molecule under pulling force of the electrodes, (II) junction with the molecule in its relaxed configuration, and (III) compression results in a shortening of the overall junction length. The simulated conductance (in units of the conductance quantum G0 = 2e2/h) as a function of the applied mechanical stress is displayed as the drawn line; the three cases (I–III) are indicated by the colored circles.

Results

The employed molecule and the conceptual idea behind the mechanical conductance manipulation are displayed in Figure 1. The molecule consists of a motif in which two ethynylphenylthiols are bound to PC in such a way that the connection resembles a para substitution in benzene.22,23 The thiol groups are connected in the para position of the outer benzene rings with respect to the PC building block, directing the current path through the PC and offering considerable mechanical stability between gold electrodes.24 The molecular motif and substitution pattern allow for flexibility by stretching of the PC; the ethynylphenylthiol building block, however, only offers limited movement upon application of a pulling force on the molecule (Figure 1c). High-pressure solid state absorption experiments on PC derivatives show shortened distances between 25 When the thiol groups are moved apart, the applied tensile force is relayed to the central PC unit along the axis connecting the anchoring groups (Figure S4). Our DFT calculations show that the alkynes are more susceptible to compressive motions, whereas the PC subunit only stretches after these are fully extended. It is noteworthy that electrical transport studies through monolayers consisting of the proposed molecular rods and similar PC-containing subunits have been reported.23,26 However, the limited control over the number of molecules inside the junction made the interpretation of the results challenging.

Single-Molecule Experiments

The target molecule was synthesized by adapting literature-known procedures;27,28 its structure was unambiguously verified by single-crystal X-ray analysis (Figure 1b). Details of the synthetic protocols are provided in the Supporting Information, together with the analytical data corroborating its identity, which is in agreement with the data already reported.23 The molecular conductance was investigated using the MCBJ technique under ambient conditions. In this technique, atomically sharp electrodes are formed in a lithographically defined gold wire and repeatedly opened and closed with sub-nanometer accuracy. The measurement of the conductance as the electrodes are continuously moved further apart constitutes a so-called breaking trace. Further details about the MCBJ setup and the measuring technique have been described elsewhere.29,30

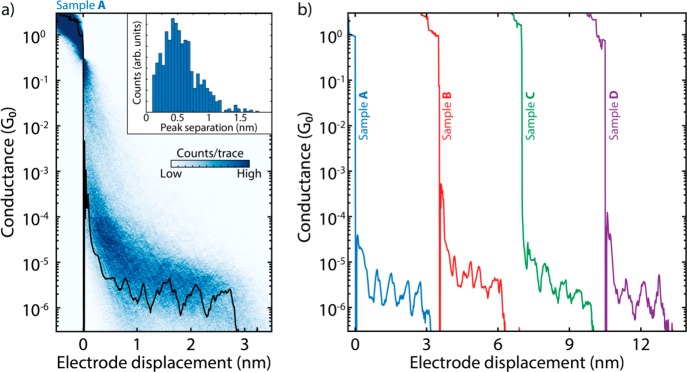
Fast-breaking measurements were performed to characterize the conductance of the OPE-linked PC molecules.31 The two-dimensional histogram in Figure 2a shows the distribution of conductance versus electrode displacement. Fitting a log-normal distribution to the one-dimensional histogram constructed from the same data (Figure S5a) reveals that the most-probable conductance value is 3.7 × 10–6 G0, where G0 = 2e2/h is the quantum of conductance. Interestingly, inspection of individual traces shows the appearance of pronounced oscillations in the conductance as the electrodes are pulled from one another, as illustrated in Figure 2b for four different samples. These oscillations are found in a large fraction of the molecular traces (40%) and have an amplitude up to an order of magnitude. The inset of Figure 2a presents a histogram of the spacing of the individual peaks, showing a periodicity of about 0.5 nm (see Supporting Information section II-1 for more details). Note that such oscillations are absent in the control measurements without the molecule (Figure S10).

Figure 2.

Figure 2

Open in a new tab

(a) Two-dimensional histogram built from 3000 consecutive breaking traces collected after deposition of the solution containing the molecule displayed in Figure 1. The applied bias is 100 mV, and the electrode speed is 4.0 nm/s. A single breaking trace (black line) has been overlaid as an example. The inset shows the peak-separation distribution. (b) Examples of breaking traces, showing oscillations in conductance as a function of displacement. The traces are taken from four different samples and are offset in the x-axis for clarity. The first trace comes from sample A, shown in panel a; samples B–D are presented in Figures S6–S9 alongside more examples of breaking traces.

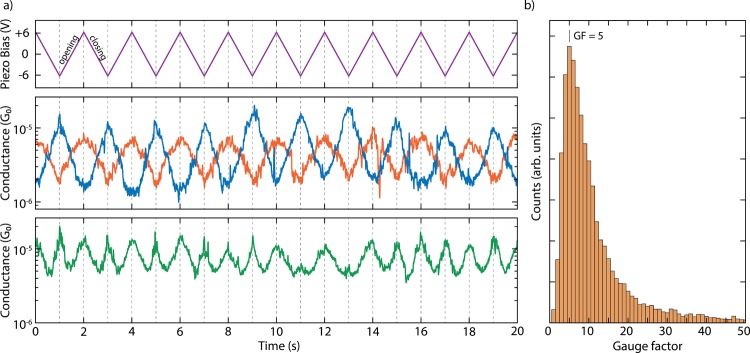
To investigate in more detail the dependence of the molecular conductance on the electrode displacement, we performed conductance measurements with modulated electrode spacing.32 In this experiment, the MCBJ was initially stretched to a few-atoms width (about 3 G0) and allowed to self-break by its surface tension to form atomically sharp electrodes.33 Next, the electrodes were separated by a distance equal to the length of the molecule to recognize, by evaluating the conductance, whether the trapping of a molecule occurred: if the conductance is found to be larger than 10–6 G0, a molecule is presumably connected between the two electrodes, and a triangular wave is applied to the piezoelectric stack that controls the electrode positions (Figure 3a). Note that a higher voltage on the piezoelectric stack corresponds to a larger electrode separation. Hundreds of such so-called distance-modulation traces are collected and from them a conductance histogram is built, similar to that obtained for fast-breaking measurements. Fitting a log-normal distribution to this histogram yields a peak at 2.7 × 10–6 G0, a value close to that found for fast-breaking measurements (Figure S5b). Thus, molecular traces in this measurement appear at approximately the same conductance values as found for the fast-breaking measurements and have a long lifetime, consistently surviving for the entire modulation time of 120 s.

Figure 3.

Figure 3

Open in a new tab

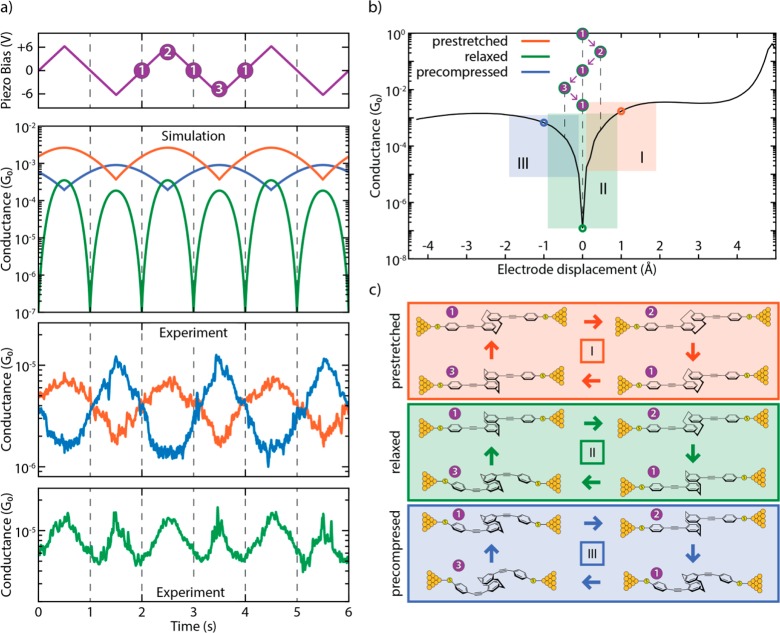
(a) Examples of distance-modulation traces (sample B). The blue, orange, and green lines (middle and bottom panel) represent three different conductance measurements, whereas the purple line (top panel) represents the voltage applied to the piezoelectric stack. The applied piezo voltage translates into a peak-to-peak distance of 5.0 Å, and a positive voltage corresponds to a larger electrode distance. The total modulation time is 120 s at a frequency of 0.5 Hz. The conductance responds to the electrode-separation modulation either in-phase (orange), in antiphase (blue), or with double the modulation frequency (green). An example of a full measurement, extending over 120 s, is shown in Figures S17 and S19. (b) Distribution of absolute values of gauge factors obtained from 123 selected traces of the distance-modulation measurements performed on sample B. The number in the figure corresponds to the peak value of the distribution.

As illustrated in Figures 3a and S12–S16, as the gap size increases, the conductance can either increase or decrease. In the former case, we define the conductance changes to be in phase with the gap size modulation (orange curve in Figure 3a). In the latter, it is the other way around: the conductance change is in antiphase with the gap-size modulation (blue curve in Figure 3a). About 32% of the molecular traces show in-phase conductance variations, 28% appear to respond in antiphase, and about 40% show a mixture of both or a more-complex response (Figures S13–S17). Most of the conductance traces show these conductance variations at the same frequency as the driving modulation (Figure S18); however, surprisingly, many (31%) respond at double the driving frequency. The green curve in Figure 3a is an example of this.

Theoretical Calculations

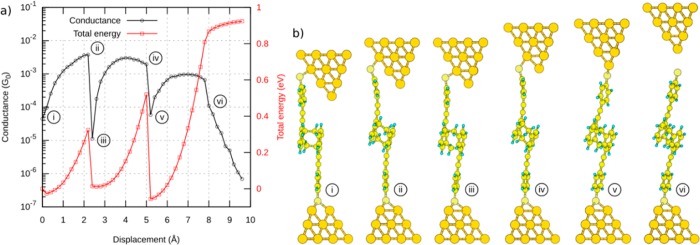
To shed more light on these experimental observations, DFT-based calculations were carried out. For the evaluation of the conductance, we used a proprietary framework.34 To start, we place the molecule between two pyramidal gold leads, as shown in Figure 4b. The upper electrode exhibits an atomically sharp tip, while the tip atom is removed for the lower one. By the placement of a terminal sulfur atom of the molecule at the hollow site of the lower pyramid, it binds to three gold atoms. Compared to the sulfur–gold bonding at the top lead, the stronger bonding of the sulfur atom to the hollow site ensures a stable mechanical connection, and the sulfur atom at the upper electrode starts sliding down the gold facets as the contact is being stretched.

Figure 4.

Figure 4

Open in a new tab

(a) Calculated conductance and total energy of the system during gap opening. (b) Selection of snapshots illustrating the stick–slip motion. A video of the simulated stick–slip motion can be found in the Supporting Information.

The total energy and conductance of this system show pronounced jumps at certain displacements during the gap opening. The snapshots at these displacements are shown in Figure 4b and reveal the expected movement of the sulfur atom. The displacement between snapshots iii and v (just after the sulfur atom jumped to the next gold atom) amounts to 2.8 Å, which is close to the gold–gold bond length of 2.89 Å in the simulated leads. The molecule in snapshots i, iii, and v is close to its relaxed gas-phase configuration (discussed below) and exhibits a low conductance. Upon further stretching, the conductance rises until it eventually levels off and reaches a local maximum at snapshots ii and iv. At this point, the sulfur anchor slips onto the next gold atom, thus releasing the mechanical tension in the molecule and restoring the conductance to a low value (panels iii and v). After the sulfur atom has reached the last gold atom of the upper lead, it finally loses its connection: the junction breaks and the molecule snaps back, as shown in snapshot vi. Thus, distancing of the electrodes leads to a stick–slip-like motion of the molecule along the surface of one of the electrodes.

In a detailed analysis of the displacement-dependent conductance, we study the molecule between two hollow leads, in which each sulfur binds to three gold atoms of the respective lead. This allows us to concentrate on the deformations of the actual molecule: the rigid bonding of the hollow–hollow configuration ensures that the lead displacement is directly passed to the molecule, minimizing deformations of the lead-molecule bonds. Starting from the configuration with minimal energy, corresponding to a molecule close to its relaxed state in the gas phase, the leads are either separated farther apart (positive displacement) or brought closer together (negative displacement), thereby stretching or compressing the molecule. The resulting conductance shows a pronounced dip at a well-determined displacement, which we define here as zero (see Figure 5b). The conductance rapidly increases when the molecule is either stretched or compressed from this position. The deformation in the stretched molecule is mainly identified with the shifting of the stacked benzene rings.

Figure 5.

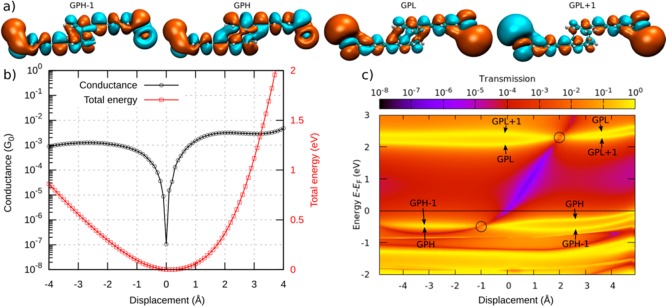
Figure 5

Open in a new tab

(a) Frontier orbitals of the molecule. The orbitals are either symmetric (GPH and GPL) or antisymmetric (GPH–1 and GPL+1) with respect to the center of the molecule. The frontier orbitals are shown in the gas phase for clarity (with the sulfur atoms “terminated” with one gold atom each) because they do not change significantly when the gold leads are attached to the molecule. (b) Conductance (horizontal black line in panel c) and total energy. (c) Transmission map of the molecule between two leads from DFT calculations. The horizontal yellow traces in the map arise from orbitals that can be related to the gas-phase frontier orbitals. An anti-resonance is observed between the frontier orbital traces. It shifts in energy as the displacement is varied. The positions at which the pairs of GPH–1 and GPH and of GPL and GPL+1 degenerate are marked with circles.

By evaluating the transmission in an energy range between −2 and +3 eV around the Fermi energy EF for each displacement step, we obtain the transmission map in Figure 5c. It reveals a transmission valley (purple diagonal line) between the traces related to the molecular frontier orbitals (yellow horizontal lines). The conductance dip in Figure 5b can be traced back to the intersection of the transmission valley and the Fermi energy. In other words, the energy position of the dip can be tuned by the lead separation. In the following, we present the underlying mechanism based on quantum interference of the molecular frontier orbitals.

A closer look at Figure 5c reveals HOMO and LUMO pairs that arise from the HOMO and LUMO states of the OPE units and are typically slightly split by the weak coupling through the PC core. To distinguish the character of the HOMO–1, HOMO, LUMO, and LUMO+1, we relate them to the frontier orbitals in the gas phase. For this purpose, we introduce the abbreviations GPH–1 to GPL+1, where GPH and GPL denote the gas-phase HOMO and LUMO, respectively. The orbitals are either symmetric (GPH and GPL) or anti-symmetric (GPH–1 and GPL+1) with respect to the center of the molecule. The crucial aspect is now that the energy of the frontier orbitals depends on the displacement. The states within HOMO and LUMO pairs, GPH–1 and GPH as well as GPL and GPL+1, eventually change their energetic order in the studied displacement window between around −4 to +4 Å. The displacements of the degeneracy points, at which these reversals take place, differ for the occupied and unoccupied states. They are located at d = −1.0 and +2.0 Å, respectively, as marked by circles in Figure 5c. According to the theory of quantum interference12,35 the orbital symmetry leads to a pronounced destructive interference feature in the HOMO–LUMO gap between displacements from −1.0 to +2.0 Å when the HOMO and LUMO pairs are ordered as in the gas phase. Outside of this displacement window, the molecular orbital pairs GPH–1 and GPH or GPL and GPL+1 rearrange in energy, thereby lifting the condition for destructive interference. Indeed, we can reproduce the main features of the conductance map by considering the displacement-dependent energies of the four frontier orbitals and their symmetries, as corroborated further in section III of the Supporting Information.

Discussion and Concluding Remarks

With the insights provided by the DFT calculations, the pronounced conductance oscillations can be explained through quantum interference of frontier orbitals in combination with the molecule acting as a spring when subject to mechanical deformations. Its relaxed conformation corresponds to the situation in which the anti-resonance originating from destructive interference of the HOMO and LUMO is in the vicinity of the Fermi energy, yielding a low-conductance state. By stretching or compressing the molecule, the anti-resonance is moved away from the Fermi energy, which leads to an increase of the conductance. The experimentally observed oscillations in conductance during continuous opening of the junction (Figure 2b) can then be associated with the stick–slip motion of the anchoring sulfur atoms on the gold surface, as this process releases the built-up mechanical strain in a semi-periodic fashion. Ab initio molecular-dynamics calculations at room temperature predict that Au–Au bonds should break instead of the Au–S bonds.36 However, if a gold adatom attached to a sulfur anchor was dragged along the gold electrode instead of the S itself, this would not lead to a qualitative change of the stick–slip picture.

The different behaviors (in-phase, antiphase, and frequency doubling) observed in the distance-modulation measurements (simulation: second panel in Figure 6a; experiment: bottom two panels in Figure 6a) can be attributed to variations in the initial molecular configuration at the beginning of the modulation. Traces that are in phase with the gap modulation are related to molecules that are pre-stretched in the starting configuration (orange panel in Figure 6c and the “pre-stretched” video in the Supporting Information). The starting point is at positive displacement and the oscillation takes place at the right lobe of the conductance curve (orange area in Figure 6b): an increase in electrode displacement corresponds to a higher conductance (and a decrease to a lower conductance). Along a similar line, traces in antiphase with the gap modulation can be related to molecules that are pre-compressed in the starting configuration (blue panel in Figure 6c and the “pre-compressed” video in the Supporting Information) and therefore correspond to oscillations at the left lobe of the conductance curve (blue area in Figure 6b). Traces with a doubled frequency (such as the green trace in Figure 6a and the “relaxed” video in the Supporting Information) are related to molecules that are close to the relaxed gas-phase geometry, in which the Fermi energy of the leads is aligned with the position of the interference dip (green panel, Figure 6c). In this case, the conductance dip is crossed two times during each piezo-modulation period, therefore doubling the frequency of the measured conductance, as can be seen by following the purple steps in Figure 6b. The appearance of the doubled frequency is thus a direct proof of the existence of the destructive interference dip. Importantly, the ability to mechanically tune the position of this dip to be located at the Fermi energy can be exploited in future studies and applications of quantum interference effects.

Figure 6.

Figure 6

Open in a new tab

(a, top panels) Simulation of conductance traces (second panel) when the electrode displacement is periodically modulated (top panel) for three different trapping configurations: pre-stretched (orange), relaxed (green), and pre-compressed (blue). Centers of oscillation at +1, 0, and −1 Å, respectively; amplitude of 0.5 Å. (a, bottom panels) Zoomed-in panel showing the experimental distance-modulation traces presented in Figure 3. (b) Calculated conductance vs electrode displacement. The blue, green, and orange areas (I, II, and III, respectively) show the portion of the curve spanned in the case of different starting positions (pre-compressed, relaxed, and pre-stretched, represented by circles in the same colors). The numbers in the purple circles represent the position of the electrodes along the oscillation period in the case of a relaxed trapping configuration. (c) Schematics of the molecular configurations along a period of electrode distance modulation. Different starting configurations are represented with different colors: pre-stretched in orange, relaxed in green, and pre-compressed in blue. White numbers in purple circles represent the position of the electrodes along the oscillation period. Note that the molecular compression and elongation in the simulation is 0.5 Å, a value smaller than the gap-size variation in the experiment. This can be rationalized by the elastic response of the sulfur–gold connections and of the gold atoms in the electrodes themselves.

We note that the conductance variations as a function of displacement can be used to estimate the gauge factor, characterizing the piezoresistive response of the molecular spring. The gauge factor is defined as the relative conductance change divided by displacement normalized to the molecular length (see Figure 3b and Supporting Information section II-4 for more details). We find gauge factors exhibiting a wide distribution with a peak located at GF = 5 and a tail at higher values, reaching up to 40 orders of magnitude larger than those that have been reported on single DNA molecules.37 We expect that thermally occupied ring rotations of the OPE rods at room temperature will reduce the electronic coupling in the molecule and the electron delocalization and, hence, the conductance. Besides the known shortcomings of DFT with regard to the description of level alignments,38 this could explain part of the over-estimation of the theoretically predicted conductance values in our static DFT geometries. In addition, longitudinal vibrations, as well as thermal fluctuations, will lead to gap-size modulations and an effective averaging over a range of junction configurations. Such vibrationally induced decoherence effects will wash out the interference-induced conductance minimum.39 Therefore, a precise control of the temperature may turn out to be crucial in the optimization of gauge factors, and the molecule studied here appears to be an ideal candidate with which to investigate quantum interference effects at lower temperatures and to quantify if decoherence limits the room-temperature performance.39−41 To achieve even-higher gauge factors, it would also be interesting to explore different chemical designs based on the mechanical manipulation principle of quantum interference.

Methods

MCBJ Experiments

For MCBJ experiments, a thin (<100 nm) gold wire is lithographically fabricated and suspended on a flexible substrate. Atomically sharp electrodes are formed when rupturing the wire in a three-point bending configuration. After the breaking of the wire, the electrodes can be fused together again by reducing the mechanical force used to bend the substrate. This opening and closing of the gap can be controlled with sub-nanometer accuracy on the position of the electrodes. Further details about the MCBJ setup and the measuring technique have been described elsewhere.29,30 The molecule was dissolved in dichloromethane, and the solution was drop-cast on the MCBJ sample after the characterization of the bare device (Figure S10). All measurements were performed in air at room temperature after the evaporation of the solvent. Concentrations of 9 μM (samples A and B), 90 μM (sample C), and 900 μM (sample D) have been used, but no significant dependence on the concentration has been observed.

Fast-Breaking Measurements

Fast-breaking measurements were performed by applying a bias of 100 mV and using a constant pulling speed of the electrodes of 4.0 nm/s. The conductance is recorded until it falls below the noise level, which is about 5·10–7 G0 in our setup. At this point the electrodes are fused back and a new trace is recorded. A total of 3000 such traces were recorded for samples A–C and 5000 for sample D. Further information on the technique can be found in Frisenda et al.31

Distance-Modulation Measurements

In these measurements, the electrode spacing was modulated to periodically increase and decrease.32 The MCBJ was initially stretched to a few-atom width (3 G0) and allowed to self-break by its surface tension to form atomically sharp electrodes. Then, the electrodes were separated by 1.75 nm, which is approximately the estimated length of the unstretched molecule. At this point, a 0.5 Hz triangular wave was applied to the piezoelectric stack that controls the electrode positions with a peak-to-peak gap size variation of 5.0 Å (Figure 3) or 2.5 Å (Figure S12), depending on the amplitude of the applied piezo voltage. Note that a higher voltage on the piezoelectric corresponds to a larger electrode separation.

The initial opening of the junction allows us to recognize if trapping of a molecule occurs because, for a displacement of 1.75 nm, the tunnelling conductance in the absence of a molecule is below the noise level of our setup. The modulation was kept for 120 s, after which the junction was stretched until the noise level was reached and fused back again to start a new cycle. It should be noted that the initial configuration in a distance-modulation experiment cannot be controlled.

Simulations

DFT calculations were carried out with TURBOMOLE.42 We used the def-SVP basis set and the PBE functional.43,44 During structural relaxations the total energy was converged to 10–6 au and the maximum norm of the Cartesian gradient to 10–3 au. The electronic transmission was evaluated with a proprietary cluster-based framework. The procedure includes the separation of the system into semi-infinite leads and a central part, which contains the molecule and parts of the electrodes. The energy-dependent transmission function is expressed in terms of non-equilibrium Green’s functions (NEGFs) of the leads and the central part. The bulk parameters of the leads were extracted from a cluster of 1415 gold atoms. Further details on the method can be found in Pauly et al.34

Acknowledgments

The authors in Basel and Delft acknowledge financial support by the European FP7-ITN MOLESCO (project no. 606728) and the H2020 FET QuIET (project no. 767187). The work at the University of Basel was also supported by the Swiss National Science Foundation (SNF, grant no. 200020-178808) and the Swiss Nanoscience Institute (SNI); the work at TU Delft was supported by the EU through an advanced ERC grant (Mols@Mols). M.S. and F.P. acknowledge funding through the Collaborative Research Centre (SFB) 767 of the German Research Foundation (DFG) as well as computational resources provided by the state of Baden-Württemberg through bwHPC and the DFG through grant no. INST 40/467-1 FUGG. Device fabrication was done at the Kavli Nanolab at Delft. D.S. thanks Riccardo Frisenda for fruitful discussions. K.J.W. thanks Markus Neuburger for single-crystal X-ray analysis.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b02810.

  • Details on the synthesis and characterization of the molecules, crystal data and structure refinement, additional fast-breaking and distance-modulation measurements, statistical analysis, and the transport calculations (PDF)

  • A movie showing a simulation of the stick-slip motion (MPG)

  • A movie showing a simulation of a distance-modulation trace with a molecule pre-stretched in the starting configuration (MPG)

  • A movie showing a simulation of a distance-modulation trace with a molecule pre-compressed in the starting configuration (MPG)

  • A movie showing a simulation of a distance-modulation trace with a molecule relaxed in the starting configuration (MPG)

Author Contributions

D.S., K.J.W., and M.S. contributed equally. D.S., C.H., K.J.W., M.M.m and H.S.J.Z. conceived of and designed the experiment. M.L.P. assembled the MCBJ setup. M.L.P., D.S., and C.H. wrote the software used for the experiments. D.S. and C.H. performed the break-junction experiments and the data analysis. K.J.W. and M.M. provided and characterized the molecule. M.S. and F.P. performed transport calculations. All authors wrote the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nl8b02810_si_001.pdf (3.8MB, pdf)
nl8b02810_si_002.mpg (190.8KB, mpg)
nl8b02810_si_003.mpg (4.6MB, mpg)
nl8b02810_si_004.mpg (4.5MB, mpg)
nl8b02810_si_005.mpg (4.6MB, mpg)

References

  1. van der Molen S.; Naaman R.; Scheer E.; Neaton J.; Nitzan A.; Natelson D.; Tao N.; van der Zant H.; Mayor M.; Ruben M.; Reed M.; Calame M. Nat. Nanotechnol. 2013, 8, 385–389.23736209 [Google Scholar]
  2. Aradhya S.; Venkataraman L. Nat. Nanotechnol. 2013, 8, 399–410. 10.1038/nnano.2013.91. [DOI] [PubMed] [Google Scholar]
  3. Sun L.; Diaz-Fernandez Y.; Gschneidtner T.; Westerlund F.; Lara-Avila S.; Moth-Poulsen K. Chem. Soc. Rev. 2014, 43, 7378–7411. 10.1039/C4CS00143E. [DOI] [PubMed] [Google Scholar]
  4. Xiang D.; Wang X.; Jia C.; Lee T.; Guo X. Chem. Rev. 2016, 116, 4318–4440. 10.1021/acs.chemrev.5b00680. [DOI] [PubMed] [Google Scholar]
  5. Wang L.; Wang L.; Zhang L.; Xiang D. Top. Curr. Chem. 2017, 375, 85. 10.1007/s41061-017-0149-0. [DOI] [PubMed] [Google Scholar]
  6. Quek S.; Kamenetska M.; Steigerwald M.; Choi H.; Louie S.; Hybertsen M.; Neaton J.; Venkataraman L. Nat. Nanotechnol. 2009, 4, 230–234. 10.1038/nnano.2009.10. [DOI] [PubMed] [Google Scholar]
  7. Su T.; Li H.; Steigerwald M.; Venkataraman L.; Nuckolls C. Nat. Chem. 2015, 7, 215–220. 10.1038/nchem.2180. [DOI] [PubMed] [Google Scholar]
  8. Li Y.; Haworth N.; Xiang L.; Ciampi S.; Coote M.; Tao N. J. Am. Chem. Soc. 2017, 139, 14699–14706. 10.1021/jacs.7b08239. [DOI] [PubMed] [Google Scholar]
  9. Frisenda R.; Harzmann G.; Celis Gil J.; Thijssen J.; Mayor M.; van der Zant H. Nano Lett. 2016, 16, 4733–4737. 10.1021/acs.nanolett.5b04899. [DOI] [PubMed] [Google Scholar]
  10. Wu S.; González M.; Huber R.; Grunder S.; Mayor M.; Schönenberger C.; Calame M. Nat. Nanotechnol. 2008, 3, 569–574. 10.1038/nnano.2008.237. [DOI] [PubMed] [Google Scholar]
  11. Schneebeli S.; Kamenetska M.; Cheng Z.; Skouta R.; Friesner R.; Venkataraman L.; Breslow R. J. Am. Chem. Soc. 2011, 133, 2136–2139. 10.1021/ja111320n. [DOI] [PubMed] [Google Scholar]
  12. Nozaki D.; Lücke A.; Schmidt W. J. Phys. Chem. Lett. 2017, 8, 727–732. 10.1021/acs.jpclett.6b02989. [DOI] [PubMed] [Google Scholar]
  13. Solomon G.; Vura-Weis J.; Herrmann C.; Wasielewski M.; Ratner M. J. Phys. Chem. B 2010, 114, 14735–14744. 10.1021/jp103110h. [DOI] [PubMed] [Google Scholar]
  14. Frisenda R.; Janssen V.; Grozema F.; van der Zant H.; Renaud N. Nat. Chem. 2016, 8, 1099–1104. 10.1038/nchem.2588. [DOI] [PubMed] [Google Scholar]
  15. Lambert C. Chem. Soc. Rev. 2015, 44, 875–888. 10.1039/C4CS00203B. [DOI] [PubMed] [Google Scholar]
  16. Schwarz F.; Kastlunger G.; Lissel F.; Egler-Lucas C.; Semenov S.; Venkatesan K.; Berke H.; Stadler R.; Lörtscher E. Nat. Nanotechnol. 2016, 11, 170–176. 10.1038/nnano.2015.255. [DOI] [PubMed] [Google Scholar]
  17. Koole M.; Thijssen J.; Valkenier H.; Hummelen J.; van der Zant H. Nano Lett. 2015, 15, 5569–5573. 10.1021/acs.nanolett.5b02188. [DOI] [PubMed] [Google Scholar]
  18. Darwish N.; Díez-Pérez I.; Da Silva P.; Tao N.; Gooding J.; Paddon-Row M. Angew. Chem., Int. Ed. 2012, 51, 3203–3206. 10.1002/anie.201107765. [DOI] [PubMed] [Google Scholar]
  19. Atesci H.; Kaliginedi V.; Celis Gil J.; Ozawa H.; Thijssen J.; Broekmann P.; Haga M.; van der Molen S. Nat. Nanotechnol. 2018, 13, 117–121. 10.1038/s41565-017-0016-8. [DOI] [PubMed] [Google Scholar]
  20. Li X.; Staykov A.; Yoshizawa K. Bull. Chem. Soc. Jpn. 2012, 85, 181–188. 10.1246/bcsj.20110256. [DOI] [Google Scholar]
  21. Brown C.; Farthing A. Nature 1949, 164, 915–916. 10.1038/164915b0.15407665 [DOI] [Google Scholar]
  22. Vorontsova N.; Rozenberg V.; Sergeeva E.; Vorontsov E.; Starikova Z.; Lyssenko K. A.; Hopf H. Chem. - Eur. J. 2008, 14, 4600–4617. 10.1002/chem.200701683. [DOI] [PubMed] [Google Scholar]
  23. Carlotti M.; Kovalchuk A.; Wächter T.; Qiu X.; Zharnikov M.; Chiechi R. Nat. Commun. 2016, 7, 13904. 10.1038/ncomms13904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Häkkinen H. Nat. Chem. 2012, 4, 443–455. 10.1038/nchem.1352. [DOI] [PubMed] [Google Scholar]
  25. Zafra J.; Molina Ontoria A.; Mayorga Burrezo P.; Peña-Alvarez M.; Samoc M.; Szeremeta J.; Ramírez F.; Lovander M.; Droske C.; Pappenfus T.; Echegoyen L.; López Navarrete J.; Martin N.; Casado J. J. Am. Chem. Soc. 2017, 139, 3095–3105. 10.1021/jacs.6b12520. [DOI] [PubMed] [Google Scholar]
  26. Seferos D.; Trammell S.; Bazan G.; Kushmerick J. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 8821–8825. 10.1073/pnas.0500002102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Bondarenko L.; Dix I.; Hinrichs H.; Hopf H. Synthesis 2004, 2004, 2751–2759. 10.1055/s-2004-834872. [DOI] [Google Scholar]
  28. Shi Z.; Wang L.; Wang H.; Cao X.; Zhang H. Org. Lett. 2007, 9, 595–598. 10.1021/ol062793l. [DOI] [PubMed] [Google Scholar]
  29. Martin C.; Ding D.; van der Zant H.; van Ruitenbeek J. New J. Phys. 2008, 10, 065008. 10.1088/1367-2630/10/6/065008. [DOI] [Google Scholar]
  30. Martin C.; Smit R.; van Egmond R.; van der Zant H.; van Ruitenbeek J. Rev. Sci. Instrum. 2011, 82, 053907. 10.1063/1.3593100. [DOI] [PubMed] [Google Scholar]
  31. Frisenda R.; Perrin M.; Valkenier H.; Hummelen J.; van der Zant H. Phys. Status Solidi B 2013, 250, 2431–2436. 10.1002/pssb.201349236. [DOI] [Google Scholar]
  32. Xia J.; Diez-Perez I.; Tao N. Nano Lett. 2008, 8, 1960–1964. 10.1021/nl080857a. [DOI] [PubMed] [Google Scholar]
  33. Tsutsui M.; Shoji K.; Taniguchi M.; Kawai T. Nano Lett. 2008, 8, 345–349. 10.1021/nl073003j. [DOI] [PubMed] [Google Scholar]
  34. Pauly F.; Viljas J.; Huniar U.; Häfner M.; Wohlthat S.; Bürkle M.; Cuevas J.; Schön G. New J. Phys. 2008, 10, 125019. 10.1088/1367-2630/10/12/125019. [DOI] [Google Scholar]
  35. Yoshizawa K.; Tada T.; Staykov A. J. Am. Chem. Soc. 2008, 130, 9406–9413. 10.1021/ja800638t. [DOI] [PubMed] [Google Scholar]
  36. Krüger D.; Fuchs H.; Rousseau R.; Marx D.; Parrinello M. Phys. Rev. Lett. 2002, 89, 186402. 10.1103/PhysRevLett.89.186402. [DOI] [PubMed] [Google Scholar]
  37. Bruot C.; Palma J.; Xiang L.; Mujica V.; Ratner M.; Tao N. Nat. Commun. 2015, 6, 8032. 10.1038/ncomms9032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Quek S.; Venkataraman L.; Choi H.; Louie S.; Hybertsen M.; Neaton J. Nano Lett. 2007, 7, 3477–3482. 10.1021/nl072058i. [DOI] [PubMed] [Google Scholar]
  39. Ballmann S.; Härtle R.; Coto P.; Elbing M.; Mayor M.; Bryce M.; Thoss M.; Weber H. Phys. Rev. Lett. 2012, 109, 056801. 10.1103/PhysRevLett.109.056801. [DOI] [PubMed] [Google Scholar]
  40. Selzer Y.; Cabassi M.; Mayer T.; Allara D. Nanotechnology 2004, 15, 483–488. 10.1088/0957-4484/15/7/057. [DOI] [Google Scholar]
  41. Kamenetska M.; Widawsky J.; Dell’Angela M.; Frei M.; Venkataraman L. J. Chem. Phys. 2017, 146, 092311. 10.1063/1.4973318. [DOI] [Google Scholar]
  42. Ahlrichs R.; Bär M.; Häser M.; Horn H.; Kölmel C. Chem. Phys. Lett. 1989, 162, 165–169. 10.1016/0009-2614(89)85118-8. [DOI] [Google Scholar]
  43. Schäfer A.; Horn H.; Ahlrichs R. J. Chem. Phys. 1992, 97, 2571–2577. 10.1063/1.463096. [DOI] [Google Scholar]
  44. Perdew J.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl8b02810_si_001.pdf (3.8MB, pdf)
nl8b02810_si_002.mpg (190.8KB, mpg)
nl8b02810_si_003.mpg (4.6MB, mpg)
nl8b02810_si_004.mpg (4.5MB, mpg)
nl8b02810_si_005.mpg (4.6MB, mpg)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES