AptaBlocks: Designing RNA complexes and accelerating RNA-based drug delivery systems

Abstract

RNA-based therapeutics, i.e. the utilization of synthetic RNA molecules to alter cellular functions, have the potential to address targets which are currently out of scope for traditional drug design pipelines. This potential however hinges on the ability to selectively deliver and internalize therapeutic RNAs into cells of interest. Cell internalizing RNA aptamers selected against surface receptors and discriminatively expressed on target cells hold particular promise as suitable candidates for such delivery agents. Specifically, these aptamers can be combined with a therapeutic cargo and facilitate internalization of the cargo into the cell of interest. A recently proposed method to obtain such aptamer-cargo constructs employs a double-stranded “sticky bridge” where the complementary strands constituting the bridge are conjugated with the aptamer and the cargo respectively. The design of appropriate sticky bridge sequences however has proven highly challenging given the structural and functional constraints imposed on them during synthesis and administration. These include, but are not limited to, guaranteed formation and stability of the complex, non-interference with the aptamer or the cargo, as well as the prevention of spurious aggregation of the molecules during incubation. In order to address these issues, we have developed AptaBlocks - a computational method to design RNA complexes that hybridize via sticky bridges. The effectiveness of our approach has been verified computationally, and experimentally in the context of drug delivery to pancreatic cancer cells. Importantly, AptaBlocks is a general method for the assembly of nucleic acid systems that, in addition to designing of RNA-based drug delivery systems, can be used in other applications of RNA nanotechnology. AptaBlocks is available at https://github.com/wyjhxq/AptaBlocks.

INTRODUCTION

Synthetic RNA molecules are increasingly utilized to alter the behavior of genes and cells (1–4). A list of examples, although by no means complete, includes RNA interference (RNAi) as a highly sequence-specific gene silencing mechanism and programmable RNAs engineered to enact and tune gene regulatory mechanisms through mediating interactions with the cellular machinery (2). Furthermore, cis-acting RNAs are subject to regulation through interactions with trans-acting small RNAs (sRNAs), which enable or block their formation, creating inducible genetic control elements (2,3). RNA-based therapeutics hence hold a promise for targeting currently undruggable genes and treating a diverse array of diseases including cancer (5,6). However targeted delivery of RNAs remains challenging. One line of attack is to use nanoparticles which can accomplish tumor targeted drug delivery via specific design or conjugated ligands, such as antibodies, folates, and peptides (reviewed in (7,8).)

Recently, RNA aptamers emerged as promising drug delivery agents (reviewed in (9–11)). Aptamers are short RNA or DNA molecules identified through iterative rounds of in vitro selection (12,13) to specifically recognize and bind cognate targets. Importantly, aptamers that bind to specific cell receptors can often be internalized into the cells that express these receptors on their surface (9,14) making them ideal candidates as cell specific vehicles to deliver therapeutic cargoes.

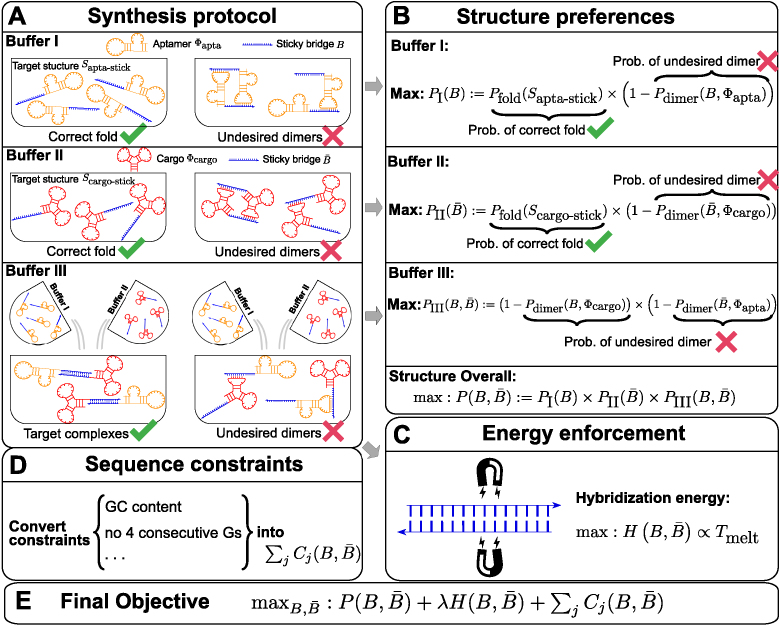
Initially, aptamer based delivery systems were assembled by conjugating aptamers with cargoes of interest through synthesis of long RNA molecules containing both sequences (15–17). This strategy however suffers from the considerable disadvantage of requiring the synthesis of long RNA molecules. Recently, Zhou, et al. (18,19) proposed an alternative approach that relies on conjugating complementary RNA strands to the aptamer and the cargo to form aptamer-stick and cargo-stick conjugates respectively. When incubating the conjugates together in a subsequent step, these complementary strands would hybridize to form a double-stranded “sticky bridge” connecting the aptamer with its cargo (Figure 1) (18,19). The experimental design hence follows a three-step procedure where aptamer-stick and cargo-stick are first synthesized and allowed to fold in separate buffers (Step 1-2, Figure 1A-Buffer I and A-Buffer II), followed by an annealing phase in a binding buffer to form the final aptamer-sticky bridge-cargo complex (Figure 1A-Buffer III).

Figure 1.

(A) The synthesis protocol (18) that AptaBlocks relies on. (A-Buffer I) Production of the first intermediate, corresponding to the conjugation Φ_apta-stick(B) of the aptamer Φ_apta and the sticky bridge B folding into structure S_apta-stick. Notably, S_apta-stick includes all structures where B is unpaired. (A-Buffer II) Production of the second intermediate, which is the conjugation Φ_cargo-stick(S) of the cargo Φ_cargo and the sticky bridge forming into structure S_cargo-stick. Importantly, S_cargo-stick includes all structures where is unpaired. (A-Buffer III) Generation of the final RNA complex. (B) Converting structure preferences in each buffer into thermodynamic probabilities. (C) Enforcing strong binding between sticky bridges to increase melting temperature. is defined in Equation (5). (D) Formulation of sequence constraints into indicator functions. (E) Final objective function that incorporates structure preferences, energy enforcement and sequence constraints.

As described later in this paper, this procedure not only reduces the length of the sequences to be synthesized but, if designed appropriately, allows to reuse the aptamer-stick as a universal delivery agent for several different cargoes. Notably, current design pipelines for sticky bridges tend to be solely informed by the experimentalists expertise and, in practice, manual designs based on trial and error strategy tend to be costly, time consuming, and not always successful. This observation can be contributed to three main challenges which emerge at different stages of the assembly. First, the covalently added “sticky bridge sequences” must hybridize to form a stable double helix. Second, they cannot interfere with any secondary and tertiary structural elements of the aptamer and the cargo and third, unwanted aggregation of the molecules, such as cargo sticky bridge interactions, must be avoided.

To address these challenges, we propose AptaBlocks, an efficient computational method for designing sticky-bridge based RNA complexes. In this paper we refer to the assembled molecules as “aptamer” and “cargo” but the method is general and can be used in other applications of RNA nanotechnology. Accounting for the three-step procedure (18,19), we formulate the sticky bridge sequence design as an optimization problem utilizing an objective function which reflects the biophysical characteristics of the assembly process. Specifically, we designed the objective function considering the equilibrium probabilities of the target structures over all possible structures of the aptamer-stick and cargo-stick, the probability of the interaction between the aptamer-stick and cargo-stick at equilibrium, the hybridization energy between the sticky bridge sequences, and additional sequence constraints including but not limited to the GC content. We further provide a simulated annealing algorithm that enables efficient estimation of the corresponding combinatorial optimization problem. We want to emphasize that AtpaBlocks is the first algorithm that is able to tackle this problem. Nupack Design (20,21) can be modified to design sticky bridges but it was not developed based on the the three-step procedure (18,19) and utilizes an over-simplified model that cannot address the full scope of the design problem.

When tested on simulated data, AptaBlocks successfully preserved the structures of both, the aptamers and cargoes, while achieving high binding affinity between the complementary strands of the sticky bridges. Next, we measured the performance of our approach to design universal sticky bridges for one aptamer and multiple distinct cargoes by varying the number and the sequence similarity of the latter. Our results indicate that AptaBlocks is capable of designing universal sticky bridges for either many cargoes with similar sequences or a smaller number of cargoes with distinct sequences.

In addition to validating AptaBlocks in silico, we applied our method to synthesize sticky bridges for an aptamer-siRNA conjugate. Specifically, we used AptaBlocks to design a sticky bridge conjugating pancreatic cancer specific RNA aptamer tP19 (22) and the NGF siRNA, previously shown to inhibit pancreatic cancer progression (23). We validated the successful formation of the conjugate in vitro. Pancreatic cancer is notorious for its high mortality rate, for which, despite significant efforts, only limited progress towards effective therapeutics has been made. Conjugate based therapeutics provide a promising strategy to improve treatment for these type of cancers in large part due to the high target affinity and specificity of aptamers (19,22). Hence, informing traditional conjugate design pipelines with in silico optimized sticky bridges using AptaBlocks not only provides the opportunity for accelerating this line of research, but represents a powerful and universal tool for the optimization of sticky bridges in other areas of research.

MATERIALS AND METHODS

Method overview

AptaBlocks takes two or more RNA molecules (the building blocks) as input and designs an RNA complex containing these molecules while preserving their individual secondary structures and thus their biological functions. In a typical application, one of the molecules is an RNA aptamer (a delivery agent), while the other molecule, the so called “cargo”, is a therapeutic with the potential of modifying the cell’s function after being internalized. Note that designing aptamer-cargo complexes is a special case of the problem of designing RNA complexes with particular properties (20,24). Indeed, our method is general and can be applied to more complex settings such as combining more than two RNA molecules. To facilitate such designs, AptaBlock does not require that the sticky bridge is necessarily at the termini of the assembled molecules. Furthermore, for designing an RNA complex that includes a larger number of RNA molecules, more than one sticky bridge can be used.

In the case of two building blocks, an aptamer and a cargo, AptaBlocks aims at designing two complementary RNA sequences B and 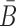, so that when B is conjugated with the aptamer and 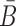is conjugated with the cargo, the desired aptamer-cargo complex is successfully formed through hybridization between B and .

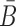Note that this model assumes a specific order of assembly as described in (18) where the building blocks are synthesized and folded separately and then incubated together to allow formation of the final complex (Figure 1A). Consistent with this experimental setup, AptaBlocks designs two intermediates, Φ_apta-stick and Φ_cargo-stick, the former referring to the aptamer conjugated with B and the latter to the cargo conjugated with 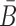while satisfying the following conditions:

• B and 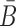are unstructured in Φ_apta-stick and Φ_cargo-stick and, in particular, do not perturb the structures of the aptamer and the cargo. Examples of these target structures are shown in Figure 1A- Buffer I and A-Buffer II (target structure).

• Two or more Φ_apta-stick molecules should not bind to each other to form undesired dimers or larger aggregates. The same condition has to be satisfied by Φ_cargo-stick. Examples of these undesired dimers are shown in Figure 1A-Buffer I and A-Buffer II.

• When Φ_apta-stick and Φ_cargo-stick incubate together, the sticky bridge strand B in Φ_apta-stick should not interact with the cargo strand in Φ_cargo-stick. Similarly, the sticky bridge strand 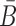in Φ_cargo-stick should not interact with the aptamer strand in Φ_apta-stick. Examples of these off-target interactions are shown in Figure 1A-Buffer III (undesired dimer).

• To maximize stability of the complex, the melting temperature of the sticky bridge that controls complex formation is maximized, i.e. the binding free energy between B and 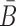is minimized.

Additional constraints on the sticky bridge sequences, such as the exclusion of long chains of G’s due to their difficulty of being synthesized, can also be added. AptaBlocks employs a biophysically inspired theoretical model capturing the complex objectives of the design specified above and yet is simple enough to allow for efficient parameter estimation. Given the developed model, the sticky bridge sequence is optimized using a Monte Carlo algorithm based on heat-bath transitions (see the following section). Note, that optimization procedure does depend on the relative concentration of the reactants. In a typical setting the concentrations are equal. If needed, the optimal concentration of the aptamer-cargo complex can be achieved by setting the concentrations of the aptamer and cargo based on the model proposed in (25) after the design of the sticky bridge.

In practical applications, the goal is often to target a specific cell using an appropriate aptamer and to deliver a cargo, optimized to manipulate specific pathways. If, for instance, the aim is to silence a gene using siRNA, this task can typically be accomplished by more than one siRNA species. Furthermore, silencing a particular gene might require the use of multiple siRNAs for multiple targets in the same pathway. However, synthesizing a different B and 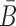for each possible aptamer-cargo pair is highly impractical, time consuming, and cost intensive. Notably, our flexible model enables to bypass this issue by extending our approach to allow for designing a universal sticky bridge for a specific aptamer but multiple different cargoes (see the following section).

The AptaBlocks algorithm

We describe our method in more details in the following. First, weoutline our biophysics based model to compute the probabilities that characterize the structural properties mentioned above. Then, we elucidate the heat-bath algorithm, a Monte Carlo method closely related to the classical (Metropolis-based) simulated annealing, that AptaBlocks uses to optimize these probabilities as well as the melting temperature, subject to possible additional constraints the user might impose on B and .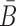

Preserving the original functionality of interacting RNA molecules

The function of a molecule is dependent on both - its sequence and structure. Therefore conjugating B with the aptamer and 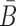with the cargo respectively can affect the desired, and functionally active, structures of the aptamer and cargo. Thus the aptamer-stick conjugate Φ_apta-stick(B) is required to attain a specific target structure S_apta-stick that consists of the aptamer part folded in the same manner as before it was conjugated with B while ensuring that B does not interact with the aptamer and remains unfolded (Figure 1 A-Buffer I). Preserving the target structure therefore translates into maximizing the probability P_fold(S_apta-stick|Φ_apta-stick(B)) (26–28) (a detailed description of P_fold can be found in Supplementary Material C.1) that the sequence Φ_apta-stick(B) folds into S_apta-stick. To achieve this, it suffices to enforce all nucleotides of B to be unpaired in Φ_apta-stick(B). Recall that in the experimental protocol, Φ_apta-stick(B) molecules are initially present in one buffer (e.g. Buffer I), opening the possibility of binding to each other (Figure 1 A-Buffer I). Assuming that the aptamers themselves do not dimerize, dimerization between the Φ_apta-stick(B) molecules at the sticky bridge strand B must still be prevented. Denoting P_dimer(B, Φ_apta) as the probability of undesired binding between the B strand of one molecule with the Φ_apta part in another, we can formulate the structural preferences mentioned above for Φ_apta-stick(B) as Equation (1) (Figure 1B for Buffer I) and further maximize Equation (1) to secure structural properties for Φ_apta-stick(B).

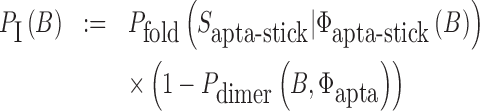(1)

Similarly, to ensure the cargo-stick species in Buffer II fold into the target structure S_cargo-stick which preserves the fold of the cargo and restricts 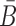to be unpaired, as well as to prevent the formation of undesired dimerizations, we maximize 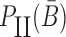defined as (Figure 1B for Buffer II)

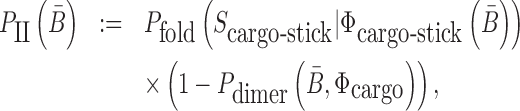(2)

where 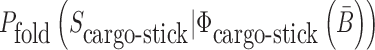is the probability that the cargo-stick species folds into S_cargo-stick for given 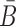(26,27), and 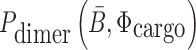corresponds to the dimerization probability between 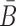and Φ_cargo across species. In case of a double stranded cargo such as a siRNA, 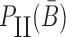is computed differently from a single-stranded RNA molecule and we refer the reader to Supplementary Material A for a detailed discussion.

To generate the final RNA complex, the above two intermediates are mixed together in a third buffer, expecting the complementary sticky bridge strands B and 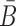to hybridize together. To avoid undesired interactions between sticky bridge strands and loop-structures (functional components (29,30)) of the aptamer and the cargo, we reduce the probability of those off-target dimerizations (as shown in Figure 1 A-Buffer III) by maximizing 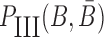(Figure 1B for Buffer III):

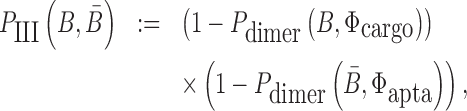(3)

where P_dimer(B, Φ_cargo) is the dimerization probability between sticky bridge B and cargo strand Φ_cargo and 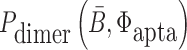stands for the dimerization probability between sticky bridge 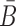and aptamer strand Φ_apta.

Overall, the sticky bridge strands B and 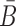have to simultaneously maximize P_I(B), 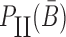, and 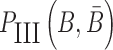to guarantee the production of two intermediates and the final aptamer-sticky bridge-cargo RNA complex. Hence, we define the overall structure objective 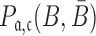for aptamer 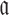and cargo as

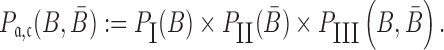(4)

Optimizing the melting temperature

To increase the melting temperature between B and 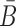, which is proportional to the free energy of their hybridization (31), we minimize the hybridization free energy between the sticky bridge sequences B and 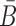by maximizing the energy objective function defined as

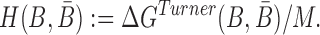(5)

where the hybridization energy 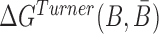is computed based on the Turner RNA folding model (32). M is used to normalize 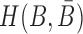into [0,1], which can be set to the smallest .

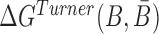Sequence constraints for sticky bridges

Besides conforming to structural preferences and optimizing melting temperature, further specific sequence requirements might have to be satisfied. In addition to ensuring complementarity between B and 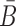, one might for instance require a particular GC content or must take into account chemical synthesis constraints prohibiting the inclusion of 4 consecutive guanines in the primary structure. Assuming C is a sequence constraint, we define an indicator function C as

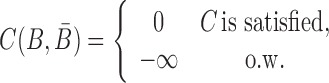(6)

for inclusion into the final model as outlined below.

Final formulation

Considering the structure preferences, energy enforcement and sequence constraints, we formulate the sticky bridge design problem as

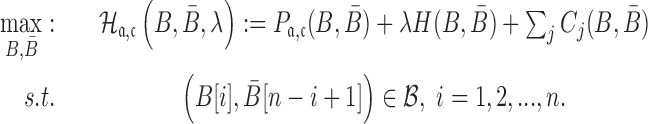(7)

where the constraint enforces B and 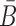to be complementary and 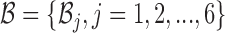corresponds to a set of all possible 6 base pairs with 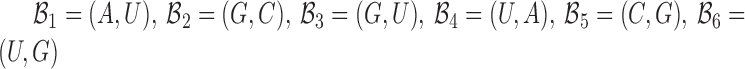. The length of the sticky bridge sequences is defined as 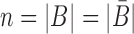whereas C_j corresponds to the j-th sequence constraint.

To take advantage of the complementary property between B and 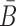, we define 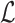, where , and therefore transform the problem of designing sequences B and into designing base pairs for . After abuse of the notations, we convert problem (7) into

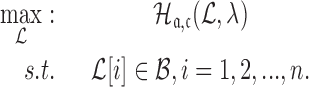(8)

Extension to multiple cargoes setting

In practical applications, the goal is often to target a specific cell using an appropriate aptamer and deliver a cargo optimized to manipulate specific pathways. If, for instance, we aim at silencing a gene using siRNA, we are typically not limited to a single siRNA species to perform this task. In addition, if we are not successful in silencing a gene we might try to silence another gene in the same pathway. However, synthesizing a different B and 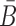for each possible aptamer-cargo pair is highly impractical, time consuming, and cost intensive. Notably, our flexible model enables to bypass this issue by extending our approach to allow for designing a universal sticky bridge for a specific aptamer but multiple different cargoes. Let 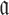be an aptamer of interest and 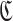be a set of cargoes that need to be delivered. Then we can attempt to find the optimal universal stick bridge sequences for all aptamer-cargo combinations by solving

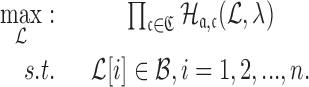(9)

The optimization procedure

To optimize our target function, subject to all imposed constraints, we use a heat-bath Monte Carlo optimization strategy - a strategy similar to the classical simulated annealing. While both, simulated annealing and the heat-bath, are conceptually very similar, the classical simulated annealing is based on the Metropolis approach to compute transition probabilities without computing partition functions which is computationally intractable in many applications. In our setting however, efficient computation of the partition function is not a challenge, allowing us to use the alternative heat-bath transitions probabilities which are known to have better performance (33,34).

Let 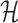represent the Hamiltonian, the objective function of the combinatorial problem. We apply the single spin heat-bath update rule, which updates the system energy when making a base pair change for a given position i in 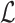from base pair 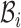to base pair 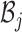while keeping the rest of the base pairs in 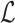fixed: 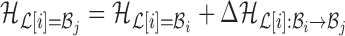. The probability of making the base pair change is proportional to the exponential of the corresponding energy change of the entire system, i.e

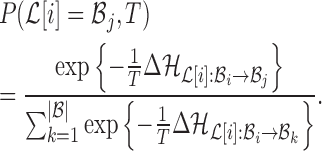(10)

The details of the AptaBlocks algorithm are elaborated in Algorithm 1. Given the complex interplay between multiple objectives described in (7), a trade-off between optimizing one over another exists. Thus, AptaBlocks varies λ and generates several alternative solutions with their respective scores so that they can be further investigated if required. Those solutions are actually on the pareto front of the equivalent multi-objective function (35).

Efficient approximation

Solving problems (8) and (9) using the AptaBlocks algorithm is computationally expensive. Based on Equation (10), in the AptaBlocks algorithm Algorithm 1, the calculation of the Hamiltonian 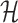is a fundamental operation and is repeatedly executed. The time complexity of computing 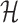is dominated by calculating the dimerization probability P_dimer( ·, ·) required in Equations (1), (2), and (3). P_dimer( ·, ·) can be computed based on an RNA-RNA interaction model (36–38) therefore defining the time complexity of computing 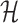as O(m⁶), where m = max (|Φ_apta|, |Φ_cargo|).

To reduce the time complexity, we propose to prevent undesired dimerization through minimizing 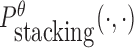instead of P_dimer( ·, ·). 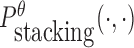is the probability of strong stacking hybridization between pairwise interacting RNAs where the binding free energy is less than θ. Based on Lemma 1 in Supplementary Materials B, we prove

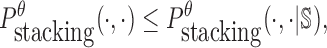(11)

where 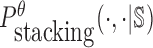is the probability of strong stacking hybridization with free energy less than θ conditioned on that the pairwise RNAs indeed bind together only through stacking hybridization. Therefore, computing and minimizing 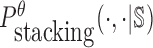, the upper bound of 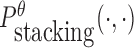, can eventually minimize 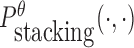to avoid strong binding across species.

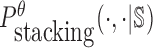can be computed in O(m³) based on the model used by RNAup (38) (see Supplementary Materials B). In summary, we replace P_dimer( ·, ·) in Equations (1), (2), and (3) by 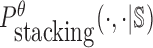allowing the time complexity of computing to be reduced to O(m³).

RESULTS

Results on simulation data

Designing sticky bridges for single aptamer-cargo pairs

As the first step towards validation of our approach we applied AptaBlocks to simulated data. For this, we generated 100 aptamer sequences and 100 ssRNA cargo sequences at random. Next, we arbitrarily combined these two sets into 100 aptamer-cargo pairs. Finally, we set the length of the sticky bridge to be 10 base pairs for all aptamer-cargo pairs. The parameters used to generating the simulation data are available in Supplementary Materials D.1.

Currently, there is no algorithm equivalent to AptaBlocks. Thus, we compared AptaBlocks with an approach in which sticky bridges were obtained as random complementary sequences of the given length. In addition, out of the existing methods, Nupack Design (20) is the closest tool that could, in theory, design sequences for sticky bridges. However, Nupack Design utilizes an oversimplified model (it concatenates two RNAs and treats them as one) and cannot properly optimize the hybridization energy nor protect against forming spurious dimers. To test if AptaBlocks was able to achieve its goals without compromising objectives common to both programs, we added Nupack Design to the comparison. Detailed description of Nupack Design can be found in Supplementary Materials G.

Performance was determined by testing whether the original structures of aptamers and cargoes are preserved, by the strength of the binding affinity between the sticky bridges, and whether undesired dimerizations are present. Hence, we measured the preservation of the original structures of aptamers by computing the probabilities that the sticky bridges stay unpaired using both a secondary structure model without pseudoknots (26,27,39) and a secondary structure model with pseudoknots (21,40) (a detailed description of the computation is elaborated in Supplementary Materials C.1). We stress that our structure optimization procedure did not include pseudoknots due to the prohibitive cost of such computations. Similarly, we determined the preservation of the structures of cargoes by computing the probabilities that the sticky bridges stay unpaired in cargo-stick conjugates using both the secondary structure models with and without pseudoknots. The binding affinity of sticky bridges can be estimated by the probability that the sticky bridge strands hybridize across aptamer-stick and cargo-stick conjugates using an RNA-RNA interaction model (36,37). Finally, the probability of undesired dimerizations is estimated by our stacking hybridization model introduced in Supplementary Materials B. We designed 10 sticky bridges for each aptamer-cargo pair and used the average of the above probabilities in our comparison.

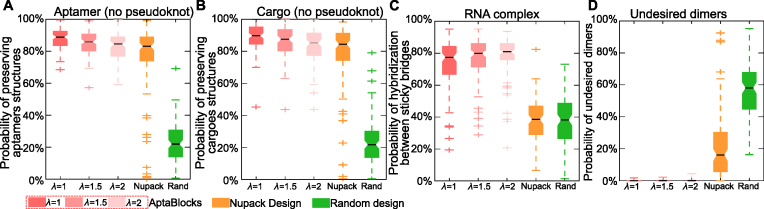
The comparisons between AptaBlocks and other approaches are detailed in Figure 2. Figure 2A and B show that AptaBlocks outperforms other approaches on preserving structures of aptamers and cargoes. Despite that AptaBlocks’ design does not take pseudoknots into account, it performed quite well on the energy model with pseudoknots (see Supplementary Figure S2), again significantly outperforming its competitors. Furthermore, we observe that, by a large margin, the sticky bridges designed by AptaBlocks have higher probabilities to hybridize than other designs (see Figure 2C), but lower probabilities to incur undesired dimerizations (see Figure 2D). Last but not least, we checked the influence of λ, which is a parameter that AptaBlocks uses to balance between structure preferences and energy enforcement. As shown in Figure 2, larger λ leads to the design of sticky bridges that have strong binding between aptamers and cargoes (see Figure 2C) but lower probability to preserve the structures of aptamers and cargoes (see Figure 2A and B). For additional validation of AptaBlocks using aptamers and cargoes of larger sizes and controlling for stability we refer the reader to Supplementary Materials F.

Figure 2.

Comparison of the competing algorithms. (A) Comparison of conserving the secondary structure of aptamers. The probability of sticky bridges being unpaired is computed using a secondary structure model without pseudoknots. (B) Comparison of conserving the secondary structure of cargoes. The probability of sticky bridges being unpaired is computed using a secondary structure model without pseudoknots. (C) Comparison of binding affinity. The binding affinity is approximated by computing the probability of hybridization between sticky bridges using an RNA-RNA interaction model. (D) Comparison on incurring undesired dimers. The probability of undesired dimers is computed by our proposed model in Supplementary Materials B. Larger λ indicates that AptaBlocks focuses more on increasing the melting temperature of sticky bridges.

Next, we tested the impact of the length of the sticky bridge on each method. In this setting, we used the same simulation data but varied the sticky bridge sizes and analyze the performance of preserving the structures of aptamers, cargoes, and binding affinity of the sticky bridges as the function of the length of the latter.

We applied AptaBlocks and Nupack Design to the simulation data and compared their performance using identical criteria as described in our previous comparison using fixed sized sticky bridges. The overall averages of the 100 aptamer-cargo pairs are shown in Figure 3 whereas the experimental details can be found in Supplementary Materials D.2.

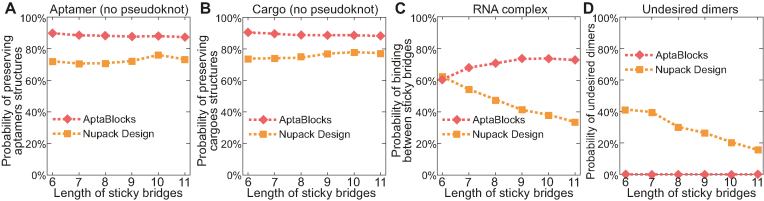
Figure 3.

Comparison of the competing algorithms on different sticky bridge sizes. The conditions under which the comparisons depicted in (A) through (D) were performed are identical to those described in Figure 2.

Figure 3 illustrates the comparison between AptaBlocks and Nupack Design. Figure 3A and B indicate that AptaBlocks is more capable of preserving the structures of aptamers and cargoes for the sticky bridges with increasing length than Nupack Design. Figure 3C shows that AptaBlocks achieves better binding affinity than Nupack Design, which loses control of binding between sticky bridges when the length of the sticky bridges increases. In contrast, we find that the longer the sticky bridges are, the better the binding affinity AptaBlocks can achieve. After a certain length however, the binding affinity remains constant suggesting that we can determine the optimal length of the sticky bridges by observing the changes of the binding affinity for AptaBlocks as shown in Figure 3C. Figure 3D illustrates that comparing to Nupack Design the sticky bridges designed by AptaBlocks rarely lead to undesired dimerizations.

Designing universal sticky bridges

Using the same 100 simulated aptamer-cargo pairs as in the previous section, we further analyzed AptaBlocks performance on the task of designing universal sticky bridges for a single aptamer and multiple alternative cargoes. For this, we selected the cargo sequence as the seed for each aptamer-cargo pair and generated additional cargo sequences by mutating the seed at random. We used sequence similarity, the percentage of identical bases between sequences, to measure similarity between cargo sequences and verified the pairwise similarities between all pairs of cargo sequences in the same group to be identical. The generation of the simulation data is elaborated in Supplementary Materials D.3.

Analogous to the previous sections, we then evaluated the performance by computing the probabilities of preserving the original structures of aptamers and cargoes, as well as the probabilities of hybridization between sticky bridges. For each design, we run AptaBlocks and Nupack Design 10 times and computed the average over those probabilities. For more details regarding the implementation of this experiment, we refer the reader to Supplementary Materials D.3. Notably, Nupack Design (20) was not originally designed for this task but can be used to generate sticky sequences by treating the aptamer-stick and each cargo-sticks as reactants and each aptamer-sticky bridge-cargo species as an intermediate (20).

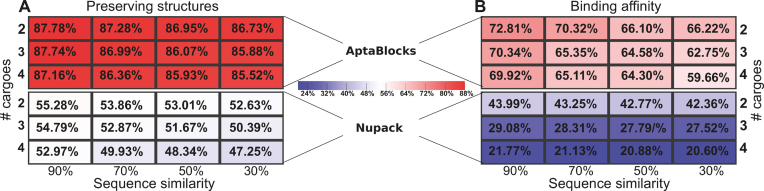
Figure 4 depicts the comparison between AptaBlocks and Nupack Design on designing universal sticky bridges. Figure 4A and B show that AptaBlocks outperforms Nupack Design by a large margin. In addition, Figure 4A implies that the original structures of cargoes and aptamers become hard to preserve when the number of cargoes increase and the cargo sequences become more distinct. Similarly, as shown in Figure 4B, the binding affinity between universal sticky bridges weakens with increasing number of cargoes and distance across cargo sequences. Overall, the experiment suggests that AptaBlocks can design promising universal sticky bridges for a large number of cargoes of similar sequences or a small number of cargoes with highly distinct sequences.

Figure 4.

Quality of universal sticky bridge design of AptaBlocks and Nupack Design for various number of cargoes and sequence similarity between cargoes. (A) Probabilities of preserving the original structures of the aptamers and cargoes (based on the secondary structure model without pseudoknots) for different number of cargoes and different sequence similarity between cargoes. (B) Probabilities of binding between the designed universal sticky bridges for different number of cargoes and different sequence similarity between cargoes. Note that Nupack Design was not originally designed for this purpose and while it can be used to perform this task as described in the text, it does not ensure high binding affinity nor structural preservation.

De novo construction of the tp19 aptamer-NGF siRNA conjugate

Complementing the in silico validation of AptaBlocks, we also validated its ability to design sticky bridges in vitro. In fact, a preliminary version of AptaBlocks has already been used to design a sticky bridge between a pancreatic cancer cell aptamer and a potent anti-mitotic agent (22). Because of the drug’s high toxicity, a non-specific delivery to all cells was not an option. The design was proven to be successful, leading to inhibition of cancer cell proliferation with minimal cytotoxicity in normal cells (22).

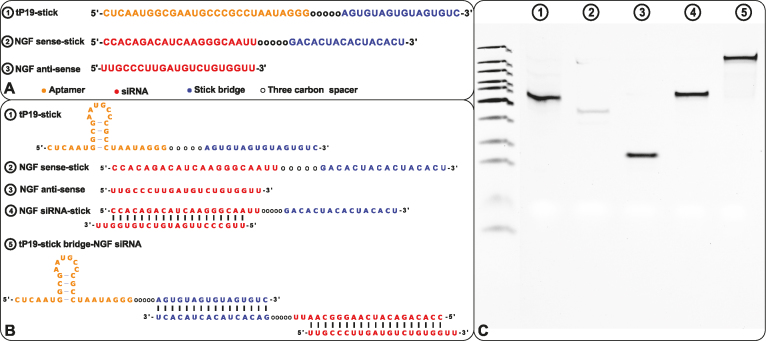
Here we design and test in vitro a more challenging case where the delivered cargo is an RNA molecule. Specifically, we used the same pancreatic cell aptamer as described in (22) and an independently designed NGF siRNA (as shown in Figure 5) whose effectiveness to inhibit pancreatic cancer progression has been experimentally verified (23). In this de novo, real-world application, the aptamer to be combined with the siRNA was 28 nucleotides in size whereas the latter had a length of 21 bases. The resulting molecules as suggested by AptaBlocks were consequently synthesized and allowed to form the final complex in accordance with steps 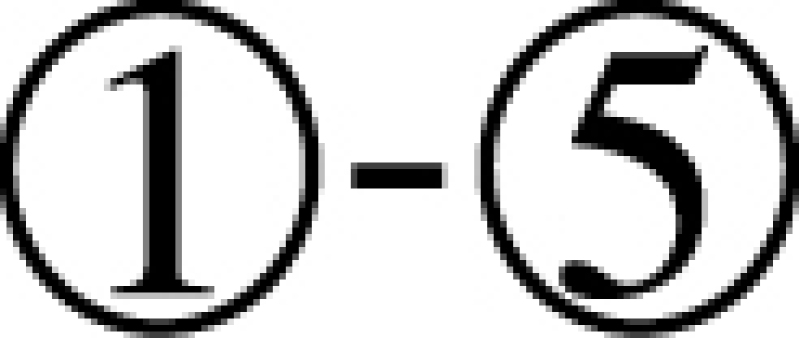in Figure 5B. The successful formation of each molecule and/or conjugate was monitored by running an agarose gel for each step (Figure 5C). The bands verify the presence of the complex without noticeable undesired dimerizations.

Figure 5.

(A) The sequences for tP19-stick, NGF sense-stick, and NGF anti-sense. (B) Predicted structures of each strand introduced in (A) and the conformations for the final RNA tP19-stick bridge-NGF siRNA complexes. (C) The agarose gel image for all species showing the successful formation of all species without undesired dimerizations.

DISCUSSION

Aptamer based drug delivery systems provide unparalleled opportunities for targeted drug therapies mainly due to the ability of designing aptamers to recognize specific cells and thus delivering intervention only to these cells. Indeed, the aptamer-drug conjugates designed using our AptaBlocks strategy reported in (22) were shown to significantly inhibit cell proliferation of pancreatic cancer cells in a dose-dependent manner while at the same time showing minimal cytotoxicity in normal cells and in the control MCF7 cell lines.

Despite our focus on ssRNA or dsRNAs as cargoes, it is important to note that our approach extends naturally to a multitude of other cargoes. As a case in point, a universal bridge designed with AptaBlocks is currently explored in an experimental setting, facilitating the conjugation of cytotoxic drugs and RNA aptamer tP19, targeting pancreatic tumor cell growth (22). Given the rapid development of efficient in vitro selection technologies allowing for the generation of highly target-specific and target-affine aptamers. AptaBlocks can also be applied in general RNA nanotechnology settings not necessarily related to drug design.

Synthesizing long conjugates containing a concatenation of an aptamer and a cargo has several drawbacks and thus a more flexible method based on non-covalent conjugation using a sticky bridge has been recently proposed (18,19). While improving the experimental procedure, the method hinges on the successful design of the sticky bridges connecting aptamers and cargoes. This design task initially relied on an expensive and time consuming trail and error approach and its success was highly dependent on the experimentalists expertise. This challenge, together with a high failure rate, showed that creating sticky bridges for a diverse array of applications could greatly benefit from a computationally informed design approach.

Until now, to the best of our knowledge, only Nupack Design (20,21) could be adopted to tackle the problem. However, Nupack Design was not able to consistently provide a satisfying solution even for the simplest variant of the problem that considers only one aptamer and one cargo. The main reason was that Nupack Design is making assumptions that are not consistent with our experimental setting. Nupack Design concatenated input molecules which, in the context of our application, has lead to spurious designs. In addition, Nupack Design ignores the interactions between different RNA strands that might cause undesired dimerization which is the most frequent reason for designs failing in vitro.

Thanks to the carefully designed theoretical model, AptaBlocks has proven to be successful in computational and experimental settings. It not only incorporates structural constraints required for a correct synthesis, but also optimizes hybridization strength of complementary strands in the sticky bridge, and minimizes formations of undesired dimerization and higher order aggregations. While in this paper, we focus on two key applications of AptaBlocks, designing a sticky bridge for two RNA molecules (an aptamer and a cargo), and designing a universal sticky bridge allowing for conjugating the same aptamer with several alternative cargoes, the method is general and can be applied to other RNA complex design. For example, although in all our application the “sticky bridge” was attached at the end of the respective molecules, it is also possible to use AptaBlock to optimize a sticky bridge that is to be inserted anywhere into the sequence. Given the broad utility of the approach in the context of RNA-based drug delivery systems and its success in a variety of experimental settings, AptaBlocks has the potential to greatly accelerate research efforts in this area.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Intramural Research Program of the National Institutes of Health, National Library of Medicine [Y.W., J.H., T.M.P.]; The DNA/RNA Synthesis Core, the Chemical GMP Synthesis Facility of the City of Hope, funded in part by Cancer Center Support Grant (National Cancer Institute of the National Institutes of Health under award number P30CA033572), to the City of Hope Comprehensive Cancer Center [Y.L., T.A., P.S.].

Conflict of interest statement. None declared.