Computationally Assisted Design of Polarizing Agents for Dynamic Nuclear Polarization Enhanced NMR: The AsymPol Family

Abstract

We introduce a new family of highly efficient polarizing agents for dynamic nuclear polarization (DNP)-enhanced nuclear magnetic resonance (NMR) applications, composed of asymmetric bis-nitroxides, in which a piperidine-based radical and a pyrrolinoxyl or a proxyl radical are linked together. The design of the AsymPol family was guided by the use of advanced simulations that allow computation of the impact of the radical structure on DNP efficiency. These simulations suggested the use of a relatively short linker with the intention to generate a sizable intramolecular electron dipolar coupling/J-exchange interaction, while avoiding parallel nitroxide orientations. The characteristics of AsymPol were further tuned, for instance with the addition of a conjugated carbon–carbon double bond in the 5-membered ring to improve the rigidity and provide a favorable relative orientation, the replacement of methyls by spirocyclohexanolyl groups to slow the electron spin relaxation, and the introduction of phosphate groups to yield highly water-soluble dopants. An in-depth experimental and theoretical study for two members of the family, AsymPol and AsymPolPOK, is presented here. We report substantial sensitivity gains at both 9.4 and 18.8 T. The robust efficiency of this new family is further demonstrated through high-resolution surface characterization of an important industrial catalyst using fast sample spinning at 18.8 T. This work highlights a new direction for polarizing agent design and the critical importance of computations in this process.

Introduction

High-field dynamic nuclear polarization (DNP) is currently changing significantly the scope of solid-state nuclear magnetic resonance (NMR) spectroscopy with new applications ranging from biomolecular systems to material science.¹⁻⁵ One of the key steps in this process is the development of tailored molecules that can act as efficient polarizing agents. A major milestone was reached with the introduction of nitroxide biradicals as polarizing agents for magic angle spinning dynamic nuclear polarization (MAS-DNP).⁶ Such biradicals show much improved performance because they fulfill the requirement of having two strongly coupled electron spins for MAS-DNP via the cross-effect mechanism (CE).⁷⁻⁹ Considerable effort has been directed toward further improvement of such biradical polarizing agents by adjusting their water solubility,¹⁰⁻¹² increasing their molecular weight,¹³ using rigid linkers,¹⁴ and replacing methyl groups that are adjacent to the nitroxides;^13,15,16 the water solubility allows for compatibility with biomolecular studies, whereas the other chemical modifications were performed to improve the properties of the electron spins (e.g., relaxation times). As such, various state-of-the-art designer polarizing agents for MAS-DNP experiments have been produced allowing high performance even at low concentration.^{10,11,13,15−19} This has enabled the acquisition of data that was previously deemed unobtainable, opening up NMR spectroscopy to intricate surface studies,² biomolecular reaction intermediates,²⁰ and structural studies of organic aggregates through ¹³C–¹³C and ¹³C–¹⁵N connections at natural isotopic abundance (1.1% and 0.1% for ¹³C and ¹⁵N, respectively).^21,22 In addition to the use of bis-nitroxides, recent efforts have been devoted to the introduction of mixed biradicals for DNP applications, such as trityl-nitroxide^18,23,24 and BDPA-nitroxide.^25,26

Nevertheless, the efficiency of DNP is still far from optimal at high magnetic field (>9 T), both in terms of DNP gain and hyperpolarization buildup times. We estimate that the polarization gain (compared to Boltzmann equilibrium) using CE DNP is around ∼10% of the theoretical limit at 9.4 T and drops to only ∼5% at 18.8 T, 100 K, and using a MAS frequency of 10 kHz.²⁷ Therefore, there is still a critical need to provide more efficient polarizing agents at high magnetic fields, even if many nitroxide biradical structures have recently been tested.^15,16

In this work, we demonstrate a new route toward this goal. We show that advanced simulations can be used to help produce improved polarizing agents. Thanks to this approach, we introduce a new family of asymmetric biradicals, stable and straightforward to synthesize, that yield a 2-fold improvement in sensitivity, as compared to current high-performing and ubiquitous standards. This is demonstrated at both 9.4 and 18.8 T and explained through advanced MAS-DNP simulations. The robust efficiency of this new family is further demonstrated through high-resolution surface characterization of an important industrial catalyst using fast sample spinning at 18.8 T.

Results and Discussion

Computationally Assisted Design of Polarizing Agents: The AsymPol Family

The design of the family was driven by recent understanding provided by MAS-DNP simulation tools,^8,9,27,28 as well as recent methodological efforts toward improving accurate evaluation of MAS-DNP efficiency,^21,23,27,28 accounting for instance for depolarization effects.^27,29 This resulted in the choice of relatively short and electron rich linkers (amide or ester-based) in order to generate a sizable intramolecular electron dipolar coupling/J-exchange interaction between either 5- or 6-membered ring nitroxides (see Figure S1). This approach allowed the increase of the electron–electron dipolar interaction to 50 MHz or more, while also introducing a large J-exchange interaction (greater than 50 MHz according to solution-state EPR). The design also avoided parallel nitroxide orientations for all of the molecules that were synthesized in this family (see Figure S1). Previous 3-spin MAS-DNP simulations have been used to show that parallel nitroxide orientations lead to inefficient MAS-DNP and that current bis-nitroxides already have good relative orientations of their nitroxides.^9,30

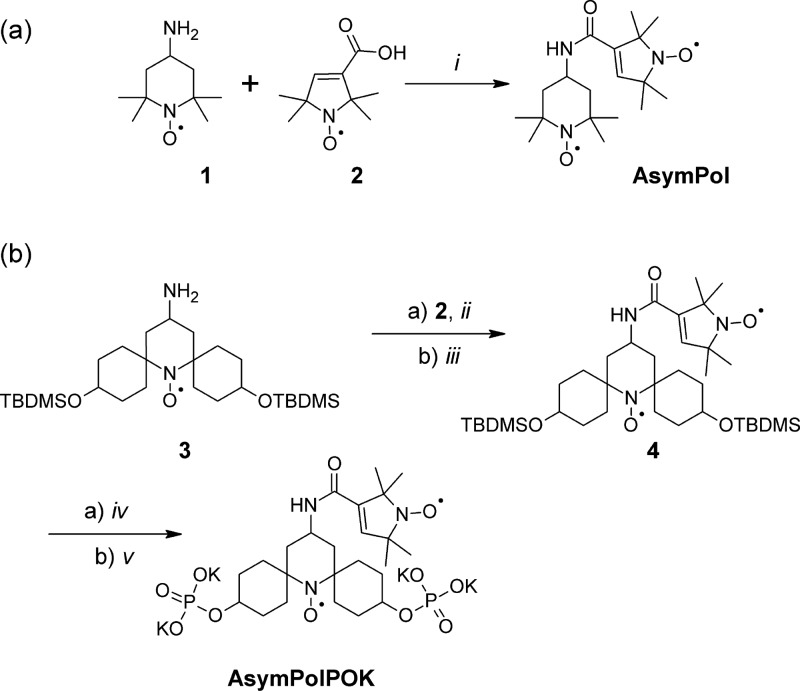
Among them we focused on AsymPol and AsymPolPOK (Scheme 1), which have relative nitroxide orientations that favor efficient MAS-DNP.^9,14,30 Both are composed of two asymmetric bis-nitroxides in which piperidine-based radicals and a pyrrolinoxyl radical are linked with a short tether. AsymPol contains a TEMPO moiety (Scheme 1a) whereas AsymPolPOK (Scheme 1b) contains a spirocyclohexanolyl-derived piperidine radical.¹⁷ The latter has increased molecular weight, which is known to slow the electron spins’ relaxation,³¹⁻³³ and phosphate groups to increase the water-solubility while avoiding possible aggregation.

Scheme 1. (a) Synthesis of AsymPol (337 g mol^–1); (b) Synthesis of AsymPolPOK (765 g mol^–1).

i: DCC, HOBt, Et₃N, CH₂Cl₂, 83%.

ii: 2, DCC, HOBt, Et₃N, CH₂Cl₂, 58%; iii: TBAF/THF, DOWEX/CaCO₃, MeOH, 49%; iv: 5-(Benzylthio)-1H-tetrazole, bis(2-cyanoethyl) diisopropylphosphoramidite, tBuOOH, CH₃CN, 35%; v: Et₃N, H₂O/KOH, H₂O, 91%.

Conjugation of 4-amino-TEMPO (1) to 3-carboxy-pyrrolinoxyl nitroxide (2) yielded AsymPol (Scheme 1a), for which an X-ray crystal structure was obtained (see Supporting Information). Coupling of the spirocyclohexanolyl derivative 3(17,32) with 2, followed by removal of the TBDMS protecting groups yielded biradical 4. Phosphitylation and deprotection yielded AsymPolPOK (Scheme 1b), which showed excellent solubility in water (640 mM) and glycerol/water (>1 M).

AsymPol and AsymPolPOK Are Highly Efficient Polarizing Agents for High and Very High Magnetic Fields

Recent developments have highlighted the importance of determining the relative signal intensity per unit square root of time obtained via DNP as a measure of polarizing agent performance.^23,34−37Figure 1 compares this “relative DNP sensitivity” for AsymPol and AsymPolPOK at 9.4 T with the ubiquitous and high-performing bis-nitroxide, AMUPol.¹¹Figure 1a plots the relative DNP sensitivity, expressed as ε_B × (T_B)^−1/2 and Figure 1b plots ε_B, both as a function of MAS frequency, where ε_B represents the polarization gain compared to Boltzmann equilibrium and T_B stands for the polarization buildup time constant. Notably, AsymPolPOK outperforms AMUPol by more than a factor of 2 in terms of relative DNP sensitivity, which corresponds to more than a factor of 4 in time-savings, enabling new sensitivity-limited experiments. For instance, at 9.4 T and 10 kHz MAS frequency, the relative DNP sensitivity is 27 and 68 s^–1/2 for AMUPol and AsymPolPOK respectively (see Table 1). The corresponding less-water-soluble version, AsymPol, gives 39 s^–1/2 in d₆-DMSO/D₂O/H₂O (8:1:1; v:v). The fact that the efficiency is reduced for AsymPol as compared to AsymPolPOK was expected for two main reasons: first, AsymPol’s molecular weight is lower and it contains more methyl groups, leading to increased relaxation rates of the electron and local nuclear spins,^13,31−33 and second, the corresponding ¹H T_1n of an undoped sample (at ∼100 K and 9.4 T) is much shorter in d₆-DMSO/D₂O/H₂O (8:1:1; v:v) than in d₈-glycerol/D₂O/H₂O (6:3:1; v:v).^8,9,28 Even so, and very notably (considering ε_on/off, vide infra), AsymPol is also more efficient than AMUPol at 9.4 T.

Figure 1.

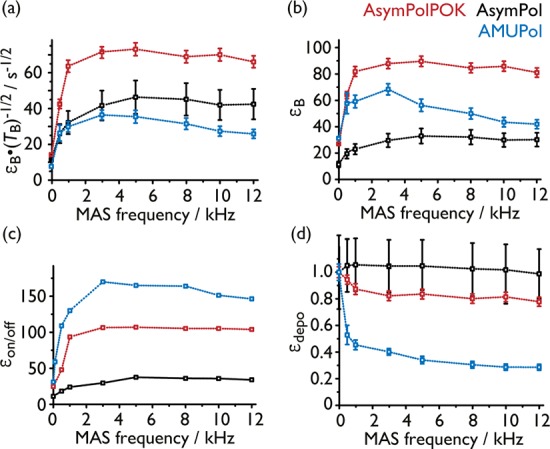
Experimental performance of AsymPol (black) and AsymPolPOK (red), with a comparison to AMUPol (blue), as a function of MAS frequency. The data were recorded using 10 mM biradical in d₆-DMSO/D₂O/H₂O (8:1:1; v:v) (for AsymPol) or d₈-glycerol/D₂O/H₂O (6:3:1; v:v) (for AsymPolPOK and AMUPol) at 9.4 T and 105 K. All samples contain 20 mM ¹³C-urea. Note that AsymPolPOK and AMUPol data can thus be compared directly since the same DNP matrix was used. The plots show (a) the relative DNP sensitivity (expressed as ε_B × (T_B)^−1/2), (b) the proton polarization gain compared to Boltzmann equilibrium, ε_B, (c) the ratio between the NMR signal obtained with and without microwave irradiation, ε_on/off, and (d) the nuclear depolarization, ε_depo, expressed here as the ratio between the obtained ¹H NMR signal integral and that recorded without sample spinning, both in the absence of microwave irradiation. The latter (static case) represents the Boltzmann equilibrium polarization. Lines are added as a guide. The larger errors for AsymPol reflect the very short T_B (see Table 1). A similar analysis was conducted using 5 mM biradical concentration (see Figure S2). Interestingly, the relative DNP sensitivity ε_B × (T_B)^−1/2 is similar for 5 and 10 mM biradical concentration for the three biradicals studied here. Note, an ε_on/off ∼ 210 has been shown to be obtained for 12 mM AMUPol with 2 M ¹³C-urea in d₈-glycerol/D₂O/H₂O (6:3:1; v:v:v).²⁷ Here we chose to use 20 mM ¹³C-urea so as to be sure to not perturb the glassy matrix or induce biradical–urea interactions. Similarly large ε_on/off ∼ 150 and 200 were obtained with 10 and 5 mM AMUPol, respectively, but using a much smaller content of urea.

Table 1. Experimental Parameters That Characterize the DNP Performance of AsymPol and AsymPolPOK, with a Comparison to AMUPol.

			Buildup Time TB/s		εon/off
	DNP sensitivity εB·TB(MAS)–1/2	DNP gain εB(MAS)	Static	MAS	Static	MAS
9.4 T
AMUPola	27 s–1/2	43	16.3	2.5	28	151
AsymPolb	39 s–1/2	30	1.0	0.6	11	32
AsymPolPOKa	68 s–1/2	83	3.5	1.5	25	105
18.8 T
AMUPolc	5.5 s–1/2	14	26.5	6.5	5	21
AsymPolPOKc	10 s–1/2	24	–	5.8	–	27

^a10 mM biradical in d₈-glycerol/D₂O/H₂O (6:3:1; v:v) with 20 mM ¹³C-urea, 10 kHz MAS rate, at 105 K and 9.4 T.

^bSame as footnote a but 10 mM biradical in d₆-DMSO/D₂O/H₂O (8:1:1; v:v).

^cSame as footnote a but at ∼130 K and 8 kHz MAS rate using a 3.2 mm rotor.

Further insight can be given by looking at both the DNP enhancement factor ε_on/off (the ratio of the intensity of the signals measured with and without microwave irradiation) and the depolarization factor ε_depo (that describes the effect of biradical doping and sample spinning on the measured ¹H polarization in absence of microwave irradiation). Nuclear depolarization is observed when the coupled electrons’ polarization difference is less than the nuclear polarization. Under these conditions, the nucleus (partially) transfers its polarization to the electrons, resulting in a depolarized nuclear state compared to Boltzmann equilibrium (P_B).^23,27 This situation generally occurs for nitroxides and protons in the absence of microwave irradiation in combination with MAS. Such an effect can be particularly severe at very low temperature (first demonstrated at ∼20 K²⁹) and/or when using polarizing agents with long electron spin relaxation times, T_1e, (such as AMUPol) and/or in the presence of inefficient electron–electron polarization exchange.^27,28 Recent work has highlighted the drawbacks in using only ε_on/off to evaluate polarizing agent efficiency;²⁹ instead, one should rely on the product of ε_on/off × ε_depo, which gives ε_B, as well as T_B.³⁴⁻³⁷

Figure 1d, which plots ε_depo as a function of MAS frequency for the three biradicals, illustrates that nuclear depolarization can be substantial, as in the case of AMUPol. For the experimental conditions used for Figure 1, i.e., 9.4 T, 105 K, and 10 mM biradical concentration, AMUPol yields nuclear depolarization up to 70% (i.e., ε_depo = 0.3). The situation is very different in the case of AsymPol and AsymPolPOK, both of which show limited depolarization effects. The rationale behind this observation was predicted by simulations (vide infra) and notably relies on the presence of the large J-exchange interaction between the electron spins of the bisnitroxides in the AsymPol family. It is clear when the traditional DNP enhancement factor ε_on/off (Figure 1c) is scrutinized against the polarization gain compared to Boltzmann equilibrium, (ε_B, Figure 1b), that one cannot use ε_on/off alone to judge the biradical efficiency due to the bias introduced through the large depolarization observed for AMUPol. Indeed, AMUPol yields the highest ε_on/off while actually being less efficient in terms of absolute polarization gain (ε_B) compared to AsymPolPOK (Figure 1b).

Additional experiments were also conducted at 18.8 T for AsymPolPOK and AMUPol. A comparison of the results obtained at 9.4 and 18.8 T (Table 1) shows that AsymPolPOK is also substantially more efficient than AMUPol at 18.8 T. For MAS frequencies around 8–10 kHz, the returned sensitivity is about 2 times higher using AsymPolPOK than AMUPol in glycerol/D₂O/H₂O (6:3:1; v:v). Another important feature is that these new polarizing agents, AsymPol and AsymPolPOK, have much shorter polarization buildup times than AMUPol, which is essential to maximize the overall sensitivity. More specifically, using the same biradical concentration in the same DNP matrix, i.e., d₈-glycerol/D₂O/H₂O (6:3:1; v:v), the buildup time is about 40% shorter for AsymPolPOK than for AMUPol. This is directly related to the presence of large electron dipolar coupling/J-exchange interactions, as predicted by simulations. Because this work utilizes multiple 3-spin systems, the effect of nuclear-spin diffusion has been neglected and the hyperpolarization build-up rates are then only relative between biradicals and fully represent the DNP efficiency. For a further description of the effect of nuclear spin diffusion on CE MAS-DNP, the reader is referred to reference (28).

It is important to stress that a shorter CE DNP buildup time does not necessarily correspond to shorter nuclear coherence lifetimes (or dephasing times). Indeed, the refocusable transverse decay time, ^13CT₂′, of the ¹³C-urea resonance in glycerol/water has been shown to be impacted by the addition of paramagnetic polarizing agents,³⁶ but at 105 K and 9.4 T similar decay constants (30 and 23 ms for 10 mM AsymPolPOK and AMUPol, respectively) were obtained. A shorter ^13CT₂′ would be deleterious for recording multidimensional NMR experiments because the returned sensitivity is also highly dependent on nuclear coherence lifetimes.

Another very useful aspect of these new biradicals is their short T_B under static conditions, T_B(static). It can be seen from Table 1 that T_B(static) is longer than T_B for spinning samples (T_B(MAS)) and notably that T_B(static) is relatively long for AMUPol. Therefore, these new biradicals are also extremely pertinent for static DNP studies.^38,39

Efficient CE MAS-DNP at 18.8 T and fast MAS

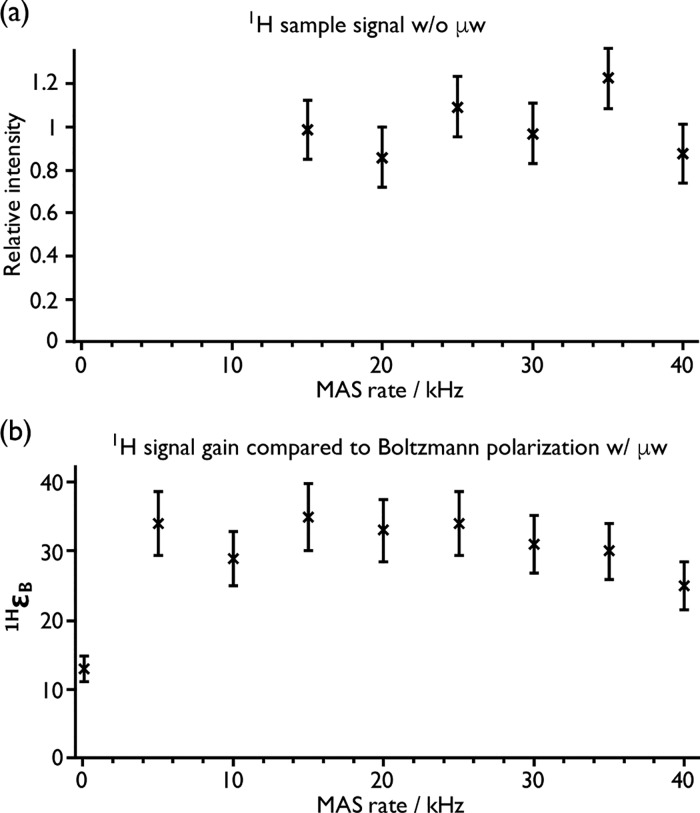
The impressive results obtained with AsymPolPOK at 18.8 T are also related to its robustness with respect to very high spinning frequencies. This is illustrated in Figure 2a that shows the evolution of the ¹H signal of an AsymPolPOK-doped sample measured under fast MAS conditions using a 1.3 mm diameter sample holder at 18.8 T, without microwave irradiation. From 15 to 40 kHz, there is no measurable loss in signal intensity. This is very different from what has been recently reported for AMUPol in the same regime,⁴⁰ where a 50% decrease in ¹H signal was measured going from 5 to 40 kHz MAS frequency at 18.8 T. These results demonstrate the large nuclear depolarization with AMUPol and that the depolarization effect seems absent with AsymPolPOK at 18.8 T. Consequently, the Boltzmann enhancement factor (^1Hε_B), plotted in Figure 2b as a function of MAS frequency, demonstrates the good efficiency of AsymPolPOK for 18.8 T measurements and the robustness of this efficiency to high MAS frequencies. These observations are again attributable to the presence of a large J-exchange interaction. The situation is significantly different for AMUPol, as seen recently under similar experimental conditions,⁴⁰ where the overall signal intensity substantially decreases by going from 10 to 40 kHz spinning frequencies.

Figure 2.

Experimental evolution of the ¹H signal intensity without microwave irradiation (a) and evolution of the polarization gain ^1Hε_B (b) for a 5 mM AsymPolPOK, 2 M ¹³C-urea, d₈-glycerol/D₂O/H₂O (6:3:1; v:v) solution using a 1.3 mm diameter sample holder at 18.8 T and a sample temperature of ∼125 K.

High-Field EPR and MAS-DNP Simulations

To further understand the observed DNP properties of AsymPolPOK, we analyzed its electron paramagnetic resonance (EPR) spectrum, in the solution state at X-band and as a frozen solution at high-field/frequency (∼8.5 T/240 GHz;^41,42Figure 3a). The solution-state EPR spectrum of AsymPolPOK in water revealed an exchange interaction of 80.5 MHz (see Figure S3). The AsymPol crystal structure (see Figure S4 and Table S1) was used as a starting geometry to conduct the EasySpin⁴³ simulated fit of the solid-state EPR spectrum. Even if the returned fit is not fully satisfactory, we tentatively estimate the mean dipolar and J-exchange couplings between the two electron spins of AsymPolPOK to be in the order of 56 and −70 ± 10 MHz, respectively. Note that in this work, we only tried to fit the g-values and a single J-exchange interaction. However, it is clear from the EPR spectrum that higher exchange interactions are also present, maybe due to different conformations and/or microenvironments. Further improvement would require a multifrequency EPR analysis,⁴⁴ as well as to account for the fact that we have a distribution of dipolar/J-exchange couplings or even g-relative orientations. This is beyond the scope of this publication. Finally, we checked with MAS-DNP simulations²⁸ that the DNP field profile, obtained using the extracted values from this EPR fit, was qualitatively consistent with the experimental data (Figure S6). Once again, a better description of the dipolar and J-exchange couplings distribution would certainly allow improving on the agreement between experiment and simulation. For completeness, the effect of the J-exchange couplings on the field sweep profile is reported in Figure S9.

Figure 3.

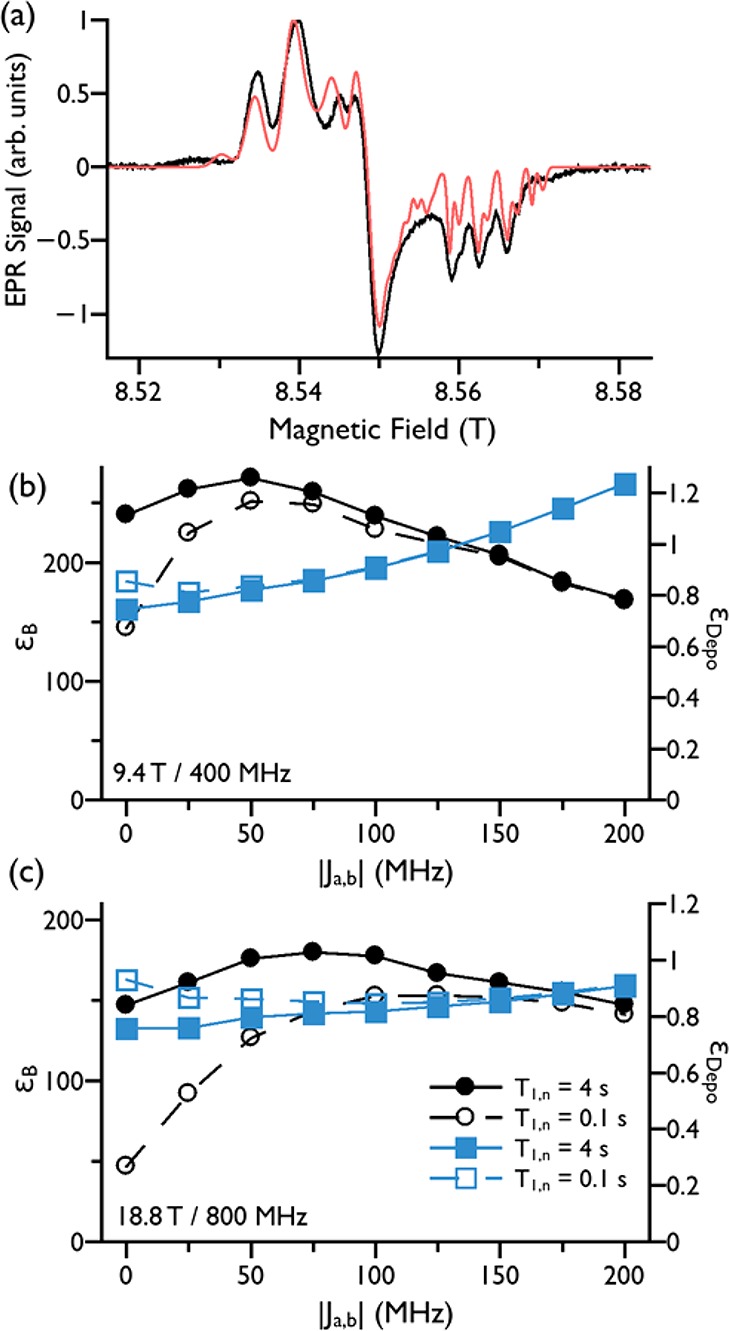
(a) High-field EPR spectrum (∼8.5 T/240 GHz) of 10 mM AsymPolPOK and 20 mM ¹³C Urea in d₈-glycerol/D₂O/H₂O (6:3:1; v:v) at 110 K (black) and best fit with a single biradical conformation (red). MAS-DNP simulations of ε_B (black circles) and ε_Depo (blue squares) as a function of the exchange interaction intensity at (b) 9.4 T/400 MHz (c) 18.8 T/800 MHz. The filled symbols were obtained assuming a nuclear relaxation time T_1,n = 4 s and the open symbols T_1,n = 0.1 s. Lines are added as a guide. Further details of the simulations are provided in the Supporting Information.

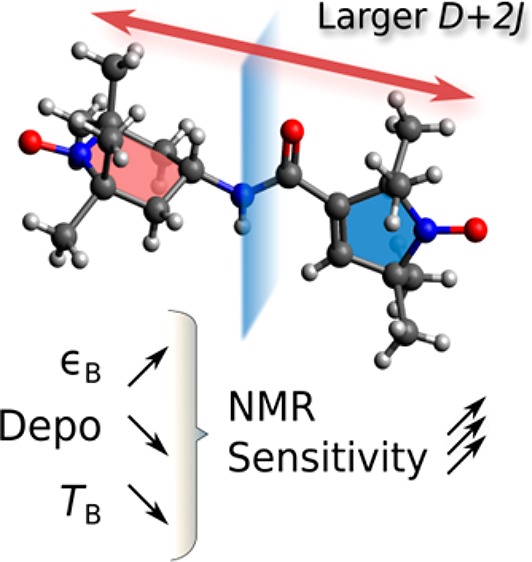
The theoretical analysis of AsymPolPOK’s performance relies on two essential points revealed by previous theoretical work.^9,28 For each biradical, the microwave irradiation generates a polarization difference (ΔP_e) between each nitroxide of the biradical,⁹ large dipolar/exchange interactions help to maintain it,^9,28 and this ΔP_e is transferred to the surrounding nuclei via the CE rotor-events, which are themselves proportional to the sum of the dipolar and J-exchange interaction (D+2J).^7−9,45 Accordingly, a fast equilibration between ΔP_e and the nuclear polarization (P_n) occurs when the dipolar and J-exchange interactions are large, leading to short buildup time T_B.^9,28 The equilibration P_n ≤ ΔP_e is then obtained at steady state.⁹

Using a simple three-spin theoretical model that takes the structure of AsymPolPOK into account, the effect of the exchange interactions on ε_B and ε_Depo were probed within two limits of the nuclear relaxation time. The results of the calculations, performed for 9.4 and 18.8 T, are represented in Figure 3b,c, respectively. At both magnetic fields, ε_B is maximum for a |J_a,b| of approximately 50 MHz for the limit of a slowly relaxing nucleus (T_1,n = 4 s), where the condition P_n ≈ ΔP_e is easily met. Weaker exchange interactions lead to a reduced ΔP_e, and consequently to a lower ε_B, whereas very strong exchange interactions modify the DNP field profile drastically (see Figure S9) leading to a decrease in ε_B and eventually the CE ceases to be active when the exchange interaction exceeds half the nuclear Larmor frequency.^18,23,46

For the fast limit of nuclear relaxation, (T_1,n = 0.1 s), weaker CE rotor-events struggle to compensate the effect of the fast nuclear relaxation, leading to P_n < ΔP_e. To achieve higher ε_B, stronger exchange interactions are then needed for short T_1,n, particularly at higher magnetic fields as the efficiency of the CE rotor-events depends on the Larmor frequency and EPR line width (cf. Figure 3b,c).

The depolarization mechanism relies on the same principles. If the electron spins present a ΔP_e it can be reduced if the dipolar/exchange interaction is weak under MAS as the electron spins exchange their polarization inefficiently (at dipolar/J rotor-events).^23,27 For the limit of slow nuclear relaxation, the depolarization is higher than for the fast limit. With AsymPolPOK’s structure, a larger ΔP_e is maintained as the exchange interaction increases and the depolarization decreases accordingly for the limit of a slowly relaxing nucleus. This observation remains true for the fast relaxing nucleus but, as for the case of hyperpolarization, relatively stronger exchange interactions are required in this limit.

Overall, the simulations confirm that AsymPolPOK’s exchange interaction of −70 ± 10 MHz, is responsible for its very good efficiency at both 9.4 and 18.8 T. It is large enough to allow high polarization gain even for fast relaxing protons at both fields. It should be stressed that the three-spin simulations are used to only highlight trends, and not absolute values. The simulations show that depolarization should be expected from AsymPolPOK, but at the same time reveal that its larger exchange interaction reduces this effect. Simulations involving many biradicals and many nuclei, which allow for more accurate absolute values, cannot be used here due to the large exchange interaction coupling.²⁸

Application at 18.8 T

MAS-DNP has been shown to be particularly pertinent for studying the surface of functional materials^2,47 including aluminas.^48,49 Indeed, under certain conditions ({¹H-}²⁷Al CP) MAS-DNP can permit highly sensitive studies of nuclei in only the first surface layer of aluminas, enabling primostrato NMR.⁵⁰ For quadrupolar nuclei, such as ²⁷Al, high magnetic fields can be extremely beneficial in terms of spectral resolution since there is a second order spectral broadening induced by the quadrupolar coupling that is inversely proportional to magnetic field strength. As such, the highest available fields for MAS-DNP have begun to be employed for quadrupolar nuclei, such as ¹⁷O.^51,52 However, the CE efficiency decreases with the magnetic field strength, so using polarizing agents that give the most NMR sensitivity is vital. As an example of the very good efficacy of AsymPolPOK as a polarizing agent for MAS-DNP, a DNP-enhanced primostrato ²⁷Al MQMAS experiment⁵⁰ was performed on nanoparticulate γ-alumina (see Figure 4), an important industrial catalyst and catalyst–support. Here, at one of the highest magnetic fields currently available for MAS-DNP, 18.8 T, and at a MAS frequency of 24 kHz (chosen as an optimum compromise for cross-polarization and MQMAS efficiencies), this high-resolution, surface selective experiment could be recorded overnight (in 14 h). Previous MAS-DNP studies at 9.4 T have shown that there is an important penta-coordinated Al site and that it resides only in the first surface layer.⁵⁰ However, the NMR signal and the resolution of this penta-coordinated site were poor. Here, thanks to the high magnetic fields and the sensitivity provided through MAS-DNP with AsymPolPOK, it is extremely clear that this surface site exists, as shown in Figure 4. This opens many perspectives for all types of materials, for example containing quadrupolar nuclei or many overlapping resonances, where the highest possible magnetic fields and sensitivity are required.

Figure 4.

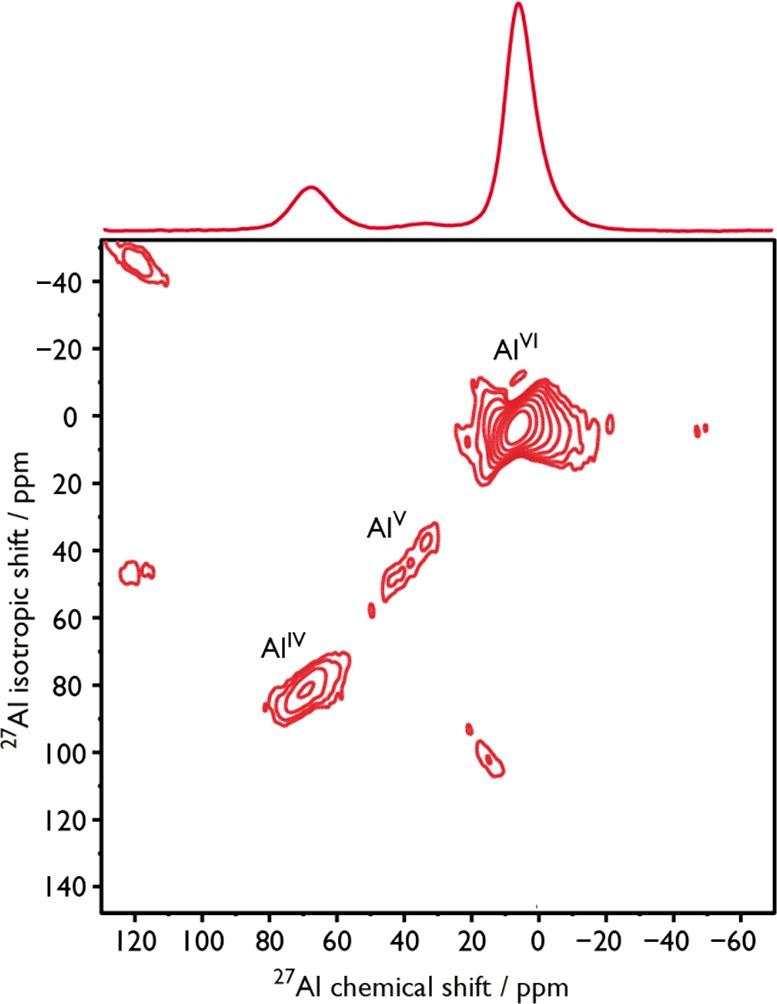
DNP-enhanced {¹H-}²⁷Al CP MQMAS NMR spectrum of γ-alumina, recorded at 18.8 T, a sample temperature of ∼125 K, and with a MAS frequency of 24 kHz. Above, a {¹H-}²⁷Al CP NMR spectrum of γ-alumina recorded under the same conditions as a comparison. The γ-alumina was impregnated with a 5 mM AsymPolPOK, 2 M ¹³C-urea, d₈-glycerol/D₂O/H₂O (6:3:1; v:v) solution. ε_on/off = 38 (see Figure S17).

Conclusions

We have introduced a new family of readily prepared biradical polarizing agents for DNP. This family, based on a simple amide/ester bond between piperidinyl and pyrrolinoxyl radicals, exhibits very advantageous MAS-DNP properties, including fast hyperpolarization build up times and little or no nuclear depolarization at very high field and fast MAS frequencies. These properties notably arise from the large dipolar- and J-exchange interactions between the two electron spins. Moreover, the highly water-soluble AsymPolPOK, a phosphate-derivatized biradical prepared for applications in structural biology, produces twice the NMR sensitivity of AMUPol, even at 18.8 T and with MAS frequencies of up to 40 kHz. In addition, the AsymPol family is stable and relatively straightforward to synthesize and purify, as compared to Trityl-based biradicals, such as TEMTriPol-1, that have also shown good potential for high-field MAS-DNP.²³

The power of AsymPolPOK as a polarizing agent was demonstrated in a DNP regime that is still far from optimal, namely very high magnetic field and fast MAS, by the acquisition of high resolution and surface-selective NMR spectra of catalytic γ-alumina. Under fast MAS and at 18.8 T, the γ-alumina surface could be easily detected through CP, with AsymPolPOK providing a DNP enhancement factor of ∼38. This improvement in sensitivity thus allowed a high-resolution surface-selective ²⁷Al MQMAS experiment at 18.8 T on a catalyst material.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b04911.

• Further information concerning the effect of biradical concentration, EPR data and simulations, MAS-DNP simulations, X-ray crystal structure (xyz coordinates), syntheses and characterization of the AsymPol family of biradicals and MAS-DNP solid-state NMR experiments (PDF)

Author Contributions

^⊥ These authors contributed equally.

The authors declare no competing financial interest.