Representing the UMLS as an Object-oriented Database

Abstract

Objective: The Unified Medical Language System (UMLS) combines many well-established authoritative medical informatics terminologies in one knowledge representation system. Such a resource is very valuable to the health care community and industry. However, the UMLS is very large and complex and poses serious comprehension problems for users and maintenance personnel. The authors present a representation to support the user's comprehension and navigation of the UMLS.

Design: An object-oriented database (OODB) representation is used to represent the two major components of the UMLS—the Metathesaurus and the Semantic Network—as a unified system. The semantic types of the Semantic Network are modeled as semantic type classes. Intersection classes are defined to model concepts of multiple semantic types, which are removed from the semantic type classes.

Results: The authors provide examples of how the intersection classes help expose omissions of concepts, highlight errors of semantic type classification, and uncover ambiguities of concepts in the UMLS. The resulting UMLS OODB schema is deeper and more refined than the Semantic Network, since intersection classes are introduced. The Metathesaurus is classified into more mutually exclusive, uniform sets of concepts. The schema improves the user's comprehension and navigation of the Metathesaurus.

Conclusions: The UMLS OODB schema supports the user's comprehension and navigation of the Metathesaurus. It also helps expose and resolve modeling problems in the UMLS.

The Unified Medical Language System (UMLS),^1,2,3,4,5 designed by the National Library of Medicine, combines many well-established medical informatics terminologies in a unified knowledge representation system. It consists of four knowledge sources—the Metathesaurus, the Semantic Network, the Specialist Lexicon, and the Information Sources Map—that provide information about medical terminologies. The UMLS can be used by a wide variety of application programs to overcome the retrieval problems caused by differences in the way the same medical concept is expressed in different sources.⁶ Such a resource is very valuable to medical researchers and to the health care industry.

The scope and complexity of the UMLS pose serious comprehension problems for users and even developers, however. The magnitude of presented knowledge is overwhelming for human comprehension, and the UMLS is difficult to maintain and use without proper comprehension. Designers, maintainers, and users of the UMLS need tools to help with their work. Most existing tools for retrieval and manipulation of the content of the UMLS^7,8,9,10 are insufficient. Additional tools are needed to help professionals reach the level of comprehension they need to perform their tasks.

In previous work,^11,12 we developed a methodology for representing controlled medical terminologies (CMTs)^13,14 as object-oriented databases (OODBs) to help users comprehend them. The methodology is based on the grouping of concepts with the same set of properties as instances of the same object class. The comprehension support was achieved by introducing the two layers of the OODB representation of a controlled medical terminology (CMT)—the schema layer and the concept layer. The additional schema layer gives an abstract view of the large and complex source CMT, which aids in the comprehension of its structure and content. At the concept layer, users can directly access objects that denote concepts of the original CMT and obtain the detailed terminologic knowledge they require. In other publications,^15,16 we describe how our previous work on the schema layer of the Medical Entities Dictionary (MED)¹⁷ helped its designer uncover and correct some errors and inconsistencies in the MED's original modeling and improve its content.

In this paper, we use an OODB representation to capture the knowledge of the two major components of the UMLS—the Metathesaurus and the Semantic Network—in a simplified and homogeneous way. The Metathesaurus is the largest and most complex of the UMLS knowledge sources. It is a compilation of terms, concepts, relationships, and associated information drawn from more than 40 medical terminologies and classifications. The 1998 release of the Metathesaurus contains 1,051,901 term names mapped into 476,313 concepts. The Semantic Network contains information about types or categories (e.g., Disease or Syndrome, Virus) and the permissible relationships among these types (e.g., Virus “causes” Disease or Syndrome).^18,19,20 Each concept in the Metathesaurus is assigned to one or more semantic types from the Semantic Network. The 1998 release of the Semantic Network contains 132 semantic types and 53 relationships.

To model the Metathesaurus and the Semantic Network as an OODB, it is natural to represent all semantic types in the Semantic Network as classes in the OODB schema. In this paper, we discuss why this straightforward approach to modeling the UMLS is unsatisfactory and introduce a more sophisticated approach. All concepts assigned to only one semantic type become instances of the corresponding class. Each concept assigned to multiple semantic types becomes an instance of a new kind of class, called an intersection class. As a result of this modeling, each class abstracts a semantically uniform set of concepts. In this paper, we also describe a rule to systematically define subclass relationships for all intersection classes. Furthermore, the intersection classes expose some problems existing in the current UMLS, such as concept omissions, classification errors, and ambiguities of concepts. The resulting UMLS OODB schema has a deeper and more refined structure than that of the Semantic Network of the UMLS. We explain why this is a modeling improvement that is completely in line with the design goals of the UMLS.²⁰ The UMLS OODB schema also supports the improved comprehension and navigation of the Metathesaurus.

The rest of this paper is organized as follows: The next section describes the derivation of the classes of the UMLS OODB schema. The third section presents the rule to specify the subclass relationships between classes. Benefits of the OODB representation of the UMLS are described in the fourth section, followed by our conclusions in the fifth.

00DB Class Representation of the Semantic Types

The connection between the Semantic Network and the Metathesaurus, two components of the UMLS, is described by McCray and Nelson²¹ as follows: “The Semantic Network encompasses and provides a unifying structure for the Metathesaurus constituent vocabularies.” An OODB system also consists of two layers—the schema layer, describing the structure of the data, and the instance layer, containing the data itself organized as objects with properties. This analogy suggests the use of an OODB to model the Semantic Network and the Metathesaurus. This modeling unifies the two components into one system, which provides several natural advantages to the UMLS. In this section, we describe the process by which the classes of the OODB are derived.

The Semantic Type Classes

As previously noted, the Metathesaurus and the Semantic Network of the UMLS are related by the association of each concept of the Metathesaurus with one or more semantic types. The Semantic Network provides a high-level abstract view of the Metathesaurus. Let us note that this is in contrast to our previous OODB modeling of CMTs,^11,12,15,16 where the CMTs lacked an existing high-level view. In general, a class in an OODB schema represents a group of objects (or instances) that exhibit the same properties and have common semantics. The OODB schema gives an abstract view of a database. To model the UMLS as an OODB, it is sensible to represent the semantic types as classes in the OODB schema and the concepts as instances of those classes. In the next subsection, we describe a different kind of class.

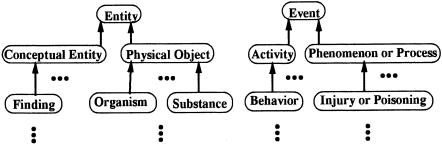
The Semantic Network of the UMLS contains 132 semantic types, which are arranged in an IS-A hierarchy. Entity and Event are two roots of the hierarchy. ▶ shows a few semantic types of the Semantic Network. In the modeling process, every semantic type in the Semantic Network is mapped into a class of the OODB schema. The name of a class in the OODB schema is identical to the name of the corresponding semantic type in the Semantic Network. This kind of a class is called a semantic type class. Every IS-A link in the Semantic Network is mapped into a subclass relationship in the OODB schema. For example, Substance IS-A Physical Object and Physical Object IS-A Entity in the Semantic Network are mapped as follows into the OODB schema: “Substance,” “Physical Object,” and “Entity” are three semantic type classes. “Substance” is a subclass of “Physical Object,” which is a subclass of “Entity.”

Figure 1.

Extract from the Semantic Network. A semantic type is represented by a rounded-corner rectangle with its name written inside. An IS-A link is represented by a bold arrow directed from a semantic type to a parent semantic type.

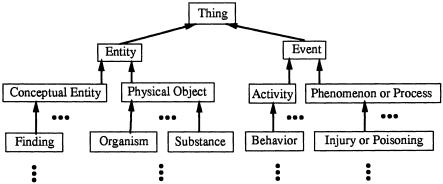
After we map all semantic types into the OODB schema, we obtain an OODB schema with two root classes, “Entity” and “Event,” since the hierarchy of the Semantic Network contains two roots. For traversal purposes, we assume a hierarchy to be singly rooted. Thus, we need to introduce an artificial root into the schema. A new class, called “Thing,” is added into the schema. The root classes mentioned above become the subclasses of “Thing.” At this point, an OODB schema with 133 semantic type classes corresponding to all semantic types in the Semantic Network has been created. ▶ shows a partial schema. Since the semantic type hierarchy of the Semantic Network consists of two disjoint trees, the corresponding OODB schema is also a tree.

Figure 2.

A subschema of the OODB schema corresponding to ▶. A class is represented by a rectangle, and a subclass relationship is indicated by a bold arrow directed upward from the subclass to the superclass.

Now we need to assign the concepts of the Metathesaurus to classes. As mentioned before, each concept is assigned to at least one semantic type. If a concept is assigned to only one semantic type, we can immediately make it an instance of the corresponding semantic type class. For instance, the concept Air of the semantic type Substance becomes an instance of the class “Substance.” In this way, 357,804 concepts in the Metathesaurus that are assigned to only one semantic type can be immediately represented as instances of the corresponding semantic type classes in the OODB schema.

Concepts may belong to more than one semantic type, however. For example, the concept Cotton belongs to two semantic types, Substance and Plant; the concept Norepinephrine preparation belongs to four semantic types, Organism, Pharmacologic Substance, Neuroreactive Substance or Biogenic Amine, and Hormone. Of the 476,314 concepts in the 1998 release of the Metathesaurus, 118,510 are assigned to two or more semantic types. ▶ provides more details on the distribution of concepts.

Table 1.

Distribution of Concepts in the Semantic Network

No. Assigned Semantic Types	No. Concepts
1	357,804
2	108,905
3	9,262
4	331
5	10
6	2

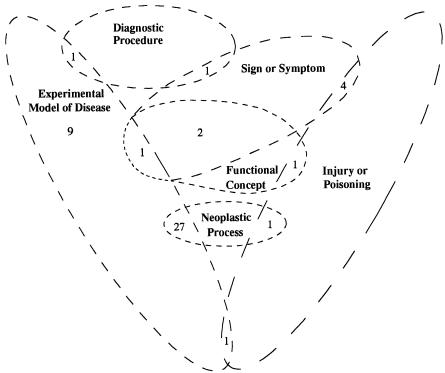
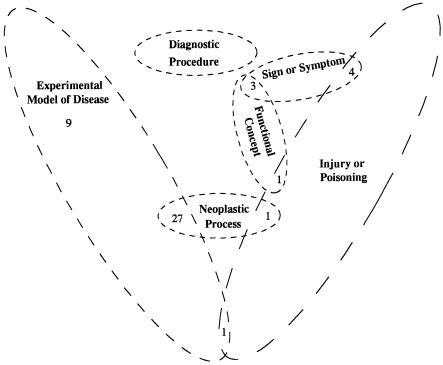
Because a concept may belong to additional semantic types, the set of concepts of one semantic type may be nonuniform. For example, the semantic type Experimental Model of Disease has 39 assigned concepts. Besides this semantic type, the concept Radiation Injuries, Experimental has one additional semantic type, Injury or Poisoning. The concept Water Deprivation has one additional semantic type, Diagnostic Procedure. Another 27 concepts have one additional semantic type, Neoplastic Process. The concept Lesion, NOS has two additional semantic types, Functional Concept and Sign or Symptom. Only nine concepts belong exclusively to the semantic type Experimental Model of Disease. It is difficult to comprehend and use the information contained in such a nonuniform semantic type. The problem we face is how to group concepts with multiple semantic types into uniform sets.

The Intersection Classes

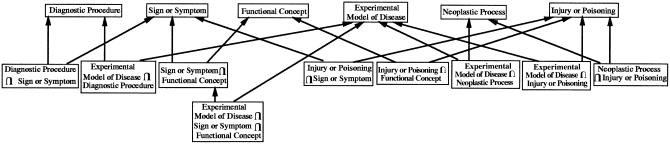
Following the above approach, a concept that is assigned to more than one semantic type should be represented as an instance of more than one class in the OODB schema. In OODBs, all instances of a class must have the same structure and the same semantics. In the UMLS, the semantics of a concept are provided by its semantic types. If a concept is assigned to only one semantic type, then it has simple semantics. Otherwise, if a concept is assigned to a set of semantic types, it has compound semantics, defined by the combination of its different semantic types. Thus, looking at the example we gave before, the concepts of the semantic type Experimental Model of Disease do not share the same semantics. For example, the concept Alloxan Diabetes has the simple semantics of “Experimental Model of Disease,” and the concept Radiation Injuries, Experimental has the compound semantics of “Experimental Model of Disease ∩ Injury or Poisoning.” The symbol ∩ indicates the intersection, meaning that the concept Radiation Injuries, Experimental is both an experimental model of disease and an injury or poisoning. In ▶, we show all intersections among six semantic types, Experimental Model of Disease and the five semantic types with which it intersects. Each intersection contains concepts that belong to two or more semantic types. From the figure, we see that all 39 concepts of Experimental Model of Disease are classified into five groups with different semantics. The concepts of one group have simple semantics, while the four other groups express compound semantics.

Figure 3.

Six semantic types and the nine intersections among them.

We cannot assign all concepts of a given semantic type to the same class corresponding to this semantic type because, as we have shown, some of the concepts may have different semantics. We need to differentiate between these concepts and represent them as instances of different classes in the schema. Each of these classes needs to have unique semantics. Each concept, even if it has multiple semantic types, will be represented as an instance of only one class, whose instances have the same combination of semantic types. The current “semantic type classes” corresponding to the semantic types are, therefore, not sufficient to represent all concepts. An additional kind of class is needed.

To keep the semantic type classes uniform, we disallow all concepts belonging to several semantic types from being instances of each of the semantic type classes. Hence, each semantic type class corresponds to concepts belonging to only this semantic type. To fulfill the goal of representing all concepts as instances of classes of uniform semantics, a new kind of class, called an intersection class, is introduced into our schema. This kind of class represents the combination of two or more semantic types.

Every concept that belongs to more than one semantic type is represented as an instance of one intersection class. To create intersection classes, all concepts with multiple semantic types are partitioned into groups, so that each group contains the concepts that belong to the same set of semantic types and thus have the same compound semantics. The corresponding intersection classes are created to represent all those concept groups. Furthermore, the concepts in each group become the instances of the corresponding intersection class. ▶ shows a refined classification of the concepts assigned to the semantic type Experimental Model of Disease, partitioned into classes with uniform semantics.

Table 2.

Partitioning of Concepts of Semantic Type Experimental Model of Disease

Experimental Model of Disease

Alloxan Diabetes Arthritis, Adjuvant Diabetes, Mellitus, Experimental Disease Models, Animal Encephalomyelitis, Allergic Liver Cirrhosis, Experimental Neuritis, Experimental Allergic Streptozotocin Diabetes Murine-acquired Immunodeficiency Syndrome

Experimental Model of Disease ∩ Injury or Poisoning

Radiation Injuries, Experimental

Experimental Model of Disease ∩ Diagnostic Procedure

Water Deprivation

Experimental Model of Disease ∩ Neoplastic Process

Avian Leukosis Carcinoma 256, Walker Carcinoma, Ehrlich Tumor Carcinoma, Krebs 2 Carcinoma, Lewis Lung Hepatoma, Experimental Hepatoma, Morris Hepatoma, Novikoff Leukemia, Experimental Leukemia, L1210 Leukemia, L5178 Leukemia P388 Liver Neoplasms, Experimental Mammary Neoplasms, Experimental Melanoma, B16 Melanoma, Cloudman S91 Melanoma, Experimental Melanoma, Harding-Passey Sarcoma 37 Sarcoma 180 Sarcoma, Avian Sarcoma, Engelbreth-Holm-Swarm Sarcoma, Experimental Sarcoma, Jensen Sarcoma, Rous Sarcoma, Yoshida Tumor Virus Infections

Experimental Model of Disease ∩ Functional Concept ∩ Sign or Symptom

Lesion, NOS

In ▶, we show six semantic types and nine intersections among them. All six original semantic types are represented as six semantic type classes. Each concept belonging to only one of these six semantic types is represented as an instance of the corresponding semantic type class. Nine intersection classes—e.g., “Experimental Model of Disease ∩ Diagnostic Procedure”—are created to represent the nine intersections. All concepts residing in the intersections become the instances of the corresponding intersection classes.

Regarding the naming of intersection classes, the list of intersecting semantic types of each intersection class should be reviewed by domain experts to identify simpler names whenever possible. For example, the intersection class “Pharmacologic Substance ∩ Organic Chemical” can be renamed “Organic Pharmacologic Substance.” Another example, the intersection class “Body Part, Organ, or Organ Component ∩ Medical Device” can be renamed “Prosthesis,” as suggested by one of our expert readers. If, however, no appropriate name is identified, the intersection is used to clarify the compound semantics of the class. After the creation of the intersection classes, all 476,314 concepts in the Metathesaurus are represented, each as an instance of one class in the schema. The whole schema consists of 1,296 classes. Of these, 1,163 are intersection classes.

In this paper, we call the set of instances of a class C the extent E(C); we call the set of concepts of a semantic type S the extent E(S); and we call the set of concepts of the Metathesaurus M the extent E(M). It may seem that with the intersection classes we lose the access to the extents of the original semantic types. However, in the next section, we show that this information can be reconstructed on demand from the OODB schema.

The Subclass Relationships in the UMLS OODB Schema

Straightforward Model: One Level of Intersection Classes

After introducing the intersection classes, we face the problem of how to determine the subclass relationships originating with an intersection class.

As described earlier, an intersection class represents the combination of more than one semantic type. Its semantics are more specific than those of each original intersected semantic type class. Now we need to decide what the superclasses of each intersection class are. One feasible approach is to use all its original intersected semantic type classes. We call this approach the “straightforward model.” Thus, an intersection class is one level lower than its intersected semantic type classes in the initial schema. In this approach, no intersection class is a superclass of other intersection classes. The extended schema has only one more level than the initial schema. For example, in ▶ the intersection class “Experimental Model of Disease ∩ Sign or Symptom ∩ Functional Concept” has three superclasses, “Experimental Model of Disease,” “Sign or Symptom,” and “Functional Concept.” For the six semantic type classes shown in the figure, one extra level of nine intersection classes and 19 additional subclass relationships is added to the original six semantic type classes.

Figure 4.

Straighforward model of defining subclass relationships for the schema shown in ▶.

The initial OODB schema of the semantic type classes was a tree with a depth of nine. ▶ shows the distribution of classes in each level of the UMLS schema, which is the result of the application of the straightforward model to the whole Metathesaurus. ▶ shows the distribution of the number of the superclasses of all classes, including both semantic type classes and intersection classes of the UMLS schema. From ▶ and ▶, we can derive the fact that 1,163 intersection classes and 2,874 subclass relationships are added to the initial Semantic Network schema, resulting in a ten-level DAG schema. The designers of the UMLS considered the increase in the depth of the Semantic Network desirable²⁰ Thus, the straightforward UMLS OODB schema represents a modeling improvement over the Semantic Network.

Table 3.

Distribution of Classes in Each Level of the UMLS Schema, Obtained by Use of the Straightforward Model

Level	No. Classes	No. Intersection Classes
1	1	0
2	2	0
3	4	0
4	20	0
5	41	62
6	23	218
7	23	172
8	17	240
9	2	401
10	0	70

Table 4.

Distribution of Superclasses for All Classes in the UMLS Schema, Obtained by Use of the Straightforward Model

No. Superclasses of a Class	No. Classes
0	1
1	132
2	714
3	358
4	84
5	6
6	1

▶ shows a subschema of the resulting UMLS schema, obtained by use of the straightforward model. It contains 15 semantic type classes and 6 intersection classes distributed over nine levels.

Figure 5.

A subschema of the UMLS schema, obtained by use of the straightforward model.

A Refined Model: Intersection Classes of Intersection Classes

In OODBs, the subclass relationships point from specific classes to general classes. By transitivity, every specific class is implicitly a subclass of all ancestors of its superclasses. (By ancestors we mean classes reachable following a chain of subclass relationships.) Because of that, we do not need explicit subclass relationships to ancestors of the superclasses. For example, in ▶ we see an intersection class “Experimental Model of Disease ∩ Sign or Symptom ∩ Functional Concept,” which is a subclass of three classes—“Experimental Model of Disease,” “Sign or Symptom,” and “Functional Concept.” The class “Sign or Symptom ∩ Functional Concept” is a subclass of the classes “Sign or Symptom” and “Functional Concept.” If we compare these two intersection classes, we see that the semantics of “Experimental Model of Disease ∩ Sign or Symptom ∩ Functional Concept” are more specific than the semantics of “Sign or Symptom ∩ Functional Concept.” It is natural to have a subclass relationship from the more specific intersection class to the more general intersection class. Hence, “Experimental Model of Disease ∩ Sign or Symptom ∩ Functional Concept” should become a subclass of “Sign or Symptom ∩ Functional Concept.” Since “Sign or Symptom ∩ Functional Concept” is a subclass of “Sign or Symptom” and “Functional Concept,” the transitivity implies that “Experimental Model of Disease ∩ Sign or Symptom ∩ Functional Concept” is a subclass of both “Sign or Symptom” and “Functional Concept.” Thus, there is no need to have explicit subclass relationships from “Experimental Model of Disease ∩ Sign or Symptom ∩ Functional Concept” to “Sign or Symptom” and “Functional Concept” as shown in ▶. ▶ shows the alternative modeling. Compared with ▶, which shows 19 subclass relationships, ▶ shows only 18 subclass relationships. In previous papers,^22,23 we defined the complexity of a schema as the ratio between the number of relationships and the number of classes of the schema. Thus, when two schemas contain the same number of classes, the one with more relationships is of higher complexity. Hence, the schema shown in ▶ is simpler than the one shown in ▶. Furthermore, it is more accurate semantically, since it captures subclass relationships between intersection classes.

Figure 6.

Model of subclass relationships for the schema shown in ▶, obtained by use of the subclass definition rule.

In view of this example, we discuss an alternative approach for defining subclass relationships for the intersection classes. The refined model is designed to capture semantic relationships between intersection classes that were not reflected in the straightforward model. We may make an intersection class a subclass of another intersection class. As a result, intersection classes appear in multiple levels. We do not want a class to have an unnecessary subclass relationship to a more general class if this relationship is implied by transitivity. A class that is an intersection of two classes needs to be made a subclass of those two classes. However, for the intersection of more than two classes, there may be more than one way to define the subclass relationships. In such a case, subclass relationships that are unnecessary because of transitivity may be eliminated. To systematically define the subclass relationships of intersection classes, we need a rule. Before we describe such a rule, we need to define the notions of direct superclass and indirect superclass.

• Direct Superclass: Let A and B be two classes in a schema. If A is a superclass of B and there does not exist a class C such that A is a superclass of C and C is a superclass of B, then A is a direct superclass of B.

• Indirect Superclass: Let A and B be two classes in a schema. If A is a superclass of B and there exists at least one class C such that A is a superclass of C and C is a superclass of B, then A is an indirect superclass of B.

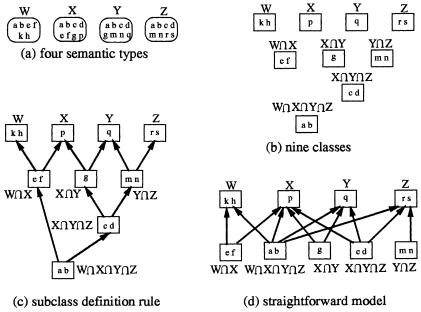
For example, ▶ shows four semantic types —W, X, Y, and Z—and the concepts assigned to them. (To illustrate our partitioning process, the concept names are placed inside the semantic type icons.) Since concepts a, b, c, d, e, f, g, m, and n are assigned to more than one of the W, X, Y, and Z semantic types, they are removed from the semantic types W, X, Y, and Z and partitioned into five groups. Thus, as shown in ▶, four semantic type classes are created to represent the four semantic types W, X, Y, and Z, and five intersection classes are created to represent those five groups.

Figure 7.

Example of OODB modeling for a few semantic types.

Since the intersection class “X ∩ Y ∩ Z” is more specific than classes “X,” “Y,” “Z,” “X ∩ Y,” and “Y ∩ Z,” all these classes are superclasses of “X ∩ Y ∩ Z.” However, only “X ∩ Y” and “Y ∩ Z” are direct superclasses of “X ∩ Y ∩ Z.” The classes “X,” “Y,” and “Z” are indirect superclasses of “X ∩ Y ∩ Z.” Also, “W,” “X,” “Y,” “Z,” “X ∩ Y,” and “Y ∩ Z” are indirect superclasses of “W ∩ X ∩ Y ∩ Z,” while the intersection classes “W ∩ X” and “X ∩ Y ∩ Z” are direct superclasses of “W ∩ X ∩ Y ∩ Z.”

We give the following rule to define the subclass relationships:

• Subclass Definition Rule: Let C be an intersection class in the schema. Then subclass relationships are defined from C to all its direct superclasses only.

As we mentioned before, because of the transitivity of the subclass relationship we do not need to explicitly define subclass relationships from a class to its indirect superclasses.

This rule is guaranteed to increase the depth of the schema by transforming intersection classes of more than two semantic type classes into subclasses of other intersection classes. As McCray and Hol²⁰ note, it is considered desirable to increase the depth of the Semantic Network. ▶ shows the schema following the rule, which has four levels and ten subclass relationships. ▶ shows the schema following the straightforward model, which has two levels and 13 subclass relationships. The straightforward model produces a schema of higher complexity than the schema obtained by the subclass definition rule.

Unfortunately, there is no guarantee that the subclass definition rule will always provide a schema of lower complexity than one obtained from the straightforward model. It may result in a schema of higher complexity. For instance, if we assume that there is one intersection class that is an intersection of all six semantic type classes shown in ▶, six more subclass relationships are added, yielding a total of 25 subclass relationships using the straightforward model. However, eight more subclass relationships are added, yielding 26 subclass relationships, if we use the subclass definition rule. Nevertheless, we shall see that in the UMLS schema obtained, the first situation occurs much more often than the second, and the total number of subclass relationships is reduced, resulting in a schema of lower complexity.

▶ and ▶ show some details of the refined schema. Following the refined approach, we get an OODB schema with a depth of 14. To obtain this schema, 2,677 relationships are added. Comparing ▶ and ▶, we see that intersection classes are pushed to lower levels in the refined schema. There are fewer intersection classes in levels 5 to 9, but more in level 10, which has grown from 70 to 212 classes. The new levels 11 to 14 contain 109 classes. Comparing ▶ and ▶, we see a systematic reduction in the number of intersection classes with more than two superclasses. The number of intersection classes with two superclasses increases from 714 to 857. The number of intersection classes with three, four, and five superclasses decreases. One class with seven superclasses, which does not exist in the straightforward schema, is created. This class demonstrates the rare phenomenon of the creation of a class with an increased number of superclasses, mentioned before.

Table 5.

Distribution of Classes in Each Level of the UMLS Schema, Obtained by Use of the Subclass Definition Rule

Level	No. Classes	No. Intersection Classes
1	1	0
2	2	0
3	4	0
4	20	0
5	41	56
6	23	203
7	23	163
8	17	186
9	2	234
10	0	212
11	0	89
12	0	16
13	0	3
14	0	1

Table 6.

Distribution of Superclasses of All Classes in the UMLS Schema, Obtained by Use of the Subclass Definition Rule

No. Superclasses of a Class	No. Classes
0	1
1	132
2	857
3	267
4	36
5	1
6	1
7	1

To summarize, we created 1,163 intersection classes and added 2,677 new subclass relationships. All 476,314 concepts in the Metathesaurus are represented as instances of unique classes. The whole schema contains 1,296 classes. Compared with the straightforward approach, where all intersection classes are subclasses of nonintersection classes, the refined approach adds more layers and fewer subclass relationships to the initial schema. Both approaches produce semantically more accurate schemas than the original Semantic Network. However, the refined approach produces a semantically more accurate schema of lower complexity than does the straightforward approach.

▶ shows a subschema of the resulting UMLS schema using the subclass definition rule. It contains 15 semantic type classes and 6 intersection classes distributed over 11 levels. In comparison, the same classes appear in ▶ in a schema modeled by the straightforward approach, but this schema has only nine levels and two additional subclass relationships.

Figure 8.

A subschema of the UMLS schema, obtained by use of the subclass definition rule.

Earlier, in the discussion of intersection classes, we noted an apparent loss of information caused by our improved modeling. To recover the extent of a semantic type, we combine the extent of its semantic type class with the extents of all the intersection class descendants (defined with regard to the subclass relationship) of its semantic type class.

Advantages of the OODB Representation

The extra comprehension afforded by the OODB representation makes it possible to identify various modeling and classification errors in the UMLS as well as make general representational improvements, as described in the following sections.

Exposing Problems in the Current UMLS

Representing the intersection classes and their instances enables researchers to study the extents of such intersection classes. In our previous experience^15,16 with the CPMC MED,¹⁷ this led to the identification of modeling problems in the MED. We have found a few similar problems in the UMLS, which are described below, and we conjecture that many more problems will be found. The resolution of these problems by domain experts would lead to a better new release of the UMLS.

Omissions

Let us give an example of omissions. In the UMLS schema, there is an intersection class “Body Part, Organ, or Organ Component ∩ Medical Device.” Studying the extent of this class, we found only four concepts in it—Dental abutments, Conduit with xenograft valve, Conduit with homograft valve, and Incubator. pediatric. However, many medical devices in body parts are missing, including various heart valves. These missing concepts should be added as instances of this intersection class.

Another example of omissions can be found in the intersection class “Injury or Poisoning ∩ Experimental Model of Disease.” This class has only one concept, Radiation Injuries, Experimental. However, many injury or poisoning experimentals are missing and should be added as instances of this intersection class. The extents of intersection classes will give the professionals in charge of the maintenance of the UMLS a useful view to discover omissions from the Metathesaurus.

Redundant Classifications

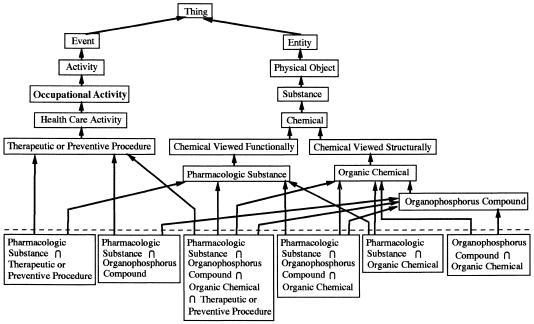
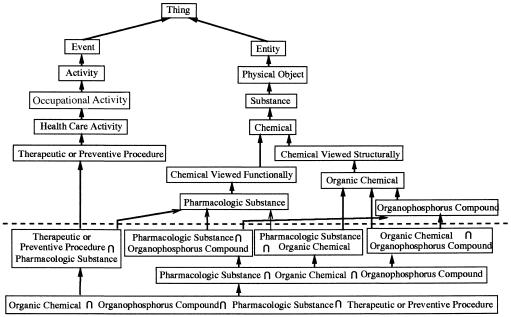
By creating intersection classes, we discovered that 8,622 concepts in the Metathesaurus are assigned to several semantic types that stand in parent-child or ancestor-descendant relationships in the UMLS Semantic Network. For example, in ▶ the intersection class “Organic Chemical ∩ Organophosphorus Compound” has two superclasses, “Organic Chemical” and “Organophosphorus Compound.” However, “Organophosphorus Compound” is itself a subclass of “Organic Chemical.” The creation of this intersection class was due to the fact that there are 127 concepts assigned to both the semantic types Organic Chemical and Organophosphorus Compound. This situation is not in line with the intentions of the UMLS designers. McCray and Nelson,²¹ discussing the assignment of concepts to semantic types, stated that “In all cases the most specific semantic type available in the hierarchy is assigned to a term.” Therefore, those 127 concepts should be assigned only to the semantic type Organophosphorus Compound. As a result, the intersection class “Organic Chemical ∩ Organophosphorus Compound” ceases to exist. Thus, we get a new subschema (▶), replacing the one shown in ▶.

Figure 9.

The subschema shown in ▶ after removal of redundant classifications.

If all the redundant classifications are removed from the UMLS (that is, if all 8,622 concepts are assigned to only one semantic type), 77 intersection classes disappear from the UMLS schema. These redundant classifications may have resulted from the assignment of concepts to semantic types by different experts for the different UMLS sources. However, the use of intersection classes has helped us uncover such redundancies.

A list of the 8,622 concepts and their correct semantic types was submitted to the National Library of Medicine. We have been notified that these redundant classifications will be removed from the next version of the UMLS.

Classification Errors

Intersection classes highlight some classification errors in the UMLS. For example, the concept Encephalitis Viruses is the only instance of the intersection class “Virus ∩ Disease or Syndrome.” But it pertains to viruses only and should not be classified as a disease. Hence, it should be an instance of the “Virus” semantic type class. Furthermore, since Encephalitis Viruses is the only instance of the intersection class “Virus ∩ Disease or Syndrome,” this intersection class is not needed. Several other such cases are shown in ▶. Each intersection class shown in the first column there will be deleted from the UMLS OODB schema. Notice that the information in the last row of the table is taken from ▶ and ▶.

Table 7.

Examples of Classification Errors

Intersection Class	Concept	Revised Class of Concept
Bacterium ∩ Laboratory Procedure	Scotch Tape Mount	Laboratory Procedure
Organism ∩ Biomedical or Dental Material	Urea Formaldehyde Resin	Biomedical or Dental Material
Congenital Abnormality ∩ Body Location or Region ∩ Disease or Syndrome	Alagille Syndrome	Congenital Abnormality ∩ Disease or Syndrome
Experimental Model of Disease ∩ Functional Concept ∩ Sign or Symptom	Lesion, NOS	Functional Concept ∩ Sign or Symptom

Ambiguity

Intersection classes helped us discover ambiguities of concepts in the UMLS. For example, the intersection class “Plant ∩ Disease or Syndrome” has only one instance, Toxicodendron. However, Toxicodendron, known popularly as poison ivy, refers to two different concepts, one a plant and the other a disease. To differentiate them, two concepts should be created, so that one is an instance of the class “Plant” and the other is an instance of the class “Disease or Syndrome.” Since the intersection class has only this instance, it can be eliminated.

Let us look at another example. The concept Paronychia of toe is the only instance of the intersection class “Anatomical Structure ∩ Disease or Syndrome.” The classification exposes the need for two different concepts. One represents the diseased toe, to be named Toe with Paronychia, which is a body part and should be an instance of the class “Anatomical Structure.” The other represents the paronychia of toe, which should be an instance of the class “Disease or Syndrome.” Thus, no such intersection class is necessary.

The third example of ambiguity is the concept Water Deprivation, shown in ▶, which is the only instance of the intersection class “Experimental Model of Disease ∩ Diagnostic Procedure.” We need two separate concepts—Water Deprivation, as an instance of the class “Experimental Model of Disease,” and Water Deprivation Procedure, as an instance of “Diagnostic Procedure.” Hence, the intersection class “Experimental Model of Disease ∩ Diagnostic Procedure” can be eliminated from the UMLS OODB schema, as well as from ▶ and ▶.

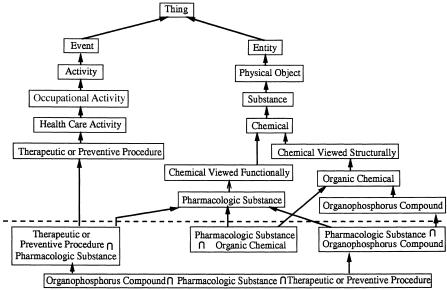
Another case of ambiguity, taken from ▶, concerns the concept Wrist Clonus, which is the only concept of the intersection class “Diagnostic Procedure ∩ Sign or Symptom.” We need two separate concepts—Wrist Clonus, belonging to the class “Sign or Symptom,” and Wrist Clonus Elicitation, belonging to the class “Diagnostic Procedure.” Hence, the intersection class “Diagnostic Procedure ∩ Sign or Symptom” can be eliminated from the UMLS OODB schema and from ▶. ▶ shows the revised ▶, taking into account the three changes described here. The reduced complexity of the revised diagram shows how the review of intersection classes may improve and simplify the UMLS classification.

Figure 10.

The revised diagram of semantic types and intersections shown in ▶.

Nonuniform Classification

The extents of some intersection classes indicate that a nonuniform classification was employed for some concepts in the UMLS. For example, the concept Prematurity is the only instance of the intersection class “Organism Attribute ∩ Temporal Concept.” The classification of Prematurity to both semantic types, “organism attribute” and “temporal concept,” is definitely legitimate. However, if this organism attribute is modeled as a temporal concept, then other organism attributes should also be classified as temporal concepts, e.g., the concept Senility. Hence, while the extent of the intersection class does not expose an error, it exposes nonuniformity in the way concepts were classified into semantic types in the UMLS. This nonuniformity is not surprising, given that many experts were involved in the classification of concepts into semantic types. Such feedback should be communicated to domain experts, who should try to make the classification more uniform, either by adding other relevant concepts to the intersection class or by deleting the existing ones (in which case the intersection class becomes empty).

Problems in a Sample of Intersection Classes

In the UMLS schema, 422 intersection classes have only one instance. One author (J.J.C.) checked the first 100 such intersection classes and their instances. For 11 of the 100 intersection classes, the classification of concepts is correct. For 55 intersection classes, the multiple classifications are wrong and the intersection classes should be deleted from the UMLS OODB schema. For 32 intersection classes, the classified concepts indicate nonuniform classifications, as described above. Two intersection classes are cases of redundant classification. These results suggest that many more classification problems may be found in the UMLS.

Representational Improvements for the UMLS

Deeper Schema

McCray and Hole,²⁰ in a description of the structure of the first version of the UMLS, state that “The current scope of the [Semantic] Network is quite broad, yet the depth is fairly shallow. We expect to make future refinements and enhancements to the Network, based on actual use and experimentation.” Introducing intersection classes and subclass relationships among them provides extra refinement and extra layers to the information contained in the Semantic Network. The resulting UMLS schema is larger and has greater depth than the Semantic Network.

Uniform Semantic Classification

As discussed earlier, the concepts belonging to a semantic type may not be uniform, since some of them may belong to one or more additional semantic types. Because of this lack of uniformity, it is difficult for a user to comprehend and use the set of concepts of such a semantic type. In the UMLS OODB representation, all concepts with the same simple semantics are instances of the same semantic type class. Also, all concepts with the same compound semantics—that is, the same combination of semantic types—are instances of the same intersection class with the same semantics. Thus, the extent of every class of the UMLS OODB representation is uniform in its semantics. Having such classes simplifies the comprehension and use of the information contained in their concepts.

Reduced Average Extent Size

In the original Semantic Network, the extents of many semantic types are too large for human comprehension. In the 1998 version, every semantic type corresponds to about 5,000 concepts on average. (Remember that many concepts belong to more than one semantic type.) Since the extents of semantic types are not uniform in size, some of them have many more than 5,000 concepts. It can be difficult for a user to comprehend such concepts.

Adding the intersection classes to the UMLS schema reduces the average number of concepts in each semantic type class to about 2,700. The average number of concepts in each intersection class is 100, which is comparatively few. Having an OODB representation with a reduced average number of instances per class facilitates comprehension and simplifies the use of the Metathesaurus.

Traversal

Since the Semantic Network and the Metathesaurus are unified into an OODB, the OODB representation captures a dual representation of the schema layer and the instance (concept) layer. The OODB schema is smaller than the Metathesaurus by two orders of magnitude, and thus provides a compact abstract representation that helps user orientation to the Metathesaurus. This class representation with its compact schema enables combined traversal, which is faster and shorter than traversal of the Metathesaurus itself.

Suppose that we want to find information on a concept stored in the UMLS, but we do not know the term of the concept. We would, however, recognize the concept if we encountered it. For this purpose, we need to traverse the hierarchies of the Metathesaurus, using our knowledge about the target to guide our choices at different levels of the Metathesaurus. Typically, we would start our traversal with a relevant Metathesaurus concept with which we are familiar. However, if no such concept is identified, the search starts with a relevant root of the Metathesaurus.

Instead of traversing the Metathesaurus through its many levels, we can take a better approach. Using the OODB representation of the UMLS, we can traverse the OODB schema until the proper class—say, S—is identified. The traversal starts either with a relevant semantic type or, if no such type is identified, with the root of the OODB schema. We are normally able to do this, since we need to make only a very general judgment about whether the concept we are looking for fits into the given class. Once the proper class is identified, we need to switch to the subnetwork of the instance level that contains only the extent of the class S. The traversal runs through the levels of this subnetwork until the desired concept is recognized (or its absence is noted).

Since traversal requires repeated scanning through lists of children and choosing one of them, it is faster at the schema level than at the instance level. This is because the number of subclasses of a class in the schema is typically much smaller than the number of children of a concept in the Metathesaurus. As an intuitive analogy, think about driving on a major highway to reach a destination. Usually, after exiting the highway near the destination, a person needs to travel on local roads. Using the schema is like driving on a highway, while traversing the subnetwork of the Metathesaurus is like driving on the local roads. Traveling to a distant destination using local roads is usually slower than using a highway.

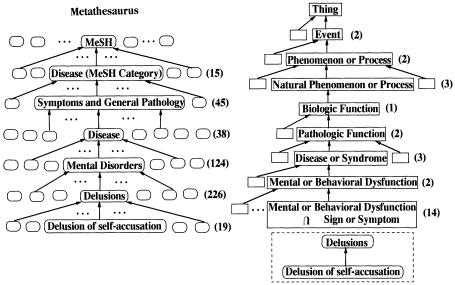
Let us give a traversal example, looking for the concept Delusion of self-accusation without, however, being able to name the concept. We now list a sequence of Metathesaurus concepts corresponding to this traversal. For each concept, we list in parentheses the number of its children. We need to scan this list to pick one child at every step of our traversal. We may, for example, start the traversal at the relevant “Mental Disorders” concept. Or, if no such relevant concept is identified, we need to start the traversal at a root of the Metathesaurus. We describe the complete traversal of the second case, which contains the first case as a later part of the traversal. However, there are 35,352 roots in the Metathesaurus, and we need to pick one of them. The right concept to choose is Medical Subject Headings (15 children). Traversing through Diseases (MeSH Category) (45), Symptoms and General Pathology (38), Disease (124), Mental Disorders (226), and Delusions (19), we finally reach the target, Delusion of self-accusation. The traversal of this path of seven concepts requires us to scan a total of 467 children (▶). (The partial traversal, of a path of three concepts, requires the scanning of 245 children.)

Figure 11.

Comparison of the Metathesaurus traversal (left) and the combined traversal of the schema and instance layers (right). In the Metathesaurus traversal, the number of concepts at each level is shown in parentheses; the total number of scanned children was 467. In the combined traversal, the number of classes at each level is shown in parentheses, and the total number of scanned children was 48.

We now contrast this traversal with another traversal to the same target, which uses the OODB schema in its first phase. A relevant semantic type may be “Mental or Behavioral Dysfunction,” or we can start with the root class; “Thing” (2), of the OODB schema. (The number inside the parentheses here is the number of subclasses of the given class.) The traversal path from “Thing” leads to “Event” (2), “Phenomenon or Process” (3), “Natural Phenomenon or Process” (1), “Biologic Function” (2), “Pathologic Function” (3), “Disease or Syndrome” (2), “Mental or Behavioral Dysfunction” (14), and the intersection class “Mental or Behavioral Dysfunction ∩ Sign or Symptom.” At this stage in our traversal, we switch to the concept level. The concept Delusions (19) is a root of the concept network of this intersection class. We continue on to the child Delusion of self-accusation, which is the concept we are looking for (▶).

The partial traversal starting at “Mental or Behavioral Dysfunction” passes through two classes with 14 children and two concepts with 19 children, or a total of 33 scanned children. The full traversal passes through nine classes with 29 children and two concepts with 19 children, or a total of 48 scanned children. The total number of scanned children for either traversal is much smaller than the number required in the earlier example—467 for the full traversal or 245 for the partial. The combined traversal search path in this second example is longer than that in the first, because the Metathesaurus has many roots and the time spent searching for the proper root to start the traversal is not reflected in the length of the search started at Medical Subject Headings. However, this disadvantage is clearly outweighed by the smaller number of children that need to be scanned. Altogether, the combined traversal supported by the UMLS OODB schema is a faster traversal.

Another advantage of browsing the schema level is that, after a while, the user becomes familiar with the schema and more efficient in traversing it. On the other hand, the size of the Metathesaurus does not enable a user to become familiar with the whole extent of the Metathesaurus.

Conclusions

The UMLS integrates many medical terminologies and coding systems. It plays a major role in overcoming terminological differences in the design of computerized health care information systems. However, the size and complexity of the UMLS make it difficult to maintain and use. To help overcome this problem, we have developed a methodology for representing two components of the UMLS, the Metathesaurus and the Semantic Network, as a unified OODB. This has led to the recognition of classification problems and possible improvements in the UMLS classification. Examples of classification problems include redundant and nonuniform classifications, omissions, and ambiguities. The resulting UMLS OODB schema enhances the Semantic Network by adding more layers and refining it. The UMLS OODB schema also supports a fast two-level traversal of the Metathesaurus. It makes comprehension of the Metathesaurus easier by partitioning its extent into semantically uniform classes.