Abstract
Salinity gradient energy is a sustainable, renewable, and clean energy source. When waters with different salinities are mixed, the change in Gibbs free energy can be harvested as energy and only brackish water remains. Reverse electrodialysis is one of the technologies that can harvest this sustainable energy source. High power densities have been obtained in small lab scale systems, but translation to large industrial scale stacks is essential for commercialization of the technology. Moreover, power density is an important parameter, and efficiency, i.e., the amount of energy harvested compared to the amount of energy available in the feed waters, is critical for commercial processes. In this work, we systematically investigate the influence of stack size and membrane type on power density, thermodynamic efficiency, and energy efficiency. Results show that the residence time is an excellent parameter for comparing differently sized stacks and translating lab scale experimental results to larger pilot stacks. Also, the influence of undesired water permeability and co-ion diffusion (as reflected in permselectivity) is clearly visible when measuring the thermodynamic efficiency. An averaged thermodynamic efficiency of 44.9% is measured using Fujifilm Type 10 anion exchange and cation exchange membranes that have low water permeability and high permselectivity. This value comes close to the thermodynamic maximum of 50%.
Introduction
Salinity gradient energy is a sustainable and renewable clean energy source. When waters with different salinities are mixed, the change in Gibbs free energy can be harvested as salinity gradient energy and only brackish water remains. The theoretical potential of salinity gradient energy is huge,1,2 and the technologies for harvesting this salinity gradient energy are developing toward their introduction into the commercial market.3−6 Reverse electrodialysis (RED) is one of the technologies that can harvest this sustainable energy source (Figure 1). A RED stack consists of repeating cells comprised of alternating cation (CEM) and anion (AEM) exchange membranes. Feed waters, i.e., seawater and river water, flow alternatingly through the feed compartments between the membranes. The ion exchange membranes (IEMs) are selective for cations (CEMs) or anions (AEMs). The salinity gradient over each ion exchange membrane creates a voltage difference (the Donnan potential), and this is the driving force for the process. When alternating CEMs and AEMs are stacked, this voltage difference accumulates. When the RED stack is connected to an external load, this driving force results in a flux of ions through the membranes. To allow the ionic flux, both ends of the pile of membranes are in contact with an electrode and a redox couple recirculating between the electrodes to transform the ionic flux into an electrical current. This process in which solutions with different salinities are mixed in a controlled way can be used to harvest the change in Gibbs energy as renewable energy to power an external load.7
Figure 1.
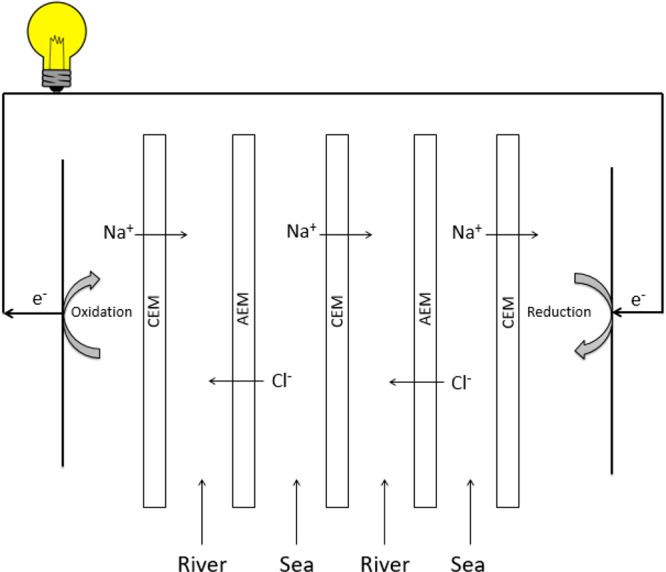
Principle of a RED stack, in which a redox couple transforms the ionic flux into an electrical current.
Most research on REDs is performed using small laboratory stacks with 0.2 m2 of active membrane area, i.e., a 10 cm × 10 cm flow compartment and 10 membrane cell pairs. Promising results have been obtained with such small stacks.8−10 A first series of experiments investigating the performance of a scaled-up RED stack was performed by Veerman et al.11 using a stack of 25 cm × 75 cm equipped with 50 cell pairs and an active membrane area of 18.75 m2. The authors concluded that the design of the stack, especially the flow direction and the inlet manifolds, was the key parameter determining the power density output when increasing the size of the stack. Tedesco et al.12 used RED technology to harvest energy from brackish water and brine (in contrast to river and seawater). A RED stack equipped with a 44 cm × 44 cm compartment area, 125 cell pairs, and a total active membrane area of 48 m2 was investigated. Using natural sources, i.e., brackish water and brine, a power output of 40 W (0.83 W/m2) was obtained. The authors also observed a constant performance during a 5 month operation when using natural feed waters and changing operational conditions. In a follow-up paper,13 the same system was scaled up from 125 to 500 cell pairs, achieving an active membrane are of 194 m2, and the authors concluded that the scaling up process did not lead to any reduction of specific performance indicators. A power density of 0.84 W/m2 was achieved when using natural sources.
Vermaas et al.14 theoretically investigated the energy efficiency in a RED using different stack configurations (flow directions) with single and multiple electrode pairs. An analytical model was used for this purpose, maximizing the gross energy efficiency output. The model assumed ideal IEMs and no concentration polarization effects. Results showed that by optimizing the mixing ratio of seawater and river water and by using a single-electrode segment, one could theoretically obtain efficiencies of ≤95%. The limitations of the model of Vermaas et al. were partially solved in a follow-up paper,15 in which IEM imperfections were included in the model. Co-ion transport, osmotic water transport, and electro-osmosis were analyzed, and after a careful selection of the operating conditions and stack parameters, an energy efficiency of ≤37% could be predicted. Most of the available energy was dissipated by the internal stack resistance and losses from uncontrolled mixing of the feed waters due to imperfections in the IEM.
Laboratory scale experiments are easy to perform and give valuable information about the research phase. Although high power densities have been obtained in such small lab scale systems, up to a 2.9 W/m2 gross power density,8−10 the translation to large industrial scale stacks is essential for commercialization of the technology. Moreover, power density is an important parameter, and efficiency, i.e., the amount of energy harvested compared to the amount of energy available in the feed waters, is critical for commercial processes. So far, all described experiments were performed under different conditions; therefore, performances cannot be compared, nor is it possible to draw conclusions about the effect of stack size on performance and possible consequences for upscaling. In the work presented here, we systematically investigate the translation of small lab scale stacks to larger systems. For that, four stacks with a different active area per membrane are used: 6 cm × 6 cm, 10 cm × 10 cm, 22 cm × 22 cm, and 44 cm × 44 cm. Each stack contains 50 cell pairs, corresponding to total active membrane areas of 0.36, 1.00, 4.84, and 19.36 m2 per stack, respectively. Stacks are compared in terms of power density and efficiency, and the influence of membrane type and stack size on performance is discussed.
Materials and Methods
Stack Configuration
Effect of Stack Size
To investigate the effect of stack size, four cross-flow reverse electrodialysis stacks (REDstack BV) with different dimensions were used. Details about the design of the stacks can be found elsewhere.7,8,10 The stacks had dimensions of 6 cm × 6 cm, 10 cm × 10 cm, 22 cm × 22 cm, and 44 cm × 44 cm. Each stack contained 50 cell pairs, corresponding to total active membrane areas of 0.36, 1.00, 4.84, and 19.36 m2 per stack, respectively. Each single-membrane cell pair consisted of a CEM and an AEM. As a CEM, a new type of homogeneous profiled membrane was used (T1 CEM P150), while a reference standard grade homogeneous type I membrane was used as an AEM. All membranes were separated by 155 μm woven net-spacers (Deukum GmbH), unless using T1 CEM P150 profiled membranes, which integrate the membrane and spacer functionality. All membranes in this research were supplied by Fujifilm Manufacturing Europe BV.
Effect of the Stack Configuration and Membrane Properties
To investigate the effect of membrane type on RED performance, three cross-flow stacks all with dimensions of 22 cm × 22 cm (total active area of 4.84 m2) were used. Each stack contained 50 cell pairs but different membrane types. The reference stack was equipped with a standard grade type I AEM and a multivalent-permeable T1 CEM. These membranes are commonly used for RED experiments.16 The second stack was equipped with a standard grade type I AEM and a new type of profiled homogeneous multivalent-permeable CEM (T1 CEM P150). The use of a profiled membrane with an integrated spacer functionality allowed us to operate the stack without net-spacers, as the integrated profile maintains the intermembrane distance in the feedwater compartment. In this research, the profiled membrane was used in only the river water compartment, while the seawater compartment contained the standard reference AEM (type I AEM). The third stack was equipped with a type 10 CEM and a type 10 AEM. These membranes were chosen because of their low water permeability and high permselectivity compared to those of the other membranes. Also, all these membranes were supplied by Fujifilm Manufacturing Europe BV.
The relevant properties of all membranes used in this study are summarized in Table 1.
Table 1. Membrane Types and Characteristicsa.
| membrane | description | membrane thickness (μm) | electrical resistance (Ω cm2) | permselectivity (%) (0.1–0.5 M NaCl) | water permeability (mL bar–1 h–1 m–2) |
|---|---|---|---|---|---|
| type I AEM | reference | 115 | 1.3 | 91.9 | 15 |
| type 10 AEM | low water permeability | 125 | 1.5 | 94.5 | 8 |
| T1 CEM P150 | multivalent-permeable profile | 115/150b | 2.2 | 92 | 15 |
| T1 CEM | multivalent-permeable | 115 | 1.7 | 89.5 | 15 |
| type 10 CEM | low water permeability | 125 | 2.3 | 94.7 | 9 |
Data provided by the manufacturer (Fujifilm Manufacturing Europe BV).
Profile height.
Details of the RED stacks are summarized in Table 2.
Table 2. Specifications of the three RED stacks with different configurations.
| stack 1 | stack 2 | stack 3 | |
|---|---|---|---|
| membrane material | type I AEM/T1 CEM | type I AEM/T1 CEM P150 | type 10 AEM/Type 10 CEM |
| membrane characteristics | reference | profile | low water permeability |
| membrane surface | flat | profile | flat |
| intermembrane distance (μm) | 155 | 150 ± 5 | 155 |
| compartment support | woven spacer 155 μm | membrane profile RW/woven spacer 155 μm SW | woven spacer 155 μm |
All stacks used titanium electrodes (mesh of 1.7 m2 of active surface area/m2 of electrode) with a mixed ruthenium/iridium mixed metal oxide coating as the anode and cathode (Magneto Special Anodes BV), placed at both sides of the membrane pile. The electrode rinse solution used to facilitate the redox reactions at the electrodes consisted of 0.2 M K3Fe(CN)6, 0.2 M K4Fe(CN)6, and 0.25 M NaCl in demineralized water. The electrode rinse solution was recirculated at selected flow rates along the electrodes by using a peristaltic pump (Cole-Parmer, Masterflex L/S Digital drive). At both ends of the membrane pile, next to the electrodes, a double-shielding cation exchange membrane (type 10) was placed to close the electrolyte compartments and to prevent leakage of the electrolyte into the feedwater compartments.
Feed Waters
Artificial seawater and river water were used at concentrations of 0.507 M (30 g of NaCl/kg of water) and 0.017 M (1 g of NaCl/kg of water), respectively. These solutions were made with NaCl (technical grade, ESCO) dissolved in water. The solutions were kept at 25 ± 0.5 °C with a heater (2000 W standard immersion heather, IHP). Measurements were performed over 360 s per flow velocity, at flow velocities of 0.25, 0.50, 1.00, 1.50, and 2.00 cm/s in random order to avoid history effects. This corresponds to flow rates ranging from 70 to 557 mL/min for the 6 cm × 6 cm stack, from 116 to 9308 mL/min for the 10 cm × 10 cm stack, from 256 to 2048 mL/min for the 22 cm × 22 cm stack, and from 512 to 4096 mL/min for the 44 cm × 44 cm stack. The artificial solutions were pumped continuously through the stack by using two peristaltic pumps (Cole-Parmer, Masterflex L/S Digital drive). The residence time (seconds) of the feedwaters inside the stack is calculated by dividing the length of the stack (centimeters) by the flow velocity (centimeters per second).
Two differential pressure transmitters (Vegadif 65, Vega BV) were placed to measure the pressure drop over the seawater and river water compartments. Data were collected using a data logger (Symex MultiCon CMC 99 PS3). The pressure drop values used to calculate the consumed pumping energy were the averaged pressure drop values per flow velocity during the full duration of the measurement (360 s).
Effluent sampling was performed during the experiments to quantify the changes in salinity gradient and volume. Sampling was performed only during the constant current stage. The salinity and conductivity were measured with a conductivity meter (Cond 3110 + TetraCon 325, WTW-Xylem), and the sample volume was measured by using a precision balance (Kern).
Electrochemical Measurements
A chrono-amperometric series was applied using a potentiostat (Ivium Technologies, The Netherlands). It involves an initial stage of 60 s without any current for the determination of the open circuit voltage (OCV), followed by a stage of 300 s measuring the current at a constant voltage equal to half of the OCV, i.e. at maximum power density.17 The gross power can be calculated as follows:8,12
| 1 |
where Pgross is the gross power (watts), V is the voltage (volts), and I is the current (amperes). The power required to pump the feed waters is determined from the measured pressure drop over the stack (hydraulic losses). The pumping power (watts) can be calculated as11,18
| 2 |
where Φr and Φs are the flow rates (cubic meters per second) of river and seawater, respectively, and Δpr and Δps are the pressure drops (pascals) over the river and seawater compartments, respectively.
The net power, Pnet (watts), is calculated as the difference between the gross power, Pgross (watts), and the power consumed for pumping the feed waters, Ppump (watts):
| 3 |
Dividing eqs 1–3 by the total active membrane area, Astack (square meters), we obtain the gross power density, the pumping power density, and the net power density.
Efficiency Calculations
The gross energy efficiency and thermodynamic efficiency calculations are based on exergy,19 which is the amount of available energy that can be extracted from a system reaching equilibrium. The most accepted way of calculating exergy (the energy available to do useful work) in RED is by calculating the Gibbs free energy of mixing (ΔGmix) (Supporting Information). The gross energy efficiency of a RED stack is defined as the ratio of extracted useful electrical energy over the total chemical energy supplied to the stack in the form of the salinity gradient (exergyin). Instead of using the number of moles to calculate the Gibbs free energy, in this work the molar flow rate (moles per second) is used. Therefore, the Gibbs free energy of mixing is expressed as a power (watts), which for efficiency calculations can be combined with the power produced by the RED stack (Pgross). The gross energy efficiency (ηgross) of a RED system can then be calculated using the expression
| 4 |
where Pgross is the (maximum) gross power produced (watts) and exergyin is the available chemical energy supplied to the stack per second (watts).
If the pumping power, Ppumping (watts), is subtracted from the gross power, Pgross (watts), then the net energy efficiency of the process can be calculated using the expression
| 5 |
where Pnet is the net power produced (watts). Moreover, when both outlet concentrations of a RED stack (i.e., the river and seawater streams exiting the stack) are not fully mixed, some salinity gradient energy is still available to be extracted. For this, when the flow rates and outlet concentrations are known, the thermodynamic efficiency (ηthermodynamic) of a RED stack can be calculated using the following expression:
| 6 |
where Pgross is the gross power (watts) and exergyout (watts) is the unused exergy exiting the stack per second.
The exergy dissipated, i.e., irreversible loss, in the stack can be calculated by subtracting the useful work obtained (Pgross) and the unused energy (exergyout) from the total chemical energy supplied to the stack (exergyin)
| 7 |
Results and Discussion
In this section, the influence of stack size and membrane type on power density and energy efficiency is evaluated and discussed.
Influence of Stack Size on Power Density and Energy Efficiency
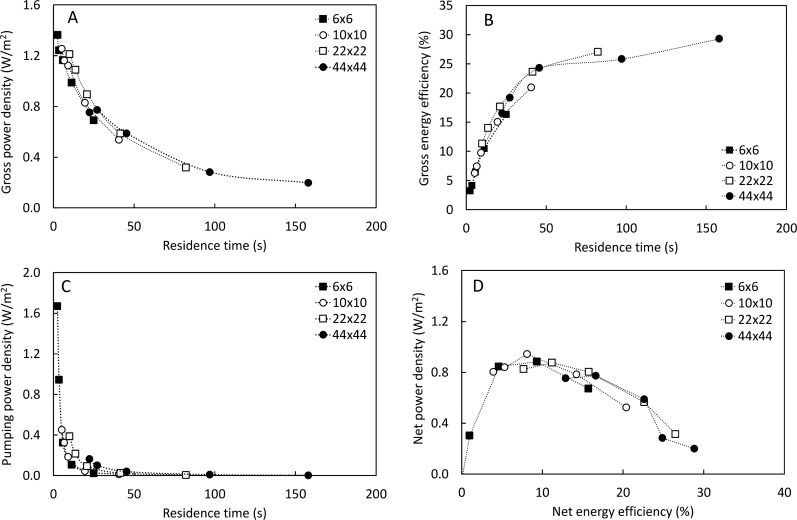
The gross power density and the gross energy efficiency against the residence time of the feedwater are plotted in panels A and B of Figure 2, respectively.
Figure 2.
RED performance indicators for all stack sizes at different flow velocities (0.25, 0.5, 1.0, 1.5, and 2.0 cm/s): (A) gross power density, (B) gross energy efficiency, and C) pumping power density vs residence time and (D) net power density vs net energy efficiency.
Figure 2A shows that stacks with different sizes and different flow velocities, but equipped with the same membranes and spacers, have an equal gross power density at equal residence times. The larger stack shows a slightly higher gross power density at the same residence time compared to that of the smaller stack. This is due to the fact that the larger stack needs a higher flow velocity to achieve the same residence time in the feedwater compartments, and thus concentration polarization effects are weaker.20 This higher velocity comes at the expense of an increased pumping energy (as presented later in Figure 2C). At low residence times (high velocities), only operation of the smaller stacks is possible as such high flow rates cannot be obtained in the larger stacks due to limitations of the pumping capacity. Consequently, the highest gross power density is achieved by the smallest stack (6 cm × 6 cm) at a residence time of 3 s (flow velocity of 2 cm/s). This is as expected, as at high flow velocities, the salinity gradient along the flow compartments and thus the voltage difference (the driving force) over the membranes for ion transport is high and maintained. At the other extreme, at high residence times (i.e., low flow velocities), the lowest gross power density is achieved by the largest stack (44 cm × 44 cm) at a residence time of 176 s (flow velocity of 0.25 cm/s). The gross energy efficiency, on the other hand, is highest at high residence times, i.e., for large stacks at low flow velocities (Figure 2B). Under fixed conditions, the residence time inside the stack determines to a large extent the amount of energy that can be extracted but at the same time also increases the amount of losses due to irreversible dissipation because of the internal resistance, concentration polarization, ionic shortcut currents, and osmotic transport.21
In Figure 2C, the consumed pumping power density is plotted versus the residence time. In general, the pumping power density decreases with an increase in residence time, i.e., decreasing flow velocity. Higher flow velocities result in higher friction and increased losses and consequently a higher pumping power density. Also, the smallest stack requires a higher pumping power density to pass the water through the compartments at the same flow velocity compared to that of the larger stacks because the major contribution to the hydrodynamic losses is located in the inlet of the stack and not along the feedwater compartment.8 Therefore, smaller stacks have relatively larger hydrodynamic losses. However, membrane areas are also smaller in smaller stacks, and consequently, the impact of stack size on pumping power density is marginal.
Figure 2D reports the net power density versus the net energy efficiency. The smaller stacks have high pumping energy densities at high velocities, and therefore, the power density is highly affected upon subtraction of the pumping power density needed to pass the solutions through the compartments from the gross power density to calculate the net power density. The large stacks on the other hand have lower pumping energy densities and are less affected by these losses. Remarkably, the results described above show that the stack design is highly scalable. Independent of the size of the stack, all performance indicators overlap, so when stacks with differents sizes but equal conditions are investigated, the residence time of the feed waters is a perfect indicator for comparison.11
Influence of Stack Size on Energy Efficiency at an Equal Flow Velocity
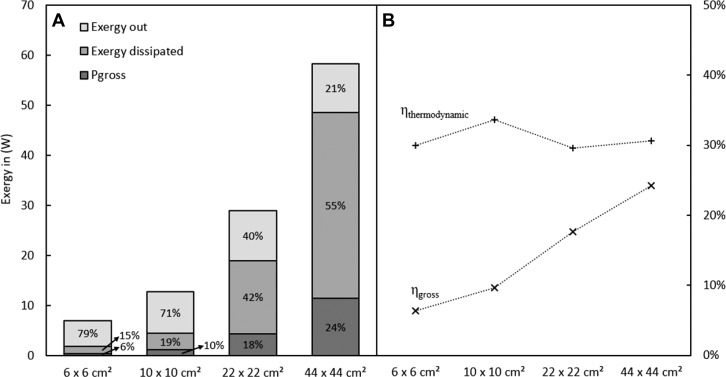
The total chemical energy supplied by the influent (exergyin) can be split into the power obtained as useful work (Pgross), the exergy dissipated or lost in the stack (exergydis), and the unused exergy (exergyout). The relative contribution of each of these terms is presented in Figure 3A for all stack sizes. The percentages mentioned in the bars in Figure 3A are the gross power, the exergy dissipated, and the exergy out relative to the total exergy in. In Figure 3B, the gross energy efficiency and the thermodynamic energy efficiency are plotted for all stack sizes. Stacks are all operated at the same flow velocity of 1 cm/s corresponding to residence times of 6, 10, 22, and 44 s for the 6 cm × 6 cm, 10 cm × 10 cm, 22 cm × 22 cm, and 44 cm × 44 cm stacks, respectively.
Figure 3.
(A) Available exergy in the influent split in gross power, exergy dissipated, and exergy out and (B) associated gross energy efficiency (ηgross) and thermodynamic energy efficiency (ηthermodynamic) for all stack sizes at a flow velocity of 1 cm/s.
Figure 3 shows that the amount of chemical energy supplied to each stack increases with an increasing stack size. As the flow velocity is the same for all stacks and the flow area for the larger stacks is larger than for the smaller stacks, the amount of chemical energy supplied to the larger stacks is larger. Moreover, the exergy supplied to the system is directly proportional to the absolute flow rate (and at an equal flow velocity to the inflow area) in each stack. The 6 cm × 6 cm stack is the least efficient stack with only 6% gross energy efficiency. Most of the exergy supplied is not dissipated or obtained but remains in the effluent as unused exergy. With an increasing stack size, the gross power or useful energy extracted from the system significantly increases and also the exergy dissipated increases, both at the expense of the percentage of unused energy (exergy out), which decreases with stack size. For the stack with a membrane area of 44 cm × 44 cm and the longest residence time, the gross energy efficiency is already 24% while the exergy dissipated is 55%, and thus, only 21% of the exergy supplied at the inlet is still available in the effluent as unused exergy. This gross energy efficiency increase with an increasing stack size is clearly visible in Figure 3.
The exergy dissipated includes, for example, the losses due to the use of non-ideal membranes that exhibit significant co-ion diffusion and water permeation. The levels of both co-ion diffusion and water permeation obviously increase with increasing residence times. The ratio of Pgross (due to desired controlled mixing) to dissipated exergy (due to undesired co-ion diffusion and water permeation) is equal for all stack sizes. This suggests that the ratio of controlled (to generate useful power) to uncontrolled (co-ion diffusion and water permeation) mixing is independent of the residence time and stack size.
During the experiments, RED stacks are operated by applying an external load maximizing the power output. Under this condition, a maximum of 50% of the total exergy supplied to the stacks at the influent can be harvested theoretically.21−24 Therefore, the maximum thermodynamic efficiency that a stack can achieve is 50%. When the stack is operating at maximum power density, the other 50% of the exergy will be dissipated by the stack internal resistances as irreversible loss. The thermodynamic efficiency can be increased by increasing the stack load relative to the stack internal resistance; however, this will reduce the power density, and therefore, a larger membrane area will be needed to achieve the same amount of power output.
The stacks presented in Figure 3B show an average thermodynamic efficiency of 31%. This thermodynamic efficiency is also the maximum gross energy efficiency that the stacks can achieve. The thermodynamic efficiency can be increased by minimizing all irreversible losses in the stacks. This is possible by using better membranes that are less sensitive to co-ion transport (i.e., have a higher permselectivity) and undesired water permeation. Moreover, at longer residence times, the thermodynamic efficiency can be increased by balancing the internal and external resistance along the path length of the stack. Although this last aspect is not investigated in this study, previous work showed that segmented electrodes with adjustable external resistances indeed allow optimization for maximal gross energy efficiency leading to a 15% increase in gross energy efficiency.23
Influence of Stack Configuration and Membrane Type
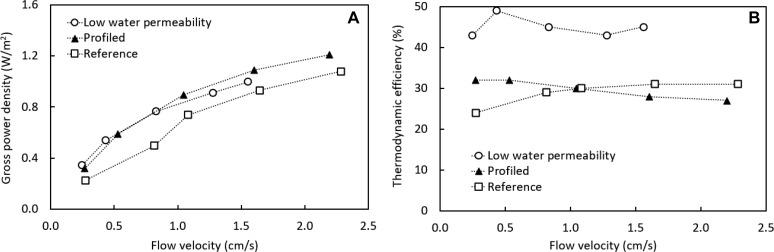
Continuing on reducing internal losses and increasing thermodynamic efficiency, we investigated the influence of membrane type and corresponding membrane properties (electrical resistance, permselectivity, and water permeability) and stack configuration (standard flat membranes and profiled membranes). Three stacks of equal size (22 cm × 22 cm) but equipped with different ion exchange membranes were used (see Table 2). Figure 4 reports the gross power density (A) and the thermodynamic efficiency (B) versus the flow velocity for the reference system, the system with profiled membranes instead of spacers (Profiled), and the systems equipped with membranes with low water permeabilities (Low water permeability).
Figure 4.
(A) Gross power density and (B) thermodynamic efficiency vs gross power density for all stack configurations.
The gross power density (Figure 4A) increases with flow rate for all membrane combinations investigated. At higher flow rates, there is a better resupply of feedwater, which keeps the concentration gradient along the length of the compartments high. Higher flow rates also improve the mixing and reduce the level of concentration polarization. The highest gross power density measured is achieved with the stack with profiled cation exchange membranes because of the lower ohmic resistance of the stack with profiled membranes. In such a stack, the membrane and the nonconductive net spacer together are replaced by an ion conductive profiled membrane integrating the membrane and spacer functionality.18 As no nonconductive net-spacers are used in such a system, less non-ion conductive material is used in the stack and therefore a lower internal stack resistance is obtained.25 Consequently, the use of profiled membranes improves the gross power density output.
The stack equipped with membranes with a lower water permeability and a higher permselectivity (type 10 AEM and CEM) has gross power densities comparable to those of the stack with profiled CEMs but power densities significantly higher than the values obtained for the stack equipped with the reference membranes (type I AEM and T1 CEM). The higher membrane resistance of these low-water permeability membranes apparently is counterbalanced by the increased voltage difference over the membranes due to the lower water permeability and higher permselectivity, especially at low flow rates. Unfortunately, low-water permeability type 10 profiled membranes are not available, but if these were to exist, an even stronger increase in gross power energy output would be expected because of the decrease in stack resistance.
In terms of thermodynamic efficiency on the other hand, the behavior changes drastically (Figure 4B). The thermodynamic efficiency is rather independent of the flow velocity, as the thermodynamic efficiency is based on the chemical energy supplied to the stack (exergy in–exergy out) (see eq 6). The stack equipped with membranes with a low water permeability has a thermodynamic efficiency much higher than those of the other two stacks equipped with standard membranes. This high thermodynamic efficiency is a result of the improved membrane properties, which reduce the extent of water permeation and co-ion diffusion. Consequently, the salinity gradient is not irreversibly lost because of unwanted mixing by co-ion diffusion and water permeation. With an average thermodynamic efficiency of 44.9%, the stack with the low-water permeability membranes operates close to the maximum of 50% that can be achieved when operating at maximum power.
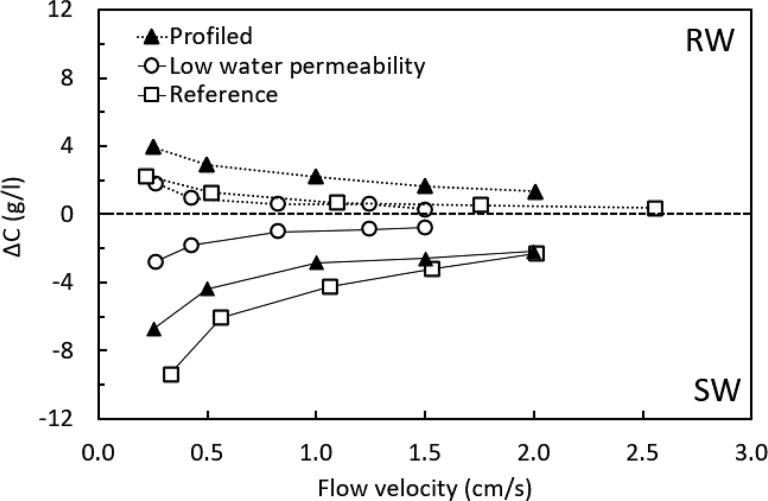
The undesired mixing due to water permeation and co-ion diffusion is shown in more detail in Figure 5. In this figure, the change in concentration over the inlet and outlet of the stack compartments, i.e., river water (RW) and seawater (SW), under open circuit conditions (Y-axis) is plotted at different flow velocities (X-axis) for all stack configurations (stack size of 22 cm × 22 cm). Under open circuit conditions, there is no desired ion transport from seawater to river water as there is no current. Therefore, the change in concentration over the length of the stack due to desired ion transport is zero. In that situation, only undesired, uncontrolled water permeation and co-ion transport occur, resulting in a change in the concentration in both the seawater and the river water compartment over the length of the stack, indicated as undesired losses. As such, Figure 5 thus quantifies the net effect of undesired water permeation and co-ion diffusion and thus the undesired losses in the three stacks at different flow rates.
Figure 5.
Concentration difference between the inlet and the outlet of both the river water (RW) and the seawater (SW) compartment under open circuit conditions vs the flow velocity for all stack configurations and flow. The stack size is 22 cm × 22 cm.
In an ideal situation with perfect, 100% selective non-water-permeable membranes, this change in concentration over the length of the stack would be zero (no losses). However, when using non-ideal membranes, the concentrations will change due to water permeation because of osmosis and co-ion diffusion.26 When the change in concentration is due to co-ion diffusion, the change in concentration will be symmetrical for both compartments, because in that case only ions will be transported. As such, the decrease in concentration difference between the inlet and the outlet of one feed compartment will be exactly equal to the increase in concentration difference between the inlet and the outlet of the other feed compartment. On the other hand, when the change in concentration between the inlet and the outlet is a result of osmotic water permeation, the change between both compartments is asymmetrical. The reason for this is that the impact of water transport is higher in the seawater compartment (due to its higher concentration) than in the river water compartment (which has a low concentration).
From Figure 5, all membranes suffer from undesired water permeation and co-ion diffusion (i.e., undesired losses), as the concentration change under open circuit conditions is not equal to zero. Obviously, this effect is smaller when a membrane with a low water permeability and a high ion selectivity (i.e., low co-ion diffusion) is used. Also, in all cases, an increase in flow velocity decreases the losses due to the reduced residence times at higher flow velocities. As for the reference membranes and the profiled membranes, the change in concentration with flow rate is nonsymmetrical; losses predominantly stem from undesired water permeation. For the stack equipped with optimized membranes with low levels of water permeation and co-ion diffusion, the change in concentration for both water compartments is much more symmetrical, suggesting that losses mainly stem from co-ion diffusion.
Outlook
In this study, the effect of stack size and membrane type on performance indicators in RED is studied. The influence of stack size on the power density, energy efficiency, and pumping power density can be directly related to the residence time of the feedwater in the stack. At equal residence times, data of all stacks with different sizes overlap. As such, the residence time is an excellent parameter to compare differently sized stacks and to translate lab scale experimental results to those of larger pilot stacks. Also, the influence of water permeability and permselectivity is clearly visible when measuring the thermodynamic efficiency. An averaged thermodynamic efficiency of 44.9% is measured using Fujifilm type 10 AEM and CEM membranes that have low water permeability and high permselectivity. This value comes close to the thermodynamic maximum of 50%.
Acknowledgments
This work was performed in the TTIW-cooperation framework of Wetsus, European Centre of Excellence for Sustainable Water Technology (www.wetsus.nl). Wetsus is funded by the Dutch Ministry of Economic Affairs, the European Union Regional Development Fund, the Province of Fryslân, the City of Leeuwarden, and the Northern Netherlands provinces. Several projects of REDstack are also co-funded by these organizations. The authors thank Elisa Huerta, Damnearn Kunteng, and Chris Coutinho for the discussions and the participants of the research theme “Blue Energy” for the fruitful collaboration and their financial support. The authors sincerely thank the participants of the “Blue Energy” research theme for the strong collaboration, the many fruitful discussions, and the financial support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.8b01886.
(PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Weinstein J. N.; Leitz F. B. Electric Power from Differences in Salinity: The Dialytic Battery. Science (Washington, DC, U. S.) 1976, 191 (4227), 557–559. 10.1126/science.191.4227.557. [DOI] [PubMed] [Google Scholar]
- Logan B. E.; Elimelech M. Membrane-Based Processes for Sustainable Power Generation Using Water. Nature 2012, 488 (7411), 313–319. 10.1038/nature11477. [DOI] [PubMed] [Google Scholar]
- Loeb S.; Van Hessen F.; Shahaf D. Production of Energy from Concentrated Brines by Pressure-Retarded Osmosis, II. Experimental Results and Projected Energy Costs. J. Membr. Sci. 1976, 1, 249–269. 10.1016/S0376-7388(00)82271-1. [DOI] [Google Scholar]
- Gerstandt K.; Peinemann K. V.; Skilhagen S. E.; Thorsen T.; Holt T. Membrane Processes in Energy Supply for an Osmotic Power Plant. Desalination 2008, 224, 64–70. 10.1016/j.desal.2007.02.080. [DOI] [Google Scholar]
- Brogioli D.; Zhao R.; Biesheuvel P. M. A Prototype Cell for Extracting Energy from a Water Salinity Difference by Means of Double Layer Expansion in Nanoporous Carbon Electrodes. Energy Environ. Sci. 2011, 4 (3), 772–777. 10.1039/c0ee00524j. [DOI] [Google Scholar]
- Brogioli D. Extracting Renewable Energy from a Salinity Difference Using a Capacitor. Phys. Rev. Lett. 2009, 103, 058501. 10.1103/PhysRevLett.103.058501. [DOI] [PubMed] [Google Scholar]
- Vermaas D. A.; Kunteng D.; Saakes M.; Nijmeijer K. Fouling in Reverse Electrodialysis under Natural Conditions. Water Res. 2013, 47 (3), 1289–1298. 10.1016/j.watres.2012.11.053. [DOI] [PubMed] [Google Scholar]
- Moreno J.; Slouwerhof E.; Vermaas D. A. A.; Saakes M.; Nijmeijer K. The Breathing Cell: Cyclic Intermembrane Distance Variation in Reverse Electrodialysis. Environ. Sci. Technol. 2016, 50 (20), 11386–11393. 10.1021/acs.est.6b02668. [DOI] [PubMed] [Google Scholar]
- Kim H.-K.; Lee M.-S.; Lee S.-Y.; Choi Y.-W.; Jeong N.-J.; Kim C.-S. High Power Density of Reverse Electrodialysis with Pore-Filling Ion Exchange Membranes and a High-Open-Area Spacer. J. Mater. Chem. A 2015, 3 (31), 16302–16306. 10.1039/C5TA03571F. [DOI] [Google Scholar]
- Vermaas D. A.; Saakes M.; Nijmeijer K. Doubled Power Density from Salinity Gradients at Reduced Intermembrane Distance. Environ. Sci. Technol. 2011, 45 (16), 7089–7095. 10.1021/es2012758. [DOI] [PubMed] [Google Scholar]
- Veerman J.; Saakes M.; Metz S. J.; Harmsen G. J. Electrical Power from Sea and River Water by Reverse Electrodialysis: A First Step from the Laboratory to a Real Power Plant. Environ. Sci. Technol. 2010, 44 (23), 9207–9212. 10.1021/es1009345. [DOI] [PubMed] [Google Scholar]
- Tedesco M.; Scalici C.; Vaccari D.; Cipollina A.; Tamburini A.; Micale G. Performance of the First Reverse Electrodialysis Pilot Plant for Power Production from Saline Waters and Concentrated Brines. J. Membr. Sci. 2016, 500, 33–45. 10.1016/j.memsci.2015.10.057. [DOI] [Google Scholar]
- Tedesco M.; Cipollina A.; Tamburini A.; Micale G. Towards 1 kW Power Production in a Reverse Electrodialysis Pilot Plant with Saline Waters and Concentrated Brines. J. Membr. Sci. 2017, 522, 226–236. 10.1016/j.memsci.2016.09.015. [DOI] [Google Scholar]
- Vermaas D. A.; Veerman J.; Yip N. Y.; Elimelech M.; Saakes M.; Nijmeijer K. High Efficiency in Energy Generation from Salinity Gradients with Reverse Electrodialysis. ACS Sustainable Chem. Eng. 2013, 1 (10), 1295–1302. 10.1021/sc400150w. [DOI] [Google Scholar]
- Yip N. Y.; Elimelech M. Thermodynamic and Energy Efficiency Analysis of Power Generation from Natural Salinity Gradients by Pressure Retarded Osmosis. Environ. Sci. Technol. 2012, 46 (9), 5230–5239. 10.1021/es300060m. [DOI] [PubMed] [Google Scholar]
- Rijnaarts T.; Huerta E.; van Baak W.; Nijmeijer K. Effect of Divalent Cations on RED Performance and Cation Exchange Membrane Selection to Enhance Power Densities. Environ. Sci. Technol. 2017, 51, 13028. 10.1021/acs.est.7b03858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Post J. W.; Veerman J.; Hamelers H. V. M. M.; Euverink G. J. W. W.; Metz S. J.; Nymeijer K.; Buisman C. J. N. N. Salinity-Gradient Power: Evaluation of Pressure-Retarded Osmosis and Reverse Electrodialysis. J. Membr. Sci. 2007, 288 (1–2), 218–230. 10.1016/j.memsci.2006.11.018. [DOI] [Google Scholar]
- Vermaas D. A.; Saakes M.; Nijmeijer K. Power Generation Using Profiled Membranes in Reverse Electrodialysis. J. Membr. Sci. 2011, 385–386 (0), 234–242. 10.1016/j.memsci.2011.09.043. [DOI] [Google Scholar]
- Veerman J.; de Jong R. M.; Saakes M.; Metz S. J.; Harmsen G. J. Reverse Electrodialysis: Comparison of Six Commercial Membrane Pairs on the Thermodynamic Efficiency and Power Density. J. Membr. Sci. 2009, 343 (1–2), 7–15. 10.1016/j.memsci.2009.05.047. [DOI] [Google Scholar]
- Yip N. Y.; Vermaas D. A.; Nijmeijer K.; Elimelech M. Thermodynamic, Energy Efficiency, and Power Density Analysis of Reverse Electrodialysis Power Generation with Natural Salinity Gradients. Environ. Sci. Technol. 2014, 48 (9), 4925–4936. 10.1021/es5005413. [DOI] [PubMed] [Google Scholar]
- Veerman J.; Post J. W. W.; Saakes M.; Metz S. J. J.; Harmsen G. J. J. Reducing Power Losses Caused by Ionic Shortcut Currents in Reverse Electrodialysis Stacks by a Validated Model. J. Membr. Sci. 2008, 310 (1–2), 418–430. 10.1016/j.memsci.2007.11.032. [DOI] [Google Scholar]
- Veerman J.; Saakes M.; Metz S. J.; Harmsen G. J. Reverse Electrodialysis: Performance of a Stack with 50 Cells on the Mixing of Sea and River Water. J. Membr. Sci. 2009, 327 (1–2), 136–144. 10.1016/j.memsci.2008.11.015. [DOI] [Google Scholar]
- Veerman J.; Saakes M.; Metz S. J. J.; Harmsen G. J. J. Reverse Electrodialysis: A Validated Process Model for Design and Optimization. Chem. Eng. J. 2011, 166 (1), 256–268. 10.1016/j.cej.2010.10.071. [DOI] [Google Scholar]
- Kim D.-K.; Duan C.; Chen Y.-F.; Majumdar A. Power Generation from Concentration Gradient by Reverse Electrodialysis in Ion-Selective Nanochannels. Microfluid. Nanofluid. 2010, 9 (6), 1215–1224. 10.1007/s10404-010-0641-0. [DOI] [Google Scholar]
- Długołęcki P. E.; Dąbrowska J.; Nijmeijer K.; Wessling M. Ion Conductive Spacers for Increased Power Generation in Reverse Electrodialysis. J. Membr. Sci. 2010, 347 (1–2), 101–107. 10.1016/j.memsci.2009.10.011. [DOI] [Google Scholar]
- Tedesco M.; Hamelers H. V. M; Biesheuvel P. M. Nernst-Planck Transport Theory for (Reverse) Electrodialysis: II. Effect of Water Transport through Ion-Exchange Membranes. J. Membr. Sci. 2017, 531, 172–182. 10.1016/j.memsci.2017.02.031. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.