Statistical Models of Signal and Noise and Fundamental Limits of Segmentation Accuracy in Retinal Optical Coherence Tomography

Abstract

Optical coherence tomography (OCT) has revolutionized diagnosis and prognosis of ophthalmic diseases by visualization and measurement of retinal layers. To speed up quantitative analysis of disease biomarkers, an increasing number of automatic segmentation algorithms have been proposed to estimate the boundary locations of retinal layers. While the performance of these algorithms has significantly improved in recent years, a critical question to ask is how far we are from a theoretical limit to OCT segmentation performance. In this paper, we present the Cramèr-Rao lower bounds (CRLBs) for the problem of OCT layer segmentation. In deriving the CRLBs, we address the important problem of defining statistical models that best represent the intensity distribution in each layer of the retina. Additionally, we calculate the bounds under an optimal affine bias, reflecting the use of prior knowledge in many segmentation algorithms. Experiments using in vivo images of human retina from a commercial spectral domain OCT system are presented, showing potential for improvement of automated segmentation accuracy. Our general mathematical model can be easily adapted for virtually any OCT system. Further, the statistical models of signal and noise developed in this paper can be utilized for future improvements to OCT image denoising, reconstruction, and many other applications.

I. Introduction

Optical coherence tomography (OCT) is a photonic imaging technology developed in the early 1990s for 3-dimensional imaging of reflectance [1]. OCT can be viewed as an optical analogue to ultrasound, in that it rejects multiple-scattered photons based on their arrival time. This is accomplished using an interferometer and either a broadband or wavelength-swept light source. OCT acquires a depth profile of reflectance, or A-scan, at a single location and then laterally samples the region of interest to produce a cross-sectional or volumetric image. A-scans in a single plane are frequently grouped together into 2-D images known as B-scans. Modern clinical OCT systems acquire the entire A-scan simultaneously using a technique called Fourier Domain OCT (FD-OCT). FD-OCT can be performed either in the spectral domain (SD) using a broadband source and a spectrometer, or using a spectrally swept source (SS). OCT has been adapted for a variety of applications including diagnosis and prognosis of cancer [2], [3], cardiovascular diseases [4], [5], and neurodegenerative diseases [6], [7].

The highest-impact application of OCT is the diagnosis of ophthalmic diseases, including age-related macular degeneration (AMD) [8], [9], diabetes [10]–[12] and glaucoma [13], [14]. A critical task for retinal diagnostics is segmentation of the retina into its anatomical layers, which correspond to different functional regions. An OCT image of the retina with expert manual segmentation is shown in Figure 1.

Fig. 1.

Manually segmented 2-D OCT image (B-scan) of the retina, centered on the fovea. The layers shown are the vitreous, the nerve fiber layer (NFL), the ganglion cell layer (GCL) and inner plexiform layer (IPL) complex, the inner nuclear layer (INL), the outer plexiform layer (OPL), the outer nuclear layer (ONL) and photoreceptor inner segment (IS), the photoreceptor outer segment (OS), the retinal pigment epithelium (RPE), and the choroid.

Manual segmentation of large OCT datasets requires significant time and attention from expert graders. Therefore, several techniques have been developed to automatically segment the layers of retinal OCT images. These include boundary tracking/dynamic programming (Djikstra’s algorithm) techniques [15]–[17], pixel classification [18], active contours [19], [20], graph search [8], [21], kernel regression [10], and deep learning [22], [23]. These segmentation algorithms are benchmarked against expert manual graders, the current gold standard. While the performance of these algorithms has been significantly improved in the recent years, a critical question has not yet been addressed: “how far is OCT segmentation performance from its theoretical limit?” The answer to this question justifies further investment of time and financial resources to gain further segmentation accuracy.

A popular tool for determining the theoretically achievable accuracy of an estimator is the Cramèr-Rao Lower Bound (CRLB). The CRLB has been extensively used to quantify the performance limits of image processing tools such as image denoising [24], registration [25], particle displacement [26], frequency estimation [27], digital super-resolution [28], signal-to-noise ratio (SNR) estimation [29], stellar photometry [30], ballistic photon based object detection in scattering media [31], and spectral peak estimation [32]. The CRLB has also been used previously to evaluate the performance of several segmentation methods [33]–[36]. Two of these methods are of particular interest for the segmentation of retinal OCT images: determining the location of changes in a steplike signal [35] and the more general problem of 2D image segmentation [36].

The work of [35] provides a useful point of reference, because the layer boundaries in an OCT A-scan can be modeled as steplike changes. However, this method does not perfectly match the problem at hand, because the shape of a steplike change in OCT comes from the convolution of a step function with a system-specific point spread function (PSF), usually modeled as a Gaussian [37]. This convolution yields an error function-shaped curve, whereas [35] uses a logistic curve. Moreover, [35] assumes an un ed estimator, which does not reflect a priori models utilized in many modern image segmentation algorithms. The work of [36] provides an excellent general framework for fuzzy segmentation of 2D images and introduces an optimal affine bias model to determine the CRLB for biased operators. However, as we discuss below, the layered structure of the retina lends itself better to non-fuzzy segmentation.

An additional critical shortcoming that precludes direct application of the studies in [35] and [36] to OCT images is their simplistic modeling of noise as uniform additive white Gaussian (UAWG). While UAWG is a reasonable model for some consumer electronic imaging applications, this is not an accurate model of noise in OCT images. This is because at least two processes, detection noise and speckle, affect OCT images.

The detection noise results from many sources and has a lower limit determined by shot noise (i.e. bandlimited quantum noise). In FD-OCT, the detection noise can be approximated as an additive circular complex Gaussian produced by the detection process [37]. Speckle is an artifact of coherent imaging processes; it is deterministic based on the interaction of light with subvoxel features and is best modeled as multiplicative noise [38]. Henceforth in this paper, we will refer to the value of the observed signal (including noise) as intensity, in keeping with standard image processing terminology. This intensity is linearly proportional, but not equivalent, to the optical intensity of the backscattered light.

Various probability density functions (PDFs) of the intensity have been proposed to model speckle in OCT. The negative exponential distribution [39]–[42] and the gamma distribution [43]–[45] are among the more popular models. More recently, the negative exponential distribution and the K distribution have been compared for modeling OCT intensity in microsphere phantoms and skin [46], [47]. However, there has not been a full, comparative accounting of all the suggested distributions on a commercially available OCT system, especially for in vivo human retinal OCT images.

Multiple manuscripts in the literature have now specifically used noise distributions for OCT denoising [41], [42]. Both Ralston et al. [41] and Yin et al. [42] derive OCT denoising methods by modeling the noise as Gaussian in the log domain. However, the Gaussian distribution has not been empirically and statistically validated in the retina. Indeed, we will show below that it is possible to reject the Gaussian distribution with statistical significance. Therefore, we hope to provide superior and validated noise distributions both to calculate the CRLB and so that other techniques may be improved.

Notably, none of these studies take into account the effect of detection noise. Moreover, as the cellular composition varies between different retinal layers, a single distribution might not efficiently model the speckle pattern in each layer.

We note that a recent paper has attempted to statistically model noise in retinal OCT images with Normal-Laplace PDF, which is shown to have a lower chi-square error than Gaussian [48]. However, neither distribution is a good fit to their experimental data, as is evident in Fig. 4 of [48]. The denoising technique described in [48] is an example of the applications which we hope will benefit from using empirically validated noise distributions.

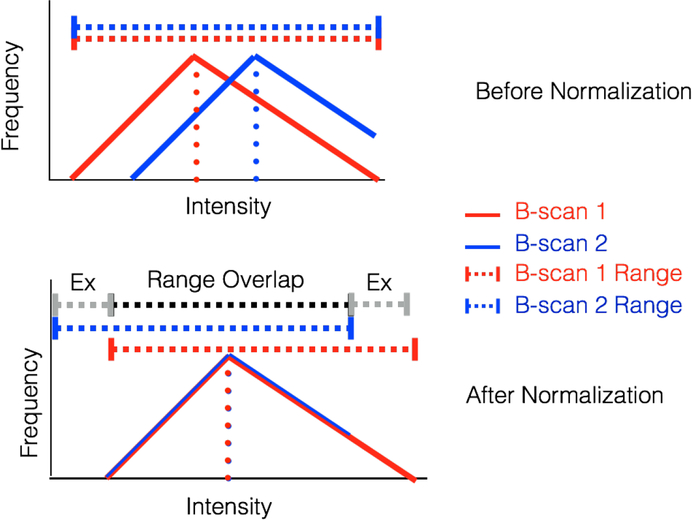
Fig. 4.

Schematic diagram of B-scan intensity normalization and range exclusion. The diagram shows the histograms of two layers before and after normalization (top and bottom, respectively). Before normalization, the histograms have the same shape and range but are separated; after normalization, the histograms overlap but the ranges have shifted. The range used in analysis is the intersection of all ranges, denoted in black; the ranges excluded from analysis are denoted in grey.

The novelty of our paper is as follows: 1) we developed physically derived and empirically validated layer-specific statistical models of the intensity in retinal OCT images; 2) using these models, we calculated the unbiased and biased CRLB for estimating the layer boundary locations in retinal OCT images. The impact of our paper goes beyond ophthalmic OCT applications as our proposed approach is general and can be adopted for modeling many other speckle dominated imaging scenarios.

The rest of the paper is organized as follows: Section II describes our calculation of the unbiased CRLB for OCT A-Scans and the biased CRLB for OCT B-scans. Section III describes our use of clinical OCT images to construct empirical statistical models of intensity. The results of both the modeling and the CRLB calculations are described in Section IV. Finally, in Section V, we discuss the results in context of the previous literature.

II. Boundary Segmentation CRLB for Layered Structures

Given a noisy signal g[k; h] dependent on a parameter vector h and position k, the CRLB states that the covariance of an unbiased estimator of h is bounded by:

$$\text{Cov\hspace{0.17em}}\left[\widehat{h}\right]\ge J^{-1},$$ (1)

where J is the Fisher information matrix. The elements of J are given by

$$J_{ij}={\displaystyle \sum }_k\text{E\hspace{0.17em}}\left[-\frac{{\partial }^2\text{\hspace{0.17em}ln}\left(p\left(g\left[k;h\right],k\right)\right)}{\partial h_i\partial h_j}\right],$$ (2)

where E[] is the expected value operator, p(g[k; h], k) is the probability of observing the intensity g[k; h] at position k and h_i and h_j are the ith and jth elements of h [49].

A. Calculation of Unbiased CRLB at Layer Boundaries in Single A-scan

In this section, we define our signal model for OCT A-scans. Then, based on that signal model, we derive a expression for the unbiased CRLB of a single-layer boundary position estimate. Taking into account both additive detection noise w_add[k; h] and speckle w_sp[k; h], the observed intensity of an OCT A-scan can be modeled as

$$\begin{array}{lll}g\left[k;h\right]\hfill & =\hfill & s\left[k;h\right]w_{\text{sp}}\left[k;h\right]+w_{\text{add}}\left[k;h\right]\hfill \\ \hfill & =\hfill & s_0\left(\left|\text{PSF\hspace{0.17em}}\left(k/f_s\right)\right|\otimes R\left(\frac{k}{2f_s};h\right)\right)w_{\text{sp}}\left[k;h\right]+w_{\text{add}}\left[k;h\right],\hfill \end{array}$$ (3)

where s[k; h] is the noiseless intensity at depth pixel number k, f_s is the axial spatial sampling frequency such that the optical depth is k/f_s, s₀ is a constant factor related to the system configuration, PSF(k/f_s) is the OCT axial PSF, R(k/f_s; h) is the depth reflectivity profile of the sample, and ⊗ is the convolution operator [37].

Each g[k; h] is a random variable with PDF p(g[k; h]) determined by s[k; h] and the PDFs of the additive and multiplicative noise processes. We rewrite this noise as purely additive to enhance mathematical tractability. This is accomplished by expressing g[k; h] as a fixed mean intensity $\overline{g}\left[k;\mathbf{h}\right]$ plus a random noise variable w[k; h] with a zero expected value (ZEV) PDF $q\left(w\left[k;\mathbf{h}\right]\right)=p\left(w\left[k;\mathbf{h}\right]+\overline{g}\left[k;\mathbf{h}\right],k\right)$.

To apply the CRLB to OCT segmentation, we first consider a model dependent only on a single parameter, the position of the ith layer boundary z_i. We model the noiseless signal in a single A-scan near the ith boundary as a Heaviside step function H(x) at position z_i convolved with a Gaussian OCT PSF [37]:

$$s_i\left[k;z_i\right]=A{\text{log}}_{10}\left[\left(I_i+\left(I_{i+1}-I_i\right)H\left(\frac{k}{f_s}-z_i\right)\right)\otimes \frac{1}{\sqrt{2\pi }{\sigma }_{\text{PSF}}}\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-\frac{{\left(k/f_s\right)}^2}{2{\sigma }_{\text{PSF}}^2}\right)\right]$$ (4)

$$=A{\text{log}}_{10}\frac{1}{2}\left[I_i\left(1+\text{\hspace{0.17em}erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)\right)\right]+A{\text{log}}_{10}\frac{1}{2}\left[I_{i+1}\left(\text{erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)\right)\right],$$ (5)

where A is a system-dependent scaling factor, I_i and I_i+1 are the average intensities of the layers above and below the boundary, σ_PSF is the standard deviation of the axial PSF, erf() is the error function, and erfc() is the complementary error function. Additionally, because most OCT images are viewed in the log domain to enhance the visibility of dimmer layers [50], we carry out these calculations in the log domain.

We make two physically and anatomically rational assumptions about noise in retinal layers. First, we note that the cellular and sub-cellular structures in each layer differ in shape and size. Thus, each layer has unique speckle characteristics and the noise is not stationary for the whole image. Moreover, because of optical blurring, the noise smoothly transitions from one layer’s noise PDF to the other. Therefore, we treat the noise PDF near the ith layer boundary w_i[k; z_i] as

$$w_i\left[k;z_i\right]=n_i\left[k\right]\frac{1}{2}\left(1+\text{\hspace{0.17em}erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)\right)+n_{i+1}\left[k\right]\frac{1}{2}\left(\text{erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)\right),$$ (6)

where n_i and n_i+1 are the noise in layer i and i + 1, respectively, and each n_i is drawn from a ZEV PDF q_i(n_i).

The observed signal near the ith layer boundary g_i[k; z_i] is therefore:

$$g_i\left[k;z_i\right]=A{\text{log}}_{10}\left[I_i+\frac{I_{i+1}-I_i}{2}\text{erf\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)\right]+n_i\left[k\right]\frac{1}{2}\left(1+\text{\hspace{0.17em}erf\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2{\sigma }_{\text{PSF}}}}\right)\right)+n_{i+1}\left[k\right]\frac{1}{2}\left(\text{erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2{\sigma }_{\text{PSF}}}}\right)\right).$$ (7)

The PDF of g_i[k; z_i] is then:

$$p\left(g_i\left[k;z_i\right]\right)=\frac{1}{2}\left(1+\text{\hspace{0.17em}erf\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2{\sigma }_{\text{PSF}}}}\right)\right)q_i\left(g\left[k\right]-s\left[k;z_i\right]\right)+\frac{1}{2}\text{erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)q_{i+1}\left(g\left[k\right]-s\left[k;z_i\right]\right).$$ (8)

To calculate the CRLB, we use the scalar version of Eq. (2) for a single variable h [49]:

$$J_h={\displaystyle \sum }_k\text{E\hspace{0.17em}}\left[{\left(\frac{\partial \text{\hspace{0.17em}ln}\left(p\left(g_i\left[k\right]\right)\right)}{\partial h}\right)}^2\right].$$ (9)

We then calculate the Fisher Information for each layer boundary:

$$\begin{array}{lll}{J}_{z_i}\hfill & =\hfill & \sum _k\text{E\hspace{0.17em}}\left[{\left(\frac{\partial \text{\hspace{0.17em}ln}\left(p\left(g_i\left[k\right],k\right)\right)}{\partial z_i}\right)}^2\right]\hfill \\ \hfill & =\hfill & {\displaystyle \sum }_k\underset{w_i\left[k\right]=-\infty }{\overset{\infty }{{\displaystyle \int }}}\frac{1}{p{\left(g_i\left[k\right],k\right)}^2}{\left[\frac{e^{-{\left(k/f_s-z_i\right)}^2/{\sigma }_{\text{PSF}}^2}}{\sqrt{2\pi }{\sigma }_{\text{PSF}}}\left(-q_i\left(w_i\left[k\right]\right)+q_{i+1}\left(w_i\left[k\right]\right)\right)\frac{1}{2}\frac{\partial s_i\left[k;z_i\right]}{\partial z_i}\left(\left[1+\text{\hspace{0.17em}erf\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)\right]q_i^{\prime }\left(w_i\left[k\right]\right)-\text{\hspace{0.17em}erfc\hspace{0.17em}}\left(\frac{k/f_s-z_i}{\sqrt{2}{\sigma }_{\text{PSF}}}\right)q_{i+1}^{\prime }\left(w_i\left[k\right]\right)\right)\right]}^{2}d{w}_i,\hfill \end{array}$$ (10)

where $q_i^{\prime }\left(n_i\right)=\frac{\partial }{\partial n_i}{q}_i\left(n_i\right)$. For many non-Gaussian noise distributions, the above integral cannot be evaluated analytically. In such cases, we numerically calculated the integral in Mathematica.

B. Biased CRLBs for Segmentation of B-scans

Most OCT layer segmentation algorithms achieve improved performance by utilizing a priori information and thus are categorized as biased estimators. These include the popular assumption that the layer boundaries are smooth, which can be exploited by analyzing a whole B-scan rather than an individual A-scan [15], [16], [51]. Biased estimators can lead to improved performance, defined as reduced mean square error (MSE) [52]. Thus, to further broaden the applicability of our bounds, we extend our CRLB findings to the case of biased estimators.

Our approach follows Peng and Varshney’s [36] use of an optimal affine bias model to determine the CRLB for a biased fuzzy segmentation estimator. The optimal affine bias CRLB puts a bound on the covariance of a biased estimate ĥ of a parameter vector h. If the bias ψ = E[ĥ] − h is affine, i.e. ψ = Kh + u, then it can be shown that the covariance of ĥ is bounded by [36]

$$\text{Cov\hspace{0.17em}}\left[\widehat{h}\right]\ge CRL{B}_{\text{Biased}}=J^{-1}-J^{-1}{\left(J^{-1}+\text{\hspace{0.17em}Cov\hspace{0.17em}}\left[h\right]\right)}^{-1}{J}^{-1}.$$ (11)

We justify the use of an affine bias model for a whole B-scan in Appendix A. When segmenting a whole B-scan, the parameter vector h contains all eight layer boundary locations in each constitutent A-scan. Consequently, the diagonal elements of J⁻¹ are the unbiased CRLBs for each layer boundary, repeated for every A-scan. The diagonal of CRLB_Biased gives the lower bound on the variance of the layer boundary positions across the B-scan. We average the bound across the B-scan for each boundary to obtain an average bound for a biased estimator, which is a useful comparison to the position-independent bound for an unbiased estimator.

We estimate Cov [h] using the same set of expert segmented B-scans used for generating the empirical distributions (see Section III-A). We use a statistical bootstrapping technique as per Peng and Varshney [36] to generate more accurate estimates of the covariance. Starting with 100 B-scans as sample data, we picked 100 B-scans with replacement and calculated the covariance of the boundary locations between the B-scans. We repeated this procedure 100 times and averaged the covariance matrices from each set of generated data to give an accurate estimate of the true covariance matrix of boundary positions in B-scans.

III. Empirical Model of OCT Intensity

In this section, we describe our method to construct an empirical, layer-specific model of the signal and noise in retinal OCT images. First, we discuss the acquisition and segmentation of the data. Then, we discuss the data processing performed to generate accurate representations of intensity across the entire population. Next, we discuss the different distributions and parameter selection process for modeling the retinal layers. Finally, we discuss how to choose the best model and estimate the mean intensity and ZEV noise PDF for each layer. The steps of this process are shown in Figure 2.

Fig. 2.

Schematic indicating the process by which we construct empirical, layer-specific intensity models.

A. Collection and Processing of OCT Data

While our technique to obtain layer-specific intensity models is general, for this study we utilized an SD-OCT system from Bioptigen Inc. (Research Triangle Park, NC). We chose this system because it is commercially available, performs minimal image processing, and offers ready access to raw data.

We acquired volumetric scans (6.7 × 6.7 mm) from 10 normal adult subjects under an IRB approved protocol. The Bioptigen SD-OCT system had a Gaussian axial PSF with a full-width at half-maximum (FWHM) resolution of 4.6 μm (in tissue), an axial pixel sample spacing of 3.23 μm, and a total axial depth range of 3.3 mm. The illumination from the SD-OCT had a central wavelength of 830 nm with a FWHM bandwidth of 50 nm. The volumetric scans had lateral and azimuthal pixel sampling spacings of 6.7 μm and 67 μm (1000 A-scans scans per B-scan, 100 B-scans per volume), respectively [15]. Each B-scan was cropped laterally to the central 800 A-scans, for a final image size of 800 × 1024. The intensity of each voxel in the volume was represented by a 16-bit integer normalized from 0 to 255.

A grader semi-automatically segmented 10 evenly spaced B-scans from each subject by using DOCTRAP software [9]. In some layers, blood vessels and specular reflections led to intensity distortions above and below the vessel. Therefore, a separate grader manually removed A-scans containing large vessels or specular reflections. We excluded these A-scans from the subsequent analysis. An example of an excluded vessel is shown in the green box of Figure 3.

Fig. 3.

Raw OCT B-scan showing a retinal ghost/autocorrelation artifact (red box) and intensity distortions from blood vessels (green box).

Additionally, particularly bright images can yield autocorrelation artifacts in OCT images [37]. The result of this is a ghost image of the retina with a prominent peak corresponding to the autocorrelation between the NFL and the RPE, at a depth determined by the difference between the RPE and NFL depths. Manual examination of the OCT images indicated that the autocorrelation artifact only occupies the top 0.55 mm of the 3.3 mm-deep scan. In most OCT images, the OCT photographer attempts to ensure that the NFL does not overlap with the autocorrelation artifact. Therefore, to represent the typical OCT image, we ignored any pixels in the top 0.55 mm of the B-scans. An example of an autocorrelation artifact is shown in the red box of Figure 3.

B. Normalization of B-scans

Differences in beam placement, ocular or corneal clarity, or other factors may change the recorded intensity from the layers of the retina by a constant multiplicative factor between B-scans from a single subject, as well as between subjects. Additionally, different amounts of absorption or scattering in OCT images can lead to a secondary, layer-specific multiplicative factor. In the log domain, this appears as a constant increase or decrease of all pixel intensities in a particular B-scan or layer, as illustrated schematically in Figure 4.

To compensate for this imaging artifact, we calculated the average intensity of each layer across all B-scans. We then added a constant value to the same layer region of each B-scan so that its average intensity value is equal to the global average intensity for that layer. As shown in Figure 4, this procedure results in a different gray-scale range for each post-normalization layer. Therefore, when considering the combined intensity histograms of multiple layers (see Section III-C), we ignored post-normalization gray-scale values that were not within the range of all other layers.

C. Generation of OCT Intensity Histograms

For each B-scan, we utilized the segmented retinal layer boundaries to isolate individual layers. First, we isolated each layer, defined as all pixels at or between the segmented boundaries. Then, to minimize the effect of possible segmentation errors, we excluded pixels in a 3 pixel-wide region next to the borders, as shown in Figure 5. Noting that the choroid lower boundary is not visible in all B-scans, we set it at 13 pixels below the RPE/choroid segmentation line. Since the vitreous has no upper boundary, we represented it as the region 10 to 20 pixels above the vitreous/NFL segmentation line.

Fig. 5.

Diagram of the boundaries used for each layer. The data for each layer is taken from between the lines with colors corresponding to that layer in the legend. These lines are calculated from segmentation lines with an offset to account for possible segmentation inaccuracies.

We then created a histogram from the intensity values for each layer in each B-scan with one gray-scale value wide bins. Finally, we added the histograms for each layer from all B-scans across all subjects to produce global layer-specific histograms.

D. Mathematical Modeling of Intensity Histograms

We considered three categories of mathematical models to represent the probability distribution of the intensity histograms: distributions based on theoretical models of speckle and additive noise in OCT images, mixture models based on the theoretical distributions, and Gaussian related distributions.

1). Theoretical Models:

In this section, based on first principles, we derive progressively more complex models of noise. In Section IV, we will experimentally evaluate the practical suitability of these complex models versus their more simplistic counter parts for representing OCT signal intensity.

First, we consider the speckle in OCT images. Although in principle speckle is a deterministic process, it is best modeled using stochastic tools because it is the result of the coherent addition of myriad sub-voxel scatterers. The intensity of a single, fully-developed speckle pattern I_sp has a negative exponential distribution [38]:

$$p_{\text{NegExp}}\left(I_{\text{sp}}|{\sigma }_S\right)=\frac{1}{\sigma s}\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-\frac{I_{\text{sp}}}{{\sigma }_S}\right),$$ (12)

where σ_S is the expected value of the distribution. If the layer varies such that σ_S is distributed according to a Gamma distribution with shape parameter α and expected value μ, the intensity for the whole layer will have a special form of the K distribution [47] with PDF:

$$p_{\text{Spec\hspace{0.17em}-\hspace{0.17em}K}}\left(I_{\text{sp}}|\alpha ,\mu \right)=\frac{2}{\Gamma \left(\alpha \right)}{I}_{\text{sp}}^{\frac{\alpha -1}{2}}{\left(\frac{\alpha }{\mu }\right)}^{\frac{\alpha +1}{2}}{\text{K}}_{\alpha -1}\left(2\sqrt{I_{\text{sp}}\alpha /\mu }\right),$$ (13)

where K_α (x) is the modified Bessel function of the second kind with order α. The presence of different polarizations, frequencies, and scatter angles can lead to multiple uncorrelated speckle realizations being added incoherently in the OCT images. We note that if m uncorrelated speckle patterns are present, the PDF is a full K distribution with PDF:

$$p_{\text{K}}\left(I_{\text{sp}}|\alpha ,\mu ,m\right)=\frac{2}{\Gamma \left(\alpha \right)\Gamma \left(m\right)}{I}_{\text{sp}}^{\frac{\alpha +m-2}{2}}{\left(\frac{\alpha m}{\mu }\right)}^{\frac{\alpha +m}{2}}{\text{K}}_{\alpha -m}\left(2\sqrt{I_{\text{SP}}m\alpha /\mu }\right).$$ (14)

Second, we account for the additive noise. The additive noise takes the form of a complex Gaussian added to a deterministic phasor with intensity I_sp [37]. The PDF of the signal’s intensity is therefore a modified Rice distribution:

$$p_{\text{ModRice}}\left(I;{\sigma }_R,I_{\text{SP}}\right)=\frac{1}{{\sigma }_R}\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-\frac{I+I_{\text{sp}}}{{\sigma }_R}\right){\text{I}}_0\left(\frac{2\sqrt{I{I}_{\text{sp}}}}{{\sigma }_R}\right),$$ (15)

where σ_R is a scale parameter and I₀(x) is the modified Bessel function of the first kind with order zero [37]. Because we model I_sp as a random variable, the PDF of the total intensity I will be a compound distribution between the modified Rice distribution p_ModRice(I|σ_R, I_sp) and the PDF of the multiplicative speckle noise p_sp(I_sp):

$$p\left(I\right)=\underset{I_{s\text{p}}=0}{\overset{\infty }{{\displaystyle \int }}}{p}_{\text{ModRice}}\left(I|{\sigma }_R,I_{\text{sp}}\right)p_{\text{sp}}\left(I_{\text{sp}}\right)d{I}_{\text{sp}}.$$ (16)

If p_sp(I_sp) is a negative exponential distribution, p(I) is also a negative exponential distribution with scale parameter σ_C = σ_S + σ_R. If p_sp(I_sp) is a K distribution (either the special case or full K distribution), the compound distribution integral cannot be evaluated analytically and must be examined with numerical methods as described in Section III-E. Due to computational complexity the only compound method that we could feasibly evaluate was the special K-Rice compound.

2). Mixture Models:

In addition to the purely theoretical distributions, we considered the biologically plausible case that there are two well-defined populations of voxel intensities within a layer (e.g. two dominant types of cellular substructures). To account for these cases, we used a mixture of two negative exponential distributions with PDF:

$$p\left(I|B,{\sigma }_{S1},{\sigma }_{S2}\right)=B{p}_{\text{NegExp}}\left(I|{\sigma }_{S1}\right)+\left(1+B\right)p_{\text{NegExp}}\left(I|{\sigma }_{S2}\right),$$ (17)

where B is the proportionality constant. Similarly, the PDF for a mixture of two special-case K distributions is:

$$p\left(I|B,{\alpha }_1,{\alpha }_2,{\mu }_1,{\mu }_2\right)=B{p}_{\text{Spec-K}}\left(I|{\alpha }_1,{\mu }_1\right)+\left(1+B\right)p_{\text{Spec-K}}\left(I|{\alpha }_2,{\mu }_2\right),$$ (18)

and finally, the PDF for a mixture of two full K distributions is:

$$p\left(I|B,{\alpha }_1,{\alpha }_2,{\mu }_1,{\mu }_2,m_1,m_2\right)=B{p}_{\text{K}}\left(I|{\alpha }_1,{\mu }_1,m_1\right)+\left(1-B\right)p_{\text{K}}\left(I|{\alpha }_2,{\mu }_2,m_2\right).$$ (19)

3). Gaussian-Related Models:

We also considered two models related to the Gaussian noise because of its explicit or implicit prevalence in the OCT literature. First of these models is the lognormal distribution, used in papers that assume the log domain OCT images are corrupted by Gaussian noise [53], [54]. The PDF of the lognormal distribution is:

$$p_{LN}\left(I|\sigma ,\mu \right)=\frac{1}{I\sqrt{2\pi \sigma }}\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-\frac{{\left(\text{ln\hspace{0.17em}I\hspace{0.17em}}-\mu \right)}^2}{2{\sigma }^2}\right),$$ (20)

where μ is the location parameter and σ is the scale parameter.

Second, we considered multiplicative Gaussian noise, which assumes a truncated Gaussian distribution in the linear, rather than log, domain. Note that the multiplicative noise cannot take negative values and therefore the Gaussian distribution must be truncated at 0. The resulting normalized PDF is:

$$p_{\text{TG}}\left(I|\sigma ,\mu \right)=\frac{1}{\left(1-\Phi \left(-\frac{\mu }{\sigma }\right)\right)\sqrt{2\pi }\sigma }\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-\frac{{\left(I-\mu \right)}^2}{2{\sigma }^2}\right),$$ (21)

where μ is the location parameter, σ is the scale parameter, and Ф(z) is the cumulative distribution function (CDF) of the standard normal distribution.

E. Signal Modeling and Parameter Estimation

Because OCT images are commonly viewed in the log domain to enhance visibility of the dimmer layers [50], we transform each of the above distributions to the log domain. The log domain intensity of a pixel with intensity I is I_L = A log₁₀(I), where A is a deterministic scaling factor determined by the OCT system’s software. Therefore, the log domain PDF, given linear domain PDF P(I), is given by the chain rule:

$$p_L\left(I_L\right)=p\left({10}^{I_L/A}\right)\times \frac{d{10}^{I_L/A}}{d{I}_L}.$$ (22)

For all distributions except the Rice-K compound, we determined the best parameter values by fitting the log domain distributions to the data based on a weighted nonlinear least squares criterion. We used a two-step procedure for parameter estimation. In the first step, we gave the data at bin k with count number M[k] weight 1/M[k], as per [55]. The fit of the jth distribution to the ith layer’s data with these weights was a_ij[k], our initial estimate. This estimate might be affected by the over-emphasis of the bins with fewer counts [56]. Therefore, following [56], we refit the distribution giving the data at bin k weight 1/a_ij[k]. The fit of the jth distribution to the ith layer’s data with these new weights was b_ij[k], our second and final estimate.

We calculated the goodness of fit for each model using Pearson’s χ² test, which provides a quantitative p-value. First, we calculated the test statistic:

$$X_{ij}^2={\displaystyle \sum }_{k,b_{ij}\left[k\right]\ge 1}\frac{{\left(b_{ij}\left[k\right]-M\left[k\right]\right)}^2}{\text{max\hspace{0.17em}}\left(b_{ij}\left[k\right],1\right)}.$$ (23)

We then calculated a p-value from the $X_{ij}^2$ value:

$$p_{ij}=\underset{x=0}{\overset{X_{ij}^2}{{\displaystyle \int }}}{X}^2\left(x,N_{\text{bins}}-d_j-1\right)dx,$$ (24)

where χ²(x, v) is the PDF of the χ² distribution with v degrees of freedom (DOF) at value x, N_bins is the number of bins where b_ij[k] ≥ 1 and the gray-scale ranges of all B-scans overlap, and d_j is the number of parameters in the jth distribution.

The Rice-special K compound distribution cannot be evaluated analytically and thus we numerically calculated the PDF at every point in a 200 × 200 × 200 grid in parameter space, for parameters α, μ, and σ_R. For every Rice-special K PDF/layer combination, we then calculated a χ² test statistic as above. For each layer, we examined the 100 PDFs with the lowest χ²s and calculated the mean τ and range ρ of the corresponding parameters. We then performed a refined search for each layer on a 100 × 100 × 100 point grid, where each parameter spanned the range τ ± max(ρ, τ × 0.02)/2. Again, we calculated the χ² test statistics. We considered the distribution with minimum χ² to be the best Rice-special K compound distribution for a given layer.

To determine the best distribution to use for each layer, we calculated the Aikake Information Criterion (AIC) value for each distribution/layer combination. The AIC value is given by

$$\text{AIC\hspace{0.17em}=\hspace{0.17em}2\hspace{0.17em}}\ast \text{\hspace{0.17em}d\hspace{0.17em}}-2\ast L,$$ (25)

where L is the log-likelihood value of the data given the distribution and d is the number of parameters of the distribution [57]. In this case, we approximated each the counts in each bin as an independent Poisson process and calculated the log-likelihood L of the model f[k] on the data M[k] as:

$$L\left(M\left[k\right]|f\left[k\right]\right)={\displaystyle \sum }_k\text{log\hspace{0.17em}}\left(\frac{f{\left[k\right]}^M\left[k\right]\text{\hspace{0.17em}exp\hspace{0.17em}}\left(-f\left[k\right]\right)}{M\left[k\right]!}\right).$$ (26)

For each layer, we chose the model with the lowest AIC value. This is the most parsimonious model, i.e. the model that describes the data best without overfitting [57]. We then used the chosen intensity distribution p̂_i(I) to calculate an expected value,

$$I_i=\underset{I=-\infty }{\overset{\infty }{{\displaystyle \int }}}I{\widehat{p}}_i\left(I\right)dI,$$ (27)

and a ZEV noise distribution,

$$q_i\left(w\right)={\widehat{p}}_i\left(w+I_i\right).$$ (28)

IV. Results

A. Empirical Model

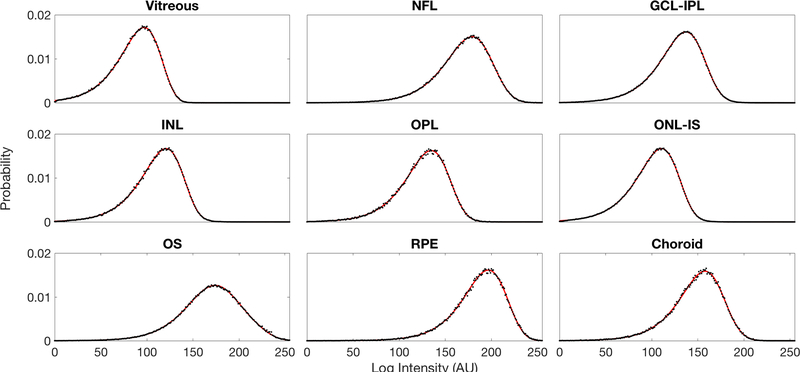
We used the AIC model selection process as discussed in Section III-E to attain the most parsimonious distribution representing each retinal layer intensity. The AIC values are shown in Table I. The summary of resulting AIC-chosen intensity distributions and parameters for each layer are shown in Table II. Among the nine models considered for representing retinal layers, three K-family models were found to be most suitable for our data: the full K mixture model for the vitreous, GCL-IPL, INL, OPL, ONL-IS, and OS; the special case K mixture model for the NFL, and Choroid; and the special case K model for RPE. Each of the chosen models has a χ² p-value of at least 0.34, indicating that these models should not be rejected on the basis of goodness of fit. The intensity distributions of each layer from our experimental data are plotted along with the best theoretical models in Figure 6. For each layer based on the corresponding best model, we calculated the average intensity I_i and ZEV noise distributions q_i(n) shown in Figure 7.

Table I.

Table indicating AIC values of each distribution/layer combination. A smaller AIC Value indicates a more parsimonious model.

Layer	Neg. Exp.	Neg. Exp. Mix.	Spec. K	Spec. K Mix.	K	KMix	Gaussian	Lognormal	Rice-K
Equation Reference	12	17	13	18	14	19	20	21	16
Vitreous	2152	1669	1807	1579	1798	1578	68423	5148	1875
NFL	16315	2061	1856	1844	1858	1848	45295	28505	11420
GCL-IPL	31621	3230	3900	1972	3484	1964	91303	39925	9109
INL	5894	1805	2246	1634	2148	1634	43465	9808	2966
OPL	4164	1662	1663	1532	1625	1531	17457	5857	1885
ONL-IS	21416	2726	4871	1908	4405	1889	82173	43559	9470
OS	62798	2749	3790	1692	3429	1685	7149	24294	5508
RPE	1801	1453	1453	1458	1452	1459	9164	3980	1675
Choroid	5898	1679	1683	1603	1653	1607	18631	8322	3338

Table II.

Per-layer distributions and parameters for the empirical model. Each distribution was chosen by an AIC selection process. The high χ² p-values indicate that the fits should not be rejected.

Layer	Distribution Name	B	μ1	μ2	α1	α2	m1	m2	X2	p-Value
Vitreous	Spec. K Mix.	0.999215	96.58	509.9	50	31.66	–	–		0.9945
NFL	Spec. K Mix.	0.86722	5974.7	4004.1	3.149	49.998	–	–		0.68358
GCL-IPL	Full K Mix.	0.062305	1676.5	677.32	1.8277	8.3798	1.8313	1.0009		0.6193
INL	Spec. K Mix.	0.9296	300	564.85	22.254	2.7856	–	–		0.97519
OPL	Full K Mix	0.12893	809.09	615.85	1.3218	9.3597	1.3283	1.0317		0.67172
ONL-IS	Full K Mix.	0.87569	193.9	228.85	14.084	1.0442	1.0855	1.0425		0.81396
OS	Full K Mix.	0.66416	9887.9	3328.1	1.0645	1.9204	1.0704	1.7793		0.6062
RPE	Full K	–	11747	–	6.7792	–	1.014	–		0.77231
Choroid	Spec. K Mix.	0.70409	1613.8	2854.7	9.6091	5.799	–	–		0.68537

Fig. 6.

Experimental PDFs (black dots) compared to the proposed best theoretical model PDFs (red line) for each layer. The data for the experimental PDFs comes from intensity-normalized data.

Fig. 7.

Expected value (left) and ZEV additive noise PDFs (right) derived from the chosen intensity distributions for each of the nine retinal layers.

B. CRLBs for Layer Boundary Locations

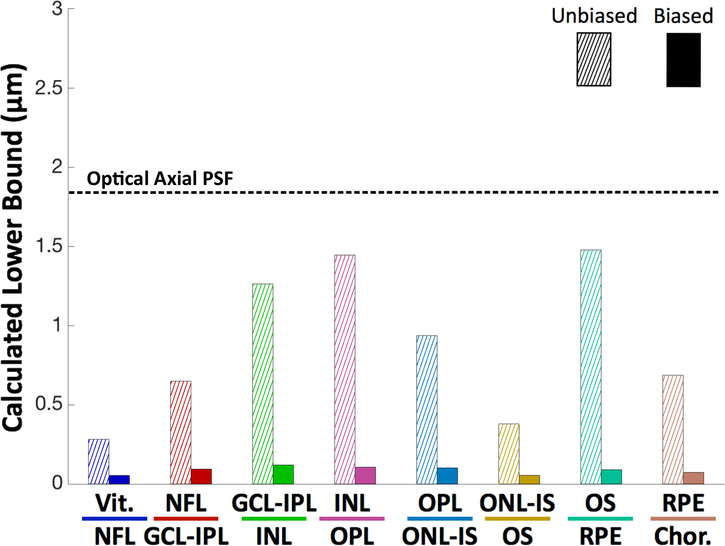
Following the methodology of Section II, we calculated unbiased and biased CRLBs for each of the eight retinal boundary positions. The unbiased $\sqrt{\text{CRLB}}$ estimator for the boundary location in a single A-scan is shown by the hatched bars of Figure 8.

Fig. 8.

CRLBs for the locations of layer boundaries in the unbiased single A-scan case (hatched) and laterally averaged biased single B-scan case (solid). For the sake of comparison, the dashed horizontal line indicates the accuracy of automatic retinal layer segmentation algorithms for normal subjects. The optical resolution of the OCT system is indicated by the dotted line.

We compared the unbiased $\sqrt{\text{CRLB}}\text{s}$ to the optical axial resolution of the Bioptigen OCT system, defined as the standard deviation of the axial PSF. We also tested the performance of a state-of-the-art deep learning based OCT layer segmentation algorithm [23] and the publicly available OCTExplorer software (downloaded at: https://www.iibi.uiowa.edu/content/iowa-reference-algorithms-human-and-murine-oct-retinal-layer-analysis-and-display [58]–[60], on this dataset and compared their results with the manually corrected segmentations. The layer-specific RMS error values for the Deep Learning and OCTExplorer, respectively, are as follows: Vitreous/NFL: 2.41 μm and 3.39 μm; NFL/GCL-IPL: 7.16 μm and 6.47 μm; GCL-IPL/INL: 5.21 μm and 5.38 μm; INL/OPL: 5.05 μm and 5.29 μm; OPL/ONL-IS: 4.36 μm and 7.86 μm; ONL-IS/OS: 2.46 μm and 2.93 μm; OS/RPE: 3.23 μm and 4.92 μm; RPE/Choroid: 4.96 μm and 4.45 μm.

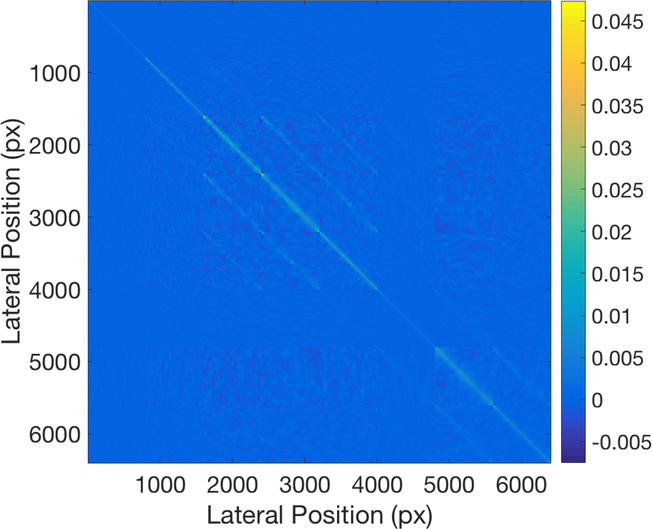
The biased $\sqrt{\text{CRLB}}$ minimum covariance matrix for the 8 boundary positions at 800 A-scan positions in each B-scan is shown in Figure 9, and the position-dependent $\sqrt{\text{CRLB}}\text{s}$ are shown in Figure 10. For the sake of comparison, we also show the biased $\sqrt{\text{CRLB}}\text{s}$ averaged across the 800 A-scans in each B-scan as the solid bars Figure 8.

Fig. 9.

Position-dependent lower bounds on the covariance of each layer’s location. The axes are arranged so that the first 800 pixels correspond to the Vitreous/NFL boundary at positions 1–800, the second 800 pixels correspond to the NFL/GCL-IPL boundary at positions 1–800, and so on.

Fig. 10.

Position-dependent $\sqrt{\text{CRLB}}\text{s}$ for a biased estimator of each layer boundary’s location at each A-scan of a B-scan.

V. Discussion

The empirical K distribution family based models of the intensity in each layer of the retina derived in this work are logical extensions to existing knowledge about the structure of the eye and the nature of speckle and detection noise. Note that the the special K distribution used was previously suggested for modeling OCT intensity [47]. However, we showed that the special K distribution used by [47] is only the best model for one out of the nine layers studied in this work. The other layers all conformed better to two other K distribution mixtures, indicating that the complex nature of retinal tissue cannot be fully described with a single distribution. Additionally, six of the layers conformed best to the non-special K distribution mixture, which has two more parameters than the special K distribution mixture. This may indicate additional complexity in the layer structure or inter-subject variance.

Although R² is popular for evaluating goodness of fit [46], [47], it is not quantitatively meaningful for nonlinear models such as these [61]. Therefore, we used the χ² goodness of fit metric and its corresponding p-value, which gives a true quantitative metric for goodness of fit.

The results of the unbiased CRLB are intuitive $\sqrt{\text{CRLB}}\text{s}$_. The bounds are on the order of microns; the higher-contrast layers (for example, Vitreous/NFL) have bounds lower than the resolution of the system (as defined by the FWHM of the PSF), and the lower-contrast layers have bounds of less than two times the resolution.

The biased $\sqrt{\text{CRLB}}\text{s}$ follow the same trend but were markedly smaller. The smallest averaged biased bound, at 0.06 μm, was far below subcellular resolution. The largest biased averaged bound, at 0.14 μm, was still quite small and over an order of magnitude below the resolution of the system. This can be attributed to the smoothness of the retinal surfaces; the retina’s shape is so highly correlated that many A-scans effectively act as independent measurements for adjacent A-scans. The averaged biased bounds are also more than order of magnitude smaller than the the accuracy of the published segmentation techniques as per Section IV-B. This indicates that there is potential to improve the performance of retinal layer segmentation algorithms.

An exciting novel development in retinal layer segmentation is the utilization of deep learning based algorithms [22], [23]. While it is hard to model the prior learned in these black-box algorithms, smoothness discussed in this paper is expected to be their major component. Note that no deep learning paper to date has provided a significantly more accurate segmentation of normal tissue than classic segmentation techniques. The utility of deep learning methods has been mainly on improving the performance of diseased eyes in segmenting hard to segment features, at an accuracy similar to normal tissue. Of course, the method for CRLB estimation presented in this paper is general and the prior utilized in this work can be easily replaced by alternate priors, including those learned via deep learning. Future studies on this topic are warranted to better characterize the limits on segmentation accuracy of deep learning techniques.

The position-dependent biased bounds are space variant. The bounds are larger at the edges of the image due to two sources. First, OCT images are blurrier at the edges, leading to increased variance in manual segmentation [62]. Second, fewer A-scans surround each individual A-scan in the image boundaries and thus negatively affecting the utility of smoothness prior.

We constructed the covariance data for our biased CRLBs from the manual segmentation of expert graders. Although manual segmentation is the gold standard, it is not perfect due to the noise and limited resolution of OCT images. The results of the biased CRLB must therefore be regarded as the lower bound of algorithmic segmentation against this particular set of human graders, not against the true anatomical structure of the retina. Indeed, it is practically impossible to discuss the theoretical bounds on all different OCT machines, retinal diseases, or alternative manual segmentation results in one paper. However, since the proposed methodology is general, one can attain bounds for different imaging scenarios by simply replacing the test dataset.

Noting that in diseased eyes layer boundary delineation is often less clear than the normal tissue, we expect that the lower bounds derived here for normal tissue to be valid for some (but not all) diseased tissues. To achieve tighter (and less optimistic) bounds, we are also pursuing the modeling and segmentation bounds of non-healthy retinas. This requires new datasets and segmentations, but with those segmentations completed, diseased tissue of the retina can be effectively modeled with the approach outlined in this manuscript. To ease adaptation of the proposed method to diseased eyes, we have released the source code of our paper so that the readers can incorporate our findings with alternative datasets. We have made the open-source code for our paper freely available online at http://people.duke.edu/~sf59/Dubose TMI 2018.htm to allow other researchers to test and modify the algorithm for their specific applications and dataset.

In conclusion, we present retina layer-specific statistical intensity models of the OCT images and biased and unbiased CRLBs for segmentation of those layers. The intensity in the OCT images was best modeled by the K distribution family. For our dataset, the unbiased $\sqrt{\text{CRLB}}\text{s}$ were on the order of microns, and the biased $\sqrt{\text{CRLB}}\text{s}$ were on the order of hundreds of microns. These results suggest that there may be room to improve the accuracy of OCT segmentation techniques. In our future work, we will extend our work to include diseased retina, other OCT imaging systems and 3-D segmentation algorithms.

Appendix A Justification of the Affine Bias Model

As stated in Section II-B, we used an affine model to approximate the bias introduced by segmentation algorithms.

In this appendix, we justify the optimum affine bias model for layer segmentation and demonstrate empirically how it accurately reflects the bias of most layer segmentation algorithms towards a smooth layer boundary.

Each B-scan is composed of A-scans of the form g[k] = s[k] + w[k], where s[k] is the true signal value and w[k] is a noise value. If we consider each boundary separately as in [15], a signal model for a single boundary in a single A-scan is a Heaviside step function at true boundary locations z convolved with a Gaussian as per Section II. The derivative of this signal is a Gaussian centered at the boundary location. A reasonable unbiased estimator for the boundary locations ẑ in the A-scan can thus be expressed as the centroid of the derivative of the A-scan:

$$\widehat{z}=CDg\left[k\right],$$ (29)

where C is a centroiding matrix and D is the derivative matrix. Given several adjacent A-scans, we can produce a biased estimate ẑ’ by a weighted averaging with the estimates of N adjacent A-scans

$$\widehat{z}\prime =W\widehat{z},$$ (30)

where W is a weighting matrix that might take into account, for example, distance and radiometric similarity of the noisy A-scans. The expected value of the estimate ẑ’ is

$$\begin{array}{lll}\text{E\hspace{0.17em}}\left[\widehat{z}\prime \right]\hfill & =\hfill & \text{E\hspace{0.17em}}\left[W\widehat{z}\right]=\text{\hspace{0.17em}E\hspace{0.17em}}\left[WCDg\left[k\right]\right]=\text{\hspace{0.17em}E\hspace{0.17em}}\left[WCD\left(s\left[k\right]+w\left[k\right]\right)\right]\hfill \\ \hfill & =\hfill & \text{E\hspace{0.17em}}\left[\text{WCD}s\left[k\right]\right]+\text{\hspace{0.17em}E\hspace{0.17em}}\left[WCDw\left[k\right]\right]\hfill \\ \hfill & =\hfill & Wz+E\left[WCDw\left[k\right]\right].\hfill \end{array}$$ (31)

The bias is then

$$\begin{array}{lll}\psi \hfill & =\hfill & \text{E\hspace{0.17em}}\left[\widehat{z}\prime \right]-z=Wz+\text{\hspace{0.17em}E\hspace{0.17em}}\left[WCDw\left[k\right]\right]-z\hfill \\ \hfill & =\hfill & \left(W-I\right)z+\text{\hspace{0.17em}E\hspace{0.17em}}\left[WCDw\left[k\right]\right],\hfill \end{array}$$ (32)

which conforms to the bias model ψ = Kh + u.