Abstract
Chemical synapses enable neurons to communicate rapidly, process and filter signals and to store information. However, studying their functional properties is difficult because synaptic connections typically consist of multiple synaptic contacts that release vesicles stochastically and exhibit time-dependent behavior. Moreover, most central synapses are small and inaccessible to direct measurements. Estimation of synaptic properties from responses recorded at the soma is complicated by the presence of nonuniform release probability and nonuniform quantal properties. The presence of multivesicular release and postsynaptic receptor saturation at some synapses can also complicate the interpretation of quantal parameters. Multiple-probability fluctuation analysis (MPFA; also known as variance-mean analysis) is a method that has been developed for estimating synaptic parameters from the variance and mean amplitude of synaptic responses recorded at different release probabilities. This statistical approach, which incorporates nonuniform synaptic properties, has become widely used for studying synaptic transmission. In this chapter, we describe the statistical models used to extract quantal parameters and discuss their interpretation when applying MPFA.
Keywords: Synapse, Vesicle, Active zone, Release probability, Release site, Quantal analysis, MPFA, Variance-mean analysis
1. Introduction
Fluctuations in the amplitude of evoked end-plate potentials recorded intracellularly from frog muscle fibers bathed in high Mg2+-containing solution (1, 2) together with their similarity to spontaneous end-plate potentials (which was first thought to be noise (3)) lead to the quantum hypothesis - the idea that neurotransmitter is released in discrete multimolecular packets or quanta. The probabilistic nature of this all-or-none process was rigorously tested using a number of different approaches (2). This work showed that fluctuations in the evoked end-plate potentials could be predicted with Poisson statistics under low probability conditions. Soon after, early electron microscopy studies revealed the presence of synaptic vesicles in motor nerve terminals (4), providing a structural basis for the “quantum” (5).
Quantal analysis refers to a group of methods that use statistical models to extract the basic functional properties of synapses from postsynaptic responses, which are typically measured at the soma. Quantal analysis can provide insights into the function of synapses and identify the locus of changes in synaptic efficacy. Three quantal parameters are now commonly used to determine the properties of synaptic transmission: the first is the maximum number of vesicles that could be released at a synaptic connection by an action potential and is often referred to as the number of independent functional release sites (N), the second is the probability of vesicular release (P) and third, the amplitude of the postsynaptic response following the release of a single vesicle or quantum (Q). The size of the postsynaptic responses and its variability from trial-to-trial are determined by the values of these quantal parameters. Presynaptic modulation is associated with P, while postsynaptic changes are associated with Q. Formation of new contacts (or increasing P from zero at existing release sites) would be associated with a change in N.
Early attempts to apply quantal analysis to central synapses met with mixed success due to difficulties in resolving individual quantal events (6). Nevertheless, it was recognized that binomial rather than Poisson statistical models were more appropriate given the relatively high release probability and few release sites present (6). Considerable efforts were made to extract quantal parameters from amplitude distributions in subsequent studies, but this approach was challenging and it was often difficult to determine the reliability of the end results because the amplitude of quantal events often fell below the noise at central synapses (7–11). Moreover, during this period, there was growing evidence of nonuniform quantal properties (12, 13). The complications arising from such nonuniform quantal size and nonuniform release probability were highlighted in a simulation study that demonstrated the difficulties of using traditional quantal analysis approaches for studying central synaptic transmission (14).
To overcome these problems a different statistical approach was developed to estimate quantal parameters at central synapses, which has its roots in non-stationary fluctuation analysis of ion channels (15) and synaptic currents (16, 17). Multiple-probability fluctuation analysis (MPFA) (18) or alternatively variance-mean analysis (19–21) does not require that quantal events be distinguished from the background noise. Moreover, the statistical model underlying MPFA is multinomial and can therefore take into account nonuniformities in P and Q. MPFA has been used to determine the quantal parameters of transmitter release at low frequency (22, 23) and has been extended to short repetitive trains of synaptic responses (24–26). It has also been combined with analysis of covariance between successive stimuli within trains (27, 28). MPFA is a valuable tool to quantify the pre- and postsynaptic contributions to short-term plasticity changes (18, 25, 26, 29–33). This quantal analysis method has also been used to determine whether long-term plasticity changes are expressed pre- or postsynaptically (19, 34, 35).
In this chapter, we describe the statistical basis of MPFA, including the binomial and the multinomial models of synaptic transmission. We also describe how to apply MPFA at central synapses and discuss the interpretation of the quantal parameters with this method.
2. Statistical models of synaptic transmission
2.1. Binomial model
The binomial model assumes that each vesicle is released independently, that the release is synchronous, that P is uniform across vesicles and that Q is uniform both at the level of a single release site and across release sites. Under these assumptions the mean peak amplitude of the synaptic current response (I) can be expressed as a function of the number of functional release sites (N), the quantal amplitude (Q) and the probability of vesicular release (P) as follows:
| (1) |
and the associated variance can be expressed as:
| (2) |
The relationship between the variance and the mean synaptic amplitude is therefore:
| (3) |
These results suggest that if a synaptic connection operates in a simple binomial manner, the relationship between the variance and the mean amplitude of synaptic responses is parabolic. Fitting a function of the form y = Ax – Bx2, (where y is the variance and x is the mean postsynaptic current) to the relationship between the variance and mean current recorded at different release probabilities can provide estimates of N and Q (Figure 1). P can be then calculated from equation (1).
Figure 1.
Binomial model of synaptic transmission. (a) Postsynaptic currents for a synapse with N = 5, Q = -20 pA at P = 0.1, 0.5 and 0.9 were simulated stochastically (20 superimposed traces in grey and average trace of 200 events in black). (b) The dots represent the theoretical values of variance and mean amplitude at the 3 different release probabilities tested. The empty squares are values from a set of 200 simulated postsynaptic currents. The variance-mean relationship of the theoretical values was fitted using equation (3). (modified from ref 58 with permission from Elsevier)
2.2. Multinomial model
Several studies have shown that the assumptions of uniform release probability and quantal size required for a simple binomial model are not valid for most central synapses (12, 36–38). These considerations lead to the application of a multinomial model for transmitter release (18, 39).
2.2.1. Nonuniform quantal size
In the multinomial model, quantal variability can be accommodated both at the single-site level (intrasite or type I variability; Figure 2a) (17, 37) and across sites (intersite or type II variability; Figure 2b) (37, 40). Intrasite quantal variability arises from fluctuations in the size of quantal events from an individual release site from trial-to-trial and from fluctuations in their latencies. These sources of type I variance can be defined in terms of their coefficient of variation (CVQS and CVQL respectively). Intersite variability arises from sampling quanta from different release sites, each of which has different mean quantal sizes. This type II variance can be defined in terms of the coefficient of variation CVQII.
Figure 2.
Multinomial model of synaptic transmission. Intrasite (or type I) (a) and intersite (or type II) (b) quantal variabilities are illustrated. Intrasite variability arises from a single connection while intersite variability arises from a connection with multiple terminals or from a single synapse containing multiple release sites. (c) Postsynaptic currents simulated stochastically for the same parameters as in figure 1a except that intra- and intersite variability was introduced in the simulations (CVQI = 0.3 and CVQII = 0.3). (d) Theoretical variance-mean relationship representing nonuniform quantal size (in black, fitted with equation (7)). Nonuniform release probabilities were added with an α value equal to 1 and fitted with equation (13) (dotted line). The open squares are the values from a set of 200 simulated postsynaptic currents with nonuniformity in quantal size while the release probability was kept uniform. The circles show the effect of adding nonuniform release probability (α = 1). The grey line line represents the simple binomial function as in figure 1b. The variance contribution from intrasite and intersite quantal variation is indicated by the broken lines.
Equation (1) can be extended to include nonuniform quantal behavior as follows:
| (4) |
where is the mean quantal size at the time of the peak of the mean synaptic current and is therefore affected by asynchronous release (Figure 2c, d) (for details see ref 41). The variance is then given by:
| (5) |
Where CVQI combines all the variability observed at a single-site level:
| (6) |
The relationship between the variance and the mean I is therefore:
| (7) |
The sum of the intra- and intersite variability can be defined in terms of the coefficient of variation as follows:
| (8) |
More details on how the different quantal variances can be estimated are given in section 3.3.
2.2.2. Nonuniform release probability
Studies in the spinal cord (12), hippocampal cultures (13, 36, 42), and hippocampal slices (43) have shown that the probability of release is nonuniform across individual synapses. The presence of nonuniform release probability tends to reduce the variance when compared to the uniform case. The impact on the variance of nonuniform P is largest at high P, leading to a wedge-shaped distortion of the variance-mean relationship (Figure 2d) at high levels of nonuniformity (18, 41). This behavior can be captured in the multinomial model relatively neatly assuming that there is no correlation between release probability and quantal amplitude across sites (18, 39). In this case the mean current and the variance are given by:
| (9) |
| (10) |
where is the mean release probability at the time of the peak of the current and CVP represents the coefficient of variation of release probability across sites. The relationship between the variance and the mean amplitude is then:
| (11) |
Given that P is bounded by 0 and 1, CVP changes as a function of . CVP and how it changes has been modeled using families of beta functions β(α,β) (41).These functions mimic the distribution of release probability across release sites and describe how the distribution might change when varies. Furthermore, beta distributions approximate distributions that have been measured in hippocampal synapses in culture (36). Using this approach CVP can be expressed as a function of the mean release probability and a family of beta distributions defined by a single parameter α:
| (12) |
Substituting for CVP in equation (11) gives:
| (13) |
adding only one additional free parameter to the expression. Low α values (<2) indicate nonuniform release probability, while higher values indicate that the probability of release is uniform (41). However, the beta function is an approximation and α is the least well-constrained parameters in equation (13); thus estimates of CVP should be considered as a rough indicator of the level of nonuniformity in release probability.
2.3. MPFA during short-term plasticity
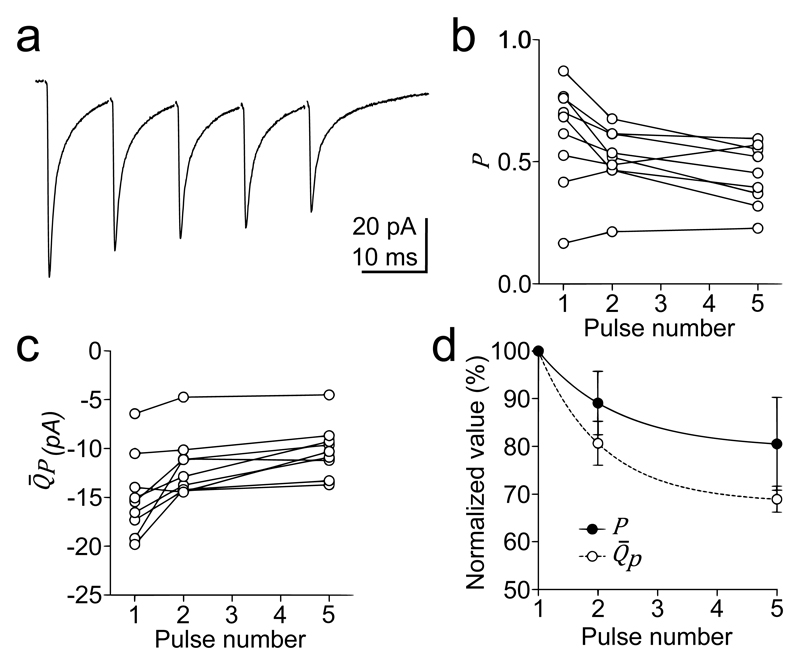
MPFA can be extended to examine how quantal parameters change during bursts of activity by determining the quantal parameters from first evoked postsynaptic current (PSC) in the burst and then analyzing the fluctuations in the subsequent events with CV analysis (Figure 3) (25). P can be estimated from the CV of evoked PSCs with the following equation:
| (14) |
Figure 3.
(a) Mean EPSCs of 5 stimuli at 100 Hz at mossy fiber-granule cell synapse. Changes of P (b) and (c) during the 100 Hz train of 9 different recordings. The graph in (d) shows the mean amplitude of P and during the 100 Hz train relative to their inital value, with associated exponential fits. (adapted from ref 25)
Changes in can be then calculated from equation (4) during the train, assuming N is constant. While simple to implement, this approach does assume that release probability is relatively uniform.
2.4. Interpretation of quantal parameters
The multinomial model provides a statistical description of release that incorporates both nonuniform presynaptic and postsynaptic properties. However, other synaptic properties, notably the occupancy of the postsynaptic receptors, affect the interpretation of the quantal parameters estimated with MPFA. This section describes how to interpret the synaptic parameters obtained with MPFA, discusses potential errors, and outlines some additional tests that can be performed to check that the interpretation is correct.
2.4.1. Interpretation of the number of release sites
When the postsynaptic quantal responses sum linearly, the amplitude of the PSC reflects the number of vesicles released. Under these conditions N the maximum number of readily release vesicles that could be released by the synaptic connection following an action potential. N therefore corresponds to the number of anatomically distinct synaptic contacts only if a maximum of one vesicle is released per synaptic contact (univesicular release) (22, 30, 41).
In the case of multivesicular release, when multiple vesicles are released at each synaptic contact (31, 44, 45), N will still reflect the total number of functional release sites or equivalently the maximum number of readily release vesicles that could be released by the synaptic connection following an action potential, if quanta sum linearly. But if the postsynaptic receptors become saturated (46), quantal events no longer sum up because the postsynaptic membrane becomes insensitive to subsequent transmitter release. In the extreme case, where a single vesicle saturates the receptors at a synaptic contact, N would correspond to the number of synaptic contacts where release can occur rather than reflecting the maximum number of vesicles that can be released at those sites (which could be much larger) (17). Thus, the interpretation of N depends on whether the postsynaptic receptors become saturated or not. Luckily, this can be tested by examining whether the postsynaptic receptor occupancy changes as a function of release probability using rapidly equilibrating low-affinity competitive antagonists (see section 3.4) (22).
At some synapses, spillover of neurotransmitter from neighboring release sites gives rise to a slow current component (47–49). This spillover-mediated current can introduce a small low variance current component that can lead to an overestimation of N (22). At cerebellar mossy fiber-granule cell synapses, spillover current can be observed in isolation when direct release fails (47). If the spillover current and direct release summate linearly, the mean spillover current and its variance can simply be subtracted at the time of the peak of the postsynaptic response at each probability of release (22).
2.4.2. Interpretation of CVP and
As for N, interpretation of also depends on whether quantal responses sum linearly or not. Under conditions when quanta sum linearly, represents the mean probability that a vesicle is released by the time of the mean peak postsynaptic response following an action potential, i.e., the integral of the release rate per functional release site up to that time (50). can be described in terms of the product of the mean probability of a vesicle being in the release-ready state () and the mean probability that a release-ready vesicle will undergo fusion following an action potential () (51, 52):
| (15) |
This interpretation is valid for both univesicular and multivesicular release, if the postsynaptic response is linear. On the other hand, if the postsynaptic receptors are saturated by a single vesicle, indicates the mean probability that one or more vesicles have been released at each synaptic contact.
At many synaptic connections, release probability has been found to be reasonably uniform leading to a parabolic variance-mean relationship. When CVP is large, the variance-mean relationship takes on an increasingly wedge-like shape due to the loss of variance at high (41). The distribution of release probability and how it changes with can be approximated by a family of beta distributions with the same α value. This approximation is unlikely to give the fine details of P distribution but gives a rough estimate of nonuniformity in P under linear conditions. However, a combination of multivesicular release and receptor saturation could also reduce the variance at high . This possibility can be tested for by examining whether receptor occupancy changes with release probability using low-affinity competitive antagonists (see section 3.4) (20, 24, 41). Low-affinity antagonists can also help prevent the build up of desensitization during trains (53).
2.4.3. Interpretation of the quantal size
Estimation of the mean quantal amplitude from the initial slope of the variance-mean relationship is robust to synaptic nonuniformities, because at low the variance is little affected by nonuniform release probability. However, mean quantal amplitude at the time of the peak (), estimated from MPFA, does not correspond to the mean peak amplitude of the quantal waveforms unless the vesicular release time course (together with any temporal dispersion arising from axonal delays) is much shorter than the initial decay time course of the PSC. This is because when release is asynchronous, quantal events can occur and partially decay before the time of the peak of the evoked PSC. In cerebellar granule cells, estimated from MPFA is about 20% lower than rise time-aligned quantal events (22). Estimation of is also robust in the presence of multiquantal release and receptor saturation because these tend to occur at intermediate to high . However, the presence of slow spillover-mediated currents can lead to an underestimate of if it is not corrected for (22).
3. Methods
In the following sections, we describe the experimental and analysis procedures to perform MPFA and explain how to estimate quantal variances and to discriminate between univesicular and multivesicular release at central synapses.
3.1. Experimental protocol
To perform MPFA, different release probability conditions should be imposed by changing the Ca2+ concentration ([Ca2+]) and [Mg2+] in the extracellular medium (18, 19, 25). The divalent cation concentration and thus membrane charge screening can be kept approximately constant by adjusting the ratio of these two ion species (18). The osmolarity should also be kept constant by adjusting the concentration of glucose and a phosphate-free solution can be used to avoid phosphate precipitation in high [Ca2+]. The presence of NMDA receptor antagonists is useful for preventing Ca2+-induced plasticity and high [Ca2+] conditions should be applied at the end of the recording to minimize the impact of plasticity induction.
Measuring synaptic responses under voltage clamp minimizes errors arising from changes in driving force and activation of voltage-gated channels in electrically compact cells such as cerebellar granule cells. However, voltage-clamp recordings from the soma are subject to errors in cells where synaptic inputs are located on electrically remote regions of the dendritic tree (54, 55). Voltage-clamp error can be reduced by using capacitance and electrode series resistance compensation functions of the amplifier (but series resistance should be monitored throughout the experiment to ensure it remains constant). While this can improve voltage clamp of the soma and proximal dendrites, it does not compensate for poor voltage control of electrically remote regions of the cell. In cases where synapses are far from the recording site and the “space-clamp” is poor, postsynaptic potentials should be recorded and corrected for the deviation in driving force (56). However, if synapses are located at different electrotonic locations, dendritic filtering will contribute to type II quantal variance and voltage-dependent dendritic conductances could complicate the variance-mean relationship by shaping postsynaptic potentials as they spread to the soma.
3.2. Data acquisition
Data acquisition and analysis can be performed with a variety of software applications and hardware configurations. We use NeuroMatic (http://www.neuromatic.thinkrandom.com/), a freely available acquisition and analysis package running under IgorPRO (Wavemetrics).
The sampling frequency of the recorded signal should be at least 2-fold higher than the highest-frequency component of the signal; otherwise the signal will be distorted by aliasing (57). Aliasing can be avoided by filtering the data with a low-pass Bessel filter before digitizing and ensuring the cut-off frequency of filter is <1/3 of the digitization frequency. Moreover, low-pass filtering the data will reduce the background noise and increase the signal-to-noise ratio. In practice, reliable reconstruction of fast AMPAR-mediated currents can be achieved by low-pass filtering at 10kHz and digitized at 50-100kHz (22, 25).
During MPFA experiments, the number of stimulated synapses should be constant. This can be achieved by using paired recordings (56) or minimal extracellular stimulation protocol (18, 23). In case of extracellular stimulation, changes in excitability or stimulation threshold could occur as a result of the different extracellular [Ca2+] solutions or stimulation frequencies. These should be controlled for by establishing thresholds under the different conditions, monitoring failures and if possible measuring the afferent fiber volley. A minimum of 50 stimuli should be recorded for each release probability condition although more may be required to constrain the fit if few release probability conditions are used. In the case of uniform release probability, a minimum of three different release probability conditions is required and at least four in the nonuniform case.
The higher the frequency the more rapidly the data set can be acquired, but it should not be so high as to induce synaptic depression or facilitation. Time stability of the synaptic responses used to calculate the mean and the variance of the PSC amplitude is essential. Time stability of the amplitude of evoked PSCs can be tested with the Spearman rank order test (18), while amplitude stability across release probability conditions should be checked by returning to a specific condition (e.g., 2mM [Ca2+]) and testing whether the mean PSC amplitude has changed.
3.3. Estimation of quantal variance
Unless a simple binomial model is used, quantal variance must be determined. Total quantal variance, CVQT, can be measured from PSCs evoked under conditions of low release probability, when failures of release reach 80-90%, because the proportion of multiquantal events is negligible regardless of the number of functional release sites (22, 41). Recording under such low release probability conditions has several advantages: 1) quantal events can be measured from stimulus-aligned PSCs, minimizing the effect of spontaneous currents, allowing a precise measurement of the mean and variance; 2) it minimizes interactions between vesicles at synapses where multivesicular release occurs, and 3) it reduces postsynaptic interactions by reducing the build up of neurotransmitter via spillover.
In another variant of this approach, CVQT can be estimated by evoking PSCs while replacing Ca2+ by Sr2+ in the extracellular medium in order to induce asynchronous release of quanta (18, 23, 33, 46). CVQT can also be estimated from the distribution of miniature postsynaptic currents (mPSCs) recorded in TTX. However, this has the serious disadvantage that quantal events arise from all the synapses impinging onto the cell rather than being restricted to an individual synaptic connection.
Once the total quantal variability is determined, the contributions made by intra- and intersite variability can be estimated (41). For rare cases where there is a single functional release site per synaptic connection, CVQI can be measured directly from the peak of stimulus-aligned PSCs (17). However, for synaptic connections with multiple functional release sites, direct estimation of CVQI is not possible. In this case CVQI can be inferred from the PSC variance remaining when P is maximal. If quanta release is independent between release sites, then the variance remaining at the peak of PSCs should arise purely from intrasite quantal amplitude variability and quantal asynchrony (i.e., ). CVQI can be determined from the remaining variance by dividing it by I and square rooting. CVQI can also be decomposed into CVQS and CVQL using equation (6), since CVQL can be determined from the difference in variability in the peak amplitude between stimulus-aligned and rise time-aligned events (22). Once CVQI is known, CVQII can be calculated from CVQT using equation (8). If estimation of CVQI is not possible, assuming that CVQI = CVQII, is likely to introduce relatively little error (41).
3.4. Distinguish between univesicular and multivesicular release
In order to distinguish between univesicular and multivesicular release, PSCs should be recorded in the presence of a rapidly equilibrating low-affinity competitive antagonist (such as γ-DGG or kynurenic acid for AMPA receptors), under low and high probabilities of release (20, 22, 44, 45, 56). In the case of multivesicular release, the fractional block of the evoked PSC by the competitive antagonist will be less at high release probabilities than low release probabilities, because the postsynaptic AMPA receptors will be exposed to a higher concentration of neurotransmitter, which displaces the antagonist more effectively. Thus, if there is significant dependence of the agonist block on the release probability, this implies the presence of multivesicular release. Moreover, if the [Ca2+]-dependence of release changes in the presence of antagonist, this implies that the postsynaptic receptors become saturated at high release probabilities. Under these conditions MPFA should be performed in the presence of a competitive antagonist (46). However, if the fractional block of the PSC by the antagonist is independent of release probability, this suggests that the postsynaptic receptor occupancy is constant across release probabilities and the interpretation of quantal parameters is straightforward. In this case MPFA should give the same number of functional release sites in the presence or the absence of a competitive antagonist.
3.5. Data analysis
The peak amplitude of PSCs should be measured from a window (Wp) centered around the maximum of the mean peak PSC and the baseline subtracted using a 1-2 ms window before the stimulus (Wb; Figure 4). Time stability of the PSC recorded for each condition should be assessed by using statistical tests such as linear regression or the Spearman rank order test. The variance arising from the background noise should be measured from each event using a window (Wn) that is similar to the one used to measure the amplitude at the time of the peak (e.g., 0.1 ms) (Figure 4). The two measurement windows (Wn and Wp) should be equidistant to ensure that both measurements pick up similar frequency components of the background noise. The baseline variance can then be calculated and subtracted from the variance of the synaptic amplitude.
Figure 4.
200 postsynaptic currents were simulated with a multinomial model under a low and uniform probability of release (P = 0.05) which gives rise to 70% of failures. 50 stimulus-aligned events are shown in grey. The average trace is displayed in black. Wb shows the window for the baseline correction and Wn and Wp the window for the measurement of the mean and variance of the baseline noise and the peak of the postsynaptic current, respectively. (modified from ref 64 with permission from Springer)
and N and their uncertainties can be estimated by performing a weighted fit of the variance-mean relationship to a binomial (equation 3), a multinomial model of release with nonuniform quantal size and uniform release probability (equation 7) or a model that also includes nonuniformity of release probability (equation 13). The initial slope is related to , the degree of curvature to P and the size to N. P can be calculated for each release probability condition from the ratio of the mean current to NP (the maximal possible response). Fits should be accepted when the χ2 value gives p ≥ 0.05. P should be greater than 0.6 at high [Ca2+] for an accurate estimate of N (41, 58).
3.6. Weighted least squares method
Conventional least squares fitting (equations (7) and (13)) assumes that the errors estimating the mean PSC amplitude are negligible, but a more sophisticated expression for the weights can be used when the errors in the current cannot be neglected (58). Errors in the estimation of variance can be determined with unbiased estimators of the variance that can be obtained using sample moments (58). A general expression of the variance of the sample variance s2 is given by:
| (16) |
where n is the number of traces acquired and m2 and m4 are sample central moments about the mean and can be calculated as , where m2 is the variance. Equation (16) is valid even when small sample sizes are used. Maximizing the number of samples improves the estimators’ reliability and is therefore anyway desirable. The use of weighted least squares improves the reliability in parameter estimation up to 30% (58).
4. Discussion
4.1. Summary of technique
MPFA (18), which is also known as variance-mean analysis (19, 20), is a simple and robust method for estimating the quantal parameters of synaptic connections. MPFA overcomes the technical difficulties encountered with more traditional methods that involved identifying and interpreting peaks in amplitude histograms (14, 59, 60), allowing estimation of quantal parameters at central synaptic connections, where quantal parameter are nonuniform, quantal variance is large, and where the signal-to-noise ratio is often low.
4.2. Limitations of MPFA
While MPFA is straightforward to apply, the accuracy of the results depends on the quality of the experimental data and the particular properties of the synapse under study. Time stable recordings of PSCs at multiple release probabilities are essential. Uncertainty in the values of quantal parameters can be reduced by increasing the number of recordings per release probability condition and the number of different release probabilities recorded, but clearly, for a finite length experiment, there is a trade-off between these two experimental parameters. At many central synapses the assumption that quantal events sum linearly has been borne out. Multiquantial release is not an issue for MPFA if postsynaptic receptor occupancy is in the low-to-intermediate range, but if postsynaptic receptors saturate following quantal release, the postsynaptic responses are no longer linear reporters of vesicular release. Under these conditions it is essential to lower receptor occupancy with rapidly equilibrating antagonists (20, 24, 41, 53), to bring the postsynaptic response back into a linear regime. But perhaps the biggest limitation for this technique is that good quality voltage clamp is only feasible for synapses close to the soma. While this method can be applied to current clamp conditions, the impact of dendritic filtering and the impact of active dendritic conductances are difficult to control for.
As for all quantal analysis methods, MPFA relies on a statistical model of synaptic transmission. The results therefore depend on the accuracy of the model. Previous quanta analysis methods have been limited by their ability to account for nonuniform quantal parameters and the presence of high quantal variance. While MPFA can account for a wide range of nonuniformities including those arising from release probability and quantal size, it can only estimate the mean values of the quantal parameters and how they change during plasticity. While this is sufficient for many questions, a deeper understanding of the release process, including separation of mean probability of a vesicle being in the release-ready state and the mean probability that a release-ready vesicle will undergo fusion, requires more powerful descriptions of the release process (25–27, 52) that include short-term plasticity (61).
4.3. Comparison of MPFA to other methods
Several quantitative methods have been developed for studying synaptic function over the last decade that extends the basic MPFA approach. These include combining variance-mean approaches with covariance analysis (27, 62) and combining deconvolution and variance analysis enabling estimation of both the quantal properties and the time course of the release rate (22, 63). These approaches together with other more direct methods of measuring release (50) provide valuable additional information on the time course of release. Combining variance-mean analysis and model of short-term plasticity is also effective for investigating the relationship between the quantal properties and short-term plasticity at central synapses (25, 26, 33, 64).
Statistical models based on Bayesian inference have been used to extract information from the fluctuations of the postsynaptic response (65, 66). This technique assumes that the fluctuations in synaptic signals are described by mixtures of Gaussian distributions. Simulations show that a Bayesian Quantal Analysis (BQA) algorithm can accurately estimate the quantal parameters from a small data set with only two conditions of release probability (66) compared to MPFA which needs at least 3 release probability conditions (41). This could be advantageous if recording stability is a problem. The BQA algorithm does not make the distinction between intra- and intersite variability but characterizes their distributions using the “quantal likelihood function”. Nevertheless, BQA performed comparably well to MPFA when compared using the same datasets (66).
4.4. Optical approaches and future directions
Most quantitative studies of synaptic connections have used electrophysiological recordings to assess synaptic function. However, optical approaches are potentially very powerful because they can also provide spatial information, thereby enabling the study of individual synaptic contacts (36, 67–70). Optical approaches have shown, for example, that the probability of neurotransmitter release is nonuniform across release sites (36). However, using postsynaptic Ca2+ changes in spines as an assay of glutamate release is complicated by the presence of voltage-gated channels. The small number of NMDARs activated by a quantum (38) can also complicate interpretation of failures. Nevertheless, optical quantal analysis has been used to probe the locus of expression of short-term plasticity (67, 68). Presynaptic calcium imaging has also been used to assess changes of probability of release during long-term (69) and short-term plasticity (43, 70). However, these techniques provide only part of the quantal description of the synapse compared to electrophysiology-based MPFA. Moreover, unlike MPFA, which can be applied to both excitatory and inhibitory synapses, optical quantal analysis can only be applied to synapses that have Ca2+-permeable receptors. However, the development of new fluorescent reporters that sense transmitter directly, like glutamate-sensing fluorescent reporter (iGluSnFR) (71), and high speed 2-photon imaging methods that can monitor synapses distributed in 3D space (72, 73) suggest that several of the limitations of optical quantal analysis could soon be overcome.
5. Conclusions
The quantum hypothesis was proposed to explain the stochastic nature of chemical synaptic transmission. However, the Poisson statistics that describe transmission at the neuromuscular junction under low release conditions are not applicable to most central synapses due to the low number of release sites. Another difficulty at central synapses is that the underlying release probability and quantal size are not uniform. MPFA is a simple approach for determining synaptic properties at synapses with nonuniform quantal parameters. It is robust to noise and large quantal variance, in contrast to more traditional methods that relied on identifying quantal peaks in amplitude histograms. MPFA has been widely used to determine quantal parameters at both glutamatergic (18, 22, 23, 35) and GABAergic synapses (30) and has been applied to trains of responses to determine which quantal parameters change during short-term plasticity (18, 25, 29, 46). The quantal parameters estimated with MPFA can also be combined with models of short-term plasticity (25, 26, 64), thereby providing a more complete picture of the quantal transmission at central synapses (74).
Acknowledgements
We thank Antoine Valera for comments on the manuscript. FL is supported by an IEF Marie Curie fellowship (FP7) and RAS holds a Wellcome Trust Principal Research Fellowship and an ERC Advanced Grant.
References
- 1.Fatt P, Katz B. Spontaneous Subthreshold Activity at Motor Nerve Endings. The Journal of Physiology. 1952;117:109–128. [PMC free article] [PubMed] [Google Scholar]
- 2.del Castillo J, Katz B. Quantal components of the end-plate potential. The Journal of Physiology. 1954;124:560–573. doi: 10.1113/jphysiol.1954.sp005129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fatt P, Katz B. Some Observations on Biological Noise. Nature. 1950;166:597–598. doi: 10.1038/166597a0. [DOI] [PubMed] [Google Scholar]
- 4.De Robertis E, Bennett HS. Some Features of the Submicroscopic Morphology of Synapses in Frog and Earthworm. Journal of Biophysical and Biochemical Cytology. 1955;1:47. doi: 10.1083/jcb.1.1.47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Katz B. The release of neural transmitter substances. Liverpool University Press; 1969. [Google Scholar]
- 6.Kuno M. Quantal components of excitatory synaptic potentials in spinal motoneurones. The Journal of Physiology. 1964;175:81–99. doi: 10.1113/jphysiol.1964.sp007504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Malinow R, Tsien RW. Presynaptic enhancement shown by whole-cell recordings of long-term potentiation in hippocampal slices. Nature. 1990;346:177–180. doi: 10.1038/346177a0. [DOI] [PubMed] [Google Scholar]
- 8.Bekkers JM, Stevens CF. Presynaptic mechanism for long-term potentiation in the hippocampus. Nature. 1990;346:724–729. doi: 10.1038/346724a0. [DOI] [PubMed] [Google Scholar]
- 9.Larkman A, Stratford K, Jack J. Quantal analysis of excitatory synaptic action and depression in hippocampal slices. Nature. 1991;350:344–347. doi: 10.1038/350344a0. [DOI] [PubMed] [Google Scholar]
- 10.Edwards F. Neurobiology. LTP is a long term problem. Nature. 1991;350:271–272. doi: 10.1038/350271a0. [DOI] [PubMed] [Google Scholar]
- 11.Kullmann DM, Nicoll RA. Long-term potentiation is associated with increases in quantal content and quantal amplitude. Nature. 1992;357:240–244. doi: 10.1038/357240a0. [DOI] [PubMed] [Google Scholar]
- 12.Walmsley B, Edwards FR, Tracey DJ. Nonuniform release probabilities underlie quantal synaptic transmission at a mammalian excitatory central synapse. Journal of Neurophysiology. 1988;60:889–908. doi: 10.1152/jn.1988.60.3.889. [DOI] [PubMed] [Google Scholar]
- 13.Rosenmund C, Clements JD, Westbrook GL. Nonuniform probability of glutamate release at a hippocampal synapse. Science. 1993;262:754–757. doi: 10.1126/science.7901909. [DOI] [PubMed] [Google Scholar]
- 14.Walmsley B. Interpretation of “quantal” peaks in distributions of evoked synaptic transmission at central synapses. Proceedings of the royal society. Biological sciences / The Royal Society. 1995;261:245–250. doi: 10.1098/rspb.1995.0144. [DOI] [PubMed] [Google Scholar]
- 15.Sigworth FJ. The variance of sodium current fluctuations at the node of Ranvier. The Journal of Physiology. 1980;307:97–129. doi: 10.1113/jphysiol.1980.sp013426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Traynelis SF, Silver RA, Cull-Candy SG. Estimated conductance of glutamate receptor channels activated during EPSCs at the cerebellar mossy fiber-granule cell synapse. Neuron. 1993;11:279–289. doi: 10.1016/0896-6273(93)90184-s. [DOI] [PubMed] [Google Scholar]
- 17.Silver RA, Cull-Candy SG, Takahashi T. Non-NMDA glutamate receptor occupancy and open probability at a rat cerebellar synapse with single and multiple release sites. The Journal of Physiology. 1996;494(Pt 1):231–250. doi: 10.1113/jphysiol.1996.sp021487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silver RA, Momiyama A, Cull-Candy SG. Locus of frequency-dependent depression identified with multiple-probability fluctuation analysis at rat climbing fibre-Purkinje cell synapses. The Journal of Physiology. 1998;510(Pt 3):881–902. doi: 10.1111/j.1469-7793.1998.881bj.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Reid CA, Clements JD. Postsynaptic expression of long-term potentiation in the rat dentate gyrus demonstrated by variance-mean analysis. The Journal of Physiology. 1999;518(Pt 1):121–130. doi: 10.1111/j.1469-7793.1999.0121r.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Clements JD, Silver RA. Unveiling synaptic plasticity: a new graphical and analytical approach. Trends in Neurosciences. 2000;23:105–113. doi: 10.1016/s0166-2236(99)01520-9. [DOI] [PubMed] [Google Scholar]
- 21.Clamann HP, Mathis J, Lüscher HR. Variance analysis of excitatory postsynaptic potentials in cat spinal motoneurons during posttetanic potentiation. Journal of Neurophysiology. 1989;61:403–416. doi: 10.1152/jn.1989.61.2.403. [DOI] [PubMed] [Google Scholar]
- 22.Sargent PB, Saviane C, Nielsen TA, et al. Rapid vesicular release, quantal variability, and spillover contribute to the precision and reliability of transmission at a glomerular synapse. Journal of Neuroscience. 2005;25:8173–8187. doi: 10.1523/JNEUROSCI.2051-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lanore F, Labrousse VF, Szabo Z, et al. Deficits in Morphofunctional Maturation of Hippocampal Mossy Fiber Synapses in a Mouse Model of Intellectual Disability. Journal of Neuroscience. 2012;32:17882–17893. doi: 10.1523/JNEUROSCI.2049-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Meyer AC, Neher E, Schneggenburger R. Estimation of quantal size and number of functional active zones at the calyx of held synapse by nonstationary EPSC variance analysis. Journal of Neuroscience. 2001;21:7889–7900. doi: 10.1523/JNEUROSCI.21-20-07889.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Saviane C, Silver RA. Fast vesicle reloading and a large pool sustain high bandwidth transmission at a central synapse. Nature. 2006;439:983–987. doi: 10.1038/nature04509. [DOI] [PubMed] [Google Scholar]
- 26.Hallermann S, Fejtova A, Schmidt H, et al. Bassoon Speeds Vesicle Reloading at a Central Excitatory Synapse. Neuron. 2010;68:710–723. doi: 10.1016/j.neuron.2010.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Scheuss V, Neher E. Estimating synaptic parameters from mean, variance, and covariance in trains of synaptic responses. Biophysical Journal. 2001;81:1970–1989. doi: 10.1016/S0006-3495(01)75848-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Neher E, Sakaba T. Combining deconvolution and fluctuation analysis to determine quantal parameters and release rates. Journal of Neuroscience Methods. 2003;130:143–157. doi: 10.1016/j.jneumeth.2003.09.020. [DOI] [PubMed] [Google Scholar]
- 29.Oleskevich S, Clements J, Walmsley B. Release probability modulates short-term plasticity at a rat giant terminal. The Journal of Physiology. 2000;524(Pt 2):513–523. doi: 10.1111/j.1469-7793.2000.00513.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Biró AA, Holderith NB, Nusser Z. Quantal size is independent of the release probability at hippocampal excitatory synapses. Journal of Neuroscience. 2005;25:223–232. doi: 10.1523/JNEUROSCI.3688-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Biró AA, Holderith NB, Nusser Z. Release probability-dependent scaling of the postsynaptic responses at single hippocampal GABAergic synapses. Journal of Neuroscience. 2006;26:12487–12496. doi: 10.1523/JNEUROSCI.3106-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Humeau Y, Doussau F, Popoff MR, et al. Fast changes in the functional status of release sites during short-term plasticity: involvement of a frequency-dependent bypass of Rac at Aplysia synapses. The Journal of Physiology. 2007;583:983–1004. doi: 10.1113/jphysiol.2007.139899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Valera AM, Doussau F, Poulain B, et al. Adaptation of Granule Cell to Purkinje Cell Synapses to High-Frequency Transmission. Journal of Neuroscience. 2012;32:3267–3280. doi: 10.1523/JNEUROSCI.3175-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sola E, Prestori F, Rossi P, et al. Increased neurotransmitter release during long-term potentiation at mossy fibre-granule cell synapses in rat cerebellum. The Journal of Physiology. 2004;557:843–861. doi: 10.1113/jphysiol.2003.060285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fourcaudot E, Gambino F, Humeau Y, et al. cAMP/PKA signaling and RIM1alpha mediate presynaptic LTP in the lateral amygdala. Proceedings of the National Academy of Sciences. 2008;105:15130–15135. doi: 10.1073/pnas.0806938105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Murthy VN, Sejnowski TJ, Stevens CF. Heterogeneous release properties of visualized individual hippocampal synapses. Neuron. 1997;18:599–612. doi: 10.1016/s0896-6273(00)80301-3. [DOI] [PubMed] [Google Scholar]
- 37.Bekkers JM, Richerson GB, Stevens CF. Origin of variability in quantal size in cultured hippocampal neurons and hippocampal slices. Proceedings of the National Academy of Sciences. 1990;87:5359–5362. doi: 10.1073/pnas.87.14.5359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Silver RA, Traynelis SF, Cull-Candy SG. Rapid-time-course miniature and evoked excitatory currents at cerebellar synapses in situ. Nature. 1992;355:163–166. doi: 10.1038/355163a0. [DOI] [PubMed] [Google Scholar]
- 39.Frerking M, Wilson M. Effects of variance in mini amplitude on stimulus-evoked release: a comparison of two models. Biophysical Journal. 1996;70:2078–2091. doi: 10.1016/S0006-3495(96)79774-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Borst JG, Lodder JC, Kits KS. Large amplitude variability of GABAergic IPSCs in melanotrophs from Xenopus laevis: evidence that quantal size differs between synapses. Journal of Neurophysiology. 1994;71:639–655. doi: 10.1152/jn.1994.71.2.639. [DOI] [PubMed] [Google Scholar]
- 41.Silver RA. Estimation of nonuniform quantal parameters with multiple-probability fluctuation analysis: theory, application and limitations. Journal of Neuroscience Methods. 2003;130:127–141. doi: 10.1016/j.jneumeth.2003.09.030. [DOI] [PubMed] [Google Scholar]
- 42.Branco T, Staras K, Darcy KJ, et al. Local dendritic activity sets release probability at hippocampal synapses. Neuron. 2008;59:475–485. doi: 10.1016/j.neuron.2008.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Holderith N, Lörincz A, Katona G, et al. Release probability of hippocampal glutamatergic terminals scales with the size of the active zone. Nature Neuroscience. 2012;15:988–997. doi: 10.1038/nn.3137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wadiche JI, Jahr CE. Multivesicular release at climbing fiber-Purkinje cell synapses. Neuron. 2001;32:301–313. doi: 10.1016/s0896-6273(01)00488-3. [DOI] [PubMed] [Google Scholar]
- 45.Christie JM, Jahr CE. Multivesicular release at Schaffer collateral-CA1 hippocampal synapses. Journal of Neuroscience. 2006;26:210–216. doi: 10.1523/JNEUROSCI.4307-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Foster KA, Regehr WG. Variance-mean analysis in the presence of a rapid antagonist indicates vesicle depletion underlies depression at the climbing fiber synapse. Neuron. 2004;43:119–131. doi: 10.1016/j.neuron.2004.06.022. [DOI] [PubMed] [Google Scholar]
- 47.DiGregorio DA, Nusser Z, Silver RA. Spillover of glutamate onto synaptic AMPA receptors enhances fast transmission at a cerebellar synapse. Neuron. 2002;35:521–533. doi: 10.1016/s0896-6273(02)00787-0. [DOI] [PubMed] [Google Scholar]
- 48.Barbour B, Hausser M. Intersynaptic diffusion of neurotransmitter. Trends in Neurosciences. 1997;20:377–384. doi: 10.1016/s0166-2236(96)20050-5. [DOI] [PubMed] [Google Scholar]
- 49.Sakaba T, Schneggenburger R, Neher E. Estimation of quantal parameters at the calyx of Held synapse. Neuroscience Research. 2002;44:343–356. doi: 10.1016/s0168-0102(02)00174-8. [DOI] [PubMed] [Google Scholar]
- 50.Minneci F, Kanichay RT, Silver RA. Estimation of the time course of neurotransmitter release at central synapses from the first latency of postsynaptic currents. Journal of Neuroscience Methods. 2012;205:49–64. doi: 10.1016/j.jneumeth.2011.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Vere Jones D. Simple stochastic models for the release of quanta of transmitter from a nerve terminal. Australian Journal of Statistics. 1966;8:53–63. [Google Scholar]
- 52.Quastel DM. The binomial model in fluctuation analysis of quantal neurotransmitter release. Biophysical Journal. 1997;72:728–753. doi: 10.1016/s0006-3495(97)78709-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wong AYC, Graham BP, Billups B, et al. Distinguishing between presynaptic and postsynaptic mechanisms of short-term depression during action potential trains. Journal of Neuroscience. 2003;23:4868–4877. doi: 10.1523/JNEUROSCI.23-12-04868.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Spruston N, Jaffe DB, Williams SH, et al. Voltage- and space-clamp errors associated with the measurement of electrotonically remote synaptic events. Journal of Neurophysiology. 1993;70:781–802. doi: 10.1152/jn.1993.70.2.781. [DOI] [PubMed] [Google Scholar]
- 55.Bar-Yehuda D, Korngreen A. Space-Clamp Problems When Voltage Clamping Neurons Expressing Voltage-Gated Conductances. Journal of Neurophysiology. 2008;99:1127–1136. doi: 10.1152/jn.01232.2007. [DOI] [PubMed] [Google Scholar]
- 56.Silver RA, Lubke J, Sakmann B, et al. High-probability uniquantal transmission at excitatory synapses in barrel cortex. Science. 2003;302:1981–1984. doi: 10.1126/science.1087160. [DOI] [PubMed] [Google Scholar]
- 57.Nyquist H. Certain Topics in Telegraph Transmission Theory. Transactions AIEE. 1928;47:617–644. [Google Scholar]
- 58.Saviane C, Silver RA. Errors in the estimation of the variance: implications for multiple-probability fluctuation analysis. Journal of Neuroscience Methods. 2006;153:250–260. doi: 10.1016/j.jneumeth.2005.11.003. [DOI] [PubMed] [Google Scholar]
- 59.Redman S. Quantal analysis of synaptic potentials in neurons of the central nervous system. Physiological reviews. 1990;70:165–198. doi: 10.1152/physrev.1990.70.1.165. [DOI] [PubMed] [Google Scholar]
- 60.Stricker C, Field AC, Redman SJ. Statistical analysis of amplitude fluctuations in EPSCs evoked in rat CA1 pyramidal neurones in vitro. The Journal of Physiology. 1996;90(Pt 2):419–441. doi: 10.1113/jphysiol.1996.sp021155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tsodyks M, Pawelzik K, Markram H. Neural networks with dynamic synapses. Neural Computation. 1998;10:821–835. doi: 10.1162/089976698300017502. [DOI] [PubMed] [Google Scholar]
- 62.Scheuss V, Neher E, Schneggenburger R. Separation of presynaptic and postsynaptic contributions to depression by covariance analysis of successive EPSCs at the calyx of held synapse. Journal of Neuroscience. 2002;22:728–739. doi: 10.1523/JNEUROSCI.22-03-00728.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sakaba T, Neher E. Quantitative relationship between transmitter release and calcium current at the calyx of held synapse. Journal of Neuroscience. 2001;21:462–476. doi: 10.1523/JNEUROSCI.21-02-00462.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Saviane C, Silver RA. Estimation of quantal parameters with multiple-probability fluctuation analysis. Methods in molecular biology. 2007;403:303–317. doi: 10.1007/978-1-59745-529-9_19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Turner DA, West M. Bayesian analysis of mixtures applied to post-synaptic potential fluctuations. Journal of Neuroscience Methods. 1993;47:1–21. doi: 10.1016/0165-0270(93)90017-l. [DOI] [PubMed] [Google Scholar]
- 66.Bhumbra GS, Beato M. Reliable evaluation of the quantal determinants of synaptic efficacy using Bayesian analysis. Journal of Neurophysiology. 2013;109:603–620. doi: 10.1152/jn.00528.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Oertner TG, Sabatini BL, Nimchinsky EA, et al. Facilitation at single synapses probed with optical quantal analysis. Nature Neuroscience. 2002;5:657–664. doi: 10.1038/nn867. [DOI] [PubMed] [Google Scholar]
- 68.Yuste R, Majewska A, Cash SS, et al. Mechanisms of calcium influx into hippocampal spines: heterogeneity among spines, coincidence detection by NMDA receptors, and optical quantal analysis. The Journal of neuroscience. 1999;19:1976–1987. doi: 10.1523/JNEUROSCI.19-06-01976.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Emptage NJ, Reid CA, Fine A, et al. Optical quantal analysis reveals a presynaptic component of LTP at hippocampal Schaffer-associational synapses. Neuron. 2003;38:797–804. doi: 10.1016/s0896-6273(03)00325-8. [DOI] [PubMed] [Google Scholar]
- 70.Sylantyev S, Jensen TP, Ross RA, et al. Cannabinoid- and lysophosphatidylinositol-sensitive receptor GPR55 boosts neurotransmitter release at central synapses. Proceedings of the National Academy of Sciences. 2013;110:5193–5198. doi: 10.1073/pnas.1211204110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Marvin JS, Borghuis BG, Tian L, et al. An optimized fluorescent probe for visualizing glutamate neurotransmission. Nature Methods. 2013;10:162–170. doi: 10.1038/nmeth.2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kirkby PA, Srinivas Nadella KMN, Silver RA. A compact Acousto-Optic Lens for 2D and 3D femtosecond based 2-photon microscopy. Optics express. 2010;18:13721–13745. doi: 10.1364/OE.18.013720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Fernández-Alfonso T, Nadella KMNS, Iacaruso MF, et al. Monitoring synaptic and neuronal activity in 3D with synthetic and genetic indicators using a compact acousto-optic lens two-photon microscope. Journal of Neuroscience Methods. 2014;222:69–81. doi: 10.1016/j.jneumeth.2013.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Rothman JS, Silver RA. Data-driven modeling of synaptic transmission and integration. Progress in molecular biology and translational science. 2014;123:305–350. doi: 10.1016/B978-0-12-397897-4.00004-8. [DOI] [PMC free article] [PubMed] [Google Scholar]