Abstract
A comparative study of 36 molecular descriptors derived from the topological distance matrix and van der Waals space is carried out within this paper. They are partitioned into 16 generalized topological distance matrix indices, 11 topological distance indices known in the literature (seven obtained from eigenvalues/eigenvectors of distance matrix), and 9 van der Waals molecular descriptors. The generalized topological distance indices, kδλ (λ = 1 – 3, k = 1 – 4), are introduced in this work on the basis of reciprocical distance matrix. Intercorrelation analysis reveals that topological distance indices mostly contain the same type of information, while van der Waals indices can be bound to the shape or the size of molecules. Furthermore, we found that topological distance indices are good for describing molecular size, and they may be viewed as bulk parameters. The most accurate QSPR models for predicting boiling point of alkanes are based on some of the generalized, eigenvalues/eigenvectors topological distance indices and the van der Waals descriptors of molecular size.
Keywords: QSPR, topological distance indices (TDI), van der Waals molecular descriptors (vdWMD)
Introduction
The most important problem in QSPR and QSAR analysis is to convert chemical structure into mathematical molecular descriptors that are relevant to the physical, chemical or biological properties [1]. Molecular structure is one of the basic concepts of chemistry, since properties and chemical and biological behaviors of molecules are determined by it. One can distinguish three levels for quantifying molecular structure: topological (based on atomic connectivity) [2], metric (bond length, valence and torsion angles) [3] and electronic (quantum-mechanical evaluation of detailed dynamics of electrons and nuclei) [4]. Within many congener series of chemical compounds the variations of molecular geometry (as measured by van der Waals descriptors), and electronic structure are small [5,6]. Consequently, one can consider that many of molecular properties are conditioned only by topology of molecules and quantify the structural information contained in their molecular graphs by means of so-called topological indices (TIs). These are numerical quantities based on various invariants or characteristics of molecular graph. Among them, more detailed topological information is provided by the topological distance matrix D, whose entries dij represent topological distances between vertices i and j, that is the number of edges (bonds) along the shortest path between these vertices (atoms). Therefore, many TIs used in QSPR and QSAR studies have been developed on the basis of D.
From their definitions, one may admit many TIs derived from D may code two structural steric factors, namely the size and shape of the molecule [7]. Although TIs do not have a precise physical meaning, they are measures for topological shape, i.e. the degree of branching or cyclicity and they correlate well with molecular volume or surface [1]. However, extensive studies on this topic do not yet exist.
On the other hand, the idea that the molecular van der Waals (vdW) space is responsible for molecular properties affords an adequate reason for introducing vdW molecular descriptors (vdWMDs) with a clear physical meaning [3,5]. They were frequently used as molecular descriptors by themselves [3,6,8] or as a starting point for deriving other parameters, e.g. lipophilicity/ hydrophilicity [9], surface tension parameters [10], Weighted Holistic Invariant Molecular (WHIM) descriptors [11] and so on.
In this paper we present our efforts to develop some topological distance indices (TDIs) [5,12,13,14,15,16,17] and vdWMDs [3,5,6,18,19] and investigate if there exists a linear relationship between these two groups of structural parameters, situated at the first and second level of molecular structural information, respectively. One type of TDIs, the generalized (global) topological distance indices (GTDIs), denoted by kδλ, λ=0,1,2,3 and k=1,2,3,4,…, is generalized here on the basis of reciprocal distances from a molecular graph Γ (reciprocal distance matrix [20]). The other type was developed with the aid of real number local vertex invariants (LOVIs) based on the graph eigenvalues [12,13,14]. Eigenvectors corresponding to the largest negative eigenvalue of the distance matrix, D, can serve as LOVIs. Various TDIs have been obtained from these LOVIs by various operations (simple summation, or application of Randić-type formulas) [12]. All TDIs presented here were tested in correlations against boiling points of alkanes, with satisfactory results for some of them, also reported in this work. It must be mentioned that Trinajstić et al. [21] compared five TDIs and five topographical (3D) distance indices in order to answer the questions as to what extent the distance indices are intercorrelated and how they perform in a given QSAR for the boiling points of the first 150 alkanes with 2-10 carbon atoms.
Among calculated vdWMDs, [5] we selected here as molecular structural descriptors only the vdW volume VW and surface SW, VW/SW, vdW volume of molecule considered as ellipsoids VWE, semi-axes of the ellipsoid (a,b,c) which embeds a given molecule (viewed as a collection of atomic spheres distributed in 3D-space, each atomic sphere having a radius equal with its vdW radius) and two globularity measures [3,5,6,12].
The results obtained by correlation analysis of all the above described molecular structural descriptors and a QSPR study of boiling temperatures of the first alkanes with 2-9 carbon atoms are also reported. They permit some insights about the physical meaning of the investigated TDIs.
Description of Selected Topological Distance Indices
The distance matrix D(Γ) = {dij} of a graph Γ is an important graph-invariant. Its entries dij, called distances, are equal to the number of edges connecting the vertices i and j on the shortest path between them. Thus all dij are integers, and dij =1 for nearest neighbors; by definition, dii = 0. Therefore, the distance matrix D = D(Γ) of a labeled connected graph Γ is a real symmetric matrix NxN whose elements dij are defined as [21,22]:
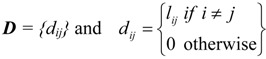 |
(1) |
where lij is the topological length of the shortest path, i. e. the minimum number of edges between the vertices i and j in Γ. The length of the shortest path lij is also called [22] the distance between the vertices i and j in Γ, hence the name “distance matrix” for D.
Many TDIs have been developed on the basis of D. We selected some of these for the present study, in which we analyze the relationship between TDIs and molecular vdW space. Among the TDIs that can be derived from D, the most popular investigated and applied is the Wiener number [23]. Besides the Wiener number [24,25] we will briefly present the following TDIs used in our analysis: the polarity number [24,25,26], the Platt index [26], the Balaban J index [27,28], and TDIs based on graph eigenvalues and eigenvectors [12,13,14]. We also generalize here the TDIs derived [5,15,16,17] from reciprocal distance matrix [20,21], denoted by kδλ.
(a) Wiener index
The Wiener index, W, [24,25] was defined as the sum of the number of bonds separating all pairs of atoms in an acyclic molecule. It is easily to shown that this index equal to the half-sum of the off-diagonal elements of D [29]:
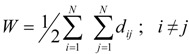 |
(2) |
where N is the total number of vertices (atoms) in Γ.
(b) Polarity number
Wiener has also introduced the so-called polarity number, P. P is the number of pairs of vertices separated by three edges, that is half of the number of distances of length three:
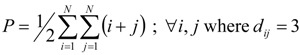 |
(3) |
In relation (3) N represents the total number of vertices in Γ.
The ½ factor before the sums in (3) compensates for the fact that the three edges between the vertices i and j in Γ are accounted for two times (both ways). W and P have been applied to correlations with boiling points, heat of formation and vaporization and other physical properties of alkanes [24,25,26].
(c) Platt index
Platt (nearest-neighbor edges) index F is calculated by summing for each edge the number of its adjacent edges [26]:
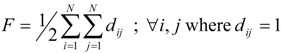 |
(4) |
(d) Balaban index
Balaban [27,28] has proposed a topological index, which can be described as the average distance sum connectivity. The Balaban topological index J of a molecular graph Γ is defined as [27]:
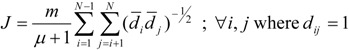 |
(5) |
where m is the number of edges in Γ, μ is the cyclomatic number, and the vertices i and j are adjacent.
The average distance sum for a vertex k in Γ represents the sum of all entries of the kth row or column in the distance matrix, D [27]:
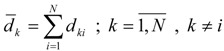 |
(6) |
The cyclomatic number μ = μ(Γ), i.e. the number of cycles in Γ, is given by [28]
| μ = m – n + 1 | (7) |
where N is the number of vertices in Γ. Relation (7) is the known Euler equation connecting the number of vertices (N), edges (m) and cycles (μ) in a planar graph. Average distance sums were used in relation (5) instead of distance sums because distance sums increase approximately parallel with m for the same type of branching. The ciclomatic number μ, defined in (7), was introduced in the definition of J because the presence of cycles markedly reduces the distance sums [7].
(e) Graph eigenvalues or eigenvector –based indices
Lowest and highest eigenvalues and corresponding eigenvectors of matrices A and D have also been used as topological indices and local vertex invariants (LOVIs) [12,13,14,30]. We present here only TDIs derived by us [12,13,14] from D of all alkanes with 2-9 carbon atoms. From the largest negative eigenvalues of D, denoted by E(D), and corresponding eigenvectors we introduced the following TDIs [13]:
| VAD1 = - E(A) | (8) |
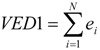 |
(9) |
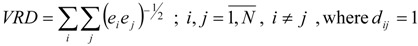 |
(10) |
where ei are the elements (LOVIs) of the first eigenvector derived from E(D) and N is the number of carbon atoms.
Two kinds of normalizations against the number N of carbon atoms of the alkane were carried out. Each of these led to a type of TDIs, denoted below by VxDk, distinguished by the final number k = 2 or k = 3:
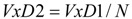 |
(11) |
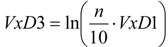 |
(12) |
where x = A, E.
Up to eight carbon atoms no degeneracy was found in the TDIs values as estimated by relations (8)–(12). However, for nine carbon atoms, just one pair of isomers for VED-type indices was found to have degenerate values [13].
The VxDk (with x=A and E, and k=1,3) and VRD indices were calculated here for the first alkanes with 2-9 carbon atoms by means of our IRS [31] computer package. The values were compared with those obtained with the aid of DRAGON [32]. The W, P, F, J, VADk and VEDk (k=1,3), VRD indices for 72 alkanes with N=1–9 carbon atoms are given in Table 1a.
Table 1a.
Topological Distance Indices and Boiling Points of the First 72 Alkanes
| Alkane | BP | W | P | F | J | VAD1 | VAD2 | VAD3 | VED1 | VED2 | VED3 | VRD |
| C2 | -88.5 | 1 | 0 | 0 | 1.0000 | 1.0000 | 0.5000 | -1.6094 | 1.4142 | 0.7071 | -1.2629 | 1.4142 |
| C3 | -44.5 | 4 | 0 | 2 | 1.6330 | 2.7321 | 0.9107 | -0.1989 | 1.7156 | 0.5719 | -0.6642 | 3.7224 |
| C4 | -0.5 | 10 | 1 | 4 | 1.9747 | 5.1623 | 1.2906 | 0.7251 | 1.9742 | 0.4935 | -0.2361 | 6.5255 |
| 2-M-C3 | -10.5 | 9 | 0 | 6 | 2.3238 | 4.6458 | 1.1614 | 0.6197 | 1.9723 | 0.4931 | -0.2371 | 6.9009 |
| C5 | 36.5 | 20 | 2 | 6 | 2.1906 | 8.2882 | 1.6576 | 1.4217 | 2.2036 | 0.4407 | 0.0970 | 9.7395 |
| 2M-C4 | 27.9 | 18 | 2 | 8 | 2.5395 | 7.4593 | 1.4919 | 1.3163 | 2.2020 | 0.4404 | 0.0962 | 10.1583 |
| 22MM-C3 | 9.5 | 16 | 0 | 12 | 3.0237 | 6.6056 | 1.3211 | 1.1948 | 2.2040 | 0.4408 | 0.0971 | 10.7414 |
| C6 | 68.7 | 35 | 3 | 8 | 2.3391 | 12.1093 | 2.0182 | 1.9832 | 2.4118 | 0.4020 | 0.3696 | 13.3165 |
| 3M-C5 | 63.2 | 31 | 4 | 10 | 2.7542 | 10.7424 | 1.7904 | 1.8634 | 2.4085 | 0.4014 | 0.3682 | 13.8800 |
| 2M-C5 | 60.2 | 32 | 3 | 10 | 2.6272 | 11.0588 | 1.8431 | 1.8924 | 2.4117 | 0.4020 | 0.3695 | 13.6798 |
| 23MM-C4 | 58.1 | 29 | 4 | 12 | 2.9935 | 10.0000 | 1.6667 | 1.7918 | 2.4121 | 0.4020 | 0.3697 | 14.1487 |
| 22MM-C4 | 49.7 | 28 | 3 | 14 | 3.1685 | 9.6702 | 1.6117 | 1.7582 | 2.4111 | 0.4019 | 0.3693 | 14.4073 |
| C7 | 98.4 | 56 | 4 | 10 | 2.4475 | 16.6254 | 2.3751 | 2.4543 | 2.6036 | 0.3720 | 0.6002 | 17.2230 |
| 3E-C5 | 93.5 | 48 | 6 | 12 | 2.9923 | 14.8636 | 2.1234 | 2.3422 | 2.6009 | 0.3716 | 0.5992 | 17.7855 |
| 3M-C6 | 91.8 | 50 | 5 | 12 | 2.8318 | 14.2970 | 2.0424 | 2.3034 | 2.5975 | 0.3711 | 0.5979 | 18.0592 |
| 2M-C6 | 90.0 | 52 | 4 | 12 | 2.6783 | 13.0698 | 1.8671 | 2.2136 | 2.6005 | 0.3715 | 0.5990 | 18.5519 |
| 23MM-C5 | 89.8 | 46 | 6 | 14 | 3.1442 | 15.4048 | 2.2007 | 2.3780 | 2.6050 | 0.3721 | 0.6008 | 17.5136 |
| 33MM-C5 | 86.0 | 44 | 6 | 16 | 3.3604 | 14.1760 | 2.0251 | 2.2949 | 2.6067 | 0.3724 | 0.6014 | 17.8657 |
| 223MMM-C4 | 80.9 | 42 | 6 | 18 | 3.5412 | 13.6346 | 1.9478 | 2.2559 | 2.6027 | 0.3718 | 0.5999 | 18.1940 |
| 24-MMC5 | 80.5 | 48 | 4 | 14 | 2.9532 | 13.6353 | 1.9479 | 2.2560 | 2.6038 | 0.3720 | 0.6003 | 18.2007 |
| 22MM-C5 | 79.2 | 46 | 4 | 16 | 3.1545 | 12.3945 | 1.7706 | 2.1606 | 2.6066 | 0.3724 | 0.6014 | 15.8479 |
| C8 | 125.8 | 84 | 5 | 12 | 2.5301 | 21.8364 | 2.7295 | 2.8604 | 2.7824 | 0.3478 | 0.8002 | 21.4335 |
| 3E-C6 | 118.9 | 72 | 7 | 14 | 3.0744 | 19.5420 | 2.4428 | 2.7494 | 2.7787 | 0.3473 | 0.7989 | 22.0645 |
| 3M-C7 | 118.8 | 76 | 6 | 14 | 2.8621 | 19.7628 | 2.4704 | 2.7607 | 2.7810 | 0.3476 | 0.7997 | 21.9365 |
| 34MM-C6 | 118.7 | 68 | 8 | 16 | 3.2925 | 18.7788 | 2.3474 | 2.7096 | 2.7762 | 0.3470 | 0.7979 | 22.3387 |
| 3E-3M-C5 | 118.2 | 64 | 9 | 18 | 3.5832 | 16.6705 | 2.0838 | 2.5905 | 2.7768 | 0.3471 | 0.7982 | 23.1188 |
| 4M-C7 | 117.7 | 75 | 6 | 14 | 2.9196 | 17.4187 | 2.1773 | 2.6344 | 2.7789 | 0.3474 | 0.7989 | 22.7102 |
| 2M-C7 | 117.6 | 79 | 5 | 14 | 2.7158 | 17.6759 | 2.2095 | 2.6491 | 2.7799 | 0.3475 | 0.7993 | 22.5967 |
| 3E-2M-C5 | 115.6 | 67 | 8 | 16 | 3.3549 | 17.4427 | 2.1803 | 2.6358 | 2.7789 | 0.3474 | 0.7989 | 22.7488 |
| 23MM-C6 | 115.3 | 70 | 7 | 16 | 3.1708 | 20.4792 | 2.5599 | 2.7963 | 2.7849 | 0.3481 | 0.8011 | 21.6556 |
| 233MMM-C5 | 114.6 | 62 | 9 | 20 | 3.7083 | 19.1115 | 2.3889 | 2.7272 | 2.7878 | 0.3485 | 0.8021 | 21.9131 |
| 234MMM-C5 | 113.4 | 65 | 8 | 18 | 3.4642 | 18.3964 | 2.2996 | 2.6890 | 2.7838 | 0.3480 | 0.8007 | 22.2412 |
| 33MM-C6 | 112.0 | 67 | 7 | 18 | 3.3734 | 18.1815 | 2.2727 | 2.6773 | 2.7815 | 0.3477 | 0.7999 | 22.3829 |
| 223MMM-C5 | 110.5 | 63 | 8 | 20 | 3.6233 | 16.8079 | 2.1010 | 2.5987 | 2.7851 | 0.3481 | 0.8011 | 22.7627 |
| 24MM-C6 | 109.4 | 71 | 6 | 16 | 3.0988 | 16.0683 | 2.0085 | 2.5537 | 2.7826 | 0.3478 | 0.8002 | 23.1970 |
| 25MM-C6 | 108.4 | 74 | 5 | 16 | 2.9278 | 18.4133 | 2.3017 | 2.6899 | 2.7843 | 0.3480 | 0.8009 | 22.2507 |
| 22MM-C6 | 107.0 | 71 | 5 | 18 | 3.1118 | 17.0338 | 2.1292 | 2.6121 | 2.7878 | 0.3485 | 0.8021 | 22.6056 |
| 2233MMMM-C4 | 106.0 | 58 | 9 | 24 | 4.0204 | 16.3152 | 2.0394 | 2.5690 | 2.7838 | 0.3480 | 0.8007 | 23.0345 |
| 224MMM-C5 | 99.3 | 66 | 5 | 20 | 3.3889 | 14.9373 | 1.8672 | 2.4807 | 2.7892 | 0.3487 | 0.8026 | 23.5670 |
| C9 | 150.6 | 120 | 6 | 14 | 2.5951 | 27.7422 | 3.0825 | 3.2176 | 2.9505 | 0.3278 | 0.9766 | 25.9281 |
| 33EE-C5 | 146.2 | 88 | 12 | 20 | 3.8247 | 25.0208 | 2.7801 | 3.1143 | 2.9471 | 0.3275 | 0.9755 | 26.5488 |
| 3E-C7 | 143.0 | 104 | 8 | 16 | 3.0922 | 23.6799 | 2.6311 | 3.0593 | 2.9429 | 0.3270 | 0.9740 | 26.9873 |
| 3M-C8 | 143.0 | 110 | 7 | 16 | 2.8766 | 21.7527 | 2.4170 | 2.9744 | 2.9458 | 0.3273 | 0.9750 | 27.4391 |
| 4M-C8 | 142.5 | 108 | 7 | 16 | 2.9548 | 22.6204 | 2.5134 | 3.0135 | 2.9491 | 0.3277 | 0.9761 | 27.0595 |
| 2M-C8 | 142.5 | 114 | 6 | 16 | 2.7467 | 22.2705 | 2.4745 | 2.9979 | 2.9448 | 0.3272 | 0.9747 | 27.3590 |
| 3E-23MM-C5 | 141.6 | 86 | 12 | 22 | 3.9192 | 25.4119 | 2.8236 | 3.1299 | 2.9505 | 0.3278 | 0.9766 | 26.3543 |
| 2334MMMM-C5 | 141.5 | 84 | 12 | 24 | 4.0137 | 24.0988 | 2.6776 | 3.0768 | 2.9457 | 0.3273 | 0.9750 | 26.7923 |
| 4E-C7 | 141.2 | 102 | 8 | 16 | 3.1753 | 21.3349 | 2.3705 | 2.9550 | 2.9439 | 0.3271 | 0.9744 | 27.6869 |
| 3E-3M-C6 | 140.6 | 92 | 10 | 20 | 3.6174 | 22.2198 | 2.4689 | 2.9956 | 2.9461 | 0.3273 | 0.9751 | 27.2876 |
| 23MM-C7 | 140.5 | 102 | 8 | 18 | 3.1553 | 20.7438 | 2.3049 | 2.9269 | 2.9501 | 0.3278 | 0.9765 | 27.6329 |
| 334MMM-C6 | 140.5 | 88 | 11 | 22 | 3.8024 | 19.8563 | 2.2063 | 2.8832 | 2.9481 | 0.3276 | 0.9758 | 28.0907 |
| 2233MMMM-C5 | 140.3 | 82 | 12 | 26 | 4.1447 | 23.0687 | 2.5632 | 3.0331 | 2.9507 | 0.3279 | 0.9767 | 26.8886 |
| 34MM-C7 | 140.1 | 98 | 9 | 18 | 3.3248 | 22.6789 | 2.5199 | 3.0161 | 2.9473 | 0.3275 | 0.9755 | 27.1235 |
| 234MMM-C6 | 139.0 | 92 | 10 | 20 | 3.5758 | 22.6772 | 2.5197 | 3.0160 | 2.9482 | 0.3276 | 0.9759 | 27.1184 |
| 233MMM-C6 | 137.7 | 90 | 10 | 22 | 3.7021 | 20.3172 | 2.2575 | 2.9061 | 2.9490 | 0.3277 | 0.9761 | 27.8661 |
| 33MM-C7 | 137.3 | 98 | 8 | 20 | 3.3301 | 26.2722 | 2.9191 | 3.1632 | 2.9537 | 0.3282 | 0.9777 | 26.0911 |
| 3E-24MM-C5 | 136.7 | 90 | 10 | 20 | 3.6776 | 24.7896 | 2.7544 | 3.1051 | 2.9575 | 0.3286 | 0.9790 | 26.2728 |
| 35MM-C7 | 136.0 | 100 | 8 | 18 | 3.2230 | 23.9292 | 2.6588 | 3.0697 | 2.9542 | 0.3282 | 0.9779 | 26.5647 |
| 25MM-C7 | 136.0 | 104 | 7 | 18 | 3.0608 | 23.5441 | 2.6160 | 3.0535 | 2.9506 | 0.3278 | 0.9767 | 26.7803 |
| 26MM-C7 | 135.2 | 108 | 6 | 18 | 2.9147 | 21.1839 | 2.3538 | 2.9479 | 2.9525 | 0.3281 | 0.9773 | 27.4273 |
| 44MM-C7 | 135.2 | 96 | 8 | 20 | 3.4311 | 23.5541 | 2.6171 | 3.0539 | 2.9507 | 0.3279 | 0.9767 | 26.7833 |
| 4E-2M-C6 | 133.8 | 98 | 8 | 18 | 3.3074 | 22.0627 | 2.4514 | 2.9885 | 2.9549 | 0.3283 | 0.9781 | 27.0476 |
| 3E-22MM-C5 | 133.8 | 88 | 10 | 22 | 3.7929 | 21.1970 | 2.3552 | 2.9485 | 2.9515 | 0.3279 | 0.9770 | 27.4362 |
| 24MM-C7 | 133.5 | 102 | 7 | 18 | 3.1513 | 20.7945 | 2.3105 | 2.9293 | 2.9490 | 0.3277 | 0.9761 | 27.7030 |
| 2234MMMM-C5 | 133.0 | 86 | 10 | 24 | 3.8776 | 19.3005 | 2.1445 | 2.8548 | 2.9542 | 0.3283 | 0.9779 | 28.1080 |
| 22MM-C7 | 132.7 | 104 | 6 | 20 | 3.0730 | 23.9635 | 2.6626 | 3.0712 | 2.9540 | 0.3282 | 0.9778 | 26.5871 |
| 223MMM-C6 | 131.7 | 92 | 9 | 22 | 3.5887 | 22.4662 | 2.4962 | 3.0067 | 2.9585 | 0.3287 | 0.9793 | 26.8263 |
| 235MMM-C6 | 131.3 | 96 | 8 | 20 | 3.3766 | 21.6063 | 2.4007 | 2.9676 | 2.9548 | 0.3283 | 0.9781 | 27.1920 |
| 244MMM-C6 | 126.5 | 92 | 8 | 22 | 3.5768 | 20.1263 | 2.2363 | 2.8967 | 2.9602 | 0.3289 | 0.9799 | 27.5398 |
| 224MMM-C6 | 126.5 | 94 | 7 | 22 | 3.4673 | 21.2250 | 2.3583 | 2.9498 | 2.9512 | 0.3279 | 0.9769 | 27.4608 |
| 225MMM-C6 | 124.0 | 98 | 6 | 22 | 3.2807 | 19.7257 | 2.1917 | 2.8766 | 2.9565 | 0.3285 | 0.9786 | 27.8260 |
Reciprocal Distance – Based Indices
Another graph-invariant is the reciprocal distance matrix RD = 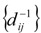 , i,j = 1,N, where N is the total number of graph vertices. This is a symmetrical matrix whose elements are reciprocal of the topological distance [5,16,17,20,33]. The first TDIs proposed on the basis of RD have been developed by a two-steps process as follows [5,16,17].
, i,j = 1,N, where N is the total number of graph vertices. This is a symmetrical matrix whose elements are reciprocal of the topological distance [5,16,17,20,33]. The first TDIs proposed on the basis of RD have been developed by a two-steps process as follows [5,16,17].
-
(i)The LOVI of each vertex in a molecular graph Γ, denoted later by μi, was defined from the RD using the following relation [5,16]:
In relation (13) dij is the topological distance between the vertices i and j, N represents the total number of vertices (i.e. non-hydrogen atoms) in Γ, and summation is made over all possible paths, from dij = 1 to dij = max(dij). Thus, each vertex is well characterized; it contains global information of the topological structure of Γ, the topological interaction between vertices i and j decreasing as distance dij is increasing. That is, for each vertex i, the quantity μi may be viewed as a measure if the influence of all others vertices in a given graph Γ on the vertex i.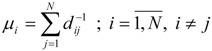
(13) -
(ii)The LOVIs μi were condensed into a TDI, hδ, with the aid of the Randić-type formula [34], the generalized molecular connectivity [35], as follows [5,16]:
These topological distances connectivity indices (TDCIs) [5,16], also called topological distance measure connectivity indices (TDMCIs) [17], of order higher than three, have not been used in correlation due to the expected small contributions to the molecular properties.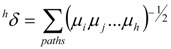
(14)
TDCIs of order one (1δ), two (2δ) and three (3δ) have been calculated by the following relations [5,16]:
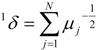 |
(15) |
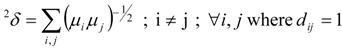 |
(16) |
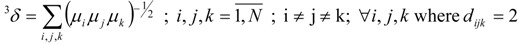 |
(17) |
Monoparametric correlations with molecular properties such as boiling temperatures (at normal pressure), gas chromatographic retention indices, atomization enthalpies, and molar refractions for alkanes were performed. The reported results for 2δ are very good, the correlation coefficients r being in the range 0.983 – 0.991 [5,16].
In this paper we extend TDCIs by generalization of relation (13) as follows:
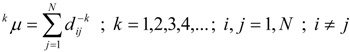 |
(18) |
Thus, we obtain a set of generalized topological distances indices (GTDIs), kδλ, where k is the same as in relation (18), which can be calculated with the following formulas:
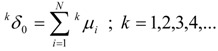 |
(19) |
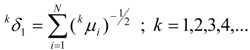 |
(20) |
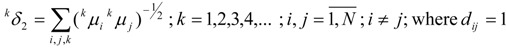 |
(21) |
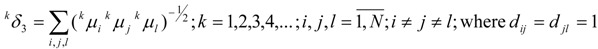 |
(22) |
One may easily observe that the TDMCIs in relations (15)-(17) are included in GTDIs in relations (19)-(22), and there exists a formal identity between λδ and 1δλ (λ=1,3).
The sixteen GTDIs corresponding to 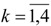 in relations (19)-(22) have been calculated with the IRS computer program [31] for 72 alkanes with
in relations (19)-(22) have been calculated with the IRS computer program [31] for 72 alkanes with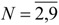 carbon atoms. The obtained results are given in Table 1b.
carbon atoms. The obtained results are given in Table 1b.
Table 1b.
Generalized Topological Distance Indices for the First 72 Alkanes
| Alkane | 1 δο | 2 δο | 3 δο | 4 δο | 1 δ1 | 2 δ1 | 3 δ1 | 4 δ1 | 1 δ2 | 2 δ2 | 3 δ2 | 4 δ2 | 1 δ3 | 2 δ3 | 3 δ3 | 4 δ3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C2 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | 4.0000 | 4.0000 | 4.0000 | 4.0000 |
| C3 | 5.0000 | 4.5000 | 4.2500 | 4.1250 | 2.3401 | 2.4960 | 2.5927 | 2.6474 | 2.3094 | 2.5298 | 2.6667 | 2.7440 | 5.4042 | 6.3143 | 6.9139 | 7.2644 |
| C4 | 8.6667 | 7.2222 | 6.5741 | 6.2747 | 2.7420 | 3.0476 | 3.2273 | 3.3217 | 2.6684 | 3.1746 | 3.4867 | 3.6562 | 5.9369 | 7.7158 | 8.8912 | 9.5537 |
| 2-M-C3 | 9.0000 | 7.5000 | 6.7500 | 6.3750 | 2.6987 | 3.0268 | 3.2606 | 3.4058 | 2.4495 | 2.8284 | 3.0984 | 3.2660 | 6.6104 | 8.5612 | 10.1027 | 11.1232 |
| C5 | 12.8333 | 10.0694 | 8.9294 | 8.4322 | 3.1512 | 3.6103 | 3.8698 | 4.0001 | 3.0184 | 3.8281 | 4.3204 | 4.5786 | 6.4421 | 9.1923 | 11.0331 | 12.0504 |
| 2M-C4 | 13.3333 | 10.4444 | 9.1481 | 8.5494 | 3.1005 | 3.5870 | 3.9085 | 4.0918 | 2.8014 | 3.4922 | 3.9664 | 4.2431 | 6.7078 | 9.4432 | 11.5347 | 12.8389 |
| 22MM-C3 | 14.0000 | 11.0000 | 9.5000 | 8.7500 | 3.0298 | 3.5237 | 3.9112 | 4.1707 | 2.5298 | 3.0237 | 3.4112 | 3.6707 | 7.6649 | 10.6547 | 13.3420 | 15.3090 |
| C6 | 17.4000 | 12.9967 | 11.3007 | 10.5929 | 3.5580 | 4.1756 | 4.5145 | 4.6794 | 3.3552 | 4.4798 | 5.1562 | 5.5026 | 6.9256 | 10.6698 | 13.1919 | 14.5611 |
| 3M-C5 | 18.1667 | 13.5139 | 11.5775 | 10.7316 | 3.4944 | 4.1486 | 4.5609 | 4.7810 | 3.1171 | 4.1359 | 4.8312 | 5.2222 | 6.8584 | 10.4033 | 13.1037 | 14.7234 |
| 2M-C5 | 18.0000 | 13.4167 | 11.5347 | 10.7147 | 3.5062 | 4.1508 | 4.5533 | 4.7718 | 3.1536 | 4.1548 | 4.8105 | 5.1729 | 7.1146 | 10.8819 | 13.7111 | 15.4109 |
| 23MM-C4 | 18.6667 | 13.8889 | 11.7963 | 10.8488 | 3.4495 | 4.1170 | 4.5856 | 4.8619 | 2.9495 | 3.8299 | 4.4719 | 4.8606 | 7.1742 | 10.8019 | 13.8032 | 15.7592 |
| 22MM-C4 | 19.0000 | 14.1667 | 11.9722 | 10.9491 | 3.4206 | 4.0819 | 4.5653 | 4.8647 | 2.8604 | 3.6769 | 4.2923 | 4.6781 | 7.5167 | 11.2053 | 14.4129 | 16.6341 |
| C7 | 22.3000 | 15.9794 | 13.6813 | 12.7551 | 3.9603 | 4.7412 | 5.1599 | 5.3589 | 3.6800 | 5.1280 | 5.9921 | 6.4268 | 7.3893 | 12.1384 | 15.3525 | 17.0740 |
| 3E-C5 | 23.5000 | 16.7083 | 14.0382 | 12.9216 | 3.8752 | 4.7084 | 5.2169 | 5.4731 | 3.3959 | 4.7553 | 5.6906 | 6.2028 | 6.9966 | 11.3769 | 14.7713 | 16.7592 |
| 3M-C6 | 23.2333 | 16.5661 | 13.9801 | 12.9001 | 3.8924 | 4.7120 | 5.2071 | 5.4618 | 3.4464 | 4.7880 | 5.6738 | 6.1525 | 7.2633 | 11.8383 | 15.2911 | 17.3058 |
| 2M-C6 | 22.9667 | 16.4239 | 13.9220 | 12.8786 | 3.9090 | 4.7153 | 5.1983 | 5.4513 | 3.4927 | 4.8103 | 5.6491 | 6.0982 | 7.5534 | 12.3402 | 15.8714 | 17.9278 |
| 23MM-C5 | 24.0000 | 17.0833 | 14.2569 | 13.0388 | 3.8348 | 4.6756 | 5.2385 | 5.5521 | 3.2543 | 4.4670 | 5.3366 | 5.8418 | 7.3034 | 11.7589 | 15.4142 | 17.7128 |
| 33MM-C5 | 24.5000 | 17.4583 | 14.4757 | 13.1560 | 3.7987 | 4.6369 | 5.2219 | 5.5613 | 3.1509 | 4.3008 | 5.1632 | 5.6840 | 7.4491 | 11.8284 | 15.5991 | 18.1020 |
| 223MMM-C4 | 25.0000 | 17.8333 | 14.6944 | 13.2731 | 3.7592 | 4.6011 | 5.2358 | 5.6326 | 3.0182 | 4.0264 | 4.8121 | 5.3131 | 7.7694 | 12.2923 | 16.3997 | 19.2855 |
| 24-MMC5 | 23.6667 | 16.8889 | 14.1713 | 13.0050 | 3.8562 | 4.6864 | 5.2345 | 5.5428 | 3.3081 | 4.4977 | 5.3100 | 5.7725 | 7.6854 | 12.5026 | 16.3675 | 18.7859 |
| 22MM-C5 | 24.1667 | 17.2639 | 14.3900 | 13.1222 | 3.8200 | 4.6450 | 5.2116 | 5.5459 | 3.2087 | 4.3428 | 5.1438 | 5.6140 | 7.8246 | 12.5789 | 16.5845 | 19.2393 |
| C8 | 27.4857 | 19.0030 | 16.0677 | 14.9182 | 4.3576 | 5.3063 | 5.8056 | 6.0386 | 3.9943 | 5.7728 | 6.8275 | 7.3510 | 7.8354 | 13.5967 | 17.5119 | 19.5871 |
| 3E-C6 | 28.9667 | 19.8406 | 16.4568 | 15.0933 | 4.2637 | 5.2701 | 5.8641 | 6.1546 | 3.7022 | 5.3951 | 6.5311 | 7.1334 | 7.3777 | 12.7893 | 16.9615 | 19.3494 |
| 3M-C7 | 28.5333 | 19.6289 | 16.3767 | 15.0655 | 4.2885 | 5.2756 | 5.8524 | 6.1415 | 3.7698 | 5.4364 | 6.5110 | 7.0777 | 7.7008 | 13.2928 | 17.4546 | 19.8252 |
| 34MM-C6 | 29.7333 | 20.3578 | 16.7336 | 15.2320 | 4.2109 | 5.2319 | 5.8921 | 6.2430 | 3.5361 | 5.0896 | 6.1974 | 6.8225 | 7.4466 | 12.7169 | 17.0353 | 19.6753 |
| 3E-3M-C5 | 30.5000 | 20.8750 | 17.0104 | 15.3707 | 4.1627 | 5.1871 | 5.8802 | 6.2603 | 3.4063 | 4.8953 | 6.0230 | 6.6881 | 7.4129 | 12.4814 | 16.8736 | 19.6994 |
| 4M-C7 | 28.6333 | 19.6739 | 16.3920 | 15.0702 | 4.2834 | 5.2746 | 5.8538 | 6.1428 | 3.7575 | 5.4330 | 6.5155 | 7.0829 | 7.6393 | 13.2499 | 17.4739 | 19.8881 |
| 2M-C7 | 28.2000 | 19.4622 | 16.3119 | 15.0424 | 4.3072 | 5.2797 | 5.8435 | 6.1309 | 3.8189 | 5.4601 | 6.4857 | 7.0227 | 7.9891 | 13.7942 | 18.0287 | 20.4407 |
| 3E-2M-C5 | 29.8333 | 20.4028 | 16.7488 | 15.2366 | 4.2051 | 5.2305 | 5.8943 | 6.2452 | 3.5201 | 5.0765 | 6.1945 | 6.8241 | 7.3998 | 12.6984 | 17.1022 | 19.8072 |
| 23MM-C6 | 29.4667 | 20.2156 | 16.6755 | 15.2105 | 4.2265 | 5.2371 | 5.8846 | 6.2330 | 3.5770 | 5.1171 | 6.1800 | 6.7729 | 7.6750 | 13.1693 | 17.5974 | 20.2978 |
| 233MMM-C5 | 31.0000 | 21.2500 | 17.2292 | 15.4878 | 4.1270 | 5.1511 | 5.8919 | 6.3299 | 3.2923 | 4.6369 | 5.6781 | 6.3186 | 7.7163 | 12.9264 | 17.6277 | 20.8159 |
| 234MMM-C5 | 30.3333 | 20.7778 | 16.9676 | 15.3538 | 4.1686 | 5.1968 | 5.9131 | 6.3223 | 3.3990 | 4.8047 | 5.8459 | 6.4638 | 7.6951 | 13.0744 | 17.7163 | 20.7199 |
| 33MM-C6 | 30.0667 | 20.6356 | 16.9095 | 15.3323 | 4.1883 | 5.1979 | 5.8690 | 6.2431 | 3.4731 | 4.9521 | 6.0113 | 6.6197 | 7.7662 | 13.1951 | 17.7780 | 20.7155 |
| 223MMM-C5 | 30.8333 | 21.1528 | 17.1863 | 15.4710 | 4.1365 | 5.1563 | 5.8887 | 6.3236 | 3.3155 | 4.6580 | 5.6766 | 6.2961 | 7.8598 | 13.2227 | 18.0216 | 21.2749 |
| 24MM-C6 | 29.3000 | 20.1183 | 16.6327 | 15.1936 | 4.2360 | 5.2451 | 5.8878 | 6.2329 | 3.5965 | 5.1282 | 6.1730 | 6.7523 | 7.8211 | 13.4491 | 17.9496 | 20.6859 |
| 25MM-C6 | 28.9333 | 19.9311 | 16.5594 | 15.1675 | 4.2564 | 5.2519 | 5.8805 | 6.2228 | 3.6463 | 5.1511 | 6.1455 | 6.6950 | 8.1313 | 13.9817 | 18.5400 | 21.2935 |
| 22MM-C6 | 29.5333 | 20.3511 | 16.7934 | 15.2893 | 4.2183 | 5.2087 | 5.8567 | 6.2256 | 3.5484 | 5.0012 | 5.9848 | 6.5405 | 8.2150 | 14.0130 | 18.7422 | 21.7600 |
| 2233MMMM-C4 | 32.0000 | 22.0000 | 17.6667 | 15.7222 | 4.0599 | 5.0746 | 5.8780 | 6.3994 | 3.0987 | 4.2357 | 5.1633 | 5.7769 | 8.1946 | 13.5658 | 18.7685 | 22.6023 |
| 224MMM-C5 | 30.3333 | 20.8611 | 17.0579 | 15.4203 | 4.1649 | 5.1758 | 5.8899 | 6.3159 | 3.3789 | 4.6995 | 5.6511 | 6.2177 | 8.3047 | 14.1290 | 19.2053 | 22.6104 |
| C9 | 32.9214 | 22.0579 | 18.4580 | 17.0818 | 4.7502 | 5.8708 | 6.4512 | 6.7183 | 4.2996 | 6.4144 | 7.6624 | 8.2752 | 8.2660 | 15.0456 | 19.6696 | 22.1000 |
| 33EE-C5 | 37.0000 | 24.4167 | 19.5764 | 17.5932 | 4.5127 | 5.7311 | 6.5397 | 6.9614 | 3.6315 | 5.4611 | 6.8712 | 7.6900 | 7.3862 | 13.1373 | 18.2140 | 21.4143 |
| 3E-C7 | 34.6000 | 22.9589 | 18.8626 | 17.2603 | 4.6523 | 5.8320 | 6.5097 | 6.8346 | 4.0103 | 6.0358 | 7.3669 | 8.0585 | 7.8024 | 14.2310 | 19.1250 | 21.8706 |
| 3M-C8 | 34.0524 | 22.7080 | 18.7724 | 17.2302 | 4.6811 | 5.8389 | 6.4977 | 6.8212 | 4.0843 | 6.0809 | 7.3466 | 8.0021 | 8.1361 | 14.7428 | 19.6123 | 22.3387 |
| 4M-C8 | 34.2190 | 22.7775 | 18.7944 | 17.2364 | 4.6733 | 5.8372 | 6.4993 | 6.8226 | 4.0669 | 6.0763 | 7.3521 | 8.0080 | 8.0534 | 14.6879 | 19.6343 | 22.4074 |
| 2M-C8 | 33.6714 | 22.5266 | 18.7041 | 17.2063 | 4.7009 | 5.8437 | 6.4889 | 6.8105 | 4.1340 | 6.1054 | 7.3213 | 7.9470 | 8.4147 | 15.2408 | 20.1847 | 22.9532 |
| 3E-23MM-C5 | 37.5000 | 24.7917 | 19.7951 | 17.7104 | 4.4802 | 5.6951 | 6.5492 | 7.0295 | 3.5326 | 5.2173 | 6.5325 | 7.3221 | 7.6733 | 13.5674 | 18.9279 | 22.4681 |
| 2334MMMM-C5 | 38.0000 | 25.1667 | 20.0139 | 17.8275 | 4.4477 | 5.6592 | 6.5587 | 7.0975 | 3.4337 | 4.9735 | 6.1938 | 6.9541 | 7.9605 | 14.0001 | 19.6539 | 23.5480 |
| 4E-C7 | 34.7667 | 23.0283 | 18.8846 | 17.2666 | 4.6441 | 5.8303 | 6.5118 | 6.8364 | 3.9904 | 6.0269 | 7.3706 | 8.0640 | 7.7226 | 14.1724 | 19.1455 | 21.9393 |
| 3E-3M-C6 | 36.4667 | 24.1322 | 19.4602 | 17.5502 | 4.5420 | 5.7452 | 6.5280 | 6.9427 | 3.7049 | 5.5319 | 6.8675 | 7.6236 | 7.7215 | 13.8285 | 19.0539 | 22.3194 |
| 23MM-C7 | 35.1000 | 23.3339 | 19.0814 | 17.3775 | 4.6176 | 5.7992 | 6.5297 | 6.9128 | 3.8964 | 5.7645 | 7.0174 | 7.6982 | 8.0909 | 14.6099 | 19.7581 | 22.8174 |
| 334MMM-C6 | 37.2333 | 24.6494 | 19.7371 | 17.6889 | 4.4945 | 5.7029 | 6.5450 | 7.0214 | 3.5669 | 5.2523 | 6.5375 | 7.3006 | 7.8283 | 13.8587 | 19.2586 | 22.8134 |
| 2233MMMM-C5 | 38.5000 | 25.5417 | 20.2326 | 17.9447 | 4.4191 | 5.6198 | 6.5332 | 7.0972 | 3.3628 | 4.8363 | 6.0255 | 6.7821 | 8.1344 | 14.1916 | 20.0131 | 24.1679 |
| 34MM-C7 | 35.5333 | 23.5456 | 19.1614 | 17.4052 | 4.5950 | 5.7918 | 6.5385 | 6.9241 | 3.8412 | 5.7309 | 7.0389 | 7.7534 | 7.8077 | 14.1126 | 19.2166 | 22.2610 |
| 234MMM-C6 | 36.4667 | 24.1322 | 19.4602 | 17.5502 | 4.5377 | 5.7501 | 6.5661 | 7.0132 | 3.6731 | 5.4219 | 6.7052 | 7.4444 | 7.8294 | 14.0204 | 19.3366 | 22.6855 |
| 233MMM-C6 | 36.9667 | 24.5072 | 19.6790 | 17.6674 | 4.5090 | 5.7095 | 6.5388 | 7.0119 | 3.6029 | 5.2825 | 6.5257 | 7.2548 | 8.0118 | 14.2671 | 19.7998 | 23.4304 |
| 33MM-C7 | 35.7667 | 23.7783 | 19.3221 | 17.5009 | 4.5789 | 5.7599 | 6.5143 | 6.9230 | 3.7952 | 5.6017 | 6.8504 | 7.5460 | 8.1623 | 14.6262 | 19.9391 | 23.2389 |
| 3E-24MM-C5 | 36.6667 | 24.2222 | 19.4907 | 17.5594 | 4.5272 | 5.7459 | 6.5684 | 7.0162 | 3.6479 | 5.4013 | 6.7009 | 7.4473 | 7.7455 | 13.9657 | 19.4139 | 22.8677 |
| 35MM-C7 | 35.2667 | 23.4033 | 19.1034 | 17.3837 | 4.6087 | 5.8019 | 6.5413 | 6.9232 | 3.8696 | 5.7494 | 7.0335 | 7.7318 | 7.9742 | 14.4001 | 19.5371 | 22.5891 |
| 25MM-C7 | 34.8333 | 23.1917 | 19.0233 | 17.3560 | 4.6310 | 5.8100 | 6.5342 | 6.9130 | 3.9217 | 5.7757 | 7.0071 | 7.6745 | 8.2729 | 14.9280 | 20.1221 | 23.1915 |
| 26MM-C7 | 34.4333 | 23.0006 | 18.9517 | 17.3312 | 4.6515 | 5.8159 | 6.5261 | 6.9026 | 3.9707 | 5.7989 | 6.9809 | 7.6190 | 8.5582 | 15.4324 | 20.6972 | 23.8055 |
| 44MM-C7 | 35.9667 | 23.8683 | 19.3526 | 17.5102 | 4.5695 | 5.7574 | 6.5165 | 6.9252 | 3.7743 | 5.5942 | 6.8580 | 7.5555 | 8.0562 | 14.5324 | 19.9493 | 23.3281 |
| 4E-2M-C6 | 35.4333 | 23.4728 | 19.1253 | 17.3900 | 4.5999 | 5.7998 | 6.5442 | 6.9259 | 3.8467 | 5.7313 | 7.0295 | 7.7335 | 7.9109 | 14.3765 | 19.6153 | 22.7325 |
| 3E-22MM-C5 | 37.1667 | 24.5972 | 19.7095 | 17.6766 | 4.4979 | 5.7064 | 6.5440 | 7.0172 | 3.5737 | 5.2601 | 6.5330 | 7.2796 | 7.9123 | 14.1177 | 19.7050 | 23.3971 |
| 24MM-C7 | 35.0333 | 23.2817 | 19.0538 | 17.3652 | 4.6216 | 5.8060 | 6.5343 | 6.9139 | 3.9032 | 5.7719 | 7.0149 | 7.6829 | 8.1669 | 14.8378 | 20.1251 | 23.2669 |
| 2234MMMM-C5 | 37.6667 | 24.9722 | 19.9282 | 17.7938 | 4.4646 | 5.6723 | 6.5601 | 7.0926 | 3.4691 | 5.0036 | 6.1899 | 6.9201 | 8.1948 | 14.4912 | 20.3010 | 24.2834 |
| 22MM-C7 | 35.1000 | 23.4450 | 19.1925 | 17.4546 | 4.6130 | 5.7721 | 6.5017 | 6.9051 | 3.8764 | 5.6527 | 6.8222 | 7.4653 | 8.6219 | 15.4526 | 20.8955 | 24.2724 |
| 223MMM-C6 | 36.7000 | 24.3650 | 19.6209 | 17.6459 | 4.5226 | 5.7161 | 6.5348 | 7.0046 | 3.6339 | 5.3072 | 6.5210 | 7.2279 | 8.1914 | 14.6038 | 20.1965 | 23.8601 |
| 235MMM-C6 | 35.9333 | 23.8478 | 19.3441 | 17.5072 | 4.5656 | 5.7667 | 6.5637 | 7.0037 | 3.7352 | 5.4631 | 6.6812 | 7.3734 | 8.1979 | 14.7547 | 20.2447 | 23.6759 |
| 244MMM-C6 | 36.6333 | 24.3128 | 19.5933 | 17.6336 | 4.5258 | 5.7253 | 6.5466 | 7.0132 | 3.6349 | 5.3030 | 6.5169 | 7.2233 | 8.2476 | 14.7385 | 20.4006 | 24.0912 |
| 224MMM-C6 | 36.3667 | 24.1706 | 19.5353 | 17.6121 | 4.5394 | 5.7322 | 6.5428 | 7.0060 | 3.6656 | 5.3281 | 6.5138 | 7.1978 | 8.4249 | 15.0656 | 20.7876 | 24.5142 |
| 225MMM-C6 | 35.9000 | 23.9383 | 19.4467 | 17.5814 | 4.5628 | 5.7423 | 6.5373 | 6.9966 | 3.7170 | 5.3520 | 6.4847 | 7.1383 | 8.7454 | 15.6258 | 21.3973 | 25.1226 |
| 2244MMMM-C5 | 37.5000 | 24.9583 | 19.9757 | 17.8435 | 4.4696 | 5.6607 | 6.5422 | 7.0877 | 3.4658 | 4.9149 | 5.9990 | 6.6664 | 8.8457 | 15.6909 | 22.0017 | 26.4205 |
van der Waals Molecular Descriptors
No general theory of the quantitative relationship between molecular structure and molecular properties in organic chemistry (QSPR) or biological activities in medicinal chemistry (QSAR) can reasonably be regarded as satisfactory unless it provides a sound basis for predicting and interpreting linear relationships among molecular quantities.
A satisfactory theoretical model for linear correlations in organic and/or medicinal chemistry should allow reliable predictions to be made as easily as possible concerning both the circumstances in which correlations should occur (e.g., between which properties and for which compounds) and the magnitudes of the regression coefficients.
The concepts used in the model – for example, analysis into electronic (polar and resonance), hydrophobic, and steric effects – should be defined in such a way that knowledge gained through the interpretation of the linear correlations can be readily used in other areas or organic or medicinal chemistry (e.g., in elucidating the reaction mechanisms or receptor-drug molecule interaction).
Therefore, the design of molecular descriptors with very clear physical meaning is a very important task in this area of research. Analysis of the informational content of TDISs and their possible steric nature [7] as described by vdW molecular descriptors are also presented in this paper. To do this we used a set of van der Waals descriptors [3,5,6], such as the vdW molecular volume (VW) [19,36,37,38] and surface (SW) [18], and other descriptors of shape and size of alkane molecules, e.g. the volume of the ellipsoid which embeds the whole molecule extended along the Ox axes of Cartesian system of coordinates, VEL, semi-axes of this ellipsoid [3,5,6], EX, EY, EZ, along Ox, Oy, and Oz axes, respectively, two measures of globularity [12], denoted by GLOB, GLEL and a measure of molecular packing, RWV.
(a) Molecular van der Waals Volume
The concept of molecular volume and surface area have found many applications, not only in QSAR, but also in the studies of molecular interactions, especially in relating the bulk properties of substances like crystal packing with molecular structures [39]. The molecular volume is a measure of the space around atomic nuclei filled by electrons [40,41] and is defined geometrically as the combined volume of overlapping spheres centred on the nuclei, similar in shape to a space-filling molecular model. The van der Waals radii are used for the radii of the atomic spheres. The molecular surface area is the area of the surface that wraps the molecular volume. Exact calculation of the molecular volume and surface area is, however, a formidable task due to multiple overlap of spheres of different radii.
A molecular van der Waals envelope, ζ, can be defined in the “hard-spheres” approximation as the external surface resulted from the intersection of all vdW spheres corresponding to the atoms of molecule Μ. The points (x,y,z) inside the envelope satisfy at least one of the following inequalities:
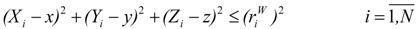 |
(23) |
where N represents the number of atoms of Μ. Consequently, the total volume embedded by the envelope is the molecular vdW volume (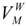 ) of the molecule M.
) of the molecule M.
The following integral:
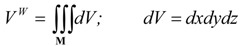 |
(24) |
can be intuitively justified as a volume [3,5,19]. This assumption is natural because the properties of molecular vdW space can be considered independent from the nature of the atoms, even in the case when domains of the vdW atomic spheres intersect.
To estimate the integral (24), the molecule (23) is inserted into a bounding parallelepiped with the volume Vp. The random points are generated into the parallelepiped, which includes the domain M. If nt is the total number of generated points and ns the number of points that which satisfy the inequalities in (23) than the van der Waals volume is:
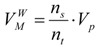 |
(25) |
In order to avoid multiple computation of the same volume, resulted from multiple atom spheres overlapping, we applied a Monte Carlo technique [42]. The accuracy ε of the estimate (25) for a given maximum probability, δ, is inversely proportional to the square root of the number of trials, or
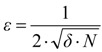 |
(26) |
Taking into consideration the precision and the accuracy of chemical and biological experiments, for ε = 0.05 and δ = 0.01, the number of necessary points is N = 10,000. This makes the Monte Carlo method not difficult to apply, due to the performances of nowadays computers. In order to increase the accuracy of the method the calculus must be repeated at least 10 to 20 times for each calculated volume. The final result, i.e. the mean value of these computed volumes, is validated by statistical methods.
(b) Molecular van der Waals Surface
The van der Waals volume of the envelope, ζ, defined in the previous paragraph, can be a measure of the molecules’ size. Obviously, this envelope is a surface, and there were methods developed to compute the area of this surface [5,18,42,43]. Some of them are based on a Monte Carlo method [5,18], others on an analytical algorithm [44]. The computed surfaces were especially used to characterize the shape and the similarity of the molecules, their graphical representation [44,45], and so on. A Monte Carlo algorithm [5,18] implies the generation of an uniform grid on each sphere of the molecule, followed by the detection of the number of points generated on the surface (nt) and of those (ne) that do not satisfy the inequalities in (23). For every “hard sphere” i, one computes the outer part of each sphere’s surface, 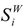 :
:
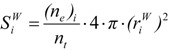 |
(27) |
The final surface is computed as a sum of exterior surface of each sphere, 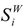 :
:
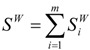 |
(28) |
See refs. [5,18] for details about how to generate a uniform grid.
(c) Synthetic van der Waals descriptors of molecular shape
The shape of molecules is doubtlessly the main element of most chemical interactions. Quantitative treatment of molecular shape, that is the development of appropriate molecular descriptors able to synthesize the characteristics of 3D extension of molecules, is a very difficult problem. Most procedures are based either on comparing molecules with a reference structure, or on dividing them and defining the sectors by means of Euclidean distance between certain atoms or with the aid of Cartesian coordinates of those sectors.
Using a hard-spheres model, we developed a series of van der Waals indicators of the molecular shape. This model allowed the introduction of several synthetic descriptors of molecular shape, which are presented as follows.
A first set of indicators was developed starting from the fact that a molecule can be characterized by the surface of molecular envelope described by equations (23) (with the sign “=”).
The equation (29) represents a 2nd -degree equation describing a general surface [5]:
| a11∙x2 + a22∙y2 + a33∙z2 + 2a14 + 2a24∙y 2a34∙z + a44 = 0 | (29) |
By transformations of coordinates (translation), equation (29) is simplified and reduced to one of the fifteen equations composed of four terms [46]. For obvious physical reasons related to spatial extension of substituents, we neglected both singular quadrics and the equations that do not have real solutions – and, therefore, do not represent geometrical figures. From the five non-singular surfaces of 2nd degree which remain and represent geometrical figures (ellipsoid, ellipsoidal and hyperbolic paraboloid, and one-sheet and two-sheet hyperboloid), only the ellipsoid fulfils the physical conditions so that by assimilating the molecule with this geometrical figure the physical meaning of the calculated parameters is maintained.
It is known that the relationship:
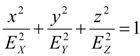 |
(30) |
represents an ellipsoid, namely a spheroid (or conoid). If EX < EY = EZ equation (30) represents a prolate ellipsoid. If EX = EY > EZ the relationship (30) represent an oblate ellipsoid of revolution, and if EX = EY = EZ we have a sphere.
The molecules are oriented along the Ox axes of the Cartesian coordinate system and the volume of the ellipsoid (30) and its vdW centre are estimated by a Monte Carlo algorithm implemented in the IRS computer program [31]. Then, the semi-axes of the ellipsoid are calculated.
Starting from the concept of packing density and from the fact that the experimental determination of the cross-section area of a molecule [47] is performed by assimilating it to a sphere, and assuming a maximal packing of molecule spheres, one may consider as a quantitative measure of the steric characteristics of molecules the descriptor RWV, defined as follows:
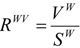 |
(31) |
where VW and SW are the calculated vdW volume and surface, respectively (see above the corresponding sections)
(d) Globularity measures
With the help of the molecular vdW descriptors computed, two other parameters can be defined. The first is defined only for acyclic molecules, named globularity measure (GLOB), and is given by relation [5,12]:
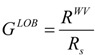 |
(32) |
where RWV is defined by relation (31) and Rs represents the ratio between the volume and the surface of an equivalent sphere, which surrounds the molecule, with the radius equal to the half of the longest dimension of the parallelepiped that embeds the molecule. The above relation cannot be used for cyclic molecules, because the volume of the equivalent sphere includes the internal empty space, which is not included in the van der Waals volume.
The second one is defined by the following equation:
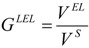 |
(33) |
where VEL is the volume of the ellipsoid surrounding the whole molecule, and VS is the volume of a sphere with a radius equal to half of the longest ellipsoid axe. This parameter should be more useful for characterizing globularity because it includes the volume of all holes which may appear.
These two parameters can be used to describe the shape of acyclic molecules. The globularity measure decreases with the growth of the linear chains and increases toward unity when the molecule is highly branched or compacted.
Intercorrelation of Topological Distance Indices and van Der Waals Molecular Descriptors
In this section we analyze the extent to which the molecular descriptors presented in this paper are linearly intercorrelated. The correlation analysis was performed on all TDIs and vdWMDs considered in this report for a set of 72 alkanes of up to 9 carbon atoms. For this purpose alkanes are convenient systems because they represent structurally rather simple chemical structures, and skeletal branching is their only complicated structural feature [21]. In this way we can establish to what extent the molecular descriptors from Table 1a and 1 are orthogonal. This orthogonality is absolutely necessary for molecular descriptors in QSPR relations because it avoids the artificial strengthening of correlations. It also assures that a quantity of information is independent of the parameters of the obtained linear model, thus very useful for physical interpretations of the model. If, on the other hand, the MDs are not orthogonal, it is possible that they predominantly express the same type of structural information, with differences residing in the scaling factors.
We have investigated the linear relationship between the pairs of molecular descriptors presented here, MDa and MDb,
| MDa = α + β∙MDb | (34) |
where MDa and MDb are TDIs, GTDIs and vdwMDs.
The correlation coefficient, r, is a measure of linear relationship described in relation (34). If r = 0 no linear relationship exists between MDa and MDb. If r = 1, there is a direct linear relationship, and if r = -1 , there is an inverse linear relationship between MDa and MDb. The correlation coefficient r ≥ 0.900 was proposed as the criterion for the intercorrelated pairs of molecular descriptors [48]. Strongly intercorrelated pairs of the molecular descriptors are those with r ≥ 0.980.
The results of the correlation analysis are displayed as the intercorrelation matrices with the correlation coefficient r. In Table 3a, Table 3b, Table 3c and Table 3d we give the intercorrelation matrices reflecting pairwise linear correlation for all molecular descriptors from Table 1 and Table 2: 11 selected TDIs, 16 GTDIs extended here from the reciprocical distance matrix, and 9 vdWMDs. The Table 3a, Table 3b and Table 3c contain the intercorrelation matrices corresponding to TDIs, GTDIs and vdWMDs, respectively. Since the matrices are symmetric, we give only the upper triangle. In Table 3d we report the intercorrelation matrix of TDIs and GTDIs.
Table 3a.
Intercorrelation Matrix of Topological Distance Indices for Alkanes with up to 9 Carbon Atoms
| W | P | F | J | VAD1 | VAD2 | VAD3 | VED1 | VED2 | VED3 | VRD | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| W | 1.000 | 0.719 | 0.716 | 0.523 | 0.945 | 0.860 | 0.862 | 0.915 | -0.810 | 0.874 | 0.952 |
| P | 1.000 | 0.842 | 0.850 | 0.825 | 0.766 | 0.784 | 0.821 | -0.744 | 0.793 | 0.838 | |
| F | 1.000 | 0.933 | 0.757 | 0.666 | 0.802 | 0.861 | -0.805 | 0.842 | 0.873 | ||
| J | 1.000 | 0.113 | 0.094 | 0.278 | 0.281 | -0.344 | 0.312 | 0.241 | |||
| VAD1 | 1.000 | 0.968 | 0.918 | 0.934 | -0.854 | 0.905 | 0.933 | ||||
| VAD2 | 1.000 | 0.927 | 0.897 | -0.866 | 0.890 | 0.849 | |||||
| VAD3 | 1.000 | 0.982 | -0.989 | 0.993 | 0.927 | ||||||
| VED1 | 1.000 | -0.967 | 0.993 | 0.978 | |||||||
| VED2 | 1.000 | -0.990 | -0.901 | ||||||||
| VED3 | 1.000 | 0.950 | |||||||||
| VRD | 1.000 |
Table 3b.
Intercorrelation Matrix of Generalized Topological Distance Indices for Alkanes with up to 9 Carbon Atoms
| 1δ ο | 2δο | 3δο | 4δο | 1δ1 | 2δ1 | 3δ1 | 4δ1 | 1δ2 | 2δ2 | 3δ2 | 4δ2 | 1δ3 | 2δ3 | 3δ3 | 4δ3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1δο | 1.000 | 0.999 | 0.996 | 0.993 | 0.965 | 0.978 | 0.990 | 0.994 | 0.809 | 0.859 | 0.899 | 0.922 | 0.837 | 0.939 | 0.967 | 0.972 |
| 2δο | 1.000 | 0.999 | 0.996 | 0.967 | 0.980 | 0.992 | 0.997 | 0.810 | 0.858 | 0.898 | 0.921 | 0.855 | 0.948 | 0.973 | 0.979 | |
| 3δο | 1.000 | 0.999 | 0.978 | 0.988 | 0.997 | 1.000 | 0.835 | 0.879 | 0.915 | 0.936 | 0.868 | 0.959 | 0.979 | 0.981 | ||
| 4δο | 1.000 | 0.986 | 0.994 | 0.999 | 1.000 | 0.856 | 0.897 | 0.930 | 0.948 | 0.872 | 0.965 | 0.981 | 0.979 | |||
| 1δ1 | 1.000 | 0.998 | 0.991 | 0.982 | 0.931 | 0.958 | 0.976 | 0.985 | 0.861 | 0.967 | 0.967 | 0.952 | ||||
| 2δ1 | 1.000 | 0.997 | 0.991 | 0.908 | 0.941 | 0.964 | 0.977 | 0.862 | 0.967 | 0.973 | 0.962 | |||||
| 3δ1 | 1.000 | 0.999 | 0.873 | 0.912 | 0.942 | 0.959 | 0.867 | 0.965 | 0.979 | 0.974 | ||||||
| 4δ1 | 1.000 | 0.845 | 0.887 | 0.922 | 0.941 | 0.872 | 0.963 | 0.981 | 0.981 | |||||||
| 1δ2 | 1.000 | 0.994 | 0.980 | 0.967 | 0.745 | 0.872 | 0.837 | 0.795 | ||||||||
| 2δ2 | 1.000 | 0.996 | 0.988 | 0.754 | 0.891 | 0.867 | 0.831 | |||||||||
| 3δ2 | 1.000 | 0.998 | 0.769 | 0.907 | 0.893 | 0.864 | ||||||||||
| 4δ2 | 1.000 | 0.780 | 0.918 | 0.910 | 0.885 | |||||||||||
| 1δ3 | 1.000 | 0.959 | 0.944 | 0.937 | ||||||||||||
| 2δ3 | 1.000 | 0.994 | 0.982 | |||||||||||||
| 3δ3 | 1.000 | 0.997 | ||||||||||||||
| 4δ3 | 1.000 |
Table 3c.
Intercorrelation Matrix of van der Waals Molecular Descriptors for Alkanes with up to 9 Carbon Atoms
| VW | SW | VEL | EX | EY | EZ | GLOB | GLEL | RWV | |
|---|---|---|---|---|---|---|---|---|---|
| VW | 1.000 | 0.994 | 0.924 | 0.852 | 0.751 | 0.566 | -0.661 | -0.220 | 0.839 |
| SW | 1.000 | 0.944 | 0.891 | 0.806 | 0.511 | -0.729 | -0.294 | 0.782 | |
| VEL | 1.000 | 0.906 | 0.822 | 0.538 | -0.764 | -0.288 | 0.652 | ||
| EX | 1.000 | 0.850 | 0.270 | -0.825 | -0.413 | 0.528 | |||
| EY | 1.000 | 0.018 | -0.978 | -0.761 | 0.351 | ||||
| EZ | 1.000 | 0.056 | 0.564 | 0.757 | |||||
| GLOB | 1.000 | 0.812 | -0.240 | ||||||
| GLEL | 1.000 | 0.178 | |||||||
| RWV | 1.000 |
Table 3d.
Intercorrelation Matrix of Generalized Topological Distance Indices (GTDIs) against Topological Distance Indices (TDIs) for Alkanes with up to 9 Carbon Atoms
| W | P | F | J | VAD1 | VAD2 | VAD3 | VED1 | VED2 | VED3 | VRD | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1δο | 0.923 | 0.885 | 0.914 | 0.801 | 0.937 | 0.857 | 0.925 | 0.975 | -0.896 | 0.947 | 0.991 |
| 2δο | 0.912 | 0.881 | 0.920 | 0.817 | 0.932 | 0.861 | 0.939 | 0.982 | -0.916 | 0.960 | 0.989 |
| 3δο | 0.921 | 0.866 | 0.905 | 0.799 | 0.938 | 0.874 | 0.952 | 0.990 | -0.930 | 0.971 | 0.991 |
| 4δο | 0.931 | 0.852 | 0.888 | 0.778 | 0.944 | 0.884 | 0.959 | 0.994 | -0.936 | 0.975 | 0.992 |
| 1δ1 | 0.959 | 0.789 | 0.802 | 0.672 | 0.955 | 0.910 | 0.965 | 0.989 | -0.936 | 0.973 | 0.981 |
| 2δ1 | 0.954 | 0.817 | 0.832 | 0.710 | 0.955 | 0.903 | 0.964 | 0.993 | -0.937 | 0.975 | 0.988 |
| 3δ1 | 0.939 | 0.844 | 0.871 | 0.758 | 0.948 | 0.890 | 0.961 | 0.995 | -0.937 | 0.976 | 0.993 |
| 4δ1 | 0.925 | 0.857 | 0.897 | 0.789 | 0.939 | 0.876 | 0.956 | 0.992 | -0.934 | 0.974 | 0.992 |
| 1δ2 | 0.924 | 0.582 | 0.534 | 0.375 | 0.887 | 0.882 | 0.882 | 0.880 | -0.842 | 0.870 | 0.858 |
| 2δ2 | 0.947 | 0.660 | 0.598 | 0.452 | 0.922 | 0.904 | 0.907 | 0.913 | -0.865 | 0.898 | 0.899 |
| 3δ2 | 0.958 | 0.724 | 0.659 | 0.526 | 0.945 | 0.918 | 0.929 | 0.940 | -0.887 | 0.924 | 0.930 |
| 4δ2 | 0.960 | 0.760 | 0.698 | 0.573 | 0.955 | 0.923 | 0.941 | 0.956 | -0.900 | 0.938 | 0.947 |
| 1δ3 | 0.780 | 0.555 | 0.824 | 0.696 | 0.752 | 0.719 | 0.880 | 0.891 | -0.905 | 0.904 | 0.850 |
| 2δ3 | 0.916 | 0.694 | 0.844 | 0.694 | 0.888 | 0.837 | 0.945 | 0.972 | -0.939 | 0.965 | 0.956 |
| 3δ3 | 0.912 | 0.755 | 0.894 | 0.756 | 0.897 | 0.833 | 0.942 | 0.979 | -0.934 | 0.966 | 0.973 |
| 4δ3 | 0.892 | 0.780 | 0.927 | 0.797 | 0.885 | 0.813 | 0.930 | 0.972 | -0.923 | 0.958 | 0.970 |
Table 2.
Van der Waals Molecular Descriptors of the First 72 Alkanes
| Alkane | VW | SW | VEL | EX | EY | EZ | GLOB | GLEL | RWV |
|---|---|---|---|---|---|---|---|---|---|
| C2 | 45.672 | 71.059 | 114.658 | 3.021 | 3.145 | 2.881 | 0.613 | 0.880 | 0.643 |
| C3 | 62.678 | 93.293 | 160.367 | 3.516 | 3.780 | 2.881 | 0.533 | 0.709 | 0.672 |
| C4 | 79.733 | 115.287 | 190.706 | 3.763 | 4.200 | 2.881 | 0.494 | 0.615 | 0.692 |
| 2-M-C3 | 79.699 | 114.746 | 217.825 | 3.889 | 3.781 | 3.536 | 0.536 | 0.884 | 0.695 |
| C5 | 96.825 | 137.555 | 247.324 | 4.252 | 4.820 | 2.881 | 0.438 | 0.527 | 0.704 |
| 2M-C4 | 96.719 | 135.905 | 264.984 | 4.182 | 4.248 | 3.561 | 0.503 | 0.825 | 0.712 |
| 22MM-C3 | 96.112 | 135.069 | 254.783 | 3.875 | 3.766 | 4.168 | 0.512 | 0.840 | 0.712 |
| C6 | 113.685 | 159.426 | 284.774 | 4.503 | 5.241 | 2.881 | 0.408 | 0.472 | 0.713 |
| 3M-C5 | 113.597 | 156.104 | 318.161 | 4.307 | 4.899 | 3.599 | 0.446 | 0.646 | 0.728 |
| 2M-C5 | 113.775 | 157.987 | 339.431 | 4.687 | 4.811 | 3.594 | 0.449 | 0.728 | 0.720 |
| 23MM-C4 | 113.295 | 154.842 | 332.325 | 4.503 | 4.220 | 4.175 | 0.488 | 0.869 | 0.732 |
| 22MM-C4 | 113.230 | 155.351 | 311.724 | 4.215 | 4.235 | 4.168 | 0.516 | 0.979 | 0.729 |
| C7 | 131.027 | 181.788 | 352.736 | 4.988 | 5.861 | 2.881 | 0.369 | 0.418 | 0.721 |
| 3E-C5 | 130.432 | 176.805 | 390.419 | 4.661 | 4.931 | 4.055 | 0.449 | 0.777 | 0.738 |
| 3M-C6 | 130.657 | 178.137 | 369.805 | 4.503 | 5.352 | 3.664 | 0.411 | 0.576 | 0.733 |
| 2M-C6 | 130.675 | 180.112 | 389.158 | 4.940 | 5.265 | 3.572 | 0.413 | 0.637 | 0.726 |
| 23MM-C5 | 130.175 | 174.531 | 397.190 | 4.681 | 4.859 | 4.168 | 0.460 | 0.826 | 0.746 |
| 33MM-C5 | 130.438 | 173.979 | 373.215 | 4.344 | 4.921 | 4.168 | 0.457 | 0.748 | 0.750 |
| 223MMM-C4 | 130.086 | 173.065 | 340.481 | 4.587 | 4.251 | 4.169 | 0.492 | 0.842 | 0.752 |
| 24-MMC5 | 130.472 | 177.729 | 363.282 | 4.746 | 5.027 | 3.635 | 0.438 | 0.683 | 0.734 |
| 22MM-C5 | 130.431 | 177.235 | 390.649 | 4.663 | 4.799 | 4.168 | 0.460 | 0.844 | 0.736 |
| C8 | 147.814 | 204.050 | 397.254 | 5.240 | 6.281 | 2.881 | 0.346 | 0.383 | 0.724 |
| 3E-C6 | 147.572 | 199.053 | 423.503 | 4.662 | 5.378 | 4.033 | 0.414 | 0.650 | 0.741 |
| 3M-C7 | 147.843 | 200.529 | 459.253 | 5.026 | 5.961 | 3.660 | 0.371 | 0.518 | 0.737 |
| 34MM-C6 | 146.984 | 194.367 | 422.458 | 4.536 | 5.351 | 4.156 | 0.424 | 0.658 | 0.756 |
| 3E-3M-C5 | 147.192 | 193.627 | 428.593 | 4.792 | 4.950 | 4.314 | 0.461 | 0.844 | 0.760 |
| 4M-C7 | 147.596 | 200.355 | 450.614 | 4.972 | 5.854 | 3.696 | 0.378 | 0.536 | 0.737 |
| 2M-C7 | 147.868 | 201.974 | 478.805 | 5.432 | 5.861 | 3.591 | 0.375 | 0.568 | 0.732 |
| 3E-2M-C5 | 147.146 | 193.534 | 427.292 | 4.946 | 4.910 | 4.201 | 0.461 | 0.843 | 0.760 |
| 23MM-C6 | 147.319 | 196.670 | 452.909 | 4.852 | 5.351 | 4.165 | 0.420 | 0.706 | 0.749 |
| 233MMM-C5 | 147.226 | 191.854 | 411.251 | 4.769 | 4.944 | 4.164 | 0.466 | 0.813 | 0.767 |
| 234MMM-C5 | 147.420 | 194.534 | 397.214 | 4.780 | 4.962 | 3.998 | 0.458 | 0.776 | 0.758 |
| 33MM-C6 | 147.539 | 195.769 | 422.747 | 4.523 | 5.353 | 4.168 | 0.422 | 0.658 | 0.754 |
| 223MMM-C5 | 147.123 | 193.437 | 401.790 | 4.740 | 4.854 | 4.169 | 0.470 | 0.839 | 0.761 |
| 25MM-C6 | 147.027 | 200.288 | 492.840 | 5.286 | 5.260 | 4.232 | 0.417 | 0.797 | 0.734 |
| 22MM-C6 | 147.747 | 199.191 | 456.496 | 4.961 | 5.270 | 4.168 | 0.422 | 0.744 | 0.742 |
| 2233MMMM-C4 | 146.856 | 188.312 | 338.229 | 4.563 | 4.239 | 4.175 | 0.513 | 0.850 | 0.780 |
| 224MMM-C5 | 147.018 | 196.564 | 410.699 | 4.714 | 5.036 | 4.130 | 0.446 | 0.768 | 0.748 |
| C9 | 164.641 | 226.192 | 476.615 | 5.723 | 6.901 | 2.881 | 0.316 | 0.346 | 0.728 |
| 33EE-C5 | 164.061 | 211.324 | 459.204 | 4.769 | 5.035 | 4.566 | 0.463 | 0.859 | 0.776 |
| 3E-C7 | 164.668 | 221.159 | 532.315 | 5.028 | 6.010 | 4.206 | 0.372 | 0.585 | 0.745 |
| 3M-C8 | 164.821 | 222.363 | 518.339 | 5.259 | 6.396 | 3.680 | 0.348 | 0.473 | 0.741 |
| 4M-C8 | 164.737 | 222.348 | 518.784 | 5.214 | 6.354 | 3.739 | 0.350 | 0.483 | 0.741 |
| 2M-C8 | 164.651 | 224.148 | 535.314 | 5.679 | 6.300 | 3.572 | 0.350 | 0.511 | 0.735 |
| 3E-23MM-C5 | 163.900 | 210.954 | 455.680 | 5.057 | 5.038 | 4.269 | 0.461 | 0.841 | 0.777 |
| 2334MMMM-C5 | 163.486 | 209.776 | 419.044 | 4.812 | 5.003 | 4.155 | 0.467 | 0.799 | 0.779 |
| 4E-C7 | 164.814 | 220.815 | 487.239 | 5.054 | 5.713 | 4.029 | 0.392 | 0.624 | 0.746 |
| 3E-3M-C6 | 164.119 | 215.689 | 472.306 | 4.804 | 5.410 | 4.338 | 0.422 | 0.712 | 0.761 |
| 23MM-C7 | 164.329 | 218.824 | 558.982 | 5.408 | 5.934 | 4.158 | 0.380 | 0.639 | 0.751 |
| 334MMM-C6 | 163.840 | 212.499 | 440.007 | 4.587 | 5.505 | 4.160 | 0.420 | 0.629 | 0.771 |
| 2233MMMM-C5 | 163.704 | 205.939 | 400.956 | 4.676 | 4.902 | 4.176 | 0.486 | 0.813 | 0.795 |
| 34MM-C7 | 163.970 | 215.894 | 522.987 | 5.081 | 5.921 | 4.150 | 0.385 | 0.601 | 0.759 |
| 234MMM-C6 | 164.105 | 214.473 | 460.278 | 4.964 | 5.428 | 4.078 | 0.423 | 0.687 | 0.765 |
| 233MMM-C6 | 164.180 | 213.892 | 455.137 | 4.831 | 5.398 | 4.167 | 0.427 | 0.691 | 0.768 |
| 33MM-C7 | 164.007 | 217.971 | 529.200 | 5.085 | 5.962 | 4.168 | 0.379 | 0.596 | 0.752 |
| 3E-24MM-C5 | 164.363 | 216.103 | 427.188 | 5.057 | 5.064 | 3.982 | 0.451 | 0.785 | 0.761 |
| 35MM-C7 | 164.491 | 218.873 | 533.826 | 5.433 | 5.307 | 4.420 | 0.415 | 0.795 | 0.752 |
| 25MM-C7 | 164.140 | 220.135 | 568.077 | 5.393 | 5.886 | 4.272 | 0.380 | 0.665 | 0.746 |
| 26MM-C7 | 164.715 | 222.197 | 491.514 | 5.443 | 5.995 | 3.596 | 0.371 | 0.545 | 0.741 |
| 44MM-C7 | 164.587 | 217.682 | 501.828 | 4.898 | 5.869 | 4.168 | 0.386 | 0.593 | 0.756 |
| 4E-2M-C6 | 164.549 | 219.575 | 436.658 | 5.125 | 5.414 | 3.757 | 0.415 | 0.657 | 0.749 |
| 3E-22MM-C5 | 164.151 | 214.491 | 446.559 | 5.003 | 5.113 | 4.168 | 0.449 | 0.798 | 0.765 |
| 24MM-C7 | 165.047 | 220.278 | 507.519 | 5.480 | 5.752 | 3.844 | 0.391 | 0.636 | 0.749 |
| 2234MMMM-C5 | 163.603 | 209.897 | 410.677 | 4.731 | 5.047 | 4.106 | 0.463 | 0.763 | 0.779 |
| 22MM-C7 | 164.016 | 221.271 | 554.019 | 5.411 | 5.865 | 4.168 | 0.379 | 0.656 | 0.741 |
| 223MMM-C6 | 163.938 | 215.620 | 456.468 | 4.911 | 5.286 | 4.197 | 0.431 | 0.738 | 0.760 |
| 235MMM-C6 | 163.921 | 216.403 | 486.875 | 5.275 | 5.384 | 4.093 | 0.422 | 0.745 | 0.757 |
| 244MMM-C6 | 164.263 | 214.907 | 478.821 | 5.128 | 5.402 | 4.127 | 0.424 | 0.725 | 0.764 |
| 224MMM-C6 | 164.000 | 216.617 | 471.400 | 5.085 | 5.392 | 4.104 | 0.421 | 0.718 | 0.757 |
| 225MMM-C6 | 164.103 | 219.201 | 495.366 | 5.365 | 5.269 | 4.184 | 0.419 | 0.766 | 0.749 |
| 2244MMMM-C5 | 164.104 | 214.571 | 408.276 | 4.639 | 5.042 | 4.168 | 0.455 | 0.761 | 0.765 |
From Table 3 we learn several interesting points:
-
1)
The intercorrelation matrix of the selected topological indices presented in Table 3a reveals that these indices are not strongly intercorrelated, that is their information content about topological structure of the 72 alkanes from table 1 is somewhat independent. Only the indices derived from eigenvalues and eigenvectors are better intercorrelated. The TDIs belonging to this group are very poorly correlated with Balaban’s J-index. Besides, J is also independent when compared to W, and very weakly linked to P. On the other hand it seems to correlate very well with F (r = 0.933). From this point of view it is necessary to avoid the simultaneous use of these indices for studying physical properties in QSPR relations.
-
2)
The majority of GTDIs, kδλ (k = 1,2,3,4; λ = 0,1,2,3) counterparts are strongly intercorrelated. Taking as criterion for strong correlations r ≥ 0.980 one notices that there exists a strong correlation inside each class λ, which slightly decreases along with the increase in k. This fact is entirely explainable, if we take into consideration the way in which LOVIs are constructed; the more the dimensionality of the space is increased, the interaction between atoms that are separated by the same topological distance decreases, and the influence gets smaller as the distance and the dimensionality of the space get larger. The degree of correlation between indices kδλ of different classes are generally smaller, except those corresponding to λ = 1 and λ = 2, which are greater than r = 0.960.
-
3)
Van der Waals molecular descriptors, vdWMDs, are much more independent relative to each other than the GTDIs and TDIs. A strong correlation was observed only between the volume (VW) and the corresponding vdW surface (SW) of the 72 alkanes having 2 – 9 carbon atoms (r = 0.994). This significant correlation was obtained between the vdW volume and surface, but also between them and the molecular vdW volume of alkanes treated as molecules with a more or less ellipsoidal shape. The shift of alkanes to an extended, intercalated conformation greatly influences the volume of the ellipsoid and progressively smaller the vdW surface area and the vdW volume. On the other hand, conformational variations on orthogonal directions are affecting these descriptors on a much smaller measure. Our intercorrelation results suggest the possibility of simultaneously using these indices in QSAR and QSPR relations for global testing of vdW space occupied by molecules (space-filling), along with bulk steric parameters (VW, SW, VEL, GLOB, GLEL, RWV), or certain directions within them (EX, EY, EZ). The simple and fast calculus for any molecular structure and the possibility of immediately testing the degree of orthogonality ensures their large applicability for any series of compounds.
-
4)
Generalized topological distance indices derived from the reciprocical distance matrix, GTDIs, present significant correlations with topological indices derived from eigenvalues and eigenvectors of the distance matrix, D. Repeatedly, the strongest are those between kδλ (k = 1,2,3,4, λ = 0,1) and VRD. In this case a more rigorous statistical analysis is imposed on the relation between distance indices, kδλ, and the VADi and VEDi parameters, i = 1,2,3. The intercorrelation between GTDIs and the first indices defined on the distance matrix is decreasing in the following order: W, F, P. Although, generally speaking, the Wiener index, W, correlates well with GTDIs, there are two surprising exceptions for indices 1δ3 and 4δ3. Investigating the physical meaning of GTDIs could emerge interesting information on other topological indices. The work is in progress.
-
5)
Are the topological indices steric measures of molecular van der Waals space? Although some reported that they correlate well with molecular volume [7] or surface area, extensive studies on this subject have not yet been performed. In Table 4 we present the intercorrelation matrix of molecular vdW descriptors and of topological indices described in this work. The best results were obtained for the correlations with the van der Waals molecular volume (VW) and surface (SW) against Wiener indices (W), derived from eigenvectors and eigenvalues of the distance matrix, and GTDIs, kδλ, except for indices with λ = 2 and k = 1 (r = 0.886), and λ = 3 and k = 1 (r = 0.869). Except for P, F and J indices, the others should be viewed as bulk steric parameters, as measured by vdW volume and surface of tested alkanes. The steric component of most topological indices is poorly explained by vdW volumes of ellipsoid-assimilated alkanes (revolving around r = 0.900). Weak correlations were also obtained for P, F and J. The results suggest the impossibility of testing the vector nature of steric effects by means of topological distance indices, which is rather important for modeling biological interactions. This is a possible explanation for the lesser utility of topological indices for QSAR studies.
Table 4.
Intercorrelation Matrix of All Topological Distance Indices (TDIs and GTDIs) against van der Walls Molecular Descriptors (vdWMDs)
| VW | SW | VEL | EX | EY | EZ | GLOB | GLEL | RWV | |
|---|---|---|---|---|---|---|---|---|---|
| W | 0.944 | 0.958 | 0.930 | 0.873 | 0.830 | 0.386 | -0.741 | -0.373 | 0.642 |
| P | 0.834 | 0.778 | 0.666 | 0.519 | 0.416 | 0.636 | -0.274 | 0.074 | 0.913 |
| F | 0.859 | 0.809 | 0.687 | 0.559 | 0.354 | 0.751 | -0.237 | 0.191 | 0.937 |
| J | 0.743 | 0.677 | 0.537 | 0.392 | 0.179 | 0.820 | -0.073 | 0.343 | 0.970 |
| VAD1 | 0.951 | 0.950 | 0.895 | 0.831 | 0.779 | 0.455 | -0.680 | -0.295 | 0.747 |
| VAD2 | 0.896 | 0.902 | 0.847 | 0.826 | 0.795 | 0.386 | -0.722 | -0.358 | 0.711 |
| VAD3 | 0.965 | 0.965 | 0.890 | 0.857 | 0.761 | 0.540 | -0.702 | -0.258 | 0.840 |
| VED1 | 0.996 | 0.990 | 0.916 | 0.854 | 0.744 | 0.581 | -0.664 | -0.211 | 0.856 |
| VED2 | -0.940 | -0.939 | -0.860 | -0.832 | -0.717 | -0.570 | 0.670 | 0.215 | -0.849 |
| VED3 | 0.978 | 0.975 | 0.898 | 0.851 | 0.738 | 0.581 | -0.672 | -0.213 | 0.860 |
| VRD | 0.991 | 0.981 | 0.910 | 0.820 | 0.718 | 0.572 | -0.618 | -0.191 | 0.829 |
| 1δο | 0.986 | 0.965 | 0.880 | 0.776 | 0.656 | 0.621 | -0.546 | -0.112 | 0.878 |
| 2δο | 0.989 | 0.968 | 0.881 | 0.782 | 0.656 | 0.632 | -0.550 | -0.107 | 0.892 |
| 3δο | 0.995 | 0.979 | 0.897 | 0.808 | 0.687 | 0.616 | -0.587 | -0.142 | 0.880 |
| 4δο | 0.998 | 0.986 | 0.909 | 0.827 | 0.714 | 0.597 | -0.618 | -0.173 | 0.865 |
| 1δ1 | 0.994 | 0.999 | 0.944 | 0.890 | 0.812 | 0.504 | -0.733 | -0.303 | 0.783 |
| 2δ1 | 0.999 | 0.998 | 0.936 | 0.869 | 0.779 | 0.541 | -0.694 | -0.256 | 0.813 |
| 3δ1 | 1.000 | 0.991 | 0.920 | 0.841 | 0.732 | 0.585 | -0.640 | -0.194 | 0.850 |
| 4δ1 | 0.997 | 0.983 | 0.905 | 0.820 | 0.698 | 0.612 | -0.601 | -0.151 | 0.873 |
| 1δ2 | 0.886 | 0.926 | 0.916 | 0.932 | 0.951 | 0.229 | -0.913 | -0.574 | 0.532 |
| 2δ2 | 0.922 | 0.953 | 0.934 | 0.919 | 0.925 | 0.305 | -0.872 | -0.510 | 0.600 |
| 3δ2 | 0.950 | 0.971 | 0.941 | 0.905 | 0.893 | 0.373 | -0.828 | -0.445 | 0.665 |
| 4δ2 | 0.965 | 0.980 | 0.943 | 0.895 | 0.869 | 0.416 | -0.797 | -0.402 | 0.706 |
| 1δ3 | 0.869 | 0.876 | 0.809 | 0.808 | 0.633 | 0.542 | -0.598 | -0.151 | 0.738 |
| 2δ3 | 0.968 | 0.975 | 0.913 | 0.881 | 0.752 | 0.533 | -0.689 | -0.239 | 0.775 |
| 3δ3 | 0.978 | 0.974 | 0.900 | 0.843 | 0.699 | 0.589 | -0.621 | -0.165 | 0.827 |
| 4δ3 | 0.972 | 0.959 | 0.875 | 0.804 | 0.647 | 0.626 | -0.561 | -0.103 | 0.858 |
Correlations with Boiling Points of Alkanes
In order to check whether the selected topological indices, generalized topological distance indices and van der Waals molecular descriptors can be used in correlations with experimentally measured properties (in QSPR) we focused on boiling points. The choice was motivated by the fact that boiling points are known to depend on molecular constitution (graph topology). The true nature of the intermolecular forces involved and the entropy change in the transition from liquid to gas phase are not considered in detail. We are interested here to test the correlation ability of the considered molecular descriptors, topological indices and van der Waals structural indices.
Monoparametric correlations with boiling points (at normal pressure) for all 72 alkanes with N = 2 – 9 carbon atoms were tested for the 36 described molecular descriptors (MD) following a linear equation,
| BP = α∙(±Δα)+ β∙(±Δβ)∙MD | (35) |
where MD = TDIs, GTDIs and vdWMDs, and statistical characteristics of each correlation were considered (see Table 4). In Table 5 r is the correlation coefficient, s is the standard deviation, EV is the explained variance, t is the Student test for r and F is the Fisher test for 72 degrees of freedom.
Table 5.
Statistical Characteristics of Structure – Boiling Point Models (35) with 11 Selected Topological Distance Indices, 16 Generalized Topological Distance Indices and 9 van der Waals Molecular Descriptors
| Eq. | Xi | r | α | ±Δα | β | ±Δβ | s | F | EV | t |
|---|---|---|---|---|---|---|---|---|---|---|
| 36 | W | 0.916 | 4.31 | 5.70 | 1.42 | 0.07 | 18.715 | 374.5 | 0.837 | 19.4 |
| 37 | F | 0.834 | 19.13 | 7.43 | 13.18 | 1.03 | 25.728 | 164.3 | 0.691 | 12.8 |
| 38 | P | 0.803 | -8.29 | 10.53 | 6.99 | 0.61 | 27.783 | 130.6 | 0.640 | 11.4 |
| 39 | J | 0.722 | -85.26 | 21.97 | 60.77 | 6.87 | 32.260 | 78.3 | 0.514 | 8.8 |
| 40 | VAD1 | 0.947 | -29.08 | 5.66 | 7.57 | 0.30 | 14.910 | 631.5 | 0.896 | 25.1 |
| 41 | VAD2 | 0.925 | -103.00 | 10.34 | 95.04 | 4.60 | 17.714 | 426.4 | 0.854 | 20.6 |
| 42 | VAD3 | 0.984 | -36.40 | 3.18 | 56.68 | 1.20 | 8.259 | 2221.0 | 0.968 | 47.1 |
| 43 | VED1 | 0.989 | -294.47 | 6.95 | 146.42 | 2.52 | 6.744 | 3366.1 | 0.979 | 58.0 |
| 44 | VED2 | 0.960 | 370.10 | 9.15 | -731.86 | 25.02 | 12.985 | 855.6 | 0.921 | 29.3 |
| 45 | VED3 | 0.984 | 24.68 | 1.96 | 112.36 | 2.36 | 8.177 | 2267.0 | 0.969 | 47.6 |
| 46 | VRD | 0.962 | -44.30 | 5.28 | 6.82 | 0.23 | 12.802 | 882.2 | 0.924 | 29.7 |
| 47 | 1δο | 0.956 | -43.28 | 5.66 | 5.12 | 0.19 | 13.716 | 759.3 | 0.912 | 27.6 |
| 48 | 2δο | 0.963 | -63.35 | 5.82 | 8.51 | 0.28 | 12.635 | 907.7 | 0.926 | 30.1 |
| 49 | 3δο | 0.973 | -77.71 | 5.31 | 11.24 | 0.32 | 10.786 | 1272.2 | 0.946 | 35.7 |
| 50 | 4δο | 0.979 | -85.16 | 4.79 | 12.85 | 0.31 | 9.439 | 1683.2 | 0.958 | 41.0 |
| 51 | 1δ1 | 0.988 | -218.36 | 6.16 | 78.24 | 1.47 | 7.341 | 2830.3 | 0.975 | 53.2 |
| 52 | 2δ1 | 0.987 | -166.85 | 5.25 | 53.23 | 1.01 | 7.403 | 2781.4 | 0.974 | 52.7 |
| 53 | 3δ1 | 0.983 | -146.99 | 5.74 | 43.90 | 0.98 | 8.675 | 2006.0 | 0.965 | 44.8 |
| 54 | 4δ1 | 0.975 | -137.52 | 6.59 | 39.85 | 1.06 | 10.260 | 1413.6 | 0.951 | 37.6 |
| 55 | 1δ2 | 0.911 | -235.00 | 18.32 | 97.53 | 5.20 | 19.205 | 352.0 | 0.828 | 18.8 |
| 56 | 2δ2 | 0.941 | -140.75 | 10.66 | 49.69 | 2.11 | 15.817 | 553.1 | 0.883 | 23.5 |
| 57 | 3δ2 | 0.963 | -122.07 | 7.70 | 38.08 | 1.26 | 12.603 | 912.7 | 0.926 | 30.2 |
| 58 | 4δ2 | 0.974 | -117.21 | 6.23 | 34.00 | 0.93 | 10.534 | 1337.3 | 0.948 | 36.6 |
| 59 | 1δ3 | 0.832 | -299.41 | 32.01 | 52.84 | 4.15 | 25.849 | 162.1 | 0.688 | 12.7 |
| 60 | 2δ3 | 0.941 | -158.93 | 11.41 | 20.34 | 0.86 | 15.800 | 554.5 | 0.884 | 23.5 |
| 61 | 3δ3 | 0.945 | -118.22 | 9.37 | 12.88 | 0.53 | 15.304 | 595.7 | 0.891 | 24.4 |
| 62 | 4δ3 | 0.932 | -100.17 | 9.65 | 10.23 | 0.47 | 16.877 | 477.0 | 0.867 | 21.8 |
| 63 | VW | 0.986 | -140.62 | 5.06 | 1.71 | 0.03 | 7.852 | 2464.6 | 0.971 | 49.6 |
| 64 | SW | 0.984 | -165.00 | 5.89 | 1.40 | 0.03 | 8.339 | 2177.0 | 0.968 | 46.7 |
| 65 | VEL | 0.911 | -83.11 | 10.35 | 0.45 | 0.02 | 19.229 | 351.0 | 0.827 | 18.7 |
| 66 | EX | 0.849 | -291.59 | 29.28 | 82.60 | 6.05 | 24.600 | 186.4 | 0.718 | 13.7 |
| 67 | EY | 0.790 | -178.72 | 26.28 | 54.54 | 4.99 | 28.575 | 119.5 | 0.619 | 10.9 |
| 68 | EZ | 0.523 | -112.71 | 42.28 | 55.91 | 10.73 | 39.718 | 27.1 | 0.264 | 5.2 |
| 69 | GLOB | 0.710 | 383.22 | 32.62 | -642.13 | 75.10 | 32.829 | 73.1 | 0.497 | 8.6 |
| 70 | GLEL | 0.285 | 176.94 | 28.50 | -101.46 | 40.22 | 44.673 | 6.4 | 0.069 | 2.5 |
| 71 | RWV | 0.833 | -1060.80 | 91.34 | 1568.38 | 122.68 | 25.773 | 163.4 | 0.690 | 12.8 |
It can be seen from Table 5 that the correlation coefficients are satisfactory for the majority of generalized topological distance indices (except 1δ3) and eigenvalues and eigenvectors based indices VxDn (x = A, E; n = 1 – 3), and unsatisfactory for P, F and especially J topological distance indices and van der Waals molecular descriptors that measure globularity (GLOB, GLEL and RWV) and various directions in molecular van der Waals space of alkanes (EX, EY and EZ). The best results are obtained for VED1, VED3, 1δ1, 2δ1, 3δ1, VW and SW (r > 0.980). These topological indices contain in a great measure a bulky component and there is a strong relation between them and the whole space of alkane molecules. Van der Waals volume and surface seem to be essential for explaining the structural variation of the boiling points of alkanes. This is easy to explain if we consider the nature of the physical interactions which appear between molecules in the liquid phase and in the gas phase.
The r values for EX, EY, GLOB and RWV are lower than those obtained for VW, SW and VEL. The correlation coefficient for P and F topological indices are also fairly low. Poor values for r are especially observed for GLEL and EZ, although there is no strong linear relation between them (the coefficient of intercorrelation is r = 0.761 – see Table 3c). This fact demonstrates that these indices contain little (EX, EY, GLOB and RWV) or no information (J, EZ, and GLEL) about the size of alkane molecules.
The most accurate models are (42), (43), (45), (51) – (53), (63) and (64), where r > 0.980, F are in the intervals 2000 – 3366 (for VED1) and standard deviations vary from 6.74 to 8.66, that is they are less than 3.6% from the whole domain of boiling points. The correlation equations above explain more than 96% from the variance of the experimentally measured boiling points.
The topological distance indices W, P, F and J, and also the van der Waals molecular descriptors (EX, EY), GLOB and RWV are less successful in modeling boiling points than the generalized and eigenvalues/eigenvectors distance indices. The worst correlation was obtained with GLEL, probably because this globularity vdW descriptor, which contains information about the shape of molecules, is normalized; its value tends towards 1 when the shape of the molecule gets closer to a sphere [49].
The results here obtained suggest that the shape of the molecules seems to be less important than the size for structure-based modeling of boiling points of alkanes. Obviously, the shape is also a more abstract concept than size, thus it is also more difficult to estimate it quantitatively (through a single number) than size.
Concluding remarks
In this work we carried out a comparative study of 36 molecular descriptors derived from the distance matrix and molecular van der Waals space. This study belongs to our interest to develop molecular descriptors with clear physical meaning. Among the studied indices were 9 van der Waals descriptors of molecular size and shape and 27 topological distance indices. We also introduced here a generalized formula for deriving topological indices from the reciprocical distance matrix.
We analyzed the correlation among some classical distance matrices (W, P, F and J), distance indices derived by us from eigenvalues and eigenvectors of distance matrix and generalized distance indices, kδλ (k = 1 – 4, λ = 1 – 3), and their relation with a series of van der Waals molecular descriptors of molecular size (volume and surface area) and shape (globularity measures and ellipsoidal characteristics). The analysis of the link between the topological molecular space and the molecular van der Waals space allowed some insights on the physical meaning of topological indices. The obtained results suggest the possibility of considering topological distance indices as descriptors of the molecule’s size. They can be regarded as bulk parameters. In the series under study the informational content is progressively decreasing in the following approximate order: VRD, kδλ, VxDn, W, F, P, J.
The correlation analysis on the first 72 alkanes revealed that many counterparts are characterized by their topological distance indices. The meaning of this result is that the topological distance indices contain similar structural information about the molecular graph. On the contrary, the intercorrelation analysis of van der Waals molecular descriptors shows that the size descriptors are weakly linked to shape descriptors. In other words, although there is some connection between the molecular shape and its size, this connection is not strong. These results lead to the conclusion that while topological distance indices contain similar information about the molecular size, they contain less information about its shape. A comparison of performance between the 36 distance indices in structure – boiling point correlations for 74 alkanes of up to 9 carbon atoms showed that the most accurate QSPR models were obtained with VxDn (x = A, n = 3; x = A, n = 1,3) and kδλ (λ = 1, k = 1,2,3) topological indices and van der Waals descriptor of molecular size, i.e. volume (VW) and surface (SW).
Studies concerning the physical meaning of structural descriptors are therefore extremely useful. They allow the distillation of the informational content of such descriptors, preventing their misuse in QSPR studies.
Acknowledgements
We thank Prof. V. Gogonea from Cleveland State University (Ohio) and Dr. Sorel Muresan from AstraZeneca for helpful discussions concerning the subject of this paper.
References
- 1.Balaban A.T. In: QSPR/QSAR Studies by Molecular Descriptors. Diudea M.V., editor. NOVA Science; Huntington: 2001. pp. 1–30. [Google Scholar]
- 2.Devillers J., Balaban A.T., editors. Topological Indices and Related Descriptors in QSAR and QSPR. Gordon and Breach; Reading, UK: 1999. [Google Scholar]
- 3.Ciubotariu D., Gogonea V., Medeleanu M. In: QSPR/QSAR Studies by Molecular Descriptors. Diudea M.V., editor. NOVA Science; Huntington: 2001. pp. 281–315. [Google Scholar]
- 4.Szabo A., Ostlund N.S. Modern Quantum Chemistry, Introduction to Advanced Electronic Theory. McGraw-Hill; New York: 1989. [Google Scholar]
- 5.Ciubotariu D. PhD Thesis. Polytechnical Institute of Bucharest; 1987. Structure-Reactivity Relations in the Series of Carbonic Acide Derivatives. [Google Scholar]
- 6.Niculescu-Duvaz I., Ciubotariu D.A., Simon Z., Voiculetz N. In: Modeling of Cancer Genesis and Prevention. Voicultez N., Balaban A.T., Niculescu-Duvaz I., Simon Z., editors. CRC Press; Boca Raton: 1991. pp. 157–214. [Google Scholar]
- 7.Balaban A.T., Motoc I., Boncher D., Mekenyan O. Topological Indices for Structure-Activity Correlations. Top. Curr. Chem. 1983;114:21–55. [Google Scholar]
- 8.de Brujin J, Heruvens J. Relationship between Octanol/Water Partition Coefficients and Total Molecular Surface Area and Total Molecular Volume of Hydrophobic Organic Chemicals. Quant. Struct.-Act. Relat. 1990;9:11–21. [Google Scholar]
- 9.Heiden W, Moeckel G., Brickmann K. A New Approach to Analysis and Display Lipophilicity/Hydrophilicity Mapped on Molecular Surfaces. J. Comput.-Aided Mol. Design. 1993;7:503–514. doi: 10.1007/BF00124359. [DOI] [PubMed] [Google Scholar]
- 10.Hermann R.B. Modeling Hydrophobic Solvation of Non-Spherical Systems: Comparison of Useof Molecular Surface Area with Accessible Surface Area. J. Comput. Chem. 1997;18:115–125. [Google Scholar]
- 11.Todeschini R., Gramatica P. 3D-Modelling and Prediction by WHIM Descriptors. Part 5. Theory Development and Chemical Meaning of WHIM Descriptors. Quant. Struct.-Act. Relat. 1997;16:113–119. [Google Scholar]
- 12.Medeleanu M. PhD Thesis. Politechnical University of Bucharest; 1997. Structure - Properties Correlations by Topological Methods. [Google Scholar]
- 13.Balaban A.T., Ciubotariu D., Medeleanu M. Topological Indices and Real Vertex Invariants Based on Graph Eigenvalues or Eigenvectors. J. Chem. Inf. Comput. Sci. 1991;31:517–523. [Google Scholar]
- 14.Medeleanu M., Balaban A.T. Real-Number Vertex Invariants and Schultz-Type Indices Based on Eigenvectors of Adjacency and Distance Matrices. J. Chem. Inf. Comput. Sci. 1998;38:1038–1047. [Google Scholar]
- 15.Ciubotariu D., Medeleanu M., Gogonea V. Quantitative Treatment of Organic Molecules. I. Distance Connectivity Index d as Similarity Measure and Correlation Parameter for Alkanes. Chem. Bull. Univ. Tech. (Timisoara) 1995;40:21–36. [Google Scholar]
- 16.Ciubotariu D., Medeleanu M., Gogonea V. Quantitative Treatment of Organic Molecules. II. A New Topological Index Based on Distance Matrix. Chem. Bull. “Politehnica” Univ. (Timisoara) 1996;41:19–24. [Google Scholar]
- 17.Balaban A.T., Ciubotariu D., Invanciuc O. Design of Topolofical Indices. Part 2. Distance Measure Connectivity Indices. Math. Chem.(MATCH) 1990;25:41–70. [Google Scholar]
- 18.Gogonea V., Ciubotariu D., Deretey E., Popescu M., Iorga I., Medeleanu M. Surface Area of Organic Molecules: a New Methodof Computation. Rev. Roum. Chim. 1991;36:465–471. [Google Scholar]
- 19.Ciubotariu D., Deretey E., Medeleanu M., Gogonea V., Iorga I. New Shape Descriptors for Quantitative Treatment of Steric Effects. 1. The Molecular van der Waals Volume. Chem. Bull. PIT. 1990;35:83–92. [Google Scholar]
- 20.Ivanciuc O., Balaban T.S., Balaban A.T. Design of Topological Indices. Part 4. Reciprocical Distance Matrix, Related Local Vertex Invariants and Topological Indices. J. Math. Chem. 1993;12:309–318. [Google Scholar]
- 21.Mihalić Z., Nikolić S., Trinajstić N. Comparative Study of Molecular Descriptors Derived from the Distance Matrix. J. Chem. Inf. Comput. Sci. 1992;32:28–37. [Google Scholar]
- 22.Harary F. Graph Theory. Addison-Wesley; Reading: 1971. 2nd edition. [Google Scholar]
- 23.Rouvray D.H. Predicting Chemistry from Topology. Sci.Am. 1986;254:36–43. doi: 10.1038/scientificamerican0986-40. [DOI] [PubMed] [Google Scholar]
- 24.Wiener H. Structural Determination of Paraffin Boiling Points. J. Am. Chem. Soc. 1947;69:17–20. doi: 10.1021/ja01193a005. [DOI] [PubMed] [Google Scholar]
- 25.Wiener H. Correlation of Heats of Isomerization and Differences in Heats of Vaporization of Isomers among the Paraffinic Hydrocarbons. J. Am. Chem. Soc. 1947;69:2636–2638. [Google Scholar]
- 26.Platt J.R. Prediction of Isomeric Differences in Paraffin Properties. J. Phys. Chem. 1952;56:328–336. [Google Scholar]
- 27.Balaban A.T. Highly Discriminating Distance-Based Topological Index. Chem. Phys. Lett. 1982;80:399–404. [Google Scholar]
- 28.Balaban A.T. Topological Indices Based on Topological Distances in Molecular Graphs. Pure Appl. Chem. 1983;55:199–206. [Google Scholar]
- 29.Hosoya H. Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons. Bull. Chem. Soc. Jpn. 1971;44:2332–2339. [Google Scholar]
- 30.Gutman I., Markovic S. Benzenoid Graphs with Maximal Eigenvalues. J. Math. Chem. 1993;13:213–215. [Google Scholar]
- 31.Ciubotariu C., Medeleanu M., Ciubotariu D. IRS – a Computer Program Package for QSAR and QSPR Studies. Chem. Bull. “POLITEHNICA” Univ. of Timisoara. 2004;49 in press. [Google Scholar]
- 32.Todeschini R., Consonni V., Pavan M. Dragon Software ver 2.1. Milano Chemometrics and QSAR Research Group; 2002. [Google Scholar]
- 33.Plavšić D., Nikolić S., Trinajstić N., Mihalić Z. On the 42-Harrary Index for Characterization of Chemical Graphs. J. Math. Chem. 1993;12:235–253. [Google Scholar]
- 34.Randić M. On the Characterization of Molecular Branching. J. Am. Chem. Soc. 1975;97:6609–6615. [Google Scholar]
- 35.Kier L.B., Hall L.H., Murray W.J., Randić M. Molecular Connectivity. Part 1. Relation to Nonspecific Local Anesthetics. J. Pharm. Sci. 1975;64:1971–1974. doi: 10.1002/jps.2600641214. [DOI] [PubMed] [Google Scholar]
- 36.Ciubotariu D., Holban S., Motoc I. Computation of Molecular van der Waals Volume by means of Monte Carlo Method. Preprint, Univ. Timisoara, Fac. St. Nat., Sect. Chimie. 1975;3:1–8. [Google Scholar]
- 37.Ciubotariu D., Gogonea V., Iorga I., Deretey E., Medeleanu M., Muresan S., Bologa C. New Shape Descriptors for Quantitative Treatment of Steric Effects. II. The Molecular van der Waals Volume: Two Monte Carlo Algorithms. Chem. Bull. Tech. (Timisoara) 1993;38:67–75. [Google Scholar]
- 38.Muresan S., Sulea T., Ciubotariu D., Kurunczi L., Simon Z. Van der Waals Intersection Envelope Volumes as a Possible Basis for Steric Interaction in CoMFA. Quant. Struct.-Act. Relat. 1996;15:31–32. [Google Scholar]
- 39.Desiraju G.R. Crystal Engineering the Design of Organic Solids. Elsevier; Amsterdam: 1989. pp. 27–62. [Google Scholar]
- 40.Bondi A.J. van der Waals Volumes and Radii. J. Phys. Chem. 1964;68:441–451. [Google Scholar]
- 41.Francl M.M., Hout J.R., Hehre R.F. Representation of Electron Densities. I. Sphere Fit to Total Electron Density Surfaces. J. Am. Chem. Soc. 1984;106:563–570. [Google Scholar]
- 42.Demidovich B.P., Maron I.A. Computation Mathematics. Mir Publishers; Moscow: 1987. pp. 649–674. [Google Scholar]
- 43.Pearlmann R.S. SAREA Program. 1983. QCPE Nr. 413.
- 44.Gogonea V. PhD. Thesis. Toyohashi Univ. of Technology; Japan: 1996. An Approach to Solvent Effect Modelling by the Combined Scaled-Particle Theory and Dielectric Continuum-Medium Method. [Google Scholar]
- 45.Cohen C. In: Computer Assisted Drug Design. Olson E.C., Christoffersen R.E., editors. Vol. 112. ACS Symp. Ser.; Washington, DC: 1979. pp. 371–382. [Google Scholar]
- 46.Vranceanu Gh., Hangan Th., Teleman C. Geometrie elementară din punct de vedere modern. Tehnică; Bucureşti: 1967. pp. 56–78. [Google Scholar]
- 47.Mayer A.Y., Farin D., Avair D. Cross-Sectional Areas of Alkanoic Acids. A Comparative Study Applying Fractal Theory of Adsorption and Considerations of Molecular Shape. J. Am. Chem. Soc. 1986;108:7897–7905. [Google Scholar]
- 48.Motoc I., Balaban A.T. Topological Indices: Intercorrelations, Physical Meaning, Correlational Ability. Rev. Roum. Chim. 1981;26:305–306. [Google Scholar]
- 49.Medeleanu M., Ciubotariu C., Ciubotariu D. A New Globularity Measure for Quantitative Treatment of Molecular Shape. Chem. Bull. “POLITEHNICA” Univ. of Timisoara. 2004;49 in press. [Google Scholar]


