The neural code for tactile roughness in the somatosensory nerves

Abstract

Roughness is the most salient perceptual dimension of surface texture but has no well-defined physical basis. We seek to determine the neural determinants of tactile roughness in the somatosensory nerves. Specifically, we record the patterns of activation evoked in tactile nerve fibers of anesthetized Rhesus macaques to a large and diverse set of natural textures and assess what aspect of these patterns of activation can account for psychophysical judgments of roughness, obtained from human observers. We show that perceived roughness is determined by the variation in the population response, weighted by fiber type. That is, a surface will feel rough to the extent that the activity varies across nerve fibers and varies across time within nerve fibers. We show that this variation-based neural code can account not only for magnitude estimates of roughness but also for roughness discrimination performance.

NEW & NOTEWORTHY Our sense of touch endows us with an exquisite sensitivity to the microstructure of surfaces, the most salient aspect of which is roughness. We analyze the responses evoked in tactile fibers of monkeys by natural textures and compare them to judgments of roughness obtained for the same textures from human observers. We then describe how texture signals from three populations of nerve fibers are integrated to culminate in a percept of roughness.

everyday manual interactions activate multiple kinds of mechanoreceptors in the glabrous skin of the hand, each sensitive to different aspects of skin deformation. The nerve fibers that innervate these receptors inherit their response properties: slowly adapting type 1 (SA1) afferents respond preferentially to slowly changing, local, large-amplitude skin deflections, Pacinian (PC) fibers prefer small-amplitude, high-frequency oscillations that propagate large distances across the skin, and rapidly adapting (RA) afferents prefer local skin deformations over an intermediate range of frequencies. Signals from these three populations of afferents are routinely combined to extract sensory information from objects (Saal and Bensmaia 2014) to support interactions with them (Johansson and Flanagan, 2009). How information from these disparate sensory channels is integrated is not yet well understood.

The study of tactile texture processing is uniquely suited to address the integration of signals from the various modalities. Indeed, tangible textural features span a wide range of spatial scales, ranging from hundreds of nanometers (Skedung et al. 2013) to tens of millimeters (Connor et al. 1990) and each tactile submodality (that is, SA1, RA, and PC fibers) is apt to encode textures over a subrange of spatial scales (Weber et al. 2013). SA1 fibers are sensitive only to surface features measured in millimeters. PC responses exhibit precise, texture-specific temporal spiking patterns to surface features on the order of micrometers but saturate with larger features. RA fibers are sensitive over a wide range of spatial scales but less sensitive than their SA1 and PC counterparts at the large and small extremes, respectively.

For many years, texture perception was thought to be primarily mediated by SA1 afferents, based on an elegant series of studies of the neural basis of perceived roughness, one of the major dimensions of texture (Hollins et al. 2000), in the somatosensory nerves (Blake et al. 1997; Connor et al. 1990; Connor and Johnson 1992; Yoshioka et al. 2001). This conclusion, however, seems to have been an artifact of the Braille-like embossed dot patterns used in these studies, the processing of which happens to be dominated by the response of SA1 fibers (Goodman and Bensmaia 2017). Indeed, we have recently shown that all classes of nerve fibers convey texture information and contribute to our perceptual experience of texture (Weber et al. 2013).

In this article, we investigate in more detail how signals from the different submodalities contribute to the tactile perception of roughness. To this end, we reexamined previously published recordings of neuronal responses evoked in the nerves of anesthetized nonhuman primates by natural textures and incorporated a new set of psychophysical judgments obtained from human observers to a previously collected one to establish how perception arises from nerve activity. First, we show that signals from all three afferent classes account for judgments of perceptual roughness across the full range of natural textures. Indeed, whereas SA1 responses are predictive of perceived roughness for coarsely textured surfaces, RA responses provide much more finely graded information about roughness for both coarse and fine surfaces. Furthermore, PC responses are necessary to account for the familiar roughness of sandpapers, which evoke comparatively weak responses in SA1 and RA fibers. Second, we show that different afferents convey information about texture not in the strength of their responses but in their variation or inhomogeneity, as was first suggested in the aforementioned studies on roughness coding (Connor et al. 1990). Moreover, we demonstrate that spatial variation in SA1 and RA afferents (the degree to which firing rates vary across fibers) and temporal variation in RA and PC fibers (the degree to which firing rates vary over time in individual fibers) determine how rough a surface will feel. Finally, we discuss how the hypothesized spatial and temporal variation computations are reflected in the responses properties of neurons in primary somatosensory cortex.

MATERIALS AND METHODS

The neurophysiological data and some of the psychophysical data (from the magnitude estimation experiment) were presented previously (Weber et al. 2013).

Stimuli

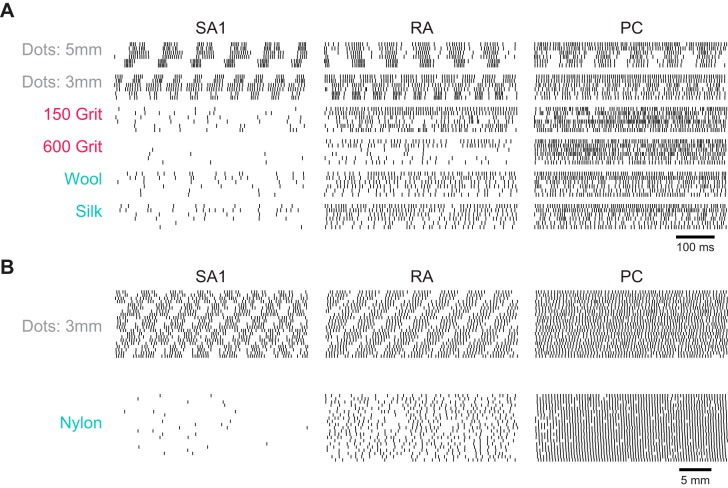
Textured surfaces were presented to the fingertips of both human participants (vibrometry, psychophysics) and nonhuman primates (neurophysiology) using a custom-built rotating drum stimulator (Weber et al. 2013) (Fig. 1A). The 55 textures included gratings (height = 0.74 mm) and tetragonal arrays of embossed dots (truncated cones: height = 0.74 mm, base diameter = 1 mm, tip diameter = 0.5 mm, inter-dot spacing range: 2–6 mm, arranged as in Connor et al. 1990), created using a photosensitive polymer (Printight; Toyobo), which have been extensively used in previous roughness studies (Cascio and Sathian 2001; Connor et al. 1990b; Darian-Smith and Oke 1980; Phillips et al. 1988), as well as finer, more naturalistic textures such as fabrics and sandpapers (Table 1, Fig. 1B). Each textured strip (2.5 cm wide × 16 cm long) was wrapped around an acrylic drum (25.4 cm in diameter and 30.5 cm in length) to cover its surface completely. On each trial, the drum began to rotate and was lowered onto the fingertip when its desired speed had been achieved to exert a contact force of 50 g (±10 g) on the finger. Textures were presented for 2.4, 1.2, or 0.8 s at 40, 80, and 120 mm/s, respectively, and the interstimulus interval was 3.5 s to prevent afferent adaptation (Bensmaïa et al. 2005; Leung et al. 2005). In all analyses of neurophysiological data, we only consider neuronal responses during the steady-state period when both desired speed and force have been achieved.

Fig. 1.

Experimental apparatus, sample textures, and roughness judgments. A: rotating drum stimulator. B: the surface microstructure (profilometry) of 9 example textures, ordered from smoothest (top left) to roughest (bottom right; across rows, then columns). Fine textures are colored in cyan, coarse textures in gray, and sandpapers in red. C: perceived roughness for each texture, split by texture group (C, coarse; F, fine; S, sandpaper). Each point represents a single texture. Bars denote mean roughness across the group, and error bars denote SD. Units of roughness are such that the mean roughness of all 55 textures is normalized to 1.

Table 1.

Texture set

Vinyl (20 gauge) [0.29, F]	Swimwear lining (polyester/Spandex) [0.47, F]	Sparkle vinyl black [0.75, F]	Denim (cotton) [0.98, F]	Corrugated paper [1.63, C]
Faux leather (polyester) [0.32, F]	Sueded Cuddle (polyester) [0.47, F]	Foam drapery tape* [0.76, F]	Grating, 3 mm (plastic) [1.01, F]	Sandpaper, 320 grit [1.65, S]
Premier velvet (polyester) [0.35, F]	Velvet [0.48, F]	Sandpaper, 800 grit [0.77, S]	Stretch denim (cotton/Lycra) [1.04, F]	Embossed dots, 2 mm (plastic) [1.67, C]
Grating, 1 mm (plastic) [0.35, F]	Leather, suede* [0.50, F]	Designer wool [0.83, F]	Silk, crinkled* [1.07, F]	Grating, 8 mm (plastic) [1.81, C]
Velour (polyester) [0.37, F]	Thin corduroy [0.51, F]	Chiffon [0.84, F]	Silk jacquard [1.08, F]	Sandpaper, 240 grit [1.83, S]
Microsuede (polyester) [0.37, F]	Satin [0.52, F]	Nylon (200 denier) [0.85, F]	Upholstery [1.12, F]	Sandpaper, 150 grit* [1.84, S]
Stretch velvet [0.38, F]	Taffeta [0.56, F]	Silk, metallic (silk/metal) [0.90, F]	Wool, blend* [1.18, F]	Grating, 12 mm (plastic) [1.87, C]
Snowflake fleece fuzz (polyester) [0.44, F]	Careerwear flannel (cotton) [0.58, F]	Wool crepe [0.92, F]	Sandpaper, 600 grit* [1.39, S]	Embossed dots, 3 mm (plastic)* [2.14, C]
Smooth leather [0.45, F]	Blizzard fleece (polyester) [0.61, F]	Thick corduroy [0.93, F]	Hucktowel (cotton) [1.51, C]	Embossed dots, 4 mm (plastic) [2.27, C]
Empire velveteen (cotton) [0.46, F]	Organza [0.74, F]	Wool/rayon felt [0.94, F]	Grating, 5 mm (plastic)* [1.55, C]	Embossed dots, 6 mm (plastic) [2.42, C]
Snowflake fleece knit (polyester) [0.47, F]	Wool gabardine [0.75, F]	Medium corduroy [0.95, F]	Sandpaper, 400 grit [1.58, S]	Embossed dots, 5 mm (plastic)* [2.46, C]

All 55 textures are shown ordered by perceived roughness (by column and then by row). Square brackets show the roughness of each texture and whether the textures were grouped as fine (F), coarse (C), or sandpapers (S).

^*Texture is shown in Fig. 1.

Sequential scanning protocol.

To reconstruct the spatial image conveyed by different afferent populations, we selected a subset of 12 textures to obtain spatial even plots (SEPs; cf. Johnson and Phillips 1988). Briefly, we repeatedly passed the texture stimulus over the receptive field of a nerve fiber, at 80 mm/s, with a 500-μm lateral shift (along the axis of rotation) between each presentation. Thus a different patch of texture was scanned across the receptive field on each successive run (Johnson and Phillips 1988). Each texture was presented twice at 21 different locations along the axis of rotation, creating an SEP that was 1 cm wide. Because afferent responses are relatively similar across afferents of a given type, spike trains elicited in a single mechanoreceptive afferent by different portions of the stimulus can be used to estimate the spatial pattern of activation elicited by the stimulus across the afferent population (Fig. 2B). Indeed, spatial variation computed from the responses of individual tactile fibers has been shown to provide a good approximation of the variation computed from different afferents (Yoshioka et al. 2001). Data from this protocol were used to compare spatial and temporal variation and revealed that these two quantities were highly correlated for the set of textures used.

Fig. 2.

Afferent responses to natural textures. A: spiking responses to 6 different textures from SA1, RA, and PC fibers (responses to 2 repeated presentations of each texture from 3 example afferents of each type). Textures are ordered from roughest (top) to smoothest (bottom); colors correspond to the texture categories as indicated in Fig. 1. B: spatial event plots for 2 textures reconstructed from the responses of one afferent of each type (5 mm corresponds to 62.5 ms at 80 mm/s) obtained in a dedicated protocol (see materials and methods). Each patch consists of repeated parallel scans of the texture across the receptive field of the afferent, each shifted perpendicular to the scanning direction by 0.5 mm, yielding a spatial image (cf. Johnson and Phillips 1988).

Profilometry.

The three-dimensional (3-D) surface profile of the 7-mm × 7-mm texture samples was recorded using a laser measuring microscope (LEXT OLS4000; Olympus, Tokyo, Japan), with a resolution of 2.5 μm in the x–y plane and 0.05 μm along the z-axis. Our reported texture profiles are detrended for clarity and downsampled to a 10-μm resolution in the x–y plane.

Psychophysics

All procedures were approved by the Institutional Review Board of the University of Chicago, and all subjects provided informed consent. Subjects sat with the left arm supinated and resting on a support under the drum. Stimuli were presented to the left index fingerpad of each subject. In the present study, we seek to relate psychophysical judgements obtained from human subjects to the responses of tactile fibers measured from anesthetized primates, because the response properties of afferents are quite similar in the two species (Johansson et al. 1982; Phillips et al. 1990, 1992).

Magnitude estimation experiments.

For these experiments (8 subjects: 6 men, 2 women; ages 18–31 yr), on each trial, the subject was passively presented with 1 of 55 textures (80 mm/s, 50 ± 10 g) and asked to produce a rating proportional to its perceived roughness, where a rating of 0 denoted a perfectly smooth surface. If texture B was perceived to be twice as rough as texture A, it was ascribed a number that was twice as large. Subjects were encouraged to use fractions and decimals. Each texture was presented once in each of six experimental blocks; ratings were normalized by the mean of each block and averaged, first within and then across subjects. Ratings of roughness were highly consistent across subjects (intersubject correlation: 0.91 ± 0.03, mean ± SD).

Roughness discrimination experiments.

For these experiments (6 subjects: 3 men, 3 women; ages 19–31 yr), a subset of six textures was selected from the fine group: fleece (fuzzy), velveteen, suede (cuddle), flannel, organza, and wool gabardine. On each trial, the subject was passively presented with a pair of textures (for 1 s each, separated by a 1-s interstimulus interval, 15 unique comparisons, 80 mm/s, 50 ± 10 g) and asked to judge which of the two felt rougher. Each pair of textures was presented 20 times in pseudorandom order. Roughness discrimination performance was consistent across the subjects (intersubject correlation: 0.85 ± 0.16, mean ± SD).

Neurophysiology

Extracellular single-unit recordings were collected from the median and ulnar nerves innervating the distal fingertips of six Rhesus macaques (Macaca mulatta) using established procedures (Muniak et al. 2007; Talbot et al. 1968). Anesthesia was maintained using pentobarbital. Data were collected from 17 SA1 fibers, 15 RA fibers, and 7 PC fibers. Units were classified as SA1, RA, or PC using standard methods (Muniak et al. 2007). All procedures complied with the NIH Guide for the Care and Use of Laboratory Animals and were approved by the Animal Care and Use Committee of the University of Chicago.

Analysis

Our large, diverse stimulus set (Table 1) allowed us to test the hypothesis that different tactile submodalities are differentially informative about surface microgeometries at different spatial scales. Having noted that, with the exclusion of sandpapers, our textures naturally split into two clearly separated groups (Fig. 1C), we split textures into three categories: 1) fine textures, 2) coarse textures, and 3) sandpapers, which, although they tended to be rough, evoked qualitatively different responses in PC fibers than did other textures.

Temporal variation.

As a starting point, we tested the hypothesis, put forth in our previous study (Weber et al. 2013), that perceived roughness could be predicted from the temporal variation in afferent responses, with the caveat that the previously published analysis did not make a strong distinction between temporal and spatial variation (see below). To this end, we implemented a simple temporal variation filter, with only two parameters, that allowed us to directly evaluate 1) the timescale over which roughness is computed and 2) the extent to which roughness relies on a rate code or a variation code. In our previously study (Weber et al. 2013), we had used a more complex filter to replicate results from one of the foundational papers on roughness coding (Connor and Johnson 1992). However, in subsequent testing, we found that a simple filter achieved comparable fits to the more complex one, and we consequently adopted it.

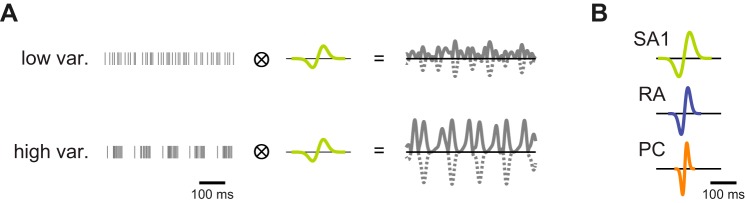
To compute variation, we first counted the number of whole and fractional interspike intervals within each 1-ms bin, an approach that yields variation values that increase smoothly with firing rate at low response rates in contrast to the standard binning technique (cf. Blake et al. 1997; Connor et al. 1990; Connor and Johnson 1992; Yoshioka et al. 2001). Next, we convolved these binned responses with a 1-D variation filter:

$$f\left(t\right)=\left[p·\frac{t}{\sigma }+\left(1-p\right)\right]\text{exp}\left[\frac{-t^2}{2{\sigma }^2}\right],$$

where σ is the characteristic width (in ms) of the filter, and p, which ranges from 0 to 1, represents the strength of the bimodality in the filter: p = 0 denotes Gaussian smoothing, and p = 1 denotes symmetric differentiation, analogous to the filters used in previous roughness studies (Blake et al. 1997; Connor et al. 1990; Connor and Johnson 1992). This mathematical description of the filter was adopted because it captures the range of filters observed for the integration of afferent signals in somatosensory cortex (Saal et al. 2015). The resulting signal was then full-wave rectified, the equivalent of implementing two half-wave rectified, phase-inverted filters (cf. Connor and Johnson 1992), and then averaged to compute a single variation value per spike train (see Fig. 3A). Note that the variation values obtained using half-wave and full-wave rectification were almost indistinguishable (R² = 1.0, 0.99, and 0.95 for SA1, RA, and PC fibers, respectively).

Fig. 3.

Variation computation and filter shapes. A: spikes are binned and convolved with a temporal filter. The output of the filter is then rectified [all negative values (dashed line) are set to their absolute value (solid line)] and averaged to obtain a single variation value (var., variation). B: illustration of the variation filters used for SA1, RA, and PC spiking data.

Filters were fit individually to responses, from each afferent population separately, to textures that elicited an average of at least 10 spikes per second in that population (if too many low-spiking textures were included in the fitting, parameters became unstable). Variation was calculated for individual spike trains and then averaged over trials and afferents to get a mean variation value for each texture in each afferent population. Filter parameters were optimized to achieve the highest correlation between response variation and perceived roughness. The optimal p was 0.85, 0.90, and 1.0 for SA1, RA, and PC afferents, respectively, suggesting strong differentiation (Fig. 3B). The optimal σ was 20.7, 12.8, and 8.0 ms, suggesting that SA1 responses are integrated over longer time windows than are their PC counterparts, with RA signals exhibiting intermediate integration times, consistent with previous findings (Saal et al. 2015). If these filters are interpreted in spatial terms (see below), then the corresponding distances between filter peaks are 3.36, 2.08, and 1.28 mm, respectively, given the scanning speed of 80 mm/s, consistent with previous findings (Connor et al. 1990). These parameters are used for all analyses throughout this article, with the exception of the speed analysis in Fig. 9, in which σ is varied over a range (with p fixed at its optimal value).

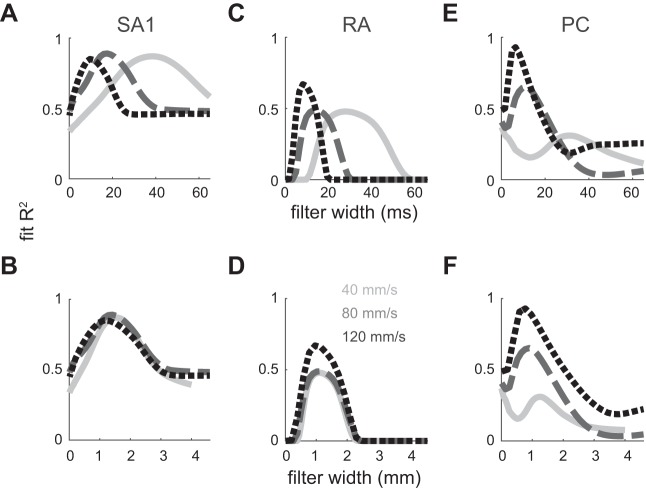
Fig. 9.

Spatial vs. temporal variation and roughness predictions. Coefficients of determination between variation and perceived roughness (coarse textures only) are plotted for SA1 (A), RA (B), and PC afferents (C) at 3 different speeds (solid line, 40 mm/s; 80 mm/s, dashed line; 120 mm/s, dotted line) plotted against the filter width parameter σ (in ms, top; see materials and methods) as the other filter parameter (p) is held constant. R² values were rectified such that when the correlation coefficient was negative (r < 0), R² was set to 0. When these functions are plotted in spatial units (in mm, bottom), the curves peak in the same location, particularly for SA1 and RA fibers, consistent with a spatial variation code for roughness, at least for SA1 and RA fibers.

Spatial variation.

We sought to determine the degree to which temporal variation could be used as a proxy for spatial variation given our texture set. To this end, we measured the spatial variation in SA1 and RA responses of a subset of textures using previously established methods (developed by Connor and Johnson 1992). Briefly, SEPs were binned in 0.5-mm × 0.5-mm bins (corresponding to 6.25 ms along the scanning direction) and then convolved with a 2-D Gabor filter:

$$f\left(x,y\right)=\sin \left\{\frac{2\pi \left[x·\sin \left(\theta \right)-y·\cos \left(\theta \right)\right]}{\lambda }+\phi \right\}·\exp \left[\frac{-\left(x^2+y^2\right)}{2{\sigma }_s{}^2}\right],$$

where (x, y) is the center of the filter, θ is the orientation of its sinusoidal component, λ is its spatial period, φ is the phase of the sinusoidal component relative to the center, and σ_s is the standard deviation of the 2-D Gaussian component. Spatial variation was calculated at a range of rotations and translations of the Gabor filter across the field of the SEP and then averaged to obtain the overall spatial variation. To compare temporal and spatial variation, we matched the shape of the spatial filter to that of the temporal filter by setting σ_s = 2σ·(80 mm/s) and λ = 2.5σ_s, which yields filters with matched peak-to-peak distances. For SA1 and RA afferents, we measured the correlation between the mean temporal variation across the 21 rows of the SEP to the measured spatial variation of that same SEP, across all recorded cells, textures, and trials. We did not compute the spatial variation of PC responses because this population of tactile fibers innervates the skin too sparsely for a spatial code to be viable at the relevant spatial scales.

Model validation.

To compare models with different numbers of parameters (e.g., single vs. multiple regressions), we performed a leave-one-out cross-validation procedure. For each texture, we refit our model on variation and roughness data from the 54 other textures and used this new model to predict the roughness of the texture that was left out; then, over the full set of 55 predicted values, we calculated the mean error normalized by total variance:

$$e=\frac{{{\displaystyle \sum }}_i{\left(y_i-f_i\right)}^2}{{{\displaystyle \sum }}_i{\left(y_i-\overline{y}\right)}^2},$$

where f_i is the predicted roughness of ith texture, y_i is the psychophysical roughness of ith texture, and ȳ is the mean measured roughness. For the non-cross-validated case, 1 − e = R². To test whether a given model provided significantly better predictions than another, we calculated a bootstrapped error (sampling textures with replacement 10,000 times) and counted the proportion of times a given model performed more accurately than another.

These errors are summed over subsets of textures (fine, coarse, sandpaper) and reported in Fig. 5A and Fig. 8A. Because our cross-validation procedure occasionally yielded large outliers (caused by an idiosyncratic sample), these errors are reported as medians and median absolute deviations.

Fig. 5.

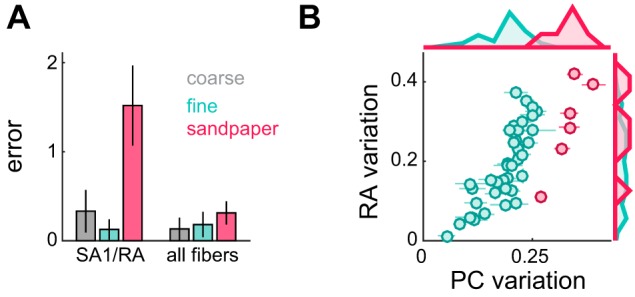
PC contribution to roughness perception: the case of sandpapers. A: comparison between 2 regression models: one using only SA1/RA afferent responses and one using all 3 afferent types. Cross-validated errors (leave-one-out procedure; see materials and methods) are plotted as medians ± median absolute deviations. With PC variation, model performance significantly improves. B: RA variation vs. PC variation for fine textures and sandpapers. Each point represents the mean response across afferents to a single texture. Error bars denote SE. Marginal histograms are plotted at top and right. RA sandpaper responses are very similar to fine texture responses, despite the fact that sandpapers are significantly rougher. PC responses separate sandpapers from fine textures.

Fig. 8.

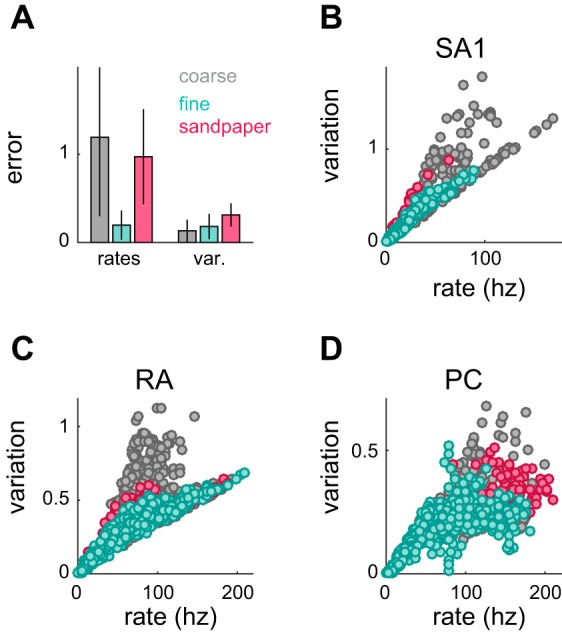
Response rate vs. variation and roughness predictions. A: comparison between 2 models, one using only firing rates from all 3 afferent types and one using response variation from all 3 afferent types. Cross-validated errors (leave-one-out procedure; see materials and methods) are plotted as medians ± median absolute deviations and are broken down by texture subtype. The model using variation greatly reduces the error in predicting the roughness of coarse textures and sandpapers. B–D: variation vs. firing rate for SA1 (A), RA (B), and PC fibers (C). Coarse texture responses exhibit a wider range of variation values for a given firing rate.

Principal components analysis.

We used principal components analysis (PCA) to characterize the extent to which the roughness signal was redundant across afferent populations. First, we treated the response variation response of each afferent as a separate dimension, yielding 55 points in a 39-dimensional space. Next, we normalized each afferent’s response across textures such that all three subpopulations of afferents (SA1, RA, PC) accounted for an equal proportion of the variance across the total space. Specifically, each response variation value was normalized by the standard deviation (across textures) of each afferent’s variation values divided by the square root of the number of afferents of that type in the sample. Thus each subspace (comprising 15, 17, and 7 dimensions corresponding to SA1, RA, and PC fibers) had unity variance, and the contribution to that variance of each fiber of each type was equal. Next, we used PCA to produce a sorted list of 39 orthonormal vectors (principal axes), the coordinates of the textures in this new orthonormal basis (principal components), and the variance explained by each basis. Finally, we performed regressions to quantify the relationship between individual principal components and roughness ratings. The main conclusions of the resulting analyses were consistent across strategies to normalize the variation values (including no normalization).

Afferent reliability.

We characterized afferent reliability in two ways: 1) how reliably could two textures be discriminated on the basis of responses of an individual afferent? and 2) how reliably could two textures be discriminated on the basis of responses of pairs of afferents? In other words, we wanted to test the degree to which individual afferents conveyed consistent roughness signals and the degree to which different afferents conveyed roughness signals that were consistent with each other. To quantify within-fiber consistency, we computed how often comparisons based on single-trial responses of a given afferent to each texture in a pair yielded results consistent with the comparison of the trial-averaged responses of that afferent to those two textures. That is, if texture t₂ had a larger mean variation than texture t₁, we assessed how often the variation in the single-trial response to t₂ was greater than that from t₁. We averaged this performance over all texture pairs to obtain a measure of how consistent each afferent’s response was across repeated presentations of each texture. For each afferent class we averaged this performance over all cells, with a performance of 0.5 indicating no consistency, 1 indicating perfect consistency, and less than 0.5 indicating that the majority of afferents did not reflect the mean tendency.

To quantify across-fiber consistency, we computed how often comparisons of the mean variation from individual afferents gave results consistent with the comparison of the mean variation across afferents. That is, if texture t₂ had a larger mean variation (across trials and fibers) than texture t₁, we assessed how often the mean variation (across trials) in each afferent’s responses to t₂ was greater than that the mean variation in another afferent’s responses to t₁. To the extent that the ordinal relationship in the response variation was consistent across nerve fibers, this measure tended toward 1 (with 0.5 indicating no consistency).

Roughness discrimination.

We implemented an ideal observer analysis to determine the extent to which a combined signal from all three afferent types could discriminate the roughness of pairs of textures. First, we combined single-trial variation values from equal numbers of SA1, RA, and PC afferents chosen at random, using weights from the full multiple regression. We measured the proportion of times that this new metric was higher for the rougher of the two textures (from magnitude estimation). The performance for a given texture pair was averaged over many combinations of trials and combinations of afferents to create a mean discrimination performance. We tested groups of afferents from sizes 3 to 21 (1 to 7 of each afferent type) and found that groups of size 15 (5 of each type) closely matched psychophysical performance. We used an equal number of afferents of each type for this analysis, despite the fact that PC fibers innervate the skin much less densely than do RA or SA1 fibers, because the high-frequency vibrations evoked during texture scanning propagate long distances across the skin and activate PC afferents far from the contact area (Delhaye et al. 2012; Manfredi et al. 2012). This recruitment results in a substantial amplification of the PC signal and counters the effects of the lower innervation density of PC fibers.

As expected, ideal observer performance systematically improved as the roughness difference between two textures increased. To obtain best-fit curves of this relationship, we averaged the discrimination performance for each texture pair across nerve fibers of each type and plotted this performance against the mean log ratio of roughness. Psychometric curves were fit with a sigmoid function:

$$f\left(r\right)=\frac{1}{1+e^{-r/T}},$$

where r is the log ratio of variation or roughness, and T is a slope parameter that corresponds to the threshold log ratio given a criterion discrimination performance of 0.73 [= 1/(1 + e⁻¹)]. The Weber fraction is then given by e^−T − 1. Note that the Weber fraction in this case is computed on the basis of perceptual judgments rather than a physical continuum (as is typically done) and so cannot be directly compared with previously measured Weber fractions (based on grit size or spatial period, for example) (Hollins et al. 2001; Miyaoka et al. 1999; Sutu et al. 2013). However, we used the same perceptual judgments for the psychophysical and neurometric analyses, so the comparison of the two is appropriate.

RESULTS

We recorded the activity evoked in 17 SA1, 15 RA, and 7 PC afferents as each of 55 textured surfaces was scanned across the finger using a rotating drum stimulator (Fig. 1A). For the purposes of comparison, stimuli were divided into three groups: 39 fine textures, which consisted mostly of fabrics; 10 coarse textures, which included Braille-like dot patterns, gratings, and coarse fabrics; and 6 sandpapers varying in grit size (from 150 to 800) (Table 1, Fig. 1B). In paired psychophysical experiments, eight human observers rated the perceived roughness of these same textures, also presented using the drum stimulator, in a free magnitude estimation paradigm (Fig. 1C), and another five human observers performed a roughness discrimination task in which they judged which of two paired textures was rougher. We sought to understand which aspects of the activity in the three classes of afferents (Fig. 2) accounted for reports of perceived roughness.

Predicting Mean Roughness Judgments on the Basis of Afferent Responses

In a previous study using the same data, we showed that the variation in the responses evoked in the three classes of tactile nerve fibers, weighted by fiber type, was a reliable predictor of perceived roughness (Weber et al. 2013). Variation is defined as the inhomogeneity in the peripheral response, in space (how much does the response vary response across afferents?) or in time (how much does the response of individual afferents vary over time?). We wanted to further examine the relationship between neural response variation and roughness and assess how consistent this relationship was across the range of tangible textures. To quantify variation, we convolved afferent spike trains with a differentiating filter (Fig. 3; see materials and methods). We first limited our analysis to coarse textures in an attempt to replicate results using dot patterns and gratings (Blake et al. 1997; Connor et al. 1990; Connor and Johnson 1992). We found that variation in SA1 responses tended to outperform both RA and PC variation, consistent with previous studies (Fig. 4, coarse textures in gray; R² = 0.90, 0.63, and 0. 80 for SA1, RA, and PC variation, respectively). In contrast, as previously reported (Weber et al. 2013), we found that SA1 variation was a poor predictor of perceived roughness of fine textures and was easily outperformed by both RA and PC variation (Fig. 4, cyan; R² = 0.46, 0.91, and 0.67 for SA1, RA, and PC variation, respectively). SA1 and PC signals were poor predictors of the roughness of sandpapers compared with RA afferents (Fig. 4, red; R² = 0.62, 0.93, and 0.82 for SA1, RA, and PC variation, respectively). In fact, over the full range of textures, RA variation outperformed both SA1 and PC variation (leave-one-out cross-validation, P < 0.05, R² = 0.72, 0.89, and 0.82 for SA1, RA, and PC variation, respectively). That SA1 responses performed poorly in the discrimination of sandpapers suggests that these nerve fibers are not simply coarse texture “specialists,” as had been previously proposed (Bensmaïa and Hollins 2005; Hollins et al. 2001). Rather, aspects of the roughness signal seem to be distributed across fiber types.

Fig. 4.

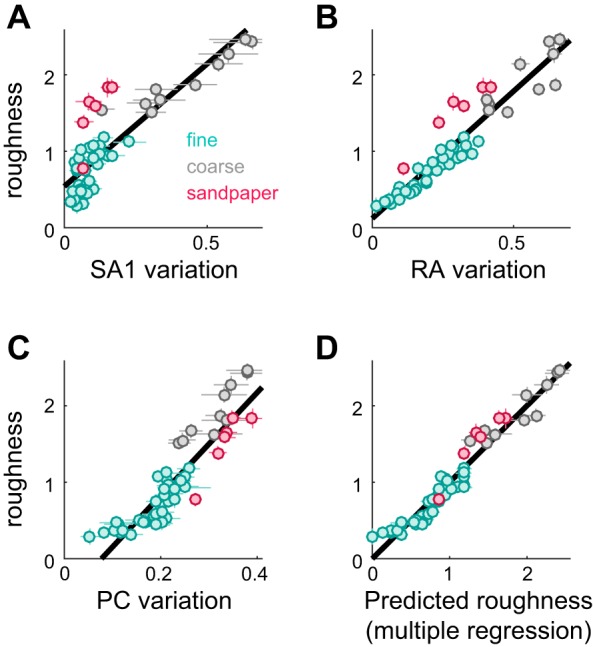
Candidate neural codes for roughness. A–C: roughness ratings are plotted against SA1 variation (A; R² = 0.72), RA variation (B; R² = 0.89), and PC variation (C; R² = 0.82). Cyan markers denote fine textures, gray markers denote coarse textures, and red markers denote sandpapers. Error bars denote SE. Lines of best fit are plotted in black. D: roughness ratings are plotted against the output of a multiple regression model that was fit on the mean variation values from all 3 afferent types (R² = 0.94, standardized regression weights = 0.11, 0.25, and 0.25 for SA1, RA, and PC, respectively). Error bars denote SE. (Reproduced from Weber et al. 2013.).

Although our data suggest that SA1 afferents cannot account for roughness and that RA afferents provide the strongest linear relationship with roughness judgments, there is no reason to believe that any given perceptual function (texture perception, for example) will be mediated by a single population of afferents (Saal and Bensmaia 2014). In fact, we found that a linear combination of response variation in the three afferent types outperformed any individual afferent type (Fig. 4D; R² = 0.94): all three predictors were significantly greater than zero [standardized regression, coefficients = 0.11, 0.25, and 0.25 for SA1, RA, and PC, respectively; ΔR² F-test: F(1,51) = 6.5, 19.5 and 48.8, with P < 0.05], and the combined model performed significantly better than any model including only responses from a single afferent population (leave-one-out cross-validation, P < 0.01) (cf. Weber et al. 2013). According to this model, then, RA and PC signals contribute to a greater extent to perceived roughness than do SA1 signals, a finding that stands in stark contrast to those of studies with embossed dot patterns and gratings.

PC signals are poor predictors of the roughness of dot patterns and gratings (Connor et al. 1990; Yoshioka et al. 2001) and predict fine texture roughness less accurately than do RA afferents. Nevertheless, they were a significant predictor in the linear regression. One way to illustrate the role of PC afferents in texture perception is to examine their contribution to the coding of sandpapers. Specifically, if we compare a model built from just SA1 and RA signals to a model using all three afferents, we find that adding PC afferents significantly reduced the error when predicting sandpaper roughness (Fig. 5A; leave-one-out cross-validation, P < 0.001). Indeed, SA1 and RA afferents consistently underestimate the relative roughness of sandpapers (see Fig. 4, A and B), but PC responses are nearly saturated for these textures (see Fig. 4C). In other words, PC responses are the reason why sandpapers feel so rough (Fig. 5B).

Although texture responses differ across fiber types, they are all relatively good predictors of roughness. One possibility, then, is that roughness is determined by the shared variance across afferent types. To test this possibility, we ran a PCA on the variation in texture-evoked responses (see materials and methods) and found that 60% of the variance in response variation was accounted for by the first principal component. Importantly, this single dimension could predict roughness ratings nearly as well as our multiple regression of mean afferent variation (R² = 0.93). Furthermore, the 38 remaining principal axes, which in combination accounted for 40% of the response variance, explained essentially nothing about roughness (R² = 0.07). In other words, roughness may be best understood as the extent to which response variation covaries across afferent types.

Reliability of Roughness Signals

In the preceding analysis, we showed that mean psychophysical ratings of roughness could be accounted for from the sum of the mean variation in afferent responses, weighted by afferent type. Next, we wanted to assess the reliability of this neural code for roughness. To this end, we investigated how reliable response variation was within and across fibers and assessed whether this neural population code could account for roughness discrimination performance.

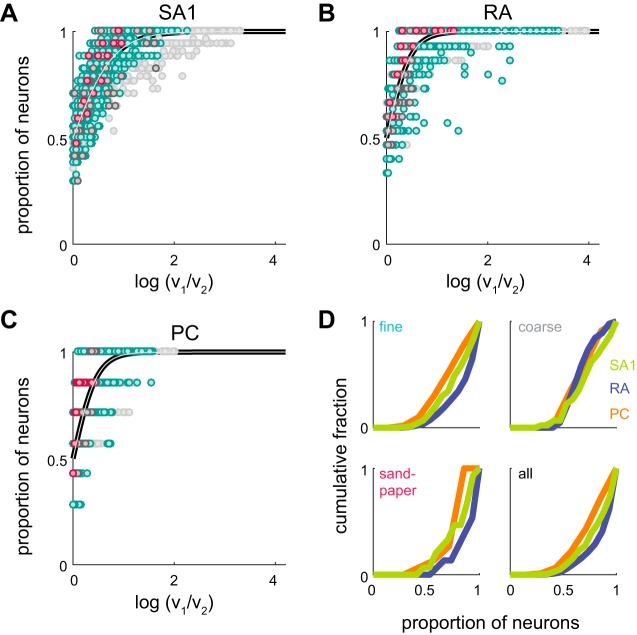
First, we found that variation was highly consistent across repeated presentations of a stimulus for each afferent. Indeed, the ordinal relation in the response variations evoked by a pair of textures, i.e., which of the two textures yielded the higher variation value, was highly consistent within fibers (mean within-afferent consistency, all texture pairs: 0.93, 0.95, and 0.91 for SA1, RA, and PC fibers, respectively). On the other hand, different afferents of a given type conveyed less consistent signals about roughness. That is, one fiber might yield a higher variation for texture A than for texture B, whereas another fiber of the same type might reverse that relation (Fig. 6, A–C). SA1 fibers tended to be the most consistent for the coarse textures, and RA fibers were the most consistent for fine textures and sandpapers, as well as over the full set of textures (Fig. 6D; mean across-fiber consistency, all texture pairs: 0.83, 0.88, and 0.79 for SA1, RA, and PC fibers, respectively). In other words, individual fibers are extremely consistent, but there is some disagreement across fibers of a given type as to the roughness of a texture, and this disagreement, rather than stochasticity in the response, most likely drives the uncertainty in roughness judgments.

Fig. 6.

Afferent reliability. A–C: across-fiber consistency. For every possible texture pair, the proportion of afferents with a higher mean variation for one texture than another is plotted against the log ratio of variation values (mean across afferents) for those textures. These values are plotted for SA1 (A), RA (B), and PC fibers (C). Pairs of fine textures are plotted in cyan, coarse textures in dark gray, and sandpapers in red. All other pairs (only mixed pairs, e.g., a sandpaper and a fine texture) are plotted in light gray. The black and gray line denotes the best fit sigmoid (see materials and methods). D: cumulative distributions of across-fiber consistency (SA1 afferents in light green, RA afferents in dark blue, PC afferents in orange) for pairs of fine textures (top left), coarse textures (top right), and sandpapers (bottom left). All possible texture pairs are combined at bottom right.

In the previous analysis, we assessed the consistency of response variation in each afferent population but did not directly address the relationship between these signals and perceived roughness. Next, we wanted to gauge whether the combined signals across afferent populations could account for roughness discrimination measured in human observers. To this end, we measured the performance of six human subjects in a roughness discrimination task with a subset of six textures (yielding a total of 15 pairs; Fig. 7B). Performance on this discrimination task yielded a Weber fraction of 0.17; that is, a 17% increase in perceived roughness was perceived 73% of the time. We then performed an ideal observer analysis based on afferent responses, weighted by afferent type (using weights from the multiple regression performed on the roughness estimates), to examine how accurately the putative distributed neural code could predict the discrimination of surface roughness. We found that obtaining a Weber fraction of 0.17 required only 15 nerve fibers (5 of each type; Fig. 7A). Orders of magnitude more fibers respond to a textured surface, but even individual tactile fibers have been shown to outperform human subjects (Arabzadeh et al. 2014). Furthermore, the patterns of confusions based on the psychophysical and neuronal data were highly correlated (R² = 0.85); that is, textures whose roughness tended to be confused in the psychophysical experiments also tended to be confused in the neurometric analysis. Thus a distributed code for roughness accounts not only for psychophysical ratings of roughness but also for roughness discrimination.

Fig. 7.

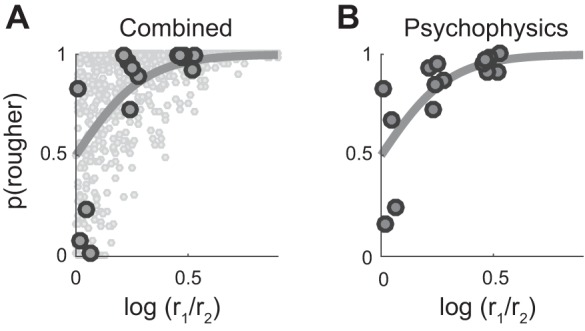
Roughness discrimination. A: ideal observer analysis based on the summed (single trial) variation of 5 afferents of each type, weighted by type, as a function of the roughness ratio (obtained in the magnitude estimation experiment) for every texture pair. Specifically, for a given pair of textures, r₁ (r₂) is the roughness rating for the rougher (smoother) of the two textures). A subset of these (larger black dots) were used in a roughness discrimination experiment. A best-fit curve is plotted in gray (threshold ratio = 0.15, yielding a Weber fraction = 0.17). Performance values below 50% fall within the margin of error of the mean ratings, highlighting the sensitivity of discrimination relative to magnitude estimation. B: mean psychophysical performance of 7 human subjects on a roughness discrimination task, for all possible pairs of 6 different textures, plotted against the log ratio of roughness judgements. A best-fit curve is plotted in gray (Weber fraction = 0.17). Performance thresholds are similar for psychophysical and neurometric judgments of texture roughness.

Does Response Rate or Response Variation Determine Roughness?

The above-described analyses were based on the premise, inspired by the work of Johnson and colleagues, that roughness was determined by the variation in afferent responses (Blake et al. 1997; Connor et al. 1990; Connor and Johnson 1992; Weber et al. 2013). However, whether response rate or response variation determine roughness has been a point of contention (Sutu et al. 2013, but see Goodman and Bensmaia 2017). With this in mind, we sought to reexamine the degree to which firing rates in populations of nerve fibers could account for perceptual judgments of roughness.

We found that a combined model using only firing rate was significantly outperformed by a model that used variation in afferent responses (P < 0.001, leave-one-out cross-validation), an effect mostly driven by an improvement in predicting the roughness of coarse textures (Fig. 8A). In light of this, we sought to examine why variation provides this advantage for some textures but not for others. We found that variation increased with firing rate in a consistently monotonic manner for fine texture responses, but much more irregularly for coarse texture responses (Fig. 8, B–D). In other words, variation and firing rate are interchangeable for fine but not coarse textures, which explains why rate and variation are equally good at predicting the roughness of fine textures but not that of coarse textures. Nonetheless, a single neural code, neural variation, accounts for perceived roughness across the range of tangible textures.

Does Temporal or Spatial Variation Determine Roughness?

Another point of inquiry is whether spatial or temporal variation is the key determinant of perceived roughness (Connor and Johnson 1992). To compute the variability of the afferent response to texture, the nervous system could plausibly compute the variability over time within individual afferents (temporal variation) or compute the degree to which responses of spatially displaced afferents differ (spatial variation). As previously reported (Weber et al. 2013), for the subset of textures for which we were able to construct spatial event plots, we found that temporal and spatial variation were nearly identical (R² = 0.93 and 0.98 for RA and SA1 afferents, respectively) and yielded indistinguishable predictions of perceived roughness (although in principle, they can be decoupled; see Connor and Johnson 1992).

However, we also examined the dependence of the filters on scanning speed. Indeed, we might expect a simple temporal variation filter to be invariant to changes in texture speed. Conversely, if our temporal filter actually reflected a spatial computation, the temporal width would contract or dilate systematically with increases or decreases in scanning speed, to map to a spatial filter of constant width. In other words, if the filters do not scale with speed, then they must be temporal. If filters do scale with speed, they may either be spatial or a more complex version of a temporal filter, the width of which is speed dependent. At each speed, we looked for the optimal timescale at which RA and SA1 response variation could best predict coarse texture roughness. We found that performance curves across speeds overlap closely when measured in spatial units, but not when measured in temporal units (Fig. 9, A–D; correlation between temporal/spatial curves, SA1: −0.08/0.95, RA: 0.11/0.99). In other words, our data are consistent with a model in which roughness is determined by spatial variation in SA1 and RA responses.

We found a similar, albeit weaker effect for PC afferents, whose responses showed more spatial than temporal constancy (Fig. 9, E and F; correlation between temporal/spatial curves, PC: 0.21/0.86). However, the innervation density of PC afferents is 1/7.5 mm², much sparser than 1/0.7 and 1/0.6 mm² for SA1 and RA afferents (Darian-Smith and Kenins 1980) and much too low to carry out spatial differentiation corresponding to the width of the PC filter (1.28 mm peak-to-peak). To the extent that the PC variation filters exhibit constancy, it is likely mediated by a speed-dependent temporal variation mechanism. Indeed, PC signals have been shown to be temporally differentiated by downstream neurons (Saal et al. 2015). Our results further suggest that the temporal differentiation filters that drive perceived roughness scale systematically with scanning speed.

DISCUSSION

Neural Code for Roughness

The main conclusions of the present study are that 1) all three afferent classes (SA1, RA, and PC afferents) contribute to roughness perception and that 2) the variation in afferent responses, rather than simply their strength, determines how rough a surface will feel. Consistent with previous reports (Blake et al. 1997; Connor et al. 1990; Connor and Johnson 1992), SA1 fibers respond strongly to textured surfaces comprising coarse spatial features. The spatial variation in this population of nerve fibers accounts for the roughness of these surfaces better than their rate. Although SA1 afferents set the limit of tactile acuity for patterns indented into the skin (Phillips and Johnson 1981), these nerve fibers are almost completely insensitive to small spatial features (measured in the hundreds of micrometers or smaller). Because most natural textures also comprise fine features, SA1 responses alone are insufficient to account for the tactile perception of texture.

Whereas RA afferents contribute less to the perceived roughness of coarse textures than do their SA1 counterparts (cf. Blake et al. 1997), these fibers are critical for the perceived roughness of textures whose features span a wide range of spatial scales. In a previous study, we proposed that RA fibers encode texture information in the temporal patterning of their responses, down to a precision of ~5 ms (Weber et al. 2013). Given the density of RA innervation, this population of fibers may also encode coarse spatial features in their spatial pattern of activation. RA signals may thus encode coarse surface features spatially and temporally and fine features temporally.

Finally, whereas PC fibers innervate the fingertip skin too sparsely to encode texture in their spatial pattern of activation, they produce strong responses to scanned surfaces that span the range of tangible textures (Weber et al. 2013). Whether the contribution of the PC signal is in the rates or in the variation is not clear: our model’s ability to predict texture roughness is unchanged if we replace PC variation with PC rate. The differentiation filter for PC responses may therefore not be necessary in the roughness computation. However, one might argue that the responses of all three afferent populations may be processed analogously to extract a given stimulus quantity (roughness), which would support the inclusion of PC variation. Furthermore, PC signals have been shown to be differentiated in cortex (see below).

In summary, all three populations of nerve fibers contribute to the perception of roughness. In fact, perceived roughness seems to be driven by a redundant signal carried by all three afferent populations. This finding adds to a body of evidence showing that signals from the three tactile submodalities are not functionally segregated, as was once believed, but rather are integrated to extract stimulus information and elicit in a tactile percept (Saal and Bensmaia 2014).

Spatial vs. Temporal Coding

A major limitation of the present study is the failure to conclusively distinguish spatial coding, where stimulus information is conveyed in the pattern of responses across populations of fibers, from temporal coding, where information is conveyed in temporal patterning in the spiking responses of individual fibers. Indeed, for the set of texture for which both could be explicitly measured and compared, the spatial and temporal variations were highly correlated. We can exclude spatial coding in PC fibers, at least at the relevant spatial scales, given their sparse innervation and enormous RFs. We can also, in principle, exclude spatial coding for fine textures, because their spatial periods are orders of magnitude smaller than what can be resolved spatially, even in SA1 and RA responses. However, we cannot exclude (and in fact believe it to be rather likely) that RA fibers encode coarse textural features both spatially and temporally. The main evidence for the spatial code for roughness is that the optimal variation filter scales with scanning speed as predicted by a spatial code. However, the ability to distinguish textures with spatial periods less than ~1 mm implies temporal coding in RA and PC fibers (Weber et al. 2013).

Downstream Mechanisms

In the proposed model of roughness coding, the spatial representation of coarse features, carried by SA1 and perhaps RA fibers, is spatially differentiated at a specific spatial scale. The receptive fields of a large proportion of neurons in area 3b, characterized by an excitatory center flanked by one or more inhibitory subfields, separated by 2–4 mm (DiCarlo and Johnson 2000), carry out precisely the implied computation. Indeed, the spatial variation filter used to predict roughness from afferent responses, the Gabor function, provides an accurate fit for this receptive field structure (Bensmaia et al. 2008). This spatial processing draws a strong analogy with vision: receptive fields in primary visual cortex are also well approximated by Gabor functions (Hubel and Wiesel 1959; Jones and Palmer 1987). The spatial differentiation structure in visual cortex is thought to be an adaptation to natural image statistics (Olshausen and Field 1996), and the same is likely true of its counterpart in somatosensory cortex (Pack and Bensmaia 2015).

In the model, the contribution of fine textural features to perceived roughness is driven primarily in the temporal variation of RA and PC afferents. In support of this hypothesis, a subpopulation of neurons in area 3b perform a differentiation of their RA and PC input (Saal et al. 2015). That is, the contribution of RA and PC signals to the responses of many cortical neurons are well approximated by using differentiating filters that are mathematically equivalent to those used to predict roughness.

Thus both the spatial and temporal computations implied by the present model of roughness have been inferred from responses of neurons in somatosensory cortex in very different experimental contexts.

Conclusion

The perception of roughness is mediated by the three populations of tactile nerve fibers that innervate the glabrous skin of the hand. Perceived roughness is driven not by the strength of the response in these afferents, but rather by the variation therein, either spatial (SA1, RA) or temporal (RA, PC). This model of roughness is bolstered by the fact that evidence for the implied variation computation has been observed in primary somatosensory cortex.

GRANTS

This work was supported by National Science Foundation Grants IOS-1150209, IIS-1518614, and DGE-0903637.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.D.L., A.I.W., and S.J.B. conceived and designed research; A.I.W. performed experiments; J.D.L. and X.X. analyzed data; J.D.L., X.X., and S.J.B. interpreted results of experiments; J.D.L. and S.J.B. drafted manuscript; J.D.L. and S.J.B. edited and revised manuscript; J.D.L., A.I.W., and S.J.B. approved final version of manuscript.