Abstract
A model of the rat nephron (Weinstein. Am J Physiol Renal Physiol 308: F1098–F1118, 2015) has been extended with addition of medullary vasculature. Blood vessels contain solutes from the nephron model, plus additional species from the model of Atherton et al. (Am J Physiol Renal Fluid Electrolyte Physiol 247: F61–F72, 1984), representing hemoglobin buffering. In contrast to prior models of the urine-concentrating mechanism, reflection coefficients for DVR are near zero. Model unknowns are initial proximal tubule pressures and flows, connecting tubule pressure, and medullary interstitial pressures and concentrations. The model predicts outer medullary (OM) interstitial gradients for Na+, K+, CO2, and , such that at OM-IM junction, the respective concentrations relative to plasma are 1.2, 3.0, 2.7, and 8.0; within IM, there is high urea and low , with concentration ratios of 11 and 0.5 near the papillary tip. Quantitative similarities are noted between K+ and urea handling (medullary delivery and permeabilities). The model K+ gradient is physiologic, and the urea gradient is steeper due to restriction of urea permeability to distal collecting duct. Nevertheless, the predicted urea gradient is less than expected, suggesting reconsideration of proposals of an unrecognized reabsorptive urea flux. When plasma K+ is increased from 5.0 to 5.5 mM, Na+ and K+ excretion increase 2.3- and 1.3-fold, respectively. The natriuresis derives from a 3.3% decrease in proximal Na+ reabsorption and occurs despite delivery-driven increases in Na+ reabsorption in distal segments; kaliuresis derives from a 30% increase in connecting tubule Na+ delivery. Thus this model favors the importance of proximal over distal events in K+-induced diuresis.
Keywords: kidney medulla, urine-concentrating mechanism, microcirculation, acid-base, ammonia, diuresis
the principal distinction between a nephron model and a kidney model is that in the nephron model, peritubular or interstitial conditions are specified, whereas in the kidney, transport by tubules and blood vessels determine the peritubular environment. The mathematical difficulty of a kidney model derives from the fact that within the renal medulla, both proximal and distal nephron segments contribute to the interstitial composition, so that late events impact early events along the tubule. Kidney models have been few in number, and basically three have been nurtured, those by Stephenson and colleagues (54, 56), by Layton and Layton (26, 28), and that of Wexler and coworkers (74) advanced by Thomas (35, 60). All of these models have been dedicated to understanding renal water conservation, specifically maximizing urine osmolality in the antidiuretic state. With rare exception, these models have been stripped down to two solutes, neutral NaCl and urea, with proximal and distal cortical transport serving as boundary conditions for the medullary flows. What these models have provided is insight into the role of the tapering multinephron and multivessel configuration, and of segmental permeability differences, in protecting deep interstitial solute gradients. What is missing is how water conservation holds up once electrolytes are included, for example, when one acknowledges that collecting duct (CD) K+ delivery may exceed Na+ delivery, and that half of this flowing K+ undergoes reabsorption. There have been no model predictions of the medullary acid-base milieu (, CO2, or ammonia concentrations).
In the present work, the previously developed nephron model (71) is extended to a kidney model with inclusion of medullary vessels, and solution of the equations for the medullary interstitial solute profile. The model’s solutes are those that have been required to capture the important aspects of tubular epithelial transport, including acid excretion. The vascular configuration and permeabilities have relied heavily on the work of Pallone and coworkers (40). Notably, both descending and ascending vasa recta show negligible osmotic effect of small solutes, suggesting the configuration of large paracellular pores in both sets of vessels. The implication of such permeabilities is that descending vessel flows are not attenuated with medullary depth. Although robust vessel flow is at cross-purposes for maximizing countercurrent exchange, it does provide a measure of protection against sludging of a hyperviscous vascular compartment, as well as adequate delivery of adequate metabolic substrate. An important ingredient of the vessel model is the extra pH buffering provided by hemoglobin species, and this has been adapted from the work of Atherton et al. (4). The number of model solutes makes this a relatively large computational problem, and thus precludes fine resolution of the medullary interstitial concentration profile. Nevertheless, despite substantial blood flow, the model provides estimates for a hypertonic, hyperkalemic, and acidotic interstitium. In this work, no attempt is made to recalibrate the nephron parameters to achieve target interstitial gradients. The model is used to examine the renal response to hyperkalemia, and the resulting natriuresis is congruent to observations in vivo. The model identifies the source of this natriuresis as proximal tubule.
Model Formulation
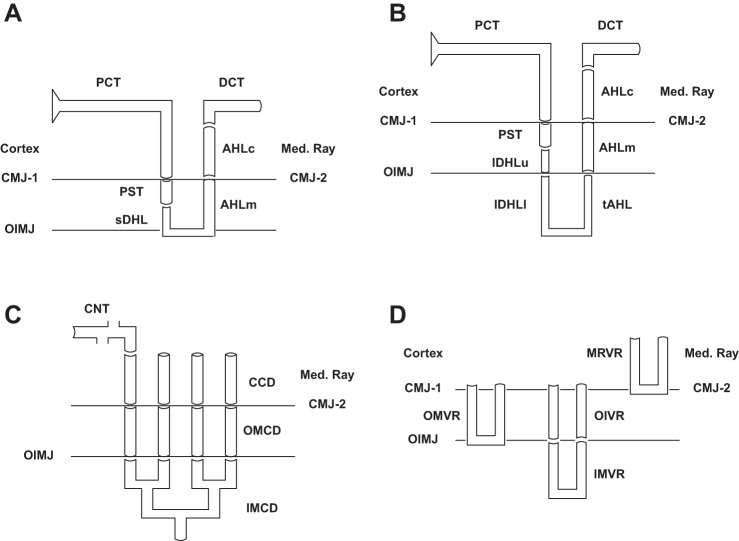
The components of this kidney model are shown in Fig. 1, A–D: superficial (SF) and juxtamedullary (JM) nephrons, through their distal convoluted tubules (DCT); the distal nephron ensemble, from connecting segments (CNT) through inner medullary collecting ducts (IMCD); and the medullary vasculature. The model nephrons are identical to those previously published (70, 71), consisting of 24,000 SF, and 12,400 JM nephrons of varying length. JM nephron number declines with inner medullary depth, and this is captured in the model by solving for 5 distinct classes of JM nephrons: 6,400 turn at 1 mm; 3,200 at 2 mm; 1,600 at 3 mm; 800 at 4 mm; and 400 span the full 5 mm of inner medulla. Each of the 6 model nephrons must have its own AHL and DCT, due to the different depths from which ascending flows reach the outer medulla. By virtue of distinct tubuloglomerular feedback (TGF) signals, each of the JM nephrons must have its own proximal convoluted tubule (PCT) and descending segments. The model nephrons merge at the initial CNT, where the 6 luminal flows mix to define the composition of entering CNT fluid, and the 6 end-DCT hydrostatic pressures must all be equal to the initial CNT pressure. The CNT coalesce (constant circumference-to-cross-section ratio) exponentially within the arcades of CNT to 7,200 cortical collecting ducts (CCD), outer medullary collecting ducts (OMCD), and initial IMCD; the IMCD coalesce exponentially to 112 papillary collecting ducts. Within Fig. 1, there is reference to the medullary ray (MR), within the cortex, and penetrating into the outer medulla. This makes explicit a feature of the prior nephron models, in which peritubular conditions of cortical ascending Henle limbs (AHLc) were distinct from the concentrations within the cortical interstitium, to be able to reproduce realistically high luminal ammonia concentrations of tubule fluid returning to the cortex (68). Inclusion of this distinct interstitial compartment mandates distinct vasculature, identified as medullary ray vasa recta (MR-VR) in Fig. 1D.
Fig. 1.
Schematic for model geometry of tubules and vessels. In each pane, bulk “Cortex” and “Medullary Ray” are distinguished. CMJ-1 refers to the boundary between Cortex and OM, and CMJ-2 to the boundary between Medullary Ray and OM; OIMJ is the outer-inner medullary junction. A: superficial (SF) nephron. sDHL denotes the short descending Henle limb, and AHLm and AHLc are medullary and cortical thick AHL. AHLc sits within the Medullary Ray; DCT is in the Cortex. B: juxtamedullary (JM) nephron. lDHLu and lDHLl are upper and lower portions of the long descending Henle limb; tAHL is thin AHL. There are 5 distinct populations of JM nephron, descending 1 to 5 mm into IM. C: distal nephron. SF and JM DCT coalesce at the start of the connecting segment, CNT, which lies within the Cortex. CCD descends within the Medullary Ray. D: model vessels. There are 2 populations of OMDVR (short VR), which descend 1 or 2 mm into OM. The long VR are denoted OIVR (outer-inner VR) within the OM, and then IMVR within IM; there are 5 populations of long VR, descending 1 to 5 mm into IM. The Medullary Ray has a single MRVR.
The critical feature of this kidney model is computation of medullary interstitial solute concentrations and pressures, rather than prespecifying peritubular conditions. This requires representation of both renal tubules and the medullary vasculature. These vasa recta derive from efferent arterioles of the JM glomeruli, with multiple descending vasa recta (DVR) supplied by a single arteriole (5). Short loop VR turn within OM, either within the inner stripe or at the outer-inner medullary junction (OIMJ), and are designated OM-VR in Fig. 1D (6). In this model, there are 20,000 OM-VR, of which 12,000 turn at 1 mm depth (border of outer and inner stripes), and 8,000 turn at the OIMJ. Long VR are fewer, and the model assumes 3,875 long VR penetrate to the IM; they are designated OI-VR within OM and IM-VR within IM. There are 5 distinct IM-VR, distinguished by their turning at successive 1-mm depths within IM; their numbers are 2,000, 1,000, 500, 250, and 125. The 5:1 ratio of short to long VR in this model may be compared with the 4:1 DVR and 6:1 AVR ratio assumed by Layton and Layton (28). Throughout the medulla, ascending vasa recta (AVR) outnumber descending vasa recta (DVR) (40), and in this model the ratio has been taken as 2:1 in all regions. Within the medullary ray, it has been assumed that there are 7,200 DVR and a 2:1 AVR:DVR ratio.
For the model tubules, the 15 solutes are Na+, K+, Cl−, , H2CO3, CO2, , , urea, NH3, , and H+, as well as , H2CO2, and glucose. The principal problem in formulating conservation equations for blood vessel flows is to represent the substantial buffering capability of hemoglobin within erythrocytes. Toward this end, Atherton et al. (4) devised a model in which the cell and plasma spaces are effectively merged as a single compartment. That scheme has been used previously with slightly different notation (62), and is used again here. Within each vessel, there are the 15 model solutes, a term for plasma proteins, and the additional 14 species from Atherton et al., which represent hemoglobin buffering. These buffer species include amino and carbamino groups, as well as two additional “equivalent” buffer sites; all species are either oxygenated or deoxygenated (Table fr1). Formulating conservation equations for this buffer system follows the approach used for the tubules: one begins with source terms representing generation of each species at each point in the vessel, sC, as the sum of any increase in axial flow, FC, plus export, JCS, across the vessel wall
Table 1.
Capillary model solutes
| Plasma solutes | |
| 1. Na+ | 9. Urea |
| 2. K+ | 10. NH3 |
| 3. Cl− | 11. |
| 4. | 12. H+ |
| 5. H2CO3 | 13. |
| 6. CO2 | 14. H2CO2 |
| 7. | 15. Glucose |
| 8. | 16. Protein |
| Hemoglobin buffers | |
| 17. HbO2NH2 | 24. HbXH |
| 18. HbNH2 | 25. HbO2X− |
| 19. | 26. HbX− |
| 20. | 27. HbO2YH |
| 21. | 28. HbYH |
| 22. | 29. HbO2Y− |
| 23. HbO2XH | 30. HbY− |
| (1) |
| (2) |
In Eq. 2, flows of solute i, FC(i,x), are purely convective, determined as the product of volume flow, FC(v,x), and local concentration. BC is the vessel circumference, and JCS are fluxes per unit area of vessel wall. Using these generation expressions (Eqs. 1 and 2), conservation of nonreactive species is expressed
| (3) |
| (4) |
for i = Na+, K+, Cl−, urea, glucose, and protein. For the binary plasma buffers (phosphate, ammonia, and formate) conservation of total buffer has two terms
| (5) |
| (6) |
| (7) |
whereas conservation of total CO2 contains three terms
| (8) |
Corresponding to the rapid protonation of and slower CO2 hydration/dehydration
generation of CO2 must satisfy (equation 22 in Ref. 66):
| (9) |
in which AC(x) is the vessel cross-section area. For these four plasma buffers, the four additional equations are the pH equilibrium relations displayed in Table 2. For the differential equations (Eqs. 3–9), the initial conditions are the entering flow and solute concentrations, either specified or delivered from the preceding segment. All vessels are assumed protein-impermeable, so that JCS(prot,x) = 0 in Eq 2. With the hemoglobin buffering model described below, there is provision for reaction with CO2, so that Eqs. 8 and 9 will need to be modified to accommodate those reactions.
Table 2.
Capillary model buffer equilibrium coefficients
| KEQ | pK | ||
|---|---|---|---|
| Plasma buffers | |||
| [H+]·[] | [H2CO3] | 2.69 × 10−4 | 3.57 |
| [H+]·[] | [] | 1.58 × 10−7 | 6.80 |
| [H+]·[NH3] | [] | 7.08 × 10−10 | 9.15 |
| [H+]·[] | [] | 1.74 × 10−4 | 3.76 |
| Hemoglobin buffers | |||
| [H+]·[HbO2NH2] | [] | 1.79 × 10−8 | 7.75 |
| [H+]·[HbNH2] | [] | 3.98 × 10−8 | 7.40 |
| [H+]·[HbO2X−] | [HbO2XH] | 2.14 × 10−7 | 6.70 |
| [H+]·[HbX−] | [HbXH] | 1.00 × 10−7 | 7.00 |
| [H+]·[HbO2Y−] | [HbO2YH] | 1.45 × 10−8 | 7.84 |
| [H+]·[HbY−] | [HbYH] | 8.13 × 10−9 | 8.09 |
| [H+]·[] | [CO2]·[HbO2NH2] | 1.13 × 10−5 | |
| [H+]·[] | [CO2]·[HbNH2] | 2.15 × 10−5 | |
Equilibrium coefficients or .
The 14 hemoglobin buffering species are divided among X, Y, and amino or carbamino buffer groups, with total concentrations defined as
| (10) |
| (11) |
| (12) |
Thus for each of these three buffer groups, conservation equations may be written
| (13) |
| (14) |
| (15) |
in which [following the model of Atherton et al. (4)] the relevant flow, FC(b,x), denotes vessel blood flow, rather than plasma flow, FC(v,x). For each group, the sum of the concentrations of oxygenated species, relative to total buffer, is provided by the oxygen saturation, S,
| (16) |
| (17) |
| (18) |
Hemoglobin oxygen saturation depends upon the Po2 (Hill equation) and pH (Bohr effect). An equation for S, which combines these two effects, is developed in the appendix. In model calculations, the medullary Po2 profile is taken from the model of Fry et al. (17) and is displayed below with the interstitial model variables. Then the hemoglobin oxygen saturation is computed at each point, according to local vessel pH. The remaining 8 equations are the equilibrium relations displayed in Table 2.
Atherton et al. (4) provide the initial conditions for the conservation equations as dependent upon total hemoglobin concentration and oxygen saturation. These buffer totals (mM) are then proportional to the hematocrit
| (19) |
| (20) |
| (21) |
Three additional equations are provided by specifying that the total of the oxygenated components of each of the buffers is proportional to the hemoglobin O2 saturation. The 8 equilibrium relations, using initial pH, allow calculation of all entering hemoglobin species. In these vessels, blood flow satisfies
| (22) |
with conservation of erythrocyte volume
| (23) |
or equivalently
| (24) |
At each point along the vessel, calculation of volume and blood flows, FC(v,x) and FC(b,x), provides the local hematocrit (Eq. 22).
Interconversion of the amino and carbamino species provides an additional source of CO2 within the vessels, which needs to be included in the conservation equations, corresponding to the equilibria
Equations 8 and 9 are thus modified to
| (25) |
| (26) |
The last of the conservation equations is that for protons, which can react with plasma buffers and the hemoglobin species. Those reactions must result in no net charge generation, so that one may write an electroneutrality condition
| (27) |
in which the index, i, runs over all solutes and Z(i) are their valences. Applying the conservation condition (4) for the nonreacting species, and Eq. 5 for phosphate, Eq. 27 simplifies to
| (28) |
Within the vessels, the Poiseuille flow equation relates pressure drop to blood flow,
| (29) |
in which PC(x) is the local pressure and ηC is blood viscosity. For the purpose of this model, ηC = 2.0 cP (50) is distinguished from tubule fluid viscosity, η = 0.85 cP, and is assumed to be independent of small differences in vessel diameter or hematocrit. The vessel equations are completed with the local open-circuit condition
| (30) |
Initial DVR pressures, flows, and solute concentrations are specified (see below); initial AVR pressures and concentrations are equal to those of DVR turning at that medullary depth, whereas initial AVR flows (per vessel) are one- half of those in the turning DVR (consistent with the 2:1 AVR:DVR ratio).
Renal medullary (and medullary ray) interstitial conditions are determined by the transmural volume and solute fluxes of tubules and vessels that traverse the region. Figure 2A displays these regions and identifies the relevant structures: cortex contains PCT, DCT, CNT, and cortical peritubular capillaries; medullary ray contains AHLc, CCD, and MR-VR; the inner medulla contains the lower segments of the long descending Henle limbs (lDHLl), thin AHL, IMCD, and IM-VR. The outer medulla comprises two regions: an OM containing PST, sDHL, and upper portions of long DHL (lDHLu), and OM-VR; and an outer medullary region contiguous with the medullary ray (OM-MR) containing AHLm, OMCD, and the upper portions of long VR (OI-VR). In view of the large renal cortical plasma flow, peritubular conditions in the cortex are identified with cortical plasma conditions and are not determined as distinct model variables. The structure of medullary interstitial variables is displayed in Fig. 2B: in both MR and IM, the interstitium is well mixed, meaning that there is a single set of pressures and concentrations at any depth. Although there has been considerable progress in defining and modeling the fine structure of the rat inner medulla, this anatomy may be of greater consequence with regard to oxygen transport and metabolism; the major solute profiles appear less likely to be affected (27, 48, 69). In the outer medulla, two sets of interstitial variables are recognized, with OM variables continuous with the cortex across the corticomedullary junction (CMJ-1) and OM-MR variables continuous with the medullary ray across CMJ-2. Within the outer medulla, OM and OM-MR are assumed to agree at the outer stripe-inner stripe boundary (i.e., mid-depth of the OM) and beyond. There is continuity of OM and IM variables across the OIMJ.
Fig. 2.
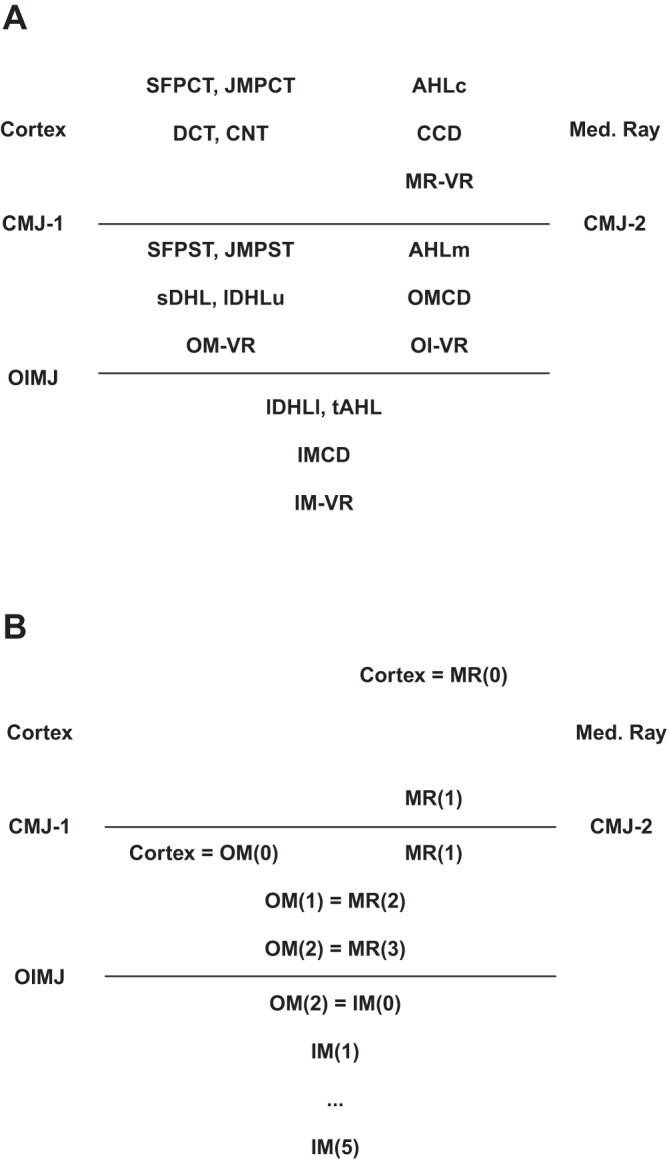
Regional distribution of tubules and vessels (A), and assignment of peritubular variables (B). Within the Cortex are PCT, DCT, and CNT, and these have assigned peritubular conditions; within the Medullary Ray are AHLc, CCD, and MRVR, for which the cortical ends have the cortical concentrations, and the CMJ-2 conditions are model variables. Within OM, there is continuity of the interstitial conditions across CMJ-1 (Cortical) and CMJ-2 (Medullary Ray), but agreement from mid-OM to the OIMJ. Within IM, there is continuity across the OIMJ and a single set of conditions at each level.
Interstitial pressure and solute concentrations are determined by solution of steady-state conservation equations at each depth, x, within each region. Thus the interstitial conservation equations must accommodate the mixing of transmural fluxes containing multiple buffers. Formulation of such problems begins by specifying an interstitial “source” or mass generation term, s, for volume, v, and each solute species, i,
| (31) |
| (32) |
In Eqs. 31 and 32, fluxes are denoted by J, with subscripts referencing the origin and destination of the flux: E and I pertain to the tubules, and denote the lateral interspaces and cytosolic compartments, and S denotes the interstitial compartment, so that ES and IS point to the interspace basement membrane and the basal cell membrane; BM and BC refer to tubule and vessel circumference. The model blood vessels lack the cellular and paracellular structure of the tubules, so that overall transmural fluxes, denoted CS, are computed. Implicit in these equations is that axial fluxes within the interstitium are negligible. With these source expressions, mass conservation for the nonreacting species is
| (33) |
| (34) |
and conservation of buffering species is
| (35) |
| (36) |
| (37) |
| (38) |
Strictly speaking, generation of CO2 is provided by the kinetics of hydration:
in which AS(x) is the cross-sectional area of the interstitial space at each level, x, of medullary depth. In view of the fact that interstitial flows are relatively sluggish and that carbonic anhydrase-laden erythrocytes are close by, we obviate the need to estimate this geometric parameter (AS), by assuming hydration equilibrium
| (39) |
For the four acid-base pairs, a second equation expresses pH equilibrium between the two solute concentrations, and these appear in Table 2. The conservation equation for protons again derives from electroneutrality of the buffer reactions
| (40) |
Finally, electrical potential within the interstitial space is assumed to be the reference for all tubules and vessels. Since luminal electrical potential for each tubule and vessel is computed from the condition of zero net current at each point, this would produce redundancy for one of the ion conservation equations. For example, if one verified all of the conservation equations for each ion except Cl−, then Eq. 34 for Cl− could be derived from those conservation equations in conjunction with the equations for zero net current across tubules and vessels at level x.1 What would be missing, however, from this system is an anchor for the difference between the sums of interstitial cations and anions. In the calculations of this model, this interstitial “anion gap” is assumed to be zero, and this is achieved by replacing the conservation Eq. 34 for Cl− by an electroneutrality condition:
| (41) |
In aggregate, Eqs. 31–41 provide a total of 16 equations for the 15 interstitial solute concentrations plus interstitial pressure.
In every kidney model of sufficient scope, there are variables that may be termed “global” in the sense that their evaluation depends upon transport in a number of tubule segments and vessels. Their evaluation requires an iterative approach, in which the full model is solved, and then initial guesses are updated. In the nephron model (71), there were 13 global unknowns: initial PCT flow and hydrostatic pressure in each nephron class (1 superficial and 5 juxtamedullary) plus lumen pressure at the coalescing point at initial CNT. The equations for these variables were the 6 TGF relations, a distal nephron flow resistance condition, and the 6 matching conditions for end-DCT pressure. Those unknowns remain unchanged in the present model, and are augmented by the medullary interstitial variables. With reference to Fig. 2B, two 1-mm sections through OM and five 1-mm sections through IM require 7 sets of interstitial variables, and a single 2-mm section of MR requires 1 additional set, for a total of 128 interstitial variables. In sum, there are 141 global variables, denoted γ, to be determined. Starting with an initial guess, γ0, the full ensemble of tubules and vessels is solved, and the “errors” in the corresponding global model equations, ϕ0, are computed. When this process is repeated systematically for perturbations of each component of γ, then a Jacobian, dϕ/dγ, is generated. Newton’s method provides a procedure to use this Jacobian to update the guesses for γ, so as to reduce the global errors by solving
| (42) |
Running on an HP Z420 workstation, and using only a single core of its Intel Xeon E5-2665 2.40 GHz 20 MB 1600 8C Processor, a single iteration of the above process required ~1 h. For the problems considered in this work, typically 4–6 iterations were needed to yield machine accuracy, which provided ~4 significant figures of the model variables, in the final iterations. It should be noted, that for OM and MR tubules and vessels, the spatial discretization of the differential equations for mass conservation was 25 μm (40 per mm), and for IM structures 10 μm (100 per mm), as in prior models. Within each 1-mm slice of medulla, peritubular and perivascular concentrations and pressures were identified with the more distal value of the interstitial values (γ) bounding that slice. Using linear interpolation between the two points of the interstitial grid to estimate peritubular and perivascular variables provoked oscillations in the Newton process, and failure to converge.
Model Calculations
In this model, medullary blood vessels are of fixed dimension and transport is represented by composite water and solute permeabilities, which reflect the amalgam of transcellular and paracellular pathways. Specifically, there are no variables representing cytosolic and lateral interspace compartments within the endothelium. For each vessel, equations for volume and solute reabsorption are (suppressing the position, x)
| (43) |
| (44) |
where ζCS(i) is a normalized electrical potential for solute, i, across the capillary wall
| (45) |
In Eqs. 43–45, pα and πα (mmHg) refer to hydrostatic and oncotic pressures in vessel and interspace, and is the logarithmic mean solute concentration across the vessel wall. The oncotic pressure of plasma protein at each point within the vessel is computed according to the Landis-Pappenheimer equation (24):
| (46) |
in which the total protein concentration is expressed in grams per deciliter.
Values for vessel water permeabilities, LpCS, reflection coefficients, σCS, and solute permeabilities, hCS, are displayed in Table 3. Instead of total vessel permeabilities, Table 3 shows component tight junction and transcellular parameters, to facilitate comparison with experimental values or to show the reasoning underlying estimates of unmeasured parameters. This view of the endothelium as a heteroporous structure, with a TJ pathway shared by solutes and water, and a water-only cellular pathway, was advanced by Pallone and Turner (43), who used it to analyze OMDVR reflection coefficients. Experimental data anchoring the table include measurements of OMDVR overall water permeability, Pf (cm/s) = 1.7 (41), 1.9 (61), and 2.0 (36), and the finding that the Na+ reflection coefficient is 0.03 (36, 43). With the assumption that TJ and endothelial reflection coefficients are 0.0 and 1.0, respectively, this suggests that the TJ is the pathway for most of the vessel water flux, and that small transmural solute concentration differences have little impact on this flux. This aspect of the model is an important departure from the models of Layton and Layton (26, 28), in which DVR reflection coefficients were taken to be 1.0. The OMDVR Na+ permeability has been measured, 76 (46) and 65 (36) cm/s × 105, and attributed to the paracellular pathway. The ratio of Cl− to Na+ permeability is 1.3 (42), also paracellular, and consistent with the ratio of the diffusion coefficients of these two ions in a large water-filled pore. Total OMDVR urea permeability is ∼5-fold greater than Na+ [360 cm/s × 105 (46)], proposed as split between paracellular and transcellular pathways (14). With the assumption that vessel permeability is dominated by a large water-filled TJ, the remaining solute permeabilities are estimated from their relative diffusion coefficients in dilute solution. In addition to urea, the only significant cell permeabilities are assumed to be those for CO2, H2CO3, NH3, and protons. For this model, the descending vessels traversing OM and destined to become IMDVR, and the descending vessels in MR have all been assumed to have properties identical to OMDVR. There has not been experimental examination of permeability properties of OMAVR, so those vessel parameters were taken to be the same as for OMDVR. With respect to IMDVR, the water permeability (45) and the Na+ permeability (46) are both similar to their values in OMDVR, and the Na+ reflection coefficient is also near zero (40). The urea permeability of IMDVR is substantially less than in OMDVR, and comparable to the Na+ permeability (42). Accordingly the IMDVR parameters in Table 3 were fashioned from OMDVR parameters, by assuming the same TJ while eliminating endothelial urea permeability. For the IMAVR, experimental observation indicates water permeability ∼8-fold greater than for DVR (31, 37), and Na+ permeability that is ∼50% greater (38, 46), with Na+ reflection coefficient near zero (38). As in IMDVR, the urea permeability is near to that of Na+ (42, 46). Accordingly, model IMAVR TJ parameters have been obtained by scaling up IMDVR water and solute permeabilities by factors of 8 and 1.5, respectively; endothelial permeabilities are comparable.
Table 3.
Vessel permeabilities
| OM/MR Vessels (R = 15 µm) |
IMDVR (R = 15 µm) |
IMAVR (R = 20 µm) |
||||
|---|---|---|---|---|---|---|
| Tight Junction | Cell | Tight Junction | Cell | Tight Junction | Cell | |
| Pf. cm/s | 1.67 | 0.06 | 1.50 | 0.06 | 13.33 | 0.05 |
| RTLp, cm/s·mOsm | 0.030 | 0.001 | 0.027 | 0.001 | 0.240 | 0.0009 |
| σ(i) | 0.000 | 1.000 | 0.000 | 1.000 | 0.000 | 1.000 |
| h(i), cm/s × 105 | ||||||
| Na | 76 | 0 | 75 | 0 | 115 | 0 |
| K | 112 | 0 | 111 | 0 | 169 | 0 |
| Cl | 116 | 0 | 114 | 0 | 176 | 0 |
| HCO3 | 67 | 0 | 67 | 0 | 102 | 0 |
| H2CO3 | 84 | 130 | 83 | 130 | 127 | 130 |
| CO2 | 110 | 15,000 | 108 | 15,000 | 166 | 15,000 |
| HPO4 | 43 | 0 | 43 | 0 | 66 | 0 |
| H2PO4 | 50 | 0 | 50 | 0 | 76 | 0 |
| Urea | 190 | 150 | 75 | 1 | 120 | 1 |
| NH3 | 120 | 1,500 | 118 | 1,500 | 182 | 1500 |
| NH4 | 113 | 0 | 111 | 0 | 170 | 0 |
| H | 257 | 2,000 | 254 | 2,000 | 389 | 2,000 |
| HCO2 | 68 | 0 | 68 | 0 | 104 | 0 |
| H2CO2 | 81 | 0 | 80 | 0 | 122 | 0 |
| Glucose | 38 | 0 | 38 | 0 | 58 | 0 |
Composite vessel permeabilities are computed as sums of TJ and Cell values:
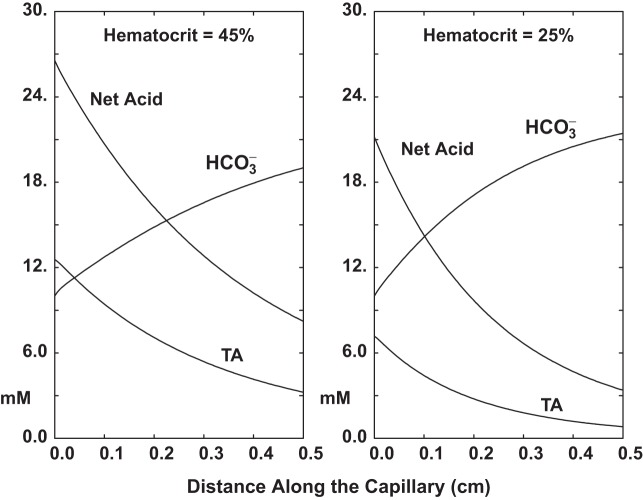
In Fig. 3 the vessel model is used to demonstrate the magnitude of hemoglobin buffering during pH equilibration of an acid lumen with a neutral bath. The vessel permeabilities are those for OMDVR, and the bath solution contains Na+ = 144, K+ = 5, Cl− = 119.5, = 24, total phosphate = 2.6, total ammonia = 0.2, total formate = 1.0, urea = 5, and glucose = 5 mM, at Pco2 = 40 mmHg (1.2 mM) and 95% O2 saturation. The luminal perfusate is similar, except for , which has been lowered to 10 mM via HCl titration. Perfusion rate is 1 nl/s, so that for a vessel radius of 15 μm, the fluid velocity is 1.4 mm/s. Both graphs display lumen and titratable acid (TA) as a function of distance along this 5-mm vessel.2 In Fig. 3 panels, the curves labeled Net Acid show the concentration of HCl needed to bring the bath solution to the composition of the luminal solution; TA is computed as the net acid, less titration. In the left pane, hematocrit is 45%, and in the right, 25%. In either case, TA is substantial, accounting for about one-half or one-third of net acid buffering, respectively. Figure 3 also demonstrates that acid equilibration is faster with lower capillary buffer content, with halfway points at 3 and 2 mm for the 45% and 25% hematocrits. As indicated below, luminal flow for this calculation is ~5- to 6-fold greater than that used in the medullary vessels of the kidney model. This implies that with these vascular permeabilities, one may expect acid equilibration within submillimeter medullary distances.
Fig. 3.
Equilibration of capillary fluid with an external bath. Capillary permeabilities are as for OMDVR. Entering luminal is 10 mM, while bath is at 24 mM, with Po2 of 40 mmHg in both lumen and bath; lumen total phosphate is 2.6 mM. Lumen perfusion rate is 1.0 nl/s. Panes on the left and right show concentration, titratable acid (TA), and net acid (NA) for hematocrits of 45% and 25%, respectively. The NA calculation includes all hemoglobin buffers.
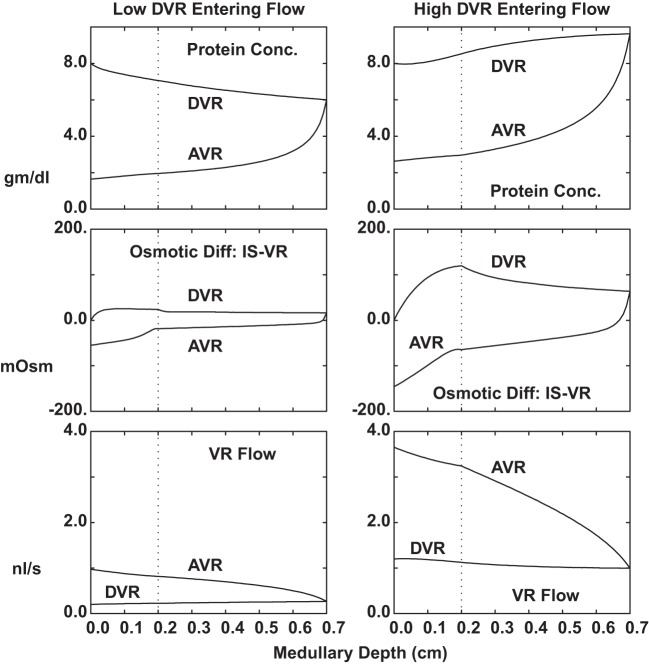
Medullary vessel configuration and transport parameters are critical to the maintenance of medullary solute gradients, insofar as they allow for adequate substrate delivery and tubule reabsorbate uptake, without washout of interstitial solutes. The calculations of Fig. 4 examine a single long model VR, running through a full OM-IM medullary region, in which the intersitial solute concentrations were assumed identical to those used in the nephron model (71). Specifically, in the OM, interstitial NaCl concentration doubles from cortex to IM border; in the IM, NaCl concentration remains high, and interstitial urea increases from 20 to 500 mM from OM to papillary tip. Initial vessel hydrostatic pressure is 10 mmHg; all interstitial hydrostatic pressures are 5 mmHg. Within each column of Fig. 4, the three panes display vessel protein concentration, plasma flow, and the osmotic difference between vessel fluid and the local interstitium. The two columns correspond to initial plasma flow of either 12 or 72 nl/min, bracketing the physiological range. The salient observation is that for either entering flow, DVR flows vary little with medullary depth. This is due to low reflection coefficients of small solutes, so that neither NaCl nor urea extracts much water. To the extent that DVR does have a small positive reflection coefficient, there can be water extraction at the higher flow, in which the osmotic difference between DVR and interstitium is greater. At the higher flow rate, DVR protein concentration increases, whereas at slower flow, solute uptake into DVR precludes water extraction. Within AVR, protein oncotic force, along with a hypertonic capillary lumen, provides for a severalfold increase in volume flow. This character of both VR flows is similar to the findings of Edwards and Pallone (14), and to the vessels within the model of Layton (26). Micropuncture of vessels within the rat inner medulla permitted measurement of DVR protein concentration, with the finding that at the papillary tip, total protein was 16% higher (52). In subsequent work, the impact of medullary solute gradients on DVR protein was demonstrated directly (47). The implication of these small changes in DVR flow is that the important limitation on IM washout must derive from reductions in depth of vessel penetration, rather than reductions in flow.
Fig. 4.
Flow and composition within a single long model VR, running through a hyperosmolar medulla. In the OM, interstitial NaCl concentration doubles from cortex to IM border; in the IM, NaCl concentration remains high, and interstitial urea increases from 20 to 500 mM from OM to papillary tip. Within each column of the figure, the three panes display vessel protein concentration (top), plasma flow (bottom), and the osmotic difference between vessel fluid and the local interstitium (middle). The two columns correspond to initial plasma flow of either 12 or 72 nl/min (0.2 and 1.2 nl/s).
The boundary and initial conditions for this kidney model include the solute concentrations within the glomerular filtrate, within cortical peritubular capillaries (surrounding PCT, DCT, and CNT), and at the initial points of descending medullary vessels (Table 4). Noteworthy among these is a cortical Pco2 = 50 mmHg (dissolved CO2 = 1.5 mM) and total ammonia 0.2 mM, both likely higher than systemic values, but intended to acknowledge that there is cortical generation of both CO2 and ammonia. At initial DVR points, solute concentrations are the same as for the cortex, with the exceptions of 10-fold higher ammonia and a 2-fold increase in urea. The higher peritubular ammonia concentration has been found necessary in prior tubule models, to achieve the measured (1–2 mM) luminal ammonia concentrations in AHL fluid returning to the cortex. The higher vessel urea concentration (10 mM) presumes some degree of countercurrent exchange before the corticomedullary boundary. It was taken slightly higher than the (8 mM) value used by Layton and Layton (28), to facilitate comparison of urea handling between the two models. (In this model, PST urea concentration is computed, and is about one-half the value assumed by Layton and Layton.) Hydrostatic pressures in cortical and initial medullary vessels were taken to be 12 mmHg; initial PCT hydrostatic pressure is a model unknown. Similarly, initial PCT flows (SNGFR) are also unknowns, computed for each nephron class from the equations for TGF. The initial plasma flows per DVR vessel were all taken to be 9.6 nl/min, so that total DVR flow is 192 μl/min to vessels turning within OM, and 74 μl/min to vessels that reach into IM. This total medullary plasma flow, 266 μl/min, is ∼25% of GFR for one kidney, and thus ∼5% of renal plasma flow. This fractional medullary plasma flow is consistent with observations of Roman and Smits (51), who estimated papillary blood flow in older rats at 0.31 ml·min−1·g−1 papilla and whole kidney blood flow of 6 ml·min−1·g−1. These conditions are also comparable to those of Layton and Layton (28), who simulated a kidney of 30,000 nephrons, with ~22,800 short DVR and 6,100 long DVR, each perfused at 8 nl/min, so that OM and IM plasma flows were 183 and 49 μl/min, respectively. Scaled up to the 36,000 nephrons of this kidney, the flows would be 219 and 58 μl/min, for a total 277 μl/min.
Table 4.
Initial vessel and tubule concentrations; cortical peritubular conditions; initial vessel flows
| Tubule Lumen (SFPCT, JMPCT) | Cortex (SFPCT, JMPCT, DCT, CNT) | Vessel Lumen (OMDVR, OIDVR, MRDVR) | |
|---|---|---|---|
| Initial concentrations/conditions | |||
| P, mmHg | 12 | 12 | |
| Imp, mmHg | 31.65 | ||
| Imp, mM | 0.00 | 2.00 | 1.64 |
| C, mM | |||
| Na | 144.00 | 144.00 | 144.00 |
| K | 5.00 | 5.00 | 5.00 |
| Cl | 118.60 | 118.60 | 120.37 |
| HCO3 | 25.00 | 25.00 | 25.00 |
| H2CO3 | 4.4E-03 | 4.4E-03 | 4.4E-03 |
| CO2 | 1.50 | 1.50 | 1.50 |
| HPO4 | 2.00 | 2.00 | 2.00 |
| H2PO4 | 0.60 | 0.60 | 0.60 |
| Urea | 5.00 | 5.00 | 10.00 |
| NH3 | 2.9E-03 | 2.9E-03 | 2.9E-02 |
| NH4 | 0.20 | 0.20 | 1.97 |
| HCO2 | 1.00 | 1.00 | 1.00 |
| H2CO2 | 2.7E-04 | 2.7E-04 | 2.7E-04 |
| Glucose | 5.00 | 5.00 | 5.00 |
| Protein, g/dl | 0.00 | 8.00 | |
| Hematocrit | 0.45 | ||
| Hb buffers, mM | |||
| HbO2NH2 | 1.919 | ||
| HbNH2 | 0.141 | ||
| 5.092 | |||
| 0.168 | |||
| 0.685 | |||
| 0.096 | |||
| HbO2XH | 5.298 | ||
| HbXH | 0.494 | ||
| HbO2X− | 23.867 | ||
| HbX− | 1.041 | ||
| HbO2YH | 32.97 | ||
| HbYH | 1.934 | ||
| HbO2Y− | 10.065 | ||
| HbY− | 0.331 | ||
| Initial Vessel Flows | Per Vessel, nl./min | Vessel Number | Per Kidney, μl/min |
| OMDVR (1 mm) | 9.6 | 12,000 | 115.2 |
| OMDVR (2 mm) | 9.6 | 8,000 | 76.8 |
| OIDVR (1 mm) | 9.6 | 4,000 | 38.4 |
| OIDVR (2 mm) | 9.6 | 2,000 | 19.2 |
| OIDVR (3 mm) | 9.6 | 1,000 | 9.6 |
| OIDVR (4 mm) | 9.6 | 500 | 4.8 |
| OIDVR (5 mm) | 9.6 | 250 | 2.4 |
| MRDVR | 9.6 | 7,200 | 69.1 |
One aspect of tubule function, which has not been included in prior tubule models, is metabolic generation of CO2, based on the magnitude of active transport. In view of the notably high Pco2 of the renal medulla (11), it was important to introduce this CO2 source into the tubules of the present model. In prior work, peritubular Pco2 had been specified, and net generation of cellular CO2 was assumed to be zero (i.e., conservation of total CO2). In this work, for each of the cells of each nephron segment, total CO2 generation was set equal to metabolic generation of CO2
| (47) |
in which sI is cytosolic generation of the indicated species, and MI is metabolic CO2 generation. In turn, MI(CO2,x) is the sum of three terms, each proportional to active transport by the Na,K-ATPase, H,K-ATPase, and H+-ATPase in any cell membrane. Those proportionality constants reflect the generation of 5 ATP per O2 (29), and a stoichiometry of 3Na+ per ATP for the Na,K-ATPase and 2H+ per ATP for both of the proton ATPases. Thus, assuming a respiratory quotient of CO2 to O2 equal to 1.0 (4), there is one CO2 generated for active transport of 15 Na+ or 10 H+. Those proportions ignore basal oxygen consumption, estimated to be ∼15% of total renal oxygen consumption (16). Otherwise, there were only minor adjustments from the prior nephron model (71). Recalling the TGF equation
| (48) |
for SF and JM nephrons, the reference flows, Fv0, were maintained at 30 and 60 nl/min, respectively, and ΔFv0 = 1.0 for both; the reference Cl− concentrations for end-cortical AHL, CI0(Cl), are now 18.0 and 27.0 mM, and had been 18.0 and 22.0 mM. Initial CNT hydrostatic pressure satisfies the relation
| (49) |
in which the distal hydraulic resistance, ΩDN, has now been reduced from 0.050 to 0.033 mmHg/(μl/min), so that for a baseline distal delivery a little over 0.2 ml/min, initial CNT pressure is ∼7 mmHg and PCT pressures are now close to 12 mmHg.
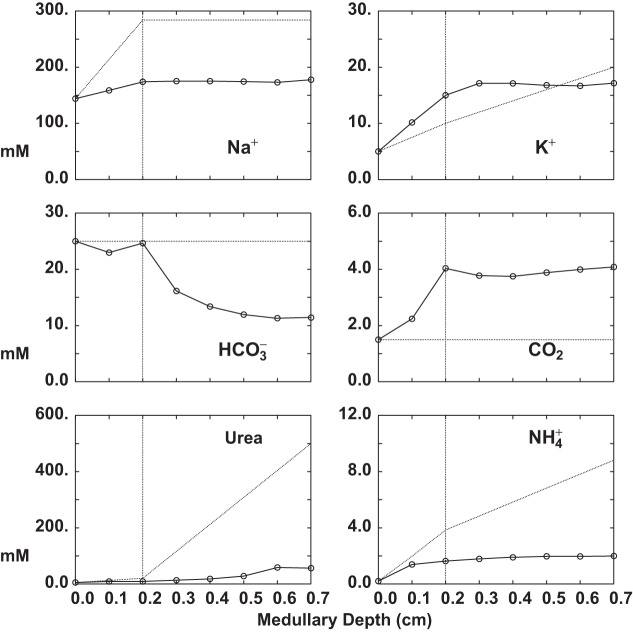
Tables 5–7 and Figs. 5–8 display the solution of the model under baseline conditions. The model variables themselves appear in Table 5, and key interstitial concentrations are plotted in Fig. 5. At baseline, TGF is situated near its inflection point (i.e., its point of maximum sensitivity), at which PCT inlet flow (SNGFR) is close to the reference values of 30 and 60 nl/min for SF and JM nephrons, respectively. JM nephrons, at half the number of SF nephrons, thus receive a comparable filtered load. Interstitial solute concentrations show an increase in Na+, K+, and Cl− and also CO2 and within the OM, and these largely reflect the transport activity of medullary AHL. The increase in CO2 can be attributed to its generation from titration, as well as to the reactions of active transport (Eq. 47). Interstitial urea increases in the distal portion of IM, due to the restriction of high IMCD urea permeability to that portion of the tubule. The interstitial profile is more complex, being neutral and flat through OM, and progressively acid within IM. This profile can be understood by focusing on transport by the tubule segments (Table 6), as this dominates ammonia fluxes by an order of magnitude. Within OM, there is brisk reabsorption by medullary AHL and OMCD, acting to support the interstitial concentration. Within IM, however, there is no longer proton secretion into the loop of Henle, so that secretion into tAHL dominates, and is not compensated by reabsorption from IMCD. Within the renal medulla, both total phosphate and glucose enter and leave the interstitial space from the vasculature, i.e., there is only minor tubular transport. In OM their concentrations fall, reflecting the balance of convective uptake into, and diffusive efflux from, both DVR and AVR (Table 7). Within IM, there is a shift from to , reflecting the fall in pH, but total phosphate is stable. Interstitial glucose concentration falls throughout IM. Within the medullary ray, there are increases in K+, CO2, and above their cortical concentrations, reflecting reabsorption from cortical AHL (Table 6). In Fig. 5, dotted curves are the interstitial concentrations that had been specified in prior tubule models (70). Of those prior estimates of the peritubular environment, only the K+ profile is really concordant with the model predictions. In the case of Na+, urea, and , the predicted curves are substantially lower, and this could reflect either deficient tubular reabsorption of the solute, or excessive vascular washout. These possibilities will be considered below as model fluxes are reviewed. The high medullary Pco2 is consistent with measurements by DuBose (11) of papillary Pco2 from -infused hydropenic rats, but this was higher than the near-systemic value for Pco2 he found in control rats. Of note, this model assumes full carbonic anhydrase activity within the interstitium (Eq. 39), so that delayed CO2 hydration cannot be responsible for the high Pco2. Other explanations for high medullary Pco2 in the model include excessive delivery of to deep tubule segments, unrealistically high metabolic production of CO2, poor vascular washout, or alternatively, experimental bias toward low Pco2 in the micropuncture protocol. With respect to the medullary interstitial concentration, the prior estimate of 25 mM had little experimental guidance. In the model, these values for medullary CO2 and provide interstitial pH equal to 6.70 at the IM base, and 6.52 at the tip. It is notable that the model predicts small negative inner medullary hydrostatic pressures, in order to balance tubular water reabsorption and AVR uptake. Negative interstitial pressures were also a finding of Edwards et al. (13) in their VR model. This effect of negative interstitial pressure, could be achieved by an oncotic force within medullary interstitium, and there is experimental support for interstitial protein (39), but estimation of interstitial protein fluxes is beyond the scope of this model.
Table 5.
Model variables at baseline: interstitial pressures and concentrations; initial pressures and flows
| MR(0) | MR(1) | OM(0) | OM(1) | OM(2) | IM(1) | IM(2) | IM(3) | IM(4) | IM(5) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Interstitial pressures and concentrations | ||||||||||
| PS, mmHg | 12.0 | 5.2 | 12.0 | 9.1 | 9.6 | −2.3 | −2.0 | −1.1 | 0.9 | −1.3 |
| CS, mM | ||||||||||
| Na | 144.0 | 148.0 | 144.0 | 158.7 | 173.8 | 175.0 | 175.0 | 174.2 | 172.9 | 177.7 |
| K | 5.0 | 8.0 | 5.0 | 10.2 | 15.0 | 17.1 | 17.1 | 16.8 | 16.7 | 17.1 |
| Cl | 118.6 | 131.0 | 118.6 | 143.6 | 163.1 | 175.2 | 178.2 | 178.6 | 178.0 | 183.1 |
| HCO3 | 25.0 | 23.5 | 25.0 | 23.0 | 24.7 | 16.1 | 13.4 | 12.0 | 11.3 | 11.4 |
| H2CO3 | 4.4E-03 | 7.2E-03 | 4.4E-03 | 6.5E-03 | 1.2E-02 | 1.1E-02 | 1.1E-02 | 1.1E-02 | 1.2E-02 | 1.2E-02 |
| CO2 | 1.5 | 2.5 | 1.5 | 2.2 | 4.0 | 3.8 | 3.8 | 3.9 | 4.0 | 4.1 |
| HPO4 | 2.0 | 1.0 | 2.0 | 1.3 | 0.8 | 0.7 | 0.7 | 0.6 | 0.6 | 0.6 |
| H2PO4 | 0.6 | 0.5 | 0.6 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0 | 1.0 |
| Urea | 5.0 | 7.3 | 5.0 | 8.6 | 8.9 | 13.2 | 17.9 | 27.9 | 58.5 | 56.1 |
| NH3 | 2.9E-03 | 1.3E-02 | 2.9E-03 | 1.3E-02 | 9.0E-03 | 6.8E-03 | 6.1E-03 | 5.4E-03 | 5.0E-03 | 5.0E-03 |
| NH4 | 0.2 | 1.5 | 0.2 | 1.4 | 1.6 | 1.8 | 1.9 | 2.0 | 2.0 | 2.0 |
| HCO2 | 1.0 | 0.5 | 1.0 | 0.5 | 0.4 | 0.3 | 0.2 | 0.2 | 0.1 | 0.1 |
| H2CO2 | 2.7E-04 | 2.6E-04 | 2.7E-04 | 2.4E-04 | 2.7E-04 | 3.0E-04 | 2.7E-04 | 2.4E-04 | 1.9E-04 | 1.5E-04 |
| Glucose | 5.0 | 2.8 | 5.0 | 2.8 | 2.1 | 1.7 | 1.4 | 1.1 | 0.8 | 0.7 |
| Osmolality | 307.9 | 326.7 | 307.9 | 352.9 | 395.1 | 405.9 | 410.5 | 418.1 | 445.8 | 453.9 |
| Vessel Po2, mmHg | 65 | 35 | 35 | 35 | 35 | 35 | 35 | 13 | 10 | 7 |
| SF | JM-1 | JM-2 | JM-3 | JM-4 | JM-5 | CNT | |
| Initial pressures and flows | |||||||
| SNGFR, nl/min | 29.2 | 58.9 | 58.9 | 59.0 | 59.7 | 59.6 | |
| Tubules | 24,000 | 6,400 | 3,200 | 1,600 | 800 | 400 | |
| GFR, μl/min | 701 | 377 | 189 | 94 | 48 | 24 | |
| PM, mmHg | 12.0 | 12.2 | 12.7 | 13.1 | 13.6 | 14.1 | 6.9 |
Table 7.
Vessel delivery and fluxes at baseline conditions
| Short VR | OMDVR | OMAVR | End |
|---|---|---|---|
| Delivery | |||
| Na, µmol/min | 27.65 | 39.60 | 50.05 |
| K | 0.96 | 2.93 | 3.08 |
| HCO3 | 4.80 | 6.02 | 6.98 |
| NH4 | 0.378 | 0.357 | 0.401 |
| Net acid | −4.42 | −5.66 | −6.58 |
| Urea | 1.92 | 2.13 | 2.51 |
| FvC, µl/min | 192.00 | 244.74 | 322.86 |
| Reabsorption | Total | ||
| Na, µmol/min | −11.95 | −10.45 | −22.40 |
| K | −1.97 | −0.15 | −2.12 |
| HCO3 | −1.22 | −0.96 | −2.18 |
| NH4 | 0.021 | −0.044 | −0.022 |
| Net acid | 1.24 | 0.91 | 2.15 |
| Urea | −0.21 | −0.37 | −0.59 |
| FvC, µl/min | −52.73 | −78.12 | −130.86 |
| Long VR | OIDVR | IMDVR | IMAVR | OIAVR | End | ||
| Delivery | |||||||
| Na, µmol/min | 5.36 | 8.62 | 9.10 | 11.30 | 12.83 | ||
| K | 0.19 | 0.74 | 0.89 | 1.09 | 0.81 | ||
| HCO3 | 0.93 | 1.31 | 0.84 | 1.14 | 1.93 | ||
| NH4 | 0.073 | 0.081 | 0.096 | 0.114 | 0.114 | ||
| Net acid | −0.86 | −1.22 | −0.75 | −1.03 | −1.81 | ||
| Urea | 0.37 | 0.45 | 1.11 | 0.86 | 0.69 | ||
| FvC, µl/min | 37.20 | 50.88 | 53.77 | 66.42 | 82.08 | ||
| Reabsorption | Total | All OM | All IM | ||||
| Na, µmol/min | −3.26 | −0.49 | −2.20 | −1.52 | −7.47 | −27.19 | −2.69 |
| K | −0.56 | −0.14 | −0.21 | 0.28 | −0.63 | −2.390 | −0.351 |
| HCO3 | −0.38 | 0.46 | −0.30 | −0.78 | −1.00 | −3.336 | 0.164 |
| NH4 | −0.007 | −0.015 | −0.018 | 0.001 | −0.040 | −0.029 | −0.034 |
| Net acid | 0.37 | −0.48 | 0.28 | 0.79 | 0.96 | 3.308 | −0.197 |
| Urea | −0.08 | −0.66 | 0.25 | 0.17 | −0.32 | −0.498 | −0.405 |
| FvC, µl/min | −13.68 | −2.88 | −12.66 | −15.68 | −44.90 | −160.22 | −15.54 |
| MR | MRDVR | MRAVR | End |
| Delivery | |||
| Na, µmol/min | 9.95 | 13.44 | 17.34 |
| K | 0.35 | 0.73 | 0.91 |
| HCO3 | 1.73 | 2.26 | 2.60 |
| NH4 | 0.136 | 0.139 | 0.163 |
| Net acid | −1.59 | −2.12 | −2.44 |
| Urea | 0.69 | 0.68 | 0.81 |
| FvC, µl/min | 69.12 | 92.88 | 119.34 |
| Reabsorption | Total | ||
| Na, µmol/min | −3.49 | −3.90 | −7.39 |
| K | −0.38 | −0.18 | −0.57 |
| HCO3 | −0.53 | −0.35 | −0.87 |
| NH4 | −0.002 | −0.025 | −0.027 |
| Net acid | 0.53 | 0.32 | 0.85 |
| Urea | 0.01 | −0.13 | −0.12 |
| FvC, µl/min | −23.74 | −26.51 | −50.25 |
Fig. 5.
Interstitial solute concentrations as a function of medullary depth, OM through IM (MR is not shown). Marked points were computed by the kidney model, and appear in Table 5; dotted curves are the interstitial concentrations that had been specified in the prior nephron model (70).
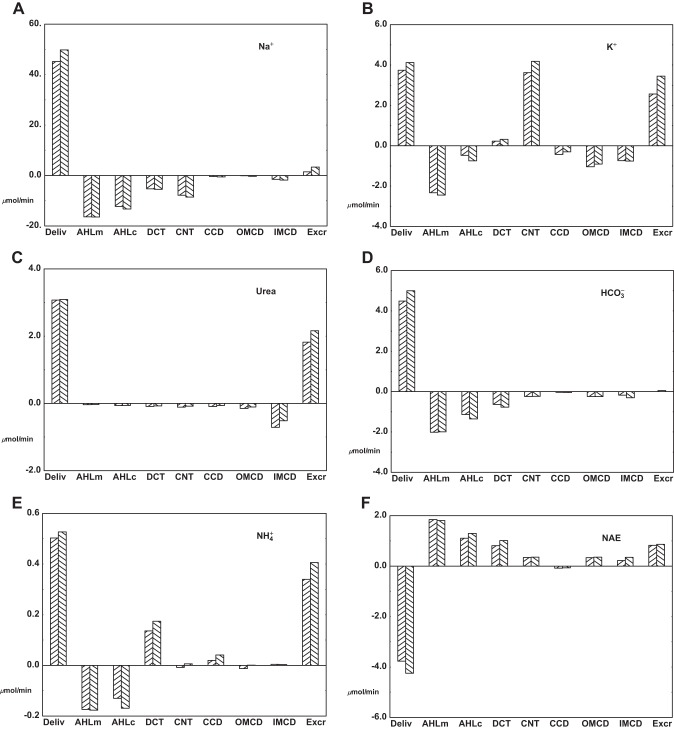
Fig. 8.
Aggregate VR flux (DVR plus AVR) of volume and solute for each medullary slice, from OM through IM. Negative values indicate net vessel uptake (i.e., reabsorption from tubule segments); positive values denote net export from the vessel to the interstitium. The rightmost bar is the (end-IMCD) excretory flow, for comparison. In pane E, the three bars to each set denote , dissolved CO2, and total CO2.
Table 6.
Segmental delivery and fluxes at baseline conditions
| SF | PCT | PST | sDHL | AHLm | AHLc | DCT |
|---|---|---|---|---|---|---|
| Delivery | ||||||
| Na, µmol/min | 100.92 | 28.94 | 24.19 | 23.72 | 13.00 | 6.05 |
| K | 3.51 | 1.15 | 1.48 | 1.66 | 0.61 | 0.47 |
| HCO3 | 17.53 | 2.66 | 2.39 | 2.53 | 1.21 | 0.62 |
| NH4 | 0.138 | 0.119 | 0.258 | 0.266 | 0.156 | 0.111 |
| Net acid | −17.33 | −2.45 | −2.02 | −2.12 | −0.90 | −0.29 |
| Urea | 3.51 | 1.47 | 1.38 | 1.32 | 1.31 | 1.28 |
| FvM, µl/min | 700.80 | 200.64 | 151.80 | 134.82 | 127.80 | 112.86 |
| Reabsorption | ||||||
| Na, µmol/min | 72.00 | 4.75 | 0.47 | 10.72 | 6.94 | 3.23 |
| K | 2.36 | −0.34 | −0.17 | 1.05 | 0.14 | −0.13 |
| HCO3 | 14.87 | 0.27 | −0.14 | 1.32 | 0.59 | 0.29 |
| NH4 | 0.019 | −0.139 | −0.007 | 0.110 | 0.044 | −0.059 |
| Net acid | −14.89 | −0.42 | 0.10 | −1.22 | −0.61 | −0.36 |
| Urea | 2.03 | 0.10 | 0.05 | 0.01 | 0.03 | 0.05 |
| FvM, µl/min | 500.40 | 48.82 | 16.99 | 7.03 | 14.93 | 17.75 |
| JM - All | PCT | PST | lDHLu | lDHLl | tAHL | AHLm | AHLc | DCT |
| Delivery | ||||||||
| Na, µmol/min | 105.36 | 28.09 | 23.50 | 22.65 | 22.14 | 21.46 | 15.79 | 10.49 |
| K | 3.66 | 1.25 | 1.45 | 1.71 | 1.83 | 2.08 | 0.80 | 0.46 |
| HCO3 | 18.29 | 1.16 | 1.28 | 1.38 | 1.42 | 1.96 | 1.26 | 0.71 |
| NH4 | 0.144 | 0.225 | 0.260 | 0.276 | 0.272 | 0.238 | 0.175 | 0.089 |
| Net acid | −18.09 | −0.85 | −0.93 | −1.01 | −1.06 | −1.64 | −1.02 | −0.52 |
| Urea | 3.66 | 1.62 | 1.48 | 1.46 | 1.85 | 1.75 | 1.72 | 1.69 |
| FvM, µl/min | 731.40 | 197.82 | 149.76 | 130.32 | 123.00 | 123.00 | 121.32 | 117.06 |
| Reabsorption | ||||||||
| Na, µmol/min | 77.28 | 4.59 | 0.85 | 0.51 | 0.68 | 5.66 | 5.30 | 2.04 |
| K | 2.40 | −0.20 | −0.26 | −0.11 | −0.26 | 1.28 | 0.34 | −0.10 |
| HCO3 | 17.13 | −0.11 | −0.11 | −0.04 | −0.53 | 0.70 | 0.55 | 0.34 |
| NH4 | −0.081 | −0.035 | −0.015 | 0.003 | 0.034 | 0.063 | 0.086 | −0.077 |
| Net acid | −17.24 | 0.09 | 0.08 | 0.05 | 0.58 | −0.63 | −0.50 | −0.45 |
| Urea | 2.03 | 0.14 | 0.03 | −0.39 | 0.10 | 0.03 | 0.03 | 0.04 |
| FvM, µl/min | 533.76 | 48.07 | 19.46 | 7.32 | −0.02 | 1.66 | 4.27 | 5.54 |
| Distal | CNT | CCD | OMCD | IMCD | Excretion | ||
| Delivery | |||||||
| Na, µmol/min | 11.28 | 3.45 | 3.05 | 2.95 | 1.45 | ||
| K | 1.16 | 4.78 | 4.35 | 3.30 | 2.57 | ||
| HCO3 | 0.70 | 0.46 | 0.42 | 0.18 | 0.00 | ||
| NH4 | 0.337 | 0.329 | 0.349 | 0.336 | 0.340 | ||
| Net acid | 0.01 | 0.35 | 0.27 | 0.61 | 0.83 | ||
| Urea | 2.88 | 2.77 | 2.68 | 2.53 | 1.82 | ||
| FvM, µl/min | 206.64 | 90.60 | 56.56 | 40.57 | 32.12 | ||
| Reabsorption | Total | Total OM | Total IM | ||||
| Na, µmol/min | 7.83 | 0.40 | 0.10 | 1.50 | 204.84 | 27.14 | 2.70 |
| K | −3.62 | 0.43 | 1.04 | 0.74 | 4.60 | 2.404 | 0.369 |
| HCO3 | 0.24 | 0.04 | 0.24 | 0.17 | 35.81 | 2.165 | −0.398 |
| NH4 | 0.008 | −0.020 | 0.013 | −0.004 | −0.057 | −0.011 | 0.034 |
| Net acid | −0.35 | 0.08 | −0.34 | −0.22 | −36.25 | −2.350 | 0.418 |
| Urea | 0.11 | 0.09 | 0.15 | 0.71 | 5.34 | 0.502 | 0.419 |
| FvM, µl/min | 116.04 | 34.06 | 15.99 | 8.45 | 1400.40 | 158.02 | 15.75 |
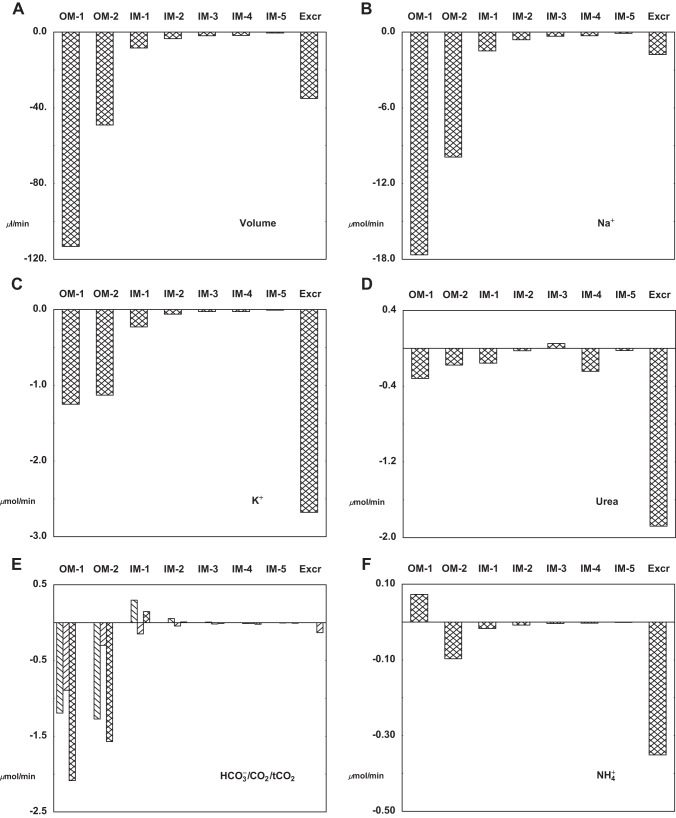
Table 6 and Fig. 6 provide tubular flows and fluxes under baseline conditions. In the table, the upper pane displays SF data and the middle pane shows data for all JM nephrons combined; the bottom pane covers the distal segments, after the nephrons have coalesced at the initial CNT. In the figure, each panel comprises three bar graphs: the first displays PCT delivery and reabsorption for SF and JM nephrons; the second shows loop of Henle and DCT fluxes, with reabsorption as a negative deflection and secretion positive; and the third bar graph contains distal segment fluxes and final urine excretion. In both SF and JM nephrons, PCT delivery and reabsorption of volume and solutes are comparable, reflecting glomerulotubular balance (i.e., greater absolute transport in tubules of higher axial flow). These similarities persist through the descending limbs of OM, but in the medullary AHL, Na+ reabsorption by the JM population is a little more than half the magnitude of that in the SF population. This reflects the fact that JM nephrons are slightly less than half the number of SF nephrons, while transporter densities within these segments were not scaled up for a higher load. Similarly, Na+ reabsorption by cortical AHL is lower for JM than for SF nephrons. These differences between SF and JM AHL had not been an issue in the prior nephron model (71), as diffusive Na+ reabsorption from JM inner medullary thin limbs was substantial. Despite the differences in loop of Henle Na+ transport, overall CNT Na+ delivery is similar in this model (11.3 μmol/min), compared with its predecessor (12.0 μmol/min, Table 1 in Ref. 71). The greatest differences between the two models are in their urea fluxes. In the prior model, when peritubular urea concentration was specified, there was urea loading of long DHL, so that urea delivery to CNT was nearly equal to the filtered load of urea [figure 3 (71)]. In the current model, IM urea secretion into loop of Henle is much reduced, and urea delivery to CNT is 40% of the total filtered load. Within IMCD, 28% of the delivered urea is reabsorbed (0.71 μmol/min), so that total renal urea excretion is 25% of filtered load. Of the IMCD urea reabsorption, secretion into long DHL accounts for more than half, with the remainder taken up by IM vessels. K+ handling by this model follows the pattern of its predecessor, with more than 80% reabsorbed before CNT, secretion of ~50% of filtered load within CNT, and then diffusive reabsorption across medullary CD. In this model, final K+ excretion is ~36% of filtered load, identical to that in the prior work (71). In the case of , delivery to CNT in this model and its predecessor are similar; however the lower medullary interstitial concentration here produces reabsorption within OMCD and little flux across IMCD. The resulting excretion is a little more than half its prior value (0.34 compared with 0.63 μmol/min). Nevertheless, that excretion rate and the rate of net acid excretion (0.83 μmol/min) is well within the envelope of values reported for the rat (see Table 4 in Ref.64).
Fig. 6.
Segmental delivery and transport of important model solutes: baseline conditions. In each tier, the left panes display glomerular filtration (first pair of bars) and proximal convoluted tubule (PCT) reabsorption (second pair of bars); the 2 bars of each pair correspond to SF and JM nephrons. The middle panes display reabsorption (negative deflection) or secretion (positive deflection) along the remainder of each nephron through the DCT (note scale change from the left panes). The right panes show delivery and transport in the distal nephron, with urinary solute excretion as the terminal bar.
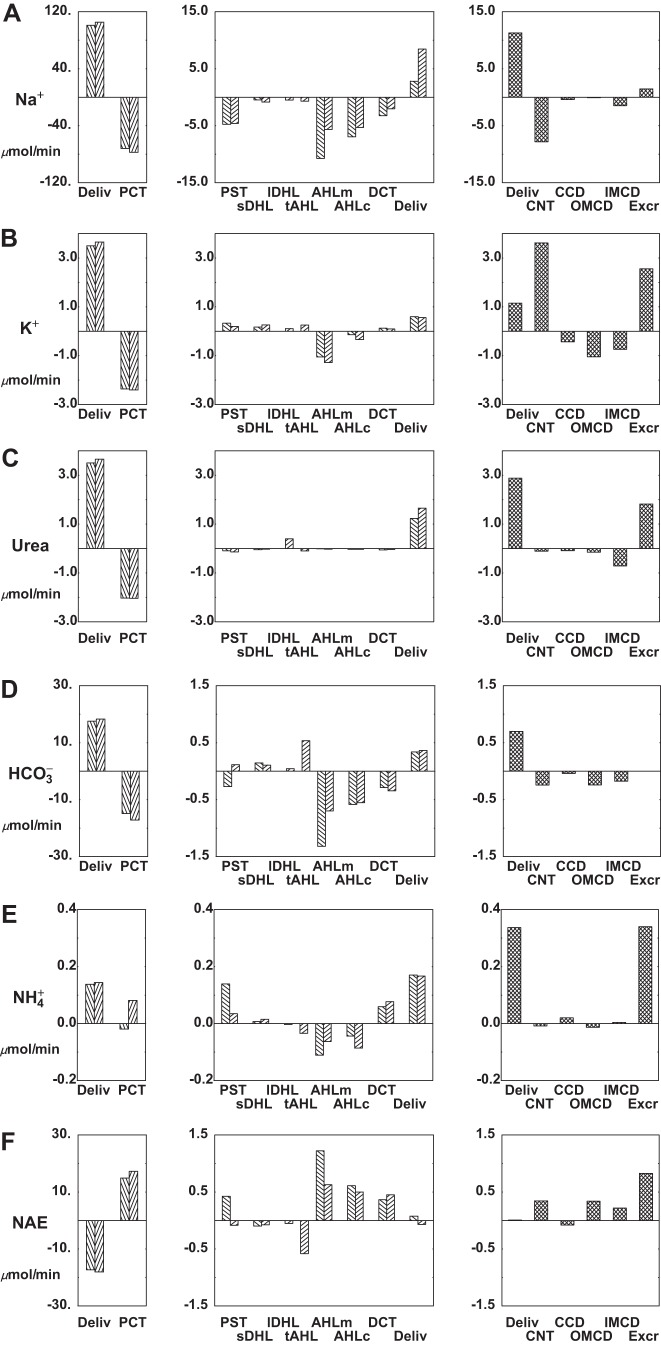
Table 7 and Fig. 7 provide whole kidney vascular flows and fluxes under baseline conditions. In the table, the upper pane shows flows and fluxes of the short VR; the middle pane displays OM and IM transport within long VR, along with flux sums across all vessels of OM and IM; and the bottom pane contains MR data. The figure follows the bookkeeping format used for the tubules: initial delivery, additions and subtractions within each vascular segment, and then exit flow in the rightmost bar. Within OM, the bars are in pairs, indicating short and long vessel (OMDVR and OIDVR) flows and fluxes. If renal plasma flow is ~5 ml/min, then volume flow to the combined OMDVR and OIDVR is 4.6% of total plasma flow, with long DVR receiving just 20% of this total. The salient observation is that for all vessels in all regions, there is volume uptake. In particular, all downstream points experience flows that are at least as large as the initial flow, so that these vessels provide no protection from washout to deeper medullary sections. This derives from the fact that vascular solute reflection coefficients are near zero, so that small solutes exert virtually no osmotic effect. Overall, in both true medulla (OM plus IM) and medullary ray, total volume uptake is ~75% of the entering flow. The pattern of Na+ flux follows that of volume, with vascular uptake in each region. If one divides total Na+ uptake by total volume uptake, this virtual reabsorbate concentration is 170 and 173 mM for OM and IM, respectively, indicating dominance of convective solutes fluxes (compared with diffusive transport) in these vessels. The uptake pattern for urea fluxes is different. In the long vessels (but not the short), there is countercurrent exchange, namely flux of urea from the vessel back into the interstitium. In the long vessels, total urea entry into the descending portions is 0.74 μmol/min, mostly in IM, and urea exit from ascending vessels is 0.42 μmol/min, split between OM and IM. Overall vascular flow of urea to renal venous blood is 3.20 μmol/min, so that relative to the returning volume flow, the returning urea concentration is 7.9 mM. Compared with the IM interstitial urea concentration, this suggests relatively effective countercurrent protection of that compartment. K+ handling has similarities to urea, with uptake by short DVR and countercurrent exchange in long DVR. Within IM, DVR and AVR together take up 0.35 μmol/min, and as they return through OM, there is exit of 0.28 μmol/min K+ from OIAVR. Of the K+ entering medullary nephrons, 2.40 μmol/min enters via PST and 3.62 μmol/min is secreted within CNT; total vascular uptake (OM plus IM plus MR) is 3.31 and urinary excretion is 2.57 μmol/min. To the extent that countercurrent exchange can protect medullary K+ gradients, it enhances renal K+ excretory capacity. Overall, the medulla is a region of generation, although this is confined to OM and MR, with uptake of 3.34 and 0.87 μmol/min, respectively; within the acidotic IM, there is 0.16 μmol/min consumption due to exit from IMDVR. With reference to Table 6, in OM tubular loss is 2.17 μmol/min, indicating that of the vascular uptake, about one-third must derive from metabolic CO2 generation within epithelial cells and buffering of H2CO3. Of ammonia reaching OM, ~0.34 μmol/min enters via PST and 0.45 μmol/min via DVR. This substantial DVR contribution derives from selection of 2 mM ammonia as a boundary condition for its entering flow. As in prior models, absence of a generous supply of to AHL results in unrealistically low returning concentrations to the cortex. With reference to Fig. 7, there are only minor vascular fluxes of ammonia, so that exit flow is little different from entering flow.
Fig. 7.
Whole kidney vascular flows and fluxes under baseline conditions. In each pane, the left bars show delivery to the vessels (initial DVR flow); middle bars are additions and subtractions with OM and IM; and the right bars show exit from the vessels (end-AVR flow). For delivery and exit flows, and within OM, the bars are in pairs indicating flows and fluxes of short (\) and long (/) vessels.
The conditions of interstitial mass balance of tubule fluxes and vessel fluxes provide the conservation equations that determine the model variables. In this work, agreement is obtained for seven slices through the true medulla (OM plus IM) and through the medullary ray. Figure 8 shows the aggregate vessel uptake of volume and solutes for each medullary slice, and for comparison, the rightmost bar in each pane is the corresponding renal excretion rate. For volume, OM uptake is dominant, and declines progressively with medullary depth. The excretory flow, 32 μl/min, is about twice total IM volume reabsorption, but only 20% of OM volume uptake. This rate of urine flow, ~2.2% of GFR, is characteristic of what is observed in micropuncture experiments (see Table 3 in Ref. 65), but is only weakly antidiuretic, and is about twice the flow that was found in the nephron model, when an antidiuretic interstitium was specified (71). Na+ uptake into medullary vessels shows a similar pattern of sharply decreasing fluxes, from OM through IM. In this case, Na+ excretion is ~0.7% of filtered load, and less than aggregate IM Na+ uptake; this excretory rate is comparable to that of the nephron model. Comparison of the patterns of volume and Na+ uptake and excretion suggests that to achieve greater antidiuresis, one would need to enhance water reabsorption within OM, with relatively little perturbation of Na+ transport. With respect to urea, the pattern is different, with urinary excretion well in excess of vessel uptake in any medullary region. In absolute magnitude, the urea fluxes are dwarfed by Na+ and even by K+ fluxes. The bump in urea uptake in the most distal IM segment reflects the restriction of IMCD urea permeability to that portion of the segment. K+ transport is substantial in both segments of OM, reflecting reabsorptive fluxes in medullary AHL and OMCD. With reference to Table 6, there is K+ secretion, 0.97 μmol/min, into PST and DHL, thus constituting a countercurrent exchange system. Figure 8 shows that for this system, the vessel uptake of K+ (i.e., washout) is about twice the rate of tubular secretion. With respect to total CO2 transport, only the fluxes of and CO2 are of importance, and neither can be excluded. For this simulation of acid urine formation, CO2 transport is largely confined to the OM; urine flow of total CO2 is just dissolved CO2, as virtually no remains in late IMCD flow. Ammonia fluxes are all small relative to ammonia excretion, especially within IM, suggesting that overall renal ammonia excretion is determined by cortical events. The pattern of vessel ammonia transport in OM, with early export and later uptake, derives from the high concentration prescribed for entering DVR. What is not visible in this picture is the countercurrent exchange of ammonia within the loop of Henle. With reference to Table 6, secretion, 0.20 μmol/min, into PST and DHL, is twice the vessel uptake, and likely reflects preferential NH3 flux into an acid tubular lumen.
Hyperkalemia is a physiological perturbation that impacts all nephron segments, and is ideally suited for examination in this model. Tables 8 and 9 and Fig. 9 display results from a simulation of an increase in blood K+ from 5.0 to 5.5 meq/l. In the model, this is achieved with addition of 0.5 meq/l KCl to fluid entering SF and JM nephrons, to peritubular fluid bathing cortical segments (PCT, DCT, and CNT), and to plasma of all DVR (OMDVR, OIDVR, and MRDVR). The salient findings are that this small K+ increase produces diuresis and natriuresis, with modest increases in K+ and urea excretion, and little change in acid-base balance. Within the medullary interstitium (Table 9), there are no important changes in most solute concentrations, with the exception of papillary urea, which falls due to the diuresis. With the higher K+, SNGFR is little changed, but tubular pressures increase from 1.1 to 1.5 mmHg, due to the higher flow. In more detail, the increase in peritubular K+ depresses PCT Na+ and volume reabsorption from 72.4% to 70.2% of filtered Na+ load, so that distal delivery increases by 2.2% of filtered load. This is due to the secondary depression of peritubular Cl− and exit, cytosolic alkalinization, and consequent decrease in NHE3 activity. Transport from AHL and beyond is shown in Fig. 9. Through the loop of Henle, there is little compensation for the increase in delivered load. Specifically, combined medullary and cortical AHL Na+ transport accounts for 13.9% and 14.4% of filtered Na+ load, comparing baseline and elevated K+. In DCT, increased Na+ delivery and higher peritubular K+ impact Na+ reabsorption in opposite directions, so that the net K+ effect is a change in Na+ flux from 2.6% to 2.7% of filtered load. In sum, the absolute increase of luminal Na+ delivery to CNT is 1.6% of the filtered Na+ load at baseline, ~75% of the K+-induced increase in exiting PCT Na+. The result constitutes a 30% increase in CNT Na+ delivery. Thus, despite small delivery-driven increases in CD Na+ reabsorption, net renal Na+ excretion increases 2.3-fold with this increase in serum K+. The constancy of Na+ reabsorption in DCT is noteworthy, inasmuch as many of the peritubular transporters present from PCT are also in DCT, and one might have expected additional depression of DCT Na+ flux (figures 11 and 12 in Ref. 66). The confounding factor here is that DCT Na+ reabsorption tends to increase with the increase in luminal Na+ delivery. The increase in kaliuresis reflects both an increase in CNT K+ secretion, due to the Na+ load, plus a decrease in K+ reabsorption within CCD and OMCD, due to lower luminal K+ concentration with diuresis. Nevertheless, the increase in K+ excretion is only modest, ~35% above baseline. This is certainly higher than the 10% increase in filtered K+, but it underscores the fact that to achieve more dramatic increases in K+ excretion, aldosterone action is required. Similarly, higher urine flow within IMCD blunts reabsorption, and enhances urea excretion by ~20%. As found in the prior examination of IMCD in isolation (64), the effect of increased luminal flow is to increase excretion of both and , so that the overall impact on net acid excretion is negligible.
Table 8.
Segmental delivery and fluxes at serum K+ = 5.5 mM
| SF | PCT | PST | sDHL | AHLm | AHLc | DCT |
|---|---|---|---|---|---|---|
| Delivery | ||||||
| Na, µmol/min | 100.62 | 31.06 | 26.47 | 26.03 | 15.23 | 7.52 |
| K | 3.84 | 1.34 | 1.67 | 1.84 | 0.71 | 0.45 |
| HCO3 | 17.47 | 2.99 | 2.68 | 2.82 | 1.51 | 0.76 |
| NH4 | 0.138 | 0.125 | 0.268 | 0.276 | 0.164 | 0.099 |
| Net acid | −17.28 | −2.77 | −2.31 | −2.39 | −1.19 | −0.44 |
| Urea | 3.49 | 1.55 | 1.46 | 1.39 | 1.38 | 1.35 |
| FvM, µl/min | 699.00 | 215.22 | 167.46 | 150.24 | 143.70 | 130.32 |
| Reabsorption | ||||||
| Na, µmol/min | 69.60 | 4.59 | 0.44 | 10.80 | 7.72 | 3.38 |
| K | 2.50 | −0.33 | −0.17 | 1.13 | 0.26 | −0.19 |
| HCO3 | 14.48 | 0.30 | −0.13 | 1.31 | 0.75 | 0.36 |
| NH4 | 0.013 | −0.143 | −0.007 | 0.112 | 0.065 | −0.091 |
| Net acid | −14.51 | −0.46 | 0.09 | −1.20 | −0.76 | −0.48 |
| Urea | 1.94 | 0.10 | 0.06 | 0.01 | 0.03 | 0.04 |
| FvM, µl/min | 483.66 | 47.75 | 17.25 | 6.51 | 13.41 | 17.14 |
| JM - All | PCT | PST | lDHLu | lDHLl | tAHL | AHLm | AHLc | DCT |
| Delivery | ||||||||
| Na, µmol/min | 105.12 | 30.32 | 25.84 | 25.02 | 24.54 | 23.78 | 18.11 | 12.56 |
| K | 4.02 | 1.47 | 1.64 | 1.90 | 2.02 | 2.28 | 0.96 | 0.47 |
| HCO3 | 18.25 | 1.34 | 1.44 | 1.54 | 1.60 | 2.18 | 1.50 | 0.89 |
| NH4 | 0.144 | 0.233 | 0.274 | 0.289 | 0.288 | 0.252 | 0.187 | 0.082 |
| Net acid | −18.05 | −1.01 | −1.08 | −1.15 | −1.21 | −1.85 | −1.24 | −0.70 |
| Urea | 3.65 | 1.72 | 1.58 | 1.55 | 1.79 | 1.70 | 1.68 | 1.65 |
| FvM, µl/min | 730.20 | 213.30 | 166.26 | 146.22 | 136.98 | 137.04 | 135.54 | 132.12 |
| Reabsorption | ||||||||
| Na, µmol/min | 74.82 | 4.47 | 0.82 | 0.48 | 0.76 | 5.67 | 5.55 | 2.10 |
| K | 2.55 | −0.18 | −0.26 | −0.12 | −0.25 | 1.32 | 0.49 | −0.12 |
| HCO3 | 16.91 | −0.10 | −0.10 | −0.05 | −0.59 | 0.69 | 0.61 | 0.41 |
| NH4 | −0.090 | −0.040 | −0.015 | 0.001 | 0.036 | 0.065 | 0.104 | −0.083 |
| Net acid | −17.03 | 0.06 | 0.07 | 0.06 | 0.64 | −0.61 | −0.54 | −0.53 |
| Urea | 1.93 | 0.14 | 0.03 | −0.24 | 0.09 | 0.02 | 0.03 | 0.03 |
| FvM, µl/min | 516.72 | 47.06 | 20.03 | 9.24 | −0.02 | 1.45 | 3.47 | 5.20 |
| Distal | CNT | CCD | OMCD | IMCD | Excretion | ||
|---|---|---|---|---|---|---|---|
| Delivery | |||||||
| Na, µmol/min | 14.59 | 6.06 | 5.49 | 5.16 | 3.35 | ||
| K | 1.24 | 5.42 | 5.12 | 4.21 | 3.45 | ||
| HCO3 | 0.88 | 0.65 | 0.60 | 0.36 | 0.05 | ||
| NH4 | 0.356 | 0.362 | 0.403 | 0.404 | 0.406 | ||
| Net acid | −0.13 | 0.23 | 0.16 | 0.52 | 0.87 | ||
| Urea | 2.93 | 2.85 | 2.78 | 2.68 | 2.16 | ||
| FvM, µl/min | 240.06 | 124.68 | 79.74 | 58.40 | 50.17 | ||
| Reabsorption | Total | Total OM | Total IM | ||||
| Na, µmol/min | 8.53 | 0.57 | 0.33 | 1.81 | 202.44 | 27.12 | 3.06 |
| K | −4.18 | 0.31 | 0.91 | 0.76 | 4.41 | 2.425 | 0.383 |
| HCO3 | 0.24 | 0.05 | 0.25 | 0.31 | 35.67 | 2.208 | −0.333 |
| NH4 | −0.006 | −0.041 | −0.001 | −0.003 | −0.125 | −0.029 | 0.034 |
| Net acid | −0.36 | 0.07 | −0.36 | −0.35 | −36.20 | −2.409 | 0.354 |
| Urea | 0.08 | 0.06 | 0.10 | 0.52 | 4.98 | 0.463 | 0.367 |
| FvM, µl/min | 115.38 | 44.93 | 21.32 | 8.23 | 1,378.80 | 161.37 | 17.45 |
Table 9.
Model variables with hyperkalemia (K+ = 5.5): interstitial pressures and concentrations; initial pressures and flows
| MR(0) | MR (1) | OM(0) | OM (1) | OM (2) | IM (1) | IM (2) | IM (3) | IM (4) | IM (5) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Interstitial pressures and concentrations | ||||||||||
| PS, mmHg | 12.0 | 8.6 | 12.0 | 9.3 | 10.6 | −1.6 | −1.5 | −0.9 | 0.5 | −1.1 |
| CS, mM | ||||||||||
| Na | 144.0 | 144.3 | 144.0 | 157.5 | 171.3 | 174.1 | 175.4 | 175.7 | 175.7 | 180.2 |
| K | 5.5 | 7.7 | 5.5 | 10.4 | 14.9 | 16.8 | 17.4 | 17.6 | 17.8 | 18.3 |
| Cl | 119.1 | 127.4 | 119.1 | 142.7 | 161.0 | 173.9 | 177.8 | 179.3 | 179.9 | 184.7 |
| HCO3 | 25.0 | 23.1 | 25.0 | 22.9 | 24.2 | 16.3 | 14.4 | 13.6 | 13.2 | 13.4 |
| H2CO3 | 4.4E-03 | 7.1E-03 | 4.4E-03 | 6.5E-03 | 1.1E-02 | 1.1E-02 | 1.1E-02 | 1.2E-02 | 1.2E-02 | 1.2E-02 |
| CO2 | 1.5 | 2.4 | 1.5 | 2.2 | 3.8 | 3.8 | 3.9 | 4.1 | 4.1 | 4.2 |
| HPO4 | 2.0 | 0.9 | 2.0 | 1.2 | 0.8 | 0.7 | 0.6 | 0.6 | 0.6 | 0.6 |
| H2PO4 | 0.6 | 0.5 | 0.6 | 0.6 | 0.6 | 0.8 | 0.9 | 0.9 | 0.9 | 0.9 |
| Urea | 5.0 | 6.4 | 5.0 | 8.3 | 8.0 | 11.5 | 14.7 | 21.5 | 43.6 | 42.4 |
| NH3 | 2.9E-03 | 1.2E-02 | 2.9E-03 | 1.2E-02 | 8.7E-03 | 6.5E-03 | 5.9E-03 | 5.5E-03 | 5.3E-03 | 5.4E-03 |
| NH4 | 0.2 | 1.4 | 0.2 | 1.3 | 1.5 | 1.7 | 1.8 | 1.8 | 1.8 | 1.9 |
| HCO2 | 1.0 | 0.5 | 1.0 | 0.5 | 0.4 | 0.3 | 0.2 | 0.2 | 0.1 | 0.1 |
| H2CO2 | 2.7E-04 | 2.4E-04 | 2.7E-04 | 2.3E-04 | 2.5E-04 | 2.8E-04 | 2.5E-04 | 2.1E-04 | 1.6E-04 | 1.3E-04 |
| Glucose | 5.0 | 2.6 | 5.0 | 2.8 | 2.1 | 1.7 | 1.3 | 1.1 | 0.8 | 0.7 |
| Osmolality | 307.9 | 317.2 | 307.9 | 350.5 | 388.6 | 401.4 | 408.4 | 416.4 | 438.5 | 447.5 |
| Po2, mmHg | 65 | 35 | 35 | 35 | 35 | 35 | 35 | 13 | 10 | 7 |
| SF | JM-1 | JM-2 | JM-3 | JM-4 | JM-5 | CNT | |
| Initial pressures and flows | |||||||
| SNGFR, nl/min | 29.1 | 58.8 | 58.8 | 58.9 | 59.4 | 59.5 | |
| Tubules | 24,000 | 6,400 | 3,200 | 1,600 | 800 | 400 | |
| GFR, μl/min | 699 | 376 | 188 | 94 | 48 | 24 | |
| PM, mmHg | 13.1 | 13.4 | 14.0 | 14.5 | 15.1 | 15.6 | 8.0 |
Fig. 9.
Comparison of distal flows and fluxes between baseline conditions (K+ = 5.0 mM) and hyperkalemia (K+ = 5.5 mM). For the same solutes of Fig. 5, the panes display distal delivery (from all nephrons, combined SF and JM), reabsorptive fluxes from each tubule segment (medullary AHL through IMCD), and total renal excretion. In each pair of bars, the left bar (/) is the baseline value, and the right bar (\) the hyperkalemic value.
DISCUSSION
With this work, the model of the rat nephron, with its full ensemble of tubule segments, advances to a model of the rat kidney, in which medullary vascular flows and interstitial composition are computed, rather than specified. That step acknowledges the fact that, in the medulla, the nephron creates its own environment, in which proximal events more directly impact distal transport. That step also brings the tubule models into the arena long-occupied by models of the urine-concentrating mechanism (UCM). Although the tubule models have been relatively comprehensive, tracking multiple electrolytes, buffer reactions, hydrostatic pressure, and voltage, UCM models have traditionally been stripped down to the essentials, volume flow, and concentrations of salt and urea, and this has allowed intense focus on maximizing urine osmolality. The step from nephron to kidney has necessitated two features, which are new to this model. The first is representation of hemoglobin buffering within the vessels, which basically doubles the capacity for acid base transport (Fig. 3). Fortunately, Atherton et al. (4) provided a convenient model of blood buffering, and this work has followed their lead. Admittedly, what is not captured with this approximation includes erythrocyte flow patterns within small vessel networks, variability in erythrocyte volume with osmolality changes, and enhanced axial K+ flows within erythrocytes. The second novelty in this kidney model is provision of equations for interstitial mass conservation of electrolytes, including multiple buffers. Those equations follow the framework set out in prior models of cytosolic buffering, but by specifying that CO2 hydration equilibrium is operative in the interstitial space, there was no need to estimate interstitial volumes at each level of medullary depth. One additional feature of this work, not usually included in UCM models, is representation of the medullary ray extending into the cortex. That was prompted by prior observation that realistically high distal tubule ammonia concentrations could not be achieved without a protected area surrounding cortical AHL. Also included within this MR are CCD and blood vessels configured for countercurrent exchange.
With inclusion of medullary blood vessels, the critical parameter choices are medullary blood flow and vessel permeability. Medullary flows entail both initial DVR flow and vessel configuration, with vessel numbers diminishing as a function of medullary depth. In this model, total medullary plasma flow is 266 μl/min (Table 4), and compared with other flows, it is ~67% of aggregate PST fluid delivery or 20% of kidney GFR (Table 6), and thus ~4% of renal plasma flow (assuming a filtration fraction of 0.2). This DVR flow is nearly identical to that used by Layton and Layton (28), when their medulla is scaled up from 30,000 to 36,000 nephrons. In the kidney model of Moss and Thomas (35) the DVR-to-PST flow ratio was 1.5, identical to that of Wexler et al. (74), but higher than 0.6 in the model of Layton and Layton (28). All of the models show a decrease of medullary vessel number as one descends through the medulla. The number of DVR extending into IM (long DVR) is 28% of total DVR in this model, 27% in Layton and Layton (28), 33% in Moss and Thomas (35), and 33% in Wexler et al. (74). Of the inner medullary models, Layton (26) shows the sharpest decrease with IM depth, with only 0.15% of long DVR reaching the papillary tip; Wexler et al. (74) and Stephenson et al. (55) have 0.78% reaching the tip; and Moss and Thomas (35) have 20% of long DVR running the length of IM. In this model, that number is 3.2% of the long DVR (Table 4). In the VR model of Edwards and Pallone (15), their analysis of prior anatomical studies of the IM vascular space suggested that 6,000 long DVR were reduced to ~190 (3.2%) at the papillary tip.
In contrast to a general consensus on vascular anatomy, a critical difference between this model and its predecessors is in the selection of the reflection coefficient for Na+ and other electrolytes attributed to the DVR. Measurements of Pallone and colleagues have demonstrated that Na+ has nearly zero osmotic force across DVR, namely a near-zero reflection coefficient (40, 44). In this work (Table 3), the endothelium has been configured as cellular and paracellular pathways in parallel, with reflection coefficients of zero for the large water-filled paracellular pore and of unity for the aquaporins in endothelial cells. The overall endothelial reflection coefficient of 0.03 thus prescribes a 30:1 ratio for the water permeability of these two pathways. With this view of the paracellular pore, and starting with a measured Na+ permeability, the other solute permeabilities were estimated according to their relative mobility in solution. Reflection coefficients for Na+ and urea are very different in prior models: Layton and Layton (28) and Layton (26) set them to 1.0 for all DVR; Moss and Thomas (35) used 0.5; Wexler et al. (74) had values between 0.3 and 0.5; and when Stephenson et al. (55) ventured from a central core configuration to represent DVR, they used reflection coefficients of 0.4 for these vessels. With those reflection coefficients, medullary hypertonicity exerts a strong osmotic force (from 30 to 100% of full effect) on DVR water flow to provide osmotic equilibration as flows descend. In turn, this concentrates DVR solutes, and limits diffusive uptake from medullary interstitium, i.e., blunting “washout.” In short, zero reflection coefficients of DVR can blunt the efficiency of countercurrent exchange. In the present model, descending vascular flows are little changed from the inflow rate, and actually increase as volume is taken up through oncotic force; delivery to deep IM is limited only by transitioning to AVR. Of note, the central core assumption of Stephenson and coworkers (56) implicitly has DVR exchanging only with AVR. In the central core, the magnitude of DVR flows is buried in an effective axial diffusion coefficient for each solute within the core. This is not an approach that is easily adapted to representing changes in vascular flows or multiple electrolyte buffers.
The medullary gradients achieved by the present work are substantially less than in prior models. What is not clear, however, is that compromised countercurrent exchange within the vessels is to blame. In the discussion above, it has been argued that the vessel configuration (i.e., limitation of vessel number reaching deep into the papilla) is consistent with model choices of others. Furthermore, although individual vessel flows do not diminish as a function of medullary depth, those flows really did not decrease much in prior models (15, 26). In an analytical model of vasa recta countercurrent exchange, Marsh and Segel (34) demonstrated that a critical parameter underlying the papillary concentration gradient was the vessel uptake of solute, relative to water, i.e., the uptake concentration. In their calculations, pertinent to antidiuretic hamster, that parameter was ~10-fold greater than systemic concentration. That principle was also evident when Edwards and coworkers extended their rat vasa recta model, by including the tubular source of solutes and water, and also varying IMCD transport patterns (13). In their calculations, they estimated overall uptake rates for water, Na+, and urea of 1%, 1%, and 40% of filtered load, so that the urea uptake concentration was 40-fold greater than in systemic plasma. Their calculations suggested that development of an IM Na+ gradient required the most distal IMCD epithelium to have both increased Na+ transport and reduced water transport (compared with IMCD closer to the papillary base). In the case of urea, the model predicted ~300 mM concentration near the papillary tip, in the case that most of the urea flux was localized there, and when IMCD water transport was uniform (figure 9 in Ref. 13). In the IMCD of this model, there is no variation in water permeability or Na+ transport along its length, but urea permeability is restricted to the most distal 40%. In the current model, IM vessel uptake of volume, Na+, and urea, were 15.5 μl/min and 2.7 and 0.4 μmol/min (Table 6), so that comparing these values with their filtration rates in Table 6, reabsorption is 1.1%, 1.3%, and 5.6% of their filtered loads. The predicted papillary urea concentration for this model is only 56 mM, but this would seem to be consistent with the result of Edwards et al., after accounting for the 7-fold reduction in papillary urea delivery. In short, the countercurrent exchange properties of the medullary vessels of this model appear to be comparable to prior work.
In the present work, model focus has shifted from maximizing water conservation to the broader bookkeeping of renal solute and acid excretion. Toward this end, the component tubule models of this kidney have all received individual scrutiny in prior studies, in which attention was paid to matching their fluxes to experimental data. The fact that most of the solute transport that determines renal solute excretion occurs in the cortex, where peritubular conditions are secure, goes a long way to ensuring fidelity in excretion rates. In order that the consequences of those tubule parameter choices could be assessed in this work, they were not adjusted from prior values to modify the computed medullary solute profiles. In view of the scope of micropuncture information on rat kidney function, concordance of this model with the physiology can be tethered to overall solute excretion rates, cortical solute flows in DCT, and a handful of determinations of papillary vasa recta solute concentrations. Measured DCT flows of the important model solutes have been previously tabulated (see Appendix in Ref. 66). In this model, renal excretion of Na+ is ~0.7% of filtered load, with 8.0% delivery to DCT; IM papillary Na+ concentration is 178 mM and the corresponding Cl− is 183 mM (Table 5). These may be compared with the measured concentrations of Na+ = 256 and Cl− = 209 mM by Diezi et al. (10), in different sets of experiments in which rats were receiving a moderate saline load3. In this model, K+ excretion is 36% of filtered load, with 13% delivery to DCT, while IM papillary interstitial K+ is 17 mM; end DHL K+ delivery of long loops is ~50% of filtered load. Diezi et al. (10) found vasa recta K+ concentrations between 6 and 54 mM, depending upon whether the animal was K+-depleted or K+-loaded. In nondiuretic rats under control conditions Jamison et al. (19) measured K+ = 44 mM in IM vasa recta; under those conditions, long-loop K+ delivery was 113% of filtered load, and whole kidney fractional K+ excretion was 38%. With respect to urea, model excretion is 25% and DCT delivery is 42% of filtered load. In late CNT, where urine is isotonic to plasma, urea concentration is 6-fold greater than plasma; IM concentration is ~56 mM. When this was first examined in the rat, Lassiter et al. (25) found that in cortical distal tubule, in segments isosmolar to plasma, urea concentration was 10.5 times greater than in plasma, with DCT urea delivery about equal to filtered load; urea excretion was 13% of filtered load. Thus the major disparity with experiment appears not so much with DCT urea flow, but more the capacity of the CD for urea reabsorption. It is interesting to compare renal handling of K+ and urea, both at systemic concentrations of 5 mM, both reabsorbed proximally, and both achieving 50 −100% of filtered-load flows within the cortical distal nephron. Within the CD, ~50% of delivered K+ is reabsorbed while 80% of urea is reabsorbed, and with urea flux restricted to a limited region of distal IMCD; IM concentrations of K+ may be 5-fold greater than plasma, while those for urea may be 50-fold greater. Although this model appears to capture K+ fluxes, the path to simulating CD urea fluxes is less certain.
With respect to acid base, model net acid excretion is 0.83 μmol/min and of this, 0.34 μmol/min is attributable to ammonia; papillary interstitial ammonia concentration is ~2 mM. Comparing these values to experimental determinations of net acid and ammonia excretion (Table 4 of Ref. 64), the discrepancies are not large. The value for IM ammonia is nearly identical to that found by Good et al. (18) in their control rats. It must be acknowledged, however, that there was effort put in to deliver enough ammonia to the medulla, just to achieve this interstitial concentration. Specifically, while arterial ammonia was not likely to be greater than 0.1 mM, renal cortical (including renal venous) ammonia concentration was assumed to be 0.2 mM, while DVR (including MRDVR) ammonia was set to 2 mM. For these concentrations, with renal plasma flow of 7 ml/min, whole kidney ammonia delivery is 0.7 μmol/min, with venous outflow of 1.4 μmol/min, or ~4-fold greater than urinary ammonia excretion. If this value for renal venous ammonia is realistic, then one obtains an upper bound for PCT ammoniagenesis, which is approximately the value that had been selected for the PCT models (70, 73). Thus any further increment in urinary ammonia would need to come from adjusting either tubular secretion or medullary washout, rather than increasing ammoniagenesis. A major surprise from this work was the predicted value of 12 mM for IM papillary interstitial concentration. Prior tubular models had uniformly used a value close to systemic , in accordance with vasa recta total CO2 reported by DuBose et al. (12). Of note, in that work, end-PCT values were acid (~8 mM, with pH = 6.8), so there was clearly medullary acid delivery. Indeed, total CO2 delivery to the bend of the loop of Henle was less than in late proximal flow, so that Dubose et al. reasoned that the higher concentration must have been produced by water reabsorption within the medulla. In the current model, low end-proximal concentration from JM nephrons doubles by the end of the longest loops, but is not restored to systemic values within OM, so that IM acidification is produced. What resists explanation is the observation of Dubose et al. (12) that medullary Pco2 (35 mmHg) was substantially less than renal cortical Pco2 (64 mmHg). This model predicts medullary Pco2 higher than in the cortex.
Eighty years ago, Keith and Binger (20) reported studies of the diuretic potential of potassium salts, noting that their work ratified observations that been accruing over the preceding 80 years. These observations have had sustained interest in the modern era, due to the salutary effect on blood pressure in people eating a high-potassium diet (2, 22). The natriuresis of potassium administration occurs even when mineralocorticoid levels are supplemented at high doses, thus reducing the amount of Na+ retention for aldo-escape (23). There is ample evidence that the natriuresis is due to a direct impact of elevated blood K+ concentration to depress renal Na+ reabsorption, and there are several plausible segmental loci for this effect. In micropuncture of rat SFPCT, raising plasma K+ acutely from 4.3 to 6.0 by KCl infusion, depressed PCT volume reabsorption (i.e., Na+ reabsorption) by 32% (7). In normal rats, acute increase in plasma K+ from 3.5 to 4.5 meq/l depressed both SFPCT volume and reabsorption by 30% (30). When phosphorus-NMR was used to assess SFPCT epithelial cell pH, whole body K+ depletion acidified the cells (pH 7.44 to 7.17), and acute KCl infusion restored cell pH to control value (1). Cytosolic alkalinization can be expected to depress Na+ reabsorption via luminal Na+/H+ exchanger (NHE3). AHL may be another site at which peritubular K+ can modulate Na+ reabsorption. Stokes (57) demonstrated that in rabbit AHL, perfused in vitro, elevation of bath K+ blunted Na+ and Cl− reabsorption. The significance of this observation for him was that increases in medullary interstitial K+ could act to augment more distal cortical K+ secretion, through enhanced Na+ delivery. Complementing this observation in vivo, proximal and distal micropuncture in the rat showed that K+ loading blunted Cl− reabsorption within the loop of Henle (21). More recently, K+ modulation of DCT NaCl transport has become a point of interest, both from the perspective of controlling CNT K+ secretion by regulating Na+ delivery (67), but also for dissecting the cellular events by which peritubular K+ can impact DCT luminal fluxes. In this regard, Terker et al. (59) examined cultured cells expressing the DCT NaCl cotransporter (NCC) and its regulating kinase cascade. They found parallel variation in cytosolic Cl− and peritubular K+, and increased phosphorylation (activation) of NCC with low Cl−, consistent with known Cl−-dependent kinases. Supporting the dominance of peritubular K+ in regulation of DCT NaCl transport are studies of aldosterone-resistant hyperkalemia in either mineralocorticoid receptor knockout mice (58) or ENaC alpha subunit knockout mice (49), in which reversal of hyperkalemia restored NCC activity and reduced natriuresis.
From the perspective of this kidney model, transport components common to PCT, AHL, and DCT include peritubular KCl cotransporters (KCC) and K+ channels. These transporters render cytosolic Cl− and concentration sensitive to changes in peritubular K+ concentration. The impact of KCC on cell Cl− is straightforward, and follows from the fact that its reabsorptive solute flux is a positive function of the electrochemical potential of the K+-Cl− pair. With respect to the K+ channel, increased peritubular K+ depolarizes the cell. To the extent that peritubular Cl− and transport is rheogenic (Cl− channels in AHL and DCT, and Na+-3 cotransporter in PCT), there will be cellular accumulation of these anions with peritubular depolarization. In PCT, luminal NHE3 activity is downregulated by cytosolic alkalinization, beyond the simple kinetic effect of the reduced proton availability (3). In a prior examination of the PCT model, a doubling of peritubular K+ was estimated to reduce total Na+ flux by 15% (figure 3 in Ref. 63). In AHL there is quadratic dependence of luminal membrane NKCC flux on cytosolic Cl− concentration, and in the AHL model of this work, an increase in peritubular K+ from 10 to 20 mM reduced NKCC flux by ~15% (figure 5 in Ref. 72). DCT Na+ flux as a function of peritubular K+ was examined in the initial model development, where a doubling of K+ from 4 to 8 mM reduced reabsorptive Na+ flux by ~10% (figure 11 in Ref. 66). That sensitivity could be amplified substantially when luminal membrane NCC density was given a linear dependence on cytosolic Cl− (59), but it is the baseline DCT model that has been used in the present kidney model. In this kidney model, all of these segmental effects were operative when peritubular K+ was increased from 5.0 to 5.5. In absolute terms, the increase in distal Na+ delivery from PCT, was largely unabated by downstream reabsorption, and provided the bulk of the natriuresis. What this model adds to the discussion is its prediction that while medullary K+ concentration may increase with mild hyperkalemia, the change in medullary K+ does not amplify the change in systemic K+. This derives from the fact that although increased plasma K+ increases interstitial K+, the diuresis of hyperkalemia also enhances medullary washout. A second model observation is the reminder that both AHL segments and DCT respond to increases in Na+ delivery with increased Na+ reabsorption. Comparing Table 8 with Table 6, one sees that for these segments, with the increase in peritubular K+, luminal and peritubular factors either balance or the impact of luminal delivery dominates. In short, the extra Na+ that arrives at CNT came from the PCT.
One thing that was not done in this work was to adjust tubule anatomy, transport rates, or permeabilities in order to capture reported interstitial concentration profiles. The component tubule models were developed individually, and this work is a report of their synthesis. It is acknowledged that modifications may be necessary. Furthermore, in its present form, this kidney model is not robust in the sense that convergence to a solution for the interstitial variables is often difficult to obtain. Figure 8 shows that IM fluxes are an order of magnitude less than OM fluxes, which in turn, are dwarfed by cortical fluxes. As a consequence, small proximal perturbations can produce major derangements in IM solute profiles and IMCD flow, and thus impact luminal hydrostatic pressure. That pressure is transmitted back to PCT, changing tubule radius, and thus altering microvillous torque. In PCT, hydrodynamic drag on microvilli is the input signal for the flow-dependent transport, and this drag varies inversely with tubule cross-section (73). Specifically, high distal pressure dilates PCT, reducing drag, blunting Na+ (and fluid) reabsorption, thus increasing distal delivery and augmenting distal pressure. Low distal pressure reduces PCT diameter, increasing drag, promoting fluid absorption, thus decreasing distal delivery and diminishing distal pressure. In short, the configuration of controllers is not self-correcting, but destabilizes with higher and lower PCT flows. Mitigating this instability are the two control mechanisms included in this model, flow-dependent transport within PCT, and TGF. Certainly, other control mechanisms are missing from the model, such as flow dependence of transport by distal nephron segments or even AHL, and tubulovascular cross-talk of the OM. Although distal flow-dependence has been demonstrated (53), there is much uncertainty regarding its operation: for example, which cells are susceptible to flow effects, or the impact of changes in luminal composition on flow-dependent fluxes. It would be expected that distal flow dependence would stabilize solute excretion. Tubulovascular cross-talk refers to medullary paracrine signals, which coordinate AHL flow and transport with vascular nutrient and oxygen delivery (9). It is expected that these signals would enhance vascular countercurrent exchange when loop of Henle flows are low, thus augmenting medullary interstitial concentration gradients. The impact of such coordinated perfusion on tubule flows and pressures is unknown.
In sum, a comprehensive nephron model has been fitted with medullary vasculature to become a kidney model. In this, the equations for coordination of tubular and vascular transport provide the medullary interstitial conditions, and bring renal electrolyte and acid-base transport models into the world of countercurrent physiology. In comparison with prior work on the urine-concentrating mechanism, reflection coefficients for DVR are near zero, so that deeper flows are slightly larger and countercurrent exchange may be less efficient. Quantitative similarities are noted between K+ and urea handling (medullary delivery and permeabilities), and the model predicts medullary gradients for both. The model K+ gradient is physiologic, and the urea gradient is several-fold steeper due to restriction of IMCD urea permeability to its distal third. Nevertheless, the predicted urea gradient is substantially less than expected for the antidiuretic rat kidney. If the K+ profile is an indication that its countercurrent exchange is realistic, then perhaps vascular exchange of urea exchange is also realistic. This suggests reconsideration of proposals of an unrecognized reabsorptive urea flux, which may be absent from one or more CD segmental models (reviewed in 33). In a simulation of mild hyperkalemia, the model captures the physiological natriuresis, with enhanced CNT Na+ delivery. The source of this additional Na+ is proximal tubule.
GRANTS
This investigation was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant R01-DK-29857.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
A.M.W. conceived and designed research; A.M.W. performed experiments; A.M.W. analyzed data; A.M.W. interpreted results of experiments; A.M.W. prepared figures; A.M.W. drafted manuscript; A.M.W. edited and revised manuscript; A.M.W. approved final version of manuscript.
appendix
Hemoglobin oxygen saturation varies along medullary depth, by virtue of variable Po2 (17). Beyond that, the Bohr effect (in which hemoglobin oxygen saturation drops at more acidic pH) may play an even greater role in modulating hemoglobin oxygen saturation within the medulla. The first of the two governing equations is the Hill equation for oxygen saturation, S, and partial pressure of oxygen, P (8):
| (A1) |
The Bohr equation states that for fixed oxygen saturation, the partial pressure of oxygen required to achieve that saturation varies according to pH:
| (A2) |
in which B is a constant, largely independent of oxygen saturation (8). The Hill equation can be rewritten in logarithmic form
| (A3) |
As indicated above, to obtain the Bohr coefficient, B, one varies pH and records the Po2 required to provide the specified oxygen saturation, S. Thus with S fixed, and because the Hill coefficient, n, is largely independent of pH (32), taking the derivative of Eq. A3 with respect to pH provides
| (A4) |
Equation A4 indicates that the Bohr coefficient also applies to P50. Returning to Eq. A3 in the case of specified P, the derivative with respect to pH is
| (A5) |
so that integration from a reference pH of 7.40 yields
| (A6) |
or
| (A7) |
Thus, starting with a medullary Po2 profile, the Hill equation provides S(P) at pH = 7.40, and Eq. A7 estimates hemoglobin saturation as a function of pH, within each vessel at each medullary depth. Actually, the impact of variable Po2 and pH on solute transport is small (<1% under baseline conditions), when compared with just assuming that medullary oxygen saturation is that of arterial blood . This is due to the fact that equilibrium binding for oxy- and deoxyhemoglobin are close (Table 2).
Footnotes
For each tubule or vessel, denoted by k, the open-circuit condition may be written, suppressing the position variable x, as
Then, recognizing the interstitial conservation equations for the non-reacting Na+ and K+ (Eq. 34), and for each of the buffer pairs (Eqs. 35–37),
To compute titratable acid for capillary flows, contributions from phosphate and from the 7 hemoglobin buffers of Table 2 are summed. Suppose acidic plasma, with buffer concentrations, B− and HB, which satisfy a Henderson-Hasselbalch equation,
Adding alkali to pH = 7.40, the buffer concentrations will shift, increasing B− and decreasing HB, each by an amount TA
Setting
the equation at neutral pH provides
In the case of the carbamino buffer, with equilibrium constant KEQ (Table 2), KB is replaced by KEQ·[CO2] in the calculation of β.
For comparison with experimental data, renal medullary interstitial concentrations near the papillary tip were used for comparison with reported vasa recta solute concentrations. In the cited experimental studies, either the DVR/AVR identification was not reported (10, 18, 19) or there were no differences between DVR and AVR measurements (12); in no case was the VR sampling site defined. In this model, differences between DVR and adjacent inner medullary interstitial concentrations were less than 10% for all solutes, and less than 5% for Na+, K+, Cl−, urea, and .
REFERENCES
- 1.Adam WR, Koretsky AP, Weiner MW. 31P-NMR in vivo measurement of renal intracellular pH: effects of acidosis and K+ depletion in rats. Am J Physiol Renal Fluid Electrolyte Physiol : F904–F910, 1986. [DOI] [PubMed] [Google Scholar]
- 2.Adrogué HJ, Madias NE. Sodium surfeit and potassium deficit: keys to the pathogenesis of hypertension. J Am Soc Hypertens : 203–213, 2014. doi: 10.1016/j.jash.2013.09.003. [DOI] [PubMed] [Google Scholar]
- 3.Aronson PS, Nee J, Suhm MA. Modifier role of internal H+ in activating the Na+-H+ exchanger in renal microvillus membrane vesicles. Nature : 161–163, 1982. doi: 10.1038/299161a0. [DOI] [PubMed] [Google Scholar]
- 4.Atherton LJ, Deen WM, Maddox DA, Gennari FJ. Analysis of the factors influencing peritubular PCO2 in the rat. Am J Physiol Renal Fluid Electrolyte Physiol : F61–F72, 1984. [DOI] [PubMed] [Google Scholar]
- 5.Beeuwkes R., III Efferent vascular patterns and early vascular-tubular relations in the dog kidney. Am J Physiol : 1361–1374, 1971. [DOI] [PubMed] [Google Scholar]
- 6.Beeuwkes R III, Bonventre JV. Tubular organization and vascular-tubular relations in the dog kidney. Am J Physiol : 695–713, 1975. [DOI] [PubMed] [Google Scholar]
- 7.Brandis M, Keyes J, Windhager EE. Potassium-induced inhibition of proximal tubular fluid reabsorption in rats. Am J Physiol : 421–427, 1972. [DOI] [PubMed] [Google Scholar]
- 8.Cartheuser CF. Standard and pH-affected hemoglobin-O2 binding curves of Sprague-Dawley rats under normal and shifted P50 conditions. Comp Biochem Physiol Comp Physiol : 775–782, 1993. doi: 10.1016/0300-9629(93)90396-L. [DOI] [PubMed] [Google Scholar]
- 9.Cowley AW Jr, Mori T, Mattson D, Zou AP. Role of renal NO production in the regulation of medullary blood flow. Am J Physiol Regul Integr Comp Physiol : R1355–R1369, 2003. doi: 10.1152/ajpregu.00701.2002. [DOI] [PubMed] [Google Scholar]
- 10.Diezi J, Michoud P, Aceves J, Giebisch G. Micropuncture study of electrolyte transport across papillary collecting duct of the rat. Am J Physiol : 623–634, 1973. [DOI] [PubMed] [Google Scholar]
- 11.DuBose TD., Jr Hydrogen ion secretion by the collecting duct as a determinant of the urine to blood PCO2 gradient in alkaline urine. J Clin Invest : 145–156, 1982. doi: 10.1172/JCI110425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.DuBose TD Jr, Lucci MS, Hogg RJ, Pucacco LR, Kokko JP, Carter NW. Comparison of acidification parameters in superficial and deep nephrons of the rat. Am J Physiol Renal Fluid Electrolyte Physiol : F497–F503, 1983. [DOI] [PubMed] [Google Scholar]
- 13.Edwards A, Delong MJ, Pallone TL. Interstitial water and solute recovery by inner medullary vasa recta. Am J Physiol Renal Physiol : F257–F269, 2000. [DOI] [PubMed] [Google Scholar]
- 14.Edwards A, Pallone TL. Facilitated transport in vasa recta: theoretical effects on solute exchange in the medullary microcirculation. Am J Physiol Renal Physiol : F505–F514, 1997. [DOI] [PubMed] [Google Scholar]
- 15.Edwards A, Pallone TL. A multiunit model of solute and water removal by inner medullary vasa recta. Am J Physiol Heart Circ Physiol : H1202–H1210, 1998. [DOI] [PubMed] [Google Scholar]
- 16.Evans RG, Harrop GK, Ngo JP, Ow CP, O’Connor PM. Basal renal oxygen consumption and the efficiency of oxygen utilization for sodium reabsorption. Am J Physiol Renal Physiol : F551–F560, 2014. 10.1152/ajprenal.00473.2013. [DOI] [PubMed] [Google Scholar]
- 17.Fry BC, Edwards A, Sgouralis I, Layton AT. Impact of renal medullary three-dimensional architecture on oxygen transport. Am J Physiol Renal Physiol : F263–F272, 2014. doi: 10.1152/ajprenal.00149.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Good DW, Caflisch CR, DuBose TD Jr. Transepithelial ammonia concentration gradients in inner medulla of the rat. Am J Physiol Renal Fluid Electrolyte Physiol : F491–F500, 1987. [DOI] [PubMed] [Google Scholar]
- 19.Jamison RL, Lacy FB, Pennell JP, Sanjana VM. Potassium secretion by the descending limb or pars recta of the juxtamedullary nephron in vivo. Kidney Int : 323–332, 1976. doi: 10.1038/ki.1976.38. [DOI] [PubMed] [Google Scholar]
- 20.Keith NM, Binger MW. Diuretic action of potassium salts. JAMA : 1584–1591, 1935. doi: 10.1001/jama.1935.02760460020005. [DOI] [Google Scholar]
- 21.Kirchner KA. Effect of acute potassium infusion on loop segment chloride reabsorption in the rat. Am J Physiol Renal Fluid Electrolyte Physiol : F599–F605, 1983. [DOI] [PubMed] [Google Scholar]
- 22.Krishna GG, Kapoor SC. Potassium depletion exacerbates essential hypertension. Ann Intern Med : 77–83, 1991. doi: 10.7326/0003-4819-115-2-77. [DOI] [PubMed] [Google Scholar]
- 23.Krishna GG, Kapoor SC. Potassium supplementation ameliorates mineralocorticoid-induced sodium retention. Kidney Int : 1097–1103, 1993. doi: 10.1038/ki.1993.154. [DOI] [PubMed] [Google Scholar]
- 24.Landis EM, Pappenheimer JR. Exchange of substances through capillary walls, In: Handbook of Physiology. Circulation. Washington, DC: Am. Physiol. Soc, 1963, p. 961–1034. [Google Scholar]
- 25.Lassiter WE, Gottschalk CW, Mylle M. Micropuncture study of net transtubular movement of water and urea in nondiuretic mammalian kidney. Am J Physiol : 1139–1147, 1961. [DOI] [PubMed] [Google Scholar]
- 26.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol : F356–F371, 2011. doi: 10.1152/ajprenal.00203.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla. II. Functional implications of three-dimensional architecture. Am J Physiol Renal Physiol : F372–F384, 2011. doi: 10.1152/ajprenal.00204.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol : F1346–F1366, 2005. doi: 10.1152/ajprenal.00346.2003. [DOI] [PubMed] [Google Scholar]
- 29.Layton AT, Vallon V, Edwards A. Modeling oxygen consumption in the proximal tubule: effects of NHE and SGLT2 inhibition. Am J Physiol Renal Physiol : F1343–F1357, 2015. doi: 10.1152/ajprenal.00007.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Levine DZ, Walker T, Nash LA. Effects of KCl infusions on proximal tubular function in normal and potassium-depleted rats. Kidney Int : 318–325, 1973. doi: 10.1038/ki.1973.123. [DOI] [PubMed] [Google Scholar]
- 31.MacPhee PJ, Michel CC. Fluid uptake from the renal medulla into the ascending vasa recta in anaesthetized rats. J Physiol : 169–183, 1995. doi: 10.1113/jphysiol.1995.sp020869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Margaria R. A mathematical treatment of the blood dissociation curve for oxygen. Clin Chem : 745–762, 1963. [PubMed] [Google Scholar]
- 33.Marsh DJ, Knepper MA. Renal handling of urea. In: Handbook of Physiology. Renal Physiology. Bethesda, MD: Am. Physiol. Soc, 1992, sect. 8, chapt. 29, p. 1317–1347. [Google Scholar]
- 34.Marsh DJ, Segel LA. Analysis of countercurrent diffusion exchange in blood vessels of the renal medulla. Am J Physiol : 817–828, 1971. [DOI] [PubMed] [Google Scholar]
- 35.Moss R, Thomas SR. Hormonal regulation of salt and water excretion: a mathematical model of whole kidney function and pressure natriuresis. Am J Physiol Renal Physiol : F224–F248, 2014. doi: 10.1152/ajprenal.00089.2013. [DOI] [PubMed] [Google Scholar]
- 36.Pallone TL. Effect of sodium chloride gradients on water flux in rat descending vasa recta. J Clin Invest : 12–19, 1991. doi: 10.1172/JCI114960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pallone TL. Resistance of ascending vasa recta to transport of water. Am J Physiol Renal Fluid Electrolyte Physiol : F303–F310, 1991. [DOI] [PubMed] [Google Scholar]
- 38.Pallone TL. Transport of sodium chloride and water in rat ascending vasa recta. Am J Physiol Renal Fluid Electrolyte Physiol : F519–F525, 1991. [DOI] [PubMed] [Google Scholar]
- 39.Pallone TL. Extravascular protein in the renal medulla: analysis by two methods. Am J Physiol Renal Integr Comp Physiol : R1429–R1436, 1994. [DOI] [PubMed] [Google Scholar]
- 40.Pallone TL, Cao C. Renal cortical and medullary microcirculations: structure and function. In: Seldin and Giebisch’s The Kidney: Physiology and Pathophysiology (5th ed.). New York: Academic, 2012, chapt 24, p. 803–857. [Google Scholar]
- 41.Pallone TL, Morgenthaler TI, Deen WM. Analysis of microvascular water and solute exchanges in the renal medulla. Am J Physiol Renal Fluid Electrolyte Physiol : F303–F315, 1984. [DOI] [PubMed] [Google Scholar]
- 42.Pallone TL, Nielsen S, Silldorff EP, Yang S. Diffusive transport of solute in the rat medullary microcirculation. Am J Physiol Renal Fluid Electrolyte Physiol : F55–F63, 1995. [DOI] [PubMed] [Google Scholar]
- 43.Pallone TL, Turner MR. Molecular sieving of small solutes by outer medullary descending vasa recta. Am J Physiol Renal Physiol : F579–F586, 1997. [DOI] [PubMed] [Google Scholar]
- 44.Pallone TL, Turner MR, Edwards A, Jamison RL. Countercurrent exchange in the renal medulla. Am J Physiol Regul Integr Comp Physiol : R1153–R1175, 2003. doi: 10.1152/ajpregu.00657.2002. [DOI] [PubMed] [Google Scholar]
- 45.Pallone TL, Work J, Jamison RL. Resistance of descending vasa recta to the transport of water. Am J Physiol Renal Fluid Electrolyte Physiol : F688–F697, 1990. [DOI] [PubMed] [Google Scholar]
- 46.Pallone TL, Work J, Myers RL, Jamison RL. Transport of sodium and urea in outer medullary descending vasa recta. J Clin Invest : 212–222, 1994. doi: 10.1172/JCI116948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pallone TL, Yagil Y, Jamison RL. Effect of small-solute gradients on transcapillary fluid movement in renal inner medulla. Am J Physiol Renal Fluid Electrolyte Physiol : F547–F553, 1989. [DOI] [PubMed] [Google Scholar]
- 48.Pannabecker TL, Layton AT. Targeted delivery of solutes and oxygen in the renal medulla: role of microvessel architecture. Am J Physiol Renal Physiol : F649–F655, 2014. doi: 10.1152/ajprenal.00276.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Perrier R, Boscardin E, Malsure S, Sergi C, Maillard MP, Loffing J, Loffing-Cueni D, Sørensen MV, Koesters R, Rossier BC, Frateschi S, Hummler E. Severe salt-losing syndrome and hyperkalemia induced by adult nephron-specific knockout of the epithelial sodium channel α-subunit. J Am Soc Nephrol : 2309–2318, 2016. doi: 10.1681/ASN.2015020154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Prothero JW, Burton AC. The physics of blood flood in capillaries. II. The capillary resistance to flow. Biophys J : 199–212, 1962. doi: 10.1016/S0006-3495(62)86849-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Roman RJ, Smits C. Laser-Doppler determination of papillary blood flow in young and adult rats. Am J Physiol Renal Fluid Electrolyte Physiol : F115–F124, 1986. [DOI] [PubMed] [Google Scholar]
- 52.Sanjana VM, Johnston PA, Robertson CR, Jamison RL. An examination of transcapillary water flux in renal inner medulla. Am J Physiol : 313–318, 1976. [DOI] [PubMed] [Google Scholar]
- 53.Satlin LM, Sheng S, Woda CB, Kleyman TR. Epithelial Na(+) channels are regulated by flow. Am J Physiol Renal Physiol : F1010–F1018, 2001. [DOI] [PubMed] [Google Scholar]
- 54.Stephenson JL. Concentration of urine in a central core model of the renal counterflow system. Kidney Int : 85–94, 1972. doi: 10.1038/ki.1972.75. [DOI] [PubMed] [Google Scholar]
- 55.Stephenson JL, Wang H, Tewarson RP. Effect of vasa recta flow on concentrating ability of models of renal inner medulla. Am J Physiol Renal Fluid Electrolyte Physiol : F698–F709, 1995. [DOI] [PubMed] [Google Scholar]
- 56.Stephenson JL, Zhang Y, Tewarson R. Electrolyte, urea, and water transport in a two-nephron central core model of the renal medulla. Am J Physiol Renal Fluid Electrolyte Physiol : F399–F413, 1989. [DOI] [PubMed] [Google Scholar]
- 57.Stokes JB. Consequences of potassium recycling in the renal medulla. Effects of ion transport by the medullary thick ascending limb of Henle’s loop. J Clin Invest : 219–229, 1982. doi: 10.1172/JCI110609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Terker AS, Yarbrough B, Ferdaus MZ, Lazelle RA, Erspamer KJ, Meermeier NP, Park HJ, McCormick JA, Yang CL, Ellison DH. Direct and indirect mineralocorticoid effects determine distal salt transport. J Am Soc Nephrol : 2436–2445, 2016. doi: 10.1681/ASN.2015070815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Terker AS, Zhang C, McCormick JA, Lazelle RA, Zhang C, Meermeier NP, Siler DA, Park HJ, Fu Y, Cohen DM, Weinstein AM, Wang WH, Yang CL, Ellison DH. Potassium modulates electrolyte balance and blood pressure through effects on distal cell voltage and chloride. Cell Metab : 39–50, 2015. doi: 10.1016/j.cmet.2014.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Thomas SR. Cycles and separations in a model of the renal medulla. Am J Physiol Renal Physiol : F671–F690, 1998. [DOI] [PubMed] [Google Scholar]
- 61.Turner MR, Pallone TL. Hydraulic and diffusional permeabilities of isolated outer medullary descending vasa recta from the rat. Am J Physiol Heart Circ Physiol : H392–H400, 1997. [DOI] [PubMed] [Google Scholar]
- 62.Weinstein AM. A mathematical model of the proximal nephron. Math Comput Model : 522–528, 1990. doi: 10.1016/0895-7177(90)90237-H. [DOI] [PubMed] [Google Scholar]
- 63.Weinstein AM. Modeling epithelial cell homeostasis: steady-state analysis. Bull Math Biol : 1065–1091, 1999. doi: 10.1006/bulm.1999.0127. [DOI] [PubMed] [Google Scholar]
- 64.Weinstein AM. A mathematical model of rat collecting duct. I. Flow effects on transport and urinary acidification. Am J Physiol Renal Physiol : F1237–F1251, 2002. doi: 10.1152/ajprenal.00162.2002. [DOI] [PubMed] [Google Scholar]
- 65.Weinstein AM. A mathematical model of rat collecting duct. II. Effect of buffer delivery on urinary acidification. Am J Physiol Renal Physiol : F1252–F1266, 2002. doi: 10.1152/ajprenal.00163.2002. [DOI] [PubMed] [Google Scholar]
- 66.Weinstein AM. A mathematical model of rat distal convoluted tubule. I. Cotransporter function in early DCT. Am J Physiol Renal Physiol : F699–F720, 2005. doi: 10.1152/ajprenal.00043.2005. [DOI] [PubMed] [Google Scholar]
- 67.Weinstein AM. A mathematical model of rat distal convoluted tubule. II. Potassium secretion along the connecting segment. Am J Physiol Renal Physiol : F721–F741, 2005. doi: 10.1152/ajprenal.00044.2005. [DOI] [PubMed] [Google Scholar]
- 68.Weinstein AM. A mathematical model of rat ascending Henle limb. III. Tubular function. Am J Physiol Renal Physiol : F543–F556, 2010. doi: 10.1152/ajprenal.00232.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Weinstein AM. Identifying renal medullary neighborhoods–when do distances matter? Am J Physiol Renal Physiol : F1411–F1412, 2013. doi: 10.1152/ajprenal.00692.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Weinstein AM. A mathematical model of rat proximal tubule and loop of Henle. Am J Physiol Renal Physiol : F1076–F1097, 2015. doi: 10.1152/ajprenal.00504.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Weinstein AM. A mathematical model of the rat nephron: glucose transport. Am J Physiol Renal Physiol : F1098–F1118, 2015. doi: 10.1152/ajprenal.00505.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Weinstein AM, Krahn TA. A mathematical model of rat ascending Henle limb. II. Epithelial function. Am J Physiol Renal Physiol : F525–F542, 2010. doi: 10.1152/ajprenal.00231.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Weinstein AM, Weinbaum S, Duan Y, Du Z, Yan Q, Wang T. Flow-dependent transport in a mathematical model of rat proximal tubule. Am J Physiol Renal Physiol : F1164–F1181, 2007. doi: 10.1152/ajprenal.00392.2006. [DOI] [PubMed] [Google Scholar]
- 74.Wexler AS, Kalaba RE, Marsh DJ. Three-dimensional anatomy and renal concentrating mechanism. I. Modeling results. Am J Physiol Renal Fluid Electrolyte Physiol : F368–F383, 1991. [DOI] [PubMed] [Google Scholar]