AN ANALYTIC SOLUTION TO SINGLE NUCLEOTIDE POLYMORPHISM ERROR-DETECTION RATES IN NUCLEAR FAMILIES: IMPLICATIONS FOR STUDY DESIGN

Abstract

Recently, there has been increased interest in using Single Nucleotide Polymorphisms (SNPs) as a method for detecting genes for complex traits. SNPs are diallelic markers that have the potential to be inexpensively produced using chip technology. It has been suggested that SNPs will be beneficial in study designs that utilize trio data (father, mother, child). In our previous work, we calculated the probability of detecting Mendelian errors at a SNP locus for a trio randomly selected from a population in Hardy-Weinberg equilibrium. The highest error-detection rate was 30%. Here we investigate the error-detection rate when additional sibs are genotyped. We define an error to be a change from a 1 allele to a 2 allele, or vice versa. Typing one additional sib increases the detection rate on average by 10 – 13%. Typing two additional sibs increases the detection rate on average by 14-19%. The increase in the detection rate is dependent on the allele frequencies. Equal allele frequencies produce the lowest detection rates, independent of true error rates and number of offspring genotyped. Typing additional siblings not only improves error-detection rates, but can also provide additional linkage information. In order to increase linkage information and error-detection rates, at least two additional siblings should be ascertained when available.

1. Introduction

Recently, there has been an increased interest in the use of Single Nucleotide Polymorphisms (SNPs) loci as a possible method for detecting genes of modest effect, i.e., for complex traits¹. SNPs occur in large numbers across the human genome and usually consist of two alleles². Statistical methods proposed for detection of genes for complex traits using SNPs include haplotype-relative risk tests³, and transmission-disequilibrium tests⁴ (TDT). In each of these tests, the sampling frame is a family trio, consisting of a father, a mother, and an affected child genotyped at a locus. In the case of TDT when testing for linkage in the presence of association, additional affected siblings may also be used⁵.

One important methodologic issue concerning markers in general and SNPs in particular is that of errors. Buetow⁶ found that, in constructing high resolution human linkage maps (3 cM or less) with highly polymorphic markers, typing errors, even at the rate of 1.5%, led to a reduction of power to discriminate orders, a dramatic inflation of map length, and significant support for incorrect over correct orders. Shields et al.⁷ also determined that the introduction of typing errors when constructing human linkage maps led to support for incorrect orders and map length inflation. Terwilliger, Weeks and Ott⁸ showed in simulation studies for a multi-allelic system that misreading an allele results in overestimation of recombination fraction and a decrease in expected lod score. Using simulated data for a multi-allelic marker, Gordon et al.⁹ showed that errors in pedigree data can significantly reduce evidence for linkage in the presence of association when using a transmission disequilibrium test. Several authors^10,11,12,13 considered the issue of errors in pedigree data, and devised methods for detecting such errors.

Regarding SNPs, Gordon et al.¹⁴ investigated the error-detection rate in trios by detecting errors through deviations from Mendel’s laws. The authors defined an error, as we do in this article, to be anything that causes a 1 allele to change to a 2 allele, or vice versa. Such errors may result from non-paternity, sample swaps in the lab, or genotyping errors. The highest detection rate for trios was slightly less than 31%. Given such a low detection rate, we seek to quantify the improvement in error-detection rates by genotyping additional siblings.

2. Materials and Methods

2.1. Detection Rate for Sib Pairs (Genotype Quartets)

For a diallelic marker with allele numbers 1 and 2, there are (up to symmetry) three possible genotypes: 1/1, 1/2, and 2/2. A genotype quartet is defined to be a 4-tuple of genotypes (Parent₁ Allele 1/Parent₁ Allele 2, Parent₂ Allele 1/Parent₂ Allele 2, Child₁ Allele 1/Child₁ Allele 2, Child₂ Allele 1/Child₂ Allele 2) in which the set of alleles is consistent with Mendel’s laws. In this 4-tuple, no distinction is made between Parent₁ and Parent₂, or Child₁ and Child₂. For example, the genotype quartets (1/2, 1/1, 1/1, 1/2) and (1/1, 1/2, 1/2, 1/1) are considered to be equivalent. No distinction is made between genotypes 2/1 and 1/2. Thus, for example, the quartet (2/1, 2/1, 2/1, 2/1) is equivalent to (1/2, 1/2, 1/2, 1/2), and so forth. For consistency, the genotypes 1/2 and 2/1 shall always be referred to as 1/2. A general quartet is defined to be any 4-tuple of genotypes in which each person has the genotypes 1/1, 1/2, or 2/2, without the restriction that the quartet displays Mendelian consistency. Here and elsewhere, the term consistency (respectively, inconsistency) implies Mendelian consistency (respectively, Mendelian inconsistency). Note that the set of genotype quartets is a subset of the set of general quartets. Also, the conjugate of a genotype quartet M (denoted M) is defined as the genotype quartet that results when each value of 1 in M is replace by a 2, and each value of 2 in M is replaced by a 1. For example, the conjugate of the quartet (1/1, 1/1, 1/1, 1/1) is (2/2, 2/2, 2/2, 2/2), the conjugate of (1/2, 1/1, 1/1, 1/1) is (1/2, 2/2, 2/2, 2/2), and so forth. The list of all genotype quartets and their conjugates may be found in Table 1. An error in a genotype quartet is defined to be one or more changes in genotypes of the quartet. For example, if the original quartet is (2/2, 2/2, 2/2, 2/2) then one error is introduced into the quartet if one and only one of the 2 alleles is replaced by a 1 allele. It is assumed that errors are introduced randomly and independently into genotype quartets at a constant rate, denoted by α.

Table 1.

List of all genotype quartets and their conjugates

Genotype Quartet M	Conjugate Genotype Quartet M
(1/1, 1/1, 1/1, 1/1)	(2/2, 2/2, 2/2, 2/2)
(1/1, 1/2, 1/1, 1/1)	(2/2, 1/2, 2/2, 2/2)
(1/1, 1/2, 1/1, 1/2)	(2/2, 1/2, 2/2, 1/2)
(1/1, 1/2, 1/2, 1/2)	(2/2, 1/2, 1/2, 1/2)
(1/1, 2/2, 1/2, 1/2)	(2/2, 1/1, 1/2, 1/2)
(1/2, 1/2, 1/1, 1/1)	(1/2, 1/2, 2/2, 2/2)
(1/2, 1/2, 1/1, 1/2)	(1/2, 1/2, 2/2, 1/2)
(1/2, 1/2, 1/1, 2/2)	(1/2, 1/2, 2/2, 1/1)
(1/2, 1/2, 1/2, 1/2)	(1/2, 1/2, 1/2, 1/2)
(1/2, 1/2, 1/2, 2/2)	(1/2, 1/2, 1/2, 1/1)
(1/2, 1/2, 2/2, 2/2)	(1/2, 1/2, 1/1, 1/1)
(1/2, 2/2, 1/2, 1/2)	(1/2, 1/1, 1/2, 1/2)
(1/2, 2/2, 1/2, 2/2)	(1/2, 1/1, 1/2, 1/1)
(1/2, 2/2, 2/2, 2/2)	(1/2, 1/1, 1/1, 1/1)
(2/2, 2/2, 2/2, 2/2)	(1/1, 1/1, 1/1, 1/1)

For each of the fifteen quartets in Table 1, anywhere from 0 to 8 errors may be introduced. In the case of either 0 or 8 errors, the resulting general quartet will always display consistency. We calculate the probability that all errors go undetected for a collection of genotype quartets in which at least one error has been introduced, and denote this quantity by β. It follows that the detection rate is 1 - β. Using basic probability theory,

$$\beta =\sum _{i=1}^8\text{Pr}(\mathit{undetected}\mathit{errors}\mid i\mathit{errors}\mathit{in}\mathit{quartet})\text{Pr}(i\mathit{errors}\mathit{in}\mathit{quartet})\cdot$$ (1)

The term i = 0 is not included in the sum (1) because only genotype quartets in which errors have been introduced are considered. If B(α; i) is defined by

$$B(\alpha ;i)=\left(\begin{array}{c}\hfill 8\hfill \\ \hfill i\hfill \end{array}\right){\alpha }^i{(1-\alpha )}^{8-i},$$

then because error introduction is assumed to be random and independent for each allele in a genotype quartet, and because only those genotype quartets that contain at least one error are considered, the quantity Pr(i errors in quartet) in formula (1) is given by

$$\text{Pr}(i\mathit{errors}\mathit{in}\mathit{quartet})=\frac{\left(\begin{array}{c}\hfill 8\hfill \\ \hfill i\hfill \end{array}\right){\alpha }^i{(1-\alpha )}^{8-i}}{1-{(1-\alpha )}^8}=\frac{B(\alpha ;i)}{\sum _{i=1}^{8}B(\alpha ;i)}.$$ (1a)

Note that the expression B(α;i) is the probability density function, evaluated at i, 1≤ i ≤ 8, for a binomial distribution with constant success rate α in each of 8 independent events. Using basic probability theory, the quantity Pr(undetected errors | i errors in quartet) in formula (1) is calculated as

$$\text{Pr}(\mathit{undetected}\mathit{errors}\mid i\mathit{errors}\mathit{in}\mathit{quartet})=\sum _{M\in S}\text{Pr}(N_0\mid M,i)\text{Pr}(M),$$ (2)

where S is the set of all fifteen genotype quartets in the first column of Table 1, N₀ is the event that all errors in a quartet go undetected, Pr(N₀ |M,i) is the probability that i errors introduced into a genotype quartet M go undetected, and Pr(M) is the population frequency of the genotype quartet M. Pr (M) is calculated using the allele frequencies p for allele 1 and q (= 1 – p) for allele 2, assuming that the alleles are in Hardy-Weinberg equilibrium. For each genotype quartet M in Table 1, Pr(M) is calculated in Table 2. For each M and each i, the probability Pr(N₀ | M,i) is equal to the proportion of resulting quartets that, after i errors have been introduced, show consistency. For example, if M = (1/1, 1/1, 1/1, 1/1) and i = 1, Pr(N₀ | M,i) = 4/8, or 1/2; of the eight general quartets that result from a change in one of the alleles, a change in any of the four parental alleles will display consistency and a change in any of the children’s alleles will display inconsistency.

Table 2.

Conditional probability that a quartet M displays consistency if i errors are introduced, 1 ≤i ≤4

Quartet = M	Pr(M)	Pr(N0|M,i)
		i=1	i=2	i=3	i=4
(1/1, 1/1, 1/1, 1/1)	P4	1/2	5/7	4/7	16/35
(1/1, 1/2, 1/1, 1/1)	P3q	7/8	15/28	15/28	4/7
(1/1, 1/2, 1/1, 1/2)	2p3q	5/8	17/28	31/56	19/35
(1/1, 1/2, 1/2, 1/2)	p3q	5/8	17/28	4/7	18/35
(1/1, 2/2, 1/2, 1/2)	2p2q2	1/2	1/2	4/7	22/35
(1/2, 1/2, 1/1, 1/1)	1/4 p2q2	3/4	17/28	15/28	19/35
(1/2, 1/2, 1/1, 1/2)	p2q2	3/4	9/14	31/56	17/35
(1/2, 1/2, 1/1, 2/2)	1/2 p2q2	1/2	9/14	4/7	4/7
(1/2, 1/2, 1/2, 1/2)	p2q2	1	9/14	1/2	18/35
(1/2, 1/2, 1/2, 2/2)	p2q2	3/4	9/14	31/56	17/35
(1/2, 1/2, 2/2, 2/2)	1/4 p2q2	3/4	17/28	15/28	19/35
(1/2, 2/2, 1/2, 1/2)	pq3	5/8	17/28	4/7	18/35
(1/2, 2/2, 1/2, 2/2)	2pq3	5/8	17/28	31/56	19/35
(1/2, 2/2, 2/2, 2/2)	pq3	7/8	15/28	15/28	4/7
(2/2, 2/2, 2/2, 2/2)	q4	1/2	5/7	4/7	16/35

We now state some lemmas whose application simplifies the calculation of Pr(N₀ |M,i) for any of the fifteen genotype quartets M in Table 1 and any i, 0 ≤ i ≤ 8. These lemmas are extensions of ones proved previously¹⁴. The lemmas in that reference apply to genotype trios, and the lemmas below follow from the observation that two genotype trios may be uniquely formed (corresponding to the two children) from any genotype quartet. For example, the quartet (1/2, 1/2, 1/1, 2/2) maps uniquely to the set of genotype trios {(1/2, 1/2, 1/1), (1/2, 1/2, 2/2)}.

Lemma 1. For any genotype quartet M and for any i, 0 ≤ i ≤ 8,

Pr(N₀ |M,i) = Pr(N₀ |M,i).

Lemma 2. For any genotype quartet M and for any i, 0 ≤ i ≤ 8,

Pr(N₀ |M,i) = Pr(N₀ |M,8 - i).

Note that any quartet M falls uniquely into one of two categories: either M = M or not. There are exactly three quartets M such that M = M : (1/2, 1/2, 1/2, 1/2), (1/1, 2/2, 1/2, 1/2) and (1/2, 1/2, 1/1, 2/2). For the remaining twelve, we divide them into six genotype quartets and their conjugates, compute Pr(N₀ |M,i) for the six quartets, and use Lemma 1 to compute this probability for the remaining six. With this information, the value Pr(undetected errors|i errors in quartet) in formula (2) is calculated. Using Table 2, it follows:

$$\begin{array}{cc}\hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,1)\text{Pr}(M)=1∕2p^4+11∕4p^{3}q+33∕8p^2{q}^2+11∕4{\mathrm{pq}}^3+1∕2q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,2)\text{Pr}(M)=5∕7p^4+33∕14p^{3}q+199∕56p^2{q}^2+33∕14{\mathrm{pq}}^3+5∕7q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,3)\text{Pr}(M)=4∕7p^4+31∕14p^{3}q+185∕56p^2{q}^2+31∕14{\mathrm{pq}}^3+4∕7q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,4)\text{Pr}(M)=16∕35p^4+76∕35p^{3}q+33∕10p^2{q}^2+76∕35{\mathrm{pq}}^3+16∕35q^4.\hfill \end{array}$$ (2.2a)

Applying Lemma 2, we observe that

$$\begin{array}{cc}\hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,5)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,3)\text{Pr}(M),\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,6)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,2)\text{Pr}(M),\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,7)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,1)\text{Pr}(M).\hfill \end{array}$$ (2.2b)

Equations (2.2a) and (2.2b) are substituted into formula (2), which are then substituted into formula (1) along with the term Σ Pr(N₀ |M,8) Pr(M) = 1, to determine β. In Table 4, error-detection rates for various values of α and p are calculated, and in Figure 1, error-detection rates for a range of values of α and p are plotted. It follows immediately from equations (2.2a) and (2.2b) that the detection rate is symmetric about the line p = 0.5. This symmetry is seen in Figure 1 as well. Therefore, for a fixed value of α, the detection rate will be the same for frequencies p and 1 – p.

Table 4.

Detection Rate 1 - β for Trios, Quartets and Quintets with various values of true error rate α and various allele frequencies p at diallelic locus.

	Frequency p of one Quartets allele = .1			Frequency p of Quartets one allele = .5
True error rate	Trios*	Quintets	Quintets	Trios*	Quintets	Quintets
.0010	.3032	.4352	.5064	.2501	.3361	.3706
.0050	.3025	.4337	.5045	.2506	.3370	.3718
.0100	.3017	.4319	.5022	.2512	.3380	.3732
.0200	.3001	.4284	.4978	.2525	.3400	.3762
.0500	.2960	.4193	.4856	.2562	.3467	.3859
.1000	.2909	.4081	.4705	.2622	.3586	.4039
.2000	.2862	.4017	.4631	.2732	.3841	.4441
.3000	.2865	.4117	.4825	.2820	.4084	.4830

^*see Reference 14, Table 4

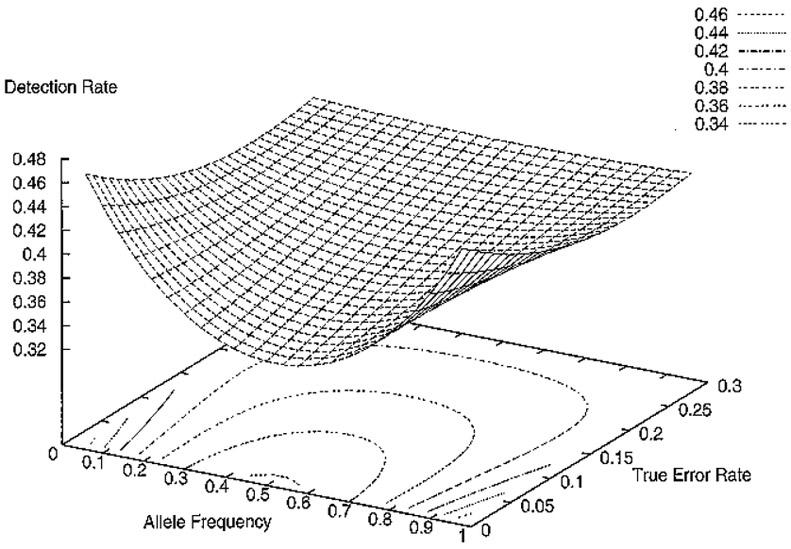
Figure 1.

Error-Detection Rate for quartets as function of allele frequency and true error rate

2.2. Detection Rate for Genotype Quintets

In the case where three offspring are available for study, definitions from the previous section are extended in the natural way to speak of genotype quintets, general quintets, conjugates and errors. The list of all genotype quintets may be found in Table 3. To compute β and the detection rate 1 - β for genotype quintets, we need only change the index in formulas (1) and (1a) so that the sum goes to 10 (corresponding to the 10 alleles in a genotype quintet). Also, in formula B(α; i) and in Lemmas 1 and 2, the value 10 is substituted for 8 everywhere. As above, extensions of Lemmas 1 and 2 are proved using the observation that any genotype quintet maps uniquely to a set of three genotype trios.

Table 3.

Conditional probability that a quintet M displays consistency if i errors are introduced, 1 ≤i ≤ 5

Quintet = M	Pr(M)			Pr(N0|M,i)
		i=1	i=2	i=3	i=4	i=5
(1/1, 1/1, 1/1, 1/1, 1/1)	P4	2/5	28/45	3/5	46/105	8/21
(1/1, 1/2, 1/1, 1/1, 1/1)	1/2 p3q	9/10	3/5	29/60	16/35	3/7
(1/1, 1/2, 1/1, 1/1, 1/2)	3/2 p3q	7/10	5/9	59/120	19/42	29/63
(1/1, 1/2, 1/1, 1/2, 1/2)	3/2 p3q	3/5	8/15	59/120	33/70	28/63
(1/1, 1/2, 1/2, 1/2, 1/2)	1/2 p3q	3/5	8/15	61/120	16/35	19/42
(1/1, 2/2, 1/2, 1/2, 1/2)	2 p2q2	2/5	19/45	13/30	52/105	65/126
(1/2, 1/2, 1/1, 1/1, 1/1)	1/16 p2q2	4/5	2/3	29/60	3/7	29/63
(1/2, 1/2, 1/1, 1/1, 1/2)	3/8 p2q2	4/5	3/5	61/120	16/35	26/63
(1/2, 1/2, 1/1, 1/1, 2/2)	3/16 p2q2	3/5	7/15	29/60	33/70	10/21
(1/2, 1/2, 1/1, 1/2, 1/2)	3/4 p2q2	4/5	31/45	31/60	91/210	3/7
(1/2, 1/2, 1/1, 1/2, 2/2)	3/4 p2q2	3/5	29/45	1/2	7/15	55/126
(1/2, 1/2, 1/1, 2/2, 2/2)	3/16 p2q2	3/5	7/15	29/60	33/70	10/21
(1/2, 1/2, 1/2, 1/2, 1/2)	1/2 p2q2	1	31/45	1/2	46/105	56/126
(1/2, 1/2, 1/2, 1/2, 2/2)	3/4 p2q2	4/5	31/45	31/60	91/210	3/7
(1/2, 1/2, 1/2, 2/2, 2/2)	3/8 p2q2	4/5	3/5	61/120	16/35	26/63
(1/2, 1/2, 2/2, 2/2, 2/2)	1/16 p2q2	4/5	2/3	29/60	3/7	29/63
(1/2, 2/2, 1/2, 1/2, 1/2)	1/2 pq3	3/5	8/15	61/120	16/35	19/42
(1/2, 2/2, 1/2, 1/2, 2/2)	3/2 pq3	3/5	8/15	59/120	33/70	28/63
(1/2, 2/2, 1/2, 2/2, 2/2)	3/2 pq3	7/10	5/9	59/120	19/42	29/63
(1/2, 2/2, 2/2, 2/2, 2/2)	1/2 pq3	9/10	3/5	29/60	16/35	3/7
(2/2, 2/2, 2/2, 2/2, 2/2)	q4	2/5	28/45	3/5	46/105	8/21

Proceeding as above and using the quantities from Table 3, we compute:

$$\begin{array}{cc}\hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,1)\text{Pr}(M)=2∕5p^4+27∕10p^{3}q+155∕40p^2{q}^2+27∕10{\mathrm{pq}}^3+2∕5q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,2)\text{Pr}(M)=28∕45p^4+11∕5p^{3}q+1229∕360p^2{q}^2+11∕5{\mathrm{pq}}^3+28∕45q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,3)\text{Pr}(M)=3∕5p^4+473∕240p^{3}q+1387∕480p^2{q}^2+473∕240{\mathrm{pq}}^3+3∕5q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,4)\text{Pr}(M)=46∕105p^4+129∕70p^{3}q+935∕336p^2{q}^2+129∕70{\mathrm{pq}}^3+46∕105q^4,\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,5)\text{Pr}(M)=8∕21p^4+151∕84p^{3}q+349∕126p^2{q}^2+151∕84{\mathrm{pq}}^3+8∕21q^4.\hfill \end{array}$$ (2.3a)

As above, note that

$$\begin{array}{cc}\hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,6)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,4)\text{Pr}(M),\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,7)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,3)\text{Pr}(M),\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,8)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,2)\text{Pr}(M),\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M,9)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,1)\text{Pr}(M),\hfill \\ \hfill & \mathrm{\Sigma }\text{Pr}(N_0\mid M10)\text{Pr}(M)=\mathrm{\Sigma }\text{Pr}(N_0\mid M,0)\text{Pr}(M)=1.\hfill \end{array}$$ (2.3b)

These equations are used to compute the detection rate for any randomly selected genotype quintet from a population in Hardy-Weinberg equilibrium. As in the case of genotype trios¹⁴ and genotype quartets above, the detection rate 1 - β is symmetric about the line p = 0.5. In Table 4, error-detection rates for various values of α and p are presented. In Figure 2, error-detection rates for a range of values of α and p are plotted.

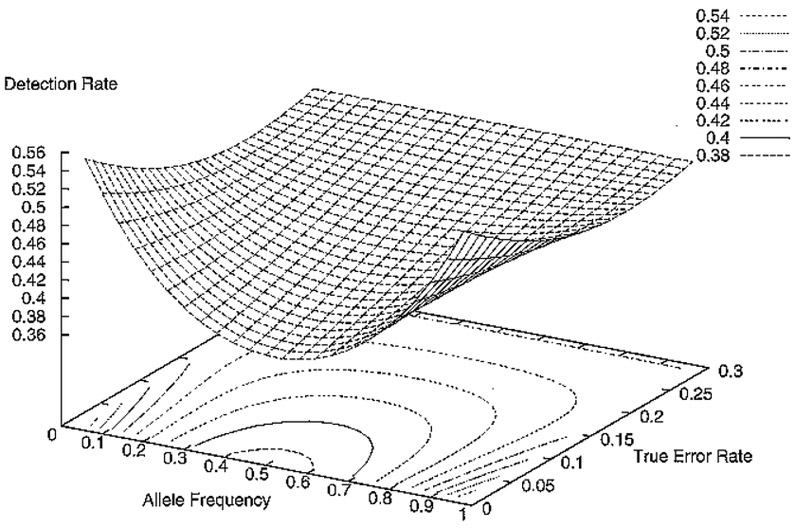
Figure 2.

Error-Detection Rate for quintets as function of allele frequency and true error rate

3. Results

In Table 4, error-detection rates for various error rates and allele frequencies when typing genotype trios (one child), quartets, and quintets are presented. Detection rates for trios were presented previously¹⁴. The main result is that typing additional siblings increases the detection rate by at least 9%. By computing the average detection rate for each sampling type (trio, quartet, and quintet), it may be seen that typing quartets or quintets increases the detection rate on average by 13% or 19% respectively when one allele frequency is 0.1. For equal allele frequencies, the change in sampling types increases the detection rate on average by 10% and 14% respectively.

This increase in detection rate holds for all error rates and allele frequencies. These results are displayed in Figures 1 and 2, which plot the detection rates for a range of true error rates from 1% to 30% and for allele frequencies (one allele) from 0.02 to 0.98. Note that detection rates are symmetric about the plane p = 0.5.

The second result is that, independent of the sampling type, detection rates are always the lowest when allele frequencies are equal (see Figures 1 and 2). However, the graphs indicate that the detection rates converge to a common detection rate, independent of allele frequencies, as the true error increases. This result holds for all sampling types.

At low error rates, a significant difference is observed between detection rates for extreme allele frequencies (one allele has frequency ≤ 0.05) and equal allele frequencies, regardless of the sampling type. To explain this observation, consider genotype quartets. When allele frequencies are extreme, then the majority of quartets sampled will have both parents homozygous for the same allele. Without loss of generality, let us assume that the 1 allele at a SNP locus has allele frequency greater than 0.95. Then the majority of the quartets are of the form M = (1/1, 1/1, 1/1, 1/1). When error rates are very low, the majority of quartets with errors will have only one error introduced. A way to reach this conclusion quantitatively is to evaluate formula (1a) for small values of α. When i in formula (1a) is greater than 1, the probability is approximately 0. It follows that the detection rate for extreme allele frequencies and small true error rates is approximately 1 - Pr(N₀| M,1) = 1 – 1/2 = 1/2, or 0.50 (Table 2).

By comparison, for the case of equal allele frequencies, all genotype quartets M appear with probability Pr(M) >> 0 (Table 2). When α is small, the detection rate is approximately 1 - Σ Pr(N₀ |M,1) Pr(M). Note that Pr(N₀ |M,1) > 1/2 for all genotype quartets M, with the exception of the quartets (1/1, 1/1, 1/1, 1/1) and (2/2, 2/2, 2/2, 2/2), and for the quartet M = (1/2, 1/2, 1/2, 1/2), Pr(N₀ |M,1) = 1, so that in computing the sum, the detection rate for equal allele frequencies is considerably less than 0.5. The same reasoning applies for trios and quintets.

4. Discussion

In this article, an analytic solution to SNP error-detection rates in nuclear families is provided. For quartets (two sibs) or quintets (three sibs), the detection rate is quantified as a function of the true error rate at a SNP locus in Hardy-Weinberg equilibrium and the allele frequency of one of the alleles. It is shown in our analysis that genotyping at least two additional siblings, when available, provides a considerable improvement in error-detection rates, on the order of 14%-19%. The authors therefore recommend that researchers who are analyzing SNP data consider results of these formulas (Table 4) when designing linkage and association studies.

There is an added benefit to genotyping additional siblings, even if unaffected. Such siblings can provide information for linkage studies. For example, in studying quantitative phenotypes with a recurrence risk of 75%, Risch and Zhang¹⁵ showed that extreme discordant sib-pairs may provide a significant amount of linkage information.

In addition, genotyping additional siblings, even if unaffected, is typically much less expensive than ascertaining an additional family with an affected child. While it is true that collection of additional families increases power to detect linkage in the presence of association, allowing errors to go undetected in pedigree data can reduce power to detect that linkage⁹, potentially negating the effects of the additionally ascertained families. Also, errors in data can make statistical tests like the TDT invalid by increasing the type I error rate¹⁶.

It is important to recognize that our formulas calculate the probability that a family is brought to the researcher’s attention because of inconsistency. Our method does not suggest the most likely location of the error. Ehm et al.¹¹ presents a likelihood method for determining typing errors in pedigree data displaying consistency, while other authors^{12, 13} present methods for determining (statistically) incorrect genotypes in pedigree data displaying inconsistency. These methods are implemented in freeware programs (see Electronic Database Information).

Regarding ascertainment, we assume that the locus studied is in Hardy-Weinberg equilibrium. However, for most studies, families are ascertained on the basis of disease. While it is true that the detection rates for SNP loci in linkage disequilibrium with a disease locus will differ from the results presented in Table 4, our recommendations regarding genotyping of additional siblings are still relevant. As previously shown¹⁴, for low error rates there is a theoretical maximum error-detection rate of 33% when sampling trios, independent of linkage disequilibrium between marker and locus, ascertainment scheme, or allele frequencies at the marker locus. This detection rate can be improved only by genotyping additional siblings, if consistency is used as the sole check for errors.