An Efficient Implementation of Deep Convolutional Neural Networks for MRI Segmentation

Abstract

Image segmentation is one of the most common steps in digital image processing, classifying a digital image into different segments. The main goal of this paper is to segment brain tumors in magnetic resonance images (MRI) using deep learning. Tumors having different shapes, sizes, brightness and textures can appear anywhere in the brain. These complexities are the reasons to choose a high-capacity Deep Convolutional Neural Network (DCNN) containing more than one layer. The proposed DCNN contains two parts: architecture and learning algorithms. The architecture and the learning algorithms are used to design a network model and to optimize parameters for the network training phase, respectively. The architecture contains five convolutional layers, all using 3 × 3 kernels, and one fully connected layer. Due to the advantage of using small kernels with fold, it allows making the effect of larger kernels with smaller number of parameters and fewer computations. Using the Dice Similarity Coefficient metric, we report accuracy results on the BRATS 2016, brain tumor segmentation challenge dataset, for the complete, core, and enhancing regions as 0.90, 0.85, and 0.84 respectively. The learning algorithm includes the task-level parallelism. All the pixels of an MR image are classified using a patch-based approach for segmentation. We attain a good performance and the experimental results show that the proposed DCNN increases the segmentation accuracy compared to previous techniques.

Introduction

Image processing is one the most important achievements and commonly used engineering techniques in all areas of science, including medical science that nowadays severely has eclipsed diagnosis and treatment of any diseases. For partitioning an image into multiple segments, the method of image segmentation can be used [1]. It is used in different applications such as medical image processing, especially in magnetic resonance imaging (MRI) [2]. MRI is one of the common methods for diagnosing brain tumors. Although surgery is the main solution, in cases where physical activity is not possible, radiation therapy and chemotherapy could help too. Since MRI compared to other diagnostic modalities (radiography, computerized tomography (CT) scan, etc.) is safe and non-invasive, and on the other hand reflects the true dimensions of organ, its use in imaging of the brain is widely considered. The most important considered characteristic in precise processing of MR images is determination and separation of borders and the edge of normal and abnormal tissues from each other. Different algorithms have been proposed for segmentation and invented which are able to identify the anatomical structure of the human body, especially the brain more precisely. For clinical purposes, medical imaging is used as a method for creating visual images of the interior of a body [3]. Medical imaging includes methods such as ionizing radiation, non-ionizing radiation, and nuclear radiation [4]. Nowadays, MRI as a non-ionizing radiation method is used commonly for the diagnosis of brain tumors [5]. Since MRI is non-invasive in comparison with other diagnostic methods (radiography, CT scan, etc.), reflects the exact dimension of the organ, its application in brain imaging has attracted considerable attention [6]. A glioma, as a type of tumor, is the most common brain tumor. Life expectancy is several years with low-grade gliomas and a maximum of 2 years with high-grade gliomas. Although some types of tumors such as meningioma can be segmented easily, some other types such as glioma and glioblastoma cannot be easily located. The images of these tumors and their edema are often spread with a low contrast and Y-shape. In addition, these tumors may be anywhere in the brain, with any shape and size [7]. Since glioblastoma tumors tend to spread, the boundaries are often fuzzy and difficult to separate from healthy tissues. To solve this problem, several isotope simultaneous MR images are used with different modalities. As the analysis of MR images is complex and time-consuming, it is indispensable to have a smart system helping doctors in this regard [8].

Algorithms for medical images segmentation are divided into three categories: the first category includes low-level techniques like application of region growing and intensity thresholds; the second category is determined using optimization techniques and uncertainty models. Third category has a higher-level knowledge like priori information about the segmentation process [9–11]. Deep Convolution Neural Network (DCNN) has been widely used in the third category. Although, various algorithms for segmentation have been developed and proposed, finding a suitable algorithm for medical image segmentation is a challenging task. This is due to noise, low contrast, and steep light variations of medical images. Tumor segmentation in MR images should be time-consuming, requiring a considerable amount of memory to segment large data. The main feature considered in the detailed processing of MR images is the segmentation and separation of the boundaries and edges of natural and non-natural tissues.

The main goal of this paper is to design and to implement a DCNN towards fast and accurate segmentation of brain MR images. In machine learning, a Convolution Neural Networks (CNN) is a type of feed-forward artificial neural network in which the pattern of binding between neurons is inspired by the mammal’s visual cortex [12]. DCNNs are a class of CNN used as a powerful tool to help to solve visual classification problems [13, 14]. The proposed DCNN includes five convolutional layers and one fully connected layer in the output. Each convolutional layer itself consists of the convolutional, pooling, and Rectified Linear Unit (ReLU). The last fully connected layer is used with a softmax classifier for the output classification. Basically, every convolution, pooling, and nonlinear operator reduces the number of features leading to a set of useful features from the image. In each layer, higher-level features are produced in comparison to the previous layer. It should be noted that if the nature of the task involved requires location information to be preserved, the pooling results in under fitting. Furthermore, in cases where it is necessary to establish a semantic relationship between two extremely distant regions in the image, the convolution imposes an incorrect prior assumption. In this paper, the overlapping pooling strategy and randomly nonlinear functions were used to enhance the segmentation accuracy in the proposed DCNN compared to other related works. In order to improve image segmentation performance, Graphic Processing Unit (GPU) hardware cores and the task-level parallelism approaches in the Caffe [15] utility were used.

This paper is organized as follows. Section 2 describes some of the conducted related works. In “The Proposed DCNN” section, the paper methodology is presented. The “Experimental Results” section expounds the experimental result. Finally, the “Conclusions” section presents conclusions and future works.

Deep Convolution Neural Network and Related Works

In this section, a brief description of DCNN and some related works are presented.

Deep Convolution Neural Network

The DCNNs are based on convolution. The convolution solves the problem of having many parameters in neural networks using sparse connections [16]. Basically, learning-based methods are either discriminative or generative. The discriminative methods do not require prior knowledge in learning, such as neural network, while generative type is based on prior knowledge in learning [17]. DCNNs are kinds of CNN consisting of multiple layers of convolutions. Each layer in the DCNN performs a simple computational operation such as a weighted sum. Unlike neural networks where each layer is connected to all previous layers, in the DCNN, each layer grid is connected to only a limited number of layers. In artificial neural networks, the network architecture is such that the neurons of each layer can be paralleled, but the successive layers must be serially executed by the CPU memory. In the DCNN, the entire network can be put into the GPU memory and the hardware cores can be used to boost network speed using deep learning tools. Due to the overlapping of neighbor layers, local correlation is used in such networks, and multiple and unique features are detected by weighing the layers in each sub-layer.

Related Work

In a CNN model, there are two nesting windows with different dimensions, that the pixels of the internal windows are labeled using the external window. The size of the windows is set in such a way that it leads to optimal results [18]. In a DCNN model, the combination of convolutional network and graphical model was used to segment the MR images. Graphical models were added for the lack of label locality in the output of the convolutional model [19]. The preliminary estimation of the fragmentation was obtained in other architectures using the CNN in the first stage, and it was added to the CNN in the second stage as input [20]. In addition to brain imaging, a full convolution method was used [21], acting independently of the input image size. Different from the architecture conventionally applied in computer vision, a new CNN architecture was presented. It benefits simultaneously both local and global contextual features. In addition, this network uses a fully connected layer as a conventional implementation, different from most traditional CNNs applications, allowing increase in speed up to 40-fold. A two-phase training procedure was also described allowing tackling the difficulties relevant to the tumor labels imbalance. At last, cascade architecture was explored in which a basic CNN output as a traditional information source is treated for a next CNN. Based on successful techniques in-depth learning, a new method for the segmentation of the brain tumor using Fully Convolutional Neural Networks (FCNNs) and Conditional Random Fields (CRFs) is proposed. In a coherent framework, in order to obtain the results of segmentation, they created spatial and apparent stability. Results showed that the first position with the Dice Similarity Coefficient metric was 0.80 for complete, 0.69 for core, and 0.61 for enhancing regions on BRATS 2015¹ [22]. A new approach for segmentation is proposed using the combination of Neural Network Abstraction Abilities. This method is based on the Hough vote, which is a strategy that allows for fully automated localization and segmentation of the anatomy desired. This approach not only uses the results of the CNN classification but also performs voting by discovering the features produced by the deepest segment of the network [23]. In brief, a multipath architecture was used and windows with different dimensions and locality degrees produced different map features that were connected to each other before the output layer. Results showed that the first position with the Dice Similarity Coefficient metric was 0.88 for complete, 0.79 for core, and 0.73 for enhancing regions on BRATS 2013² [24, 25]. An automatic CNN-based segmentation method was proposed, exploring small 3 × 3 kernels in convolutional layer. The intensity normalization application was investigated as a processing phase not routine in the techniques of CNN-based segmentation. The proposed method was validated in BRATS 2013, achieving the first position simultaneously considering the Dice Similarity Coefficients metric of 0.88 for complete, 0.83 for core, and 0.77 for enhancing regions. Furthermore, using the platform of online evaluation, the overall first position was obtained. By applying the same model, it participated also in the challenge of on-site BRATS 2015, and achieved the second place considering the Dice Similarity Coefficient metric of 0.78, 0.65, and 0.75 for the complete, core, and enhancing regions, respectively [26]. A local structure prediction approach was applied for 3D segmentation tasks, and a method of local structure approach was applied which evaluated systematically the various parameters related to the anatomical structures dense annotation. In learning algorithm, a CNN is used which is known suitable for addressing the correlation between features. In the architectural model, local structural estimation and correlation between neighbors, the labels of pixels were used for the segmentation of brain MR images. This model used k means clustering to create a dictionary of image patches. Finally, the method was evaluated on the public BRATS 2014³ dataset with three multimodal segmentation tasks, resulting in obtaining the first position with the Dice Similarity Coefficient metric, 0.84 for complete, 0.75 for core, and 0.76 for enhancing regions [27]. We already used the data-level parallelism for fuzzy inference system and the results showed that the performance improved for different image sizes [28]. In addition, we can choose parallel-based fuzzy C means clustering as the objective function and combining it with watershed algorithm to improve the performance of fuzzy C means clustering [29]. Even if for improving breast cancer detection accuracy, we proposed Modified Fuzzy Logic (MFL) then improving the performance of MFL algorithm using GPU platform [30]. GPU hardware cores and the task-level parallelism approaches in the Caffe utility were used to improve the performance of training time. Therefore, the main limitation to each packet size is the amount of the GPU memory as well as larger memories and packages. While the accuracy of these recent studies have had a lot of improvement over the conventional methods of the past, it is important to further improve the performance and optimize the training process.

The Proposed DCNN

In the DCNNs, it is possible to obtain suitable results by increasing the convolutional layers and deepening the network using precise measures such as weight decay, dropout, and pooling. Pooling is used to discard low-value data and reduce dimensions in the DCNNs. It examines the neighbor layers’ activations and considers a maximum or a mean value as the representative of each neighbor. At the final layer of the DCNNs, a fully connected layer obtained based on high-value features is usually used for classifying. The number of network output layers is equal to the number of classes needed to be identified. The proposed DCNN includes two parts: architecture and a learning algorithm. The architecture is used to design a network model and the learning algorithm is used to optimize the calculated parameters in the network training phase.

Proposed Architecture

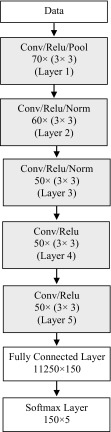
The architecture of the proposed DCNN consists of five convolutional layers with 3 ×3 windows and one fully connected layer in the output which is defined in Fig. 1. This decision has been made according to the number of data available and the conducted tests. In the training process, the number of neurons in each layer is 70, 60, 50, 50, and 50. The size of batches referring to the number of training data for updating in the optimization process was 256 with eight epochs. In the first layer of the architecture, pooling is used to maintain useful information. In the second and third layers, the normalization operation is performed online to improve the performance of the learning algorithm. Neurons in all convolutional layers are directly connected to the previous layers. Output neurons in the last convolutional layer are connected to a softmax layer. A softmax layer is finally added to the model in order to create five output classes and define the target function. This layer divides each voxel (volume pixel) into five output classes.

Fig. 1.

The proposed DCNN architecture

Proposed Learning Algorithm

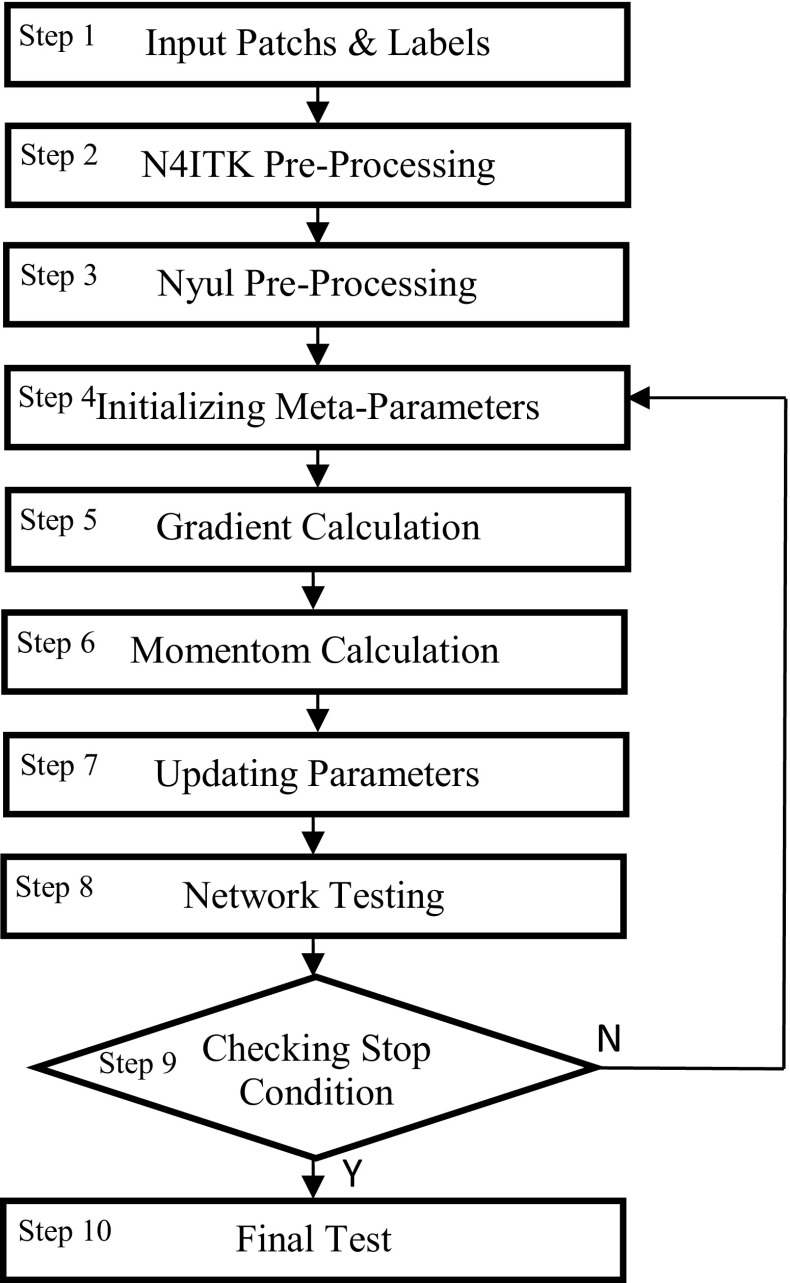
The DCNN model consists of architecture for the structure and arrangement of model components introduced in last section, and a learning algorithm for adjustable parameters. The learning algorithm is depicted in Fig. 2.

Fig. 2.

The proposed learning algorithm for DCNN

In the learning algorithms, the methods used commonly to obtain optimal parameters are gradient-based methods. In this method, the cost function moves in the parameter space to search for optimal values. In order to find the optimal values of the model parameters, the combination of methods was used, including Momentum [31], Nestrov [32], and Adam [33]. Therefore, the strengths of each method can be used simultaneously. Parameters that are fixed during training process are called hyper-parameters. Different values in hyper-parameter space is selected using random search checked using cross validation. The best result are used to train the model for getting the final results. The learning algorithm consists of ten steps that are described as follows.

1. Step 1, Input Patches and Labels: In order to compile the dataset for our DCNN, data augmentation technique was used for input images. To prepare the input dataset, the tumor pixels as one among two and the healthy pixels as one among three were selected with their related labels. Then, it moved voxel to voxel in the input four-layered MR image, and the 32 × 32 pixels were extracted and used to input data into the Caffe.

2. Step 2, N4ITK Pre-processing: The N4ITK bias correction was used for non-uniformity correction due to magnetic field changes.

3. Step 3, Nyul Pre-processing: Nyul’s lighting normalization was used for intensity normalization throughout the image.

4. Step 4, Initializing Meta-parameters: The model meta-parameters such as learning rate, momentum coefficient, and the coefficient of variation were initialized after performing N4ITK and Nyul pre-processing on the input images.

5. Step 5, Gradient Calculation: The network cost function was calculated based on the input training data patches (small packages). The output of the network reaches the expected value by using gradient-based optimization methods through multiple iterations. In order to obtain the cost function, the cross entropy between the softmax output and the given output was calculated and then maximized by changing the parameters.

6. Step 6, Momentum Calculation: Momentum calculation was used to accelerate the learning process, especially in the face of extreme curvature surfaces and noise gradients. In this step of the gradients in the previous steps, the running average was taken with a damping and the motion continued in this direction.

7. Step 7, Updating Parameters: In this step, graded gradients were updated as model parameters. Each parameter has its own learning rate. Therefore, the learning rate for parameters with a large partial derivative history was rapidly reduced and minimal reductions were observed for parameters with a small partial derivative record. Overall, the algorithm finds better calibration speeds when faced with gentle slope directions

8. Step 8, Network Testing: The data were mixed and 75% were used for training, 15% for validation and 10% for testing. After the formation of the DCNN and preparation of the expected input and output data, it is necessary to test the network.

9. Step 9, Checking Stop Condition: The vector of network parameters was updated as gradient descent. In addition, the global learning rate was reduced according to a schedule.

10. Step 10, Final Test: Final test has done in this step. There should be a continuous monitoring of the model performance accuracy for validation data, and the training process is terminated in order to prevent over-fitting, if the accuracy is not improved by an epoch. It is noteworthy that the convergence rate increases by 10% when calculating the gradient for a class using the GPU and task-level parallelism.

Experimental Results

In this section, evaluation of the proposed DCNN architecture and learning algorithm are presented.

Number of Layers, Kernels, and Neurons

At first, three convolutional layers and one fully connected layer were chosen for the proposed network architecture. Increasing convolutional layers led to change in Dice Similarity Coefficient metric. In the experimental results, we increased and decreased the number of convolutions and trained the model again. The results are presented in Table 1. Increasing the number of convolutions causes the model Dice Similarity Coefficient metric to drop because of over fitting. Also, a decrease of the number of convolutions causes the model Dice Similarity Coefficient metric to drop because of the decrease in expressive power of the model. On the other hand, increasing number of layers have no tangible changes in the results, this may be because of the size of input patches and the amount of their information content. And finally, decreasing number of layers causes the expressive power of the model to decrease, that in turn causes a drop in Dice Similarity Coefficient metric. Due to the five convolutional layers, the model accuracy for the input images was improved up to 0.90, 0.85, and 0.84 for complete, core, and enhancing regions. In the experiments, the efficient number of parameters equals five convolutional layers and one fully connected layer. The accuracy remained constant after increasing the layers. There was no change in the Dice Similarity Coefficient metric of the network performance after increasing the fully connected layers. After conducting the tests, the pooling layer was proved to be useful in the first convolutional layer and subsequent layers. In the first layer, useful information is maintained due to the overlapping of the convolutional layers.

Table 1.

The results of increasing and decreasing of convolutions

The action	Dice Similarity Coefficient metric
	Complete	Core	Enhancing regions
The base model	0.90	0.85	0.84
10% increase of number of convolutions	0.84	0.83	0.81
10% decrease of number of convolutions	0.88	0.80	0.79

The most informative features are extracted through five layers of convolution and nonlinearity in the network. Low-level features are extracted using initial layer and high-level features are extracted using deeper layers. The number of neurons in each convolution layer depends on two factors. The first factor is the size of kernel of convolution that in turn depends on width, height, and number of kernels in previous layer. The second factor is the number of kernels in present layer. The kernels dimensions are three in DCNN design. On the other hand, the number of kernels in our design follows the best practice in deep networks that says by going deeper in the network, the size of feature maps are decreased and the number of kernels are increased. The important point here is that because of memory and computational constraints and threat of over fitting, the number of kernels cannot be increased more than a limit that is usually obtained through cross validation. Softmax layer is a generalized logistic regression that can support multiple classes directly, without having to train and combine multiple binary classifiers. The idea is quite simple: when given an instance x, the Softmax regression model first computes a score for each class k, then estimates the probability of each class by applying the Softmax function to the scores. The scores here is the outputs of DCNN just before the Softmax layer computes the exponential of every score, and divides the results by the sum of all the exponentials. In this way, the output of Softmax layer is between 0 and 1 and can be interpreted as an estimation of the probability that the instance belongs to each classes. This instance calculated using Equation (1) which K is the number of classes and s(x) is a vector containing the scores of each class for the instance x. σ(s(x))_k is the estimated probability that the instance x belongs to class k given the scores of each class for that instance.

$${\widehat{p}}_k=\sigma {\left(s\left(\mathbf{x}\right)\right)}_k=\frac{e^{-s_k\left(\mathbf{x}\right)}}{{\sum }_{i=1}^K{e}^{-s_i\left(\mathbf{x}\right)}}$$ 1

A 5 × 5 and a 7 × 7 convolutions can be constructed by two and three consecutive 3 × 3 convolutions, respectively. 3 × 3 kernels were used in all of the convolutional layers. In the test conducted by increasing kernel dimensions to 5 × 5 or 7 × 7, the model Dice Similarity Coefficient metric was reduced. This decision was made due to the relatively large number of parameters available compared to the available data. Each convolution with a 3 × 3 kernel covers a 3 × 3 window of input image pixels, which is named as the receptive field. By sequencing convolutions, the receptive field gradually increases so that two pixels add in each layer of each dimension to the receptive field. In this way, we have a five convolutional network with a receptive field 3 + 2 × 4 = 11. The experimental result shows this receptive field is sufficient to detect the tumor area in MR images.

When the kernel size is multiplied by two, the number of neurons of the kernel is multiplied by four. So the computational complexity of the training and inference time are proportional to square of kernel size. To calculate dice similarity, we calculate model prediction that can be obtained using inference. So dice similarity computation complexity is proportional to square of kernel size. The smaller the dimensions of the kernels, the smaller the numbers of parameters, preventing over-fitting. In addition, another advantage of using small kernels is to reduce the computational load time.

By increasing the number of neurons to 25, the Dice Similarity Coefficient metric of the model reaches 0/75. Given the number 50 for neurons in all layers, Dice Similarity Coefficient metric is obtained at 0/80. Due to the lower number of parameters in the last three layers, the reduction of neurons in these layers leads to a change in efficiency. The number of neurons in the convolutional layers are 70, 60, 50, 50, and 50, and the number of neurons in the fully connected layer is equal to 11,250 × 150. The results were obtained without the precise adjustment of the meta-parameters. At first, number of neurons for all layers were fixed 70. As the number of neurons increases, no appreciable change occurs in the accuracy of the model, and only the computational load time increases. Because of the lower number of parameters in the last three layers, decreasing neurons in these layers led to efficient change in accuracy. In order to prevent the saturation of the neurons and accelerate the updating of the parameters, ReLU was used in all layers. In addition, to prevent the synchronization of neurons and to create an implicit hybrid classification, the dropout technique was employed.

Batch and Epoch Sizes

The batch size refers to the number of training data for an update in the optimization process. The size selection directly affects the computational cost and the update uncertainty. In the case of using smaller batches, more noise would be created, but when the error function has many local minimums, the presence of noise on the gradient prevents the algorithm from being stuck in shallow regions. On the other hand, large batches cause more operations in parallel, helping to improve convergence speed. Therefore, in order to obtain the optimal batch size, a balance must be created. In the present study, the optimal size was 256.

In the network training, the number of epochs was eight, since the network accuracy does not change with an increased number. By finalizing the meta-parameters on the input images and recording the network performance accuracy in the training procedure, the cost function is illustrated in Fig. 3. As can be observed, the network cost at the end of the 7th epoch after 7000 iterations decreased, and no change occurred after that and the cost remained constant.

Fig. 3.

The cost function of the model in the training procedure

Datasets and Evaluation Criteria

The data used in the study were extracted from the BRATS 2016⁴ Challenge, including four MRI modalities named spin-lattice relaxation (T1), spin-spin relaxation (T2), spin-lattice relaxation contrasted (T1c), and attenuation inversion recovery (FLAIR). The dataset consists of 230 brain images and 448,000 patches of size 32 × 32 are extracted random from the dataset that each patch has label of the central pixel of extracted patch. So the training data of the proposed DCNN consist of 448,000 patches and their corresponding labels. In this way, if the batch size is 256 the number of iteration per each epoch will be 1750. In order to prevent over-fitting in the learning of multi-million parameters of this network, the data augmentation technique was used in the dataset. In the existing training DCNNs, there are usually three input channels requiring the adjustment of meta-parameters such as learning rate, small size of batches, and weight decay rate. However, the input images in this model are four-channel. Finally, the proposed DCNN classifies each voxel according to a dangerous level in five different classes. The classes are shown in the following order based on the dangerous level in different colors, respectively:

• Normal Tissue (gray)

• Edema (green)

• Non-enhanced tumor (blue)

• Necrosis (red)

• Enhanced tumor (yellow).

For each class, there are two binary maps, one obtained by the model (P) and the other by the consensus of experts (T) available in the dataset. Therefore, the Dice Similarity Coefficient metric is calculated according to Eq. (2) using the model output. In other words, this metric is the ratio of the overlapping region to the average region specified by the model and the expert. The criterion of correctness for segmentation of MR images usually is presented as dice similarity. But to calculate the accuracy, Eq. (3) can be used. In the Dice Similarity Coefficient metric, P represents the model predictions, T represents the ground truth labels, and A is all the binary map. By using 2-norm in calculating the moment and applying the Nesterov technique in calculating the gradient resulted in the best outcomes, indeed accuracy of 91.1 percentage.

$$\text{Dice}\left(\mathrm{P},\mathrm{T}\right)=\frac{\left|\mathrm{P}\bigwedge \mathrm{T}\right|}{\left(\left|\mathrm{P}\right|+\left|\mathrm{T}\right|\right)/2}$$ 2

$$\text{Accuracy of proposed learning algorithm}\left(\mathrm{P},\mathrm{T}\right)=\frac{\left|\mathrm{P}\bigwedge \mathrm{T}\right|+\left|\left(\mathrm{A}-\mathrm{P}\right)\bigwedge \left(\mathrm{A}-\mathrm{T}\right)\right|}{\left|\mathrm{A}\right|}$$ 3

Platform and Results

With regard to the considerable training time in most related works, we used GPU hardware to reduce this time. The experimental platform based on NVIDIA GeForce series GeForce GTX 1080 Ti with 11G RAM, 4584 cores and Linux Ubuntu operating system were used in the experiment. Deep learning tools with task-level parallelism in the Caffe have been used, reducing the training time from 168 to 110 h. Task-level parallelism caused the nodes existing in each layer to be formed as patches with the dimensions of 32 × 32, considered as the network input.

Table 2 depicts the accuracy of the Dice Similarity Coefficient metric for the complete, core, and enhancing areas on the image dataset of BRATS using the proposed DCNN in comparison to some related works. As the table’s last row reveals the proposed DCNN, accuracy is more than other previous techniques.

Table 2.

The comparison of the measured accuracy of the proposed DCNN with some related works for MRI segmentation

Reference	Dataset (http://www.braintumorsegmentation.org/)	Dice Similarity Coefficient metric			Methods
		Complete	Core	Enhancing regions
[22]	BRATS 2015	0.80	0.69	0.61	Back propagation algorithm
[24, 25]	BRATS 2013	0.88	0.79	0.73	Parallel path + two-stage learning and architecture
[26]	BRATS 2013	0.88	0.83	0.77	3 × 3 kernels and ReLU functions with leakage
	BRATS 2015	0.78	0.65	0.75
[27]	BRATS 2014	0.84	0.75	0.76	Local structural estimation +K means clustering
#	BRATS 2016	0.90	0.85	0.84	The proposed DCNN

The results in Table 2 compare Dice Similarity Coefficient metric in complete, core, and enhancing regions. As can be seen, the proposed DCNN provides better results for complete, core, and enhancing regions. This is because in the proposed DCNN, only one pooling layer is used and normalization layers are used in second and third layers. This helps the learned features in middle layers be approximately independent of each other and be more informative.

Table 3 depicts some MR images of four different modalities (a) T1, (b) T2, (c) T1c, and (d) FLAIR and outputs of the segmented class in e column. The results in e (output) column of Table 3 show that the other regions are surrounded by non-enhancing core that is shown in blue. Also necrosis is central and other regions grow around it.

Table 3.

Some MR images of four different modalities (a) T1, (b) T2, (c) T1c, and (d) FLAIR and outputs of the segmented class in e column

Table 4 presents the confusion matrix showing the results of this phase. As a particular table layout, confusion matrix allows performance visualization of a supervised learning algorithm. The instance in each actual class is represented by each row, and the instance in a predicted class is represented by each column of the matrix. Specifically, in this application, there are five rows and columns that represent different substructures of glioma namely normal tissue (0), edema (1), non-enhancing core (2), necrotic (3), and enhancing core (4). The confusion matrix summarizes the results of testing the proposed DCNN. In other words, each pixel in a volume should be classified to one of the five labels and according to the result; the number in corresponding column is incremented by one.

Table 4.

The confusion matrix for the classification of the center points of MR image segments

Actual	Normal tissue	Edema	Non-enhanced tumor	Necrosis	Enhanced tumor
Predicted
Normal tissue	52,355	5	361	76	227
Edema	13	6013	98	215	931
Non-enhanced tumor	1360	101	42,671	1320	1023
Necrosis	40	130	365	8447	752
Enhanced tumor	150	602	250	2	10,709

In Table 4 the result of prediction of center pixel test patches are presented. We have 52,355, 6013, 42,671, 8447 and 10,709 patches of normal tissue, edema, non-enhanced tumor, necrosis, and enhanced tumor, respectively, as test set. Each column shows the result for patches of one of these classes. The patches of edema hardy can be mistaken as normal and mistaking it as enhanced tumor is more probable. This a similar reasoning can be stated for other columns. The result shown that non-enhanced and normal tissue can be predicted with higher precision.

Conclusions

In this paper, a DCNN was proposed for more accurate and faster segmentation of the brain MR images to help physicians in the diagnosis and treatment of brain tumors. The purpose was to separate damaged tissues, despite their low-contrast and Y-shaped structure in segmentation images, as well as to resolve the imbalance in the training dataset. In order to improve network performance, a pooling layer was used to summarize the information, and a ReLU was used to create a nonlinear layer. At the same time, the connection of the convolutional layers was established so that the potential for network parallelism would be high after forming independent paths. The experimental results showed the accuracy of the complete, core, and enhancing regions for BRATS 2016 in the Dice Similarity Coefficient metric is 0.90, 0.85, and 0.84 respectively. Due to the considerable training time in the DCNN, GPU hardware was employed for load balancing, exploiting task-level parallelism, and improving the performance. The DCNN architecture was conducted using the CAFFE. Nodes in each convolutional layer were patch-based with the task-level parallelism technique. The performance of the training phase was improved. Given that the number of labeled specimens in dataset is low, it is not possible to design models with greater depth for segmentation, since models with more depth would have more parameters leading to over-fitting in the conditions of data deficit. On the other hand, because of the limited memory space and the number of parallel GPUs, the use of higher-volume data is difficult to handle. With the advancement of GPUs and the use of libraries that distribute processing across multiple GPUs and multiple machines, this problem can be addressed.

For future works, the formation of three auxiliary paths will be possible in order to accommodate local and global features in the input image segment, and it then will be added to the fully connected layer with the main path. In the first auxiliary path, 15 × 15 kernels with 15 image jumps can be considered. Additionally, in the second and third paths, the average and maximum pooling of 30 × 30 can be used. The outputs of these auxiliary paths before the fully connected layer can be used in classification and segmentation by entering the main path at the same time.